Pythonで〇×ゲームのAIを一から作成する　その61　ai11s の検証と限定的な条件による問題の解決

Last updated at 2024-03-15Posted at 2024-03-11

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI のアルゴリズムは以下の通りです。

ルール	アルゴリズム
ルール1	左上から順に空いているマスを探し、最初に見つかったマスに着手する
ルール2	ランダムなマスに着手する
ルール3	真ん中のマスに優先的に着手する既に埋まっていた場合はランダムなマスに着手する
ルール4	真ん中、隅のマスの順で優先的に着手する既に埋まっていた場合はランダムなマスに着手する
ルール5	勝てる場合に勝つそうでない場合はランダムなマスに着手する
ルール6	勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する
ルール6改	勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合はランダムなマスに着手する
ルール7	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手の勝利を阻止するそうでない場合はランダムなマスに着手する
ルール7改	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合はランダムなマスに着手する
ルール8	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合は、次の自分の手番で勝利できるように、「自 2 敵 0 空 1」が 1 つ以上存在する局面になる着手を行うそうでない場合はランダムなマスに着手する
ルール9	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合は、次の自分の手番で必ず勝利できるように、「自 2 敵 0 空 1」が 2 つ以上存在する局面になる着手を行うそうでない場合は、次の自分の手番で勝利できるように、「自 2 敵 0 空 1」が 1 つ存在する局面になる着手を行うそうでない場合はランダムなマスに着手する
ルール10	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合は、次の自分の手番で必ず勝利できるように、「自 2 敵 0 空 1」が 2 つ以上存在する局面になる着手を行うそうでない場合は、以下の 2 つを総合的に判断して着手を行う次の自分の手番で勝利できるように、「自 2 敵 0 空 1」が 1 つ存在する局面になる着手を行う自分が有利になるように、「自 1 敵 0 空 2」が最も多い着手を行うそうでない場合はランダムなマスに着手する
ルール11	真ん中のマスに優先的に着手するそうでない場合は勝てる場合に勝つそうでない場合は相手が勝利できる着手を行わないそうでない場合は、次の自分の手番で必ず勝利できるように、「自 2 敵 0 空 1」が 2 つ以上存在する局面になる着手を行うそうでない場合は、以下の 3 つを総合的に判断して着手を行う次の自分の手番で勝利できるように、「自 2 敵 0 空 1」が 1 つ存在する局面になる着手を行う自分が有利になるように、「自 1 敵 0 空 2」が最も多い着手を行う相手が不利になるように、「自 0 敵 1 空 2」が最も少ない着手を行うそうでない場合はランダムなマスに着手する

ルール 11 で 評価値を計算 する際の パラメータ は以下の通りです。

	修正前	修正後
「自 2 敵 0 空 1」が 1 つの場合の評価値	1	2
「自 1 敵 0 空 2」が 1 つあたりの評価値	1	1
「自 0 敵 1 空 2」が 1 つあたりの評価値	-1	-1

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥の列は、アルゴリズム に欠陥があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
`ai1` `ai1s`	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
`ai2` `ai2s`	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
`ai3` `ai3s`	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
`ai4` `ai4s`	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
`ai5` `ai5s`	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
`ai6`	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
`ai6s`	88.6	1.9	9.5	69.4	9.1	21.5	79.0	5.5	15.5
`ai7` `ai7s`	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
`ai8s`	98.2	0.1	1.6	89.4	2.5	8.1	93.8	1.3	4.9
`ai9s`	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6
`ai10s`	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
`ai11s` 修正前	98.1	0.0	1.9	82.5	1.9	15.6	90.3	1.0	8.7	あり
`ai11s` 修正後	98.8	0.0	1.2	87.7	2.4	10.0	93.2	1.2	5.6

`ai2` VS `ai11s` の検証と `ai11s` の修正

前回の記事では、ランダムな AI である ai2 と ai11s を対戦させた結果、ai11s が 敗北する 場合があることが確認できたので、ai11s は 弱解決の AI では ありません。

そこで、その 原因を検証 するために、下記のプログラムのように、show_progress を利用することで、ai2 VS ai11s で ai11s が敗北する場合の 試合経過 を表示しました。

from ai import show_progress, ai2, ai11s
from marubatsu import Marubatsu

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn x
.O.
...
...

Turn o
.o.
.X.
...

Turn x
.o.
.x.
O..

Turn o
.o.
.x.
o.X

Turn x
Oo.
.x.
o.x

Turn o
oo.
.x.
oXx

winner o
oo.
Ox.
oxx

今回の記事では、ai11s が 敗北する理由 を検証し、敗北しない ように修正します。

`ai2` VS `ai11s` の検証

下図は、上記の show_progress で表示された ai2 VS ai11s の 試合経過 です。以前の記事と 同様の方法 で、ai11s が どのような判断 で 着手を選択したか を検証します。なお、ai2 は ランダムな着手 を行う AI なので、ai2 が行う 着手の検討 は省略します。

2 手目の検証

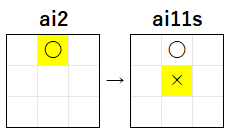
ルール 11 の 最も優先順位が高い条件 から、ai11s は 真ん中のマス に 優先的に着手 するので、この局面 では、ai11s は (1, 1) に着手します。

4 手目の検証

以前の記事と 同様の方法 で、下記のプログラムで ai11s がそれぞれの 合法手 に対して どのように 評価値を計算するかを表示し、その結果を 表にまとめます。

mb = Marubatsu()
mb.move(1, 0)
mb.move(1, 1)
mb.move(0, 2)
ai11s(mb, debug=True)

実行結果（長いのでクリックして開いてください）

Start ai_by_score
Turn x
.o.
.x.
O..

legal_moves [(0, 0), (2, 0), (0, 1), (2, 1), (1, 2), (2, 2)]
====================
move (0, 0)
Turn o
Xo.
.x.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 1,
             Markpat(last_turn=1, turn=0, empty=2): 1,
             Markpat(last_turn=1, turn=1, empty=1): 4,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 2 best score -inf
UPDATE
  best score 2
  best moves [(0, 0)]
====================
move (2, 0)
Turn o
.oX
.x.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 3,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=1, empty=0): 1})
score 1 best score 2
====================
move (0, 1)
Turn o
.o.
Xx.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 1,
             Markpat(last_turn=1, turn=1, empty=1): 3,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1 best score 2
====================
move (2, 1)
Turn o
.o.
.xX
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1 best score 2
====================
move (1, 2)
Turn o
.o.
.x.
oX.

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=1, empty=0): 1})
score 0 best score 2
====================
move (2, 2)
Turn o
.o.
.x.
o.X

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 3,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 2 best score 2
APPEND
  best moves [(0, 0), (2, 2)]
====================
Finished
best score 2
best moves [(0, 0), (2, 2)]

下記は、上記の結果 を まとめた表 です。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+1`	1 つで `-1`
1		1		1	1	2
2				3	2	1
3		1		1	2	1
4		1		2	3	1
5				2	2	0
6		1		2	2	2

上記の表 から、合法手 1 と 6 の 評価値 が 2 で 最も高くなる ことがわかります。従って、2 つの合法手 である (0, 0) と (2, 2) がそれぞれ 1 / 2 = 50 % の確率で 選択される ことが わかります。そのことは、下記の 実行結果 の 最後の 2 行 からも確認できます。

best score 2
best moves [(0, 0), (2, 2)]

従って、4 手目 では、50 % の確率 で、(2, 2) が 選択された ことがわかります。

5 手目の検証

5 手目 で ai2 が上記のように (0, 0) に着手を行った場合は、〇にとって「自 2 敵 0 空 1」が 2 つ存在 するので、〇の必勝の局面 であることがわかります。ai2 は ランダムな AI なので、必勝の局面 になってもその後で 最善手 を 選択しない可能性 がありますが、今回で検証している 下記の試合経過 のように、この後で ai2 が 最善手 を 選択し続けた場合 は、ai2 の勝利 になります。

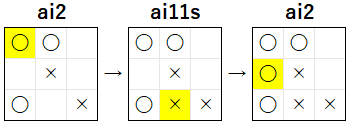
4 手目で (0, 0) に着手した場合の検証

上記から、4 手目 で ai11s が選択した (2, 2) が 最善手ではない可能性がある ことが わかりました。そのことを 確認する ために、4 手目 での ai11s の もう一つの候補 である (0, 0) に 着手した場合 の 局面の状況 の検証を行うことにします。

4 手目 で (0, 0) に着手を行った場合は、下記のような局面になります。なお、実際の対戦 では (0, 0) に 着手していない ので、そのこと を 明確にする ために、(0, 0) のマス は、黄色ではなく オレンジ色 で 塗りつぶして います。(0, 0) に着手した場合の 局面の状況 を 調べるため に、以後は 最善手のみ を選択した場合の 試合の経過 と結果を 調べます。

上記の局面 は、次の × の手番 で × が (2, 2) に着手を行うと、× の勝利 になるので、5 手目 の 〇の最善手 は (2, 2) です。下記は 5 手目 で (2, 2) に 着手を行った場合 の図です。

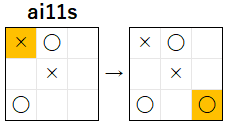
上記の局面 は、次の 〇の手番 で〇が (1, 2) に着手を行うと、〇の勝利 になるので、6 手目 の × の最善手 は (1, 2) です。下記は 6 手目 で (1, 2) に 着手を行った場合 の図です。

上記の局面 には、3 種類 の 合法手 があるので、それぞれ について 調べます。

(2, 0) に着手を行った場合は、× は 〇の勝利を阻止 するために (2, 1) に着手を行い、最後に〇が (0, 1) に着手を行い、下図のように 引き分け になります。

(2, 1) に着手を行った場合は、× は 〇の勝利を阻止 するために (2, 0) に着手を行い、最後に〇が (0, 1) に着手を行い、下図のように 引き分け になります。

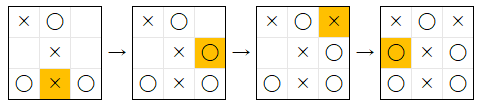
(0, 0) に着手を行った場合は、下図の局面になり、この後で × と〇が どのような着手 を行っても 引き分け になります。

上記から、4 手目 で (0, 0) に着手を行った場合に、その後で お互い が 最善手のみ を選択すると 引き分け になります。一方、(2, 2) に着手を行った場合は、お互い が 最善手のみ を選択すると 敗北する ので、4 手目 の (2, 2) は 最善手ではない ことがわかりました。

上記から わかること は、「4 手目 の局面で (2, 2) が 最善手 では ないこと」だけで、「(0, 0) が 最善手 で あること」までは わかりません。そのこと を 示すため には、残りの 合法手 2 ~ 5 に着手した局面が 引き分けの局面 か、× の必敗の局面 であることを 示す必要 があります。長くなるので本記事ではその確認を省略しますが、実際に確認 することで、(0, 0) が 最善手 の 1 つ であることが わかります。興味と余裕がある方は実際に確認してみて下さい。

パラメータの修正

ai2 VS ai11s で、ai11s が敗北した理由は、下記の局面 で ai11s が 最善手ではない (2, 2) を選択する 可能性がある ことです。また、この局面 では (2, 2) と 同じ評価値 が計算される (0, 0) を選択すると 引き分けの局面 になるので、ai11s が この局面 で (0, 0) の 評価値のみ を 最も高く計算 するように できれば、ai11s が 敗北しない ように なります。その方法を少し考えてみて下さい。

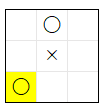
下記は、(0, 0) と (2, 2) を表す 合法手 1 と 6 の表です。この表 から、合法手 1 と 6 では、評価値 を計算する際に 利用する、いくつかの マークのパターン の数が 異なる ことが分かります。従って、それらのマークのパターンの パラメータ を うまく変更する ことで、合法手 1 の 評価値 を、合法手 6 の 評価値より も 大きくする ことが できる可能性 が あります。その方法を少し考えてみて下さい。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+1`	1 つで `-1`
1		1		1	1	2
6		1		2	2	2

そのような方法としては、以下の 2 種類 の方法が 考えられます。

「自 1 敵 0 他 2」の 1 つ当たりの 評価値 を 減らす
「自 0 敵 1 他 2」の 1 つ当たりの 評価値 を 増やす

いずれの方法 でも かまいません ので、本記事では、「自 1 敵 0 他 2」の 1 つ当たりの 評価値 を 減らす方法 を 考えてみる ことにします。興味と余裕がある方は、もう一つの方法も実際に試してみて下さい。

次に、具体的 に 評価値 を どの程度減らすか について 考える必要 があります。以前の記事で説明したように、ルールの 条件の意味 を考えると、「自 1 敵 0 他 2」の 1 つ当たりの 評価値 は 正の値 にする必要があります。そこで、この パラメータ を 0 と 1 の中間の 0.5 に設定 してみることにします。

まず、そのように パラメータ設定 した場合の、それぞれの合法手の 評価値 を、下記のプログラムで 計算してみる ことにします。「自 1 敵 0 他 2」の 1 つ当たりの 評価値を変更 しましたが、他のパラメータ は 変更していない ので、下記のように、対応する score_102 の キーワード引数のみ を記述するだけで かまいません。

mb = Marubatsu()
mb.move(1, 0)
mb.move(1, 1)
mb.move(0, 2)
ai11s(mb, score_102=0.5, debug=True)

実行結果（長いのでクリックして開いてください）

Start ai_by_score
Turn x
.o.
.x.
O..

legal_moves [(0, 0), (2, 0), (0, 1), (2, 1), (1, 2), (2, 2)]
====================
move (0, 0)
Turn o
Xo.
.x.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 1,
             Markpat(last_turn=1, turn=0, empty=2): 1,
             Markpat(last_turn=1, turn=1, empty=1): 4,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1.5 best score -inf
UPDATE
  best score 1.5
  best moves [(0, 0)]
====================
move (2, 0)
Turn o
.oX
.x.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 3,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=1, empty=0): 1})
score -0.5 best score 1.5
====================
move (0, 1)
Turn o
.o.
Xx.
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 1,
             Markpat(last_turn=1, turn=1, empty=1): 3,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.5 best score 1.5
====================
move (2, 1)
Turn o
.o.
.xX
o..

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.0 best score 1.5
====================
move (1, 2)
Turn o
.o.
.x.
oX.

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=0, empty=3): 1,
             Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=2, turn=1, empty=0): 1})
score -1.0 best score 1.5
====================
move (2, 2)
Turn o
.o.
.x.
o.X

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 3,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1.0 best score 1.5
====================
Finished
best score 1.5
best moves [(0, 0)]

下記は、上記の結果 を まとめた表 です。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+0.5`	1 つで `-1`
1		1		1	1	1.5
2				3	2	-0.5
3		1		1	2	0.5
4		1		2	3	0
5				2	2	-1
6		1		2	2	1

上記の表 から、合法手 1 の 評価値のみ が 1.5 で 最も高く なり、(0, 0) のみ が 選択される ようになります。そのことは、下記の 実行結果 の 最後の 2 行 からも確認できます。

best score 1.5
best moves [(0, 0)]

上記の修正 によって、他の 優先順位が高い 条件の 評価値の範囲 を 超えているか どうかを下記の表で確認します。特に 問題はなさそう です。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		`300`
2	自分が勝利している		`200`
4	「自 2 敵 0 空 1」が 2 つ以上存在する		`100`
5	「自 2 敵 0 空 1」が 1 つ存在する「自 1 敵 0 空 2」が x 個存在する「自 0 敵 1 空 2」が y 個存在する	`2` (`0～2`) `0.5 * x` (`0～4`) `-y` (`-8~0`)	`-8～6`
3	相手が勝利できる		`-100`

修正したパラメータでの `ai2` との対戦

修正したパラメータ で ai2 と対戦することで、問題が 解決されたか を確認することにします。その際には、下記のプログラムのように、ai_match の キーワード引数 params の ai11s に対応 する要素には、ai11s の 修正を行ったパラメータの値のみ を記述します。

from ai import ai_match

ai_match(ai=[ai11s, ai2], params=[{"score_102":0.5}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9909       0      91
x        8768      80    1152
total   18677      80    1243

ratio     win    lose    draw
o       99.1%    0.0%    0.9%
x       87.7%    0.8%   11.5%
total   93.4%    0.4%    6.2%

下記は、上記の結果 と、これまで の ai11s が ai2 と対戦した際の結果を表に まとめたもの です。なお、これまでは 修正前 と 修正前 の ai11s のように表記していましたが、今回の修正 で ai11s の種類が 3 種類 になったので、それぞれ を ai11s を 作成した順番 で ai11s ver 1 のように表記することにします。

関数名	o 勝	o 分	x 勝	x 負	x 分	勝	負	分
`ai11s` ver 1	98.1	1.9	82.5	1.9	15.6	90.3	1.0	8.7
`ai11s` ver 2	98.8	1.2	87.7	2.4	10.0	93.2	1.2	5.6
`ai11s` ver 3	99.1	0.9	87.7	0.8	11.5	93.4	0.4	6.2

上記の表から、今回の パラメータの修正 によって、× を担当 した場合の敗率が 約 2 % から、1 % 未満 に 減っている ので、先程の問題 が改善された 可能性が高い ことがわかります。ただし、依然として × を担当 した際の敗率が 0 % に なっていない ので、この修正 を行っても ai11s ver 3 は 弱解決の AI には なっていない ことがわかります。

パラメータの他の修正方法の検証

上記では、「自 1 敵 0 他 2」の 1 つ当たりの 評価値 を 1 から 0.5 に 減らしました が、1 未満 の 他の正の値 に修正することで、もしかすると、敗率が 0 % に なるかもしれません。そこで、下記のプログラムで、パラメータ を 0.9、0.75、0.25、0.1、0 に 変えて、ai2 と対戦してみることにします。

なお、正ではない 0 に変えて 対戦する理由 は、「自 1 敵 0 他 2」の マークのパターンの数 が、弱解決の AI を作る際に、実際に 役に立っていること を 確認するため です。「自 1 敵 0 他 2」の 1 つあたりの 評価値 を 0 にする ということは、「自 1 敵 0 他 2」の マークのパターンの数 を 考慮しない という意味になるので、その場合に敗率が 増えなければ、「自 1 敵 0 他 2」の マークのパターンの数 が 役に立っていない ことになります。

ai_match(ai=[ai11s, ai2], params=[{"score_102":0.9}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9895       0     105
x        8776      68    1156
total   18671      68    1261

ratio     win    lose    draw
o       99.0%    0.0%    1.1%
x       87.8%    0.7%   11.6%
total   93.4%    0.3%    6.3%

ai_match(ai=[ai11s, ai2], params=[{"score_102":0.75}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9893       0     107
x        8797      52    1151
total   18690      52    1258

ratio     win    lose    draw
o       98.9%    0.0%    1.1%
x       88.0%    0.5%   11.5%
total   93.5%    0.3%    6.3%

ai_match(ai=[ai11s, ai2], params=[{"score_102":0.25}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9893       0     107
x        8808      59    1133
total   18701      59    1240

ratio     win    lose    draw
o       98.9%    0.0%    1.1%
x       88.1%    0.6%   11.3%
total   93.5%    0.3%    6.2%

ai_match(ai=[ai11s, ai2], params=[{"score_102":0.1}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9912       0      88
x        8805      61    1134
total   18717      61    1222

ratio     win    lose    draw
o       99.1%    0.0%    0.9%
x       88.0%    0.6%   11.3%
total   93.6%    0.3%    6.1%

ai_match(ai=[ai11s, ai2], params=[{"score_102":0}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9916       0      84
x        8685     159    1156
total   18601     159    1240

ratio     win    lose    draw
o       99.2%    0.0%    0.8%
x       86.9%    1.6%   11.6%
total   93.0%    0.8%    6.2%

実行結果 から、パラメータ を 0.9、0.75、0.25、0.1 に 変えても、0.5 の場合 と結果が 変わらない ことが分かりました。また、0 に変更 した場合は、× を担当 した場合の敗率が 約 1.5 % に上昇することから、「自 1 敵 0 他 2」の マークのパターンの数 が、弱解決の AI を作る際に、実際に 役に立っている ことが確認できました。

そこで、ai11s ver 3 の「自 1 敵 0 他 2」の パラメータ を 0.5 とし、下記のプログラムのように、ai11s の score_012 の デフォルト引数値 を 0.5 に修正することにします。

from marubatsu import Markpat
from ai import ai_by_score
from pprint import pprint

def ai11s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):
以下同じなので略

プログラム全体

from marubatsu import Markpat
from ai import ai_by_score
from pprint import pprint

def ai11s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 300 を返す
        if mb.last_move == (1, 1):
            return 300
    
        # 自分が勝利している場合は、評価値として 200 を返す
        if mb.status == mb.last_turn:
            return 200

        markpats = mb.count_markpats()
        if debug:
            pprint(markpats)
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 100

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += score_201
        # 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
        # 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
        score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

from marubatsu import Markpat
from ai import ai_by_score
from pprint import pprint

-def ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=False):
+def ai11s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):
以下同じなので略

`ai2` VS `ai11s` ver 3 の検証と `ai11s` ver 3 の修正

上記から ai11s ver 3 は、弱解決の AI ではない ことがわかったので、下記のプロラムのように、再び show_progress を利用して、ai2 VS ai11s ver3 で ai11s ver 3 が敗北する場合の 試合経過 を表示し、敗北する 原因を検証 することにします。

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn x
...
...
..O

Turn o
...
.X.
..o

Turn x
O..
.x.
..o

Turn o
o..
.x.
X.o

Turn x
o.O
.x.
x.o

Turn o
oXo
.x.
x.o

winner o
oxo
.xO
x.o

`ai2` VS `ai11s` ver 3 の検証

下図は、上記の show_progress で表示された ai2 VS ai11s ver 3 の 試合経過 です。

2 手目の検証

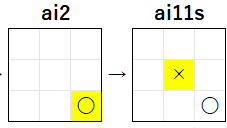
ルール 11 の 最も優先順位が高い条件 から、ai11s ver 3 は 真ん中のマス に 優先的に着手 するので、この局面 では、ai11s ver 3 は (1, 1) に着手します。

4 手目の検証

先程と 同様の方法 で、下記のプログラムで ai11s ver 3 がそれぞれの 合法手 に対して どのように 評価値を計算するかを表示し、その結果を 表にまとめます。

mb = Marubatsu()
mb.move(2, 2)
mb.move(1, 1)
mb.move(0, 0)
ai11s(mb, debug=True)

実行結果（長いのでクリックして開いてください）

Start ai_by_score
Turn x
O..
.x.
..o

legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2)]
====================
move (1, 0)
Turn o
oX.
.x.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.0 best score -inf
UPDATE
  best score 0.0
  best moves [(1, 0)]
====================
move (2, 0)
Turn o
o.X
.x.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1.0 best score 0.0
UPDATE
  best score 1.0
  best moves [(2, 0)]
====================
move (0, 1)
Turn o
o..
Xx.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.0 best score 1.0
====================
move (2, 1)
Turn o
o..
.xX
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.0 best score 1.0
====================
move (0, 2)
Turn o
o..
.x.
X.o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 1.0 best score 1.0
APPEND
  best moves [(2, 0), (0, 2)]
====================
move (1, 2)
Turn o
o..
.x.
.Xo

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 0.0 best score 1.0
====================
Finished
best score 1.0
best moves [(2, 0), (0, 2)]

下記は、上記の結果 を まとめた表 です。なお、同一局面は、同じ合法手 に まとめました。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+0.5`	1 つで `-1`
1		1		2	2	1
2		1		2	3	0

上記の表 から、合法手 1 の 評価値 が 1 で 最も高くなる ことがわかります。従って、合法手 1 の 2 つの合法手 である (2, 0) と (0, 2) がそれぞれ 1 / 2 = 50 % の確率で 選択される ことが わかります。そのことは、下記の 実行結果 の 最後の 2 行 からも確認できます。

best score 1.0
best moves [(2, 0), (0, 2)]

従って、4 手目 では、50 % の確率 で、(0, 2) が 選択された ことがわかります。

6 手目以降の検証

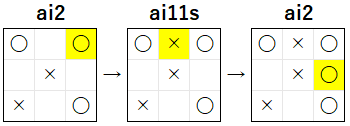
5 手目 で ai2 が上記のように (2, 0) に着手を行った場合は、〇にとって「自 2 敵 0 空 1」が 2 つ存在 するので、〇の必勝の局面 であることがわかります。ai2 は ランダムな AI なので、必勝の局面 になってもその後で 最善手 を 選択しない可能性 がありますが、今回で検証している 上記の試合経過 のように、この後で ai2 が 最善手 を 選択した場合 は、ai2 の勝利 になります。

4 手目で合法手 2 に着手した場合の検証

上記から、4 手目 で ai11s が選択した 合法手 1 である (0, 2) が 最善手ではない可能性がある ことが わかりました。そのことを 確かめる ために、4 手目 での ai11s の もう一つの候補 である 合法手 2 が 最善手であるか どうかを 調べる ことにします。

先程検証した ai2 VS ai11s ver 2 の場合の 4 手目 の局面には 合法手 が 6 種類 あったので、そのうちの 2 つ の合法手を 検証するだけ では、どの合法手 が 最善手であるか までは わかりません でした。一方、今回の場合 は、合法手 が 2 種類 しかないので、片方の合法手 を着手した場合の 局面の状況 が、もう片方の合法手 を着手した場合の 局面の状況より も 良ければ、最善手 であることが確定します。

4 手目 で 合法手 2 の 1 つ である (0, 1) に着手を行った場合は、下図の 左の局面 になります。(0, 1) が 最善手であるか どうかを 調べるため に、その後で 最善手のみ を選択した場合の 試合の経過 と結果を 調べる と、その後に出現 するいずれの局面も、そこに 着手しなければ敗北 する マスが存在 するので、そのマスが最善手 になります。下図は、最善手 を 選択し続けた場合 の図で、引き分けになる ことが わかります。

上記から、4 手目 で 合法手 2 のいずれかに着手を行った場合に、その後で お互い が 最善手のみ を選択すると 引き分け になります。一方、合法手 1 のいずれか着手を行った場合は、お互い が 最善手のみ を選択すると 敗北する ので、4 手目 の局面では 合法手 1 は 最善手ではない ことがわかりました。

パラメータの修正方法の検討

ai2 VS ai11s ver 3 で、ai11s ver 3 が敗北した理由は、3 手目 で 最善手ではない合法手 1 を選択することです。また、上記から、この局面の 合法手 2 は 最善手である ことがわかったので、ai11s ver 3 が この局面 で 合法手 2 の 評価値 を 最も高く計算 するように できれば、ai11s ver 3 が 敗北しない ように なります。その方法を少し考えてみて下さい。

下記は、先程の 合法手 1 と 2 の表を再掲したものです。図から、合法手 1 と 2 では、評価値 を計算する際に 利用する、マークのパターン の数が 異なる のは、「自 0 敵 1 他 2」のみであることが わかります。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+0.5`	1 つで `-1`
1		1		2	2	1
2		1		2	3	0

従って、「自 0 敵 1 他 2」の マークのパターン に対する パラメータ を 変える ことで、下記の式 のように、合法手 2 の 評価値 が、合法手 1 の 評価値より も 大きくなる ようにする方法を 考える ことにします。

$合法手 1 の評価値 < 合法手 2 の評価値$

「自 0 敵 1 他 2」の マークのパターン の 1 つ当たりの 評価値 を $x$ とすると、合法手 1 と 2 の 評価値 の 計算式 は、以下のようになります。

$合法手 1 の評価値 = 2 + 0.5 × 2 + 2y = 3 + 2y$
$合法手 2 の評価値 = 2 + 0.5 × 2 + 3y = 3 + 3y$

上記の式 を、目的の式 に 当てはめる と、下記の式 になります。

$3 + 2y < 3 + 3y$

この式の 両辺から $3 + 2y$ を 引くと 、下記の式 になります。

$0 < y$

上記から、「自 0 敵 1 他 2」の マークのパターン の 1 つ当たりの 評価値 を 正の数 にすることで、合法手 2 の 評価値 が 合法手 1 の 評価値より も 大きくなる ことが わかりました。

式で考えるのが 苦手な人 は、以下のように 言葉で考える ことも できます。ただし、慣れれば、式で考えたほう が、分かりやすさ や 計算のしやすさ の面ではるかに 優れている ので、式で考える方法 に 慣れる ことを お勧めします。

「自 0 敵 1 他 2」の マークのパターン の数は、合法手 2 のほうが、合法手 1 より も 1 だけ多い
従って、その パラメータ を 1 増やす と、合法手 2 の 評価値 のほうが、合法手 1 の 評価値より も、1 だけ 多く増える
現時点 では、合法手 1 の 評価値 の方が、合法手 2 の 評価値より も 1 だけ多い
従って、パラメータ を 1 より多く増やせば、合法手 2 の 評価値 の方が 合法手 1 の 評価値より も 大きくなる
現時点 の パラメータ は -1 で、$-1 + 1 = 0$ なので、パラメータ を 0 より大きい、正の値 に すればよい ことが わかる

パラメータの修正の効果の確認

問題の 解決方法 がわかったので、下記のプログラムで「自 0 敵 1 空 2」のパラメータを、正の値 である 1 に修正 して、4 手目 の局面で ai11s が計算する 評価値を表示 し、合法手 2 のみ が 選択される ようになったかどうかを確認することにします。

mb = Marubatsu()
mb.move(2, 2)
mb.move(1, 1)
mb.move(0, 0)
ai11s(mb, score_012=1, debug=True)

実行結果（長いのでクリックして開いてください）

Start ai_by_score
Turn x
O..
.x.
..o

legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2)]
====================
move (1, 0)
Turn o
oX.
.x.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 6.0 best score -inf
UPDATE
  best score 6.0
  best moves [(1, 0)]
====================
move (2, 0)
Turn o
o.X
.x.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 5.0 best score 6.0
====================
move (0, 1)
Turn o
o..
Xx.
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 6.0 best score 6.0
APPEND
  best moves [(1, 0), (0, 1)]
====================
move (2, 1)
Turn o
o..
.xX
..o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 6.0 best score 6.0
APPEND
  best moves [(1, 0), (0, 1), (2, 1)]
====================
move (0, 2)
Turn o
o..
.x.
X.o

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 2,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 2,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 5.0 best score 6.0
====================
move (1, 2)
Turn o
o..
.x.
.Xo

defaultdict(<class 'int'>,
            {Markpat(last_turn=0, turn=1, empty=2): 3,
             Markpat(last_turn=1, turn=0, empty=2): 2,
             Markpat(last_turn=1, turn=1, empty=1): 1,
             Markpat(last_turn=1, turn=2, empty=0): 1,
             Markpat(last_turn=2, turn=0, empty=1): 1})
score 6.0 best score 6.0
APPEND
  best moves [(1, 0), (0, 1), (2, 1), (1, 2)]
====================
Finished
best score 6.0
best moves [(1, 0), (0, 1), (2, 1), (1, 2)]

下記は、上記の 実行結果 を表に まとめた ものです。

		「201」	「021」	「102」	「012」	評価値
	評価値	1：`+2` 2~：`100`	`-100`	1 つで `+0.5`	1 つで `+1`
1		1		2	2	5
2		1		2	3	6

上記の表から、合法手 2 の 評価値 が 6 になり、合法手 1 の 評価値 である 5 より も 大きくなる ことが確認できます。また、合法手 2 のマスである、辺のマスのみ が 選択される ようになったことは、下記の 実行結果 の 最後の 2 行 からも確認できます。以後は、このパラメータ で 評価値 を計算する ai11s を ai11s ver 4 と表記することにします。

best score 6.0
best moves [(1, 0), (0, 1), (2, 1), (1, 2)]

次に、下記のプログラムで、ai2 と対戦してみることにします。

ai_match(ai=[ai11s, ai2], params=[{"score_012": 1}, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9887       0     113
x        9128     121     751
total   19015     121     864

ratio     win    lose    draw
o       98.9%    0.0%    1.1%
x       91.3%    1.2%    7.5%
total   95.1%    0.6%    4.3%

下記は、上記の結果 と、これまで の ai11s が ai2 と対戦した際の結果を表に まとめたもの です。

関数名	o 勝	o 分	x 勝	x 負	x 分	勝	負	分
`ai11s` ver 1	98.1	1.9	82.5	1.9	15.6	90.3	1.0	8.7
`ai11s` ver 2	98.8	1.2	87.7	2.4	10.0	93.2	1.2	5.6
`ai11s` ver 3	99.1	0.9	87.7	0.8	11.5	93.4	0.4	6.2
`ai11s` ver 4	98.9	1.1	91.3	1.2	7.5	95.1	0.6	4.3

上記の表 から、ai11s ver 4 は、× を担当 した場合の勝率が 最も高くなっている ので、改善している ように 見えるかもしれません が、敗率が 0.8 % から 1.2 % に上昇しているという問題が あります。〇×ゲーム は、引き分けのゲーム なので、前回の記事で説明した 引き分けのゲーム の場合の 弱解決の AI の性質から、弱解決の AI に 近づいているか どうかの判断としては、勝率ではなく、敗率が重要 です。従って、敗率が上昇する ということは、修正前 の ai11s ver 3 よりも、弱解決の AI から 遠ざかっている と 考えられます。何故このようなことが起きたかについて少し考えてみて下さい。

敗率が上昇した理由

下記のプログラムで ai2 VS ai11s ver 4 で ai11s ver 4 が敗北する 試合経過を表示 すると、これまで とは 異なる試合経過 で 敗北している ことが 分かります。

show_progress(ai=[ai2, ai11s], params=[{}, {"score_012": 1}], winner=Marubatsu.CIRCLE)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn x
...
.O.
...

Turn o
X..
.o.
...

Turn x
x..
.o.
..O

Turn o
x..
Xo.
..o

Turn x
x..
xo.
O.o

Turn o
xX.
xo.
o.o

winner o
xxO
xo.
o.o

パラメータの修正 によって、ai11s ver 4 は、ai2 VS ai11s ver 3 の 4 手目の局面 で、最善手 を 選択する ようになりましたが、一方で、上記のように これまで最善手 を 選択できていた 別の局面で、最善手 を 選択できなくなる ことが、敗率が 上昇した理由 です。

長くなる ので 本記事 では 検証は行いません が、興味と余裕がある方は、上記の 試合経過 を 実際に検証 することで、パラメータの修正 によって 最善手 が 選択できなく なった局面があることを確認してみて下さい。

そのようなこと が 起きた原因 は、今回行った パラメータの修正 が、ルール 11 の条件の 目的に反する ような修正だったからです。具体的には、ルール 11 の『相手が 不利になる ように、「自 0 敵 1 空 2」が 最も少ない 着手を行う』という条件から、「自 0 敵 1 他 2」の 1 つ当たりの 評価値 を 負の値 にする必要があります。これは、先程求めた、この パラメータ を 正の値 にするという 修正方法 と 両立しない ので、どのように パラメータを修正しても 目的を達成 することが できない ことが わかりました。

このように、ai11s ver 4 には 問題がある ため、本記事 では このパラメータ は 採用しない ことにします。

限定的な条件による問題の解決

上記から、ルール 11 の 条件だけ では、ai11s ver 3 の問題を解決して、弱解決の AI を作る ことは できない ことが わかりました。このような場合は、ai11s ver 3 の 問題を解決 するための、新しい条件 を 考える必要 が あります。

これまでは、ルール に ヒューリスティックな条件 を 追加する際 に、マークのパターン の数を 利用した条件 を 考えてきました が、今回の問題 は マークのパターンを利用 しても うまくいきません ので、何か 別の方法 を 考える必要 が あります。どのような方法が良いかについて少し考えてみて下さい。

汎用的な条件と限定的な条件

これまで に ルール に 加えてきた『自分が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う』などの、ヒューリスティックな条件 は、すべての局面 で 適用する、汎用的な条件 でした。しかし、物事には 例外がつきもの なので、汎用的な条件 では 対処できない 場合は、例外に 対応する ために、限定的な条件 を 加える ことが 良くあります。

例えば、現実の世界 での 具体例 としては、下記のような例が挙げられます。

信号が青 の時は 横断歩道 を 渡って良い（汎用的な条件）
ただし、救急車などの 緊急車両 が サイレンを鳴らして通る場合 は、信号が青でも 横断歩道 を 渡ってはいけない（限定的な条件）

実際に、世の中 にある ほとんどのルール には、「ただし、〇〇の場合 には ×× である」のような、限定的な条件 が存在します。

汎用的な条件と限定的な条件の性質

汎用的な条件 と、限定的な条件 には、下記のような 利点と欠点 があります。

汎用的な条件
- 利点：一つの条件 で 多くの状況 に 対処する ことが できる ので、効率的 である
- 欠点：特定の状況 に対して、想定外 の 悪影響を与える 場合がある
限定的な条件
- 利点：特定の状況以外 の状況に 悪影響を与える ことがない
- 欠点：特定の状況 にのみ 影響を与える ので、効率が悪い

条件が与える影響の範囲

上記では 汎用的な条件 と 限定的な条件 のように、2 種類 に分類しましたが、実際には、条件が影響を与える範囲は、千差万別 です。例えば、条件が影響を与える範囲として、以下のような 様々な範囲 が 考えられます。従って、条件を考える ときは、どのような範囲 に 適用できるか について 考える ことも重要です。

全世界
特定の国
特定の標高の範囲
特定の地域
特定の学校
特定の家族
特定の趣味を持つ人

ゲーム で 例を挙げる と、以下のような 様々な範囲 が 考えられる でしょう。

すべての局面
先手の手番の局面
後手の手番の局面
先手の必勝の局面
引き分けの局面
後手の必勝の局面
序盤の局面
中盤の局面
終盤の局面

条件を考える手順

問題を解決 する際に、ヒューリスティックな条件 を 考える 場合は、一般的 には下記のような手順で、最初は 効率を重視 して 広い範囲 で 適用できる の条件を考え、徐々に 範囲を狭めながら 新しい条件を 考えます。意識していないかもしれませんが、多くの人は実際に下記のような手順で問題を解決しようと試みているはずです。

なるべく多くの範囲 で 問題を解決できる ような、条件を 考える
考えた条件 で問題が 解決されなかったり、問題が起きる状況 を検討する
考えた条件 が、メリット のほうが デメリットより も 大きい場合 は採用する
手順 2 で 明らかになった問題 を 新しい問題 として設定し、手順 1 に戻る
上記を、満足のいく程度 に 問題が解決される まで 繰り返す

この方法の 問題点 としては、以下のようなものが挙げられます。多くの人は、日々そのことを実感しているのではないでしょうか。また、これらのいくつかは、以前の記事で説明した ルールベース AI の欠点でもあります。

あまり 性質の良くない条件 を設定すると、さまざまな状況 で 悪影響 が 発生する
実際には、上記の 手順 2 で 検討を行っても、考えた条件 が、どのような状況 で 悪影響を与える かが 分からない 場合が多い
実際に その条件 を用いて 問題を解決 しようと 試みた後 で 問題が判明 する 場合が多い
後から問題 が判明した場合、その問題 を 解決するため の 限定的な条件 を 追加する必要 があるが、そのような 限定的な条件 が 多くなりすぎる と、わけがわからなくなる
後から発生 した 問題を解決 するために 加えた条件 が、別の問題を発生 させたり、以前に解決 した問題が 再び発生する ような場合がある
この方法で、問題が 100 % 解決できない 場合が多い

ただし、この手順 は上記のような欠点はあるものの、他に良い方法 が 無かったり、条件が少ないうち はこの方法が 有効なことが多い ので、実際に 良く使われます。

問題が 見つかってから、条件を追加して対処 するという、場当たり的 な 対処方法 を続けると、本当に わけがわからなくなります。そのような場合は、一から 条件を 考えなおしたほうが早い ことも よくあります。

法律の条文 や 契約書 などが、長くて分かりづらい のは、すべての状況 に 対応する条件 を 漏れなく記述 しようとしているからです。ほとんどの問題 には、例外的 な 状況がある ので、それらに対応 するためには、どうしても条件が 数多く、複雑にならざるを得ません。また、完璧に 見えた 場合でも、後から欠陥が発見 されて、修正を 余儀なくされる ことは 良くあります。

プログラム のバグが 後から発見される ことが 多い理由 も、複雑な処理 を行うプログラムの場合は、100 % 正しい処理 を完璧に 記述する ことが困難だからです。

限定的な条件の追加によるルール 12 の定義

ai11s ver 3 が、ai2s に敗北 するのは、0.7 % という、かなりレアなケース です。また、下記のプログラムで、ai2 VS ai11s ver 3 で、ai11s ver 3 が敗北する 試合経過 を 何度も表示 すると、同一局面 を 考慮する と 1 つ の パターンしか存在しない ことが 分かります。興味がある方は、下記のプログラムを何度か実行して、そのことを確認してみて下さい。

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

従って、ai11s ver 3 が、ai2s に敗北 する 局面のみ を対象とする、下記の条件 を、ルール 11 の ヒューリスティックな条件より も 高い優先順位 で 追加する という方法が 考えられます。なお、この条件 による 合法手 の選択は、先程の検証 によって、最善手 であることが 確認できている ので、演繹法による条件 です。従って、この条件を加える ことによって、他の局面 に 悪影響を与える ことは ありません。

下記の いずれかの局面 の場合は、辺のマス を選択する

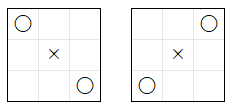
下記は、上記の条件 を ルール 11 に 加えた、ルール 12 の定義です。新しい条件 は、元の ルール 11 の 優先順位 が 1 ~ 4 の どの条件 とも 同時に満たされる ことはないので、優先順位 が 1 ~ 4 の条件の前後であれば、どこに入れても構いません。本記事では、優先順位 が 4 の条件 の次に、優先順位 が 5 の条件 として追加しました。

順位	条件	種類
1	真ん中のマスに優先的に着手する
2	勝てる場合に勝つ	十分条件
3	相手が勝利できる着手を行わない	必要条件
4	「自 2 敵 0 空 1」が 2 つ以上存在する着手を行う	十分条件
5	斜め方向に〇×〇が並び、他の 6 マスが空のマスの場合は、いずれかの辺のマスに着手を行う	十分条件
6	「自 2 敵 0 空 1」が 1 つ存在する着手を行う「自 1 敵 0 空 2」が最も多い着手を行う「自 0 敵 1 空 2」が最も少ない着手を行う
7	ランダムなマスに着手する

評価値の設定

ルール 12 の条件に対する 評価値 は、下記の表のように設定することが できます。具体的には、新しく追加 した条件の 評価値 を 100 に設定 し、それよりも 優先順位 が 高い評価値 にそれぞれ 100 を加えました。

順位	局面の状況	個別	評価値
1	真ん中のマスに着手している		`400`
2	自分が勝利している		`300`
4	「自 2 敵 0 空 1」が 2 つ以上存在する		`200`
5	片方の斜め方向に〇×〇が並び、いずれかの辺の 1 つのマスのみに × が配置されている		`100`
6	「自 2 敵 0 空 1」が 1 つ存在する「自 1 敵 0 空 2」が x 個存在する「自 0 敵 1 空 2」が y 個存在する	`2` (`0～2`) `0.5 * x` (`0～4`) `-y` (`-8~0`)	`-8～6`
3	相手が勝利できる		`-100`

`ai12s` の定義の方法

ai12s を定義するためには、ゲームの局面が「片方の 斜め方向 に 〇×〇 が並び、いずれか の辺の 1 つのマスのみ に × が配置 されている」であるか どうかを 判定する必要 が あります。どのような方法で判定できるかについて少し考えてみて下さい。

上記の条件 を 満たすため には、以下の 3 つの条件 が すべて満たされる必要 が あります。

片方の 斜め方向 に 〇×〇 が並ぶ
いずれか の辺の 1 マスのみ に × が配置 されている
他の すべてのマス は 空のマス である

片方の斜め方向に〇×〇が並ぶ

この場合は、以下の いずれか の条件が 満たされる必要 が _あります。

(0, 0) に〇、(1, 1) に ×、(2, 2) に〇が配置されている
(2, 0) に〇、(1, 1) に ×、(0, 2) に〇が配置されている

mb に Marubatsu クラス の インスタンスが代入 されている場合、上記を 判定する条件式 は、以下のようになります。このような条件式を記述する際には、and 演算子 のほうが or 演算子より も 優先順位が高い点 に注意して下さい。なお、このプログラムを 1 行で記述することもできますが、わかりづらいので、適宜改行を行っています。

(mb.board[0][0] == Marubatsu.CIRCLE and \
 mb.board[1][1] == Marubatsu.CROSS and \
 mb.board[2][2] == Marubatsu.CIRCLE) \
 or \
(mb.board[2][0] == Marubatsu.CIRCLE and \
 mb.board[1][1] == Marubatsu.CROSS and \
 mb.board[0][2] == Marubatsu.CIRCLE)

上記の 条件式 でも 問題はありません が、どちらの場合 も (1, 1) に × が配置 されていることから、下記の 2 つの条件 が すべて満たされるか どうかで判定することも できます。

(1, 1) に × が配置 されている
下記の いずれか の条件が 満たされる
- (0, 0) と (2, 2) に 〇が配置 されている
- (2, 0) と (0, 2) に 〇が配置 されている

下記は、上記を判定 する 条件式 です。どちらを使っても構いません が、プログラムが 若干短くなる ので、本記事 では 下記の条件式 を 採用する ことにします。

mb.board[1][1] == Marubatsu.CROSS and \
(mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
 mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE)

いずれかの辺の 1 マスのみに × が配置されている

この場合は、以下の いずれかの条件 が 満たされる必要 が あります。

(1, 0) に × が配置 されている
(0, 1) に × が配置 されている
(2, 1) に × が配置 されている
(1, 2) に × が配置 されている

その 条件式 は、下記のプログラムのように 記述するしかない でしょう。

mb.board[1][0] == Marubatsu.CROSS or \
mb.board[0][1] == Marubatsu.CROSS or \
mb.board[2][1] == Marubatsu.CROSS or \
mb.board[1][2] == Marubatsu.CROSS

他のすべてのマスは空のマスである

初心者の方は、この条件を判定する方法が難しく感じられるかもしませんが、ある事 にさえ 気が付けば、簡単に判定 することが できる ので、分からない方は少し考えてみて下さい。

〇×ゲーム の性質から、4 回の着手 が行われた局面で、4 つのマス に マークが配置 されていることが確認できた場合は、残りのマス は必ず 空のマス になります。4 つのマス に マークが配置 されていることは、上記の 2 つの条件式 で 判定できる ので、その条件 に 加えて、4 回の着手 が 行われている ことを判定することで、他の すべてのマス が 空のマス であることが判定できます。

Marubatsu クラス の インスタンス には、着手が 行われた回数 を表す move_count 属性 があるので、そのことは、下記の条件式 で 簡単に判定 できます。

mb.move_count == 4

判定を行う条件式

求める条件式 は、下記のプログラムのように、上記の 3 つの条件式 をすべて and 演算子 で つないだもの です。初心者の方の多くは、下記のような複雑な条件式をつくることが難しいと思うかもしれません。慣れないうち は、上記のように、個別の条件 を表す 条件式 を 順番に記述 し、最後にそれらを つなぎ合わせる という 方法を取る と 良いでしょう。なお、ある程度 プログラミング に 慣れてくれば、下記のような 複雑な条件式 を 一度に考える ことが できるようになります。

mb.board[1][1] == Marubatsu.CROSS and \
(mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
 mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
(mb.board[1][0] == Marubatsu.CROSS or \
 mb.board[0][1] == Marubatsu.CROSS or \
 mb.board[2][1] == Marubatsu.CROSS or \
 mb.board[1][2] == Marubatsu.CROSS) and \
 mb.move_count == 4

上記が わかりづらい と 思った方 は、下記のプログラムのように それぞれの条件式 の 計算結果 を、変数に代入 し、その変数を つなぎ合わせる という方法が あります。なお、変数の名前 の cond は、条件を表す condition の略です。

cond1 = mb.board[1][1] == Marubatsu.CROSS and \
        (mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
         mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE)
cond2 = mb.board[1][0] == Marubatsu.CROSS or \
        mb.board[0][1] == Marubatsu.CROSS or \
        mb.board[2][1] == Marubatsu.CROSS or \
        mb.board[1][2] == Marubatsu.CROSS
cond3 = mb.move_count == 4

cond1 and cond2 and cond3

`ai12s` の定義

上記の 条件式 を利用することで、ai12s を下記のプログラムのように定義できます。

5、9、19 行目：評価値 を修正する
23 ~ 31 行目：上記の条件式 で判定を行うプログラムを追加します

 1  def ai12s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):   
 2      def eval_func(mb):      
 3          # 真ん中のマスに着手している場合は、評価値として 400 を返す
 4          if mb.last_move == (1, 1):
 5              return 400
 6   
 7          # 自分が勝利している場合は、評価値として 300 を返す
 8          if mb.status == mb.last_turn:
 9              return 300
10
11          markpats = mb.count_markpats()
12          if debug:
13              pprint(markpats)
14          # 相手が勝利できる場合は評価値として -100 を返す
15          if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
16              return -100
17          # 次の自分の手番で自分が必ず勝利できる場合は評価値として 200 を返す
18          elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
19              return 200
20       
21          # 斜め方向に 〇×〇 が並び、いずれかの辺の 1 つのマスのみに × が
22          # 配置されている場合は評価値として 100 を返す
23          if mb.board[1][1] == Marubatsu.CROSS and \
24             (mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
25              mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
26             (mb.board[1][0] == Marubatsu.CROSS or \
27              mb.board[0][1] == Marubatsu.CROSS or \
28              mb.board[2][1] == Marubatsu.CROSS or \
29              mb.board[1][2] == Marubatsu.CROSS) and \
30             mb.move_count == 4:
31              return 100              
以下同じなので略

行番号のないプログラム

def ai12s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):   
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 400 を返す
        if mb.last_move == (1, 1):
            return 400
    
        # 自分が勝利している場合は、評価値として 300 を返す
        if mb.status == mb.last_turn:
            return 300

        markpats = mb.count_markpats()
        if debug:
            pprint(markpats)
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 200 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 200
        
        # 斜め方向に 〇×〇 が並び、いずれかの辺の 1 つのマスのみに × が
        # 配置されている場合は評価値として 100 を返す
        if mb.board[1][1] == Marubatsu.CROSS and \
           (mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
            mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
           (mb.board[1][0] == Marubatsu.CROSS or \
            mb.board[0][1] == Marubatsu.CROSS or \
            mb.board[2][1] == Marubatsu.CROSS or \
            mb.board[1][2] == Marubatsu.CROSS) and \
           mb.move_count == 4:
            return 100              

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += score_201
        # 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
        # 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
        score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)

修正箇所

-def ai11s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):   
+def ai12s(mb, score_201=2, score_102=0.5, score_012=-1, debug=False):   
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 400 を返す
        if mb.last_move == (1, 1):
-           return 300
+           return 400
    
        # 自分が勝利している場合は、評価値として 300 を返す
        if mb.status == mb.last_turn:
-           return 200
+           return 300

        markpats = mb.count_markpats()
        if debug:
            pprint(markpats)
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 200 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
-           return 100
+           return 200
        
        # 斜め方向に 〇×〇 が並び、いずれかの辺の 1 つのマスのみに × が
        # 配置されている場合は評価値として 100 を返す
+       if mb.board[1][1] == Marubatsu.CROSS and \
+          (mb.board[0][0] == mb.board[2][2] == Marubatsu.CIRCLE or \
+           mb.board[2][0] == mb.board[0][2] == Marubatsu.CIRCLE) and \
+          (mb.board[1][0] == Marubatsu.CROSS or \
+           mb.board[0][1] == Marubatsu.CROSS or \
+           mb.board[2][1] == Marubatsu.CROSS or \
+           mb.board[1][2] == Marubatsu.CROSS) and \
+          mb.move_count == 4:
+           return 100              
以下同じなので略

`ai2` との対戦

下記のプログラムで、ai2 との対戦を行います。

ai_match(ai=[ai12s, ai2])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai12s VS ai2
count     win    lose    draw
o        9907       0      93
x        8820       0    1180
total   18727       0    1273

ratio     win    lose    draw
o       99.1%    0.0%    0.9%
x       88.2%    0.0%   11.8%
total   93.6%    0.0%    6.4%

実行結果 から、ついに ai12s の敗率が、どちらの手番 を 担当した場合 でも 0 % になりました。対戦回数 が 足りない ため、偶然 ai12s が敗北する対戦が 生じなかったのではないか と 心配する方 は、実行に時間はかかりますが、下記のプログラムのように、対戦回数 を 10 倍の 10 万回 にして対戦を行ってみて下さい。なお、筆者のパソコンで、下記のプログラムの実行には約 5 分かかりました。

ai_match(ai=[ai12s, ai2], match_num=100000)

実行結果

ai12s VS ai2
count     win    lose    draw
o       98919       0    1081
x       88168       0   11832
total  187087       0   12913

ratio     win    lose    draw
o       98.9%    0.0%    1.1%
x       88.2%    0.0%   11.8%
total   93.5%    0.0%    6.5%

実行結果から、10 万回 でも 敗率が 0 % になったので、ai12s は 弱解決の AI である 可能性 が 非常に高い ことが確認できました。

下記は、上記の結果 と、これまで の ai11s が ai2 と対戦した際の結果を表に まとめたもの です。

関数名	o 勝	o 分	x 勝	x 負	x 分	勝	負	分
`ai11s` ver 1	98.1	1.9	82.5	1.9	15.6	90.3	1.0	8.7
`ai11s` ver 2	98.8	1.2	87.7	2.4	10.0	93.2	1.2	5.6
`ai11s` ver 3	99.1	0.9	87.7	0.8	11.5	93.4	0.4	6.2
`ai12s`	98.9	1.1	88.2	0.0	11.8	93.5	0.0	6.5

これで、ルールベース の AI で、弱解決の AI を作成することが できました。ai12s が 最強の AI であることは、現時点 では 証明できません が、今後の記事で 探索型の AI で 最強の AI を 作成する ので、その際 に 最強の AI と対戦 させることで、ai12s が 最強の AI であるか どうかを 確認する ことにします。

今回の記事のまとめ

今回の記事では、ai11s ver 3 の パラメータ を修正し、さらに 新しいルール を 付け加える ことで、ai12s という 弱解決の AI を作成しました。残念ながら、現時点 では、ai12s が 最強の AI であることの 証明は行えません が、ルールベース で 作成する AI としては、最も強い AI が 作れた のではないかと思います。

なお、これでルールベースの AI の話は終わったのではないかと思う人がいるかもしれませんが、あと数回ほど、ルールベースの AI の話は続きます。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

今回の記事では marubatsu.py は変更していません。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その61 ai11s の検証と限定的な条件による問題の解決

目次と前回の記事

これまでに作成したモジュール

これまでに作成した AI

ai2 VS ai11s の検証と ai11s の修正

ai2 VS ai11s の検証

2 手目の検証

4 手目の検証

5 手目の検証

4 手目で (0, 0) に着手した場合の検証

パラメータの修正

修正したパラメータでの ai2 との対戦

パラメータの他の修正方法の検証

ai2 VS ai11s ver 3 の検証と ai11s ver 3 の修正

ai2 VS ai11s ver 3 の検証

2 手目の検証

4 手目の検証

6 手目以降の検証

4 手目で合法手 2 に着手した場合の検証

パラメータの修正方法の検討

パラメータの修正の効果の確認

敗率が上昇した理由

限定的な条件による問題の解決

汎用的な条件と限定的な条件

汎用的な条件と限定的な条件の性質

条件が与える影響の範囲

条件を考える手順

限定的な条件の追加によるルール 12 の定義

評価値の設定

ai12s の定義の方法

片方の斜め方向に〇×〇が並ぶ

いずれかの辺の 1 マスのみに × が配置されている

他のすべてのマスは空のマスである

判定を行う条件式

ai12s の定義

ai2 との対戦

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その61　ai11s の検証と限定的な条件による問題の解決

`ai2` VS `ai11s` の検証と `ai11s` の修正

`ai2` VS `ai11s` の検証

修正したパラメータでの `ai2` との対戦

`ai2` VS `ai11s` ver 3 の検証と `ai11s` ver 3 の修正

`ai2` VS `ai11s` ver 3 の検証

`ai12s` の定義の方法

`ai12s` の定義

`ai2` との対戦