Go to Qiita Advent Calendar 2024 Top
LoginSignup
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@ysgeso

Pythonで〇×ゲームのAIを一から作成する　その60　弱解決の定義と性質とその判定方法

Last updated at Posted at 2024-03-08

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

ルール アルゴリズム
ルール1 左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する
ルール2 ランダム なマスに 着手 する
ルール3 真ん中 のマスに 優先的 に 着手 する
既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール4 真ん中、隅 のマスの 順 で 優先的 に 着手 する
既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール5 勝てる場合 に 勝つ
そうでない場合は ランダム なマスに 着手 する
ルール6 勝てる場合 に 勝つ
そうでない場合は 相手の勝利 を 阻止 する
そうでない場合は ランダム なマスに 着手 する
ルール6改 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は ランダム なマスに 着手 する
ルール7 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手の勝利 を 阻止 する
そうでない場合は ランダム なマスに 着手 する
ルール7改 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は ランダム なマスに 着手 する
ルール8 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う
そうでない場合は ランダム なマスに 着手 する
ルール9 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う
そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う
そうでない場合は ランダム なマスに 着手 する
ルール10 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う
そうでない場合は、以下 の 2 つを 総合的に判断 して着手を行う
  • 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う
  • 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う
そうでない場合は ランダム なマスに 着手 する
ルール11 真ん中 のマスに 優先的 に 着手 する
そうでない場合は 勝てる場合 に 勝つ
そうでない場合は 相手 が 勝利できる 着手を 行わない
そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う
そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う
  • 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う
  • 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う
  • 相手 が 不利になる ように、「自 0 敵 1 空 2」が 最も少ない 着手を行う
そうでない場合は ランダム なマスに 着手 する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名 o 勝 o 負 o 分 x 勝 x 負 x 分 勝 負 分 欠陥
ai1
ai1s 		78.1 17.5 4.4 44.7 51.6 3.8 61.4 34.5 4.1 あり
ai2
ai2s 		58.7 28.8 12.6 29.1 58.6 12.3 43.9 43.7 12.5
ai3
ai3s 		69.3 19.2 11.5 38.9 47.6 13.5 54.1 33.4 12.5
ai4
ai4s 		83.0 9.5 7.4 57.2 33.0 9.7 70.1 21.3 8.6 あり
ai5
ai5s 		81.2 12.3 6.5 51.8 39.8 8.4 66.5 26.0 7.4
ai6 88.9 2.2 8.9 70.3 6.2 23.5 79.6 4.2 16.2
ai6s 88.6 1.9 9.5 69.4 9.1 21.5 79.0 5.5 15.5
ai7
ai7s 		95.8 0.2 4.0 82.3 2.4 15.3 89.0 1.3 9.7
ai8s 98.2 0.1 1.6 89.4 2.5 8.1 93.8 1.3 4.9
ai9s 98.7 0.1 1.2 89.6 2.4 8.0 94.1 1.3 4.6
ai10s 97.4 0.0 2.6 85.6 2.6 11.7 91.5 1.3 7.2
ai11s 98.1 0.0 1.9 82.5 1.9 15.6 90.3 1.0 8.7 あり

最強の AI であるかどうかの判定

前回の記事で説明した、演繹法 を使って、最強の AI の 定義 を 完全に満たす ような ルール の 条件 で AI を 作成 した場合は、間違いなく 最強の AI です。一方、少しでも ヒューリスティック の 手法 が用いられた ルール の 条件 で 作られた AI が、本当に 最強の AI であるか を知るためには、検証 を行う 必要 が あります。

作成した AI が 最強の AI であるか どうかを 検証 するためには、下記の 最強の AI の 定義 の 通り、すべての局面 で 最善手 を 選択するか どうかを 調べる必要 が あります。

最強の AI とは、すべての局面 で、最善手 を 選択する AI のことである。

しかし、下記 のような 理由 で、そのようなことを行うのは 容易ではありません。

  • オセロ、勝利、囲碁1などのように、局面の数 が 多すぎる 場合は、現実的 に、すべての局面 で 最善手を選択するか どうかを 調べる ことが 不可能 である
  • AI が、すべての局面 で 最善手を選択する ことを 判定するため には、すべての局面 の 最善手 が 何であるか が 分かっている必要 がある。それは、最強の AI であるか どうかを 判定するため に、最強の AI が 必要になる ということであり、矛盾 する

従って、演繹法 で 最強の AI を 作れない場合 に、ヒューリスティック な 手法 で 作成された AI が 最強の AI であるか どうかを 判定する ことは、多くのゲーム では ほぼ不可能 です。ただし、最強の AI であることは わからなくても、他の AI と 比較 して、相対的に強いか どうかであれば、他の AI との 総当たり戦 や、レーティング などの 方法 で 判定 することは 可能 なので、一般的 には それらの方法 で、特定の AI の中 での、最も強い AI を 判定 します。また、実際 に、それらの方法 は さまざまな競技 で 用いられています。

弱解決 の AI であるかの判定方法

これまで の記事では、〇×ゲーム の 新しい AI を 作成 した際に、その 強さを検証 するために、ランダムな AI との 対戦 と、それまで に 作成 した 最も強い AI との 対戦 を行ってきました。それまで の 最も強い AI と 対戦する ことは、新しい AI の 強さを検証 する上で、直観的 に 理にかなっている と 思う人が多い と思います。しかし、実際 には、それまで の 最も強い AI と 対戦するだけ では、新しく作成 した AI が 強くなったか どうかを 判定できる とは 限りません。

その 理由の一つ は、対戦成績 が 良かった としても、作成した AI が 偶然 それまでの中で 最も強いの AI の 弱点 を つくことができる、相性の良い AI である 可能性がある からです。これは 対戦成績 が 悪かった場合 でも同様です。

他の理由 としては、前回の記事 で 検証 を行った、修正後 の ai11 VS ai10s で行われる 着手の図 を見ればわかるように、強い AI は、ルール の 条件 が 厳しくなる ために、特定 の 着手 のみを 選択する傾向 があります。分かりづらいと思った方は、修正前 の ai11s VS ai10s で行われる 着手の図 と 見比べて下さい。

そのため、強い AI どうし で 対戦 を行っても、〇× ゲーム の 特定の局面 に対する 検証しか行えません。従って、強い AI どうし で 対戦した際 に、出現しなかった局面 でも、新しい AI が 最善手 を 選択するか どうかの 検証 を行うことは できません。

一方、AI の強さ を 検証 する際に、明らか に 弱い AI である、ランダムな AI と 対戦 することの 必要性 に 疑問を感じた人 はいないでしょうか？ランダムな AI は、平均的 にみると 弱い AI ですが、ありとあらゆる着手 を 行う可能性がある ので、繰り返して 何度も戦う と、その中の いくつかの対戦 で 常に最善手を選択 する 可能性が生じます。実際 に、〇×ゲーム のような、局面の種類 があまり 多くないゲーム では、数万回対戦 を行うことで、その中の いくつかの試合 では ランダムな AI が 最善手のみ を 選択する ことが 期待できます。

〇×ゲーム は、ゲーム開始時 の 局面の状況 は 引き分け の局面であるので、最強の AI であれば、どのような AI と 対戦 しても、負ける ことは 決してありません。従って、ランダムな AI と 数多く対戦 した 結果、一度 も 負けることがなければ、最強の AI である 可能性が高い と 判断する ことが できます。これが、これまで の記事で、新しい AI を 作成するたび に、ランダムな AI と 対戦した これまでに説明していなかった 理由 です。

ランダムな AI と 数多く対戦する ことで、最強の AI であるか どうかを 判定する という 方法 は、〇×ゲームだけではなく、理論的 には すべて の 二人零和有限確定完全情報ゲーム に 適用できます。ただし、厳密 には、判定できる のは、最強の AI であるか どうか ではなく、この後で説明する 弱解決の AI であるか どうかの 判定 です。また、現実的 に 判定できる のは、〇×ゲームのような、局面の数 が 少ないゲーム に 限られます。

今回の記事では、そのようなことができる 具体的な理由 と 方法 について 説明 します。

ゲームの解決とその種類

ゲーム の ある局面 から、お互い が 最善手のみ を 選択 した場合の 結果 が 判明している ことを、ゲーム が 解決された（solved）と呼び、以下の 3 種類 に 分類 されています2。

  • 超弱解決（ultra weakly solved）
    ゲームの 開始時 の 局面の状態 は 判明 しているが、その 局面の状況以上 の 結果 になる 合法手 を 選択する方法 が 判明していないゲーム のこと3。本記事 では 取り扱いません

  • 弱解決（weakly solved）
    ゲームの 開始時 の 局面の状態 が 判明 しており、どのような相手と対戦 しても、その 局面の状況以上 の 結果 になる 合法手 を 選択する方法 が 判明しているゲーム のこと

  • 強解決（strongly solved）
    すべての局面 で、局面の状況 と、最善手 が 判明しているゲーム のこと

強解決 の 意味 は 簡単 で、最強の AI の 定義 から、強解決 された ゲームである ということと、最強の AI が 作れる ということは、同じ意味 を持ちます。

一方、弱解決 の 意味 は わかりづらい と思いますので、詳しく説明 します。

最強の AI どうし が、実際 に 対戦を行う場合 のことを考えると、すべての局面 で 最善手 を みつけることができる必要 は ありません。

例えば、ai11s は、ルール 11 の「真ん中 のマスに 優先的 に 着手 する」という 条件 から、〇 を担当 した際に、1 手目 では 下図 の 左 の (1, 1) の 合法手のみ を 選択 します。

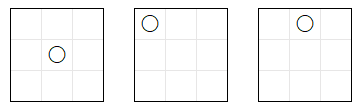
このことから、ai11s が ゲームの開始時 から 対戦を行う際 には、1 手目 で、上図 の 真ん中 や 右 のような、隅 や 辺 の マス への 着手 が行われる 局面 は 決して生じない ことが わかります。従って、ai11s は、それらの局面 で 最善手 を 選択できる必要 は ありません。

強解決 と 弱解決 の 違い は以下のようになります。

  • 強解決 されたゲームは、すべての局面 の 最善手 が 判明 している
  • 弱解決 されたゲームは、必要な局面のみ で、目的を達成 できる 合法手 が 判明 している

本記事では、弱解決 の 定義を元 に、弱解決の AI を 以下 のように 定義 します。

弱解決の AI とは、ゲーム開始時 の 局面 から、どのような AI と 対戦 しても、ゲーム開始時 の 局面の状況以上 の 結果 になる 合法手を選択 する AI のことである。

弱解決の AI という呼び方は、最強の AI と 区別するため に 筆者が作った 本記事 独自 の 呼び方 です。おそらく、他では使われていない と思います。

なお、これまで の 最強の AI のことを、強解決の AI と呼ぶこともできますが、本記事では 弱解決の AI と 強く区別したい場合 を 除いて、これまで通り 最強の AI と 表記する ことにします。

弱解決 の AI は、最善手 を 選択できる必要 がある 局面の数 が、最強の AI と 比べて大幅に少ない ので、最強の AI より は 簡単に作る ことが できます。

実際 に、オセロ は、2024 年 3 月の時点では、強解決されていません が、2023 年 10 月に 弱解決がされた という 論文 が発表 されました。

とはいえ、将棋 や 囲碁 などの、オセロより かなり 複雑なゲーム では、弱解決の AI であっても 作成 することは ほぼ不可能 だと 考えられています

弱解決でよくある誤解

上記で、「弱解決 されたゲームは、必要な局面のみ で、目的を達成 できる 合法手 が 判明 している」と説明しましたが、強解決の説明 と 同様 に、「弱解決 されたゲームは、必要な局面のみ で、最善手 が 判明 している」のように 説明しなかった点 が 気になっている 人はいないでしょうか？筆者 も 最初 は そのように考えていた のですが、よく考える とその説明では 間違っている のではないかと思いました。ただし、これは 筆者 の 勘違いかもしれない ので、間違っていたらコメントで指摘していただけると嬉しいです。

実際に、「弱解決」を 検索 すると、「ゲーム開始時の局面から、お互い が 最善手を選択 した場合の 結果がわかっている ゲームのこと」のような 説明 が いくつか発見 できました。また、下記の論文 の 96 ページ でも、弱解決 を「初期局面の勝敗が解明されていて、それを証明するのに必要な 各局面 の 最善手 も 分かっている」のように説明しています。

しかし、下記の論文の 8 ページ にある 本来 の 弱解決の定義 で 述べられている、必要な局面 で ゲームの開始時 の 局面の状況以上 になるような 合法手 を 選択できる ことと、最善手 が わかっている ことは 同じではありません。

そのことを理解するためには、弱解決の AI の 性質 を 理解する必要 があるので、その 説明を行いながら、弱解決の誤解の意味 を説明します。

弱解決 の AI の性質

二人零和有限確定完全情報ゲーム には、先手 と 後手 があります。そのため、先手を担当 した場合は 弱解決 の AI や 最強の AI であるが、後手を担当 した場合は そうではない という場合が あります。これは、先手と後手 を 入れ替えた場合 も 同様 です。

一般的 には 弱解決の AI や 最強の AI は、先手と後手 の 両方 で その性質を持つ AI のことを 指す ので、本記事 でも、そのような意味 でそれらの 表記を行います。

また、片方 の 手番だけ で 性質を満たす 場合は、先手の弱解決の AI のように、手番つけて表記 することで、区別する ことにします。

次に、弱解決の AI の 性質 を、ゲームが 先手の必勝、引き分け、後手の必勝 の 3 つの場合 と、先手 と 後手 を担当する 場合 に 分けて説明 します。

先手の必勝のゲームで、先手を担当する場合

弱解決の AI が 先手を担当 する場合は、ゲーム開始時 の 局面 は 必勝の局面 です。勝利より も 良い状況 は 存在しない ので、勝利以上 の 結果 は 勝利だけ です。従って、弱解決の AI の定義 から 弱解決の AI は、この場合は 必ず勝利 する 必要 があります。

以前の記事で説明したように、最善手を選択するか どうかで、局面の状況 は 下記 の表のようになります。この表 から、局面の状況 が 悪化した場合 は、相手 が 最善手 を 選択し続ける と、元の状況 に 戻ることはない ことが わかります。従って、どのような AI に対しても 勝利する ためには、弱解決の AI は 常に最善手 を 選択 する 必要がある 事が わかります。

局面の状況
最善手を選択する 変化しない
最善手を選択しない 悪化する

上記 を まとめる と以下のようになります。

先手の必勝のゲーム で、ゲームの開始時 の 局面 から 弱解決の AI が 先手を担当 する場合は、以下 のような 性質 がある

  • 出現 する すべての局面 で 最善手を選択 する
  • 相手 が どのような AI であっても 100 % 勝利 する
  • 最強の AI と 同じ強さ を持つ

従って、この場合 は、弱解決の AI は、最強の AI と 同じ強さ を持ち、「弱解決 されたゲームは、必要な局面のみ で、最善手 が 判明 している」という説明は 正しい説明 です。

先手の必勝のゲームで、後手を担当する場合

ゲームの 開始時の局面 が 先手の必勝の局面 の場合で、後手を担当 する場合は、後手の立場 から見ると、後手の必敗の局面 です。敗北以上 の 結果 は、勝利、引き分け、敗北 という、すべての結果 を 含みます。従って、弱解決の AI の定義 から 弱解決の AI は、出現 する すべての局面 で、どのような着手 を 選択 しても 構わない ことになります。つまり、この場合 は、すべての AI が 弱解決の AI である と 言える ということです。

別の言葉 で 説明 すると、この場合 は、弱解決の AI は、出現 するどの 局面 でも 最善手 を 知る必要がない ということです。従って、この場合は、「弱解決 されたゲームは、必要な局面のみ で、最善手 が 判明 している」という 説明 は 間違っています。

一方、最強の AI は、すべての局面 で 最善手を選択 するので、この場合 は、最強の AI と 弱解決の AI は 同じ強さ では ありません。

具体例としては、先手の必勝の局面 で、先手 が 最善手 を 選択しなかった場合 は、引き分けの局面 または 先手の必敗の局面 になります。後手 が 最強の AI であれば、そのような場合でも 常に最善手を選択 するので、決して 敗北する ことは ありません。一方、弱解決の AI は そのような局面 で 最善手を選択 するとは 限らない ので、敗北 してしまう 可能性 が あります。これが、最強の AI と 弱解決の AI の 大きな違い です。

上記 を まとめる と、以下のようになります。

先手の必勝のゲーム で 後手を担当 する場合は、以下 のような 性質 がある。

  • 勝利、引き分け、敗北の すべての結果 になる 可能性がある
  • すべての AI が 後手の場合 は 弱解決の AI である
  • 最善手 を 選択 するとは 限らない点 が、最強の AI とは 異なる

後手の必勝のゲームの場合

後手の必勝のゲーム で 先手を担当 する場合は、先手の立場 から見ると、先手の必敗の局面 です。後手の必勝のゲーム で 後手を担当 する場合は、必勝の局面 です。

従って、先手の必勝のゲーム の場合と 同様の考え方 で それぞれの性質 を 知る ことができ、下記 のように、一つにまとめる ことができます。

なお、『「先手の必勝のゲーム で、先手を担当 する」または「後手の必勝のゲーム で、後手を担当 する」』のような表記は長いので、そのことを 自分の必勝のゲーム のように 表記 することにします。自分の必敗のゲーム も 同様の意味 です。

自分の必勝のゲーム で、ゲームの開始時 の 局面 から 対戦 を行った場合は、弱解決の AI には 以下の性質 がある。

  • 出現 する すべての局面 で 最善手を選択 する
  • 相手 が どのような AI であっても 100 % 勝利 する
  • 最強の AI と 同じ強さ を持つ

自分の必敗のゲーム で、ゲームの開始時 から 対戦 を行った場合は、以下 のような 性質 がある。

  • 勝利、引き分け、敗北の すべての結果 になる 可能性がある
  • すべての AI が 自分の手番 の場合は 弱解決の AI である
  • 最善手 を 選択 するとは 限らない点 が、最強の AI とは 異なる

引き分けのゲームの場合

ゲーム開始時 の 局面の状況 が 引き分けの局面 場合は、弱解決の AI が 先手を担当 しても、後手を担当 しても、その 定義 から 結果 は 引き分け以上 になります。従って、この場合は、弱解決の AI は どのような AI と 対戦 しても 敗北する ことは ありません。そのためには、弱解決の AI が どのような合法手 を 選択 する 必要があるか について 説明 します。

相手 が 最善手 を 選択し続けた 場合、局面の状況 が 良くなる ことは ない ので、弱解決の AI は、必敗の局面 につながる 合法手 を 選択 しては いけない ことが わかります。

従って、引き分けの局面 では、弱解決の AI は、常に 最善手 を 選択する必要 が あります。

弱解決の AI が 対戦する相手 が、最善手 を 選択しない 場合は、弱解決の AI の 手番の局面 が 自分の必勝の局面 になる 場合 が あります。この場合も、弱解決の AI は 最善手 を 選択 する 必要がある と 思う人 が いるかもしれません が、そうではない 点に 注意 して下さい。

その理由は、自分の必勝の局面 から、引き分けの局面 につながるような、最善手ではない 合法手を 選択しても、引き分け以上 の 結果 になるという 条件 が 満たされる からです。この点 が、常に最善手 を 選択 する、最強の AI との 違い です。

上記 を まとめる と、以下のようになります。

引き分けのゲーム で、ゲームの開始時 の 局面 から 対戦 を行った場合は、弱解決の AI には 先手と後手 の いずれを担当 した場合でも、以下 のような 性質 がある。

  • どのような AI と 対戦 しても 敗北 する ことはない
  • 自分の必勝の局面 では 必敗の局面 につながる 合法手以外 を 選択 する。この点 が、最強の AI とは 異なる
  • 引き分けの局面 では、最善手を選択 する

弱解決の AI の性質のまとめ

弱解決の AI は、ゲームの開始時 の 局面 から 対戦 を行った際に 生じる局面 に対して、局面の状況 によって、下記 のような 合法手 を 選択 します。なお、空欄 は、そのような局面 が 生じない ことを意味します。

必勝の局面 引き分けの局面 必敗の局面
自分の必勝のゲーム 最善手
引き分けのゲーム 必敗の局面につながる
以外の合法手		 最善手
自分の必敗のゲーム 任意の合法手 任意の合法手 最善手4

表から、弱解決の AI は、ゲーム開始時 の 局面の状況 と 同じ状況の局面 では、常に最善手 を 選択 する AI であることが わかります。そのため、相手 が 常に最善手を選択 する場合は、下記の表のように、弱解決の AI と 最強の AI は 同じ結果 になります。

弱解決の AI VS 最強の AI 最強の AI VS 最強の AI
自分の必勝のゲーム 100 % 勝利 100 % 勝利
引き分けのゲーム 100 % 引き分け 100 % 引き分け
自分の必敗のゲーム 100 % 敗北 100 % 敗北

一方、試合で 相手 が 最善手以外 を 1 回以上選択 する場合は、以下 のようになります。このことから、弱解決の AI は、相手 が 最善手を選択しない という、ミス に つけこむ という 能力を持っていない ということが分かります。

弱解決の AI 最強の AI
自分の必勝のゲーム 100 % 勝利 100 % 勝利
引き分けのゲーム 勝利、引き分け 100 % 勝利
自分の必敗のゲーム 勝利、引き分け、敗北 勝利、引き分け

また、弱解決の AI は、ゲーム開始時 の 局面 から 着手の選択 を行った場合に 出現 する 可能性 のある 局面以外 では、自分の必勝の局面 であっても 最善手を選択 する 能力を持ちません。そのため、例えば 人間どうし が行った 対戦 の 途中の局面 から、弱解決 の AI が 引き継いで対戦 を行った場合に、その 局面の状況 よりも悪い結果になる場合があります。

最近では、将棋や囲碁の 対局の中継 で、AI による形成判断 が 表示される場合 が良くありますが、そのような 形成判断 は、弱解決 を 目的 として 作られた AI5 では 行えません。

ランダムな AI による弱解決の AI の判定

ここまでで説明した、弱解決の AI の 性質 から、ランダムな AI を 利用する ことで、原理的 には、AI が 弱解決の AI であるか を 判定 することが できます 。その理由と手順について少し考えてみて下さい。

弱解決の AI であることの判定手順

具体的には、下記の手順 で AI が 弱解決の AI であるか を 高確率 で 判定 することが できます。なお、条件 1 の 具体的な意味 は、この後で説明します。

  1. 判定したい AI と ランダムな AI を、先後を入れ替えて、すべての AI と 高確率 で 1 回以上対戦 することが できる ように、十分な数だけ対戦 する
  2. 下記 の いずれか の場合は、判定する AI は 弱解決の AI であり、いずれの条件 も 満たさない 場合は、弱解決の AI ではない
    • 先手 または、後手 の いずれかの場合 に 勝率 が 100 % になる
    • 先手 と 後手 のいずれも 敗率 が 0 % になる

このような、乱数（ランダムなもの）を使って 問題を解決する方法 の事を モンテカルロ法 と呼びます。モンテカルロ法 は、ヒューリスティック な 手法の一種 なので、100 % 正しい かどうかは 判定できません。従って、上記では 高確率 という 表現 を行いました。

モンテカルロ法 については、AI を作成する方法 の一つとして、今後の記事 で 取り扱う予定 です。参考までに、モンテカルロ法の Wikipedia のリンクを下記に示します。

上記の方法 で 判定できる理由 を少し考えてみて下さい。

ランダムな AI の性質

AI が 弱解決な AI であるか を 判定するため には、定義 から どのような AI と 対戦 しても、ゲーム開始 の 局面の状況 よりも 悪化しない ことを 確認する必要 があります。

単純 に 考えると、そのようなことを 判定する ことは 難しい と 思えるかも しれませんが、ランダムな AI を 利用する ことで そのような判定 を行うことが できます。その 理由 は ランダムな AI の 以下 の 性質 にあります。

ランダムな AI は、すべての局面 で、すべての合法手 を 選択 する 可能性がある AI です。従って、ランダムな AI は、世の中 に 存在 する すべての AI が 選択する着手 と、まったく同じ着手 を 選択する可能性 があります。そのため、ランダムな AI と 何度も対戦する ことで、理論上 は すべての AI と 1 回以上対戦 することが できます。また、その中 には ランダムな AI の すべての着手 が、最強の AI が 選択 する 合法手と同じ である 試合 があります。

これは、下手な鉄砲も数撃てば当たる という、でたらめな行動 であっても、何回も行えば、偶然 うまくいく場合がある という意味の ことわざ に相当します。

ただし、これはあくまで 理論上の話 で、オセロ、将棋、囲碁といった、局面の数 が 多いゲーム では、現実的 では ありません。その 理由 は、すべての AI と 1 回以上対戦 するということは、その AI が 対戦した際 に 出現 する可能性がある すべての局面 が、何度も行う対戦 の中で 1 度は出現 する 必要がある ということを 意味 するからです。

例えば、オセロ は、一回の対戦 で、基本的には 60 回の着手 を行うので、約 60 種類 の 局面 しか 出現しません。オセロ は、局面の数 が $10^{28}$ もある といわれているので、最低 でも $10^{28}$ / 60 = 約 $10^{26}$ 回以上 の 対戦 を 行わなければ、すべての局面 が 出現しません。従って、オセロでは、ランダムな AI と 対戦 することで、すべての AI と 1 回以上対戦 するためには、現実的でないほど の、途方もない回数 の 対戦 を 行う必要 が あります。

上記 を、サイコロ を使った 例え で 説明 します。サイコロ を 2 つ振った 場合の 合計 は、2 ~ 12 までの 11 種類 があります。これを ゲームの局面 に 対応 させて考えてみて下さい。サイコロの出目 は ランダム なので、サイコロ を 2 つ 、2 ~ 12 までの すべての出目 が 出現するまで振る ことは、すべての局面 が 出現するまで、ランダムな AI と対戦 することに（全く同じではありませんが）似ています。

プログラムの説明は省略しますが、下記 は 2 ~ 10 個まで の サイコロを振った 際に、何回 で すべての種類 の 出目が出現するか を 数えて表示 するプログラムです。

プログラム（興味がある方はクリックしてみて下さい） 
from random import randint

def dice(num):
    """ num 個のサイコロの合計を返す """
    total = 0
    for _ in range(num):
        # randint は実引数で指定した範囲のランダムな整数を返す
        total += randint(1, 6)
    return total

def countall(num):
    """ num 個のサイコロを振った場合に、すべての出目が出るまでの回数を返す"""
    
    # 出現した出目を記録する set
    s = set()
    # 出目の種類を計算する。最小値が num で 最大値が num * 6
    left = num * 5 + 1
    # サイコロを振った数を数える変数を初期化する
    count = 0
    # 全ての出目が出るまで繰り返す
    while left > 0:
        # サイコロを振る
        dicenum = dice(num)
        # 振った回数を増やす
        count += 1
        # s の要素に登録されているかを判定する
        if dicenum not in s:
            # 登録されていなければ、left を 1 減らし s に出目を登録する
            left -= 1
            s.add(dicenum)
    return count

# 2 ~ 10 個のそれぞれの場合の回数を表示する
for i in range(2, 11):
    print(i, countall(i))

実行結果（実行結果はランダムなので下記とは異なる場合があります）

2 45
3 333
4 3746
5 2333
6 99256
7 833719
8 4610084
9 10782768
10 51201303

実行結果 からわかるように、サイコロの数 が 増える と、すべての出目 が 出現するまで の 回数 が 大幅に増えていき、10 個振った場合 は 約 5000 万回 もかかることが わかります。なお、筆者のパソコン では、上記 の 実行 に 約 5 分 かかりました。

一方、〇×ゲーム は、局面の数 が 5478 のように6 少ない ので、１万回程度 の ランダムな AI との 対戦 で、高確率 で、すべての AI と 1 回以上対戦 することが できます。

判定手順で、弱解決の AI であることを判定できる理由

次に、先程示した、下記 の 判定手順 で、弱解決の AI であるか を 判定 することができる 可能性が高い理由 について 説明 します。なお、以降の説明 では、実際に すべての AI と 1 回以上対戦できた ことを 前提 に 説明 します。運悪く、その 前提 が 満たされなかった場合 は、弱解決の AI であると 正しく判定できない 場合が あります。それが、上記で「判定 することができる 可能性が高い」と表記した 理由 です。

  1. 判定したい AI と ランダムな AI を、先後を入れ替えて、すべての AI と 高確率 で 1 回以上対戦 することが できる ように、十分な数だけ対戦 する
  2. 下記 の いずれか の場合は、判定する AI は 弱解決の AI であり、いずれの条件 も 満たさない 場合は、弱解決の AI ではない
    • 先手 または、後手 の いずれかの場合 に 勝率 が 100 % になる
    • 先手 と 後手 のいずれも 敗率 が 0 % になる

下記は、弱解決の AI が、相手 が 最善手のみを選択 する場合と、そうでない場合 の 試合の結果 をまとめた表です。

相手が最善手のみを選択 そうでない場合
自分の必勝のゲーム 100 % 勝利 100 % 勝利
引き分けの ゲーム 100 % 引き分け 勝利、引き分け
自分の必敗のゲーム 100 % 敗北 勝利、引き分け、敗北

自分の必勝のゲーム とは、先手が必勝 のゲームで 先手を担当 する場合か、後手が必勝 のゲームで 後手を担当 する 場合 のことを表します。

自分の必敗のゲーム とは、先手が必勝 のゲームで 後手を担当 する場合か、後手が必勝 のゲームで 先手を担当 する 場合 のことを表します。

そこで、先手の必勝、後手の必勝、引き分けのゲーム に 分けて説明 することにします。

先手の必勝のゲーム

弱解決の AI が 先手を担当 する場合は、上記の表から 100 % 勝利 します。一方、弱解決の AI では ない AI の場合は、その 定義 から、ゲーム開始時 の 局面の状況 よりも 悪化する場合がある ので、すべての AI と 対戦 を行った場合は、いずれかの対戦 で 勝利できない 場合が あります。従って、勝率 は 100 % に なりません。

下記 は、上記の考察 を まとめた表 です。

勝率 引き分け率 敗率
弱解決の AI 100 % 0 % 0 %
弱解決の AI ではない 100 % 未満 0 ~ 100 % 0 ~ 100 %

先手の必勝のゲーム で、後手を担当 した場合は、先程説明したように、すべての AI が 後手の場合 は 弱解決の AI になります。従って、先手の必勝 のゲームでは、弱解決の AI であるか どうかは、その AI が 先手を担当 した 場合のみ で 判定すればよい ことが分かります。

後手を担当 した場合に、相手 が 常 に 最善手を選択 した場合は、敗北する ので、敗率 は 必ず 0 % より も 大きく なります。下記 は、上記の考察 を まとめた表 です。

勝率 引き分け率 敗率
後手を担当するすべての AI 0 ~ 100 % 未満 0 ~ 100 % 未満 0 % より大きい

下記は、先手 と 後手 の 勝率 と 敗率 の 関係 をまとめたものです。△ は、どちらの可能性もある 事を意味します。

弱解決の AI 弱解決でない AI
先手 の場合に 勝率 が 100 % になる 〇 ×
後手 の場合に 勝率 が 100 % になる × ×
先手 の場合に 敗率 が 0 % になる 〇 △
後手 の場合に 敗率 が 0 % になる × ×

上記の表 から、先手の必勝のゲーム の場合は、下記の 判定方法 が 正しい ことが分かります。なお、下記の 2 つ目の条件 は、引き分けのゲーム の場合に 必要となる条件 であり、先手の必勝のゲーム の場合は 常に満たされません。

下記 の いずれか の場合は、判定する AI は 弱解決の AI であり、いずれの条件 も 満たさない 場合は、弱解決の AI ではない

  • 先手 または、後手 の いずれかの場合 に 勝率 が 100 % になる
  • 先手 と 後手 のいずれも 敗率 が 0 % になる

後手の必勝の場合

先手 と 後手 を 入れ替えて考える ことで、上記 と 同じ考察 ができるので、後手の必勝 の場合も、上記の 判定方法 が 正しい ことが分かります。

引き分けのゲーム場合

引き分けのゲーム の場合は、先手 と 後手 の どちらを担当 しても、ゲーム開始時 の 局面の状況 は 引き分けの局面 です。従って、以下の説明は、先手を担当 した場合と 後手を担当 した場合の 両方 に 当てはまります。

引き分けのゲーム の場合は、弱解決の AI の 定義 から、どのような AI と 対戦 しても、ゲーム開始時 の 局面の状態 よりも 悪化することはない ので、敗北 することは ありません。一方、弱解決の AI では ない AI の場合は、ゲーム開始時 の 局面の状態 よりも 悪化する場合がある ので、敗率 は 0 % より も 大きくなります。

また、引き分けのゲーム の場合は、相手 が 最善手のみ を 着手 した場合に、必ず引き分けになる ので、勝率 が 100 % になることは ありません。

下記は、先手 と 後手 の 両方の場合 の 勝率 と 敗率 の 関係 をまとめたものです。

弱解決の AI 弱解決でない AI
勝率 が 100 % になる × ×
敗率 が 0 % になる 〇 ×

上記の表 から、引き分けのゲーム の場合は、下記の 判定方法 が 正しい ことが分かります。

下記 の いずれか の場合は、判定する AI は 弱解決の AI であり、いずれの条件 も 満たさない 場合は、弱解決の AI ではない

  • 先手 または、後手 の いずれかの場合 に 勝率 が 100 % になる
  • 先手 と 後手 のいずれも 敗率 が 0 % になる

なお、先手の場合 に 敗率 が 0 % になっても、後手の場合 に 敗率 が 0 % にならなければ、弱解決の AI では ない 点に注意して下さい。

以上で、先手の必勝、後手の必勝、引き分け の すべての場合 で、上記の手順 で 弱解決の AI であるか どうかを 高確率 で 判定 することが できる ことが わかりました。

繰り返しになりますが、上記 の 判定方法 は、オセロ、将棋、囲碁のような、局面の数が多いゲーム では 利用できない 点に 注意 して下さい。その 理由 は、局面の数 が 多い場合 は、ランダムな AI と対戦することで、すべての AI と 1 回以上対戦 することができる 可能性 が ほぼ 0 になる からです。

ランダムな AI との対戦による ai11s の検証

実際 に ai11s と ランダムな AI である ai2 を 対戦 させることで、ai11s が 弱解決の AI であるか を 判定する ことにします。その際に、以前の記事で、ai_match を、仮引数 params に AI の パラメータ を 代入 するように 修正 したので、以前の記事 で説明したように、下記のプログラムのように 記述する必要 がある点に 注意 して下さい。

from ai import ai_match, ai2, ai11s

param_ai11s = {
    "score_201": 2,
    "score_102": 1,
    "score_012": -1
}
ai_match(ai=[ai11s, ai2], params=[param_ai11s, {}])

実行結果（実行結果はランダムなので下記とは異なる場合があります）

ai11s VS ai2
count     win    lose    draw
o        9879       0     121
x        8767     236     997
total   18646     236    1118

ratio     win    lose    draw
o       98.8%    0.0%    1.2%
x       87.7%    2.4%   10.0%
total   93.2%    1.2%    5.6%
関数名 o 勝 o 負 o 分 x 勝 x 負 x 分 勝 負 分
ai9s 98.7 0.1 1.2 89.6 2.4 8.0 94.1 1.3 4.6
ai10s 97.4 0.0 2.6 85.6 2.6 11.7 91.5 1.3 7.2
修正前 の ai11s 98.1 0.0 1.9 82.5 1.9 15.6 90.3 1.0 8.7
修正後 の ai11s 98.8 0.0 1.2 87.7 2.4 10.0 93.2 1.2 5.6

上記は、ai9s、ai10s、修正前 と 修正後 の ai11s のそれぞれが ai2 と 対戦 した場合の 対戦結果 の表です。〇×ゲーム は、ゲーム開始時 の 局面の状態 が 引き分けのゲーム なので、表 から 以下 のようなことが わかります。

  • ai9s は 〇 を担当 した場合も、× を担当した 場合も、弱解決の AI ではない
  • ai10s と 修正前 と 修正後 の ai11s は、〇 を担当 した場合は、敗率が 0 % なので、〇 を担当 した場合のみ 弱解決の AI である 可能性が高い。従って、ルール 10 で ルール 9 に追加 した 条件 によって、〇 を担当 した場合は 弱解決の AI になった
  • いずれの AI も、× を担当 した場合に 敗率 が 0 % ではない ので、弱解決の AI ではない

次に、ai11s が 〇 を担当 した場合に 弱解決の AI ではない ことの 理由 を 検証 し、ai11s の ルール を 改善 することにします。

ai_match などの改良

ai11s が 〇 を担当 した場合に 弱解決の AI ではない ことの 理由 を 検証 する前に、このままでは、ai_match が 使いづらい ので 改良 することにします。

ai_match の問題点

先程は、下記 のような プログラム で、ai_match を 呼び出し ました。ai11s の パラメータ は、AI の ルールの修正 を 行う際 には、頻繁に変更 しますが、最適 と思われる パラメータ が 決まった後 は、頻繁に変更 することは ありません。そのため、パラメータ が 決まった後 でその AI で 対戦を行う際 に、下記のプログラムのように、毎回パラメータ を 実引数に記述 するのは かなり面倒 です。

param_ai11s = {
    "score_201": 2,
    "score_102": 1,
    "score_012": -1
}
ai_match(ai=[ai11s, ai2], params=[param_ai11s, {}])

下記 のプログラムのように、昔 の ai_match と同様 に、params を 記述しなくても AI どうしの 対戦を行える と 便利 だとは思いませんか？下記のように記述できるようにするための方法を少し考えてみて下さい。

ai_match(ai=[ai11s, ai2])

ai11s の修正

ai_match の params に 記述 した パラメータのデータ は、マッピング型の展開 によって、ai11s が 呼び出される際 に、キーワード引数 として 記述 されます。従って、ai11s の パラメータ を代入する 仮引数 を、調整済みのパラメータ を デフォルト値 とする、デフォルト引数 に 変更 することで、ai11s で 対戦する際 に、毎回 調整済のパラメータ を 記述 する 必要 が なくなります。下記 は、そのように ai11s を修正 した プログラム です。

  • 4 行目：評価値を計算 する際に 利用 する パラメータ を 代入 する 仮引数 を、調整したパラメータ を デフォルト値 とする、デフォルト引数 に 修正 する
1  from marubatsu import Marubatsu, Markpat
2  from ai import ai_by_score
3
4  def ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=False):
5      def eval_func(mb):  
元と同じなので省略
行番号のないプログラム 
from marubatsu import Marubatsu, Markpat
from ai import ai_by_score

def ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=False):
    def eval_func(mb):      
        # 真ん中のマスに着手している場合は、評価値として 300 を返す
        if mb.last_move == (1, 1):
            return 300
    
        # 自分が勝利している場合は、評価値として 200 を返す
        if mb.status == mb.last_turn:
            return 200

        markpats = mb.count_markpats()
        if debug:
            pprint(markpats)
        # 相手が勝利できる場合は評価値として -100 を返す
        if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
            return -100
        # 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
        elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
            return 100

        # 評価値の合計を計算する変数を 0 で初期化する
        score = 0        
        # 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
        if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
            score += score_201
        # 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
        score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
        # 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
        score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
        
        # 計算した評価値を返す
        return score

    return ai_by_score(mb, eval_func, debug=debug)
修正箇所 
from marubatsu import Marubatsu, Markpat
from ai import ai_by_score

-def ai11s(mb, score_201, score_102, score_012, debug=False):
+def ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=False):
    def eval_func(mb): 
元と同じなので省略

上記の修正 が 正しく動作するか を 確認 するために、下記のプログラムで、パラメータ を 実引数 に 記述せず に、ai11s を呼び出し てみます。実行結果 から、パラメータ を 記述しなくても、ai11s を 呼び出せる ことが 確認 できます。

mb = Marubatsu()
print(ai11s(mb))

実行結果

(1, 1)

また、上記の修正 により、ai_match で 対戦を行う際 には、params の 対応する要素 には、下記のプログラムのように、空の dict を 記述するだけで済む ようになります。なお、実行結果は、先程と変わらないので省略します。

ai_match(ai=[ai11s, ai2], params=[{}, {}])

ai_match の修正

デフォルト値 の パラメータ を使って、ai_match で 対戦を行う 際に、上記のプログラムのように、params の 要素 に 空の dict を 記述 するのも 面倒 です。そこで、下記のプログラムのように、ai_match の 仮引数 params を、デフォルト値 が [{}, {}] の デフォルト引数 にすることで、params に対応する 実引数 も 省略できる ようになります。

from collections import defaultdict

def ai_match(ai, params=[{}, {}], match_num=10000):
    print(f"{ai[0].__name__} VS {ai[1].__name__}")
元と同じなので省略
プログラム全体 
def ai_match(ai, params=[{}, {}], match_num=10000):
    print(f"{ai[0].__name__} VS {ai[1].__name__}")
    
    mb = Marubatsu()

    # ai[0] VS ai[1] と ai[1] VS a[0] の対戦を match_num 回行い、通算成績を数える
    count_list = [ defaultdict(int), defaultdict(int)]
    for _ in range(match_num):
        count_list[0][mb.play(ai, params, verbose=False)] += 1
        count_list[1][mb.play(ai=ai[::-1], params=params[::-1], verbose=False)] += 1

    # ai[0] から見た通算成績を計算する
    count_list_ai0 = [
        # ai[0] VS ai[1] の場合の、ai[0] から見た通算成績
        { 
            "win": count_list[0][Marubatsu.CIRCLE],
            "lose": count_list[0][Marubatsu.CROSS],
            "draw": count_list[0][Marubatsu.DRAW],
        },
        # ai[1] VS ai[0] の場合の、ai[0] から見た通算成績
        { 
            "win": count_list[1][Marubatsu.CROSS],
            "lose": count_list[1][Marubatsu.CIRCLE],
            "draw": count_list[1][Marubatsu.DRAW],
        },
    ]           

    # 両方の対戦の通算成績の合計を計算する
    count_list_ai0.append({})
    for key in count_list_ai0[0]:
        count_list_ai0[2][key] = count_list_ai0[0][key] + count_list_ai0[1][key]

    # それぞれの比率を計算し、ratio_list に代入する
    ratio_list = [ {}, {}, {} ]
    for i in range(3):
        for key in count_list_ai0[i]:
            ratio_list[i][key] = count_list_ai0[i][key] / sum(count_list_ai0[i].values())
            
    # 各行の先頭に表示する文字列のリスト
    item_text_list = [ Marubatsu.CIRCLE, Marubatsu.CROSS, "total" ]    
    
    # 通算成績の回数と比率の表示
    width = max(len(str(match_num * 2)), 7)
    diff_list = [ ("count", count_list_ai0, f"{width}d"),
                  ("ratio", ratio_list, f"{width}.1%") ]
    for title, data, format in diff_list:
        print(title, end="")
        for key in data[0]:
            print(f" {key:>{width}}", end="")
        print()
        for i in range(3):
            print(f"{item_text_list[i]:5}", end="")
            for value in data[i].values():
                print(f" {value:{format}}", end="")
            print()
        print()
修正箇所 
from collections import defaultdict

-def ai_match(ai, params, match_num=10000):
+def ai_match(ai, params=[{}, {}], match_num=10000):
    print(f"{ai[0].__name__} VS {ai[1].__name__}")
元と同じなので省略

上記の修正 を行うことで、下記 のプログラムのように、ai_match に params に対応する実引数 を 記述 する 必要 が なくなります。なお、実行結果は省略します。

ai_match(ai=[ai11s, ai2])

ai2 VS ai11s の検証

以前の記事で作成した show_progress を使って、ai2 VS ai11s で ai11s が 敗北する理由 を 検証 します。しかし、下記 のプログラムを 実行する と、実行結果のように エラーが発生 します。このようなエラーが発生する理由を少し考えてみて下さい。

from ai import show_progress

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

実行結果

略
--> 178     if mb.play(ai=ai, verbose=False) == winner:
    179         records = mb.records
    180         mb.restart()

TypeError: Marubatsu.play() missing 1 required positional argument: 'params'

上記のエラーメッセージは、以下のような意味を持ちます。

  • TypeError
    データ型（type）に関するエラー
  • play() missing 1 required positional argument: 'params'
    play メソッドに必要とされる（required）、params という位置引数（positional argument）が記述されていない（missing）

play メソッドの修正

このエラー は、play メソッドに 仮引数 params が 追加 されているのに、show_progress で、play メソッドを 呼び出す際 に、params の 実引数 が 記述されていない からです。

この問題 を 解決 する 方法 の一つは、下記 のプログラムのように、play メソッドの 仮引数 params を デフォルト引数 にするという方法です。なお、その方法は、以前の記事で説明した 関数の互換性 を持つ方法です。

def play(self, ai, params=[{}, {}], verbose=True):
元と同じなので省略

Marubatsu.play = play
プログラム全体 
def play(self, ai, params=[{}, {}], verbose=True):
    # 〇×ゲームを再起動する
    self.restart()
    # ゲームの決着がついていない間繰り返す
    while self.status == Marubatsu.PLAYING:
        # ゲーム盤の表示
        if verbose:
            print(self)
        # 現在の手番を表す ai のインデックスを計算する
        index = 0 if self.turn == Marubatsu.CIRCLE else 1
        # ai が着手を行うかどうかを判定する
        if ai[index] is not None:
            x, y = ai[index](self, **params[index])
        else:
            # キーボードからの座標の入力
            coord = input("x,y の形式で座標を入力して下さい。exit を入力すると終了します")
            # "exit" が入力されていればメッセージを表示して関数を終了する
            if coord == "exit":
                print("ゲームを終了します")
                return       
            # x 座標と y 座標を要素として持つ list を計算する
            xylist = coord.split(",")
            # xylist の要素の数が 2 ではない場合
            if len(xylist) != 2:
                # エラーメッセージを表示する
                print("x, y の形式ではありません")
                # 残りの while 文のブロックを実行せずに、次の繰り返し処理を行う
                continue
            x, y = xylist
        # (x, y) に着手を行う
        try:
            self.move(int(x), int(y))
        except:
            print("整数の座標を入力して下さい")

    # 決着がついたので、ゲーム盤を表示する
    if verbose:
        print(self)
    return self.status

Marubatsu.play = play
修正箇所 
-def play(self, ai, params, verbose=True):
+def play(self, ai, params=[{}, {}], verbose=True):
元と同じなので省略

Marubatsu.play = play

上記の修正 を行うことで、下記のプログラムを実行しても エラーが発生しなくなります。

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

実行結果（実行結果はランダムなので下記とは異なる場合があります）

Turn x
...
...
O..

Turn o
...
.X.
o..

Turn x
...
.xO
o..

Turn o
X..
.xo
o..

Turn x
x..
.xo
o.O

Turn o
x..
Xxo
o.o

winner o
x.O
xxo
o.o

show_progress の修正

上記のように、show_progress によって、ai2 VS ai11s で、ai11s が 敗北 する 試合の経過 を 表示できています が、このまま では、show_progress を 呼び出す際 に AI のパラメータ を 指定できない ので、show_progress にも下記のプログラムのように、デフォルト引数 params を 追加 し、play メソッドを 呼び出す際 に、キーワード引数 として params=params を 記述する ように 修正 します。

  • 1 行目：[{}, {}] を デフォルト値 とする デフォルト引数 params を 追加 する
  • 4 行目：play メソッドの 呼び出しの際 に、キーワード引数 として params=params を 記述する 
 1  def show_progress(ai, winner, params=[{}, {}]):
 2      mb = Marubatsu()
 3      while True:
 4          if mb.play(ai=ai, verbose=False, params=params) == winner:
 5              records = mb.records
 6              mb.restart()
 7              for x, y in records:
 8                  mb.move(x, y)
 9                  print(mb)
10              break
行番号のないプログラム 
def show_progress(ai, winner, params=[{}, {}]):
    mb = Marubatsu()
    while True:
        if mb.play(ai=ai, verbose=False, params=params) == winner:
            records = mb.records
            mb.restart()
            for x, y in records:
                mb.move(x, y)
                print(mb)
            break
修正箇所 
-def show_progress(ai, winner):
+def show_progress(ai, winner, params=[{}, {}]):
    mb = Marubatsu()
    while True:
-       if mb.play(ai=ai, verbose=False) == winner:
+       if mb.play(ai=ai, verbose=False, params=params) == winner:
            records = mb.records
            mb.restart()
            for x, y in records:
                mb.move(x, y)
                print(mb)
            break

下記 のプログラムで、上記の修正 を行っても show_progress が 正しく動作 することが 確認 できます。なお、実行結果は先ほどと同様なので省略します。

show_progress(ai=[ai2, ai11s], winner=Marubatsu.CIRCLE)

長くなりましたので、ai2 VS ai11s の検証は次回の記事で行うことにします。

今回の記事のまとめ

今回の記事では、弱解決 と 弱解決の AI の 定義 と 性質 を説明し、〇×ゲーム のように、局面の数 が 少ないゲーム では、ランダムな AI と 十分な回数の対戦 を行うことで、AI が 弱解決の AI であるか どうかを 判定できる ことを 示しました。

また、いくつかの関数 を、使いやすいように 修正 し、ai2 VS ai11s で ai11s が 敗北 する 試合経過 を表示しました。

本記事で入力したプログラム

以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。

以下のリンクは、今回の記事で更新した marubatsu.py です。

以下のリンクは、今回の記事で更新した ai.py です。

次回の記事

  1. 以前の記事で説明したように、この中で 最も局面の数 が 少ないオセロ でも、局面の数は $10^{28}$ 以上ある と 言われています ↩

  2. 本記事の説明 は、元の定義 を 少し意訳 しています。原文の定義 を知りたい方は、http://fragrieu.free.fr/SearchingForSolutions.pdf の 8 ページ を見て下さい ↩

  3. 具体例 を知りたい方は、https://www.jstage.jst.go.jp/article/sugaku/65/1/65_0651093/_pdf/-char/ja の 96 ページ を見て下さい ↩

  4. 必敗の局面 では、すべての合法手 が 最善手 です ↩

  5. 「目的 として 作られた」という 表現 になっているのは、将棋 も 囲碁 も、現時点 では 弱解決 も 強解決 も されていない からです ↩

  6. 局面の種類 の 数 が 5478 であることは、探索型の AI の 説明の際 に 示します ↩

2
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?