Pythonで〇×ゲームのAIを一から作成する その58 最強の AI と最善手の定義とその性質

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

ルール	アルゴリズム
ルール1	左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する
ルール2	ランダム なマスに 着手 する
ルール3	真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール4	真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール5	勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する
ルール6	勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール6改	勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール7	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール7改	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール8	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する
ルール9	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する
ルール10	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 2 つを 総合的に判断 して着手を行う 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う そうでない場合は ランダム なマスに 着手 する
ルール11	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う 相手 が 不利になる ように、「自 0 敵 1 空 2」が 最も少ない 着手を行う そうでない場合は ランダム なマスに 着手 する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1 ai1s	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2 ai2s	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3 ai3s	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4 ai4s	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5 ai5s	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
ai6	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
ai6s	88.6	1.9	9.5	69.4	9.1	21.5	79.0	5.5	15.5
ai7 ai7s	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
ai8s	98.2	0.1	1.6	89.4	2.5	8.1	93.8	1.3	4.9
ai9s	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6
ai10s	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
ai11s	98.1	0.0	1.9	82.5	1.9	15.6	90.3	1.0	8.7	あり

前回の記事のおさらい

前回の記事では、ai10s VS ai11s で、ai11s が × を担当 した際に、ai11s が 50 % の 確率 で 負けてしまう という 問題を修正 するために、下記 の表のように パラメータ の 修正 を行いました。

	修正前	修正後
「自 2 敵 0 空 1」が 1 つの場合の評価値	1	2
「自 1 敵 0 空 2」が 1 つあたりの評価値	1	1
「自 0 敵 1 空 2」が 1 つあたりの評価値	-1	-1

下記は、パラメータ の 修正前 と 修正後 の ai11s VS ai10s の 対戦結果 の表です。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
修正前	22.2	0.0	77.8	0.0	50.5	49.5	11.1	25.3	63.6
修正後	0.0	0.0	100.0	0.0	0.0	100.0	0.0	0.0	100.0

修正結果 からわかるように、ai11s が × を担当 した際に 負けなく なりましたが、今度は、〇 を担当 した際に、勝てなくなる という 新しい問題 が 発生 しました。

パラメータの修正の影響の検証

新しい問題 が 発生 した 原因 は、ai11s の パラメータ の 修正 が、ai10s VS ai11s の 4 手目 の局面 のみ を 考慮 して 行われた からです。そのため、4 手目 の 局面 に対しては、想定通りの処理 が行われますが、それ以外 の 局面 では、この修正 によって AI が 弱くなる ような 変化 が起きている 可能性 が 生じます。

別の言葉で説明すると、何らかの 問題を解決 する際に、特定の状況のみ を 考慮 に入れて 解決 するという、局所的 な 解決 を行うと、考慮していない状況 で 別の問題 を 引き起こし てしまう 場合がある ということです。

このようなことは、現実世界 でも よくあります。例えば、成績を向上 させるために、毎日 2 時間勉強する という 行動 は、健康である という 条件 を満たしていれば 有効 でしょう。しかし、病気になった時 に無理して 2 時間勉強 を行うと、病気が悪化して治りが遅くなり、成績 が 逆に下がってしまう ことになるでしょう。

修正前と修正後の ai11s VS ai10s の検証

上記 のようなことが 起きた こと 確認 するために、パラメータの修正 が、ai11s VS ai10s の 対戦結果 に、どのような影響 を 与えたか について 検証 することにします。

これまでと 同様の手順 で、ai11s VS ai10s の 検証 を行うことができますが、検証の作業 は 前回の記事 と ほとんど変わらない ので、検証結果 の図 だけ を 示す ことにします。興味と余裕がある方は、これまでと同様の方法で実際に検証してみて下さい。

修正前の ai11s VS ai10s の検証結果

修正前 の ai11s VS ai10s では、下図 のような 着手 が行われます。赤字 が ai11s の 勝利 につながる 着手の選択 を表します。

この表から、修正前 の ai11s は 3 手目 で下記の 2 種類 の 着手を行う ことが分かります。

• 33 % の 確率 で (2, 2) を 選択 する
  • その場合は、その次 の 4 手目 で ai10s は、66 % の 確率 で ai11s の勝利 につながる 着手 を、33 % の 確率 で 引き分け につながる 着手 を行う
• 67 % の 確率 で 引き分け につながる (2, 0) の 着手 を 選択 する

上記 から、ai11s が 勝利 する 確率 は、0.33 * 0.66 = 約 21.8 % であると 計算 できます。これは、実際 の 対戦結果 の ai11s の 勝率 である 約 22 % とほぼ 一致 します。

修正後の ai11s VS ai10s の検証

修正後 の ai11s VS ai10s では、下図 のような 着手 が行われます。

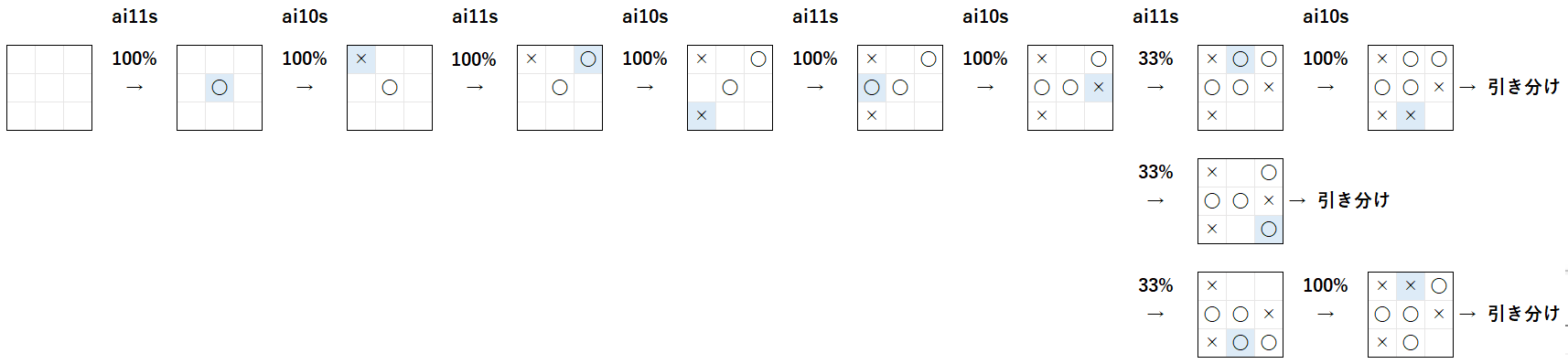
修正後 の ai11s は、修正前と異なり、3 手目 で (2, 0) の 着手 しか 選択 しないので 必ず引き分け になります。なお、3 手目 で (2, 0) の 着手 が 行われた後 の ai10s と ai11s が 選択 する 着手 は、修正前 と 修正後 で 完全に同じ です。

検証結果からの考察

上記 から、ai11s の パラメータ を 修正 することで、実際 に ai11s VS ai10s で、ai11s が 3 手目 に 選択 する 着手 が 変化する ことが 確認 できました。また、その 変化 が起きた 結果、ai11s の 勝率 が 約 22 % から 0 % に 減ってしまう ことが わかりました。

ただし、勝率が減る ことが必ずしも 悪いこと であるとは 限りません。その 理由 を 理解 するためには、最強の AI の 定義 と 性質 を 明確 にする 必要 があります。

最強の AI と最善手の定義と性質

本記事 の 目的 は、〇×ゲーム の 強い AI、すなわち 最強の AI を作る事です。しかし、これまでの記事 では、この 強い AI や 最強の AI がどのようなものを指すかについて、明確な定義 を 行ってきません でした。その理由は、AI を 作成 した 体験がない 人に対してその定義を示してもあまり 実感がわかない のではないかと 思ったから です。

ここまでの記事で、様々な AI を作成し、対戦させてきたことで、AI が どのようなルール で 着手 を 選択 するかがある程度は わかってきた のではないかと思いますので、この機会に、強い AI や 最強の AI がどのようなものであるかについて 定義を行う ことにします。

強いとは何か

一般用語 としての「強い」には、様々な意味 があり、「強い」という 用語 をどのような 意味 でとらえているかは、人 や 状況 によって 異なる でしょう。

例えば、卓球などの 個人戦 の スポーツ選手 に対する 強い という 用語 は、下記のような 様々な意味 で 使われます。もちろん、下記以外にも様々な使われ方があるでしょう。

• 試合 の 勝率が高い
• 世界ランキング が 高い
• 大きな大会 で 優勝 した 実績 がある
• 怪我をせず、年間を通じて活躍 する
• 負けてもスランプに陥いらないという、強い精神力を持つ

「強い」という 用語 が あいまい なままでは、強い AI という 表現 をしても、どのように強いか が 明確 では ありません。また、「強い」という 用語 が あいまい なままでは、最も強いという意味を持つ、最強の AI の 意味 も 明確 では ありません。

ゲームの性質の制限

本記事 は、〇×ゲーム の AI の 強さ を考えているので、ゲームの AI の 強さ を 定義 します。ただし、世の中の あらゆるゲーム の 強さを定義 する事は 簡単 なことでは ありません。その理由は、ゲームの性質 によっても、強い という 用語の意味 が 変わる からです。

例えば、〇×ゲーム のような、運の要素がない ゲームと、じゃんけん のような 運の要素がある ゲームでは、「強い」という 意味が異なる でしょう。運の要素がない ゲームは、完全 に 実力勝負 になるので、単純に 勝った方が強い ということができます。しかし、じゃんけんのような 運の要素がある ゲームは、100 % 勝つ ということは 不可能 なので、1 つの試合 の 勝敗だけ を見て どちらが強いか を 測る ことは できません。

そこで、本記事 では、話を簡単にする ために、試合の結果 が 完全 に 実力によって決まる という 性質 がある、「二人零和有限確定完全情報ゲーム」という 分類 の ゲーム の 強さ を 定義 することにします。なお、この用語 は 難しそうに見える かもしれませんが、その 意味 はそれほど 難しくはない ので安心して下さい。

「二人零和有限確定完全情報ゲーム」とは、下記 のような 性質 を持つ ゲーム です。

• 二人：文字通り、二人で遊ぶゲーム という性質
• 零和：プレイヤー の 利害 が 完全に対立する という性質。例えば、片方 が 勝てば、もう片方 が 負ける という 性質 を持ち、両方 が 同時に勝利 することは ない。二人の 利害の合計（和）が 零になる ことから、零和 と呼ぶ
• 有限：合法手 が 有限 であり、ゲームが 有限の手番 で 必ず終了する という性質。合法手 が 無限 にあったり、永遠 に 決着がつかない ようなゲーム ではない
• 確定：サイコロのような、ランダムな要素 が 存在しない という性質。着手 による 局面の変化 が 確定 する 性質 を持つゲーム
• 完全情報：ゲームの すべての情報 が 公開されている という性質

この分類 の ゲーム には、本記事が題材とする、〇×ゲーム をはじめ、将棋、チェス、オセロ¹など、数多くのゲーム があり、AI の研究 の 初期の頃 から 研究が行われてきました。

一般的 に、問題を解く際 に、このように 条件 を 限定 することで、問題 を 簡単にする ことができます。例えば、完全情報 という 性質 を 加える ことで、公開されていない情報 を 推測 する 必要 が なくなる ので、問題が簡単 になります。本記事 では、以後は、二人零和有限確定完全情報ゲーム という 条件を満たすゲーム について 説明 することにします。

この 条件を満たさないゲーム に関しては、本記事 の この後の説明 の 一部 が 当てはまらない 場合がある点に 注意 して下さい。例えば、麻雀 や、手札を明かさないトランプ のゲームは、見えない情報 が 存在する ので 完全情報 の性質を 満たしません。また、じゃんけん は、ランダムな要素 は ない ので 確定 の性質は 満たします が、自分 が 手を出す際 に、相手 が 出す手 が 見えていない ので 完全情報 の性質を 満たしません。従って、二人のプレイヤーが 同時に着手 を行うような ゲーム は、完全情報 の性質を 満たしません。

参考までに、二人零和有限確定完全情報ゲーム の Wikipedia のリンクを下記に示します。

二人零和有限確定完全情報ゲームの性質

二人零和有限確定完全情報ゲーム には、下記 の 性質 があります。なお、説明 が かなり長くなる ので、それぞれについての 厳密な証明 は 省略 しますが、〇×ゲーム に関しては、探索型の AI を 説明 する際に、実際 に 下記の性質を持つ ことを 示す 予定です。

• 原理的にはすべての局面を列挙可能
  有限 という 性質 から、原理的 には、その ゲーム の すべての局面 を 列挙可能 です。ただし、原理的 には 可能であっても、オセロ、将棋、囲碁 など、多くのゲーム では、局面の数 が 多すぎて、現実的 には すべての局面 を 列挙 することは 不可能 です。

オセロ の 局面の数 は 約 $10^{28}$、将棋 の 局面の数² は 約 $10^{69}$、囲碁 の 局面の数³ は 約 $10^{171}$ であると 言われています。オセロ の場合は、1 秒間 に 1 億 の 局面 を 列挙できた としても、すべての局面 を 列挙 するためには 1 兆年以上 かかります。

• 原理的には完全攻略が可能
  すべての局面 を 列挙 することが できれば、その ゲーム の すべての知識 を 得ることができる ということなので、原理的 にはその ゲーム の 完全攻略 が 可能⁴ です。将棋 や 囲碁 は、局面の数 が 多すぎて、現実的 には 完全攻略 は 不可能 ですが、〇×ゲーム の場合は、局面の数 は 5478 で、同一局面 を 1 つの局面 と みなした 場合は 850 しかありません。そのため、人間 であっても十分に 完全攻略 が 可能 な ゲーム です。

• すべての局面に最善手が存在する
  完全攻略ができる ということは、すべての局面 で、自分にとって 最も有利 となる 合法手 が 存在する ということです。そのような合法手 の事を 最善手 と呼びます。なお、すべての局面 に 最善手 が 存在 することは 間違いありません が、 多くのゲーム では、局面の数 が 多すぎる ため、一部の局面 でしか 最善手 を 見つける ことは できません。

現実の世界 にも、存在する ことと、見つける方法 が わかっていても、現実的 に、はそれを 見つけること が ほぼ不可能 なものが あります。例えば、現時点 で 世界 で 最も体重が重い 人は 必ず存在 します。また、全世界の人 の 体重 を 今すぐ に 同時に測って比較 することで、原理的 には その人を 見つける ことは 可能 です。しかし、現実的 には そのようなこと を 行う のは 不可能 でしょう。

最強の AI の定義

AI の 強さ を いきなり定義 する事は 困難 なので、最初に 定義しやすい、最強の AI を 定義 し、その後で 強い AI を 定義 する事にします。

本記事 では、上記の性質 を元に、二人零和有限確定完全情報ゲーム における、最強の AI を、下記 のように 定義 する事にします。「自分にとって 最も有利 になる 合法手」という、最善手 の 意味 を考えれば、あたりまえ の 定義 と言えるでしょう。

二人零和有限確定完全情報ゲーム における、最強の AI とは、すべての局面 で、最善手 を 選択する AI のことである。

従って、二人零和有限確定完全情報ゲーム の 最強の AI を作るということは、すべての局面 での、最善手を見つける ということを 意味 します。また、その 最善手 は、今後の記事 で 説明 する 探索型の AI を 作成 することによって、原理的 には みつける ことが 可能 です。

ただし、将棋 や 囲碁 などの、局面の数 が 多すぎる ゲームの 場合 は、現実的 には 探索型の AI で 最善手 を 見つける ことは 不可能 です。

二人零和有限確定完全情報ゲーム は、原理的 には すべての局面 での、最善手を見つける ことが 可能 だが、多くのゲーム では、局面の数 が 多すぎる ため、現実的 には 最強の AI を 作成 することは 不可能 である。

従って、多くのゲーム では、本記事でこれまでに行ってきた ルールベースなど の、様々な方法 を 組み合わせて、最強の AI に 近い強さ を持つ AI の作成 を 目指します。

弱点の局面の定義

最強ではない AI は、必ず いずれかの局面 で、最善手以外 の 合法手 を 選択 します。最善手以外 の 着手 を行うと、状況が悪化 することになるので、本記事 では そのような局面 のことを、AI の 弱点の局面 と 表記 することにします。

最強の AI どうしの対戦

二人零和有限確定完全情報ゲーム には、ランダム性 が 存在しない ので、局面 ごとに、お互い が 最善手 を 指し続けた場合 の 結果 が 決まっています。つまり、最強の AI どうしが 対戦 した場合、局面 ごとに、勝敗 の 結果 は 決まっている ということです。

〇×ゲーム のように、ゲームの結果 が、勝利、敗北、引き分け の 3 種類 に 分類 される場合、すべての局面 は、その局面 から 最強の AI どうしが 対戦した結果 によって、下記 の 3 つに分類 することができます。以後 は、必要に応じて 〇×ゲームの局面 を、下記 の 局面の分類 で 表記 することにします。

局面の分類	対戦結果
〇 の必勝の局面	〇 が 勝利する
× の必勝の局面	× が 勝利する
引き分けの局面5	引き分け

なお、上記の 必勝 とは、最強の AI どうし が 対戦 した場合の 結果 を表します。どのような AI が その局面 から 対戦 しても 必ず勝つ という 意味ではない 点に 注意 して下さい。

「〇 の必勝 の 局面」という、実際 に 良く使われる表現 には、「最強の AI どうし が 対戦 した 場合 は」という 主語 が 省略されている と考えて下さい。

すべての局面 で、最強の AI どうし が 対戦 した場合の 結果 が 決まっている ということは、ゲーム開始時 の 局面 でも 結果 が 決まっている ということです。

二人零和有限確定完全情報ゲーム の 性質 を持つ ゲーム は、ゲーム が 始まった時点 で、既に 最強の AI どうしが 対戦 した場合の 結果が決まっている。

また、一般的 に、ゲーム開始時 の 局面の状況 を使って、その ゲーム を「〇 の必勝 の ゲーム」や「必ず引き分け になる ゲーム」のように 呼ぶ。

〇×ゲーム は、最初の局面 が 引き分けの局面 であることが わかっている ので、〇×ゲーム は（最強の AI どうし が 対戦 した場合は）必ず引き分け になる ゲーム です。従って、最強の AI どうしが 対戦 した場合は、〇 を担当 しても × 担当し ても 引き分け になります。

本記事では扱いませんが、ゲームによっては 引き分け が 無かったり、勝利 と 敗北 だけでなく、お互いの点数差 などが 重要になる 場合があります。例えば、サッカーのワールドカップの総当たり戦では、同じ成績の場合 は、得失点差 が 多いほう が 優勝 します。そのような場合でも、基本となる考え方 は 大きく変わりません。

先後を入れ替えた場合

二人零和有限確定完全情報ゲーム は、完全情報 の性質から、二人のプレイヤー が、交互 に 着手 を行うので、ゲームの開始時 に どのプレイヤー が 着手を行う かが 決まっています。先に着手 を行う プレイヤー を 先手、後に着手 を行う プレイヤー を 後手 と 呼びます。

二人零和有限確定完全情報ゲーム は、先手の必勝 または、後手の必勝 の ゲーム である 場合が多い ので、多くの対戦 では 公平性 を考えて、先手 と 後手 を 入れ替えて、2 回対戦 し、総合成績 で 勝敗を決めます。ai_match でも そのような対戦 を行います。

下記は、ゲーム開始時 の それぞれ の 局面の状況 に対して、最強の AI どうし で、先後 を 入れ替え た 対戦結果 です。表から、いずれの場合 も 勝数 と 敗数 が 同じ になります。つまり、最強の AI どうし が 先後 を 入れ替えて戦う と、通算成績 は 引き分け になります。これは、同じ強さ の AI どうし が 戦う と 引き分けになる という 直観通りの結果 です。

ゲーム開始時の状況	先手を担当	後手を担当	勝	負	分
先手必勝	勝利	敗北	1	1	0
引き分け	引き分け	引き分け	0	0	2
後手必勝	敗北	勝利	1	1	0

最強の AI のパラドックス

最強の AI の 定義 を行いましたが、皆さんが、一般的 に「最強」という 用語 を 思い浮かべた時 に、どのような存在 を 思い浮かべる でしょうか？おそらく、どのような大会 に 参加 した場合でも 優勝する ような 存在 を 思い浮かべる 人が 多いのではないか と思います。

しかし、実際 には、先程定義した 最強の AI は、どのような大会 でも 優勝できる とは 限りません。最強 であるのに 優勝できない場合がある というような、一見 すると 矛盾 しているように 見える が、実際 には 真実 であるような 性質 のことを パラドックス と呼びます。どのような場合に優勝できないことがあるかについて少し考えてみて下さい。

なお、誰でもすぐに思いつく例として、大会に 最強の AI が 複数参加 する場合があると思いますが、最強の AI が 1 つしか参加しない 場合でも、この パラドックスは起きます。

参考までに、辞書 の パラドックス の リンク を下記に示します。

パラドックスが起きる具体例

上記の パラドックス が起きる具体的な 大会のルール、ゲームの設定、参加する AI についてそれぞれ 説明 し、どのようにパラドックス が 起きるか について 説明 します。

大会のルール

この大会では、以下のルール で 優勝 する AI が 決まります。

• 総当たり（リーグ戦）で、すべての AI どうしの 組み合わせ で 対戦を行う
• 対戦 は、先手 と 後手 を 入れ替え て 1 回ずつ 行う
• 勝率 が 最も高い AI が 優勝 する

ゲームの設定

下記 は、ゲームの設定 を表す 図 で、図の中の 記号や図形 などの 意味 は 以下の通り です。なお、探索型 の AI の 説明 を 行う際 に 詳しく説明 しますが、このような、ゲームの全貌 を表す 図 のことを、ゲーム木 と呼びます。

• 図の 番号 が書かれている 正方形 が、局面 を表す
• 局面 1 が、ゲームの 開始時の局面 を表す
• 水色 の 正方形 が、先手 が 着手 を行う 局面 を表す
• オレンジ色 の 正方形 が、後手 が 着手 を行う 局面 を表す
• 局面 から 右に伸びる線 は、その 局面 の 合法手 を表し、その 線の右 には、その 合法手 を 着手 した後の 局面 または、ゲームの 結果 を 表記 する
• 一番右 は、ゲームの 結果 を表し、青字 は 先手の勝利、黒字 は 引き分け を表す

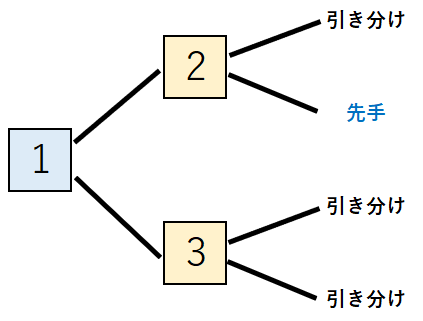
図からわかるように、このゲーム は、すべての局面 に対して、合法手 が 2 つずつ存在 し、先手 と 後手 が 1 回ずつ着手 を行うと ゲームが終了 します。

3 つの AI の設定

この大会には、3 つ の A、B、C という、すべての局面 で、ランダム な 着手 を 行わない（同じ局面 であれば、常に同じ合法手 を 選択 する）AI が参加します。

下図 は、それぞれの局面 で、それぞれの AI が 選択 する 合法手 を、線の色 で 表現 しています。例えば、最初の局面 である 局面 1 から は、赤い線 が 局面 3 に向かって 引かれている ので、A は 局面 1 で、着手すると 局面 3 になるような 合法手 を 選択 します。

3 つの AI の中で、A は 最強の AI です。その事を示します。

• 後手 の 手番 である 局面 2 は、着手を行う ことでゲームの 決着がつく ので、結果 から 明らか に図の 赤い線 の 合法手 が、後手（先手ではない 点に 注意 すること！）にとって 最も有利 になる。従って、局面 2 の 最善手 は 上の合法手 である

• 後手 の 手番 である 局面 3 は、どちら の 合法手 を 選択 しても 引き分け になる。従って、局面 3 では どちら の 合法手 も 最善手 である

• 先手 の 手番 である 局面 1 で、上の合法手 を 選択 した場合は、局面 2 になり、局面 2 で 後手 が 最善手 を 選択 すると 引き分け になる。下の合法手 を 選択 した場合は、局面 3 になり、局面 3 で 後手 が 最善手 を 選択 すると 引き分け になる。従って、局面 1 では どちら の 合法手 も 最善手 である

下記は、それぞれの 局面 の 最善手 と、それぞれの AI が 選択 する 合法手 を表します。なお、AI が 選択 する 合法手 が 最善手 の場合は、太字で表記 します。

	最善手	A	B	C	局面の状況
局面 1	上、下	下	上	下	引き分け
局面 2	上	上	下	下	引き分け
局面 3	上、下	上	上	下	引き分け

上記 から、A は、すべての局面 で 最善手を選択 しているので、A は 最強の AI です。

一方、B と C は 局面 2 以外 の 局面 では 最善手 を 選択 しますが、弱点 となる 局面 2 で 最善手 を 選択しない ので、最強の AI では ありません。

なお、上記の表から、最初の局面 である 局面 1 は、引き分けの局面 なので、このゲーム は 最強の AI どうし が 対戦 すると 引き分けになる ことが分かります。

複数の最強の AI

上記の 局面 1、3 のように、合法手 の中に 複数 の 最善手 が 存在 する場合は、最善手の中 の、どの合法手 を 選択 しても 最強の AI であることは 変わりません。従って、このゲーム の 最強の AI は、下記の A、D、E、F の 4 種類 が 存在 します。

	最善手	A	D	E	F
局面 1	上、下	下	下	上	上
局面 2	上	上	上	上	上
局面 3	上、下	上	下	上	下

合法手の中 に 複数 の 最善手 が ある 場合は、最強の AI は 複数存在 する。

AI どうしの対戦結果

次に、A、B、C で 総当たり戦 を行うと、どのような 結果 になるかを 検証 します。

分かりやすいように、先程の図 を 再掲 します。

それぞれの AI は、上図 に 従って着手 を 選択 するので、それぞれ の 組み合わせ の 対戦結果 は、局面 1 から はじまり、それぞれ の 局面 で、それぞれの AI が 選択 する 合法手 を 下記 の 表 のように 辿っていく ことで、知る ことができます。

	経過	結果
A VS B	局面 1 → 局面 3 → 引き分け	引き分け
B VS A	局面 1 → 局面 2 → 引き分け	引き分け
A VS C	局面 1 → 局面 3 → 引き分け	引き分け
C VS A	局面 1 → 局面 3 → 引き分け	引き分け
B VS C	局面 1 → 局面 2 → 先手の勝利	B の勝利
C VS B	局面 1 → 局面 3 → 引き分け	引き分け

下記は、上記の結果 を 総当たりの表 にしたものです。表の 記号 は、〇 が 勝利、△ が 引き分け、× が 敗北 を表します。

	A	B	C	勝	敗	分	勝率
A		△△	△△	0	0	4	0 %
B	△△		〇△	1	0	3	100 %
C	△△	×△		0	1	3	0 %

表から、B の勝率 が 100 % で 最も高い ので、B が優勝 することがわかります。なぜ、最強の AI ではない、B が優勝 することになったかについて、少し考えてみて下さい。

最善手の意味とパラドックスが起きる理由

先程、「自分にとって 最も有利 となる 合法手」のことを 最善手 と 説明 しましたが、この説明は 正確 では ありません。最善手 とは、正確 には、「お互い が 最善手 を 選択し続けた場合 に、自分にとって 最も有利 となる 合法手」のことです。

最善手 とは、お互い が 最善手 を 選択し続けた 場合に、自分 にとって 最も有利 となる 合法手 のことである。

つまり、相手 が 最善手 を 選択しない 場合は、自分にとって 最も有利 になるとは 限らない ということです。そのことを、具体例を挙げて説明します。

総当たり戦で、B が 優勝 する 理由 は、最強の AI である A が先手で C と 対戦 した際に 引き分け になるのに対し、最強ではない B が先手で C と 対戦 した際に B の勝利 になるという、一見 すると おかしい ように 見える ことが起きているからです。そこで、A VS B、A VS C、B VS C の 対戦 を 検証 してみることにします。

なお、A は 最強の AI なので、すべての局面 で 最善手 を 選択 します。そのため、以下の説明 では、A の 手番 で行われる 合法手の選択 の 説明 は 省略 します。

A VS B と A VS C の検証

下記は、A VS B と A VS C の 対戦の経緯 を表す表です。

	経緯
A VS B	「局面 1（A の手番） → 局面 3（B の手番） → 引き分け」
A VS C	「局面 1（A の手番） → 局面 3（C の手番） → 引き分け」

上記から、いずれも 同じ経緯 で 引き分け になることがわかります。A VS B の 経緯 の中で B が 着手 を 選択 するのは 局面 3 で、B は 下記 の 表 からわかるように 局面 3 で 最善手 を 選択 します。これは、A VS C の場合でも 同様 です。

	最善手	A	B	C	局面の状況
局面 1	上、下	下	上	下	引き分け
局面 2	下	上	下	下	引き分け
局面 3	上、下	上	上	下	引き分け

また、上記 の 表 から、局面 2 は、B と C はの 弱点の局面 ですが、上記の経緯 では、局面 2 は 出現しません。このことから、最強 ではない AI であっても、対戦の中 で 弱点の局面 が 生じなければ、相手は すべての着手 で 最善手 を 選択 することが わかります。

別の言葉 で説明すると、最強ではない AI には、必ず どこかに 弱点があります が、相手 がその 弱点を突く ことが できなければ、最強の AI と 互角の戦いができる ということです。

最強ではない AI でも、弱点 を 突かれなけれ ば（最善手 を 選択しない、弱点の局面 が 生じなければ）、最強の AI と 互角に戦う ことが できる。

このようなことは 現実の世界 でも よくある 事です。例えば、あるスポーツで、以下 のような 2 つのチーム が存在する場合、一般的 には チーム A のほうが チーム B より も 強い と 評価されます。実際 に 一年を通じて試合を行う と、チーム A は チーム B に 勝ち越す可能性が高い でしょう。しかし、チーム B の 弱点 となる 夏以外 で、試合を行う と、チーム B は チーム A と 互角に戦う ことが できます。

	特徴
チーム A	一年中 を通じて 強い
チーム B	暑さが苦手 なので 夏は弱い が、夏以外 は チーム A と 互角

B VS A や C VS A などの 試合結果 が 引き分け になる 理由 も、上記 と 同様 に、B や C の 手番 で、B や C の 弱点の局面 が 生じない からです。B VS A では、B の 弱点 の 局面 2 が 生じる と 思った人 が いるかもしれません が、その場合 の 局面 2 は A の手番 です。

B VS C の検証

B VS C は「局面 1（B の手番） → 局面 2（C の手番） → 引き分け」という 経緯 で B の勝利 になりますが、この中で C が 着手 を 選択 する 局面 2 は、下記 の 表 からわかるように C の 弱点の局面 なので、C は 最善手 を 選択しません。

	最善手	A	B	C	局面の状況
局面 1	上、下	下	上	下	引き分け
局面 2	下	上	下	下	引き分け
局面 3	上、下	上	上	下	引き分け

このことから、B VS C で B が勝利 する 理由 は、C の 弱点の局面 である 局面 2 が 生じる ような 最善手 を B が選択 したからであることがわかります。

検証結果からわかる事

上記の 検証結果 から、以下 の事が わかります。

• 最強の AI であっても、相手 の 弱点を突く ことが できなければ（弱点の局面 が 生じなければ）、ゲーム開始時 の 局面の状況 よりも 良い結果になる ことは ない。
• 最強ではない の AI であっても、相手 の 弱点を突く ことが できる（弱点の局面 が 生じる）場合は、ゲーム開始時 の 局面の状況 よりも 良い結果になる 場合が ある。

上記を 別の言葉 で説明すると、AI どうし の 対戦結果 は、最強 であるかどうかには 関係なく、お互いの 弱点を突く ことが できるか どうかによって 決まる ということです。

下記 は、検証結果 からわかったことを 一般化 した 説明 です。

X、Y、Z の 3 つの AI の間で 対戦 を行った場合に、X VS Y の 結果 が、X VS Z の 結果よりも良い 場合でも、X のほうが Y より強い とは 限らない。

また、上記を 別の言葉 で 説明 すると、以下のようになります。

2 つの AI の 強さを比較 するために、それぞれの 別の AI との 対戦結果 を 比較 しても、うまく比較できる とは 限らない。

最強ではない B が 優勝できた理由 は、A は C の 弱点 を つけなかった が、B は C の 弱点 を 突くこと が できたから であることが わかりました。ただし、だからといって、最強の AI に 価値がない わけでは ありません。次は、そのことを説明します。

一般的な意味の「最善」と「最善手」の意味の違い

一般用語 としての「最善」が「最も良い」という 意味を表す ことから、最善手 を 選択 し続けることで、最も良い結果 である 勝利することができる のように 勘違する人 が いるかもしれません が、上記の検証 からそれは 間違い であることがわかります。

実際 には ゲーム の 最善手 は、一般的なイメージ の 最善 とは 異なり、以下 のような 意味を持つ 点に 注意 して下さい。

• 最善手 を 選択 することで、現在の局面 の 状態 を 維持する。つまり、最善手 を 選択 しても、局面の状況 が 改善することはない
• 最善手以外 を 選択 した場合は、局面の状況 が 悪化 する
• 従って、局面 の 状況が改善 されるのは、相手 が 最善手以外 を 選択した場合 である

上記で、最善手 を 選択しない 場合は 局面の状況が悪化 すると 説明 しましたが、状況の悪化 には 種類 が あります。例えば、〇×ゲーム のように、必勝、引き分け、必敗 という、3 種類 の 局面の状況 がある場合は、局面の状況 の 悪化 には、「必勝 → 引き分け」、「必勝→必敗」、「引き分け→必敗」という 3 種類 があります。

状況 が 何段階悪化するか によって 分類 すると、下記の表 のようになります。この表は、局面の状況 で、それぞれに 分類される着手 を 行った場合 に、局面の状況 が どのように変化するか を表します。空欄 は 合法手 が 存在しない ことを表します。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗
必敗	必敗

表から、必敗 の 状況 では、すべての合法手 が 最善手 になることが分かります。必ず負ける の に、最善手 と呼ぶのは 変だと思うかもしれません が、最も良い結果になる ということは 事実 なので、この場合 も 最善手 と 呼びます。

最強の AI の性質

上記から、最強の AI は、どのような AI と 対戦 しても、最強の AI どうし が 対戦 した場合の 結果 と 同じか、それよりも 良い結果 になります。

従って、〇×ゲーム のように、勝利、敗北、引き分け の 3 種類 の 結果 がある ゲーム では、最強の AI は どのような AI と 対戦 しても、下記 のような 結果 になります。

局面の状況	結果
自分の必勝	必ず勝利 する
引き分け	引き分け または 勝利 する
相手の必勝	勝利、引き分け、敗北の すべての可能性がある

また、最強の AI と 最強ではない AI が 先後 を 入れ替えて対戦 した場合は、下記の表 のような 結果 になります。表からわかるように、どの場合 でも、最強の AI の 勝数 が 敗数以上 になるので、最低 でも 通算成績 は 引き分け以上 の 結果 になります。別の言い方 をすると 最強の AI は 通算成績 で 負けになる ことは 絶対にありません。

ゲーム開始時の状況	先手を担当	後手を担当	勝	負	分
先手必勝	勝利	敗北以上	1~2	0~1	0~1
引き分け	引き分け以上	引き分け以上	0~2	0	0~2
後手必勝	敗北以上	勝利	1~2	0~1	0~1

先手必勝 と 後手必勝 は、いずれも 勝利 が ある ので、勝数 は 1 以上 になります。引き分け の場合は、絶対に負けない ので、敗数 は 0 になります。

上記から、最強の AI には 下記 のような 性質がある事 が分かります。最強の AI は、必ず勝つ AI ではなく、絶対 に 局面の状況 を 悪化させない AI である点に 注意 して下さい。

最強の AI は、どのような AI と 対戦 しても、結果 が ゲーム開始時 の 局面の状況 よりも 悪くなる ことは ない。

先後 を 入れ替え て 対戦 を行った場合、最強の AI は、どのような AI と 戦っても、通算成績 は 引き分け以上 になる。すなわち、絶対 に 負けることはない。

__別の言葉__で 説明 すると、以下のようになります。

• 最強の AI は 最善手のみ を 選択 するので、局面の状況 が 悪化 することは ない
• 相手 が 最善手 を 選択するか どうかは、相手次第 なので、局面の状況 が 好転するか どうかは、相手次第（他力本願）である
• 従って、先手を担当 した場合に、先手必勝 のゲームでは、最強の AI は 必ず勝利 するが、そうでないゲーム の場合は 勝利するか どうかは、相手次第 である

一般的な意味の「最強」と「最強の AI」の違い

一般的 な 意味 での 最強 は、例えば 総当たり戦 などで 優勝 するような 意味 で 使われます。実際に、最強の AI は、先後 を 入れ替え て 対戦を行う 場合は、どのような AI と 戦っても、引き分け以上 になり、絶対 に 負けることはない ので、他の AI との 直接対決のみ で 優勝を決める ような 場合 は、他の AI と 同率で首位 になる 場合 は あるかも しれませんが、必ず優勝 します。従って、そのような意味 では 最強 であると 言える でしょう。

一方、総当たり戦 のように、直接対決以外 の 対戦結果 が 成績に反映 する 場合 は、最強の AI は 他の AI どうし の 対戦 に 影響を及ぼす ことが できないため、それらの対戦結果 によっては 優勝できない可能性 があります。現実の具体例として、最強のチーム が 優勝しないようにする ために、弱いチーム が 八百長 をして 特定のチームだけ を わざと勝たせる ようなことが行われた場合、最強のチーム であっても 優勝 することは 難しい でしょう。

最強の AI は、他の AI と 先後 を 入れ替え て 対戦 を行う場合は、絶対に負けない。

従って、直接対決のみ で 優勝を決める 場合は、最低 でも 同率 1 位 で 優勝できる という 意味 では 最強 である。

一方、直接対決 が 行われない試合がある 場合は、必ず優勝できる とは 限らない。

このように、最強の AI とは、一般的 な 最強 の イメージ と 異なり、絶対に優勝できる AI のこと ではない 点に 注意が必要 である。

複数の最強の AI の優劣

先程、このゲーム の 最強の AI は、下記の表のように、複数存在 することを 説明 しました。そのため、A 以外 の 別 の 最強の AI であれば、優勝できるのではないか と思った人がいるかもしれません。

	最善手	A	D	E	F
局面 1	上、下	下	下	上	上
局面 2	上	上	上	上	上
局面 3	上、下	上	下	上	下

実際に、局面 1 で、上の合法手 を 選択する、E と F の場合は、B と C の 弱点をつく ことが できる ので、下記の表 のような 結果 になり、優勝できます。

	E、F	B	C	勝	敗	分	勝率
E、F		〇△	〇△	2	0	2	100 %
B	×△		〇△	1	1	2	50 %
C	×△	×△		0	2	2	0 %

このことから、複数 の 最強の AI が 存在する 場合に、その中に 常に優劣が存在する と 思う人がいる かもしれませんが、そうではありません。必勝の局面でない 場合に、相手 に 勝てるか どうかは、相手 の 弱点をつくことができるか によって 変化 するからです。

具体例 を挙げて説明します。下図 のような 設定 の ゲーム では、それぞれ の 局面 の 最善手 は 以下の表 のようになります。先程 との 違い は、局面 3 で 下の合法手 を 選択 すると 先手が勝利 する点です。ただし、どの局面 の 状況 も 引き分け になる点は 同じ です。

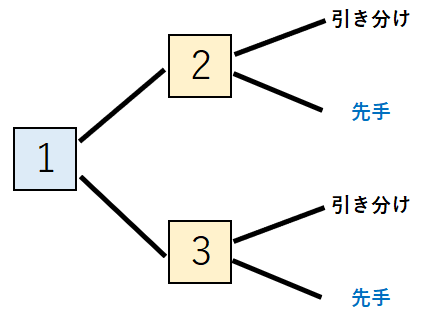
	最善手	局面の状況
局面 1	上、下	引き分け
局面 2	上	引き分け
局面 3	上	引き分け

このゲーム の 最強の AI は、下記の表の G と H の 2 種類 があります。また、下記の表や図 のような 選択 を行う、最強ではない、I と J という AI があるものとします。なお、I と J の違いは、弱点の局面 が I は 局面 2、J は 局面 3 である点です。

	最善手	G	H	I	J
局面 1	上、下	上	下	上	下
局面 2	上	上	上	下	上
局面 3	上	上	上	上	下

下記の表 は、G、H が、それぞれ I、J と 対戦 した場合の 結果 です。表からわかるように、G は I と 対戦 した場合は 勝利 しますが、 J と 対戦 した場合は 引き分け になります。一方、H はその 逆の結果 になります。

	I	J
G	G の勝利	引き分け
H	引き分け	H の勝利

このように、G と H は、それぞれ I と J の どちらかの弱点 しか つくことができない ので、G と H の 優劣 は、下記のように 状況によって異なる ことになります。

• I と 同様の弱点 を持つ AI が、J と 同様の弱点 を持つ AI よりも多い 場合は、G のほうが H より も 良い成績 になる
• I と 同様の弱点 を持つ AI が、J と 同様の弱点 を持つ AI よりも少ない 場合は、H のほうが G より も 良い成績 になる
• I と 同様の弱点 を持つ AI が、J と 同様の弱点 を持つ AI と同じ 場合は、G と H の 成績 は 同じ になる

最強の AI どうしの 優劣 は、それだけ で 決めることはできず、対戦相手 の 性質 によって 変化する。また、一般的 には、対戦相手 が 不明 の場合は、最強の AI どうし に 優劣はない と 考える 場合が 多い。

現実の世界 でも、同じくらい の 強さ を持つと考えられている ゲームの戦法 が 複数 あった場合でも、何も考えず に 戦法を選ぶ ことはあまり しない でしょう。一般的 には 対戦相手 の 苦手な戦法 を 分析 して 戦法を選択 するはずです。ただし、相手 の事が 全く分からない場合 は、ランダム に 戦法を選択 するしかないでしょう。

ランダムな着手を行う AI の場合

ここまでは、話を簡単にするために、ランダム な 着手 を 行わない 場合の AI の 性質 について 説明 しました。一方、これまでに作成 してきた ai11s などの AI では、評価値 が 最大 の 合法手 の中から ランダム に 選択 を行う AI を作成 してきました。

ランダムな着手 を 考慮に入れた 場合は、最強の AI を 無限に作成 することが できます。例えば、ある局面に 最善手 が 2 つ存在 した場合に、ランダム に 最善手 を 選択 する 方法 は、最善手 1 を 選択する確率 を x %、最善手 2 を 選択する確率 を y % とした場合、$x + y = 100$ を 満たせば、どのような値 を 設定 しても 構わない ので、無限の組み合わせ があります。必ず最善手 を 選択 するという 条件 が 満たされて いれば、ランダムな着手 を行っても、これまでに説明 した 最強の AI の 性質を満たす ことに 変わりはありません。

最強でない AI の 場合 は、合法手の中 から、最善手 を 選択する確率 と、最善手でないもの を 選択する確率 によって、AI の強さ が 毎回変わります。従って、AI どうし で 対戦 した場合に、毎回結果 が 変わる 場合が生じるようになります。

なお、すべての局面 で 最善手 を 選択 する 可能性 が ある場合 でも、そうでない可能性がある 場合は、最強の AI とは みなされない 点に 注意 して下さい。例えば、すべての局面 で ランダム な 合法手 を 選択 する ai2 は、偶然すべて の 着手 で 最善手 を 選択する可能性 がありますが、ai2 を 最強の AI だと 考える人 はおそらく 誰もいない でしょう。

下記は、AI が ランダムな着手 を 行う 場合に、最強の AI と 最強でない AI が、先後 を 入れ替え て 複数回対戦 した場合の 結果 を表す表です。

		勝率	敗率	引分率
先手必勝	先手	100 %	0 %	0 %
	後手	0 ~ 100 %	0 ~ 100 %	0 ~ 100 %
	通算	50 ~ 100 %	0 ~ 50 %	0 ~ 50 %
引き分け	先手	0 ~ 100 %	0 %	0 ~ 100 %
	後手	0 ~ 100 %	0 %	0 ~ 100 %
	通算	0 ~ 100 %	0 %	0 ~ 100 %
後手必勝	先手	0 ~ 100 %	0 ~ 100 %	0 ~ 100 %
	後手	100 %	0 %	0 %
	通算	50 ~ 100 %	0 ~ 50 %	0 ~ 50 %

上記の表 から、ランダム性がある 場合も、ランダム性がない 場合と 同様 に、局面の状況 より 悪い結果になる ことは ない ため、ランダム性がない 場合と 同様の性質 があります。

ランダム に 着手を選択するか どうかに 関わらず 、下記の性質 がある。

最強の AI は、どのような AI と 対戦 しても、結果 が ゲーム開始時 の 局面の状況 よりも 悪くなる ことは ない。

先後 を 入れ替え て 対戦 を行った場合、最強の AI は、どのような AI と 戦っても、通算成績 は 引き分け以上 になる。すなわち、絶対 に 負けることはない。

逆に言えば、他の AI と 対戦 した 結果、上記の表 のように ならない 場合は、最強の AI ではない ということが わかります。

AI の修正による結果の解釈

下記は、先程の表 を、自分の視点 で まとめ直した ものです。

局面の状況	勝率	敗率	引分率
自分の必勝	100 %	0 %	0 %
引き分け	0 ~ 100 %	0 %	0 ~ 100 %
自分の必敗	0 ~ 100 %	0 ~ 100 %	0 ~ 100 %

この表から、最強の AI は 局面の状況 ごとに 下記 の 性質がある 事が 分かります。

自分の必勝の場合

自分の必勝 の局面では、最強の AI は 引き分け や 敗北 になることは ありません。従って、この状況の局面 で、自分の AI が 他の AI と 対戦 して 引き分け や 敗北 になった場合は、自分の AI に 何らかの弱点 が 存在する ことを 意味します。

必勝の局面 で、AI を修正 した 結果、敗率 や 引分率 が 悪化 した場合は、修正 によって 欠陥が増えて おり、AI が 弱く なっている 可能性が高い。

逆に、100 % 勝利 した 場合 でも、相手の AI に 弱点 がある 可能性がある ため、それだけ で 最強の AI であると 断言する ことは できない。

引き分けの場合

引き分け の局面では、最強の AI は、必ず引き分け になります。従って、この状況の局面 で、自分の AI が 他の AI と 対戦 して 敗北 した場合は、自分の AI に 何らかの弱点 が 存在する ことを 意味します。

逆に、この状況の局面 で、自分の AI が 他の AI と 対戦 して 勝利 した場合は、相手の AI に 何らかの弱点 が 存在する ことを 意味します。

引き分けの局面 で、AI を修正 した 結果、敗率 が 悪化 した場合は、修正 によって 欠陥が増えて おり、AI が 弱く なっている 可能性が高い。

勝率が変化 した場合は、相手の AI の 弱点が原因 なので、勝率が変化 しても、自分の AI の 強さが変化 したと 断言する ことは できない。

自分の必敗の場合

自分の必敗 の局面では、最強の AI は、必ず敗北 します。従って、この状況の局面 で、自分の AI が 他の AI と 対戦 して 引き分け や 勝利 した場合は、相手の AI に 何らかの弱点 が 存在する ことを 意味します。

必敗の局面 で、AI を修正 した 結果、勝率 や 引分率 が 変化 した場合は、相手の AI の 弱点が原因 なので、自分の AI の 強さが変化 したと 断言する ことは できない。

ai11s の場合

証明 は 今後の記事 で行いますが、〇×ゲーム の 最初の局面 は、引き分け の局面です。

そのため、下記の表 のように、修正前 と 修正後 の ai11s が 〇 を担当 して、ai10s と 対戦 した場合に、修正後 のほうが 勝率が低く なっても AI が 弱くなった と 断言 することは できません。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
修正前	22.2	0.0	77.8	0.0	50.5	49.5	11.1	25.3	63.6
修正後	0.0	0.0	100.0	0.0	0.0	100.0	0.0	0.0	100.0

一方、ai11s が × を担当 する場合は、引き分けの局面 であるにも関わらず、修正前 では 約 50 % の確率 で 敗北 します。これは、修正前 の ai11s が × を担当 する場合に、弱点が存在した こと表します。また、修正後 で 負けなくなっている ことから、修正 によって、× を担当 する場合は 弱点が解消 された結果 ai11s が 強くなった ことが分かります。

ai11s のパラメータの修正によっておきたことの検証

パラメータ の 修正 によって 勝利できなくなった原因 が 相手の弱点 のせいであることを 検証 することで、修正 によって 勝利できなくなった ことが 問題ではない ことを示します。

修正前の ai11s VS ai10s の検証

下記は、修正前 の ai11s VS ai10s で行われる 着手の選択 です。

図 から、ai11s が 勝利 するのは、3 手目 で ai11s が (2, 0) に 着手 した 場合 であることがわかります。また、その後 の 4 手目 の局面で ai10s が行う 選択 は 以下 のようになっていることがわかります。

• (1, 2) を 選択 した場合は ai11s が勝利 する
• (0, 2) を 選択 した場合は 引き分け になる
• (0, 1) を 選択 した場合は ai11s が勝利 する

上記から、4 手目 の 局面 では、(0, 2) を 選択 することが、ai10s にとって 最も有利 になるので、最善手 は (0, 2) であることが 分かります。しかし、ai10s は この局面 で 最善手以外 を 選択 する 可能性 があるので、この局面 は ai10s の 弱点の局面 です。

つまり、修正前 の ai11s が ai10s に 勝利できた のは、たまたま 相手の弱点 を つけていたから に 過ぎない ということです。

修正後の ai11s VS ai10s の検証

下記は、修正後 の ai11s VS ai10s で行われる 着手の選択 です。

図から、ai11s VS ai10s の 3 手目 では、(2, 0) のみが選択され、その結果 引き分けになる ことが 確認 できました。

3 手目の検証

上記から、3 手目 で (2, 2) を 選択 した場合は、相手 が 4 手目 で 最善手 を 選択 すると 引き分け になります。また、3 手目 で (0, 2) を 選択 した場合も 引き分け になります。従って、3 手目 の 局面 の 最善手 は、(2, 2) と (0, 2) の 両方 であることがわかります。

また、2 つの図 から、3 手目 で (2, 0) に 着手 を 行った後 の 局面 では、修正前 と 修正後 の ai11s は、全く同じ選択 を 行う ことが分かります。

従って、修正前 と 修正後 の ai11s の 違い は、3 手目 で行われる 選択のみ ですが、どちらも最善手 なので、修正前 と 修正後 の ai11s は、同じ強さ であることが分かります。

このことから、ai10s に 勝利できなくなった理由 は、AI が弱くなった から ではなく、相手の弱点 を つけなくなった からであるため、問題ではない ことが 確認 できました。

ai11s をさらに修正すべきか

ai11s の パラメータ を さらに修正 し、ai11s VS ai10s で ai11s が 勝利できるようにする ことは 可能かもしれません が、そのような修正 を 行う必要 は ない でしょう。

その 理由の 1 つ は、そのような 修正を行う ことで、別の局面 で 新しい問題 が 発生する可能性 があるからです。他の理由 としては、修正前 の ai11s が ai10s に 勝利できていた のは、ai10s の 弱点 を ついている に すぎない からです。頑張ってそのような 修正 を 行っても、その弱点がない AI と 対戦 した場合には 勝利できません。

本記事では、修正後 の ai11s に 問題がない ことが 確認できた ので、これ以上の修正 を ai11s に 行わない ことにします。

AI の強さを評価する方法

ここまでで、最強の AI の 強さ の 定義 と、性質 について 説明 しましたが、最強ではない AI どうしの 強さ は どのように評価する ことができるででしょうか。

AI の強さ は、様々な方法 で 評価 されます。本記事では、その中の いくつか の 方法 について説明しますが、本記事で紹介しない方法もあります。

最強の AI の定義と類似する方法

最強の AI と そうでない AI の 違い は、すべての局面 で 最善手 を 選択するか どうかでした。それと 同様の考え方 で、2 つ の X と Y という AI に、下記 のような 関係がある場合 に、X は Y より も 強い と 定義 することができます。

下記の条件 を すべて満たす 場合に、X は Yより も 強い AI である。

• すべての局面 で、X が選択 した着手を行った 後 の 局面の状況 が、Y が選択 した着手を行った 後 の 局面の状況 と 同じ か、良い状況 になる
• 1 つ以上 の 局面 で、X が選択 した着手を行った 後 の 局面の状況 が、Y が選択 した着手を行った 後 の 局面の状況より も 良い状況 になる

上記の条件 が満たされていれば、X と Y が 最強の AI と 対戦 した場合は、同じ結果 または、X のほうが Y より も 良い結果 になります。その 理由 は、以下の通りです。

• どのような局面 でも、X のほうが、Y より も 不利 な 局面の状況 になるような 合法手 を 選択 することは ない
• 相手 が 最強の AI の場合は、相手は 最善手のみ を 選択 するので、局面の状況 が 変化 することは ない

最強の AI と 対戦 した場合は、強い AI は、弱い AI と 同じ か、それよりも良い結果 になる。逆に言えば、強い AI の 結果 が 弱い AI の 結果より悪くなる ことは ない。

また、最強の AI の場合と 全く同じ理由 で、以下の事 が言えます。

最強でない AI と 対戦 した場合は、強い AI のほうが、弱い AI よりも 良い結果になる とは 限らない。

先程の定義 が わかりづらい と思った方は、下記 のような 例 を 思い浮かべる と良いでしょう。下記は、あるゲームの 3 人 のキャラクターの 能力値 です。

この中で 最強 のキャラクターは、すべて の 能力値 が 最も高い C です。

また、B の すべて の 能力値 は、A の能力値 以上 で、なおかつ 1 つ以上 の 能力値 が A より も 高い ので、B は A より も 強い といえます。同様 の理由で、C は B より も 強く、C は A より も 強い と言えます。

	HP	強さ	かしこさ
キャラクター A	10	5	20
キャラクター B	20	5	30
キャラクター C	30	15	50

この定義の方法の問題点

上記で 強い AI の定義 を行いましたが、実際 には この定義 は 多くの場合 で あまり 役に立ちません。その 理由 は、先程の例 の、下記の表 の I と J のように、異なる局面 で 片方 は 弱点ではない が、もう片方 が 弱点 であるような 場合 が 良くある からです。特に 局面 が 多くなれば なるほど、ほとんどの AI が どちらが強い かを 判定できなく なります。

	最善手	I	J
局面 1	上、下	上	下
局面 2	上	下	上
局面 3	上	上	下

上記の 問題点 から、この AI の強さ の 定義 は、採用しない ことにします。

なお、最強の AI の定義は、そのまま利用 します。

わかりづらい と思った方は、下記 の 例 を見て下さい。下記の場合では、キャラクターどうし の 強さの関係 を、先程の定義 で 決める ことは できません。また、最強 のキャラクターを 決める ことも できません。

	HP	強さ	かしこさ
キャラクター A	20	5	10
キャラクター B	10	20	5
キャラクター C	5	10	20

最善手の選択の割合を利用する方法

すべての局面 で 最善手 を 選択する という、最強の AI の 定義 から、ゲーム の すべての局面 の中で、AI が 最善手を選択 する 局面の割合 を 計算 して AI の 強さを評価する という 方法も 考えられますが、実際 には 下記の理由 で、多くの場合 は その方法 で AI の 強さを評価 することは 不可能 です。従って、本記事では この方法 も 採用しません。

• 多くのゲームでは、局面の数 が 多すぎる
• どの合法手 が 最善手 であるかが わからない局面 が 多い
• 局面 の 出現率 が 偏っている 場合は、正しく 強さを 評価できない。例えば ゲーム開始時 の 局面 は 100 % 出現 するが、ほとんど出現しない局面 もある

総当たり と 勝ち抜き戦 による方法

複数のもの の 順位を決める方法 として、 良く使われる のが 総当たり戦 と 勝ち抜き戦 ですが、今回の記事で説明したように、総当たり戦 を行っても、AI どうし の 相性の問題 から、強い AI が 優勝する とは 限りません し、勝ち抜き（トーナメント）戦 では 限られた組み合わせ でしか 対戦 が 行われない という 問題 があり、運よく苦手な相手 が 対戦する前 に 負けてしまった ために 弱い AI が 優勝してしまう場合 が あります。

ただし、AI どうし の 相性の問題 は、多様な AI を 数多く用意 することで、ほとんど 問題 には ならなくなります。その 理由 は、相性の問題 は、一般的 に 特定の AI どうし で 発生する からです。多様な AI を 数多く用意 すれば、そのような問題 は 全体の中 の 一部 として 埋もれてしまい、全体の結果 に ほとんど影響 を 与えなくなる からです。従って、総当たり戦 は、実際 に 順位 を 決める方法 として 良く使われています。

また、その際に、同じくらいの強さ の AI を集めて 対戦を行うのが 一般的 です。現実の世界 でも、例えば サッカー の場合は、J1、J2、J3 のように、同じレベル の チーム を 集めて 総当たり戦を行い、優勝チーム を 決めています。

総当たり戦 は、参加者 の 2 乗 に 比例 した 回数 の 対戦 を行う 必要 があるという 欠点 があるため、参加者 が 非常に多い場合 には 向いていません 。そのような場合 は、参加者 をいくつかの ブロック にわけて 総当たり戦 を行い、各ブロック の 上位者 で 総当たり戦 や 勝ち抜き戦 で 順位を決める 方法が良く 用いられます。

高校野球のように、数千 の 参加者 がいる場合は、勝ち抜き戦だけ で 順位を決める 場合がありますが、勝ち抜き戦 の場合は、優勝するため には 実力以外 にも 運が必要でしょう。

レーティングによる強さの定義

AI など の 強さを測る方法 を レーティング と呼び、総当たり戦 や 勝ち抜き戦以外 にも 様々な方法 があります。その中で、数学的な裏付けがある 有名な方法として、イロレーティング があり、サッカー の FIFA ランキング など、多くの競技 で 利用 されています。

参考までに、イロレーティング の Wikipedia のリンクを示します。

将棋の AI の場合は、コンピュータ将棋連続対局場所 (floodgate) という、自作 の 将棋の AI どうし を 対戦 させる 場 があり、日々 AI どうしの対戦 が 行われています。floodgate では、AI の強さ を、先ほど説明した イロレーティング で 計測 しており、かなりの精度 で、AI の強さ を 測ることができます。

参加者が少ない場合の問題点

強さの評価 を行う際に、参加者 の 数が少ない と、どのような方法でも __強さ__を 正確に評価 することは 困難 です。参加者 が 少ない とどうしても 相性の問題 が 発生しやすかったり、集めた 参加者 が 弱すぎたり、偏ってていたり した場合などでは、そこで 1 位 に なったとしても、本当に強いか どうかが 分からないから です。

井の中の蛙 という ことわざ があるように、地方の大会 で 優勝 した人が、全国の大会 に参加した結果、ぼろ負け してしまうことは よくある ことです。

残念ながら、本記事のように、一人 で AI を作成 する場合は、多様な AI を 数多く集めて対戦 させることは 難しい ので、代わりに 基準 となる ai2 と、それまでに作成 した 最も強い AI と 対戦 させることで、AI の強さ を 測定しています。

なお、イロレーティング は、数多く の 参加者の間 で 多種多様な対戦 を行う 必要がある ので、一人で AI を作成 する場合の 〇×ゲーム の 強さの測定 には全く 向いていません。

パラドックスの例の補足

以下は、おまけの内容 なので、興味がない方 は 読み飛ばして も 構いません。

実は、今回の記事 の パラドックスの例 で説明した 下図 の ゲームの例 は、修正前 の ai11s VS ai10s を 元に して 作ったもの です。また、パラドックスの例の A、B、C という AI は、ai10s、修正前 と 修正後 の ai11s を 元に作った ものです。

局面の対応

下記は、上図 の ゲームの局面 と、修正前 の ai11s VS ai10s の 局面 の 対応 を表します。

上図のゲーム	局面 1	局面 2	局面 3
ai11s VS ai10s	3 手目の局面	3 手目で (2, 2) に 着手した局面	3 手目で (0, 2) に 着手した局面
類似点	どちらの合法手も 最善手である	引き分けと先手の 勝利になる	引き分けになる

下図 は パラドックスの例 の ゲームの局面 の図と、修正前 の ai11s VS ai10s の 着手の図 を 簡略化 した図を並べたものです。見比べる ことで、両者 が 同じ構造 を 持っている ことが わかる のではないかと思います。

AI の対応

下図は A、B、C と、ai10s、修正前 と 修正後 の ai11s の対応表です。

上図のゲーム	A	B	C
ai11s VS ai10s	修正後の ai11s	修正前の ai11s で、局面 1 で 上を選択した場合	ai10s で、局面 2 で 下を選択した場合

修正前 の ai11s や ai10s は ランダムな着手 を行いますが、修正前 の ai11s VS ai10s で、ai11s が 勝利する のは、上記 の 着手 が 選択 された 場合だけ なので、上記の表 の 着手 が 選択 された 場合 に 限定して 話を進めることにします。

下図は、A VS B、B VS C、修正前 の ai11s VS ai10s、修正後 の ai11s VS ai10s、で 上記の表 に従って 選択 する 合法手 を表します。図から、対応する AI が、同様の着手 を 選択 することが分かります。

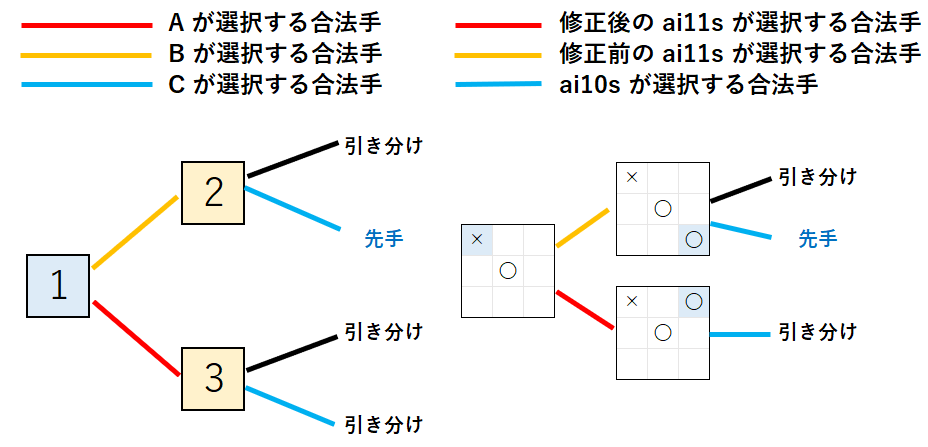
パラドックスの例による ai11s VS ai10s の説明

上記から、下記の事が分かります。

• B VS C と 修正前 の ai11s VS ai10s は 同じ理由 で B と ai11s が 勝利する
• A VS C と 修正後 の ai11s VS ai10s は 同じ理由 で 引き分けになる

従って、修正後 の ai11s が ai10s に 勝てなくなった 理由は、パラドックスの例 で 説明 した 理由 と 同じ理由 であることがわかりました。

今回の記事のまとめ

今回の記事では、これまでに曖昧なままにしてきた、最強の AI の 定義 を行うために、二人零和有限確定完全情報ゲーム という ゲームの分類 を紹介し、この分類 のゲームの 最善手 と、最強の AI の 定義 と 性質 の説明を行いました。

また、AI の修正 による 結果の解釈 について説明し、修正後 の ai11s が ai10s に 勝てなくなったこと が 問題ではない ことを示しました

最後に、AI の強さ を 測定する方法 を いくつか紹介 しました。

本記事で入力したプログラム

今回の記事では入力したプログラムはありません。

次回の記事

更新履歴

更新日時	更新内容
2024/03/06	オセロの局面の数を、26830 から 5478 に修正しました

1. Wikipedia のリンク先に記述されているように、厳密 には、チェス や 囲碁 は 有限 の性質を 満たしません が、有限でない のは 例外的 な場合だけなので、一般的 には 有限 の性質を持つと みなされる ようです ↩

2. https://www.nara-wu.ac.jp/math/personal/shinoda/legal.pdf ↩

3. https://link.springer.com/chapter/10.1007/978-3-540-75538-8_8 (有料の論文です） ↩

4. その方法 については、探索型の AI を 説明 する際に 紹介 します ↩

5. 必ず勝つ ことを「必勝」のように 表現 しますが、必ず引き分け になることを表す「必分け」のような 用語 は 存在しない ようです。誰か知っている方がいれば教えて頂ければうれしいです。 ↩