目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
これまでに作成した AI
これまでに作成した AI の アルゴリズム は以下の通りです。
| ルール | アルゴリズム |
|---|---|
| ルール1 | 左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する |
| ルール2 | ランダム なマスに 着手 する |
| ルール3 |
真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する |
| ルール4 |
真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する |
| ルール5 |
勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する |
| ルール6 |
勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する |
| ルール6改 |
勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する |
| ルール7 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する |
| ルール7改 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する |
| ルール8 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する |
| ルール9 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する |
| ルール10 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 2 つを 総合的に判断 して着手を行う
|
| ルール11 |
真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う
|
基準となる ai2 との 対戦結果(単位は %)は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 | 欠陥 |
|---|---|---|---|---|---|---|---|---|---|---|
ai1ai1s
|
78.1 | 17.5 | 4.4 | 44.7 | 51.6 | 3.8 | 61.4 | 34.5 | 4.1 | あり |
ai2ai2s
|
58.7 | 28.8 | 12.6 | 29.1 | 58.6 | 12.3 | 43.9 | 43.7 | 12.5 | |
ai3ai3s
|
69.3 | 19.2 | 11.5 | 38.9 | 47.6 | 13.5 | 54.1 | 33.4 | 12.5 | |
ai4ai4s
|
83.0 | 9.5 | 7.4 | 57.2 | 33.0 | 9.7 | 70.1 | 21.3 | 8.6 | あり |
ai5ai5s
|
81.2 | 12.3 | 6.5 | 51.8 | 39.8 | 8.4 | 66.5 | 26.0 | 7.4 | |
ai6 |
88.9 | 2.2 | 8.9 | 70.3 | 6.2 | 23.5 | 79.6 | 4.2 | 16.2 | |
ai6s |
88.6 | 1.9 | 9.5 | 69.4 | 9.1 | 21.5 | 79.0 | 5.5 | 15.5 | |
ai7ai7s
|
95.8 | 0.2 | 4.0 | 82.3 | 2.4 | 15.3 | 89.0 | 1.3 | 9.7 | |
ai8s |
98.2 | 0.1 | 1.6 | 89.4 | 2.5 | 8.1 | 93.8 | 1.3 | 4.9 | |
ai9s |
98.7 | 0.1 | 1.2 | 89.6 | 2.4 | 8.0 | 94.1 | 1.3 | 4.6 | |
ai10s |
97.4 | 0.0 | 2.6 | 85.6 | 2.6 | 11.7 | 91.5 | 1.3 | 7.2 | |
ai11s |
98.1 | 0.0 | 1.9 | 82.5 | 1.9 | 15.6 | 90.3 | 1.0 | 8.7 | あり |
前回の記事のおさらい
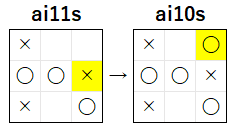
前回の記事では、ai10s VS ai11s で、ai11s が 負ける試合 で行われる 着手 の 選択 を 検証 し、下図 のような 着手 が行われることがわかりました。

4 手目で (0, 2) に着手を行った場合の検証
前回の記事では、4 手目 で ai11s が上図の (0, 2) の着手を 選択 した場合の 検証 を 行っていない ので、最初に その検証 を 行います。なお、実際 には 4 手目 で、(2, 0) に 着手 する 場合 がありますが、その場合 の 局面 は (0, 2) に着手した場合の局面と 同一局面 なので、(0, 2) に 着手 した場合の 検証 で まとめて説明 することにします。
5 手目の検証
下図は、ai11s が、4 手目 で (0, 2) に 着手 を行った場合の図です。
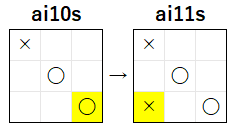
上記 の 局面 は、「自 0 敵 2 空 1」 が 1 つ存在 する 局面 です。ルール 10 には、相手の勝利を阻止する という 条件 があるので、ai10s は 必ず (1, 0) を 選択するはず です。
そのことを、下記のプログラムを実行することで 検証 して 確認 することにします。
- 4 ~ 8 行目:上図の 4 手目まで の 着手 を 行う
1 from marubatsu import Marubatsu
2 from ai import ai_match, ai10s, ai11s
3
4 mb = Marubatsu()
5 mb.move(1, 1)
6 mb.move(0, 0)
7 mb.move(2, 2)
8 mb.move(0, 2)
9 ai10s(mb, debug=True)
行番号のないプログラム
from marubatsu import Marubatsu
from ai import ai_match, ai10s, ai11s
mb = Marubatsu()
mb.move(1, 1)
mb.move(0, 0)
mb.move(2, 2)
mb.move(0, 2)
ai10s(mb, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn o
x..
.o.
X.o
legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (1, 2)]
====================
move (1, 0)
Turn x
xO.
.o.
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -100 best score -inf
UPDATE
best score -100
best moves [(1, 0)]
====================
move (2, 0)
Turn x
x.O
.o.
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score -100 best score -100
APPEND
best moves [(1, 0), (2, 0)]
====================
move (0, 1)
Turn x
x..
Oo.
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 3 best score -100
UPDATE
best score 3
best moves [(0, 1)]
====================
move (2, 1)
Turn x
x..
.oO
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=2, turn=0, empty=1): 2,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -100 best score 3
====================
move (1, 2)
Turn x
x..
.o.
xOo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score -100 best score 3
====================
Finished
best score 3
best moves [(0, 1)]
下記は、上記の結果 を まとめた表 です。
| 「201」 | 「021」 | 「102」 | 評価値 | ||
|---|---|---|---|---|---|
| 評価値 | 1:+12~: 100
|
-100 |
1 つで+1
|
||
| 1 | 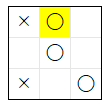 |
1 | 1 | 2 | -100 |
| 2 |  |
1 | 1 | 2 | -100 |
| 3 | 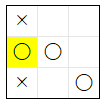 |
1 | 2 | 3 | |
| 4 | 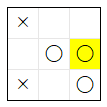 |
2 | 1 | 1 | -100 |
| 5 | 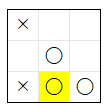 |
1 | 1 | 2 | -100 |
下記は ルール 10 の 条件 の 優先順位 です。
- 「自 0 敵 2 他 1」が 存在 する場合は -100
- 「自 2 敵 0 他 1」が 2 つ以上存在 する場合は 100
- 下記の 評価値 の 合計
1.「自 2 敵 0 他 1」が 1 つ の場合は 1
2.「自 1 敵 0 他 2」が 1 つにつき +1
上記の表 から、実際 に ai10s が 上記 の 優先順位 で 評価値 の 計算 を 行っている ことが 確認 できます。例えば、合法手 4 では、『「自 0 敵 2 他 1」が 存在 する』と『自 2 敵 0 他 1」が 2 つ以上存在 する』の 2 つの条件 が 同時 に 満たされます が、前者 の条件のほうが 優先順位 が 高い ので、評価値 は -100 に なっています。
上記の 表 から、ai10s は、最も評価値 が 高い 3 になる、合法手 3 の (0, 1) を 必ず選択する ことがわかります。そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score 3
best moves [(0, 1)]
5 手目 で ai10s が 必ず (0, 1) に 着手を行う ことが 分かった ので、その着手 が行われた 局面 に対して 6 手目 の 検証 を 行う ことにします。
6 手目の検証

上記の局面 も、「自 0 敵 2 空 1」が 1 つ存在 する 局面 で、ルール 11 にも、相手の勝利を阻止する という 条件 があるので、ai11s は 必ず (2, 1) を 選択するはず です。
そのことは、下記のプログラムで、(2, 1) に 着手 した場合の 評価値 が 0、それ以外 の場合の 評価値 が -100 になることから 確認 できます。
mb.move(0, 1)
ai11s(mb, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
Oo.
x.o
legal_moves [(1, 0), (2, 0), (2, 1), (1, 2)]
====================
move (1, 0)
Turn o
xX.
oo.
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 1})
score -100 best score -inf
UPDATE
best score -100
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
oo.
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score -100 best score -100
APPEND
best moves [(1, 0), (2, 0)]
====================
move (2, 1)
Turn o
x..
ooX
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 3,
Markpat(last_turn=1, turn=2, empty=0): 2,
Markpat(last_turn=2, turn=1, empty=0): 1})
score 0 best score -100
UPDATE
best score 0
best moves [(2, 1)]
====================
move (1, 2)
Turn o
x..
oo.
xXo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=0, turn=2, empty=1): 1,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score -100 best score 0
====================
Finished
best score 0
best moves [(2, 1)]
また、そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。なお、実行結果 を まとめた表 は、5 手目 の場合と ほとんと変わらない ので 省略 します。
best score 0
best moves [(2, 1)]
6 手目 で ai11s が 必ず (2, 1) に 着手を行う ことが 分かった ので、その着手 が行われた 局面 に対して 7 手目 の 検証 を 行う ことにします。
7 手目の検証

これまで と 同様 に、下記のプログラムで ai10s がそれぞれの 合法手 に対して どのように 評価値を 計算 するかを 表示 し、その 結果 を 表にまとめます。
mb.move(2, 1)
ai10s(mb, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn o
x..
ooX
x.o
legal_moves [(1, 0), (2, 0), (1, 2)]
====================
move (1, 0)
Turn x
xO.
oox
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=1, turn=1, empty=1): 4,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 2})
score 1 best score -inf
UPDATE
best score 1
best moves [(1, 0)]
====================
move (2, 0)
Turn x
x.O
oox
x.o
defaultdict(<class 'int'>,
{Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=1, empty=0): 4})
score 1 best score 1
APPEND
best moves [(1, 0), (2, 0)]
====================
move (1, 2)
Turn x
x..
oox
xOo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1,
Markpat(last_turn=2, turn=1, empty=0): 3})
score 1 best score 1
APPEND
best moves [(1, 0), (2, 0), (1, 2)]
====================
Finished
best score 1
best moves [(1, 0), (2, 0), (1, 2)]
下記は、上記の結果 を まとめた表 です。
| 「201」 | 「021」 | 「102」 | 評価値 | ||
|---|---|---|---|---|---|
| 評価値 | 1:+12~: 100
|
-100 |
1 つで+1
|
||
| 1 | 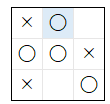 |
1 | 1 | ||
| 2 | 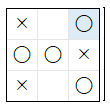 |
1 | 1 | ||
| 3 | 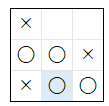 |
1 | 1 |
上記の表 から、どの合法手 でも、「自 2 敵 0 他 1」と「自 1 敵 0 他 2」の どちらか が 1 つ であるため、評価値 が 同じ 1 になります。従って、3 つの合法手 である (1, 0)、(2, 0)、(1, 2) がそれぞれ 1 / 3 = 約 33 % の 確率 で 選択される ことが わかります。そのことは、下記の 実行結果 の 最後の 2 行 からも 確認 できます。
best score 1
best moves [(1, 0), (2, 0), (1, 2)]
8 手目の検証
7 手目 の 局面 は、下記の 3 通り が あります。それぞれの局面 に対して、これまでと同様 に、ai11s を実行し、実行結果 から ai11s が 選択 する 合法手 を 検証 することが できますが、3 つの局面に対して、それぞれ プログラムを実行 してその 結果を記述 して 説明 すると、非常に長く なります。8 手目 を 着手 する 局面 では、残り のマスが 2 マスしかない ので、プログラムに頼らなくても 頭の中だけ で 簡単 に ai11 が 行う着手 を 知ることが可能 なので、その方法 で 検証する ことにします。興味と余裕がある方は、これまで通りの方法で ai11s を実行して検証してみて下さい。
7 手目で (1, 0) に着手した場合

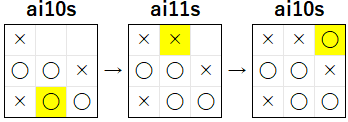
この場合 は、次 に 相手 が (1, 2) に 着手 すると 負けてしまう ので、明らかに ai11s は (1, 2) に 着手 を行います。その結果、残りのマス が 1 マスになる ので、9 手目 で ai10s は (2, 0) に 着手 を行い、下図のように 引き分け になります。

7 手目で (1, 2) に着手した場合
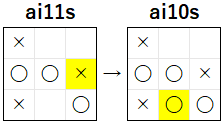
この場合 も 上記と同様 に、次 に 相手 が (1, 0) に 着手 すると 負けてしまう ので、明らかに ai11s は (1, 0) に 着手 を行います。その結果、残りのマス が 1 マスになる ので、9 手目 で ai10s は (2, 0) に 着手 を行い、下図のように 引き分け になります。
7 手目で (2, 0) に着手した場合
この場合 は、少し考えればすぐにわかると思いますが、残りのマス に × と 〇 を どのような順番 で 配置 しても 引き分け になります。従って、どのような AI どうしの対戦 であっても、この局面 になった時点で 引き分け になることが 確定 します。
8 手目の検証のまとめ
上記 から、7 手目 で 3 つの どの着手 が 選択された場合でも、必ず引き分け になります。
4 手目で (0, 2) に着手を行った場合の検証からわかること
上記の検証 から、下記 の事が わかります。
-
4 手目 で (0, 2) に 着手 が行われた場合は、
ai10sVSai11sは 7 手目まで は 必ず同一局面 になる着手を行う - 7 手目 で 選択 される 着手 は 3 種類 あるが、どの着手 が行われても 引き分け になる
上記 から、4 手目 で (0, 2) に 着手 が行われた場合は、ai10s VS ai11s は 必ず引き分けになる ことが 分かりました。
ai10s VS ai11s で行われる着手のまとめ
下図は、ai10s VS ai11s で 行われる着手 を まとめた ものです。

この図 から 以下の事 が 分かります。
-
4 手目 で
ai11sが 50 % の 確率 で (1, 2) に 着手 すると、ai11sが負ける -
4 手目 で
ai11sが 50 % の 確率 で (0, 2) に 着手 すると、引き分け になる
このことは、前回の記事で実行した、下記のプログラムによる ai11s VS ai10s の 対戦結果 で、ai11s が × を担当 した場合の 敗率 約 50 %、引き分け 約 50% と 一致 します。従って、これまでに行ってきた ai10s VS ai11s で 行われる着手 の 検証結果 に ほぼ間違いがなさそう であることが 確認 できました。
人間が行う検証 には、間違いがある可能性 があります。そのため、上記では「ほぼ間違いがなさそう」であるという 表現 にしています。
ai_match(ai=[ai11s, ai10s])
実行結果(実行結果はランダムなので下記とは異なる場合があります)
ai11s VS ai10s
count win lose draw
o 2223 0 7777
x 0 5053 4947
total 2223 5053 12724
ratio win lose draw
o 22.2% 0.0% 77.8%
x 0.0% 50.5% 49.5%
total 11.1% 25.3% 63.6%
ai11s の敗因の検証と改善
ai10s VS ai11s で行われる 着手の検証 から、以下の事 が 判明 しました。
-
ai10sとai11sが、ルール通り の 処理 を行っている 可能性が高い こと -
ai10sVSai11sでai11sが 50 % の 確率 で 負ける理由
上記の 2 つ は どちらも重要 です。AI が ルール通り の 処理を行っている ということは、AI の プログラムの実装 には 問題がない ということを表すからです。従って、問題を修正 するためには、ルールの不備 を 見つける という 作業 を 行えば良い ことが 分かります。
負ける理由 が 判明した ということは、その 理由を分析 することで、負けないよう に ルールを改善 することができる 可能性が生じる ということを意味するからです。
なお、負ける理由 のことを 敗因 と呼ぶので、以後は 敗因 と 表記 することにします。
「可能性が生じる」という 表現 にしたのは、残念ながら 原因が分かっても 問題を 解決する方法 が ない場合 や、分からない場合 が あるから です。
ai11s の敗因の検証と改善方法の検討
そこで、ai11s の 敗因 を 検証 し、ai11s を 改善する方法 を 検討する ことにします。
先ほどの 検証 から、ai10s VS ai11s の 対戦 では、ai11s が 4 手目 で (1, 2) と (0, 2) の どちらに着手 を 行うか で、敗北 と 引き分け が 決まること が 分かりました。このことから、ai10s VS ai11s で、ai11s が 敗北 した場合の 敗因 は、4 手目 で (0, 2) に 着手 したことであることが わかります。このような、負けにつながる着手 の事を 敗着 と呼びます。
次に、この 敗着 を 避ける方法 について 検討 することにします。4 手目 では、引き分け に つながる (1, 2) という 合法手 が 存在 するので、ai11s が 4 手目 で、必ず (1, 2) を 選択する ように ルールを改善 できれば、ai10s VS ai11s の 対戦 の結果は 必ず引き分け になり、その結果、ai11s が 負けること が なくなります。
上記の 改善を行う ためには、ai11s の 評価値 の 計算方法 を 修正 する 必要 があります。どのように修正すれば良いかについて少し考えてみて下さい。
ここまでで行ったことは、現実の世界 でも 実際 に 良く行われる ことです。例えば、スポーツの試合で 負けた場合 に、負けた試合 を 細かく検証 することで、敗因を発見 し、その 敗因を分析 することで 次は負けないよう に 改善します。
評価値の計算方法の修正
下記は、前回の記事で 4 手目 の 検証 を行った際に 作成した表 です。
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+12~: 100
|
-100 |
1 つで+1
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 4 | -2 | |
| 2 |  |
1 | 1 | 3 | -1 | |
| 3 |  |
2 | 3 | -1 |
上記の表 で、敗着 となる 合法手 3 が 選択 される 可能性 がある 理由 は、その評価値 が 合法手 2 の 評価値 と 並んで、最も高いから です。先程の、引き分けになる ことが分かっている 合法手 2 のみ を 選択 するという 改善方法 を 実現するため には、合法手 2 の 評価値のみ が 最も高くなる ようにする 必要 があります。そのために、ルール 11 の 評価値 の 計算方法 を どのように修正すれば良いか について少し考えてみて下さい。
評価値の計算のパラメータ
4 手目 の局面では、ルール 11 の『「自 2 敵 0 空 1」が 2 つ以上存在 する 局面になる 着手 を行う』以上 の 優先順位 の 条件 を満たす 合法手 は 存在しない ので、ai11s は、それぞれの 合法手 の 評価値 を、下記の表 で 設定 される 評価値 の 合計 で 計算 します。
| 項目 | 評価値 |
|---|---|
| 「自 2 敵 0 空 1」が 1 つ の場合 | 1 |
| 「自 1 敵 0 空 2」が 1 つあたり | 1 |
| 「自 0 敵 1 空 2」が 1 つあたり | -1 |
この表の 評価値 の 数字 は、以前の記事で 試行錯誤 して決めたものであったり、とりあえずこの値に設定する という方法で決めたものであるため、それぞれの値 が AI を強くする ために ベストな数字であるか どうかは わかっていません。実際に、以前の記事で、『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 変えて ai9s と 対戦 した 結果、対戦成績 が 変化 したことからわかるように、これらの値 を 変える ことで、AI の強さ が 変わります。
このような、何かを計算 する際に 利用 する、変更可能 な 値 を パラーメータ と呼びます。4 手目 の 局面 で、合法手 2 の 評価値のみ が 最も高くなる ような パラメータ を 見つける ことで、目的 を 達成 することが できます。
パラメータ(parameter)は、日本語 では 変数 と 訳され、プログラム用語 での 任意の値 を 代入 できる a のような 変数 も パラメータの一種 です。ただし、プログラム用語 の 変数 は、一般的 に 英語 では variable と 表記 し、parameter は 仮引数 という意味で、変数 と 区別 して 使われます1。
プログラム用語 の 変数 を、英語で variable と 表記 する のは、おそらく「変化(vary)することが できる(可変)」という 意味 を 強調したい からではないかと思います。一方、仮引数 は、関数 で行う 何らかの計算 を 行うため の 変更可能 な 値 と 考えることができる ので、parameter と 表記 するのではないかと思います。
パラメータ は、ゲーム などでは、キャラクターやアイテムの 能力値など を 表す用語 として使われます。それらの パラメータ は、個々 のキャラクターやアイテムによって 値が変化 し、戦闘 などで行われる 計算 で 利用 されます。
パラメータの修正方法の考え方
それぞれの合法手 の 現時点 の 評価値 と、目標 となる 評価値 の 関係 は 以下 の通りです。
- 現状:合法手 2 の評価値 = 合法手 3 の評価値 > 合法手 1 の評価値
- 目標:合法手 2 の評価値 > 合法手 1 の評価値、合法手 2 の評価値 > 合法手 3 の評価値
目標 の 関係 のうち、前者 の「合法手 2 の評価値 > 合法手 1 の評価値」という 関係 は 達成済 なので、後者 の「合法手 2 の評価値 > 合法手 3 の評価値」という 関係 を 達成 するように パラメータ を 変更すればよい ことが分かります。そこで、評価値 を 計算 する際に 利用 する 項目 の、合法手 2 と 合法手 3 の 性質 を 調べる ことにします。
下記は、合法手 2 と 合法手 3 のそれらの 項目 を 調べた結果 を まとめた表 です。
| 項目 | 合法手 2 | 合法手 3 | 合法手 2 と 3 の比較 |
|---|---|---|---|
| 「自 2 敵 0 空 1」が 1 つ | あり | なし | 合法手 2 のみあり |
| 「自 1 敵 0 空 2」の数 | 1 | 2 | 合法手 3 の方が多い |
| 「自 0 敵 1 空 2」の数 | 3 | 3 | 数は同じ |
上記から、以下 の事が 分かります。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値(パラメータ)を 増やす と、合法手 2 の 評価値 は 増える が、合法手 3 の 評価値 は 増えない
- 『「自 1 敵 0 空 2」が 1 つあたり』の 評価値 を 増やす と、合法手 3 の 評価値 のほうが、合法手 2 の 評価値 より 多く増える
- 『「自 0 敵 1 空 2」が 1 つあたり』の 評価値 を 変えた場合、合法手 2 と 合法手 3 の 評価値 は、同じ大きさ だけ 増減 する
従って、合法手 2 の 評価値 が 合法手 3 の 評価値より も 大きくなる ようにするためには、以下の 2 種類 の 方法がある 事が分かります。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 増やす
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす
これで パラメータ の 修正方法 が 決まりました が、この ような 修正方法 で 本当に大丈夫でしょうか?何か 忘れていることはないか、少し考えてみて下さい。
目標に複数の条件がある場合の修正方法
上記 の 修正方法 では、以下 のような 考え方 で パラメータの修正 を行いました。この 考え方 には 重大な間違い があります。何が間違っているか を少し 考えてみて下さい。
- 目標 のうち、「合法手 2 の評価値 > 合法手 1 の評価値」は 満たされている
- 目標 のうち、「合法手 2 の評価値 > 合法手 3 の評価値」は 満たされていない
- 従って、「合法手 2 の評価値 > 合法手 3 の評価値」が 満たされるよう に パラメータ を 修正すればよい
上記 の考え方の 間違い は、上記 の 考え方 に従って パラメータ を 修正 した 結果 、現状 で 満たされている「合法手 2 の評価値 > 合法手 1 の評価値」という 条件 が 満たされなくなる 可能性を 考慮 に 入れていない 点です。
ピンとこない人がいるかもしれないので、上記 に 類似する 簡単な 具体例 を挙げます。
テレビの音 が 小さすぎて よく 聞こえない ので、適切な音量 に 調整 する場合のことを考えてみて下さい。この例では、テレビの音量 を 0 ~ 50 までの 整数 で表現し、数字 が 大きい程、音量 が 大きくなる ものとします。この場合の パラメータ は、テレビの音量 です。
まず、目標 を 設定 するために、適切な音量 を 定義 する 必要 があります。ここでは、音 が 良く聞こえる音量 を 20 以上 とすることにします。また、音量 が 大きすぎる と うるさい ので、うるさい と感じられる 音量 を 30 以上 とすることにします。
現状 の 音量 を 10 とした場合、現状 と 目標 は以下のようになります。
- 現状:音量 = 10
- 目標:音量 >= 20、音量 < 30
先程 と 同じ考え方 で パラメータ を 修正する方法 を 考える と以下のようになります。
- 現状 の 音量 10 は、「音量 >= 20」は 満たしていない が、「音量 < 30」は 満たす
- 従って、「音量 >= 20」を 満たす ように パラメータ である 音量 を 修正 すれば良い
- 従って、修正方法 は、パラメータ である、音量 を 10 以上増やす ことである
音量 を 20 以上増やす という パラメータ の 修正 は、上記 の 修正方法 の 条件 を 満たします が、音量 が 30 以上 になり、「音量 < 30」が 満たされなくなる ため、目的 を 達成 することが できません。従って、上記 の 修正方法 は 間違っています。
上記の事から、下記の事がわかります。
目標 に 複数の条件 がある場合は、現状 で 条件 のうちのいくつかが 満たされているか どうかに 関係なく、すべての条件 を 満たす ような パラメータ の 修正方法 を 考える必要 がある。
複数の条件を満たすパラメータを見つける手順
上記 の事から、下記の 両方の条件 を満たす パラメータ を 見つける ことで、目的 を 達成できる ことがわかりました。このうち、「合法手 2 の評価値 > 合法手 3 の評価値」を 達成 する パラメータ の 修正方法 は 先程見つけた ので、同時 に もう一つ の「合法手 2 の評価値 > 合法手 1 の評価値」を 達成 する パラメータ の 条件 を 見つける必要 があります。
- 合法手 2 の評価値 > 合法手 1 の評価値
- 合法手 2 の評価値 > 合法手 3 の評価値
その際 に、先程「合法手 2 の評価値 > 合法手 3 の評価値」を満たす パラメータ を みつけた手順 と 同じ方法 で 見つける必要 があると 思う人 がいるかもしれませんが、その 条件を見つける のは 大変 です。もっと簡単な方法 があるので、それが何かを考えてみて下さい。
目的 を 達成するため の 複数の条件 を すべて満たす ような パラメータの条件 は、下記の手順 で 求める ことができます。
- 最初は、パラメータの条件 を「条件なし」と設定する
- 目標 を 達成するため の 複数の条件 のうち 検討していない条件 を 1 つ選択 する
- パラメータの条件 の 範囲 で、選択 した 条件 を満たす 条件 を求め、求めた条件 で、パラメータの条件 を 更新 する
- 検討していない条件 が 残っている場合 は 手順 2 に 戻る
- パラメータの条件 が 求める条件 である
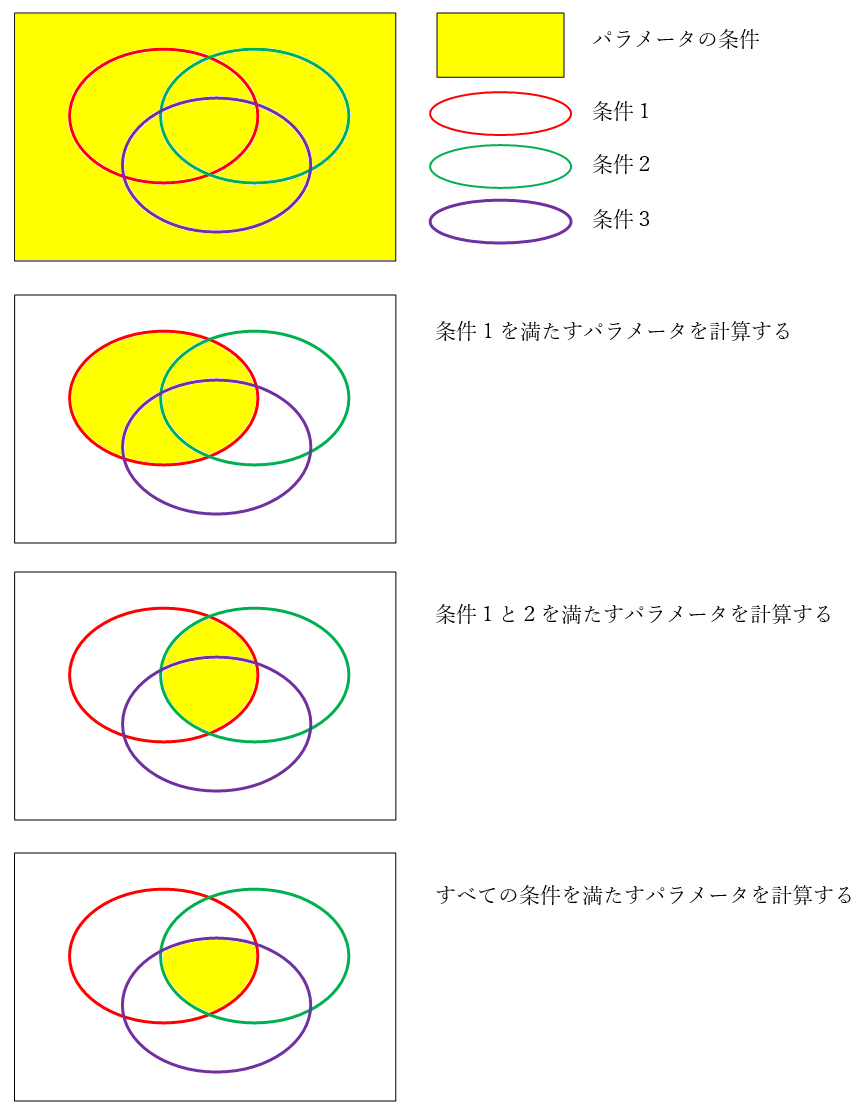
分かりづらいと思いますので、具体例と図で説明します。
目標 を 達成するため の 条件 として、「条件 1」、「条件 2」、「条件 3」があるとき、すべての条件 を満たす パラメータの条件 は 下記の手順 で 求める ことが できます。
- パラメータの条件 を「条件なし」と設定する(一番上の図)
- その条件の範囲 で、条件 1 を満たす 条件 を 計算 する
- パラメータの条件 を 計算した条件 で 更新 する(2 番目の図)
- その条件の範囲 で、条件 2 を満たす 条件 を 計算 する
- パラメータの条件 を 計算した条件 で 更新 する(3 番目の図)
- その条件の範囲 で、条件 3 を満たす 条件 を 計算 する
- パラメータの条件 を 計算した条件 で 更新 する(4 番目の図)。これが、すべての条件 を満たす パラメータの条件 である
上記の手順 の方が、簡単である ことが ピンとこない 人が いるかもしれない ので、別の 具体例 を挙げて 説明 します。たとえば、100 人の生徒 の中から、以下 の 条件 を すべて満たす生徒 を 見つける という 問題 を考えてみて下さい。
- 国語 の点数が 50 点以上
- 英語 の点数が 50 点以上
- 数学 の点数が 50 点以上
個別の条件 を それぞれ 満たす生徒 を 探し、探した生徒 の 中から、すべての条件 を満たす 生徒を探す という 方法 でこの問 題を解く 場合は、以下 の 手順 で 作業 を 行います。
この手順 では、100 人 の 中から 特定の 条件を満たす生徒 を 探す という 作業 を 3 回行う必要 があります。また、その後 で、その中から すべての条件を満たす 生徒を探す という 作業 を 行う必要 があります。
- 100 人 の 中から 国語の点数が 50 点以上の 生徒を探す
- 100 人 の 中から 英語の点数が 50 点以上の 生徒を探す
- 100 人 の 中から 数学の点数が 50 点以上の 生徒を探す
- 手順 1、2、3 で探した中で、すべてに含まれる生徒 を 探す
一方、先程 の 手順 で 探す 場合は、以下の手順 で 作業 を 行います。こちらの手順 では、作業 を 行うたび に、特定の条件を満たす 生徒を探す際 の、生徒の数 が 減っていく ため、作業 が やりやすく なります。また、最後 に 上記の手順 4 を 行う必要 は ありません。
- 100 人 の 中から 国語の点数が 50 点以上の 生徒を探す
- 手順 1 で X 人が見つかった場合、X 人 の 中から 英語の点数が 50 点以上の 生徒を探す
- 手順 2 で Y 人が見つかった場合、Y 人 の 中から 数学の点数が 50 点以上の 生徒を探す
同様 の 問題を解く際 には、おそらく、多くの方 が、無意識のうちに 後者の手順 で 作業を行っている のではないでしょうか。
すべての条件を満たすパラメータの計算
先程の手順 に従って、「合法手 2 の評価値 > 合法手 3 の評価値」と「合法手 2 の評価値 > 合法手 1 の評価値」の両方の条件を満たす パラメータ の 修正方法 を 求めます。
下記は、先程検討 した「合法手 2 の評価値 > 合法手 3 の評価値」を満たす、パラメータの 2 種類 の 修正方法 です。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 増やす
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす
先程の手順 から、この 条件 を 満たした上 で、「合法手 2 の評価値 > 合法手 1 の評価値」を満たす パラメータ の 修正方法 を考える必要があるので、この条件 を 満たした場合 の、合法手 2 の評価値 と 合法手 1 の評価値 の 関係 を 調べます。
この 2 つ の 修正方法 に関して、合法手 1 と 2 の 関係 は以下のようになっています。
- 合法手 1 と 合法手 2 は、どちらも「自 2 敵 0 空 1」が 1 つ である
- 合法手 1 と 合法手 2 は、どちらも「自 1 敵 0 空 2」の 数が同じ である
従って、上記 の どちらの修正方法 で 修正 を行っても、合法手 1 と 合法手 2 の 評価値 は 同じだけ増減する ことが 分かります。修正前 の 合法手 1 の評価値は -2 で、修正前 の 合法手 2 の評価値である -1 より 小さい ので、どちらの修正方法 で 修正 を行っても、合法手 2 の評価値の方が、合法手 1 の評価値より 常に大きくなる ことが 分かりました。
上記 から、先程 求めた「合法手 2 の評価値 > 合法手 3 の評価値」の 条件 を 満たすため の 修正方法 によって、「合法手 2 の評価値 > 合法手 1 の評価値」の 条件 も 同時に満たされる ことが分かります。従って、目的 を 満たす ための 修正方法 は 以下のいずれか です。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 増やす
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす
2 つ目の条件に対するパラメータの条件を求める場合の具体例
上記 では、複数の条件 のうちの、一つ目 の 条件 を 満たすための修正 によって、残りの条件 が 満たされました が、一般的 には そのようなこと は おきません。そこで、そのようなことが起きない 場合の 具体例 を 紹介 することにします。
なお、下記 は、説明のため に 作った、実際 の 〇×ゲーム では おきない、架空の例 です。具体的には、 下記の表 のように、4 手目 の局面で、合法手 1 を着手した場合の「自 1 敵 0 他 2」の 数 が 1 ではなく、3 だった場合に、先程 と 同様 の、下記 の 条件 を 満たす ような パラメータ の 修正方法 を 求める手順 を説明します。
- 合法手 2 の評価値 > 合法手 1 の評価値
- 合法手 2 の評価値 > 合法手 3 の評価値
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+12~: 100
|
-100 |
1 つで+1
|
1 つで-1
|
||
| 1 |  |
1 | 1 → 3 | 4 | -2 → 0 | |
| 2 |  |
1 | 1 | 3 | -1 | |
| 3 |  |
2 | 3 | -1 |
「合法手 2 の評価値 > 合法手 3 の評価値」を満たす修正方法
上記の表 では、合法手 2 と 合法手 3 の 部分 は 変わっていない ので、「合法手 2 の評価値 > 合法手 3 の評価値」の 条件 を満たす パラメータ の 修正方法 は、先程と同様 に、下記 の いずれか になります。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 増やす
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす
「合法手 2 の評価値 > 合法手 1 の評価値」を満たす修正方法
次に、上記の 条件 を 満たした上 で、「合法手 2 の評価値 > 合法手 1 の評価値」を満たす パラメータ の 修正方法 を考える必要があります。
まず、上記の 1 つ目 の 修正方法 によって、合法手 1 と 合法手 2 の 評価値 が どのように変化 するかを 考察 します。以下の点 から、上記の 1 つ目 の 修正方法 では、「合法手 2 の評価値 > 合法手 1 の評価値」の 条件 を 満たす ことは できない ことが 分かります。
- 合法手 1 と 2 では、どちらも「自 2 敵 0 空 1」の数が 1 つ である
- 従って、上記 の 1 つ目 の 修正方法 を 適用 しても、合法手 1 と 2 の 評価値 は 同じだけ増減 する
- 現状 では、合法手 1 の 評価値 は 0 であり、合法手 2 の 評価 値である -1 よりも 大きい
次に、もう一つ の 修正方法 について 考察 します。合法手 1 のほうが、合法手 2 よりも「自 1 敵 0 空 2」の 数が多い ので、「自 1 敵 0 空 2」が 1 つあたり の 評価値 を 減らす ことで、合法手 1 の 評価値 の方が、合法手 2 の 評価値より も 多く減る ことになります。
しかし、「自 1 敵 0 空 2」が 1 つあたり の 評価値 を 減らしたから と言って、必ずしも「合法手 2 の評価値 > 合法手 1 の評価値」の 条件を満たす ことが できるわけ では ありません。そのため、その条件 を 満たすため の パラメータの条件 を 調べる必要 があります。
下図は、「自 1 敵 0 空 2」が 1 つあたり の 評価値 と、合法手 1 と 2 の 評価値 の 関係 を表す グラフ です。グラフ から、「合法手 2 の評価値 > 合法手 1 の評価値」の 条件 を 満たすため には、評価値 の パラメータ を 0.5 未満 にする 必要がある ことが わかりました。
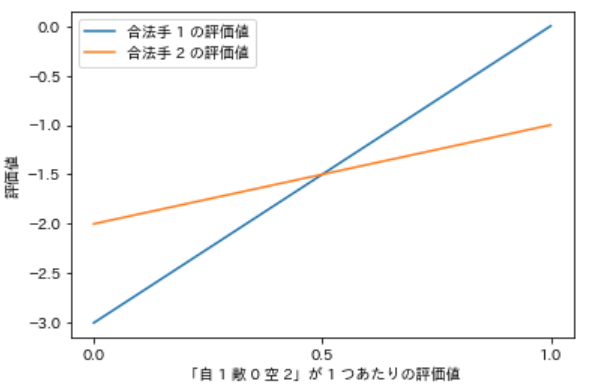
従って、下記の条件 を 満たす ための パラメータ の 修正方法 は、『「自 1 敵 0 空 2」が 1 つあたり の 評価値 を 0.5 未 満にする』ということが わかりました。
- 合法手 2 の評価値 > 合法手 1 の評価値
- 合法手 2 の評価値 > 合法手 3 の評価値
パラメータの調整のさらなる注意点 その 1
話を、4 手目 で、下記の条件 を満たす パラメータ の 修正方法 に 戻します。
- 合法手 2 の評価値 > 合法手 1 の評価値
- 合法手 2 の評価値 > 合法手 3 の評価値
先程、この条件 を 満たす ための パラメータ の 修正方法 として、下記 の いずれか の 修正 を 行えば良い と示しましたが、この条件だけ で 本当に十分でしょうか?何か忘れている ことはないか、少し考えてみて下さい。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 増やす
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす
ルール 11 の「自 1 敵 0 空 2」に関する 下記の説明 を思い出してください。
「自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う」
この条件 を 満たす ような 着手 を 選択する ためには、『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 正の値 にする 必要 があります。しかし、上記の 2 つ目 の 修正方法 は、そのこと に 言及していない ので、『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 負の値 にしても かまわない ことになります。実際 に、この パラメータ を 負の値 に 修正 することで、合法手 2 の 評価値のみ が 最も高くなる という 目的 は 達成できます が、ルール の 条件 の 意図 に 反する ような 修正 を 行ってはいけない 点に 注意が必要 です。
なお、1 つ目 の 修正方法 にも 同じこと が 言えます が、1 を 増やした場合 は、必ず正の値になる ので、そのまま でも 問題 は ありません。
従って、正しい修正方法 は 以下 のようになります。なお、1 つ目 の 元の修正方法 の「増やす」という 表現 は、あいまい なので、下記のように 具体的な表現 に 修正 しました。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 より大きな値 にする
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 1 未満 の 正の値 にする
実は、上記の修正を行っても、まだ 問題 が 残っている ので、少し考えてみて下さい。
パラメータの調整のさらなる注意点 その 2
上記の条件 の 問題点 は、ルール 11 の、より 優先順位 が 高い条件 を 考慮していない という点です。例えば、『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 から 10000 に 変更 するという 修正方法 は、上記 の 1 つ目の修正方法 の 条件 を 満たします。下記は、そのように修正 した場合の 表 です
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+100002~: 100
|
-100 |
1 つで+1
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 4 | 9997 | |
| 2 |  |
1 | 1 | 3 | 9998 | |
| 3 |  |
2 | 3 | -1 |
表から、確かに 合法手 2 の 評価値のみ が 最も大きい 9998 になることが分かりますが、この 評価値 は、より 優先順位 が 高い はずの、自分が勝利した局面 の 評価値 である 200 や、次 の 自分の手番 で 必ず 自分が 勝利できる局面 の 評価値 である 100 よりも 大きく なってしまいます。4 手目の局面には、そのような合法手は存在しませんが、他の局面 で そのような合法手 が 存在 した場合は、優先順位 が 低い条件 を満たす 合法手 が、優先順位 が 高い条件 の 合法手より も 優先 して 選択される ことになってしまいます。
このようなこと が 起きないようにする ためには、評価値 の 計算結果 が、優先順位 が 高い条件 の 合法手より も 小さくなる ように パラメータ を 修正する必要 があります。
問題 が 発生しない ことを 確認 するためには、以前の記事で作成した、優先順位 ごとの 評価値 の 表 を 作成すると良い でしょう。下記は、『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 から 2 に 修正 した場合の 表 で、問題 が 発生しない ことが 確認 できます。
| 順位 | 局面の状況 | 個別 | 評価値 |
|---|---|---|---|
| 1 | 真ん中のマスに着手している | 300 |
|
| 2 | 自分が勝利している | 200 |
|
| 4 | 「自 2 敵 0 空 1」が 2 つ以上存在する | 100 |
|
| 5 |
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
2 (0~2)x (0~8)-y (-8~0) |
-8~10 |
| 3 | 相手が勝利できる | -100 |
念のため に、上記 の 修正 を行った 場合 のそれぞれの 合法手 の 表 も 作ってみる ことにします。下記の表 から、合法手 2 の 評価値のみ が、最も高くなる ことが 確認 できます。
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+22~: 100
|
-100 |
1 つで+1
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 4 | -1 | |
| 2 |  |
1 | 1 | 3 | 0 | |
| 3 |  |
2 | 3 | -1 |
パラメータ の 修正を行う際 に、元の値 から 大きく変更する ことはあまり お勧めできません。その理由は、大きく変更 すると、上記の例のように、別の所 で 何らか の 悪影響 を 及ぼす可能性 が 高くなる からです。
現実の場合 でも、テレビの音 が 小さい場合 に、少しずつ 音量を 上げていく のが 一般的 ではないでしょうか。一気 に音量を 上げてしまう と音が 大きくなりすぎて、周りに迷惑がかかるなどの 別の問題 が 発生する可能性 が 高くなります。
この時点で、かなり うんざりした人 が 多いかもしれません が、残念ながら このような 細かい点 を 考慮せず に パラメータ を 修正してしまう と、AI が 意図通り に 着手 を 行わなくなってしまう ので、避けて通る ことは できません。これまでの記事で、何度も 何度も 表を書いて確認 してきたのはそのような 間違いを避けるため です。
ある局面 に対して、何らかの目的 を 達成 するために パラメータを修正 する場合は、修正したパラメータ が、その局面 における、ルール の すべての条件 を 満たす ことを 確認する必要 がある。
目的を達成できない場合
目的 によっては、どのように パラメータ を 修正しても 、その 目的 を 達成 することが できない場合 が あります。そのような場合は、パラメータではなく、ルール の 条件 の方を 修正 する 必要 が あります。具体例については今後の記事で紹介します。
また ルール の 条件を修正 しても 目的 が 達成できない ような 場合 もあります。そのような場合は、例えば、絶対に勝てない局面で勝利を目指すというような、目的 の 設定 そのものに 無理がある 可能性が高く、目的 のほうを 修正 する 必要 が あります。
ai11s の評価値の計算方法の修正
先程、問題がない ことを 確認 した、『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 から 2 に 修正 するという方法で ai11s を 修正 することにします。そのように パラメータ を 修正する ためには、以前の記事で 評価値の調整 を行った際と 同様 に、ai11s の下記のプログラムの 3 行目 の score += 1 で、評価値 に 加算する数値 を 1 から 2 に 変更すればよい のですが、今後、このように パラメータ を 変更する必要 が生じた場合に、ai11s のプログラムを 毎回修正する のは 大変 です。
# 次の自分の手番で自分が勝利できる場合は評価値に 1 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
score += 1
そこで、ai11s の 仮引数 に、評価値 を 計算 する際に 利用 する パラメータ を 代入する ように 修正 することで、ai11s の プログラム を 修正しなくても、実引数 に 記述 する パラメータ を 変えるだけ で、評価値 の 計算方法 を 変える ことが できるように します。
これらの パラメータ を、仮引数 に 代入する ためには、それぞれの 仮引数 の 名前 を 考える必要 があるので、仮引数 の 名前 を、下記の表 のように 名づける ことにします。
| 仮引数の名前 | |
|---|---|
| 「自 2 敵 0 空 1」が 1 つ の場合 | score_201 |
| 「自 1 敵 0 空 2」が 1 つあたり | score_102 |
| 「自 0 敵 1 空 2」が 1 つあたり | score_012 |
なお、他の 100 など の 評価値 も パラメータ の 一種 なので、それら を 仮引数 に 代入 して 変更できるよう にすることもできます。ただし、仮引数 を 多くする と 分かりづらくなる ので、今回の記事 では 上記 の 3 つ の パラメータのみ を 変更できる ようにします。
ai11s の修正
下記は、上記 の 仮引数 を 追加 し、その 仮引数 を使って 評価値を計算する ように ai11s を 修正 したプログラムです。デフォルト引数 は、通常の仮引数より も 後に記述 する 必要がある ので、新しい仮引数 は debug=False より も 前に記述 する 必要 があります。
- 5 行目:パラメータ を 代入 する 仮引数 を 追加 する
-
11 行目:「自 2 敵 0 空 1」が 1 つ の場合に、評価値 に
score_201を 加算する ように 修正 する -
13 行目:評価値 に『「自 1 敵 0 空 2」の数 ×
score_102』を 加算 するように 修正 -
15 行目:評価値 に『「自 0 敵 1 空 2」の数 ×
score_012』を 加算 するように 修正。なお、元 はscore -= 1であったが、score_102には 負の値 を 代入 することを 想定している ので、修正後 はscore += 式に 変更 する 必要 がある点に 注意 すること
1 from pprint import pprint
2 from ai import ai_by_score
3 from marubatsu import Markpat
4
5 def ai11s(mb, score_201, score_102, score_012, debug=False):
6 def eval_func(mb):
元と同じなので省略
7 # 評価値の合計を計算する変数を 0 で初期化する
8 score = 0
9 # 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
10 if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
11 score += score_201
12 # 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
13 score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
14 # 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
15 score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
16
17 # 計算した評価値を返す
18 return score
19
20 return ai_by_score(mb, eval_func, debug=debug)
行番号のないプログラム
from pprint import pprint
from ai import ai_by_score
from marubatsu import Markpat
def ai11s(mb, score_201, score_102, score_012, debug=False):
def eval_func(mb):
# 真ん中のマスに着手している場合は、評価値として 300 を返す
if mb.last_move == (1, 1):
return 300
# 自分が勝利している場合は、評価値として 200 を返す
if mb.status == mb.last_turn:
return 200
markpats = mb.count_markpats()
if debug:
pprint(markpats)
# 相手が勝利できる場合は評価値として -100 を返す
if markpats[Markpat(last_turn=0, turn=2, empty=1)] > 0:
return -100
# 次の自分の手番で自分が必ず勝利できる場合は評価値として 100 を返す
elif markpats[Markpat(last_turn=2, turn=0, empty=1)] >= 2:
return 100
# 評価値の合計を計算する変数を 0 で初期化する
score = 0
# 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
score += score_201
# 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
# 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
# 計算した評価値を返す
return score
return ai_by_score(mb, eval_func, debug=debug)
修正箇所
from pprint import pprint
from ai import ai_by_score
from marubatsu import Markpat
-def ai11s(mb, debug=False):
+def ai11s(mb, score_201, score_102, score_012, debug=False):
def eval_func(mb):
元と同じなので省略
# 評価値の合計を計算する変数を 0 で初期化する
score = 0
# 次の自分の手番で自分が勝利できる場合は評価値に score_201 を加算する
if markpats[Markpat(last_turn=2, turn=0, empty=1)] == 1:
- score += 1
+ score += score_201
# 「自 1 敵 0 空 2」1 つあたり score_102 だけ、評価値を加算する
- score += markpats[Markpat(last_turn=1, turn=0, empty=2)]
+ score += markpats[Markpat(last_turn=1, turn=0, empty=2)] * score_102
# 「自 0 敵 1 空 2」1 つあたり score_201 だけ、評価値を減算する
- score -= markpats[Markpat(last_turn=0, turn=1, empty=2)]
+ score += markpats[Markpat(last_turn=0, turn=1, empty=2)] * score_012
# 計算した評価値を返す
return score
return ai_by_score(mb, eval_func, debug=debug)
動作の確認
修正 した ai11s が 正しく動作 するかを 確認 します。
まず、下記のプログラムのように、元 の 計算方法 で 評価値 を 計算する ように、実引数 に パラメータ を 記述 し、ai10s VS ai11s の 4 手目 の 局面 で ai11s が どのように着手 を 選択 するかを 表示 します。なお、3 つ の パラメータ を 位置引数 で 記述 すると、それぞれの 意味がわかりづらくなる ので、キーワード引数 で 記述 しました。
mb = Marubatsu()
mb.move(1, 1)
mb.move(0, 0)
mb.move(2, 2)
ai11s(mb, score_201=1, score_102=1, score_012=-1, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.o.
..O
legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2)]
====================
move (1, 0)
Turn o
xX.
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -2 best score -inf
UPDATE
best score -2
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1 best score -2
UPDATE
best score -1
best moves [(2, 0)]
====================
move (0, 1)
Turn o
x..
Xo.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -2 best score -1
====================
move (2, 1)
Turn o
x..
.oX
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -1 best score -1
APPEND
best moves [(2, 0), (2, 1)]
====================
move (0, 2)
Turn o
x..
.o.
X.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1 best score -1
APPEND
best moves [(2, 0), (2, 1), (0, 2)]
====================
move (1, 2)
Turn o
x..
.o.
.Xo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -1 best score -1
APPEND
best moves [(2, 0), (2, 1), (0, 2), (1, 2)]
====================
Finished
best score -1
best moves [(2, 0), (2, 1), (0, 2), (1, 2)]
実行結果 には、修正前 の ai11s と 同じ内容 が 表示 されます。また、下記の 実行結果 の 最後の 2 行 から 修正前 と 同様 に 合法手 2 と 3 の 評価値 として -1 が 計算 され、合法手 2 と 3 の 中から選択 が 行われる ことが 確認 できます。
best score -1
best moves [(2, 0), (2, 1), (0, 2), (1, 2)]
次に、下記のプログラムで、『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 の パラメータ を 2 に 変更 した場合に ai11s が どのよう に 着手を選択 するかを 表示 します。
-
1 行目:
score_201=1をscore_201=2に 修正 する
ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=True)
修正箇所
-ai11s(mb, score_201=1, score_102=1, score_012=-1, debug=True)
+ai11s(mb, score_201=2, score_102=1, score_012=-1, debug=True)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.o.
..O
legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2)]
====================
move (1, 0)
Turn o
xX.
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1 best score -inf
UPDATE
best score -1
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score 0 best score -1
UPDATE
best score 0
best moves [(2, 0)]
====================
move (0, 1)
Turn o
x..
Xo.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1 best score 0
====================
move (2, 1)
Turn o
x..
.oX
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -1 best score 0
====================
move (0, 2)
Turn o
x..
.o.
X.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score 0 best score 0
APPEND
best moves [(2, 0), (0, 2)]
====================
move (1, 2)
Turn o
x..
.o.
.Xo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -1 best score 0
====================
Finished
best score 0
best moves [(2, 0), (0, 2)]
実行結果 から、想定通り に、下記の表 と 同じ計算 が 行われる ことが 確認 できます。
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+22~: 100
|
-100 |
1 つで+1
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 4 | -1 | |
| 2 |  |
1 | 1 | 3 | 0 | |
| 3 |  |
2 | 3 | -1 |
下記の 実行結果 の 最後の 2 行 から、合法手 2 のみ が 選択される ことが 確認 できます。
best score 0
best moves [(2, 0), (0, 2)]
ai10s との対戦
次に、ai_match を使って、ai10s と 対戦 を行い、ai11s が × を担当 した場合に、ai10s に 負けなくなったか どうかを 確認 します。
ai_match の問題点
その際に、初心者の方は、下記 のプログラムのように 記述すれば良い と 思うかもしれません が、実行 すると、実行結果 のような エラーが発生 します。
ai_match(ai=[ai11s(mb, score_201=2, score_102=1, score_012=-1), ai10s])
実行結果
略
---> 37 print(f"{ai[0].__name__} VS {ai[1].__name__}")
39 mb = Marubatsu()
41 # ai[0] VS ai[1] と ai[1] VS a[0] の対戦を match_num 回行い、通算成績を数える
AttributeError: 'tuple' object has no attribute '__name__'
上記のエラーメッセージは、以下のような意味を持ちます。
-
AttrubuteError
オブジェクトの属性(attribute)に関するエラー -
'tuple' object has no attribute 'name'
tuple というオブジェクト(object)は、__name__という属性(attribute)を持たない(has no)
上記の エラー が 発生する理由 は以下の通りです。
-
ai_matchの 仮引数aiには、[ai11s(mb, score_201=2, score_102=1, score_012=-1), ai10s]という list が 代入 される - 上記の エラーが発生 する
print(f"{ai[0].__name__} VS {ai[1].__name__}")の 行 では、ai[0]とai[1]に 対する処理 を行う -
ai[0]に 代入 されるのは、ai11s(mb, score_201=2, score_102=1, score_012=-1)というai11sの 関数呼び出し の 返り値 であり、その値 はai11sが 選択 した 着手 を表す(1, 1)のような tuple である - 従って、
print(f"{ai[0].__name__} VS {ai[1].__name__}")のai[0].__name__では、(1, 1).__name__という、tuple に対する__name__属性の値 を 参照する という 処理 が行われる -
tuple には
__name__という 属性 は 存在しない ので、上記 のような エラーが発生 する
先程のプログラムの 問題点 は、仮引数 ai に 代入 する list の要素 に、関数オブジェクト を 記述する必要 があるにも関わらず、関数呼び出し を 記述 してしまった点にあります。
ai_match への仮引数の追加
ai_match の 問題点 は、対戦 を行う AI の 処理 を行う 関数オブジェクト を 代入 する 仮引数 は 存在するが、それらの 関数 を 呼び出す際 に 記述する実引数 を 代入 する 仮引数 が 存在しない 点です。そこで、ai_match に、そのような 仮引数を追加 することにします。
まず、仮引数 に 代入 する データ の データ型 と、名前 を 決める必要 があります。ai_match は、2 種類 の AI の 関数を呼び出す 処理を行うので、それぞれの AI ごとに、個別 の パラメータのデータ を 記述 する 必要 があります。そのため、仮引数 に 代入 するデータの データ型 は list2にすればよいでしょう。list の 要素 に 記述 する データ は、AI が 評価値 を 計算する際 に 利用 する パラメータ なので、仮引数 の 名前 を parameters の 略 である params にすることにします。
従って、ai_match の 定義 の 1 行目 を 下記 のプログラムのように 修正 します。
def ai_match(ai, params, match_num=10000):
修正箇所
-def ai_match(ai, match_num=10000):
+def ai_match(ai, params, match_num=10000):
仮引数 params を利用した関数の呼び出し
次に、この 仮引数 params に 代入 する list の要素 に どのようなデータ を 記述 し、どのように して そのデータ を、AI の関数 を 呼び出す際 の 実引数に記述 するかを 説明 します。その 方法 は、初心者の方にはおそらく思いつくことはできないと思いますが、以前の記事で説明した マッピング型の展開 を使って 行う ことが できます。
おそらく忘れてしまった方が多いのではないかと思いますので、マッピング型の展開 を おさらい します。マッピング型の展開 とは、dict などの マッピング型 の データ の キー と キーの値 を、キーワード引数 に 変換 したものと みなして、関数呼び出しを行う という 処理 で、マッピング型 の 先頭 に ** を 記述 します。例えば、下記 のプログラムの 1 行目 のプログラムは、マッピング型の展開 を使って、2 ~ 7 行目 のように 記述できます。
なお、実行結果 は、先程実行した、下記の 1 行目 のプログラムの 実行結果 が 2 回続けて表示 されるので、省略 します。
1 ai11s(mb, score_201=1, score_102=2, score_012=3)
2 param = {
3 "score_201": 1,
4 "score_102": 2,
5 "score_012": 3
6 }
7 ai11s(mb, **param)
行番号のないプログラム
ai11s(mb, score_201=1, score_102=2, score_012=3)
param = {
"score_201": 1,
"score_102": 2,
"score_012": 3
}
ai11s(mb, **param)
従って、ai_match の params に 代入 する list の要素 には、それぞれの AI の 関数 を 呼び出す際 に 実引数に記述 する キーワード引数を表す dict を 記述 し、AI の関数 を 呼び出す際 に、マッピング型の展開 を 記述すれば良い ことが 分かります。
ただし、実際 の マッピング型の展開 の 記述 は、play メソッドに 記述する必要 があります。その理由は、下記のプログラムのように、AI の関数 を 呼び出す処理 は、ai_match ではなく、play メソッドで 行っている からです。
def ai_match(ai, params, match_num=10000):
略
for _ in range(match_num):
# ai_match では、play メソッドを呼び出す処理を行っている
count_list[0][mb.play(ai, verbose=False)] += 1
count_list[1][mb.play(ai=[ai[1], ai[0]], verbose=False)] += 1
略
def play(self, ai, verbose=True):
略
if ai[index] is not None:
# 実際の AI の関数呼び出しは、ここで行われている
x, y = ai[index](self)
略
play メソッドと ai_match の修正
play メソッドは 下記 のプログラムのように 修正 します。
-
1 行目:仮引数
paramsを 追加 する -
4 行目:AI の関数 を 呼び出す際 に、対応 する
paramsの 要素 の マッピング型の展開 を 実引数に記述 する(局所変数indexが 対応する AI の インデックス を表す)
1 def play(self, ai, params, verbose=True):
元と同じなので省略
2 # ai が着手を行うかどうかを判定する
3 if ai[index] is not None:
4 x, y = ai[index](self, **params[index])
元と同じなので省略
5 Marubatsu.play = play
行番号のないプログラム
def play(self, ai, params, verbose=True):
# 〇×ゲームを再起動する
self.restart()
# ゲームの決着がついていない間繰り返す
while self.status == Marubatsu.PLAYING:
# ゲーム盤の表示
if verbose:
print(self)
# 現在の手番を表す ai のインデックスを計算する
index = 0 if self.turn == Marubatsu.CIRCLE else 1
# ai が着手を行うかどうかを判定する
if ai[index] is not None:
x, y = ai[index](self, **params[index])
else:
# キーボードからの座標の入力
coord = input("x,y の形式で座標を入力して下さい。exit を入力すると終了します")
# "exit" が入力されていればメッセージを表示して関数を終了する
if coord == "exit":
print("ゲームを終了します")
return
# x 座標と y 座標を要素として持つ list を計算する
xylist = coord.split(",")
# xylist の要素の数が 2 ではない場合
if len(xylist) != 2:
# エラーメッセージを表示する
print("x, y の形式ではありません")
# 残りの while 文のブロックを実行せずに、次の繰り返し処理を行う
continue
x, y = xylist
# (x, y) に着手を行う
try:
self.move(int(x), int(y))
except:
print("整数の座標を入力して下さい")
# 決着がついたので、ゲーム盤を表示する
if verbose:
print(self)
return self.status
Marubatsu.play = play
修正箇所
-def play(self, ai, verbose=True):
+def play(self, ai, params, verbose=True):
元と同じなので省略
# ai が着手を行うかどうかを判定する
if ai[index] is not None:
- x, y = ai[index](self)
+ x, y = ai[index](self, **params[index])
元と同じなので省略
Marubatsu.play = play
次に、ai_match を、下記のプログラムの 4、5 行目 のように、play メソッドに params の 実引数 を 追加 するように 修正 します。なお、元 の プログラム の 5 行目 では、手番 を 入れ替えて対戦を行う 際に、ai の要素 の 順番 を 入れ替える処理 を ai=[ai[0], a[1]] のように記述していましたが、以前の記事で説明したように、スライス表記 を 利用する ことで、list の 要素の順番 を 逆 にした list は、ai[::-1] のように 簡潔 に 記述できる ので、今回の記事では その方法 で ai や params の 要素 を 逆にした list を 記述 しています。
1 from collections import defaultdict
2
3 def ai_match(ai, params, match_num=10000):
元と同じなので省略
4 for _ in range(match_num):
5 count_list[0][mb.play(ai, params, verbose=False)] += 1
6 count_list[1][mb.play(ai=ai[::-1], params=params[::-1], verbose=False)] += 1
元と同じなので省略
行番号のないプログラム
from collections import defaultdict
def ai_match(ai, params, match_num=10000):
print(f"{ai[0].__name__} VS {ai[1].__name__}")
mb = Marubatsu()
# ai[0] VS ai[1] と ai[1] VS a[0] の対戦を match_num 回行い、通算成績を数える
count_list = [ defaultdict(int), defaultdict(int)]
for _ in range(match_num):
count_list[0][mb.play(ai, params, verbose=False)] += 1
count_list[1][mb.play(ai=ai[::-1], params=params[::-1], verbose=False)] += 1
# ai[0] から見た通算成績を計算する
count_list_ai0 = [
# ai[0] VS ai[1] の場合の、ai[0] から見た通算成績
{
"win": count_list[0][Marubatsu.CIRCLE],
"lose": count_list[0][Marubatsu.CROSS],
"draw": count_list[0][Marubatsu.DRAW],
},
# ai[1] VS ai[0] の場合の、ai[0] から見た通算成績
{
"win": count_list[1][Marubatsu.CROSS],
"lose": count_list[1][Marubatsu.CIRCLE],
"draw": count_list[1][Marubatsu.DRAW],
},
]
# 両方の対戦の通算成績の合計を計算する
count_list_ai0.append({})
for key in count_list_ai0[0]:
count_list_ai0[2][key] = count_list_ai0[0][key] + count_list_ai0[1][key]
# それぞれの比率を計算し、ratio_list に代入する
ratio_list = [ {}, {}, {} ]
for i in range(3):
for key in count_list_ai0[i]:
ratio_list[i][key] = count_list_ai0[i][key] / sum(count_list_ai0[i].values())
# 各行の先頭に表示する文字列のリスト
item_text_list = [ Marubatsu.CIRCLE, Marubatsu.CROSS, "total" ]
# 通算成績の回数と比率の表示
width = max(len(str(match_num * 2)), 7)
diff_list = [ ("count", count_list_ai0, f"{width}d"),
("ratio", ratio_list, f"{width}.1%") ]
for title, data, format in diff_list:
print(title, end="")
for key in data[0]:
print(f" {key:>{width}}", end="")
print()
for i in range(3):
print(f"{item_text_list[i]:5}", end="")
for value in data[i].values():
print(f" {value:{format}}", end="")
print()
print()
修正箇所
from collections import defaultdict
-def ai_match(ai, match_num=10000):
+def ai_match(ai, params, match_num=10000):
元と同じなので省略
for _ in range(match_num):
- count_list[0][mb.play(ai, verbose=False)] += 1
+ count_list[0][mb.play(ai, params, verbose=False)] += 1
- count_list[1][mb.play(ai=[ai[1], ai[0]], verbose=False)] += 1
+ count_list[1][mb.play(ai=ai[::-1], params=params[::-1], verbose=False)] += 1
元と同じなので省略
修正したパラメータでの ai10s との対戦
下記は、修正後 の パラメータ で ai11s VS ai10s の 対戦 を行うプログラムです。ai10s のように、パラメータ が 存在しない 場合は、空の dict を 記述 します。これは、空の dict に対して マッピング型の展開 を行った場合は 何も行われない からです。
param_ai11s = {
"score_201": 2,
"score_102": 1,
"score_012": -1
}
ai_match(ai=[ai11s, ai10s], params=[param_ai11s, {}])
実行結果
ai11s VS ai10s
count win lose draw
o 0 0 10000
x 0 0 10000
total 0 0 20000
ratio win lose draw
o 0.0% 0.0% 100.0%
x 0.0% 0.0% 100.0%
total 0.0% 0.0% 100.0%
下記は、パラメータ の 修正前 と 修正後 の ai11s VS ai10s の 対戦結果 の 表 です。
| 関数名 | o 勝 | o 負 | o 分 | x 勝 | x 負 | x 分 | 勝 | 負 | 分 |
|---|---|---|---|---|---|---|---|---|---|
| 修正前 | 22.2 | 0.0 | 77.8 | 0.0 | 50.5 | 49.5 | 11.1 | 25.3 | 63.6 |
| 修正後 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 100.0 |
修正後 の ai11s は、4 手目 で 必ず引き分け になる 合法手を選択 するようになったので、ai11s が × を担当 した 場合 に 必ず引き分けになる のは 想定通り で 問題 は ありません。一方、ai11s が 〇 を担当 した 場合 は、修正する ことで 勝率 が 22.1 % から 0 % に 減ってしまう という、新しい問題 が 発生 しています。
長くなったので今回はここまでにします。何故このようなことが起きるかについて、少し考えてみて下さい。このようなことが起きる理由については次回の記事で説明します。
もう一つの修正方法の確認
おまけ として、『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 減らす という、下記の、2 つめ の 修正方法 でも 目的 を 達成できる ことを示します。
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 より大きな値 にする
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 1 未満 の 正の値 にする
具体的には、下記の表 のように、『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 0.5 に 減らしてみる ことにします。
| 評価値 | |
|---|---|
| 「自 2 敵 0 空 1」が 1 つ の場合 | 2 |
| 「自 1 敵 0 空 2」が 1 つあたり | 1 → 0.5 |
| 「自 0 敵 1 空 2」が 1 つあたり | -1 |
下記 は、そのように 修正 した場合の 表 です。特に 問題はなさそう です。
| 順位 | 局面の状況 | 個別 | 評価値 |
|---|---|---|---|
| 1 | 真ん中のマスに着手している | 300 |
|
| 2 | 自分が勝利している | 200 |
|
| 4 | 「自 2 敵 0 空 1」が 2 つ以上存在する | 100 |
|
| 5 |
「自 2 敵 0 空 1」が 1 つ存在する 「自 1 敵 0 空 2」が x 個存在する 「自 0 敵 1 空 2」が y 個存在する |
1 (0~1)0.5 × x (0~4)-y (-8~0) |
-8~5 |
| 3 | 相手が勝利できる | -100 |
| 「201」 | 「021」 | 「102」 | 「012」 | 評価値 | ||
|---|---|---|---|---|---|---|
| 評価値 | 1:+12~: 100
|
-100 |
1 つで+0.5
|
1 つで-1
|
||
| 1 |  |
1 | 1 | 4 | -2.5 | |
| 2 |  |
1 | 1 | 3 | -1.5 | |
| 3 |  |
2 | 3 | -2 |
下記は、4 手目 で、このパラメータ で ai11s を 実行 するプログラムです。
mb = Marubatsu()
mb.move(1, 1)
mb.move(0, 0)
mb.move(2, 2)
param = {
"score_201": 1,
"score_102": 0.5,
"score_012": -1,
}
ai11s(mb, **param)
実行結果(長いのでクリックして開いてください)
Start ai_by_score
Turn x
x..
.o.
..O
legal_moves [(1, 0), (2, 0), (0, 1), (2, 1), (0, 2), (1, 2)]
====================
move (1, 0)
Turn o
xX.
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -2.5 best score -inf
UPDATE
best score -2.5
best moves [(1, 0)]
====================
move (2, 0)
Turn o
x.X
.o.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1.5 best score -2.5
UPDATE
best score -1.5
best moves [(2, 0)]
====================
move (0, 1)
Turn o
x..
Xo.
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 4,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 1,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -2.5 best score -1.5
====================
move (2, 1)
Turn o
x..
.oX
..o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -2.0 best score -1.5
====================
move (0, 2)
Turn o
x..
.o.
X.o
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 1,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1,
Markpat(last_turn=2, turn=0, empty=1): 1})
score -1.5 best score -1.5
APPEND
best moves [(2, 0), (0, 2)]
====================
move (1, 2)
Turn o
x..
.o.
.Xo
defaultdict(<class 'int'>,
{Markpat(last_turn=0, turn=1, empty=2): 3,
Markpat(last_turn=1, turn=0, empty=2): 2,
Markpat(last_turn=1, turn=1, empty=1): 2,
Markpat(last_turn=1, turn=2, empty=0): 1})
score -2.0 best score -1.5
====================
Finished
best score -1.5
best moves [(2, 0), (0, 2)]
実行結果 から、上記の表 のように 評価値 が 計算される ことが 確認 できます。また、下記の 実行結果 の 最後の 2 行 から、合法手 2 のみ が 選択される ことが 確認 できます。
best score -1.5
best moves [(2, 0), (0, 2)]
下記は、修正後 の パラメータ で、ai10s と 対戦 するプログラムです。こちらのパラメータでも、すべての場合 で 引き分けになる ことが 確認 できました。
param_ai11s = {
"score_201": 1,
"score_102": 0.5,
"score_012": -1
}
ai_match(ai=[ai11s, ai10s], params=[param_ai11s, {}])
実行結果
ai11s VS ai10s
count win lose draw
o 0 0 10000
x 0 0 10000
total 0 0 20000
ratio win lose draw
o 0.0% 0.0% 100.0%
x 0.0% 0.0% 100.0%
total 0.0% 0.0% 100.0%
今回の記事のまとめ
今回の記事では、ai10s VS ai11s で、ai11s が 負ける 場合がある 原因 を 検証 し、その 問題点 を 解決する方法 を紹介しました。また、問題点 を 解決するため に、評価値 を 計算 するための パラメータ を 修正する方法 について紹介しました。
下記は、問題点 の 解決方法 と、パラメータ の 修正方法 です。
解決方法: 4 手目 で、(0, 2)(または (2, 0))のみ に 着手 が 行われる ようにする
パラメータの修正方法:以下の いずれか の 方法 で パラメータを修正 する
- 『「自 2 敵 0 空 1」が 1 つ の場合』の 評価値 を 1 より大きな値 にする
- 『「自 1 敵 0 空 2」が 1 つあたり 』の 評価値 を 1 未満 の 正の値 にする
一方、パラメータの修正 によって、ai11s が 負ける 場合があるという 問題 は 解決できました が、今度は ai11s VS ai10s で、ai11s が 勝てなくなる という 新しい問題 が 発生しました。次回の記事ではそのような問題が発生する原因などについて説明します。
本記事で入力したプログラム
以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。
以下のリンクは、今回の記事で更新した marubatsu.py です。
以下のリンクは、今回の記事で更新した ai.py です。
次回の記事