Pythonで〇×ゲームのAIを一から作成する その59 演繹法とヒューリスティックによる問題の解決

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

これまでに作成した AI

これまでに作成した AI の アルゴリズム は以下の通りです。

ルール	アルゴリズム
ルール1	左上から順 に 空いているマス を探し、最初に見つかったマス に 着手 する
ルール2	ランダム なマスに 着手 する
ルール3	真ん中 のマスに 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール4	真ん中、隅 のマスの 順 で 優先的 に 着手 する 既に 埋まっていた場合 は ランダム なマスに 着手 する
ルール5	勝てる場合 に 勝つ そうでない場合は ランダム なマスに 着手 する
ルール6	勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール6改	勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール7	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手の勝利 を 阻止 する そうでない場合は ランダム なマスに 着手 する
ルール7改	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は ランダム なマスに 着手 する
ルール8	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ以上 存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する
ルール9	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う そうでない場合は ランダム なマスに 着手 する
ルール10	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 2 つを 総合的に判断 して着手を行う 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う そうでない場合は ランダム なマスに 着手 する
ルール11	真ん中 のマスに 優先的 に 着手 する そうでない場合は 勝てる場合 に 勝つ そうでない場合は 相手 が 勝利できる 着手を 行わない そうでない場合は、次 の 自分の手番 で 必ず勝利できる ように、「自 2 敵 0 空 1」が 2 つ以上存在する 局面になる着手を行う そうでない場合は、以下 の 3 つを 総合的に判断 して着手を行う 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う 相手 が 不利になる ように、「自 0 敵 1 空 2」が 最も少ない 着手を行う そうでない場合は ランダム なマスに 着手 する

基準となる ai2 との 対戦結果（単位は %）は以下の通りです。太字 は ai2 VS ai2 よりも 成績が良い 数値を表します。欠陥 の列は、アルゴリズム に 欠陥 があるため、ai2 との 対戦成績 が 良くても強い とは 限らない ことを表します。欠陥の詳細については、関数名のリンク先の説明を見て下さい。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分	欠陥
ai1 ai1s	78.1	17.5	4.4	44.7	51.6	3.8	61.4	34.5	4.1	あり
ai2 ai2s	58.7	28.8	12.6	29.1	58.6	12.3	43.9	43.7	12.5
ai3 ai3s	69.3	19.2	11.5	38.9	47.6	13.5	54.1	33.4	12.5
ai4 ai4s	83.0	9.5	7.4	57.2	33.0	9.7	70.1	21.3	8.6	あり
ai5 ai5s	81.2	12.3	6.5	51.8	39.8	8.4	66.5	26.0	7.4
ai6	88.9	2.2	8.9	70.3	6.2	23.5	79.6	4.2	16.2
ai6s	88.6	1.9	9.5	69.4	9.1	21.5	79.0	5.5	15.5
ai7 ai7s	95.8	0.2	4.0	82.3	2.4	15.3	89.0	1.3	9.7
ai8s	98.2	0.1	1.6	89.4	2.5	8.1	93.8	1.3	4.9
ai9s	98.7	0.1	1.2	89.6	2.4	8.0	94.1	1.3	4.6
ai10s	97.4	0.0	2.6	85.6	2.6	11.7	91.5	1.3	7.2
ai11s	98.1	0.0	1.9	82.5	1.9	15.6	90.3	1.0	8.7	あり

今回の記事の内容

以前の記事で、〇×ゲーム の 強い AI を 作成 するための 条件 を、必要条件、十分条件、その どれでもない条件 に 分類 して 説明 を行いましたが、その際にはまだ 最強の AI とはどのようなものであるかの 説明 を 行っていません でした。

そのため、これまでの記事 で 行ってきた、さまざま な ルールの条件 を 考え、その 条件を処理 するプログラムを 記述 することで、強い AI を 作成 するという 方法 が、最強の AI の 作成 に つながる方法であるか どうかは 説明 していません。

前回の記事で、二人零和有限確定完全情報ゲーム における、最善手 と 最強の AI を 下記 のように 定義 しました。

最善手 とは、お互い が 最善手 を 選択し続けた 場合に、自分 にとって 最も有利 となる 合法手 のことである。

最強の AI とは、すべての局面 で、最善手 を 選択する AI のことである。

今回の記事では、この定義 に 基づいて、〇×ゲーム の 最強の AI を作るための 条件 を説明し、これまでの手順 と、最強の AI を 作る手順 の 関係 について 説明 します。

用語の定義

前回の記事で「最強の AI」の 定義 を行いましたが、これまでの記事 では、「これまでに作成 した 最強の AI」のように、全く同じ用語 を、異なる意味 で 利用 してきました。後者 は、「これまでに作成 した AI の中」での 最も強い AI という 意味 なので、前者 の用語とは 意味が異なります。これでは 紛らわしい ので、以後は、後者の場合 は、これまでに作成 した中で「最も強い AI」のように、用語 を 使い分ける ことにします。

用語	用語の意味
最強の AI	前回の記事で定義した、文字通り の 最強 の AI のことを表す
最も強い AI	いくつかの AI の中 で 最も強い AI という意味

〇×ゲームの最強の AI の再定義

これまで に行ってきた AI の 作成方法 によって、最強の AI を 作成できる ことを 示す ために、下記 の 最強の AI の 定義 を、別の言い方 で 再定義 することにします。

「最強の AI とは、すべての局面 で、最善手 を 選択する AI のことである」

前回の記事のノートで、下記 のような 説明 を行いました。

• 最善手 を 選択しない 場合は 局面の状況 が 悪化 する
• 〇×ゲーム の場合は、状況の悪化 には 「必勝 → 引き分け」、「必勝→必敗」、「引き分け→必敗」という 3 種類 がある
• 合法手 を、状況 が 何段階悪化するか によって 分類 すると、下記の表 のようになる

この表は、局面の状況 で、それぞれに 分類される着手 を 行った場合 に、局面の状況 が どのように変化するか を表します。空欄 は 合法手 が 存在しない ことを表します。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗
必敗	必敗

先程説明したように、最強の AI の 定義 は「すべての局面 で 最善手 を 選択 する」なので、上記の表 を使って 最強の AI の 再定義 を行うと、「すべての局面 で、下記の 太字の合法手 を 選択 する」のようになります。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗
必敗	必敗

表からわかるように、必敗の局面 では、すべて の 合法手 が 最善手 になるので、すべての AI が 必敗の局面 では 最善手 を 選択 します。従って、上記の表から 必敗の局面 の 状況 を 削除 することができます。

最強の AI とは、下記 の 表 の すべて の 局面の状況 で、太字 の 合法手 を 選択する AI である。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

これまでに作成したルールの条件の意味

これまで に 作成 した ルール の 条件 によって、最強の AI に 近づく ことができる 理由 を 説明 します。

これまで の記事で 作成 した AI の ルールの条件 は、下記 を 目指す ものです。

1. 真ん中 のマスに 着手 する
2. 自分 が 勝利できる
3. 相手 が 勝利できない
4. 自分 が 勝利できそうになる
5. 相手 が 勝利できなさそうになる

上記の条件のうちの、条件 2 と 3 は、下記 のように 言い換える ことができます。

2. 自分の必勝 の 局面 で 最善手 を 選択 する
3. 自分の必敗 の 局面以外 で、必敗の局面 になるような 合法手 を 選択しない

この 2 つ の それぞれの条件 と、最強の AI の 定義 との 関係 について説明します。

自分が勝利できる条件

「自分 が 勝利できる」条件 は、必勝の局面 で、最善手 を 選択 するという 条件 です。従って、この条件 は、必勝の局面 で 下記の表 の 青字 の合法手を 選択 し、その結果 赤字 の合法手が 選択されなくなります。一方、この条件 は、引き分けの局面 では 適用されない ので、引き分けの局面 では すべての合法手 が 選択 される 可能性 が あります。

• 太字：最強の AI が 選択 する 必要がある 合法手
• 下線：ルールの条件 によって 選択される 合法手
• 青字：ルールの条件 によって、結果 として 選択 が 行われる 合法手
• 赤字：ルールの条件 によって、結果 として 選択 が 行われなくなる 合法手
• 黒字：ルールの条件 とは 無関係 な合法手で、選択 が行われる 可能性がある 合法手

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

表から、この条件 は 引き分けの局面 で、最善手ではない、必敗の局面 につながる 合法手 が 選択 される 可能性がある という点が、最強の AI の 定義 と 異なります。

上記の場合は、「必勝」の部分に 青字 と 下線 の 両方が設定 されているので、青字 と 下線 の 違い が わかりづらい と思います。次の例 では、青字 と 下線 が 別々 に 設定される ので、その違い については 次の例 で 説明 します。

相手が勝利できない条件

「相手 が 勝利できない」条件 は、必敗の局面 に つながる合法手 を 選択しない という 条件 です。従って、この条件 によって、下図 の 取り消し線 が 引かれている、必敗の局面 に つながる合法手 が 選択されない ようにすることが できます。その結果、それ以外 の 青字 の 合法手 が 選択される ようになります。

• 取り消し線：ルールの条件 によって 選択 を 行わない 合法手

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

表から、この条件 は 必勝の局面 で、最善手ではない、引き分けの局面 につながるの 合法手 が 選択 される 可能性がある という点が、最強の AI の 定義 と 異なります。

先程 の場合と 異なり、青字 の 合法手 は、条件 によって 直接選択 される 合法手ではなく、必敗の局面 に つながる合法手 を 選択 から 除外する ことで、結果 として 選択される ようになった 合法手 です。そのため、上記 の表では、選択される 青字 の 合法手 には 下線 を 引きません。

１ つ前 の 自分が勝利できる 条件の 表で 、「必勝の局面」の 赤字 の 合法手 に 取り消し線 が 引かれていない理由 も 同様 で、赤字 の 合法手 は、ルールの条件 によって 直接除外 されている わけではなく、下線 の 合法手 を 選択する ことによって、結果 として 除外された からです。

最強の AI の 定義 を 別の言い方 で 再定義 した 理由 は、そのように定義し直すことで、ルールの条件 が 選択 する 合法手 を、最強の AI の 定義 の 表 を使って 説明できるようになる からです。

2 つの条件の組み合わせ

「自分 が 勝利できる」条件と「相手 が 勝利できない」条件を 組み合わせる ことで、下記 の表ように、選択 される 青字 の 合法手 が、最善手 を表す 太字 の 合法手のみ になるので、すべて の 局面の状況 で、最善手のみ が 選択される ようになります。従って、最強の AI を 作成する ためには、「自分 が 勝利できる」条件と、「相手 が 勝利できない」条件の 2 つの条件 を 組み合わせればよい ことが わかります。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

従って、最強の AI の 定義 を、以下 のように、さらに 再定義 することができます。

最強の AI とは、下記の 両方の条件 を 満たす AI である。

1. 必勝の局面 になる 合法手 が 存在する場合 は、必ずその合法手 を 選択する
2. 必敗以外の局面 で、必敗の局面 につながる 合法手 を 選択しない

上記の事から、これまでの 強い AI を 作成する ための ルール の中の 下記の条件 が、最強の AI を 作成 するための 正しい条件 であることが 分かります。

• 自分 が 勝利できる
• 相手 が 勝利できない

上記で 両方の条件 を 満たす と説明しましたが、1 つ目 の 条件 が 満たされた場合 は、必敗の局面 になる 合法手 を 選択していない ので、2 つ目 の 条件 は 必ず満たされます。逆に 2 つ 目 の 条件 が 満たされた 場合に、1 つ目 の条件が 満たされる とは 限らない 点に 注意 して下さい。

他の条件の考察

最強の AI の 定義 を 満たす条件 は、他にも存在 します。

例えば、「相手 が 勝利できない」という 条件 の 代わり に、「引き分けの局面 で、引き分けの局面 に つながる 合法手を 選択する」という 条件 はどうでしょうか。下記 は、そのような条件 によって 選択 される 合法手 の 表 です。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

この条件 と、「自分 が 勝利できる」条件を 組み合わせる ことで、下記 の表のように、すべて の 局面の状況 で、最善手のみ が 選択される ようになります。

局面の状況	最善手	1 段階悪化する着手	2 段階悪化する着手
必勝	必勝	引き分け	必敗
引き分け	引き分け	必敗

従って、「引き分けの局面 で、引き分けの局面 に つながる 合法手を 選択する」という 条件 でも 最強の AI を 作成 すること 可能 ですが、この条件 には 大きな欠点 が あります。それは、この条件 で 合法手 を 選択する ためには、局面の状況 が「引き分けの局面」であるか どうかを 判定 する 必要がある ことです。多くの局面 では 局面から、その 局面の状況 が どうなっているか を 判定する ことは 簡単 なこと ではありません。それに対し、「自分 が 勝利できる」という 条件 や、「相手 が 勝利できない」という 条件 は、局面の状況 を 判定 する 必要がない 点が 優れています。

もちろん、「引き分けの局面 で、引き分けの局面 に つながる 合法手を 選択する」という 条件を満たす 合法手を 見つける方法 を 思いつく ことが できれば、その方法 を使って 最強の AI を 作成する ことは 可能 です。

必勝の局面につながる合法手が複数ある場合

実は 先程定義 した下記の 最強の AI の 定義 は、必勝の局面 になる 合法手 の 数が 1 つ の場合は 正しい ですが、複数存在 する場合は 厳密 では ありません。

最強の AI とは、下記の 両方の条件 を 満たす AI である。

1. 必勝の局面 になる 合法手 が 存在する場合 は、必ずその合法手 を 選択する
2. 必敗以外の局面 で、必敗の局面 につながる 合法手 を 選択しない

必勝の局面 になる 合法手 が 複数存在 する場合は、その中 の どの合法手 を 選択 しても、最善手を選択 したことになります。従って、上記の定義 の 1 つ目の条件 は、厳密 には 下記 のようになります。

必勝の局面 になる 合法手 が 存在する場合 は、必ずその合法手 の いずれか を 選択する

例えば、必勝の局面 になる 合法手 が 複数ある 場合は、常に そのうちの 1 つのみを選択 する AI であっても、その中から ランダムに選択 する AI であっても、最強の AI の 定義 を 満たします。前回の記事で説明した、最善手 が 複数存在 する場合は、最強の AI も 複数存在 するという 説明 を 思い出してください。

2 つ目の条件 は、特に 修正する必要 は ありません が、1 つ目 と 2 つ目 の 条件 が 同時に満たされる 合法手が 複数存在した場合 に、その中の どの合法手 を 選択 しても 構わない点 は 上記と同様 です。

下記は、最強の AI の 定義 を 修正 したものです。

最強の AI とは、下記の 両方の条件 を 満たす AI である。

1. 必勝の局面 になる 合法手 が 存在する場合 は、必ずその合法手 の いずれか を 選択する
2. 必敗以外の局面 で、必敗の局面 につながる 合法手 を 選択しない

ところで、この 2 つの条件 は、ルール 8 の時点 ですでに ルール に 組み込まれている ので、ルール 8 を 実装した時点 で 最強の AI に なっていない のは 変 だと 思いませんか？実際には、それにもかかわらず、ルール 9、10、11 のように 条件を追加 することで、AI が 強くなっています。そのようなことが起きる理由について少し考えてみて下さい。

これまでのルールの条件の問題点

これまで に ルール に 組み込んだ「自分 が 勝利できる」や「相手 が 勝利できない」という 条件 には、特定の局面だけ でしか 適用できない という 問題 が あります。

ルール 11 の自分が勝利できる条件の問題点

ルール 11 の「自分 が 勝利できる」条件には 下記 の 2 つの条件 が あります。

1． 勝てる場合 に 勝つ
2． 「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う

これらの条件 が、すべて の 必勝の局面 で 最善手 を 選択 することが できない ことを 示します。下記の 3 つの局面 は、いずれも 〇 の手番 で、〇 の必勝 の 局面 です。

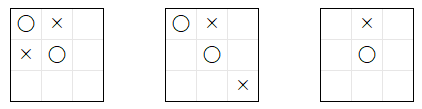
下記は、その 理由 です。

• 左の局面：(2, 2) に 着手 することで 勝利する
• 真ん中の局面：(0, 1) または (0, 2) に 着手 することで、「自 2 敵 0 空 1」が 2 つ以上存在 するようになるので、必勝の局面 である
• 右の局面：(0, 0) に 着手 すると、相手 は 〇 の勝利 を 阻止するため に (2, 2) に 着手 する 必要 がある。その結果、上記 の 真ん中の局面になる ため、必勝の局面 である

実は、右の局面 は、(1, 2) 以外 は、すべて 必勝の局面 につながる 最善手 です。興味がある方はその理由を実際に確認してみて下さい。

下記は、上記の 3 つの局面 に対して、ルール 11 の「自分 が 勝利できる」2 つの条件 で 最善手 を 選択できるか どうかを表す表です。表から わかるように、右の局面 に対して、どちらの条件 も 最善手 を 選択 することは できません。

	左の局面	真ん中の局面	右の局面
勝てる場合 に 勝つ	〇	×	×
「自 2 敵 0 空 1」が 2 つ以上 存在 する着手を行う	×	〇	×

つまり、ルール 11 の「自分 が 勝利できる」2 つの 条件だけ では、すべて の 必勝の局面 で 最善手を選択 するには、条件が足りない ということです。

ルール 11 の相手が勝利できない条件の問題点

ルール 11 の「相手 が 勝利できない」条件 は、具体的には『「自 0 敵 2 空 1」が 存在 する着手を 行わない』という条件ですが、この条件 だけでは、すべて の 必敗以外の局面 で 必敗の局面 に つながる合法手 を 選択しない ようにすることは できません。具体例 として、下図の局面 があります。証明 は 今後の記事 で行いますが、この局面の状況 は、「引き分けの状況」です。

この局面 では、(0, 0) などの 隅の合法手 が 最善手 で、(1, 0) などの 辺の合法手 は 最善手 では ありません。(1, 0) が 最善手ではない理由 は、(1, 0) に 着手 すると 先程 の図の 右の局面 になり、その局面 は 先程説明 したように、× の必敗の局面 であるからです。

しかし、『「自 0 敵 2 空 1」が 存在 する着手を 行わない』という 条件 だけでは、上記の局面 で (1, 0) の 着手 の 選択 を 阻止 することは できません。

上記 から、ルール 11 の 条件 は、最強の AI の定義 を 満たさない ことがわかります。

これまでの AI の作成の手順の意味と問題点

これまで の記事で 作成 した、下記の AI の ルールの条件 のうち、2 と 3 は、最強の AI の 定義 の 条件と同じもの です。従って、これまで の 強い AI の 作成の手順 の 方針 は 間違っていない ことが わかりました。

1. 真ん中 のマスに 着手 する
2. 自分 が 勝利できる
3. 相手 が 勝利できない
4. 自分 が 勝利できそうになる
5. 相手 が 勝利できなさそうになる

また、これまでに 作成 した ルールの条件 によって、最強の AI が 作れていない のは、それらが 最強の AI の 定義 の 条件 の 一部しか満たさない ことが 原因 です。

演繹法とヒューリスティックによる問題の解決

最強の AI を 作成 するための 条件 と、これまでに作成 してきた ルール の 問題点 が わかりました が、その 問題点 を 解決 することは 簡単ではありません。その 理由を説明 するために、問題を解決 する 手法 を 分類 し、それぞれの分類 の 性質 を 説明 します。

演繹法

演繹法 とは、問題 の 解決方法 を、問題 の 前提 から 論理的 に 導き出す方法 です

参考までに、演繹の Wikipedia のリンクを下記に示します。

例えば、ルール 11 の「自分 が 勝利できる」合法手 の 条件 である、『「自 2 敵 0 空 1」が 2 つ以上存在 する着手を行う』という条件は、以前の記事で、〇×ゲーム の 前提 となる ルールから、筋道をたてて、論理的¹ に 見つけた条件 です。このような 演繹法 で 見つけた手順 には、下記 のような 性質 があります。

• 前提 が 正しければ、演繹 によって 導き出された答え は、100 % 正しい
• 手順に従う ことができれば、100 % 問題を解決する ことが できる
• 手順の意味 を 理解できなくても、手順を覚えれば 誰でも利用 することが できる

逆に言えば、前提 が 間違っていれば、正しい答え を 導き出す ことは できません。例えば、「私は万能の神である」という 間違った前提 からは、「私は 万能なので 空を飛べる」などの、間違った答え を 導くこと が できてしまいます。従って、演繹法 では 前提が正しい ことが 非常に重要 です。

演繹法 の 代表例 としてよく取り上げられるのは、「A ならば B である」、「B ならば C である」という 事実 から「A ならば C」であるという 事実 を 導く、三段論法 があります。本記事 でこれまでに何度も行ってきた、何かを説明した後で、その 説明を元 に、「従って 〇〇である」のような 説明 は 演繹法 を使った 説明 です。

他の 演繹法 の 例 としては、下記の $ax^2 + by + c = 0$ という 二次方程式 の 解の公式 があります。この 公式 は、論理的 な 手順 で 導かれたもの であり、公式の意味 を 理解しなくても、誰でも この 公式を使って、二次方程式の解 を 求める ことが できます。

$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$

二次方程式 の 解の公式 は、複雑な問題 でも、答え を 計算する方法 さえ わかっていれば、誰でも答えを求める ことが できる という 例 として出したものです。

〇×ゲーム に 二次方程式 の 解の公式 は 必要ない ので、上記の公式の 意味 や 使い方 を 理解 する必要は ありません。

演繹法 の 問題点 は、世の中の 多くの問題 は、演繹法 を使って 答えを求める手順 を 見つける ことが できない ことです。また、手順 を みつける ことが できても、それを 実際に行う ためには、時間がかかりすぎる ような 問題 もあります。

例えば、何らかの スポーツ で 世界最強のチーム を 見つける方法 として、総当たり戦 があります。総当たり戦 を行う 手順 は、全チーム の 全ての組み合わせ で 対戦を行う というものですが、実際に 総当たり戦を行う ためには、チーム数 が $x$ の場合は、$x(x-1)/2$ 回の 対戦を行う必要 があります。例えば、100 チーム で 総当たり戦 を行う場合は $100 * 99 / 2 =$ 4950 回 もの 対戦 を 行う必要 があります。

問題 を 解くための方法 が わからない例 としては、「金持ちになる」という問題があります。おそらく、誰でも この手順を行えば、金持ちになる ことができるという 手順 は 存在しない でしょう。他にも、「嘘を見抜く」という問題に対する 確実な手順 も 存在しない でしょう。一般的 に、現実の世界 の 多くの問題 は、物事 の 因果関係²が 複雑 に 絡み合う 場合が 多い ため、問題を解く ための、方法 を みつける ことは 不可能 です。

近似解

100 % 正しい 答えを 得る手順 が わからなくても、正解 に 一定以上近い答え を 得る手順 であれば 知ることができる 場合があります。そのような答え の事を 近似解 と呼び、正しい答え と 近似解の差 の事を 誤差 と呼びます。例えば、鉛筆の長さ を 正確に求める ことは 不可能 ですが、定規 を使えば、最大で 1 mm の 誤差 で 長さを測る ことが できます。なお、近似解 を 求める方法 も、演繹法の一種 です。

近似解に対して、100 % 正しい答え の事を、最適解 と呼びます。

近似解 はには 必ず誤差 が あります が、正解より も 簡単に求める ことが できる 場合が多いので、誤差 が 問題にならない ような 場合 などで 良く使われます。

例えば、986 × 1023 という 計算を行う のは 面倒 ですが、大雑把な答え でも かまわない 場合は、どちらも 1000 に近い数字 であることから、1000 × 1000 = 100 万 という 簡単な計算 で求められる 近似解で代用 することが できます。

先程 の 100 チーム の 総当たり戦 を行う スポーツの例 では、下記の方法で、最も強いチーム の 近似解 を 求める ことが できます。

• 100 チーム を 10 チームずつ に グループ分け する
• グループごと の 10 チーム の 総当たり戦 を行う
• グループで優勝 した 10 チーム で 総当たり戦 を行う

この方法 の場合の 試合数 は 下記 の方法で 求める ことが できます。

• 10 チームの総当たり戦の 試合数 は、$10 × 9 / 2 =$ 45 試合 である
• 10 チームの総当たり戦は、10 グループ と、決勝の総当たりで、11 回 行う
• 従って、総試合数は、 $45 × 11 = $ 495 試合 である

このように、近似解 の場合の 試合数 は、先ほどの 100 チーム で 総当たり戦 を行った 場合 である 4950 試合 の 1/10 になり、大幅に減らす ことが できます。

一方、たまたま 強豪チーム が 多いグループ に 当たってしまった ため、強いチーム が グループ の リーグ戦 で 勝ち残れない というようなことがあるため、優勝チーム が 本当 に 世界一のチーム であるとは 限らない という 誤差 があります。

なお、最初から勝ち抜き戦 で 優勝を決める 場合は、試合数 は 99 試合 ですみますが、さらに精度が落ちる でしょう。夏の全国高校野球選手権 は、毎年 約 3500 もの チームが参加 するので、精度を犠牲 にして、最初から勝ち抜き戦 を 採用 しています。

ルール 11 の 下記の 3 つの条件 は、いずれも、最強の AI の 定義 の 条件 の 一部を満たす 条件なので、ルール 11 の 下記の条件 のみによって 作られた AI は、最強の AI の 近似解 ということができます。

• 勝てる時 に 勝つ
• 「自 1 敵 2 空 1」が存在 する 着手 を 行わない
• 「自 2 敵 0 空 1」が 2 つ以上存在 する 着手 を 行う

一方、近似解 であっても 求める手順 が わからなかったり、手順 を行うために 時間がかりすぎる 場合があります。また、近似解 では、精度 が 低すぎる という場合もあります。そのような場合は、ヒューリスティック という 手法 が使われます。

ヒューリスティック

ヒューリスティック は、心理学 や、コンピュータ科学 などで使われる 用語 で、その 意味 は 心理学 と コンピューター科学 で 若干異なります。

帰納法とは何か

いずれの場合 でも、経験 に 基づく、帰納法 に分類される 手法 です。帰納法 は、経験から 問題に関する 法則を推測 することで 問題を解く という方法なので、演繹法と異なり、100 % 正しい答え は 得られません が、理屈 が 分からなくても、ある程度正しい答え が得られると 考えられる方法 を 求めることができる という 利点 があります。

たとえば、毎朝日の出 を 観察 することで、その経験 から 太陽 は 東から昇る という、おそらく正しい であろう 法則を知る ことができますが、その際に、太陽が東から昇る 理由はわかりません。経験則 が必ずしも 正しいとは限らない例 として、中世まで は、太陽 が 地球の周りをまわっている という、天動説 が 信じられていた ことが挙げられます。これには 宗教的な理由 もありますが、太陽の動きを見た際 に、太陽 の方が 地球の周りをまわっている ように 見える という 経験か らの 間違った推測 も 一因 でしょう。

一方、地球の自転 や 太陽の位置 などの 法則 を 調べ、太陽 が 東から昇る ことや、地球 が 太陽の周りをまわっている ことを 論理的 に 導き出す のが 演繹法 です。

参考までに、Wikipedia の帰納とヒューリスティックのリンクを示します。

心理学におけるヒューリスティック

心理学 における、ヒューリスティック とは、その手順 で 問題を解く ことができる 保証はない が、自分の 経験など から 有効である可能性が高い と思われる 手順 を 用いる という 手法 のことです。ヒューリスティック は日本語で、発見的手法 と呼ばれますが、経験を元 に 問題を解決 することから、経験則 と 呼ばれる こともあります。

ヒューリスティック は、問題 を 厳密に解く ための 手法 や 近似解 を 求める ための 手法 が 発見されていない場合 や、問題を解くため に 時間をかけることができない 場合などで 用いられます。なお、ヒューリスティック は、経験の少なさ や、間違った経験の解釈 を行うなどの 理由 で、正しい答え を 得られない可能性 がある点に 注意 が必要です。ヒューリスティック によって生まれる、認知上の偏り を 認知バイアス と呼びます。

ヒューリスティックの例 をいくつか挙げます。

正解を知らない クイズの 問題を解く 場合に、インターネットで検索 するなどの 方法 で、時間をかければ正解を求める ことが できます が、答えるまでの 制限時間 がある場合は その方法をとる ことは できません。そのような場合は、経験から答えを推測 して 解答する必要 があります。その際に、クイズの問題 と 似た問題 を 解いた経験 が 豊富であれば、正解 の 可能性が高く なりますが、経験が乏しい場合 は 正解 の 可能性は低くなる でしょう。ただし、その方法で、100 % 正解 を 答える ことは 不可能 です。

はじめて入ったレストラン で、最も美味しい メニューを 食べよう と思った場合に、メニューの中 から 最も美味しい ものを 100 % 正しく見つける方法 はおそらく ない でしょう。そのような場合は、メニュー の「名前」、「写真」、「値段」などを 手がかり に、それまで のさまざまな レストランでの食事の経験 から 選択 するしかありません。レストランに入った 経験が多い程、美味しいメニューを選択 できる 可能性が高く なりますが、そのような方法で、最も美味しいメニュー を 100 % 選択 することは 不可能 です。

このように、ヒューリスティック は、必ず 正しい答え を得ることができる とは限りません が、短い時間 で 判断を行う ことが できる という利点があります。世の中 には、正しい答え を 見つける方法 が 分かっていない場合 や、選択するまで の 時間が限られている場合 の方が 多い ので、人間 が 日々の生活の中 で行う 判断 の 多く は、ヒューリスティック による 判断 であるといっても 間違いではない でしょう。

コンピューター科学におけるヒューリスティック

コンピュータ科学 における ヒューリスティック は、問題 を 解くための方法 が 分からない 場合や、問題を解くため に 時間がかかりすぎる 場合などで 利用される方法 で、下記 のような 手順 を、満足な結果 がでるまで 繰り返す ことで 問題を解きます。

1. 問題を解くため の、有望そうな方法 を考える
2. 考えた方法 で 問題を解き、結果を検証 する
3. 検証した結果 から、それまでの経験 を元に、以下の作業 を行い、手順 2 に戻る
   • それまでに考えた方法 を 修正する
   • 新しい方法 を考えて 加える
   • 見込みがなさそうな方法 を 破棄する

上記からわかるように、この方法は「様々な経験 を通じて 問題 の 解決方法 を 改良 する」という、試行錯誤 で問題を解く方法です。従って、経験 を 元 に 問題を解決 する点は、心理学 の ヒューリスティックと同じ です。また、そのような作業 のことを一般的に 学習 と呼びます。実際に、辞書 では、学習 を 下記 のように 説明 しています。

「人間も含めて動物が、生後に 経験を通じて知識や環境に適応 する 態度・行動 などを 身につけていくこと。不安や嫌悪 など 好ましくないもの の体得も 含まれる」

また、上記の説明からわかるように、学習 では、成功の経験 だけでなく、失敗の経験 も 重要 です。「失敗から学ぶ」という ことわざ は、まさに そのことを示しています。

学習を行う ためには、様々な方法 で 問題を解く という 試み を、何度も行う ことが できる必要 があります。逆に言えば、一度 または、数回しか行えない ような 問題 は、ヒューリスティック で解決するには 向いていません。

先程 コンピューター科学 における ヒューリスティック と 説明 しましたが、この手法 は、元々 は 人間 が 問題を解決 するために 普段行っている「学習」を、コンピューター科学 で 応用 したものです。従って、ヒューリスティック を用いて コンピュータ が 問題を解決 する 手法の事 を「機械学習」と呼びます。

下記は、現実の世界 での ヒューリスティックの例 です。

美味しいカレー の レシピを考える という 問題 は、ヒューリスティック では 下記の手順 で行います。なお、調理の手順 まで 考慮 に入れると 問題 が 複雑になる ので、問題 を 簡単にする ため、調理の手順 は 決まっている ものとします。

1. 美味しいカレーを作るための 材料 と、その 分量 を 考える
2. 実際 に カレーを作り、食べてみる
3. カレーの味 を 評価 し、以下 のような 改良方法を考え、手順 2 に戻る
   1. 材料の量 を 変える
   2. 新しい材料 を 加える
   3. 不適切 な 材料 を 破棄する

他にも、人間 は「言葉 を 覚える」、「自転車の乗り方 を 覚える」など、さまざまなこと を、ヒューリスティック な 試行錯誤 による 学習 で 身に付けていきます。

コンピューター科学の ヒューリスティック は、得られた答え の 精度 は 保証されません が、近似解 を求める より短い時間 で、平均的 に 高い精度 で 答えを求める ことが できる場合が多い という 特徴 があります。

2 つのヒューリスティックの違い

先程説明した、心理学 における ヒューリスティック と、コンピューター科学 の ヒューリスティック には 密接な関係 があります。心理学 における ヒューリスティック は、それまでの経験 で得られた 学習 を 元に して 素早く判断を行う方法 のことですが、その 経験による学習 を 行う のが、コンピューター科学 の ヒューリスティック です。

従って、それぞれ の ヒューリスティック の 意味は 以下のようになります。心理学 の場合は、判断を行う際 に、新しい学習 は 行わない点 が 異なります。

	意味
心理学	それまでに行われた学習 にもとづいて 判断を行う こと
コンピューター科学	学習を行う方法 も 含めて、判断を行う こと

ヒューリスティックと評価指標

ヒューリスティック は、経験から学ぶ 手法ですが、そのためには、問題の解決 を試みた 結果 の 良し悪しを判断 する 必要 があります。その理由は、結果の良し悪し が 判断できなければ、どこを改良するべきか が わからない からです。結果 が 良ければ その 長所を伸ばす という 改良 ができ、悪ければ その 短所を克服する という 改良 ができます。

この 結果 の 良し悪し の 判断材料 の事を 評価指標 と呼びます。評価指標 には さまざまなもの が ある ため、問題の性質 に 適した 評価指標を 選択する必要 があります。

例えば、成績を上げる という 問題 の場合は、テストの点数 が 評価指標 になります。スポーツ を 上達する という 問題 の場合は、試合の成績 が 評価指標 になるでしょう。

ただし、状況 によって 同じ評価指標 でも 良いかどうか を 判断する基準 が 変わる 点に 注意 して下さい。例えば、高校生 が、小学生のテスト で 100 点 をとったり、小学生相手 に 試合で勝利 しても、特に良い結果 であるとは 言えない でしょう。

アルゴリズムという用語の意味の違い

心理学 では、アルゴリズム という 用語 は、問題 を 100 % 解く とことができる 手順 の事を表し、ヒューリスティック の 対義語 として 使われます。

一方、コンピューター科学 での アルゴリズム は、処理 を行うための 手順 のことを表し、その際に、アルゴリズム が 問題を 100 % 解く ことが できるか どうかは一般的に 区別しません。従って、ヒューリスティック の 対義語の意味 では 使われません。例えば、「ヒューリスティック な アルゴリズム」のような 表記 が 実際 に 使われます。

このように、アルゴリズム という 用語 は、心理学 と、コンピューター科学 では 異なる使われ方 がされる点に 注意 して下さい。本記事 では、もちろん アルゴリズム という 用語 を、コンピューター科学 の 意味 で 使います。

演繹法とヒューリスティックの併用

問題を解く際に、演繹法 と ヒューリスティック の 両方 を 組み合わせる ことが 良くあります。例えば、スポーツの練習 を行う際に、最初 は スポーツの入門書 を読んで、その通りに練習 するのが 一般的 ではないかと思います。多くの 入門書 に書かれている 内容 は、科学的な方法など の 演繹法 によって 検証 された、誰でも その方法で練習することで ある程度のレベル までは 上達できる 方法です。

しかし 一般的 には、誰でもスポーツの中級者 になることができる 手順 は あっても、誰でも上級者 になるための 手順 は ありません。上級者 になるためには 自分 で 様々な経験 を積んで 試行錯誤を行う という ヒューリスティック な方法を 行う必要 があります。

下記は、そのことをまとめたものです。

• 最初 は、演繹法 を使って、ある程度 までの 精度 で 問題を解決 する
• 演繹法 では 精度を上げられないレベル に到達したら、ヒューリスティック で、自分 で 精度を上げる方法 を 見つけていく

実は、これまでの記事 で 〇×ゲーム の 強い AI を 作成する際 に、上記の手順 で作成を 行ってきました。ルール 11 の 下記の条件 は、演繹法 で求めた 条件 であり、下記の条件 を 組み込む ことで、実際 に ある程度まで の 強い AI を 作成 することができました。

• 自分 が 勝利できる
• 相手 が 勝利できない

ただし、残念ながら、ルール 11 の 上記の条件 では、すべての局面 で 最善手 を 選択 することは できません。また、すべての局面 で、最善手 を 選択する方法 は わからない ので、ここから は、ヒューリスティック な 方法 を 利用 する 必要 が あります。

ai11s で行われたヒューリスティックの手順

ルール 11 の 下記の条件 は、ヒューリスティック による 条件 です。

• 真ん中 のマスに 着手 する
• 自分 が 勝利できそうになる
• 相手 が 勝利できなさそうになる

実際 に、上記の条件 を ai11s に 組み込む際 に、下記 の ヒューリスティック による 手順 を 行っていた ことを示します。なお、真ん中 のマスに 着手する という条件は、演繹法 の 条件より も 前 に 組み込んだ ので、下記の説明では 省略 します。

1. 問題を解くため の、有望そうな方法 を考える
2. 考えた方法 で 問題を解き、結果を検証 する
3. 検証した結果 から、それまでの経験 を元に、以下の作業 を行い、手順 2 に戻る
   • それまでに考えた方法 を 修正する
   • 新しい方法 を考えて 加える
   • 見込みがなさそうな方法 を 破棄する

問題を解くための、有望そうな方法を考える

まず、すべての局面 で 最善手 を 選択する合法手 を 見つけるため の、有望そう な 判断基準 として、下記の 3 つ を考えました。下記 の 判断基準 は、いずれも それを満たすことで、すべての局面 で 最善手 を 100 % 見つける ことができることは 保証されていない ので、ヒューリスティック です。

• 次 の 自分の手番 で 勝利できる ように、「自 2 敵 0 空 1」が 1 つ存在する 局面になる着手を行う
• 自分 が 有利になる ように、「自 1 敵 0 空 2」が 最も多い 着手を行う
• 相手 が 不利になる ように、「自 0 敵 1 空 2」が 最も少ない 着手を行う

次に、上記の 3 つの条件 を 総合的 に 判断 するために、それぞれ の マークのパターン に対して 下記の表 の 評価値 を 割り当て ました。

	評価値
「自 2 敵 0 空 1」が 1 つの場合の評価値	1
「自 1 敵 0 空 2」が 1 つあたりの評価値	1
「自 0 敵 1 空 2」が 1 つあたりの評価値	-1

考えた方法で問題を解き、結果を検証する

上記の方法 で、ai11s VS ai10s の 対戦 を行い、下記 のような 結果 になりました。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
ai11s VS ai10s	22.2	0.0	77.8	0.0	50.5	49.5	11.1	25.3	63.6

結果 から、ai11s が × を担当 した場合に、50 % の確率で 敗北する という 問題点がある ことが わかりました。

検証した結果から修正を行う

何故 そのような結果になった かを 検証 し、評価値 を 計算 するための パラメータ を 下記 のように 修正 しました。

	修正前	修正後
「自 2 敵 0 空 1」が 1 つの場合の評価値	1	2
「自 1 敵 0 空 2」が 1 つあたりの評価値	1	1
「自 0 敵 1 空 2」が 1 つあたりの評価値	-1	-1

修正した方法で問題を解き、結果を検証する

修正 した方法で、ai11s VS ai10s の 対戦 を行い、下記 のような 結果 になりました。

関数名	o 勝	o 負	o 分	x 勝	x 負	x 分	勝	負	分
修正前	22.2	0.0	77.8	0.0	50.5	49.5	11.1	25.3	63.6
修正後	0.0	0.0	100.0	0.0	0.0	100.0	0.0	0.0	100.0

修正 によって、先程の問題 は 解消 されましたが、新しく 〇 を担当した際に、勝てなくなるという 問題が生じました。この問題を、検証した結果、勝てなくなっても 問題がない と 判断 し、このパラメータ で ai11s を 作成する ことに 決めました。

ヒューリスティックを用いる際の注意点

ヒューリスティック は、経験則 による 解決方法 なので、問題 を 解決する方法 を 修正 した 結果、常に 状況が好転する とは 限りません。

例えば、ai11s の 評価値 を 計算 する パラメータ を 下記 の表のように 修正 した際に、ai10s VS ai11s の 4 手目の局面のみ を 考慮 に入れて 修正 を行ったため、それ以外の局面 で パラメータ の 修正 による 悪影響 が 生じる可能性 があります。

	修正前	修正後
「自 2 敵 0 空 1」が 1 つの場合の評価値	1	2
「自 1 敵 0 空 2」が 1 つあたりの評価値	1	1
「自 0 敵 1 空 2」が 1 つあたりの評価値	-1	-1

上記の修正 によって、ai11s VS ai10s の 3 手目 の 選択 に 実際 に 影響 を 与えた ように、ai11s が 他の AI と 対戦 した際に、どこかの局面 の 選択 に 良い影響 と 悪い影響 も含めて 何らかの影響 を与えている 可能性 が あります。

他の局面 に 良い影響のみ を与えているのであれば、問題はない のですが、悪い影響 を 与えた場合 は 問題 です。しかし、残念ながら ヒューリスティック な 条件 は、絶対に正しい という 明確 な 根拠がない 条件なので、修正 することで、良い影響のみ を与えることを 保証 することは できません。

また、ヒューリスティック で 問題を解決 する場合に、お互いに 矛盾する条件 が 存在 することが 良くあります。例えば、成績をよくする ためには「勉強の時間 を 増やす」と「適度 な 休息をとる」という 条件 が 考えられます が、この 2 つの条件 は、どちらか を 増やしすぎ ると、もう片方 が 減ってしまう という、矛盾する要素 があります³。そのような場合は、それらの条件 を、バランスよく設定 する 必要 がありますが、適切なバランス を 見つける ためには、さまざま な パラメータ で 実際 に 問題の解決 を 試みて、その中で 最もバランスの良い ものを 採用する という 試行錯誤 が 必要 になります。

日本語の ことわざ に、「あちらを立てればこちらが立たず」というものがありますが、これは、まさに ヒューリスティック による 問題解決 で 良く起きる状況 を 表します。

ヒューリスティック は、常に間違う可能性 があります。特に、特定の状況 を 改善 するために パラメータを修正 したり 条件 を 追加、削除 した場合は、それ以外 の さまざまな状況 で 状況が悪化していないか どうかを 必ず検証 する 必要 があります。

今回の記事のまとめ

今回の記事 では、最強の AI の 定義 を、下記のように 定義しなおし、本記事で これまで 行ってきた AI のルール の 条件 が、下記 の 最強の AI の 定義 の 一部を満たす ような 条件である ことを示しました。

最強の AI とは、下記の 両方の条件 を 満たす AI である。

1. 必勝の局面 になる 合法手 が 存在する場合 は、必ずその合法手 の いずれか を 選択する
2. 必敗以外の局面 で、必敗の局面 につながる 合法手 を 選択しない

次に、問題 を 解決する方法 の 分類 として、演繹法 と ヒューリスティック を紹介し、これまで に行ってきた AI の作成方法 が、それらの方法 に 基づいて行われてきた ことを 示し、これまで に行ってきた AI の作成方法 で、AI の強さ を 最強の AI に 近づけていく ことが できる ことを 示しました。

本記事で入力したプログラム

今回の記事では入力したプログラムはありません。

次回の記事

1. 論理 の事を英語で ロジック（logic）、論理的 を英語で ロジカル（logical）と呼びます ↩

2. 原因と結果 の 関係 のことです ↩

3. このような、片方を増やす と、もう片方が減る ような、両立しない ようなもののことを、トレードオブ と呼びます。また、2 つ の 相反する要素 の中から 1 つを選択しなければならない ような 状況 のことを事を ジレンマ と呼びます ↩