Pythonで〇×ゲームのAIを一から作成する　その98　ゲーム木の生成過程を表示するアニメーションの改良と処理時間の計測

Last updated at 2024-07-18Posted at 2024-07-14

目次と前回の記事

これまでに作成したモジュール

以下のリンクから、これまでに作成したモジュールを見ることができます。

リンク	説明
marubatsu.py	Marubatsu、Marubatsu_GUI クラスの定義
ai.py	AI に関する関数
util.py	ユーティリティ関数の定義。現在は `gui_play` のみ定義されている
tree.py	ゲーム木に関する Node、Mbtree クラスの定義
gui.py	GUI に関する処理を行う基底クラスとなる GUI クラスの定義

ルールベースの AI の一覧

ルールベースの AI の一覧については、下記の記事を参照して下さい。

ゲーム木の生成の過程のアニメーションの改良

今回の記事では、前回の記事で作成した、ゲーム木の生成の過程を表示するアニメーションの改良を行います。どのような改良の余地があるかについて少し考えてみて下さい。

ゲーム木に追加予定のノードの表示の改良

前回の記事で作成したアニメーションは、以下のような表示を行います。

アニメーションのフレームを 0 番から数えることにする
0 番のフレームには、ルートノードが中心かつ、選択状態になった部分木を描画する
n 番のフレームには、ゲーム木に n 番目に追加されたノードが中心かつ、選択状態になった部分木を描画する

このアニメーションでは、そのフレームで追加されたノード を、赤枠の選択されたノードとして表示 することで、どのようにゲーム木が生成されたかを表現しています。そのため、選択されたノードの子ノード は、今後のフレームで追加される予定である、まだゲーム木に追加されていないノード を表しますが、そのことがわかりづらい という問題があります。

例えば 0 番のフレームには下図のような部分木が描画されます。0 番のフレームのゲーム木は、ルートノード以外のノードがまだ追加されていない、ルートノードのみのゲーム木 を表しますが、下図のように、今後のフレームで追加される予定である、ルートノードの子ノードがそのまま表示 されているので、それらのノードが 既にゲーム木に追加されているように見えてしまいます。

そこで、ゲーム木にまだ追加されていない、今後のフレームで 追加される予定のノード を 暗く表示 することで、それらのノードが まだ追加されていないことが直観的にわかる ように修正することにします。どのように修正すれば良いかについて少し考えてみて下さい。

ゲーム木に追加予定のノードを暗く表示するアルゴリズム

行いたい処理は、部分木に表示されるノードの中で、現在表示されているフレームより後にゲーム木に 追加する予定であるノードを暗く表示する というものです。

また、現状のプログラムでは、以下のようなデータが記録されています。

部分木に表示されるそれぞれの ノードとその表示範囲 が、Mbtree クラスの nodes_by_rect 属性に dict の形式で記録されている
Mbtree_Anim クラスの Play ウィジェットの value 属性に、現在表示されるアニメーションの フレームの番号が代入 されている

上記から、下記のアルゴリズムで追加する予定であるノードを暗く表示できます。

それぞれのノード が、ゲーム木に 何番目に追加されたか を計算する
その 順番と Play ウィジェットの value 属性の値を比較する ことで、そのノードが 追加する予定のノードであるか どうかを判定できる
追加する予定のノードを何らかの方法（具体的な方法は後で説明します）で暗く表示する

ノードがゲーム木に追加された順番を計算するアルゴリズム

まず、それぞれのノード が、ゲーム木に 何番目に追加されたか を計算する必要があるので、その方法を少し考えてみて下さい。

`index` メソッドによる計算

Mbtree クラスの nodelist には、ゲーム木の ノードの一覧が list の形式で代入 されています。また、その list の 要素の順番 は、ゲーム木のノードが 追加された順番に対応 します。

従って、nodelist の n 番のインデックスの要素 には、ゲーム木に n 番目に追加されたノードが代入されている ので、list の index メソッドを使って、ノードがゲーム木に何番目に追加されたかを計算することができます。

例えば、ルートノードは、下記のプログラムで 0 番目（最初から存在する）に追加されたノードであることが確認できます。

from tree import Mbtree

mbtree = Mbtree()
print(mbtree.nodelist.index(mbtree.root))

実行結果

ゲーム木の生成時の表示は省略
0

ゲーム木に最後に追加されたノードは、nodelist の最後の要素に代入されています。従って、下記のプログラムから、最後に追加されたノードは、549445 番目にゲーム木に追加されたノードであることが計算できます。

print(mbtree.nodelist.index(mbtree.nodelist[-1]))

実行結果

`index` メソッドの欠点と、timeit モジュールによる処理時間の計測

index メソッドは、list の 先頭の要素から順番 に、実引数に記述されたデータを 検索する という処理を行うので、list の 大きなインデックスの要素 を実引数に記述すると、処理に時間がかかる という 問題が生じます。そのことを実際に示します。

プログラムの 処理時間を計測する方法 の一つに、timeit モジュール を利用するという方法があります。timeit モジュールは、指定したプログラムを 何度も実行 し、その 処理時間の平均などを計測 する処理を行いますが、その際に、何回プログラムを実行するかなどの設定を行う必要がある点が少し面倒です。ただし、JupyterLab には、そのような 設定を自動的に行ってくれる、%%timeit というマジックコマンド が用意されているので、それを使えば簡単にプログラムの処理時間を計測することができます。

timeit モジュールの詳細については、下記のリンク先を参照して下さい。

具体的には、セルの先頭に %%timeit というマジックコマンドを記述 することで、セルの中に記述したプログラムを実行した際の 処理時間の平均などを計測 することができます。

下記は、先程の、ルートノードが追加された順番を計算するプログラムの処理時間を %%timeit を使って計測するプログラムです。

%%timeit
mbtree.nodelist.index(mbtree.root)

実行結果（表示される内容は、コンピュータの性能によって変わります）

45.8 ns ± 0.264 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

実行結果は以下のような意味を表し、mbtree.nodelist.index(mbtree.root) が平均すると 45.8 ナノ秒（約 1 億分の 4 秒）というかなり短い時間で処理が行われることがわかります。

セルの中のプログラムを 1000 万回（10,000,000）回繰り返す（loop）という処理が、7 回行われた。これらの回数は、自動的に適切な値が設定 される
セルの中のプログラムの処理時間の平均（mean）は 45.8 ns（ナノ秒） である
セルの中のプログラムの処理時間の 標準偏差（std¹) は 0.264 ns である

表示される時間の単位は以下のようになっています。

表記	単位	意味
s		秒
ms	ミリ（mili）	1/千秒
μs²	マイクロ（micro）	1/百万秒
ns	ナノ（nano）	1/十億万秒

標準偏差 は、統計学で使われる、計測された処理時間の ばらつきを表す量 で、上記の実行結果のように、標準偏差 が 平均と比べて小さい場合 は ほとんどの処理 が、平均値とほぼ同じ時間で行われた ことを意味します。

従って、標準偏差の値が平均値よりもかなり小さい場合 は、平均値だけを注目すれば良いでしょう。本記事でもそのような場合は、標準偏差については特に言及せずに、平均値だけを注目 することにします。

上記の結果の場合は、かなり大雑把 に言えば³、行われた処理の約 70 % が 45.8 ns ± 0.264 ns の範囲におさまっていた ということを意味します。

下記は、先程の、ゲーム木に最後に追加されたノードの順番を計算するプログラムの処理時間を %%timeit を使って計測するプログラムです。実行結果から 平均すると 30.5 ms = 約 0.03 秒 の時間がかかることがわかります。

%%timeit
mbtree.nodelist.index(mbtree.nodelist[-1])

実行結果

30.5 ms ± 752 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

上記では、一見すると平均値の 30.5 よりも標準偏差の 752 の方が多く見えるかもしれませんが、単位を考慮に入れる と、標準偏差は平均値の 約 50 分の 1 です。

実行結果からわかるように、処理が繰り返し行われる回数は、処理時間の長さによって自動的に調整されます。先程は処理時間が非常に短かったので、7 * 1000 万 = 7000 万回も処理が行われましたが、上記では 7 * 10 = 70 回しか行われません。

下記は 2 つの処理時間の平均です。なお、1 ns = 1000 ms = 100 万 ms です。

処理	平均
`mbtree.nodelist.index(mbtree.root)`	45.8 ns = 4580 万 ms
`mbtree.nodelist.index(mbtree.nodelist[-1])`	30.5 ms

上記から、処理時間の平均が約 150 万倍も異なる ことがわかります。最後のノードは、nodelist の中の 549945 = 約 50 万番目の要素に代入されているので、index が nodelist の 先頭の要素から順番に検索する ことを考えると、この 処理時間の違いは妥当 でしょう。

print が記述されたプログラム を %%timeit で計測すると、%%timeit が繰り返しプログラムを実行した数だけ、print によるメッセージが大量に表示 されてしまいます。そのため、 %%timeit で計測するプログラムには、print の処理を含めないようにしたほうが良い でしょう。

上記の計測で、print で index の結果を表示しなかったのはそのためです。

ノードを挿入した順番の記録

上記のように、要素の数が非常に多い list に対して index メソッドを実行すると処理に時間がかかる可能性が高くなる ので望ましくありません。そこで、ゲーム木に ノードを追加する際 に、追加したノードの属性に、ゲーム木に 追加された順番を代入する ことにします。そのようにすれば、ノードの属性を見るだけでそのノードが何番目にゲーム木に追加されたかがわかるようになります。

ノードの属性の名前としては、様々なものが考えられますが、ゲーム木にノードが追加された順番を表す数値は、すべてのノードで異なる数値になる ため、識別子としての役割を持つ こともできます。また、実際に良く使われる識別子は 0（または 1）から順番に整数を割り当てることが多いので、本記事では 識別子 を表す identifier の略である id という名前の属性に、ゲーム木に追加された順番を代入することにします。

この、id 属性を計算する処理は、以前の記事で説明した、「値を変更するクラスの属性の利用例」と同じ方法で、クラス属性を使って行う ことができます。

まず、Node クラスを下記のように修正します。

8 行目：ノードを作成した回数を表すクラス属性 count を 0 で初期化する
11 行目：インスタンスを作成した際に呼び出される __init__ メソッドの中で、インスタンスの id 属性に、クラス属性 count を代入する
12 行目：クラス属性 count の値に 1 を足す

 1  from copy import deepcopy
 2  from marubatsu import Marubatsu_GUI
 3  import matplotlib.pyplot as plt
 4  from tree import Rect
 5
 6  class Node:
 7      # ノードを作成した回数を表すクラス属性
 8      count = 0
 9    
10      def __init__(self, mb, parent=None, depth=0):
11          self.id = Node.count
12          Node.count += 1
13          self.mb = mb
14          self.parent = parent
15          self.depth = depth
16          self.children = []
17          self.children_by_move = {}        
元と同じなので省略

行番号のないプログラム

from copy import deepcopy
from marubatsu import Marubatsu_GUI
import matplotlib.pyplot as plt
from tree import Rect

class Node:
    # ノードを作成した回数を表すクラス属性
    count = 0
    
    def __init__(self, mb, parent=None, depth=0):
        self.id = Node.count
        Node.count += 1
        self.mb = mb
        self.parent = parent
        self.depth = depth
        self.children = []
        self.children_by_move = {}        
        
    def insert(self, node):
        self.children.append(node)
        self.children_by_move[node.mb.last_move] = node
        
    def calc_children(self):
        self.children = []
        for x, y in self.mb.calc_legal_moves():
            childmb = deepcopy(self.mb)
            childmb.move(x, y)
            self.insert(Node(childmb, parent=self, depth=self.depth + 1))
        
    def calc_height(self):
        if len(self.children) == 0:
            self.height = 4
        else:
            self.height = 0
            for childnode in self.children:
                self.height += childnode.height

    def draw_node(self, ax=None, maxdepth=None, emphasize=False, size=0.25, lw=0.8, dx=0, dy=0):
        width = 8
        if ax is None:
            height = len(self.children) * 4
            fig, ax = plt.subplots(figsize=(width * size, height * size))
            ax.set_xlim(0, width)
            ax.set_ylim(0, height)   
            ax.invert_yaxis()
            ax.axis("off")
            for childnode in self.children:
                childnode.height = 4
            self.height = height
                
        # 自分自身のノードを真ん中の位置になるように (dx, dy) からずらして描画する
        y = dy + (self.height - 3) / 2
        Marubatsu_GUI.draw_board(ax, self.mb, show_result=True, emphasize=emphasize, lw=lw, dx=dx, dy=y)
        rect = Rect(dx, y, 3, 3)
        # 子ノードが存在する場合に、エッジの線と子ノードを描画する
        if len(self.children) > 0:
            if maxdepth != self.depth:   
                plt.plot([dx + 3.5, dx + 4], [y + 1.5, y + 1.5], c="k", lw=lw)
                prevy = None
                for childnode in self.children:
                    childnodey = dy + (childnode.height - 3) / 2
                    if maxdepth is None:
                        Marubatsu_GUI.draw_board(ax, childnode.mb, show_result=True, dx=dx+5, dy=childnodey, lw=lw)
                    edgey = childnodey + 1.5
                    plt.plot([dx + 4 , dx + 4.5], [edgey, edgey], c="k", lw=lw)
                    if prevy is not None:
                        plt.plot([dx + 4 , dx + 4], [prevy, edgey], c="k", lw=lw)
                    prevy = edgey
                    dy += childnode.height
            else:
                plt.plot([dx + 3.5, dx + 4.5], [y + 1.5, y + 1.5], c="k", lw=lw)
                
        return rect

修正箇所

from copy import deepcopy
from marubatsu import Marubatsu_GUI
import matplotlib.pyplot as plt
from tree import Rect

class Node:
    # ノードを作成した回数を表すクラス属性
+   count = 0
    
    def __init__(self, mb, parent=None, depth=0):
+       self.id = Node.count
+       Node.count += 1
        self.mb = mb
        self.parent = parent
        self.depth = depth
        self.children = []
        self.children_by_move = {}        
元と同じなので省略

次に、Mbtree クラスの __init__ メソッドを下記のように修正します。この修正を行わないと、複数の Mbtree クラスのインスタンスを作成した際に、Node クラスの count 属性の値 が 0 ではなく、その前に作成した Mbtree クラスのノードの数になってしまう からです。

5 行目：Node クラスの count 属性の値を 0 で初期化する

1  from marubatsu import Marubatsu
2  from tree import Mbtree
3
4  def __init__(self):
5      Node.count = 0
6      self.root = Node(Marubatsu())
7      self.create_tree_by_bf()
8    
9  Mbtree.__init__ = __init__

行番号のないプログラム

from marubatsu import Marubatsu
from tree import Mbtree

def __init__(self):
    Node.count = 0
    self.root = Node(Marubatsu())
    self.create_tree_by_bf()
    
Mbtree.__init__ = __init__

修正箇所

from marubatsu import Marubatsu
from tree import Mbtree

def __init__(self):
+   Node.count = 0
    self.root = Node(Marubatsu())
    self.create_tree_by_bf()
    
Mbtree.__init__ = __init__

上記の修正後に下記のプログラムで、Mbtree クラスのインスタンスを作成し直した後で、ルートノードと、最後に追加されたノードの id 属性を表示すると、実行結果のようにそれぞれのノードがゲーム木に追加された順番が正しく表示されます。

mbtree = Mbtree()
print(mbtree.root.id)
print(mbtree.nodelist[-1].id)

実行結果

ゲーム木の生成時の表示は省略
0
549945

また、下記のプログラムで mbtree.nodelist[-1].id の処理時間を計測すると、実行結果の平均 42.9 ns のように、非常に短い時間で計算できることが確認できました。

%%timeit
mbtree.nodelist[-1].id

実行結果

42.9 ns ± 0.237 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

ノードを暗く表示する方法

ノードがゲーム木に追加された順番がわかるようになったので、次は現在表示されているフレームより後にゲーム木に追加された ノードを暗く表示する という処理を実装します。ノードを暗く表示する方法について少し考えてみて下さい。

背景色を変える方法とその問題点

これまでに紹介した方法を利用する場合は、ゲーム盤の背景色を灰色で表示する という方法が考えられますが、その方法では 決着がついた局面のゲーム盤の背景色までもが灰色で表示される ようになってしまうため、決着がついた局面であるかどうかがわからなくなってしまう という問題が生じます。

背景色を変える方法でこの問題を解決するためには、決着がついていない局面と 3 種類ある決着がついた局面の 4 種類の暗い色の背景色を考える必要 がありますが、それは面倒です。

半透明の黒い図形を重ねる方法

別の方法として、ゲーム盤の画像の上に、半透明の黒い図形を重ねて表示する という方法があり、この方法であれば、背景色を新しく考える必要はありません。

ipywidgets の Rectangle などの Artist を作成する関数 には、塗りつぶしの透明度 を表す 仮引数 alpha⁴ があります。alpha には 0 ~ 1 の範囲 の数値を代入し、0 が完全な透明、1 が完全に透明でない ことを表します。

下記は、左下に赤い正方形を、右上に 透明度が 0.5 の半透明な黒い正方形 を、一部が重なるように表示 するプログラムです。実行結果のように、赤い正方形の上に半透明な黒い正方形が表示され、重なった部分が暗く表示される ようになります。

import matplotlib.patches as patches

fig, ax = plt.subplots(figsize=(3, 3))
rect1 = patches.Rectangle(xy=(0, 0), width=0.75, height=0.75, fc="red")
rect2 = patches.Rectangle(xy=(0.25, 0.25), width=0.75, height=0.75, fc="black", alpha=0.5)
ax.add_artist(rect1)
ax.add_artist(rect2)

実行結果

透明度を表す alpha に 0.5 よりも大きな（1 以下の）数値を代入すると、表示される黒い正方形の色が濃くなります。興味がある方は試してみて下さい。

ノードを暗く表示する処理の実装

以前の記事では、ノードに赤枠を表示して強調する処理を実装する際に、ゲーム盤を表示する処理を行う draw_board を修正 しました。同様の方法で、ゲーム盤を暗く表示することができるように draw_board を修正するという方法が考えられます。

ただし、そのような方法で draw_board を修正するということを続けていくと、draw_board の定義が複雑になる⁵ という問題が発生します。そこで、今回の記事では draw_board ではなく、Mbtree_Anim の update_gui メソッド内で、その処理を行う ことにします。

具体的には下記のように update_gui を修正します。

draw_subtree で部分木を描画する
Mbtree クラスの nodes_by_rect の中で、現在表示されているフレームより後にゲーム木に追加されたノードの表示範囲に、半透明の黒色の正方形を重ねて描画する

下記は、そのように update_gui を修正したプログラムです。

5 行目：nodes_by_rect の全てのキーとキーの値に対する繰り返し処理を行う
6 行目：ノードが追加された順番を表す node.id が、アニメーションのフレームの番号を表す self.play.value よりも大きいかどうかを判定する
7、8 行目：大きい場合は、ノードの表示範囲に半透明の黒い正方形を重ねて描画する

 1  from tree import Mbtree_Anim
 2
 3  def update_gui(self):
元と同じなので省略    
 4      self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
 5      for rect, node in self.mbtree.nodes_by_rect.items():
 6          if node.id > self.play.value:
 7              self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width,
 8                                              height=rect.height, fc="black", alpha=0.5))
 9
10  Mbtree_Anim.update_gui = update_gui

行番号のないプログラム

from tree import Mbtree_Anim

def update_gui(self):
    self.ax.clear()
    self.ax.set_xlim(-1, self.width - 1)
    self.ax.set_ylim(0, self.height)   
    self.ax.invert_yaxis()
    self.ax.axis("off")   
    
    self.selectednode = self.mbtree.nodelist[self.play.value]
    self.centernode = self.selectednode
    if self.selectednode.depth <= 4:
        maxdepth = self.selectednode.depth + 1
    elif self.selectednode.depth == 5:
        maxdepth = 7
    else:
        maxdepth = 9
    self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
    for rect, node in self.mbtree.nodes_by_rect.items():
        if node.id > self.play.value:
            self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width,
                                                 height=rect.height, fc="black", alpha=0.5))

Mbtree_Anim.update_gui = update_gui

修正箇所

from tree import Mbtree_Anim

def update_gui(self):
元と同じなので省略    
    self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
+   for rect, node in self.mbtree.nodes_by_rect.items():
+       if node.id > self.play.value:
+           self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width,
+                                                height=rect.height, fc="black", alpha=0.5))

Mbtree_Anim.update_gui = update_gui

上記の修正後に、下記のプログラムを実行して三角形のボタンをクリックすると、実行結果の左図のように、表示されたフレーム以降に追加される予定のノードが暗く表示されるようになります。修正前の右図と比較して、そのフレームでゲーム木にまだ追加されていないノードが明確になったことを確認して下さい。

mbtree_anim = Mbtree_Anim(mbtree)

実行結果（右図は 0 ~ 19 フレームまでのアニメーションの繰り返しです。なお、左図と右図は連動していないので、表示されるフレームがずれる場合があります）

中心となるノードの改良

上記のアニメーションを見て、何かがわかりづらいと思った人はいないでしょうか？そう思った方は、その理由について少し考えてみて下さい。

わかりづらさの原因の検証

下図は、アニメーションの中の 17 番と 18 番のフレームを並べたものです。

17 番のフレームはの最後の子ノードであるが選択された部分木です。次の兄弟ノードが存在しないので 18 番のフレームはの次の兄弟ノードのの最初の子ノードであるが選択された部分木です。

上図のように、静止画をじっくり見比べた場合はそのことを理解できるのではないかと思いますが、アニメーションでは上の 2 つの画像が短い間に切り替わる ので、そのことをアニメーションを見ながら 理解することは困難でしょう。

また、選択されたノードの 親ノード であるとは、2 つのフレームで全く同じ場所に表示 されますが、アニメーションでは表示が短い間に切り替わるので、17 番と 18 番のフレームで 親ノードが変化したことを実感するのは困難でしょう。

この問題を解決する方法を少し考えてみて下さい。

中心となるノードの変更

一つの方法として、部分木の 中心となるノード を、選択されたノードの親ノードに修正 するという方法が考えられます。そのようにすることで、選択されたノードの 親ノードの兄弟ノード が部分木に 表示されるようになる ので、アニメーションで選択されたノードの 親ノードが変化したことが実感できる ようになります。おそらく言葉の説明だけではわかりづらいと思いますので、この後の修正後と修正前の処理を比較してみて下さい。

中心となるノードの深さを一つ減らした場合 は、部分木に表示するノードの数が多くなりすぎないようにするために、部分木に表示するノードの深さも同時に減らす 必要が生じますが、下記の理由から減らしても問題は発生しません。

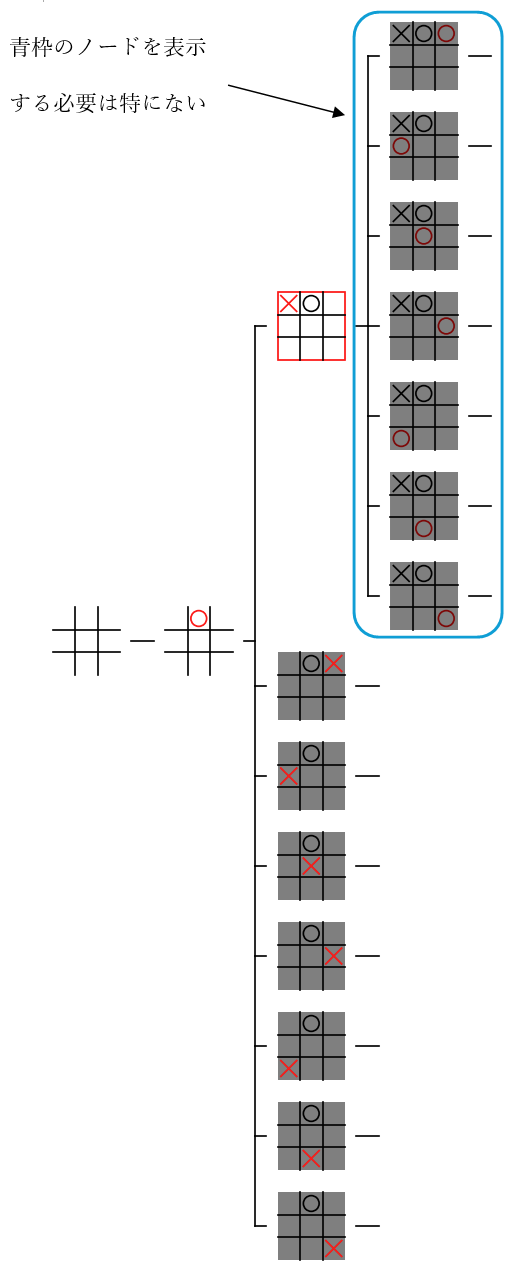
下図の青枠の中にある、選択されたノードの 子ノード は、すべて が今後のフレームで追加される予定の 暗く表示されるノード なので、表示しなくても大きな問題は発生しません。そのため、中心となるノードの深さにあわせて、部分木に表示する ノードの深さを 一つ減らして、選択されたノードの深さと同じ にしても　問題は発生しません。

下記は、そのように update_gui を修正したプログラムです。

4、5 行目：中心となるノードを、親ノードに変更する。ただし、ルートノードには親ノードは存在しない ので 深さが 0 以上の場合のみ行う 必要がある点に注意すること
6 ~ 8 行目：元のプログラムは、selectednode と centernode が同じだったので、selectednode を使って部分木の深さを計算していたのを、centernode を使って部分木の深さを計算するように修正する

 1  def update_gui(self):
元と同じなので省略
 2      self.selectednode = self.mbtree.nodelist[self.play.value]
 3      self.centernode = self.selectednode
 4      if self.centernode.depth > 0:
 5          self.centernode = self.centernode.parent
 6      if self.centernode.depth <= 4:
 7          maxdepth = self.centernode.depth + 1
 8      elif self.centernode.depth == 5:
 9          maxdepth = 7
10      else:
11          maxdepth = 9
元と同じなので省略
12
13  Mbtree_Anim.update_gui = update_gui

行番号のないプログラム

def update_gui(self):
    self.ax.clear()
    self.ax.set_xlim(-1, self.width - 1)
    self.ax.set_ylim(0, self.height)   
    self.ax.invert_yaxis()
    self.ax.axis("off")   
    
    self.selectednode = self.mbtree.nodelist[self.play.value]
    self.centernode = self.selectednode
    if self.centernode.depth > 0:
        self.centernode = self.centernode.parent
    if self.centernode.depth <= 4:
        maxdepth = self.centernode.depth + 1
    elif self.centernode.depth == 5:
        maxdepth = 7
    else:
        maxdepth = 9
    self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
    for rect, node in self.mbtree.nodes_by_rect.items():
        if node.id > self.play.value:
            self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width, height=rect.height, fc="black", alpha=0.5))

Mbtree_Anim.update_gui = update_gui

修正箇所

def update_gui(self):
元と同じなので省略
    self.selectednode = self.mbtree.nodelist[self.play.value]
    self.centernode = self.selectednode
+   if self.centernode.depth > 0:
+       self.centernode = self.centernode.parent
-   if self.selectednode.depth <= 4:
+   if self.centernode.depth <= 4:
-       maxdepth = self.selectednode.depth + 1
+       maxdepth = self.centernode.depth + 1
-   elif self.selectednode.depth == 5:
+   elif self.centernode.depth == 5:
        maxdepth = 7
    else:
        maxdepth = 9
元と同じなので省略

Mbtree_Anim.update_gui = update_gui

上記の修正後に、下記のプログラムを実行して三角形のボタンをクリックすると、実行結果の左図のように、中心となるノードが選択されたノードの親ノードになります。修正前の右図と比較して、わかりやすく表示されるようになったことを確認して下さい。

mbtree_anim = Mbtree_Anim(mbtree)

下図は、アニメーションの中の 17 番と 18 番のフレームを並べたものです。修正前と比べて、以下のような点がわかりやすくなっています。

表示する必要がない、選択されたノードの 子ノードが表示されなくなった
親ノードが中心となったため、親ノードの兄弟ノードが表示される ようになった
親ノードが変化した際に、親ノードが表示される位置が異なる ようになったので、親ノードの変化がわかりやすくなった

深いノードの表示の改良

上記の修正を行っても、まだ改良する余地は残っています。それは、例えば 深さが 9 のノードが追加 されるフレームのアニメーションを見ることで確認できます。

下図は、深さが 9 のノードが選択されたフレームとなる、500000 ~ 500019 フレームのアニメーションです。深さ 8 のノードが 中心となるノードになっている ため、表示される ノードの数が少なく、変化がわかりづらい アニメーションになっています。

この問題を解決するためには、前回の記事と同様に、中心となるノードがの深さが 6 以下 の場合は、その親ノードを辿った、深さが 6 の親ノードを中心とする部分木を描画する という方法が考えられます。

下記は、そのように update_gui を修正したプログラムです。

5、6 行目：深さが 6 になるまで centernode の親ノードを辿るようにする

1  def update_gui(self):
元と同じなので省略
2      self.centernode = self.selectednode
3      if self.centernode.depth > 0:
4          self.centernode = self.centernode.parent
5      while self.centernode.depth > 6:
6          self.centernode = self.centernode.parent
元と同じなので省略
7
8  Mbtree_Anim.update_gui = update_gui

行番号のないプログラム

def update_gui(self):
    self.ax.clear()
    self.ax.set_xlim(-1, self.width - 1)
    self.ax.set_ylim(0, self.height)   
    self.ax.invert_yaxis()
    self.ax.axis("off")   
    
    self.selectednode = self.mbtree.nodelist[self.play.value]
    self.centernode = self.selectednode
    if self.centernode.depth > 0:
        self.centernode = self.centernode.parent
    while self.centernode.depth > 6:
        self.centernode = self.centernode.parent
    if self.centernode.depth <= 4:
        maxdepth = self.centernode.depth + 1
    elif self.centernode.depth == 5:
        maxdepth = 7
    else:
        maxdepth = 9
    self.mbtree.draw_subtree(centernode=self.centernode, selectednode=self.selectednode, ax=self.ax, maxdepth=maxdepth)
    for rect, node in self.mbtree.nodes_by_rect.items():
        if node.id > self.play.value:
            self.ax.add_artist(patches.Rectangle(xy=(rect.x, rect.y), width=rect.width, height=rect.height, fc="black", alpha=0.5))

Mbtree_Anim.update_gui = update_gui

修正箇所

def update_gui(self):
元と同じなので省略
    self.centernode = self.selectednode
    if self.centernode.depth > 0:
        self.centernode = self.centernode.parent
+   while self.centernode.depth > 6:
+       self.centernode = self.centernode.parent
元と同じなので省略

Mbtree_Anim.update_gui = update_gui

上記の修正後に、下記のプログラムを実行して IntSlider の数値の部分をクリックして 500000 を入力した後で三角形のボタンをクリックすると、実行結果のような、中心となるノードが 6 になった部分木のアニメーションが表示されるようになります。

mbtree_anim = Mbtree_Anim(mbtree)

実行結果（右図は 500000 ~ 500019 フレームまでのアニメーションの繰り返しです）

興味がある方は、他の様々なフレームでアニメーションを行ってみて下さい。

アニメーションの速度の調整

現状では、Play ウィジェットの interval 属性 に 500 を代入 したので、1 秒間に 1000 / 200 = 2 回フレームを表示するという、2 fps でアニメーションが行われますが、アニメーションの 速度を調整できるようになると便利 でしょう。

そこで、この interval 属性を変更 するための IntSlider をもう一つ用意 し、jslink を使って連動 することで、アニメーションの 速度を調整できるようにする ことにします。

`create_widgets` の修正

まず、Mbtree_Anim クラスの create_widgets メソッドを下記のように修正します。

5 行目：IntSlider が 2 つに増えたので、フレームの番号を表す IntSlider を代入する属性の名前を frame_slider に修正した
6 行目：アニメーションの表示の間隔を表す IntSlider を、初期値を 500、最小値を 1、最大値を 2000、左に interval という文字列を表示するように設定して作成し、interval_slider 属性に代入する。最小値と最大値を変更したい人は自由に変更すること
8 行目：Play ウィジェットの interval 属性と、interval_slider の value 属性をリンクして、連動するようにする

 1  import ipywidgets as widgets
 2
 3   def create_widgets(self):
 4       self.play = widgets.Play(max=self.mbtree.nodenum - 1, interval=500)
 5       self.frame_slider = widgets.IntSlider(max=self.mbtree.nodenum - 1, description="frame")
 6       self.interval_slider = widgets.IntSlider(value=500, min=1, max=2000, description="interval")
 7       widgets.jslink((self.play, "value"), (self.frame_slider, "value"))    
 8       widgets.jslink((self.play, "interval"), (self.interval_slider, "value"))
元と同じなので省略
 9    
10   Mbtree_Anim.create_widgets = create_widgets

行番号のないプログラム

import ipywidgets as widgets

def create_widgets(self):
    self.play = widgets.Play(max=self.mbtree.nodenum - 1, interval=500)
    self.frame_slider = widgets.IntSlider(max=self.mbtree.nodenum - 1, description="frame")
    self.interval_slider = widgets.IntSlider(value=500, min=1, max=2000, description="interval")
    widgets.jslink((self.play, "value"), (self.frame_slider, "value"))    
    widgets.jslink((self.play, "interval"), (self.interval_slider, "value"))

    with plt.ioff():
        self.fig = plt.figure(figsize=[self.width * self.size,
                                        self.height * self.size])
        self.ax = self.fig.add_axes([0, 0, 1, 1])
    self.fig.canvas.toolbar_visible = False
    self.fig.canvas.header_visible = False
    self.fig.canvas.footer_visible = False
    self.fig.canvas.resizable = False     
    
Mbtree_Anim.create_widgets = create_widgets

修正箇所

import ipywidgets as widgets

def create_widgets(self):
    self.play = widgets.Play(max=self.mbtree.nodenum - 1, interval=500)
-   self.slider = widgets.IntSlider(max=self.mbtree.nodenum - 1, description="frame")
+   self.frame_slider = widgets.IntSlider(max=self.mbtree.nodenum - 1, description="frame")
+   self.interval_slider = widgets.IntSlider(value=500, min=1, max=2000, description="interval")
-   widgets.jslink((self.play, "value"), (self.slider, "value"))    
+   widgets.jslink((self.play, "value"), (self.frame_slider, "value"))    
+   widgets.jslink((self.play, "interval"), (self.interval_slider, "value"))
元と同じなので省略
    
Mbtree_Anim.create_widgets = create_widgets

`display_widgets` の修正

次に、display_widgets メソッドを下記のプログラムように修正します。

2 行目：interval_slider を frame_slider の右に並べて配置するようにする

1  def display_widgets(self):
2      hbox = widgets.HBox([self.play, self.frame_slider, self.interval_slider])
3      display(widgets.VBox([hbox, self.fig.canvas]))
4      
5  Mbtree_Anim.display_widgets = display_widgets

行番号のないプログラム

def display_widgets(self):
    hbox = widgets.HBox([self.play, self.frame_slider, self.interval_slider])
    display(widgets.VBox([hbox, self.fig.canvas]))
    
Mbtree_Anim.display_widgets = display_widgets

修正箇所

def display_widgets(self):
    hbox = widgets.HBox([self.play, self.frame_slider, self.interval_slider])
    display(widgets.VBox([hbox, self.fig.canvas]))
    
Mbtree_Anim.display_widgets = display_widgets

動作の確認

上記の修正後に、下記のプログラムを実行すると、実行結果のようにアニメーションの表示間隔を調整する IntSlider が表示されるようになります。実際に三角形のボタンをクリックした後で IntSlider を操作して アニメーションの速度が変更される ことを確認して下さい。

mbtree_anim = Mbtree_Anim(mbtree)

Play ウィジェットの value 属性は、interval 属性に代入されたミリ秒の間隔で増えると説明しましたが、interval の値が一定以下 の場合は その値が正しく適用されない ようです。筆者のパソコンで調べた所、interval 属性の値が 4 以下 の場合は、interval 属性に 4 が代入されたものとして処理が行われる ようでした。なお、この値はパソコンや OS の種類によって異なるかもしれません。

mbtree_anim = Mbtree_Anim(mbtree) を実行してアニメーションを行った際に、interval の IntSlider を　1 ~ 4 の間の様々な値に変更してみて下さい。frame の数字が増える速度が変化しないことがわかるのではないかと思います。

従って interval 属性には 4 以下の数値を設定しても意味がないのですが、この 4 という数値がすべてのコンピューターで共通する数値であるかが良くわからないので、本記事では interval_slider の最小値を 1 のままにすることにします。

`interval` 属性と実際の `value` 属性の増加の間隔の違い

Play ウィジェットの value 属性を増やす処理 は、以前の記事で説明した イベントループの仕組み によって行われ、イベントループには、イベントループから呼び出した処理が終了するまでは、次のイベントを処理できない という性質があります。そのため、value 属性の値が変更する間隔は実際には interval 属性の値とは異なる場合があります。

具体例として、Play ウィジェットの value 属性が増加した際に呼び出された イベントハンドラが行う処理 が interval 属性で指定した時間よりも長くかかる場合 は、value 属性の値は、interval 属性よりも 長い間隔で増加 します。Mbtree_Anim クラスを使ってアニメーションを行った際に、interval の IntSlider の値を小さくする と、間を飛ばしながらアニメーションが行われる のは、上記のような理由からです。

value 属性の値が変更する間隔が、interval 属性の値よりも長くなった場合は、value 属性の値 は時間経過の分だけ、まとめてその値が増加します。

わかりづらいと思いますので具体例を挙げます。interval 属性の値に 5 を設定した場合に、value 属性の値が 30 ミリ秒後に変更された場合は、30 / 5 = 6 回分の value 属性の増加の処理がまとめて行われるので、 6 増えることになります。

下記のプログラムは、そのことを確認するプログラムです。

1、2 行目：interval 属性に 5 を設定した Play ウィジェットを作成して、表示する
4、5 行目：Play ウィジェットの value 属性の値が変更された場合に呼び出されるイベントハンドラを定義する。このイベントハンドラは value 属性の値を表示する
7 行目：イベントハンドラと Play ウィジェットを結び付ける

1  play = widgets.Play(interval=5)
2  display(play)
3
4  def on_play_changed(changed):
5      print(play.value)
6
7  play.observe(on_play_changed, names="value")

行番号のないプログラム

play = widgets.Play(interval=5)
display(play)

def on_play_changed(changed):
    print(play.value)

play.observe(on_play_changed, names="value")

実行結果（表示される数字の間隔は、コンピュータの性能によって異なります）

上記のプログラムを実行して三角形のボタンをクリックすると、実行結果のように value 属性の値が変更された際の値が表示 されますが、その値は とびとびの値 になっています。上記の実行結果から、value 属性は 平均すると約 8 ずつ増えながら表示される ので、実際の値の増加 は 5 * 8 = 約 40 ミリ秒おきに行われた ことがわかります。

上記のように、interval 属性の値を小さくしても、1 秒間に value 属性の値が変更される回数には限度がある ようです。おそらく 60 回が限度になっているので、Play ウィジェットを使った場合のアニメーションの fps の最大値は約 60 fps だと思われます。ただし、この最大値はパソコンによって異なるかもしれません。

アニメーションが遅くなる理由

mbtree_anim = Mbtree_Anim(mbtree) でアニメーションを行った際に、interval を 10 のように かなり小さく し、frame を 500000 のように大きくする と、同じ interval でも表示されるアニメーションの フレームの更新の間隔が伸びるように感じられる と思いますが、これは 錯覚ではありません。そのようなことが起きる原因について少し考えてみて下さい。

その理由は、部分木を描画する draw_subtree の中で呼び出されている、ゲーム木の 各ノードの高さを計算する calc_node_height(maxdepth) が原因 です。calc_node_height は、ルートノードから maxdepth で指定した深さのノードまでの部分木を描画する際の、それぞれのノードの高さを計算する処理を行います。draw_subtree で描画する部分木の 深さが浅い場合 は、maxdepth の値が小さくなるので、高さを計算する必要があるノードの数は多くありません。しかし、maxdepth の値が例えば最大の 9 の場合は、50 万以上のノードのすべてのノードの高さを計算する ことになるので、処理に時間がかかります。

そのことは、下記のプログラムで確認することができます。

下記は 深さ 1 まで のゲーム木の各ノードの高さの計算の処理時間を計測するプログラムで、実行結果から平均すると 約 1.14 μs（約百万分の 1 秒） かかることがわかります。

%%timeit 
mbtree.calc_node_height(maxdepth=1)

実行結果

1.14 µs ± 3.07 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)

下記は深さ 9 までのゲーム木の各ノードの高さの計算の処理時間を計測するプログラムで、実行結果から平均すると 約 212 ms（約 0.21 秒） もの時間がかかることがわかります。高さを計算するだけで 0.21 秒もかかるということは、1000 / 213 = 約 5 なので、約 5 fps 以上のアニメーションを行うことはできない ことがわかります。

%%timeit 
mbtree.calc_node_height(maxdepth=9)

実行結果

212 ms ± 3.21 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

下図の 深さが 9 の部分木 を描画する際に 高さを計算する必要があるノード は、下図の 赤枠の中のたった 16 個のノードだけ です。それにもかかわらず 50 万以上のノードの高さを計算するのは、かなりの無駄な処理を行っている ということです。

アニメーションを行わない場合は、ノードの高さの計算に約 0.2 秒かかってもほとんど気になりませんでしたが、アニメーションのように 描画を高速に行わなければならない場合 は、このような 無駄な処理が アニメーションの fps の大きな低下につながります。そこで、必要なノードの高さだけを計算する ように calc_node_height を修正することにします。

`calc_node_height` の修正

現状の calc_node_height は、必ずルートノードから maxdepth までの部分木の各ノードの高さを計算していましたが、必要となる計算は、中心となるノードから maxdepth まで の部分木の各ノードの高さです。そこで、calc_node_height に、中心となるノードを代入する centernode という仮引数を追加する ことにします。

次に centernode から maxdepth までの部分木のノードの一覧を計算する必要がありますが、その方法は、ゲーム木を作成する create_tree_by_bf とほぼ同じ、幅優先アルゴリズムで計算 することができます。create_tree_by_bf との具体的な違いは、以下の通りです。

最初に nodelist に登録 するノードを、ルートノードから centernode に変更 する
ノードの深さ を表す depth を 0 ではなく、centernode.depth で初期化する
create_tree_by_bf では、各ノードの子ノードを作成する必要があったが、calc_node_height では ノードはすべて作成済 である
create_tree_by_bf では、ゲーム木全体 の各深さのノードの一覧を 後で利用できるようにする ために、その情報を nodelist_by_depth という属性 に代入していたが、calc_node_height で計算するのは 部分木 の各深さのノードの一覧である。また、その情報は、calc_node_height の処理が終わった後で利用することはない ので、同じ名前の ローカル変数に代入する ことにする
create_tree_by_bf では、深さ 0 のルートノードから nodelist_by_depth にデータを記録 したが、calc_node_height では centernode の深さからデータを記録する
print などの処理は必要がないので削除する

nodelist_by_depth の計算後は、元の calc_node_height と同様の方法で、 maxdepth から centernode の深さの順で、各ノードの高さを計算することができます。

下記は、そのように calc_node_height を修正したプログラムです。

全体：self.node_list_by_depth をローカル変数 node_list_by_depth に修正する
1 行目：仮引数 centernode を追加する
2 行目：nodelist を、centernode を要素とする list で初期化するようにする
3 行目：depth に centernode の深さを代入するように修正する
5 行目：depth より浅いノードの高さは計算しないが、node_list_by_depth の 0 ~ depth - 1 番の要素には何らかの値を代入しておく必要があるので、None で初期化する
6 行目：node_list_by_depth の depth の深さのデータとして、nodelist を追加する
10 ~ 12 行目：深さが depth のノードの子ノードの一覧を計算する。create_tree_by_bf と異なり、子ノードは計算済なので、node.children を順次追加するだけで良い
17 行目：maxdepth の深さから、centernode の深さまで、深い順に各ノードの高さを計算するように修正する。計算方法は元のプログラムと同じ

 1  def calc_node_height(self, centernode, maxdepth):
 2      nodelist = [centernode]
 3      depth = centernode.depth
 4      # 各深さのノードのリストを記録する変数を初期化する
 5      nodelist_by_depth = [None] * centernode.depth
 6      nodelist_by_depth.append(nodelist)
 7   
 8      # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
 9      while len(nodelist) > 0:
10          childnodelist = [] 
11          for node in nodelist:
12              childnodelist += node.children
13          nodelist_by_depth.append(childnodelist)
14          nodelist = childnodelist
15          depth += 1
16    
17      for depth in range(maxdepth, centernode.depth - 1, -1):
18          for node in nodelist_by_depth[depth]:
19              if depth == maxdepth:
20                  node.height = 4
21              else:
22                  node.calc_height()                  
23                
24  Mbtree.calc_node_height = calc_node_height

行番号のないプログラム

def calc_node_height(self, centernode, maxdepth):
    nodelist = [centernode]
    depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
    nodelist_by_depth = [None] * centernode.depth
    nodelist_by_depth.append(nodelist)
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
            childnodelist += node.children
        nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
    
    for depth in range(maxdepth, centernode.depth - 1, -1):
        for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()                  
                
Mbtree.calc_node_height = calc_node_height

修正箇所（前半部分は create_tree_by_bf との違い、for depth in・・・ 以降の後半部分は元の calc_node_height との違いです）

-def calc_node_height(self, maxdepth):
+def calc_node_height(self, centernode, maxdepth):
-   nodelist = [self.root]
+   nodelist = [centernode]
-   depth = 0
+   depth = centernode.depth
    # 各深さのノードのリストを記録する変数を初期化する
-   self.nodelist_by_depth = [ nodelist ]
+   nodelist_by_depth = [None] * centernode.depth
+   nodelist_by_depth.append(nodelist)
    
    # 深さ depth のノードのリストが空になるまで繰り返し処理を行う
    while len(nodelist) > 0:
        childnodelist = [] 
        for node in nodelist:
-           if node.mb.status == Marubatsu.PLAYING:
-               node.calc_children()
            childnodelist += node.children
-       self.nodelist_by_depth.append(childnodelist)
+       nodelist_by_depth.append(childnodelist)
        nodelist = childnodelist
        depth += 1
-       print(f"{len(nodelist):>6} depth {depth} node created")
    
-   for depth in range(maxdepth, -1, -1):
+   for depth in range(maxdepth, centernode.depth - 1, -1):
-       for node in self.nodelist_by_depth[depth]:
+       for node in nodelist_by_depth[depth]:
            if depth == maxdepth:
                node.height = 4
            else:
                node.calc_height()                  
                
Mbtree.calc_node_height = calc_node_height

上記の修正後に、下記のプログラムで深さ 6 のノードを中心とする深さ 9 までのノードの処理時間を計測すると、実行結果のように処理時間が大幅に短くなったことが確認できます。

%%timeit 
mbtree.calc_node_height(mbtree.nodelist_by_depth[6][0], maxdepth=9)

実行結果

2.73 µs ± 12.9 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

`draw_subtree` の修正

draw_subtree の修正は、下記のプログラムの 6 行目のように、calc_node_height にキーワード引数 centernode=centernode を追加するだけです。

1  def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
2      self.nodes_by_rect = {}
3
4      if centernode is None:
5          centernode = self.root
6      self.calc_node_height(centernode=centernode, maxdepth=maxdepth)
元と同じなので省略
7            
8  Mbtree.draw_subtree = draw_subtree

行番号のないプログラム

def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
    self.nodes_by_rect = {}

    if centernode is None:
        centernode = self.root
    self.calc_node_height(centernode=centernode, maxdepth=maxdepth)
    width = 5 * (maxdepth + 1)
    height = centernode.height
    parent = centernode.parent
    if parent is not None:
        height += (len(parent.children) - 1) * 4
        parent.height = height
    if ax is None:
        fig, ax = plt.subplots(figsize=(width * size, height * size))
        ax.set_xlim(0, width)
        ax.set_ylim(0, height)   
        ax.invert_yaxis()
        ax.axis("off")        
    
    nodelist = [centernode]
    depth = centernode.depth
    while len(nodelist) > 0 and depth <= maxdepth:        
        dy = 0
        if parent is not None:
            dy = parent.children.index(centernode) * 4
        childnodelist = []
        for node in nodelist:
            if node is None:
                dy += 4
                childnodelist.append(None)
            else:
                dx = 5 * node.depth
                emphasize = node is selectednode
                rect = node.draw_node(ax=ax, maxdepth=maxdepth, emphasize=emphasize, size=size, lw=lw, dx=dx, dy=dy)
                self.nodes_by_rect[rect] = node
                dy += node.height
                if len(node.children) > 0:  
                    childnodelist += node.children
                else:
                    childnodelist.append(None)
        depth += 1
        nodelist = childnodelist
        
    if parent is not None:
        dy = 0
        for sibling in parent.children:
            if sibling is not centernode:
                sibling.height = 4
                dx = 5 * sibling.depth
                rect = sibling.draw_node(ax, maxdepth=sibling.depth, size=size, lw=lw, dx=dx, dy=dy)
                self.nodes_by_rect[rect] = sibling
            dy += sibling.height
        dx = 5 * parent.depth
        rect = parent.draw_node(ax, maxdepth=maxdepth, size=size, lw=lw, dx=dx, dy=0)
        self.nodes_by_rect[rect] = parent
    
        node = parent
        while node.parent is not None:
            node = node.parent
            node.height = height
            dx = 5 * node.depth
            rect = node.draw_node(ax, maxdepth=node.depth, size=size, lw=lw, dx=dx, dy=0)
            self.nodes_by_rect[rect] = node
            
Mbtree.draw_subtree = draw_subtree

修正箇所

def draw_subtree(self, centernode=None, selectednode=None, ax=None, size=0.25, lw=0.8, maxdepth=2):
    self.nodes_by_rect = {}

    if centernode is None:
        centernode = self.root
-   self.calc_node_height(maxdepth)
+   self.calc_node_height(centernode=centernode, maxdepth=maxdepth)
元と同じなので省略
            
Mbtree.draw_subtree = draw_subtree

実行結果は省略しますが、上記の修正後に、下記のプログラムを実行し、interval を小さくしてアニメーションを行うと、frame を変更してもアニメーションの fps がほとんど変わらないようになったことを確認して下さい。

mbtree_anim = Mbtree_Anim(mbtree)

今回の記事のまとめ

今回の記事では、ゲーム木の生成の過程のアニメーションの改良を行いました。

次回の記事では、ゲーム木を生成するもう一つのアルゴリズムである、深さ優先アルゴリズム について説明する予定です。

本記事で入力したプログラム

リンク	説明
marubatsu.ipynb	本記事で入力して実行した JupyterLab のファイル
tree_new.py	今回の記事で更新した tree.py

次回の記事

std は標準偏差を表す standard deviation の略です ↩
マイクロはギリシャ文字で μ と表記します。micro の頭文字である m と表記しない理由は mili と micro の頭文字が被っているからです ↩
正確には、計測された処理時間が 正規分布に従う場合は という条件がつきます。また、プログラムを何度も実行した際の処理時間の分布は、多くの場合はほぼ正規分布に従うことが知られています。正規分布は統計学で出てくる用語で、本記事でも必要があればこの後の記事で紹介するかもしれません。興味がある方は勉強してみて下さい ↩
色を表すデジタルデータの中で、透明度を表すデータの事を α（アルファ）値と呼びます。なお、透明度を表す英単語は opacity です ↩
具体的には、仮引数が増えて複雑になる、draw_board の中で行う処理が複雑になるなどです ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up

Pythonで〇×ゲームのAIを一から作成する その98 ゲーム木の生成過程を表示するアニメーションの改良と処理時間の計測

目次と前回の記事

これまでに作成したモジュール

ルールベースの AI の一覧

ゲーム木の生成の過程のアニメーションの改良

ゲーム木に追加予定のノードの表示の改良

ゲーム木に追加予定のノードを暗く表示するアルゴリズム

ノードがゲーム木に追加された順番を計算するアルゴリズム

index メソッドによる計算

index メソッドの欠点と、timeit モジュールによる処理時間の計測

ノードを挿入した順番の記録

ノードを暗く表示する方法

背景色を変える方法とその問題点

半透明の黒い図形を重ねる方法

ノードを暗く表示する処理の実装

中心となるノードの改良

わかりづらさの原因の検証

中心となるノードの変更

深いノードの表示の改良

アニメーションの速度の調整

create_widgets の修正

display_widgets の修正

動作の確認

interval 属性と実際の value 属性の増加の間隔の違い

アニメーションが遅くなる理由

calc_node_height の修正

draw_subtree の修正

今回の記事のまとめ

本記事で入力したプログラム

次回の記事

Pythonで〇×ゲームのAIを一から作成する　その98　ゲーム木の生成過程を表示するアニメーションの改良と処理時間の計測

`index` メソッドによる計算

`index` メソッドの欠点と、timeit モジュールによる処理時間の計測

`create_widgets` の修正

`display_widgets` の修正

`interval` 属性と実際の `value` 属性の増加の間隔の違い

`calc_node_height` の修正

`draw_subtree` の修正