目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
ルールベースの AI の一覧
ルールベースの AI の一覧については、下記の記事を参照して下さい。
木構造のデータを作成する 2 つのアルゴリズム
前回の記事で説明した ゲーム木を作成する主なアルゴリズム には、幅優先 と 深さ優先 という 2 種類があります。今回の記事ではそのうちの幅優先アルゴリズムについて説明します。なお、深さ優先アルゴリズムに関しては今後の記事で紹介します。
幅優先と深さ優先という用語は、主に木構造などの グラフ構造のデータを分析 する際に用いられる「幅優先探索」、「深さ優先探索」という 探索のアルゴリズムの名前 で使われます。木構造を作成する際のアルゴリズムに「幅優先」、「深さ優先」という用語が使われているのはあまり見たことがないのですが、行う処理は探索のアルゴリズムと同様なので、本記事ではゲーム木を作成する際のアルゴリズムを「幅優先アルゴリズム」のように表記することにします。
なお、ゲーム木を分析する探索のアルゴリズムに関してはこの後で紹介します。
幅優先アルゴリズムによるゲーム木の作成
幅優先(breadth first)アルゴリズムは、ゲーム木のノードに対して、ノードの 深さの浅い順番 で、子ノードを作成する というものです。
具体的には下記のような手順でゲーム木を作成します。
- ゲーム開始時の局面 を表すノードを ルートノード とする ゲーム木を作成 する
- 子ノードを作成する処理を行う ノードの深さ d を 0 に設定 する
- 深さ d のノードが存在しない場合は、ゲーム木が完成しているので処理を終了する
- 深さ d のノードが存在する場合は、それらの 全てのノードに対して子ノードを作成 する
- 深さ d に 1 を足して 手順 3 に戻る
前回の記事で説明したように、〇×ゲーム木の ノードの深さ は、局面の手数を表します。上記のアルゴリズムでは、0 手目の局面から順番に、子ノードの作成 を行いますが、〇×ゲームは必ず 9 手目までで決着がつくので、具体的には、以下のような処理が行われます。
- ゲーム開始時の 0 手目の局面の子ノードを計算する
- 1 手目のすべての局面の子ノードを計算する
- 2 手目のすべての局面の子ノードを計算する
- 3 手目のすべての局面の子ノードを計算する
略 - 9 手目のすべての局面の子ノードを計算する
前回の記事では、〇×ゲームのゲーム木のノードを表す Node という クラスを定義 し、ノードの 子ノードを計算する calc_childnode というメソッドを定義 しました。幅優先アルゴリズム では、このメソッドを利用することでゲーム木を作成することができます。
幅優先アルゴリズムでは、ゲーム木のノードを、深さが浅い順に作成します。そのため、ゲーム木のノードを、深さが浅い順に 縦方向に表現した場合 に、横一列に並んだ同じ深さのノードが上から順番に作成されていくことになります。この様子が、横幅(breadth)の方向を優先 してゲーム木が作られるように見えるため、幅優先 いう名前が付けられました。
上記の説明でピンとこない人がいるかもしれませんので、幅優先アルゴリズムでゲーム木がどのように作られていくかについては、今後の記事で視覚化する予定です。
ゲーム木を表すクラスの定義
まず、〇×ゲームのゲーム木を表す Mbtree1 という クラスを定義 することにします。ゲーム木はゲーム開始時の局面をルートノードとして持つので、root という属性にルートノードを表す Node クラスのインスタンスを代入することにします。
なお、ノードを表すデータを、Node クラスのインスタンスと表記するのは冗長なので、以後は単に、「root 属性にノードを代入する」のように表記することにします。
下記は、Mbtree クラスの定義を表すプログラムで、インスタンスを作成する際に、root 属性にゲームの開始時の局面を表すノードを作成して代入しています。
-
6 行目:下記の処理で、ゲームの開始時の局面を表すノードを
root属性に代入する- Marubatsu クラスのインスタンスを作成する
- Marubatsu クラスのインスタンスを表す Node クラスのインスタンスを作成する
1 from marubatsu import Marubatsu
2 from tree import Node
3
4 class Mbtree:
5 def __init__(self):
6 self.root = Node(Marubatsu())
行番号のないプログラム
from marubatsu import Marubatsu
from tree import Node
class Mbtree:
def __init__(self):
self.root = Node(Marubatsu())
下記のプログラムは、MbTree のインスタンスを作成し、ルートノードの局面を表示するプログラムで、実行結果のようにゲーム開始時の局面が表示されます。
mbtree = Mbtree()
print(mbtree.root.mb)
実行結果
Turn o
...
...
...
幅優先アルゴリズムによるゲーム木を作成するメソッドの定義 その 1
次に、Mbtree クラスに、幅優先アルゴリズムでゲーム木を作成する、下記のようなメソッドを定義します。
名前:create_tree_by_bf2 という名前にする
処理:幅優先アルゴリズムによってゲーム木を作成する
入力:なし
出力:なし
今回の記事では、初心者が思いつきそうな幅優先アルゴリズムによるゲーム木を作成する方法を紹介し、その方法では深いゲーム木を作成する場合はうまくいかない ことを示します。深いゲーム木を幅優先アルゴリズムで作成する方法については、次回の記事で説明します。
深さ 1 のノードの作成
いきなり深いゲーム木を作成するのは大変なので、深さ 1 のノードから順番 に、作成するゲーム木の ノードの深さを 1 つずつ増やしながら ゲーム木を作成していくことにします。
深さ 1 のノードは、前回の記事 で行った、ルートノードの子ノードを計算する処理 によって行えます。そこで、create_tree_by_bf にその処理を、下記のプログラムのように記述することにします。なお、この処理は、1 手目の局面 のノードをゲーム木に追加する処理で、深さ 1 のゲーム木を作成 することができます。
def create_tree_by_bf(self):
self.root.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
また、下記のプログラムの 3 行目のように、__init__ メソッドの中で create_tree_by_bf を呼び出すようにすることで、Mbtree クラスの インスタンスを作成した際 に、深さ 1 のゲーム木を作成 するようにすることができます。
1 def __init__(self):
2 self.root = Node(Marubatsu())
3 self.create_tree_by_bf()
4
5 Mbtree.__init__ = __init__
行番号のないプログラム
def __init__(self):
self.root = Node(Marubatsu())
self.create_tree_by_bf()
Mbtree.__init__ = __init__
修正箇所
def __init__(self):
self.root = Node(Marubatsu())
+ self.create_tree_by_bf()
Mbtree.__init__ = __init__
上記の修正後に、下記のプログラムを実行することで、実行結果のように、ルートノードの子ノードが計算されたことが確認できます。
mbtree = Mbtree()
mbtree.root.draw_node()
実行結果(見やすいように、実際に表示される画像よりも小さく画像を表示しています)
深さ 2 のノードの作成
深さ 2 のノードの作成は、深さ 1 の全てのノードに対して calc_children を呼び出すことで作成できるので、下記のプログラムの 5、6 行目ように記述できます。
1 def create_tree_by_bf(self):
2 # 深さ 1 のノードの作成
3 self.root.calc_children()
4 # 深さ 2 のノードの作成
5 for childnode in self.root.children:
6 childnode.calc_children()
7
8 Mbtree.create_tree_by_bf = create_tree_by_bf
行番号のないプログラム
def create_tree_by_bf(self):
# 深さ 1 のノードの作成
self.root.calc_children()
# 深さ 2 のノードの作成
for childnode in self.root.children:
childnode.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
修正箇所
def create_tree_by_bf(self):
# 深さ 1 のノードの作成
self.root.calc_children()
# 深さ 2 のノードの作成
+ for childnode in self.root.children:
+ childnode.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
上記の修正後に、下記のプログラムを実行することで、実行結果のように、深さ 1 のノードの最初のノードを表す mbtree.root.children[0] の子ノードが計算されたことが確認できます。なお、ゲーム木を作成する処理を修正 したので、1 行目のように、Mbtree クラスの インスタンスを作り直す必要がある 点に注意して下さい。
mbtree = Mbtree()
mbtree.root.children[0].draw_node()
実行結果

深さ 2 のゲーム木の視覚化
上記では、深さ 1 のノードの中の、最初の 1 つのノードだけを視覚化しましたが、これでは 全体像が見えない ので、深さ 2 のゲーム木の 全体を視覚化 することにします。
まず、Mbtree クラスにゲーム木を視覚化する下記のメソッドを定義する事にします。
名前:ゲーム木を描画するので draw_tree という名前にする
処理:ゲーム木のすべてのノードを描画する
入力:なし
出力:なし
深さ 1 のノードまでのゲーム木の描画
まず、ルートノードから深さ 1 までのゲーム木を描画する処理を記述することにします。深さ 1 までのゲーム木の描画は、ルートノードとその子ノードの関係を描画すればよい ので、下記のプログラムの 3 行目のように、ルートノードに対して、前回の記事で定義した draw_node メソッドを呼び出すことで描画することができます。
1 def draw_tree(self):
2 # 深さが 0 のノードとその子ノードの関係を描画する
3 self.root.draw_node()
4
5 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self):
# 深さが 0 のノードとその子ノードの関係を描画する
self.root.draw_node()
Mbtree.draw_tree = draw_tree
上記を実行後に、下記のプログラムを実行することで、実行結果のように、ルートノードと子ノードの関係が描画され、深さ 1 までのゲーム木が描画されます。なお、先程と異なり、ゲーム木の作成の処理は変更していないので、Mbtree クラスのインスタンスを作成し直す必要はありません。
mbtree.draw_tree()
実行結果

深さ 2 のノードまでのゲーム木の描画に対する考察
深さ 2 のノードまでのゲーム木を描画するためには、それぞれのノードをどの位置に描画するか を計算する必要があります。その計算方法を考えるためには、前回の記事と同様に、深さ 2 までのゲーム木を 実際にノートなどに書いてみる ことをお勧めします。
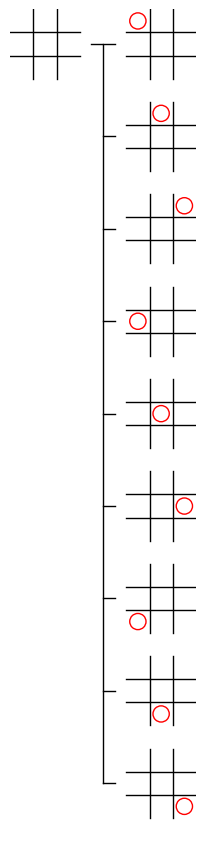
下記は、筆者が考えた深さ 2 までのゲーム木の視覚化の図です。
下図は、上図の一部を拡大したものです。赤丸で示した、深さ 1 の最初のノードと、その子ノードの関係の部分は、draw_node で描画される画像と比べると、描画する位置が異なるだけ なので、draw_node とほぼ同じ方法で描画できそう です。これは、他の深さ 1 のノードとその子ノードの関係も同様 です。そこで、最初に深さ 1 のノードとその子ノードの関係を描画する処理を記述することにします。

任意の座標に描画できるようにするための draw_node の修正
まず、draw_node に、前回の記事で draw_board を修正した場合と同様の方法で、仮引数 dx、dy を追加して、任意の Axes の座標 にノードとその子ノードの関係を 描画できるように修正 することにします。下記は draw_node を修正したプログラムです。
-
4 行目:デフォルト値を
0とするデフォルト引数dx、dyを追加する -
6 ~ 11 行目:x 座標を表す部分に
dxを、y 座標を表す部分にdyを加算することで、すべての描画を (dx, dy) の分だけずらして行う
1 import matplotlib.pyplot as plt
2 from marubatsu import Marubatsu_GUI
3
4 def draw_node(self, size=0.25, lw=0.8, dx=0, dy=0):
元と同じなので省略
5 # 自分自身のノードを (dx, dy) に描画する
6 Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
7 plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
8 # i 番の子ノードを (dx + 5, dy + i * 4) に描画する
9 for i, childnode in enumerate(self.children):
10 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
11 plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
12
13 Node.draw_node = draw_node
行番号のないプログラム
import matplotlib.pyplot as plt
from marubatsu import Marubatsu_GUI
def draw_node(self, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
# i 番の子ノードを (dx + 5, dy + i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
修正箇所
import matplotlib.pyplot as plt
from marubatsu import Marubatsu_GUI
-def draw_node(self, size=0.25, lw=0.8):
+def draw_node(self, size=0.25, lw=0.8, dx=0, dy=0):
元と同じなので省略
# 自分自身のノードを (dx, dy) に描画する
- Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
+ Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
- plt.plot([3.5, 4, 4], [1.5, 1.5, 1.5 + height - 4], c="k", lw=lw)
+ plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
# i 番の子ノードを (dx + 5, dy + i * 4) に描画する
for i, childnode in enumerate(self.children):
- Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
+ Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
- plt.plot([4 , 4.5], [1.5 + i * 4, 1.5 + i * 4], c="k", lw=lw)
+ plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
draw_node での Figure の作成処理に関する修正
draw_node で任意の座標に描画を行うことができるようになりましたが、draw_node は Figure を作成する処理を行っている ので、draw_node を実行するたび に、別々の Figure が作成されてしまいます。そこで、以下のように draw_node を修正することにします。
- ゲーム木を描画する Figure、Axes は、ゲーム木を描画する
draw_treeメソッドで作成 し、draw_nodeを呼び出す際に 実引数で Axes の値を指定 する。そのために、draw_nodeに、描画を行う Axes を代入する 仮引数axを追加 する - ただし、1 つのノードだけを
draw_nodeで描画する場合 はこれまで通りdraw_nodeで Figure を作成したほうが便利 なので、仮引数axをデフォルト値がNoneのデフォルト引数とし、Noneが代入されている場合のみFigureを作成 する処理を行うようにする
下記は、そのように draw_node を修正したプログラムです。
-
1 行目:デフォルト値を
Noneとするデフォルト引数axを追加する -
4 ~ 9:
axにNoneが代入されている場合のみ、Figure を作成するように修正する
1 def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
2 width = 8
3 height = len(self.children) * 4
4 if ax is None:
5 fig, ax = plt.subplots(figsize=(width * size, height * size))
6 ax.set_xlim(0, width)
7 ax.set_ylim(0, height)
8 ax.invert_yaxis()
9 ax.axis("off")
元と同じなので省略
10
11 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
height = len(self.children) * 4
if ax is None:
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
# i 番の子ノードを (dx + 5, dy + i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
修正箇所
-def draw_node(self, size=0.25, lw=0.8, dx=0, dy=0):
+def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
height = len(self.children) * 4
- fig, ax = plt.subplots(figsize=(width * size, height * size))
- ax.set_xlim(0, width)
- ax.set_ylim(0, height)
- ax.invert_yaxis()
- ax.axis("off")
+ if ax is None:
+ fig, ax = plt.subplots(figsize=(width * size, height * size))
+ ax.set_xlim(0, width)
+ ax.set_ylim(0, height)
+ ax.invert_yaxis()
+ ax.axis("off")
元と同じなので省略
Node.draw_node = draw_node
実行結果は先ほどの mbtree.draw_tree() と同じなので省略しますが、上記の修正後に、下記のプログラムを実行することで、draw_board に キーワード引数 ax、dx、dy を記述しなかった場合 に、これまでと同じ処理が行われる ことが確認できます。
mbtree.root.draw_node()
深さ 1 のノードの描画位置の計算
次に、深さ 1 のそれぞれのノードの描画位置を計算する必要があります。どのように計算すればよいかについて少し考えてみて下さい。
下図は、深さ 1 の上 2 つのノードの左上の点の座標を表したものです。

深さ 1 のノードの x 座標は、前回の記事でゲーム盤とゲーム盤の横の間隔を 2 としたので、ゲーム盤の幅である 3 を加えて 3 + 2 = 5 になります。
深さ 1 の 2 番目のノードの y 座標は、図から深さ 1 の 1 番目のノードの 右に 8 つの子ノードを描画する必要がある ので、1 番目のノードの 8 つ下に描画 する必要があります。ゲーム盤とゲーム盤の縦の間隔を 1 としたので、その座標は 8 × (3 + 1) = 8 × 4 = 32 となります。
深さ 1 のノード は、いずれも 8 つの子ノードを持つ ので、それぞれのノードは縦方向に 等間隔に並び、深さ 1 の i 番のインデックス のノードの座標は (5, i * 32) となります。
深さ 1 のノードの描画
Figure を作成する処理は、先程説明したように、ゲーム木を描画する draw_tree の中に記述します。その際に、ゲーム木全体を描画 することができる 大きさの Figure を作成 する必要があります。その大きさを計算する方法について少し考えてみて下さい。
Figure の横方向の大きさは、ゲーム盤の横幅が 3 でゲーム盤の間隔が 2 なので 深さが 1 あたり 5 が必要になります。そのため、深さが 0、1、2 の 3 つの深さ のノードを描画する場合は 3 + 2 + 3 + 2 + 3 = 13 であることがわかります。なお、横幅は描画する 深さの数を d とすると「5 * d - 2」で計算できます。
縦方向の大きさは、「深さ 2 のノードの総数 * (3 + 1)」になります。〇×ゲームは 1 手目で 9 通り、2 手目で 8 通りの着手を行えるので、深さ 2 のノードの数は 9 * 8 = 72 になります。従って、縦幅は 72 * 4 = 288 になります。
上記から、深さ 1 のノードを描画する処理は、下記のプログラムのように記述できます。なお、Figure の大きさと線の太さを調整できるように、draw_node と同様の仮引数 size と lw を追加しました。また、すべての内容が変更されているので修正箇所は省略します。
-
1 行目:
draw_nodeと同じ設定の仮引数sizeとlwを追加する - 2、3 行目:Figure の画像の幅と高さを変数に代入する
-
4 ~ 8 行目:
draw_nodeと同じ方法で Figure を作成する -
10、11 行目:ルートノードのそれぞれの i 番のインデックスの子ノードに対して、
enumerateを使って (5, i * 32) の位置にdraw_nodeでそのノードと子ノードの関係を描画する
1 def draw_tree(self, size=0.25, lw=0.8):
2 width = 13
3 height = 288
4 fig, ax = plt.subplots(figsize=(width * size, height * size))
5 ax.set_xlim(0, width)
6 ax.set_ylim(0, height)
7 ax.invert_yaxis()
8 ax.axis("off")
9
10 for i, childnode in enumerate(self.root.children):
11 childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=i*32)
12
13 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, size=0.25, lw=0.8):
width = 13
height = 288
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
for i, childnode in enumerate(self.root.children):
childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=i*32)
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行することで、実行結果のように、深さ 1 のノードと子ノードの関係が描画されます。
mbtree.draw_tree()
深さ 0 のノードの描画処理を行う際に必要な計算の考察
draw_node では、下記のプログラムの 3 行目のように、i 番の子ノード を、(dx, dy) を基準 とした座標から、(5, i * 4) の座標に描画しています。これは、4 行目の エッジを表す横線 を描画する処理も同様です。
# 深さ 1 のノードの i 番の子ノードを (dx + 5, dy + i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
これは、深さ 1 のノードを描画する際は正しいのですが、深さ 0 のノードの i 番のインデックスの子ノード の y 座標 は、先程説明したように、dy を基準とした座標から i * 32 の座標になります。そのため、draw_node の中の処理で、深さが 0 の子ノードを描画する際には、下記のプログラムの 3 行目のように、y 座標を dy + i * 4 ではなく、dy + i * 32 にする必要があります。これは、4 行目のエッジを表す横線を描画する処理も同様です。
# 深さ 0 のノードの i 番の子ノードを (dx + 5, dy + i * 32) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*32, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 32, dy + 1.5 + i * 32], c="k", lw=lw)
修正箇所
# 深さ 0 のノードの i 番の子ノードを (dx + 5, dy + i * 32) に描画する
for i, childnode in enumerate(self.children):
+ Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
+ Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*32, lw=lw)
- plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
+ plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 32, dy + 1.5 + i * 32], c="k", lw=lw)
上記の問題に対して、ノードの深さを調べ、その深さによってそのノードを描画する座標を計算する式を変えるようなプログラムを記述すれば良いのではないかと思った人がいるかもしれませんが、その方法は、下記のような理由でうまくいきません。
-
ゲーム木全体のノードの深さが変わる と 計算式が変わってしまう。例えば、深さが 0 のノードの i 番の子ノードの y 座標は、ゲーム木の深さによって以下のように変化する
- 深さが 1 までのゲーム木の場合は i * 4
- 深さが 2 までのゲーム木の場合は i * 32
- ゲームの 決着がついたノード には 子ノードは存在しない ので、同じ深さのノードでも、子ノードが存在する ノードと 存在しない ノードによって 計算式が変わってしまう
それぞれの ノードの y 座標 は、同じ深さの 一つ前のインデックス のノードの 高さ がわかれば 計算することができます。例えば、下図の赤枠内の深さが 2 のノードの y 座標は、その上の赤線のノードの高さがわかれば計算することができます。下図の緑枠内の深さが 1 のノードの y 座標は、その上の緑線のノードの高さがわかれば計算することができます。
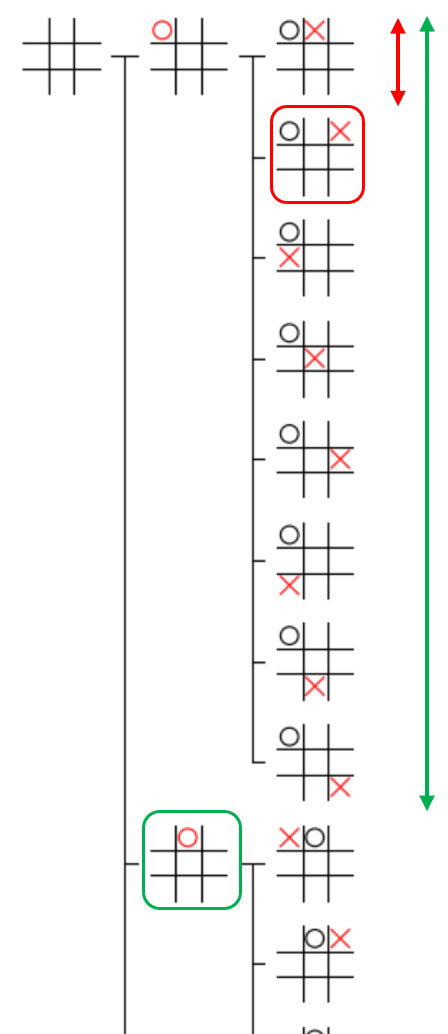
そこで、各ノードを描画した際の高さを計算 することにします。なお、以後はこの高さのことを単に「ノードの高さ」と表記します。
それぞれのノードの高さをどのように計算すればよいかについて少し考えてみて下さい。
ノードの高さを計算する処理の実装
それぞれのノードの高さは、下記のように計算することができます。
- 子ノードがあるノード の場合は、子のノードの高さの合計
- 子ノードがないノード の場合でも、自分自身のノードの高さの分 だけ次のノードを 下に描画する必要がある ので、ゲーム盤の高さ + ゲーム盤の縦の間隔 = 3 + 1 = 4
そこで、Node クラスに、ノードの高さを計算する下記のようなメソッドを定義する事にします。
名前:ノードの高さ(height)を計算するので、calc_height という名前にする
処理:ノードを描画した際の高さを計算する
入力:なし
出力:なし
計算したノードの高さはどこかに記録する必要があるので、height 属性に記録することにします。下記は calc_height の定義です。
-
2、3 行目:子ノードが存在しない場合は
height属性に 4 を代入する -
5 ~ 7 行目:子ノードが存在する場合は、子ノードの
height属性の合計を計算してheight属性に代入する
1 def calc_height(self):
2 if len(self.children) == 0:
3 self.height = 4
4 else:
5 self.height = 0
6 for childnode in self.children:
7 self.height += childnode.height
8
9 Node.calc_height = calc_height
行番号のないプログラム
def calc_height(self):
if len(self.children) == 0:
self.height = 4
else:
self.height = 0
for childnode in self.children:
self.height += childnode.height
Node.calc_height = calc_height
木のそれぞれのノードの高さを計算する処理の実装
次に、Mbtree クラスに、ゲーム木の 各ノードの高さを計算 する下記のようなメソッドを定義する事にします。どのように定義すればよいかについて少し考えてみて下さい。
名前:ゲーム木の各ノードの高さを計算するので、calc_node_height という名前にする
処理:ゲーム木のそれぞれのノードの高さを計算する
入力:なし
出力:なし
下記は、ノードの高さを計算する方法を再掲したものです。
- 子ノードがあるノード の場合は、子のノードの高さの合計
- 子ノードがないノード の場合でも、自分自身のノードの高さの分 だけ次のノードを 下に描画する必要がある ので、ゲーム盤の高さ + ゲーム盤の縦の間隔 = 3 + 1 = 4
上記から、子ノードが存在するノードの高さを計算するためには、子のノードの高さが必要になる ことがわかります。また、木の 一番深いノードには子ノードは存在しません。
このことから、ゲーム木のノードの高さを計算するためには、深い順にノードの高さを計算する必要がある ということがわかるので、calc_node_height は下記のプログラムのように定義することができます。なお、ノードの子ノードの子ノードである、2 つ下の深さのノードのことを孫(grandchild)ノードと呼びます
- 2 行目:ルートノードの子ノードである、深さ 1 のノードに対する繰り返し処理を行う
-
4、5 行目:深さ 1 のノードである
childnodeの子ノードである、深さ 2 のノードに対して、繰り返し処理でその高さを計算する -
7 行目:4、5 行目の処理で、
childnodeの全ての子ノードの高さが計算できるので、childnodeの高さを計算する - 9 行目:2 ~ 7 行目の処理で、ルートノードの全ての子ノードの高さが計算できるので、ルートノードの高さを計算する
1 def calc_node_height(self):
2 for childnode in self.root.children:
3 # 深さ 2 のノードの高さの計算
4 for grandchildnode in childnode.children:
5 grandchildnode.calc_height()
6 # 深さ 1 のノードの高さの計算
7 childnode.calc_height()
8 # 深さ 0 のノードの高さの計算
9 self.root.calc_height()
10
11 Mbtree.calc_node_height = calc_node_height
行番号のないプログラム
def calc_node_height(self):
for childnode in self.root.children:
# 深さ 2 のノードの高さの計算
for grandchildnode in childnode.children:
grandchildnode.calc_height()
# 深さ 1 のノードの高さの計算
childnode.calc_height()
# 深さ 0 のノードの高さの計算
self.root.calc_height()
Mbtree.calc_node_height = calc_node_height
下記のプログラムは、calc_height を呼び出してそれぞれのノードの高さを計算し、深さ 0 のノード、深さ 1 のノード、深さ 2 の最初のノードの高さを表示するプログラムです。それぞれ 288、32、4 という正しい値が計算されていることが確認できます。なお、深さ 2 のノードは数が非常に多いので、最初のノードの高さみを表示しました。
mbtree.calc_node_height()
print("root height", mbtree.root.height)
for childnode in mbtree.root.children:
print("child height", childnode.height)
print("grandchild height", mbtree.root.children[0].children[0].height)
実行結果
root height 288
child height 32
child height 32
child height 32
child height 32
child height 32
child height 32
child height 32
child height 32
child height 32
grandchild height 4
ゲーム木のそれぞれのノードの高さを計算する処理は、ゲーム木の それぞれのノード に対して 何らかの分析 を行う処理です。そのような処理の事をゲーム木の 探索 と呼び、ノードをどのような順番で探索するかによって、幅優先探索と深さ優先探索の 2 種類のアルゴリズムがあります。上記の calc_node_height のように、ゲーム木の深さの(浅い、または深い)順でノードの探索を行うアルゴリズムの事を 幅優先探索 アルゴリズムと呼びます。
ノードの高さの情報を利用した draw_node の修正
次に、ノードの高さの情報を利用するように draw_node を修正する必要がありますが、その際に draw_node を以下の条件で利用するように修正することにします。
-
個別のノードだけを描画 するために、キーワード引数
axを記述せずにdraw_nodeを呼び出す場合は、(子ノードに子ノードが存在するかどうかに関わらず)常に子ノードを縦に 4 の間隔で描画すれば良い ので、ノードの高さをあらかじめ計算しておく必要はない -
ゲーム木を描画 する際に、キーワード引数
axを記述してdraw_treeから呼び出す場合は、calc_node_heightによって、すべてのノードの高さが計算済 である必要がある
また、それぞれの子ノードは、以下の座標に描画します。
- 最初の子ノード は (dx + 5, dy) の位置に描画する
- すべての子ノードを描画する x 座標は
dx + 5である - 次の子ノードノードを描画する y 座標 は、現在の子ノードを描画した y 座標 に、現在の 子ノードの高さを加算 することで計算できる
従って、それぞれの子ノードを描画する座標は、下記の方法で計算できます
- (dx + 5, dy) の座標に描画する
- ただし、子ノードを描画するたびに、
dyの値にその子ノードの高さを加算する
下記は、そのように draw_node を修正したプログラムです。
-
2 ~ 11 行目:
axがNoneの場合は、draw_nodeで、自分自身のノードとその子ノードの関係だけを描画する。その場合の処理を、下記のように修正する-
3 行目:
widthの値は、このブロックの中でしか利用しないので、widthに値を代入する処理はこのブロックの中に移動した -
4 行目:この場合は、子ノードの高さは常に 4 になるので、自分自身のノードの高さを表す
heightの値は元と同じ「子ノードの数 * 4」という式で計算できる - 10、11 行目:子ノードの高さは、この後で子ノードを描画する処理で必要になるので、すべての子ノードの高さを 4 に設定する
-
3 行目:
-
12、13 行目:
axがNoneでない場合は、ゲーム木を描画するdraw_treeから、個別のノードを描画するために呼び出される。その場合は、このノードの高さは既に計算されているのでheightにはself.heightを代入する -
19 行目:繰り返し処理の中で、インデックスの番号の情報は不要になったので、
iとenumerateは削除した -
20、21 行目:子ノードを描画する際に、y 座標として
dyの位置に描画するように修正する。エッジの描画の処理も同様である -
22 行目:
dyの値を、21 行目で描画した子ノードの高さだけ増やすことで、次のノードの描画位置を計算する
1 def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
2 if ax is None:
3 width = 8
4 height = len(self.children) * 4
5 fig, ax = plt.subplots(figsize=(width * size, height * size))
6 ax.set_xlim(0, width)
7 ax.set_ylim(0, height)
8 ax.invert_yaxis()
9 ax.axis("off")
10 for childnode in self.children:
11 childnode.height = 4
12 else:
13 height = self.height
14
15 # 自分自身のノードを (dx, dy) に描画する
16 Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
17 plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
18 # 子ノードとエッジの線を描画する
19 for childnode in self.children:
20 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
21 plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
22 dy += childnode.height
23
24 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
if ax is None:
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
for childnode in self.children:
childnode.height = 4
else:
height = self.height
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
# 子ノードとエッジの線を描画する
for childnode in self.children:
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
dy += childnode.height
Node.draw_node = draw_node
修正箇所
def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
- width = 8
- height = len(self.children) * 4
if ax is None:
+ width = 8
+ height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
+ for childnode in self.children:
+ childnode.height = 4
+ else:
+ height = self.height
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
# 子ノードとエッジの線を描画する
- for childnode in enumerate(self.children):
+ for childnode in self.children:
- Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy+i*4, lw=lw)
+ Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
- plt.plot([dx + 4 , dx + 4.5], [dy + 1.5 + i * 4, dy + 1.5 + i * 4], c="k", lw=lw)
+ plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
+ dy += childnode.height
Node.draw_node = draw_node
次に、draw_tree を修正します。深さ 1 の一番上のノードは、(5, 0) の位置に描画します。また、その下のノードは先程と同様に、下記の方法で描画する座標を計算できます。
- 最初に
dyに0を代入する - 深さ 1 のノードを (5, dy) の座標に描画する
- ただし、ノードを描画するたびに、
dyの値にそのノードの高さを加算する
従って、draw_tree は、下記のプログラムのように修正できます。
- 2 行目:ゲーム木の各ノードの高さを計算する
-
4 行目:Figure の高さは、ルートノードの高さに等しく、その高さは 2 行目で計算済なので、その値を
heightに代入する - 5 行目:深さ 0 のルートノードを (0, 0) の位置に描画する
-
7 行目:深さ 1 のノードを描画する y 座標を表す
dyを 0 で初期化する -
9 ~ 10 行目:繰り返し処理で深さ 1 のノードを (5, dy) の位置に描画し、描画するたびに
dyにそのノードの高さを加算する。なお、繰り返し処理の中でインデックスの番号の情報は不要になったので、iとenumerateは削除した
1 def draw_tree(self, size=0.25, lw=0.8):
2 self.calc_node_height()
3 width = 13
4 height = self.root.height
元と同じなので省略
5 # 深さ 0 のノードの描画
6 self.root.draw_node(ax=ax, size=size, lw=lw)
7 dy = 0
8 # 深さ 1 のノードの描画
9 for childnode in self.root.children:
10 childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=dy)
11 dy += childnode.height
12
13 Mbtree.draw_tree = draw_tree
行番号のないプログラム
def draw_tree(self, size=0.25, lw=0.8):
self.calc_node_height()
width = 13
height = self.root.height
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 深さ 0 のノードの描画
self.root.draw_node(ax=ax, size=size, lw=lw)
dy = 0
# 深さ 1 のノードの描画
for childnode in self.root.children:
childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=dy)
dy += childnode.height
Mbtree.draw_tree = draw_tree
修正箇所
def draw_tree(self, size=0.25, lw=0.8):
+ self.calc_node_height()
width = 13
- height = 288
+ height = self.root.height
元と同じなので省略
# 深さ 0 のノードの描画
+ self.root.draw_node(ax=ax, size=size, lw=lw)
+ dy = 0
# 深さ 1 のノードの描画
- for i, childnode in enumerate(self.root.children):
+ for childnode in self.root.children:
- childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=i*32)
+ childnode.draw_node(ax=ax, size=size, lw=lw, dx=5, dy=dy)
+ dy += node.height
Mbtree.draw_tree = draw_tree
上記の修正後に、下記のプログラムを実行することで、実行結果のように、深さ 2 までのゲーム木が描画 されるようになります。ただし、一見すると正しく描画されているように見えるかもしれませんが、1 つだけおかしな点があります。どこがおかしいかと、何故そのようなことが起きるかについて少し考えてみて下さい。
mbtree.draw_tree()
問題の検証と修正
おかしな点は、深さ 0 のノードから深さ 1 のノードへの エッジを表す線 が、下図の赤い矢印の部分のように、最後の子ノードの下まで 突き出てしまう 点です。

深さ 1 のノードから深さ 2 のノードへのエッジを表す線が突き出ないのは、draw_node の中で、エッジのその部分の描画を行う下記のプログラムの dy + 1.5 + height - 4 という式の - 4 によって、エッジの下の y 座標を ゲーム盤 1 つ分だけ引いて短くしている からです。
plt.plot([dx + 3.5, dx + 4, dx + 4],
[dy + 1.5, dy + 1.5, dy + 1.5 + height - 4], c="k", lw=lw)
深さ 1 のノードからのエッジの場合はそれでかまいませんが、深さ 0 のノードからのエッジの場合は、4 ではなく、子ノードの 最後のノードの高さの分だけ減らす 必要があります。
そこで、draw_node の中で、下記のプログラムのように、エッジの高さ を表す edgeheight を計算 し、それを使ってエッジを描画することにします。なお、このプログラムを書いていて気づいたのですが、ノードに子供が存在しない場合 は、エッジを描画してはいけない ので、その処理も追加しています。
-
4、5 行目:
axがNoneの場合の、edgeheightを計算する。ただし、エッジは子ノードが存在する場合のみ表示するので、子ノードが存在する場合のみ計算を行う -
7、8 行目:
axがNoneでない場合のedgeheightを計算する。最後の子ノードは、インデックスに -1 を記述する ことで参照することができる。なお、heightは、この後のプログラムで利用しないので、heightにself.heightを代入する処理は削除した - 13 行目:エッジと子ノードの描画処理を、子ノードが存在する場合だけ行うようにした
-
14 行目:エッジの縦線の下端の y 座標を
dy + 1.5 + edgeheightに修正する
1 def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
2 width = 8
3 if ax is None:
元と同じなので省略
4 if len(self.children) > 0:
5 edgeheight = height - 4
6 else:
7 if len(self.children) > 0:
8 edgeheight = self.height - self.children[-1].height
9
10 # 自分自身のノードを (dx, dy) に描画する
11 Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
12 # 子ノードが存在する場合に、エッジの線と子ノードを描画する
13 if len(self.children) > 0:
14 plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
15 for childnode in self.children:
16 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
17 plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
18 dy += childnode.height
19
20 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
if ax is None:
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
for childnode in self.children:
childnode.height = 4
if len(self.children) > 0:
edgeheight = height - 4
else:
if len(self.children) > 0:
edgeheight = self.height - self.children[-1].height
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
# 子ノードが存在する場合に、エッジの線と子ノードを描画する
if len(self.children) > 0:
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
for childnode in self.children:
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
dy += childnode.height
Node.draw_node = draw_node
修正箇所
def draw_node(self, ax=None, size=0.25, lw=0.8, dx=0, dy=0):
width = 8
if ax is None:
元と同じなので省略
if len(self.children) > 0:
edgeheight = height - 4
else:
if len(self.children) > 0:
edgeheight = self.height - self.children[-1].height
# 自分自身のノードを (dx, dy) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw, dx=dx, dy=dy)
# 子ノードが存在する場合に、エッジの線と子ノードを描画する
if len(self.children) > 0:
plt.plot([dx + 3.5, dx + 4, dx + 4], [dy + 1.5, dy + 1.5, dy + 1.5 + edgeheight], c="k", lw=lw)
for childnode in self.children:
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=dx+5, dy=dy, lw=lw)
plt.plot([dx + 4 , dx + 4.5], [dy + 1.5, dy + 1.5], c="k", lw=lw)
dy += childnode.height
Node.draw_node = draw_node
上記の修正後に、下記のプログラムを実行することで、実行結果のように、深さ 2 までのゲーム木が正しく描画されるようになります。
mbtree.draw_tree()
深さ 3 以上のノードの作成と問題点
深さ 3 のノードの作成は、深さ 2 のノードの作成と同様の方法で、下記のプログラムのように記述できます。
- 8、9 行目:深さ 2 のノードを作成する ブロックの中 で、同様の繰り返し処理を記述 することで、深さ 3 のノードを作成する
1 def create_tree_by_bf(self):
2 # 深さ 1 のノードの作成
3 self.root.calc_children()
4 # 深さ 2 のノードの作成
5 for childnode in self.root.children:
6 childnode.calc_children()
7 # 深さ 3 のノードの作成
8 for grandchildnode in childnode.children:
9 grandchildnode.calc_children()
10
11 Mbtree.create_tree_by_bf = create_tree_by_bf
行番号のないプログラム
def create_tree_by_bf(self):
# 深さ 1 のノードの作成
self.root.calc_children()
# 深さ 2 のノードの作成
for childnode in self.root.children:
childnode.calc_children()
# 深さ 3 のノードの作成
for grandchildnode in childnode.children:
grandchildnode.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
修正箇所
def create_tree_by_bf(self):
# 深さ 1 のノードの作成
self.root.calc_children()
# 深さ 2 のノードの作成
for childnode in self.root.children:
childnode.calc_children()
# 深さ 3 のノードの作成
+ for grandchildnode in childnode.children:
+ grandchildnode.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
上記の修正後に下記のプログラムを実行すると、実行結果のように深さ 2 の最初のノードが正しく描画されます。
mbtree = Mbtree()
mbtree.root.children[0].children[0].draw_node()
実行結果

同様に、深さ 4 のノードは下記のプログラムで作成できます3。なお、先程とほぼ同様の修正なので、プログラムの修正の説明と修正箇所は省略します。
def create_tree_by_bf(self):
# 深さ 1 のノードの作成
self.root.calc_children()
# 深さ 2 のノードの作成
for childnode in self.root.children:
childnode.calc_children()
# 深さ 3 のノードの作成
for grandchildnode in childnode.children:
grandchildnode.calc_children()
# 深さ 4 のノードの作成
for greatgrandchildnode in grandchildnode.children:
greatgrandchildnode.calc_children()
Mbtree.create_tree_by_bf = create_tree_by_bf
上記の修正後に下記のプログラムを実行すると、実行結果のように深さ 3 の最初のノードが正しく描画されます。
mbtree = Mbtree()
mbtree.root.children[0].children[0].children[0].draw_node()
実行結果
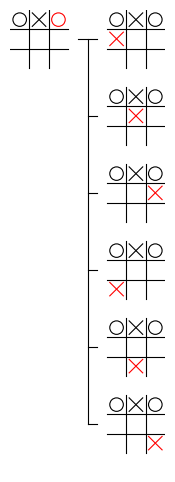
上記のプログラムの記述方法は、おそらく初心者でも思いつくことができる方法ですが、深さを 1 つ増やすたび に、増やした深さのノードを計算する 繰り返しのブロックを記述する必要があります。そのため、このようなプログラムを、〇×ゲームのゲーム木を作成する際に必要な、深さ 9 のノードまで記述 することは かなり面倒 です。
また、〇×ゲームの場合は、深さが 9 までしかないので記述しようと思えば記述できるかもしれませんが、オセロ、囲碁、将棋のような、決着するまでに数十手以上かかるゲームの場合は、そのようなプログラムを記述する のは 現実的にはほぼ不可能 になります。
次回の記事では、幅優先アルゴリズムで、任意の深さのゲーム木を作成する方法について紹介します。余裕がある方は、その方法について少し考えてみて下さい。
今回の記事のまとめ
今回の記事では、幅優先アルゴリズムで深さ 2 のゲーム木を作成し、視覚化する処理を実装しました。
本記事で入力したプログラム
以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。
今回の記事では marubatsu.py は更新していません。
以下のリンクは、今回の記事で更新した tree.py です。
次回の記事



