目次と前回の記事
これまでに作成したモジュール
以下のリンクから、これまでに作成したモジュールを見ることができます。
ルールベースの AI の一覧
ルールベースの AI の一覧については、下記の記事を参照して下さい。
探索型の AI による最強の AI の作成
今回の記事から、〇×ゲームの 探索型の AI を作成することにします。
以前の記事で説明したように、〇×ゲームは 二人零和有限確定完全情報ゲーム という性質を持つゲームです。この性質の中の、下記の「有限」、「確定」、「完全情報」という性質を持つゲームは、原理的 には、ゲーム開始時の局面から、とりうるすべての着手を行った局面を、ゲーム木 と呼ばれる データ構造で列挙 することができます。
- 有限:合法手が有限 であり、ゲームが 有限の手番で必ず終了する という性質。合法手 が無限にあったり、永遠に決着がつかないようなゲームではない
- 確定:サイコロのような、ランダムな要素が存在しない という性質。着手による 局面の変化が確定する 性質を持つゲーム
- 完全情報:ゲームの すべての情報が公開 されているという性質
〇×ゲームは、局面の数が少ないのでゲーム木を作成することが実際にできますが、オセロ、将棋、囲碁などのゲームでは、局面の数が多すぎる ため、原理的にはゲーム木を作成することはできても、現実的には作成できません。
ゲーム木と局面の数の問題については、今後の記事で説明します。
そのゲームで出現するすべての局面を表す ゲーム木を調べる ことで、そのゲームの 任意の局面の最善手を計算 することができます。ゲーム木を調べて、最善手を見つけることを、ゲーム木の 探索 と呼びます。ゲーム木を作成し、探索を行うことで、以前の記事で説明した、「すべての局面で、局面の状況と、最善手が判明している」という、ゲームを強解決することができる ので、最強の AI を作成 することができます。
木構造(tree structure)
ゲーム木は、木構造 と呼ばれる データ構造の一種 なので、木構造について説明します。
下図は、〇×ゲームの ゲーム開始時の局面 から、2 手目まで のとりうる局面の組み合わせを表したものです。〇×ゲームは、1 手目で 9 通り、2 手目で 8 通りの合法手があるので、図では 9 × 8 = 72 通りの 2 手目の局面が表示されています。なお、図がかなり縦に長いので、折りたたんで表示しました。
2 手目で 72 もの局面があることからわかるように、ゲーム終了時までのとりうる局面の数 は 膨大なものになる ので画像では示しませんが、ゲーム開始時の局面から終了時までの、とりうる すべての局面 を上図のような方法で表現することができます。
このようなデータ構造を、木構造(tree structure)と呼びます。〇×ゲームのゲーム木には、下記のような性質があります。
- 大元となる局面(ゲーム開始時の局面のこと)が 1 つだけある
- それぞれの局面 から、その局面の合法手の数だけ 次の局面が存在 し、次の局面を 線で結んで表現 する
- 図の 線には、左の局面から右の局面に移行するという、方向がある
- ただし、ゲームの決着がついた局面は次の局面が存在しない
- 有限ゲーム であるため、局面を辿っていくことで、必ず決着がついた局面にたどり着く(局面を辿っていくと、元の局面に戻るという、ループが存在しない)
また、木構造では、その名の通り、木(tree)に由来 する以下のような用語が使われます。
- 枝分かれする それぞれの局面のデータを、木の節点 に例えて ノード(node1)と呼ぶ
- ノードとノードを つなぐ線 のことを、木の枝 に例えて エッジ(edge2)と呼び、それぞれのノードは 0 個以上のエッジを持つ
- エッジは 方向を持ち、ノード A から ノード B にエッジでつながれている場合、ノード A を 親ノード(parent node)、ノード B を 子ノード(child node) と呼ぶ
- 大元となる、親ノードを持たないノード の事を、木の根(root)に例えて ルートノード(root node) と呼ぶ
- 子ノードを持たない、エッジの無い 末端のノード の事を、木の葉(leaf)に例えて リーフノード(leaf node)と呼ぶ
- それぞれのノードに対して、ルートノードから エッジを 何回辿る ことでたどり着けるかを表す数値の事を、ノードの 深さ(depth)と呼ぶ。ルートノードの深さは 0 であり、〇×ゲームの場合は、n 手目の局面 のノードの 深さは n となる
先程の図では、木構造を左から右に図示しましたが、下から上に図示 した場合、ルートノードを根 とし、リーフノードを葉 とした 木のように見える ことから、木構造 と名付けられました。なお、ゲーム木を図示する際に、上から下に図示することが多いようですが、上から下に図示すると横幅が広がりすぎて、横にスクロールしないと全体が見えなくなるので、本記事では左から右に図示します。
木構造にはノードに子ノードが 2 つしかない二分木など、様々な種類があります。
木構造のように、頂点(ノードの事)と 辺(エッジの事)で構成されるデータ構造のことを、グラフ構造 と呼びます。また、グラフ構造の中で、辺に方向が存在する ものを 有向グラフ と呼びます。
木構造 は、グラフ構造の一種 で、有向グラフで、頂点から辺の方向に従って辿ることで元の頂点に戻ることがないという性質を持ちます。
〇×ゲームのゲーム木のルートノードの作成
〇×ゲームのゲーム木をいきなり作成するのは大変なので、今回の記事では、ゲーム開始時の局面 を表すゲーム木の ルートノード のデータを Python のプログラムで作成します。
ノードを表す Node クラスの定義
ゲーム木 は、大量のノードから構成される ので、〇×ゲームのノードを表す Node という クラスを定義 し、そのインスタンスを作成して 組み合わせる ことで、〇×ゲームのゲーム木を作成することにします。
ノードは 局面のデータを持つ ので、mb という属性に局面のデータを表す Marubatsu クラスのインスタンスを代入 することにします。
下記は、Node クラスの定義です。__init__ メソッドの 仮引数 mb に 局面のデータを代入 することで、特定の局面の Node クラスのインスタンスを作成できるようにしています。
class Node:
def __init__(self, mb):
self.mb = mb
例えば、〇×ゲームの開始時の局面を表す、ゲーム木の ルートノード は、下記のプログラムで作成し、ノードが表す局面を表示することができます。
- 4 行目:ゲーム開始時の局面を表す Marubatsu クラスのインスタンスを実引数に記述して Node クラスのインスタンスを作成する
-
5 行目:Node クラスのインスタンスの
mb属性にそのノードの局面の情報が代入されているので、それをprintで表示することでゲーム盤を表示する
1 from marubatsu import Marubatsu
2
3 mb = Marubatsu()
4 rootnode = Node(mb)
5 print(rootnode.mb)
行番号のないプログラム
from marubatsu import Marubatsu
mb = Marubatsu()
rootnode = Node(mb)
print(rootnode.mb)
実行結果
Turn o
...
...
...
属性によるエッジの表現
ゲーム木は、大量のエッジからも構成されるので、エッジを表すクラスを定義する必要があるのではないかと思う人がいるかもしれません。実際に、エッジを表すクラスを定義してゲーム木を作成することも可能ですが、エッジ は 親ノードから子ノードへの参照 とみなすことができるので、変数(属性)を使ってエッジを表現 することができます。以前の記事で説明したように、変数への代入処理 は、オブジェクトの id を格納することで、オブジェクトを参照する処理 を行っていることを思い出してください。
具体的には、Node クラスのインスタンスに、子ノードを表す属性 を用意し、その属性に 子ノード を表す Node クラスのインスタンスを 代入 することで、クラスを定義することなくエッジを表現することができます。
ノードは 0 個以上の子ノード を持つので、子ノードを表すデータは、list で表現する ことができます。そこで、子ノードのデータを children という属性に、list の形式で代入することにします。
子ノードのデータをいきなり作成するのは大変なので、下記のプログラムのように、__init__ メソッド内では children 属性に 空の list を代入 し、後から子ノードのデータを追加する処理を記述することにします。
下記は、Node クラスの定義です。
class Node:
def __init__(self, mb):
self.mb = mb
self.children = []
子ノードを挿入する insert メソッドの定義
作成したばかりの Node クラスのインスタンスには、子ノードは一つも登録されていないので、子ノードを追加する処理 を記述する必要があります。そこで、ノードに子ノードを追加する下記のようなメソッドを定義する事にします。なお、木構造のデータにノードを追加する処理の事を ノードの挿入(insert)と呼ぶので、メソッドの名前は insert にしました。
名前:子ノードを挿入(insert)するので insert という名前にする
処理:実引数に記述したノードを子ノードに挿入する
入力:仮引数 node に、子ノードに挿入するノードを代入する
出力:なし
下記は、insert メソッドの定義です。
def insert(self, node):
self.children.append(node)
Node.append_child = append_child
insert が行う処理は、self.children.append(node) だけなので、このようなメソッドを定義しなくても、例えば、rootnode.children.append(node) のように、Node クラスの children 属性に対して直接 append メソッドを使って子ノードを挿入すればよいのではないかと思った人がいるかもしれません。
しかし、rootnode.children.append(node) というプログラムは、子ノードを表すデータが children という属性に、list の形式で代入されていることを 知っていなければ記述することはできない という問題があります。
また、子ノードのデータを記録するデータ構造 は、list だけではありません。後から list 以外の形式 で子ノードを記録するように Node クラスの 定義を修正した場合 は、rootnode.children.append(node) の処理が 動作しなくなる ため、そのような記述が行われている部分のプログラムを すべて修正する必要が生じます。
その点、insert というメソッドの中で子ノードの追加を行う処理を記述するようにしておけば、後から子ノードのデータ構造を変更した場合でも、insert の中の処理を変更 するという 修正だけで済みます。
なお、実際に今後の記事で、子ノードを list ではない形式で記録するように Node クラスの定義を変更する予定です。
子ノードを計算するメソッドの定義
次に、子ノードを計算する、下記のようなメソッドを定義することにします。
名前:子ノードを計算(calculate)するので calc_children という名前にする
処理:子ノードを計算し、children 属性に挿入する
入力:なし
出力:なし
子ノードの局面は、親ノードの局面に対して、それぞれの合法手を着手した局面です。従って、calc_children は、下記のプログラムのように定義できます。なお、下記の 4 行目の処理を記述しない場合は、calc_children メソッドを 2 度以上呼び出してしまう と、children 属性に同じ子ノードが 重複して登録されてしまう という問題が発生します。
-
4 行目:このメソッドを 呼び出す前 に、
children属性に ノードが登録されていた場合のことを考慮 して、children属性の値を 空の list で初期化する - 5 行目:合法手を計算し、それぞれの合法手に対する繰り返し処理を行う
-
6 行目:
self.mbに対してmoveメソッドで着手を行うと、自分自身のノードの局面が変化してしまう ことになるので、子ノードの局面を計算する際は、deepcopyでself.mbに対して 深いコピー を行う必要がある -
7、8 行目:コピーした
childmbに対して合法手の着手を行い、Node(childmb)で着手を行ったノードを作成し、insertメソッドで子ノードに挿入する
1 from copy import deepcopy
2
3 def calc_children(self):
4 self.children = []
5 for x, y in self.mb.calc_legal_moves():
6 childmb = deepcopy(self.mb)
7 childmb.move(x, y)
8 self.insert(Node(childmb))
9
10 Node.calc_children = calc_children
行番号のないプログラム
from copy import deepcopy
def calc_children(self):
self.children = []
for x, y in self.mb.calc_legal_moves():
childmb = deepcopy(self.mb)
childmb.move(x, y)
self.insert(Node(childmb))
Node.calc_children = calc_children
子ノードが正しく登録されているかどうかを確認するために、下記のプログラムで、ルートノードの子ノードの計算を行い、子ノードの局面を表示することにします。実行結果から、9 つの合法手が着手された局面が子ノードとして正しく登録されていることが確認できます。
-
1 行目:
calc_childrenで、rootnodeの子ノードを計算する -
2 行目:繰り返し処理を使って、
rootnodeの子ノードの局面をprintで表示する
rootnode.calc_children()
for node in rootnode.children:
print(node.mb)
実行結果
Turn x
O..
...
...
Turn x
.O.
...
...
Turn x
..O
...
...
Turn x
...
O..
...
Turn x
...
.O.
...
Turn x
...
..O
...
Turn x
...
...
O..
Turn x
...
...
.O.
Turn x
...
...
..O
下記のプログラムは、rootnode の 最初の子ノード である、(0, 0) に着手を行った rootnode.children[0] に対して calc_children を実行し、その子ノードを表示 するプログラムです。実行結果から、この場合でも正しく子ノードが計算できることが確認できます。
childnode = rootnode.children[0]
childnode.calc_children()
for node in childnode.children:
print(node.mb)
実行結果
Turn o
oX.
...
...
Turn o
o.X
...
...
Turn o
o..
X..
...
Turn o
o..
.X.
...
Turn o
o..
..X
...
Turn o
o..
...
X..
Turn o
o..
...
.X.
Turn o
o..
...
..X
上記から、ゲーム木の すべてのノードを指定 して calc_children を実行 すれば〇×ゲームのゲーム木を作成することができそうですが、その方法はそれほど簡単ではありません。今回の記事では、ゲーム木の作成の話はここまでにしますので、余裕がある方は次回の記事までに、どのような方法でゲーム木を作成できるかについて考えてみて下さい。
画像による親ノードと子ノード関係の視覚化
木構造に限った話ではありませんが、複雑なデータ構造 を、頭の中だけで理解することは困難です。そのような場合は、データを図示して視覚化する ことで 理解しやすくなります。
上記では、文字列で 9 つの子ノードの局面を表示して視覚化しましたが、文字列での表現は、あまりわかりやすいとは言えないでしょう。
そこで、本記事では、親ノードと子ノードの関係を 画像で視覚化 することにします。
視覚化の方針の決定
データの視覚化を行うためには、どのようにデータを視覚化するか を決める必要があります。親ノードと子ノードの場合は、下記のような方法で視覚化すること良く行われます。
- 親ノードを上 に描画し、その下に子ノードを 横に並べて描画 する
- 親ノードと子ノードを 線で結ぶ
ただし、上記のような視覚化を行うと、子ノードの数が多くなると、画像の横幅が大きくなりすぎて 1 画面に収まらなくなるので、本記事では下記のように視覚化することにします。
- 親ノードを左 に描画し、その右に子ノードを 縦に並べて描画 する
- 親ノードと子ノードを線で結ぶ
次に、上記の方針で 具体的にどのように描画を行うか を決める必要があります。その際には、ノートなどに、手書き でどのように描画を行うかを 試行錯誤すると良い でしょう。
下記は、筆者が考えた視覚化です。本記事では、この視覚化を行う方法を紹介しますが、視覚化の方法 は 1 つではありません。別の視覚化を行いたい人は自由に変更して下さい。

ゲーム盤を任意の場所に描画するメソッドの定義
上図の視覚化では、それぞれのノードが表す ゲーム盤 を、さまざまな位置に描画 しています。ゲーム盤を Figure に描画する処理は、Marubatsu_GUI クラスの draw_board メソッドで行うことができますが、draw_board は、以下のような問題があるため、上記のような画像を描画することはできません。
- Axes の 特定の座標にしか ゲーム盤を 描画できない
- 手番や、対戦カードなど、上図では表示しない 文字列を描画してしまう
そこで、Marubatsu_GUI に対して、下記のような修正を行うことにします。
- これまでの
draw_boardは、ゲーム盤の描画だけでなく、手番の文字列や、GUI のボタンの設定の変更などの GUI に関する様々な処理を行うので、draw_boardメソッドの 名前 をupdate_guiに変更 する - 元の
draw_boardが行う処理の中から、ゲーム盤を描画する処理を抜き出して修正 し、下記のようなメソッドを定義する。
名前:ゲーム盤を描画するので、draw_board という名前をそのまま利用する
処理:指定した Axes の、指定した座標に、指定した局面の画像を描画する
入力:仮引数 ax に Axes を、mb に Marubatsu クラスのインスタンスを、dx、dy3 に描画するゲーム盤の 左上の点の座標 を代入する
出力:なし
上記の draw_board は、Marubatsu_GUI クラスのインスタンスの情報は 利用しない ので、静的メソッドとして定義 する事にします。また、静的メソッドとして定義する事によって、Marubatsu_GUI の インスタンスを作成しなくても、任意の場所から利用できる ようになるので、親ノードと子ノードの関係を描画する処理で利用することができます。
修正前の draw_board では、ゲーム盤の 左上の点 を Axes の (0, 0) の座標に描画 していました。従って、ゲーム盤の 左上の点 を Axes の (dx, dy) の座標に描画 するためには、描画を行う際の x 座標と y 座標にそれぞれ dx と dy を加算すればよい ことがわかります。
下記は、そのように draw_board メソッドを修正したプログラムです。
- 3 行目:静的メソッドとして定義する
-
4 行目:静的メソッドなので、仮引数
selfを削除し、仮引数ax、mb、dx、dyを追加する。また、通常の場所にゲーム盤を描画する場合に省略できるように、仮引数dx、dyはデフォルト値が0のデフォルト引数とする - 5 行目の下にあった、ゲーム盤の描画とは関係ない処理を削除する
-
self.mbをmbに修正する。なお、axに関しては、元のプログラムでは最初にax = self.axのように、axに値を代入してから処理を行っていたので修正する必要はない -
plotとdraw_markで枠やマークを描画する際に指定する x 座標と y 座標 に、それぞれdxとdyを加算 して、ゲーム盤を 描画する位置を (dx, dy) だけずらす -
15 行目:
draw_boardを 静的メソッドとして定義 したため、selfを利用できなくなった ので、self.draw_markをMarubatsu_GUI.draw_markに修正 する。なお、draw_markは静的メソッドとして定義されているので、インスタンスから呼び出す必要はない
なお、14 行目と 15 行目の (x, y) と mb.board[x][y] の x と y は、Axes の座標ではなく、ゲーム盤のマスの座標 なので dx と dy を 加算してはいけない 点に注意して下さい。
1 from marubatsu import Marubatsu_GUI
2
3 @staticmethod
4 def draw_board(ax, mb, dx=0, dy=0):
5 # この下にあったゲーム盤の描画と関係ない処理を削除する
6 # ゲーム盤の枠を描画する
7 for i in range(1, mb.BOARD_SIZE):
8 ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k") # 横方向の枠線
9 ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k") # 縦方向の枠線
10
11 # ゲーム盤のマークを描画する
12 for y in range(mb.BOARD_SIZE):
13 for x in range(mb.BOARD_SIZE):
14 color = "red" if (x, y) == mb.last_move else "black"
15 Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color)
16
17 Marubatsu_GUI.draw_board = draw_board
行番号のないプログラム
from marubatsu import Marubatsu_GUI
@staticmethod
def draw_board(ax, mb, dx=0, dy=0):
# ゲーム盤の枠を描画する
for i in range(1, mb.BOARD_SIZE):
ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k") # 横方向の枠線
ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k") # 縦方向の枠線
# ゲーム盤のマークを描画する
for y in range(mb.BOARD_SIZE):
for x in range(mb.BOARD_SIZE):
color = "red" if (x, y) == mb.last_move else "black"
Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color)
Marubatsu_GUI.draw_board = draw_board
修正箇所(前半のゲーム盤の描画とは関係ない処理は省略しています)
from marubatsu import Marubatsu_GUI
+@staticmethod
-def draw_board(self):
def draw_board(ax, mb, dx=0, dy=0):
# ゲーム盤の枠を描画する
- for i in range(1, self.mb.BOARD_SIZE):
+ for i in range(1, mb.BOARD_SIZE):
- ax.plot([0, self.mb.BOARD_SIZE], [i, i], c="k") # 横方向の枠線
+ ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k") # 横方向の枠線
- ax.plot([i, i], [0, self.mb.BOARD_SIZE], c="k") # 縦方向の枠線
+ ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k") # 縦方向の枠線
# ゲーム盤のマークを描画する
- for y in range(self.mb.BOARD_SIZE):
+ for y in range(mb.BOARD_SIZE):
- for x in range(self.mb.BOARD_SIZE):
+ for x in range(mb.BOARD_SIZE):
- color = "red" if (x, y) == self.mb.last_move else "black"
+ color = "red" if (x, y) == mb.last_move else "black"
- self.draw_mark(ax, x, y, self.mb.board[x][y], color)
+ Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color)
Marubatsu_GUI.draw_board = draw_board
なお、上記の修正によって、Marubatsu_GUI の draw_board の定義が変更されたので、それに合わせて Marubatsu_GUI などの定義を変更する必要があります が、その修正は、親ノードと子ノードの関係の画像を表示するプログラムを記述した後で行うことにします。
draw_board を利用したゲーム盤の描画の確認
draw_board の仮引数 dx、dy は、描画するゲーム盤の左上の点の Axes の座標を表しますが、毎回「ゲーム盤の左上の点の Axes の座標」と表記するのは冗長なので、以後は単に「ゲーム盤の座標」と表記することにします。
draw_board が正しく実装できているかを確認するために、2 つの異なる局面の画像 を 横に並べて描画する ことにします。そのためには、Figure の大きさ と、2 つの局面の画像を、具体的に _どの座標に描画するか を決める必要があります。
Figure の大きさは、2 つの局面の画像をどこに描画するかを決めないと決まらないので、先に 2 つの画像の描画位置を決めることにします。
まず、1 つ目のゲーム盤 を、通常の場合と同様に (0, 0) の座標に描画 することにします。横に並べて描画するので、2 つ目のゲーム盤の y 座標は 0 になります。
〇×ゲームのゲーム盤は、縦横 3 x 3 のサイズで描画 されます。そのため、〇×ゲームのゲーム盤を横に 2 つ並べて描画するためには、2 つ目のゲーム盤の x 座標を 3 より大きな数値に設定 する必要があります。そこで、2 つ目のゲーム盤の x 座標に 4 を設定 することで、2 つのゲーム盤の 間を 1 だけ開けて描画 することにします。
座標に関する説明が分かりづらいと思った方は、グラフ用紙などの座標がわかる用紙に実際にゲーム盤を書いて確認すると良いでしょう。
上記から、2 つのゲーム盤を描画する Figure のサイズは、横幅が 3 + 1 + 3 = 7、縦幅が 3 になることが分かります。
下記は、2 つのゲーム盤を並べて描画するプログラムです。draw_board では、Axes の y 座標の上下を反転する必要がある 点に注意して下さい。なお、下記のプログラムでは、ゲーム盤の描画位置のわかりやすさを重視して、Axes の目盛りを表示しています。
- 3 行目:サイズが 7 x 3 の Figure を作成する
- 4 行目:Axes の y 軸の上下を反転させる
-
6、7 行目:Marubatsu クラスのインスタンスを作成し、
draw_boardで (0, 0) の座標にゲーム開始時の局面を描画する -
8、9 行目:(1, 1) のマスに着手を行い、
draw_boardで (4, 0) の座標にゲーム開始時の局面を描画する
1 import matplotlib.pyplot as plt
2
3 fig, ax = plt.subplots(figsize=(7, 3))
4 ax.invert_yaxis()
5
6 mb = Marubatsu()
7 Marubatsu_GUI.draw_board(ax, mb)
8 mb.move(1, 1)
9 Marubatsu_GUI.draw_board(ax, mb, dx=4, dy=0)
行番号のないプログラム
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(7, 3))
ax.invert_yaxis()
mb = Marubatsu()
Marubatsu_GUI.draw_board(ax, mb)
mb.move(1, 1)
Marubatsu_GUI.draw_board(ax, mb, 4, 0)
実行結果

各ノードのゲーム盤を描画する座標の計算
親ノードと子ノードの関係を表す先程の画像を描画するためには、上記と同様に下記の内容を具体的に決める必要があります。
- 親ノードと子ノードの関係の画像を描画する Figure のサイズ
- それぞれのノードの ゲーム盤を表示する座標
- 親ノードと子ノードを結ぶ 線の両端の座標
まず、それぞれのノードのゲーム盤を描画する座標を決めます。
下図は、先程の親ノードと子ノードの関係の図に座標の目盛りをつけたものです。

上図では、ルートノードと子ノードの左上の座標は以下のようになっています。
| x 座標 | y 座標 | |
|---|---|---|
| ルートノード | 0 | 0 |
| 子ノード | 5 | 0 からはじまり、4 ずつ増える |
親ノードと子ノードの 横の間隔は 2 になっているので、子ノード のゲーム盤の x 座標は 3 + 2 = 5 になります。
子ノードと子ノードの 上下の間隔は 1 になっているので、子ノード のゲーム盤の y 座標 は 3 + 1 = 4 ずつ増える ことになります。従って、children 属性の i 番の要素 の子ノードの局面の画像は (5, i * 4) の座標に描画 すればよいことが分かります。
また、上図から、Figure のサイズは、横が 8、縦が 35 になることがわかります。横のサイズは 3 + 2 + 3 = 8 で計算できます。縦のサイズは、子ノードの数を num とすると、num × 4 - 1 で計算できます。1 を引くのは、最後の子ノードの後の間隔は必要がない からですが、その間隔があっても大きな違いはないので、計算式を簡単にするため に、Figure のサイズは、横を 8、縦を num × 4 とすることにします。ゲーム盤がぴったりと収まる大きさの画像にしたい人は、縦幅を num × 4 - 1 にして下さい。
ノードを描画する処理の実装
次に、Node クラスに、インスタンスのノードと、その子ノードの関係を描画する下記のようなメソッドを定義する事にします。
名前:インスタンスのノードに関する内容を描画するので draw_node とする
処理:インスタンスのノードと、子ノードの関係を描画する
入力:なし
出力:なし
インスタンスのノードの局面は、draw_board を使って self.mb を (0, 0) の座標に描画すればよいので簡単に描画することができます。
子ノード のデータは、list で記録 されているので、for 文による繰り返し処理を使って、子ノードを描画することができます。子ノードを描画する (5, i * 4) という座標を計算するためには、繰り返し処理の中 で、何番の要素に対する処理を行っているか を知る必要があり、その情報は組み込み関数 enumerate を使って得ることができます。
組み込み関数 enumerate
組み込み関数 enumerate は、下記のプログラムのように、for 文 の中で、list や dict などの、反復可能オブジェクト を 実引数として記述 します。このように記述することで、繰り返し処理が行われるたびに、反復可能オブジェクトの先頭の要素から順に、(0 から数えた繰り返しの回数, 要素) という tuple が取り出される ので、下記のプログラムでは、実行結果のように list の各要素の値が、そのインデックスの値と共に表示されます。
for i, data in enumerate(["a", "b", "c"]):
print(i, data)
実行結果
0 a
1 b
2 c
enumerate の詳細に関しては、下記のリンク先を参照して下さい。
各ノードのゲーム盤の描画の実装
enumerate を利用することで、draw_node は、下記のプログラムのように定義できます。
- 2 ~ 4 行目:Figure を作成し、y 軸の上下を反転し、軸の目盛りを表示しないようにする
-
7 行目:インスタンスが表すノードの局面を
draw_boardを使って (0, 0) に描画する -
9、10 行目:for 文と
enumerate、draw_boardを使って、i番の要素の子ノードの局面を (5, i * 4) に描画する
1 def draw_node(self):
2 fig, ax = plt.subplots(figsize=(8, len(self.children) * 4))
3 ax.invert_yaxis()
4 ax.axis("off")
5
6 # 自分自身のノードを (0, 0) に描画する
7 Marubatsu_GUI.draw_board(ax, self.mb)
8 # i 番の子ノードを (5, i * 4) に描画する
9 for i, childnode in enumerate(self.children):
10 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4)
11
12 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self):
fig, ax = plt.subplots(figsize=(8, len(self.children) * 4))
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4)
Node.draw_node = draw_node
下記のプログラムを実行すると、実行結果のように、ゲーム開始時の局面を表す、ルートノードと子ノードが描画されます。
rootnode.draw_node()
実行結果

描画の範囲と画像の大きさの調整
上記の画像では、画像の 上下左右に余白 があります。これは、matplotlib が画像などを描画する際に、自動的に Axes の表示範囲を調整 して 上下左右に余白を入れる ようになっているからです。この余白は、グラフを描画する場合はグラフが見やすくなるという利点がありますが、今回の場合はこの 余白は邪魔 です。Axes の描画範囲は、set_xlim と set_ylim メソッドを使って調整できるので、余白を表示しないようにします。
また、上記の 画像が大きすぎる と感じる人が多いのではないかと思います。そこで、draw_node に、描画する 画像の大きさの倍率 を表す size という属性と追加し、画像の大きさを調整できる ようにすることにします。
下記は、そのように draw_node を修正したプログラムです。
-
1 行目:仮引数
sizeを追加する - 2、3 行目:画像の幅と高さを計算する
-
4 行目:
figsizeで、画像の幅と高さにsizeを乗算することで、画像の大きさをsize倍に調整する -
5、6 行目:
set_xlimとset_ylimを利用して、Axes の表示範囲を、余白が無くなるように調整する
1 def draw_node(self, size):
2 width = 8
3 height = len(self.children) * 4
4 fig, ax = plt.subplots(figsize=(width * size, height * size))
5 ax.set_xlim(0, width)
6 ax.set_ylim(0, height)
7 ax.invert_yaxis()
元と同じなので省略
8
9 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, size):
width = 8
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4)
Node.draw_node = draw_node
修正箇所
-def draw_node(self):
+def draw_node(self, size):
+ width = 8
+ height = len(self.children) * 4
- fig, ax = plt.subplots(figsize=(8, len(self.children) * 4))
+ fig, ax = plt.subplots(figsize=(width * size, height * size))
+ ax.set_xlim(0, width)
+ ax.set_ylim(0, height)
ax.invert_yaxis()
元と同じなので省略
Node.draw_node = draw_node
上記の修正後に、下記のプログラムを実行すると、実行結果のように、余白がなくなり、画像のサイズが小さくなります。
rootnode.draw_node(size=0.25)
実行結果
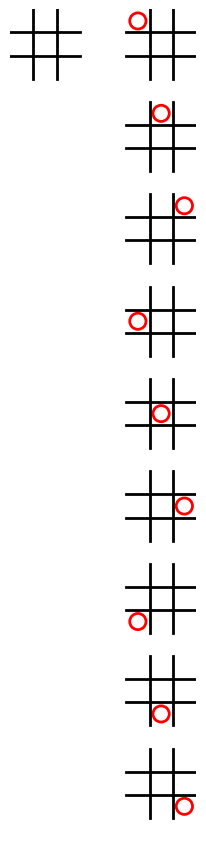
筆者は、上記の画像の大きさがちょうど良いと感じましたので、この後の修正で draw_node の仮引数 size をデフォルト値が 0.25 のデフォルト引数に修正することにします。どのくらいの画像の大きさがちょうどよいかは人によって異なるので、別の大きさが良いと感じた人は自由に変更して下さい。
枠線の太さの調整
draw_board や draw_mark では、ゲーム盤の枠線や図形の 線の太さを 2 に設定 して描画を行っていましたが、上図のように、matplotlib では、画像を小さく描画 すると、線の太さが相対的に太くなる という現象が発生するようです。上記の画像は 線が太くて見づらい 気がしますので、draw_node、draw_board、draw_mark に、線の太さを設定する 仮引数 lw を追加 することにします。
下記は、そのように draw_mark を修正したプログラムです。
4 行目:互換性を考慮して、デフォルト値に 2 を設定した仮引数 lw を追加する
6、9、10 行目:キーワード引数 lw=lw に修正することで、太さが lw の線を描画する
1 import matplotlib.patches as patches
2
3 @staticmethod
4 def draw_mark(ax, x, y, mark, color="black", lw=2):
5 if mark == Marubatsu.CIRCLE:
6 circle = patches.Circle([x + 0.5, y + 0.5], 0.35, ec=color, fill=False, lw=lw)
7 ax.add_artist(circle)
8 elif mark == Marubatsu.CROSS:
9 ax.plot([x + 0.15, x + 0.85], [y + 0.15, y + 0.85], c=color, lw=lw)
10 ax.plot([x + 0.15, x + 0.85], [y + 0.85, y + 0.15], c=color, lw=lw)
11
12 Marubatsu_GUI.draw_mark = draw_mark
行番号のないプログラム
import matplotlib.patches as patches
@staticmethod
def draw_mark(ax, x, y, mark, color="black", lw=2):
if mark == Marubatsu.CIRCLE:
circle = patches.Circle([x + 0.5, y + 0.5], 0.35, ec=color, fill=False, lw=lw)
ax.add_artist(circle)
elif mark == Marubatsu.CROSS:
ax.plot([x + 0.15, x + 0.85], [y + 0.15, y + 0.85], c=color, lw=lw)
ax.plot([x + 0.15, x + 0.85], [y + 0.85, y + 0.15], c=color, lw=lw)
Marubatsu_GUI.draw_mark = draw_mark
修正箇所
import matplotlib.patches as patches
@staticmethod
-def draw_mark(ax, x, y, mark, color="black"):
+def draw_mark(ax, x, y, mark, color="black", lw=2):
if mark == Marubatsu.CIRCLE:
- circle = patches.Circle([x + 0.5, y + 0.5], 0.35, ec=color, fill=False, lw=2)
+ circle = patches.Circle([x + 0.5, y + 0.5], 0.35, ec=color, fill=False, lw=lw)
ax.add_artist(circle)
elif mark == Marubatsu.CROSS:
- ax.plot([x + 0.15, x + 0.85], [y + 0.15, y + 0.85], c=color, lw="2")
+ ax.plot([x + 0.15, x + 0.85], [y + 0.15, y + 0.85], c=color, lw=lw)
- ax.plot([x + 0.15, x + 0.85], [y + 0.85, y + 0.15], c=color, lw="2")
+ ax.plot([x + 0.15, x + 0.85], [y + 0.85, y + 0.15], c=color, lw=lw)
Marubatsu_GUI.draw_mark = draw_mark
元のプログラムでは、間違って 9、10 行目に lw="2" のように、線の太さに文字列を指定していましたが、線の太さの設定は文字列でも問題はないようです。
下記は、draw_board を修正したプログラムです。
2 行目:互換性を考慮して、デフォルト値に 2 を設定した仮引数 lw を追加する
5、6、12 行目:キーワード引数 lw=lw を追加することで、太さが lw の線を描画する
1 @staticmethod
2 def draw_board(ax, mb, dx=0, dy=0, lw=2):
3 # ゲーム盤の枠を描画する
4 for i in range(1, mb.BOARD_SIZE):
5 ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k", lw=lw) # 横方向の枠線
6 ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k", lw=lw) # 縦方向の枠線
7
8 # ゲーム盤のマークを描画する
9 for y in range(mb.BOARD_SIZE):
10 for x in range(mb.BOARD_SIZE):
11 color = "red" if (x, y) == mb.last_move else "black"
12 Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color, lw=lw)
13
14 Marubatsu_GUI.draw_board = draw_board
行番号のないプログラム
@staticmethod
def draw_board(ax, mb, dx=0, dy=0, lw=2):
# ゲーム盤の枠を描画する
for i in range(1, mb.BOARD_SIZE):
ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k", lw=lw) # 横方向の枠線
ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k", lw=lw) # 縦方向の枠線
# ゲーム盤のマークを描画する
for y in range(mb.BOARD_SIZE):
for x in range(mb.BOARD_SIZE):
color = "red" if (x, y) == mb.last_move else "black"
Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color, lw=lw)
Marubatsu_GUI.draw_board = draw_board
修正箇所
@staticmethod
-def draw_board(ax, mb, dx=0, dy=0):
+def draw_board(ax, mb, dx=0, dy=0, lw=2):
# ゲーム盤の枠を描画する
for i in range(1, mb.BOARD_SIZE):
- ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k") # 横方向の枠線
+ ax.plot([dx, dx + mb.BOARD_SIZE], [dy + i, dy + i], c="k", lw=lw) # 横方向の枠線
- ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k") # 縦方向の枠線
+ ax.plot([dx + i, dx + i], [dy, dy + mb.BOARD_SIZE], c="k", lw=lw) # 縦方向の枠線
# ゲーム盤のマークを描画する
for y in range(mb.BOARD_SIZE):
for x in range(mb.BOARD_SIZE):
color = "red" if (x, y) == mb.last_move else "black"
- Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color, lw=2)
+ Marubatsu_GUI.draw_mark(ax, dx + x, dy + y, mb.board[x][y], color, lw=lw)
Marubatsu_GUI.draw_board = draw_board
下記は、draw_node を修正したプログラムです。
2 行目:デフォルト値に 0.8 を設定した仮引数 lw を追加する。なお、この 0.8 は、試行錯誤した結果、size が 0.25 の場合に見やすいと筆者が感じた値である
3、6 行目:キーワード引数 lw=lw を追加することで、太さが lw の線を描画する
1 def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
2 # 自分自身のノードを (0, 0) に描画する
3 Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
4 # i 番の子ノードを (5, i * 4) に描画する
5 for i, childnode in enumerate(self.children):
6 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
7
8 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, size=0.25, lw=0.8):
width = 8
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
Node.draw_node = draw_node
修正箇所
-def draw_node(self, size):
+def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
# 自分自身のノードを (0, 0) に描画する
- Marubatsu_GUI.draw_board(ax, self.mb)
+ Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
- Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4)
+ Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
Node.draw_node = draw_node
上記の修正後に、下記のプログラムを実行すると、実行結果のように枠線の太さを調整できるようになったことが確認できます。なお、上記のプログラムでは、下記の値をデフォルト値に設定しましたが、他の値が良いと思った方は自由に変更して下さい。
draw_node(rootnode, size=0.25, lw=0.8)
実行結果

エッジを描画する処理の実装 その 1
エッジを描画する方法の一つに、下図のように、親ノードの右から子ノードの左に直線を引く という方法があります。最初にこのエッジを描画する方法を紹介します。どのように下図のエッジを描画すればよいかについて少し考えてみて下さい。
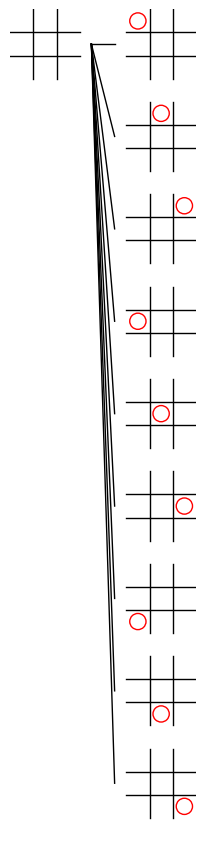
エッジの両端の座標の計算方法
上図のエッジを描画するためには、エッジの線の 両端の座標を計算する 必要があります。
下図は、親ノードと、上 2 つの子ノードを結ぶ線の両端の座標を表したものです。

上図から、親ノードと子ノードを結ぶ線の両端の座標は以下のようになることがわかります。なお、この座標の計算は先ほどのゲーム盤の座標と 考え方はほぼ同じ です。
| x 座標 | y 座標 | |
|---|---|---|
| 親ノードの右 | 3.5 | 1.5 |
| 子ノード | 4.5 | 1.5 からはじまり、4 ずつ増える |
親ノードと子ノードの ゲーム盤の左右の間隔は 2 なので、エッジの 左右の点の x 座標の間隔を 2 以下 にする必要があります。x 座標の間隔を 1 にした場合は、エッジの左の点の x 座標は 3.5、右の点の x 座標は 4.5 になります。
エッジの左の点の y 座標は、親ノードのゲーム盤の ちょうど真ん中にする と見栄えが良いでしょう。ゲーム盤の縦幅は 3 なので、真ん中の y 座標はその半分の 1.5 になります。従って、親ノードの右のエッジの端の座標は (3.5, 1.5) になります。
同様の理由で、一番上の子ノードの左のエッジの端の座標は (4.5, 1.5) になります。
子ノードの左のエッジの端の y 座標は、子ノードの座標と同じ間隔にすれば良いので、i 番のインデックスの子ノードの左のエッジの端の座標は (4.5, 1.5 + i * 4) で計算できます。
従って、下記のプログラムの 5 行目のように、子ノードを描画した後で(描画する前でもかまいません)、親ノードの右と子ノードの左を結ぶ線を plot メソッドで描画することで、エッジを描画することができます。
1 def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
2 # i 番の子ノードを (5, i * 4) に描画する
3 for i, childnode in enumerate(self.children):
4 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
5 plt.plot([3.5, 4.5], [1.5, 1.5 + i * 4], c="k", lw=lw)
6
7 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, size=0.25, lw=0.8):
width = 8
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
plt.plot([3.5, 4.5], [1.5, 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
修正箇所
def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
+ plt.plot([3.5, 4.5], [1.5, 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
上記の修正後に、下記のプログラムを実行すると、実行結果のように、親ノードと子ノードを結ぶエッジが描画されるようになります。
rootnode.draw_node()
実行結果

エッジを描画する処理の実装 その 2
上記の方法でエッジを描画すると、上図のようになりますが、下の方の子ノードのエッジは、他のエッジどうしが重なりあうため、わかりにくい図 になっています。そこで、本記事では、下図のようにエッジを描画することで、エッジどうしが重ならない ようにします。下図のエッジをどのように描画すればよいかについて少し考えてみて下さい。
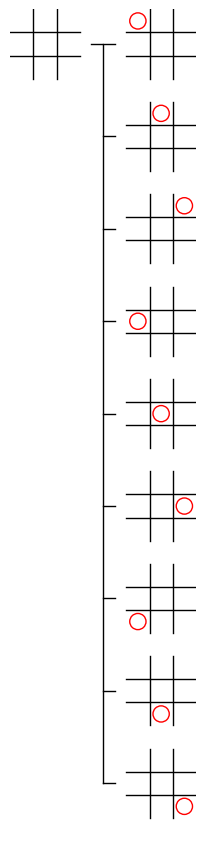
エッジの構成要素と座標の計算方法
下図は、親ノードと、上 2 つと最後の子ノードを結ぶエッジを表したものです。

図から、エッジは、下記の 2 種類の線から構成されることがわかります。
- 親ノードから右にまっすぐ伸びた後に、真下に伸びる緑色の線
- 緑色の線から真横に子ノードに伸びる線
また、図から、それぞれの線の頂点の座標は下記のようになることがわかります。緑の折れ線の一番下の点の y 座標は 1.5 + 子ノードの数 * 4 ではない 点に注意して下さい。
| 頂点の座標 | |
|---|---|
| 緑色の折れ線 | (3.5, 1.5)、(4.0,1.5)、(4.0, 1.5 + (子ノードの数 - 1) * 4) |
| 子ノードの線 | i 番の要素のノードは (4.0, 1.5 + i * 4)、(4.5, 1.5 + i * 4) |
従って、下記のプログラムのように、親ノードを描画した後で上図の緑色の折れ線を描画し(実際の描画は黒色で行います)、子ノードを描画した後で子ノードの線を描画することで、先程の図のエッジを描画することができます。
- 4 行目:上図の緑の折れ線と同じ形の線を、黒色で描画する
- 8 行目:子ノードの線を描画する
1 def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
2 # 自分自身のノードを (0, 0) に描画する
3 Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
4 plt.plot([3.5, 4, 4], [1.5, 1.5, 1.5 + height - 4], c="k", lw=lw)
5 # i 番の子ノードを (5, i * 4) に描画する
6 for i, childnode in enumerate(self.children):
7 Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
8 plt.plot([4 , 4.5], [1.5 + i * 4, 1.5 + i * 4], c="k", lw=lw)
9
10 Node.draw_node = draw_node
行番号のないプログラム
def draw_node(self, size=0.25, lw=0.8):
width = 8
height = len(self.children) * 4
fig, ax = plt.subplots(figsize=(width * size, height * size))
ax.set_xlim(0, width)
ax.set_ylim(0, height)
ax.invert_yaxis()
ax.axis("off")
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
plt.plot([3.5, 4, 4], [1.5, 1.5, 1.5 + height - 4], c="k", lw=lw)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
plt.plot([4 , 4.5], [1.5 + i * 4, 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
修正箇所
def draw_node(self, size=0.25, lw=0.8):
元と同じなので省略
# 自分自身のノードを (0, 0) に描画する
Marubatsu_GUI.draw_board(ax, self.mb, lw=lw)
+ plt.plot([3.5, 4, 4], [1.5, 1.5, 1.5 + height - 4], c="k", lw=lw)
# i 番の子ノードを (5, i * 4) に描画する
for i, childnode in enumerate(self.children):
Marubatsu_GUI.draw_board(ax, childnode.mb, dx=5, dy=i*4, lw=lw)
- plt.plot([3.5, 4.5], [1.5, 1.5 + i * 4], c="k", lw=lw)
+ plt.plot([4 , 4.5], [1.5 + i * 4, 1.5 + i * 4], c="k", lw=lw)
Node.draw_node = draw_node
上記の修正後に、下記のプログラムを実行すると、実行結果のように、親ノードと子ノードを結ぶエッジが描画されるようになります。
draw_node(rootnode, size=0.25, lw=0.8)
実行結果

他のノードと子ノードの描画
先程、rootnode の最初の子ノードに対して calc_children を実行して子ノードを計算したので、下記のプログラムで、rootnode の最初の子ノードを代入した childnode に対して draw_node を実行してみることにします。実行結果から、ルートノード以外のノードでも、draw_node で正しくノードと子ノードが描画されることが確認できます。
childnode.draw_node()
実行結果

なお、現時点では rootnode の他の子ノードに対して calc_children を実行していないので、draw_node を実行しても子ノードは描画されません。
Marubatsu、Marubatsu_GUI クラスのメソッドの修正
今回の記事では、Marubatsu_GUI クラスの draw_board メソッドを修正 したので、このままでは gui_play を実行するとエラーが発生します。そこで、draw_board の修正に合わせて、Marubatsu_GUI クラスなどの定義を修正することにします。
今回の記事の最初のほうで、元の draw_board の名前を update_gui に修正することにしたので、update_gui を下記のプログラムのように定義します。
-
1 行目:メソッドの名前を
draw_boardからupdate_guiに修正する -
2、3 行目:2 行目の下にあったゲーム盤を描画する処理を削除し、3 行目の
draw_boardの呼び出しに置き換える
1 def update_gui(self):
元と同じなので省略
2 # この下にあったゲーム盤を描画する処理を削除する
3 self.draw_board(ax, self.mb)
4
5 self.update_widgets_status()
6
7 Marubatsu_GUI.update_gui = update_gui
行番号のないプログラム
def update_gui(self):
ax = self.ax
ai = self.mb.ai
# Axes の内容をクリアして、これまでの描画内容を削除する
ax.clear()
# y 軸を反転させる
ax.invert_yaxis()
# 枠と目盛りを表示しないようにする
ax.axis("off")
# リプレイ中、ゲームの決着がついていた場合は背景色を変更する
is_replay = self.mb.move_count < len(self.mb.records) - 1
if self.mb.status == Marubatsu.PLAYING:
facecolor = "lightcyan" if is_replay else "white"
else:
facecolor = "lightyellow"
ax.figure.set_facecolor(facecolor)
# 上部のメッセージを描画する
# 対戦カードの文字列を計算する
names = []
for i in range(2):
names.append("人間" if ai[i] is None else ai[i].__name__)
ax.text(0, 3.5, f"{names[0]} VS {names[1]}", fontsize=20)
# ゲームの決着がついていない場合は、手番を表示する
if self.mb.status == Marubatsu.PLAYING:
text = "Turn " + self.mb.turn
# 引き分けの場合
elif self.mb.status == Marubatsu.DRAW:
text = "Draw game"
# 決着がついていれば勝者を表示する
else:
text = "Winner " + self.mb.status
# リプレイ中の場合は "Replay" を表示する
if is_replay:
text += " Replay"
ax.text(0, -0.2, text, fontsize=20)
self.draw_board(ax, self.mb)
self.update_widgets_status()
Marubatsu_GUI.update_gui = update_gui
修正箇所
-def draw_board(self):
+def update_gui(self):
元と同じなので省略
# ゲーム盤の枠を描画する
- for i in range(1, self.mb.BOARD_SIZE):
- ax.plot([0, self.mb.BOARD_SIZE], [i, i], c="k") # 横方向の枠線
- ax.plot([i, i], [0, self.mb.BOARD_SIZE], c="k") # 縦方向の枠線
# ゲーム盤のマークを描画する
- for y in range(self.mb.BOARD_SIZE):
- for x in range(self.mb.BOARD_SIZE):
- color = "red" if (x, y) == self.mb.last_move else "black"
- self.draw_mark(ax, x, y, self.mb.board[x][y], color)
+ self.draw_board(ax, self.mb)
self.update_widgets_status()
Marubatsu_GUI.update_gui = update_gui
draw_board の名前を update_gui に変更したので、draw_board を利用していたプログラムを修正する必要があります。
下記は、play_loop メソッドの修正です。
-
7、11 行目:
draw_boardをupdate_guiに修正する
1 def play_loop(self, mb_gui):
元と同じなので省略
2 # ゲーム盤の表示
3 if verbose:
4 if gui:
5 # AI どうしの対戦の場合は画面を描画しない
6 if ai[0] is None or ai[1] is None:
7 mb_gui.update_gui()
元と同じなので省略
8 # 決着がついたので、ゲーム盤を表示する
9 if verbose:
10 if gui:
11 mb_gui.update_gui()
元と同じなので省略
12
13 Marubatsu.play_loop = play_loop
行番号のないプログラム
def play_loop(self, mb_gui):
ai = self.ai
params = self.params
verbose = self.verbose
gui = self.gui
# ゲームの決着がついていない間繰り返す
while self.status == Marubatsu.PLAYING:
# 現在の手番を表す ai のインデックスを計算する
index = 0 if self.turn == Marubatsu.CIRCLE else 1
# ゲーム盤の表示
if verbose:
if gui:
# AI どうしの対戦の場合は画面を描画しない
if ai[0] is None or ai[1] is None:
mb_gui.update_gui()
# 手番を人間が担当する場合は、play メソッドを終了する
if ai[index] is None:
return
else:
print(self)
# ai が着手を行うかどうかを判定する
if ai[index] is not None:
x, y = ai[index](self, **params[index])
else:
# キーボードからの座標の入力
coord = input("x,y の形式で座標を入力して下さい。exit を入力すると終了します")
# "exit" が入力されていればメッセージを表示して関数を終了する
if coord == "exit":
print("ゲームを終了します")
return
# x 座標と y 座標を要素として持つ list を計算する
xylist = coord.split(",")
# xylist の要素の数が 2 ではない場合
if len(xylist) != 2:
# エラーメッセージを表示する
print("x, y の形式ではありません")
# 残りの while 文のブロックを実行せずに、次の繰り返し処理を行う
continue
x, y = xylist
# (x, y) に着手を行う
try:
self.move(int(x), int(y))
except:
print("整数の座標を入力して下さい")
# 決着がついたので、ゲーム盤を表示する
if verbose:
if gui:
mb_gui.update_gui()
else:
print(self)
return self.status
Marubatsu.play_loop = play_loop
修正箇所
def play_loop(self, mb_gui):
元と同じなので省略
# ゲーム盤の表示
if verbose:
if gui:
# AI どうしの対戦の場合は画面を描画しない
if ai[0] is None or ai[1] is None:
- mb_gui.draw_board()
+ mb_gui.update_gui()
元と同じなので省略
# 決着がついたので、ゲーム盤を表示する
if verbose:
if gui:
- mb_gui.draw_board()
+ mb_gui.update_gui()
元と同じなので省略
Marubatsu.play_loop = play_loop
下記は、create_event_handler を修正したプログラムです。
-
13、18 行目:
draw_boardをupdate_guiに修正する
1 import math
2 from datetime import datetime
3 from tkinter import Tk, filedialog
4 import pickle
5
6 def create_event_handler(self):
元と同じなので省略
7 # 待ったボタンのイベントハンドラを定義する
8 def on_undo_button_clicked(b=None):
9 if self.mb.move_count >= 2 and self.mb.move_count == len(self.mb.records) - 1:
10 self.mb.move_count -= 2
11 self.mb.records = self.mb.records[0:self.mb.move_count+1]
12 self.mb.change_step(self.mb.move_count)
13 self.update_gui()
元と同じなので省略
14 # step 手目の局面に移動する
15 def change_step(step):
16 self.mb.change_step(step)
17 # 描画を更新する
18 self.update_gui()
元と同じなので省略
19
20 Marubatsu_GUI.create_event_handler = create_event_handler
行番号のないプログラム
import math
from datetime import datetime
from tkinter import Tk, filedialog
import pickle
def create_event_handler(self):
# 乱数の種のチェックボックスのイベントハンドラを定義する
def on_checkbox_changed(changed):
self.update_widgets_status()
self.checkbox.observe(on_checkbox_changed, names="value")
# 開く、保存ボタンのイベントハンドラを定義する
def on_load_button_clicked(b=None):
path = filedialog.askopenfilename(filetypes=[("〇×ゲーム", "*.mbsav")],
initialdir="save")
if path != "":
with open(path, "rb") as f:
data = pickle.load(f)
self.mb.records = data["records"]
self.mb.ai = data["ai"]
change_step(data["move_count"])
for i in range(2):
value = "人間" if self.mb.ai[i] is None else self.mb.ai[i]
self.dropdown_list[i].value = value
if data["seed"] is not None:
self.checkbox.value = True
self.inttext.value = data["seed"]
else:
self.checkbox.value = False
def on_save_button_clicked(b=None):
name = ["人間" if self.mb.ai[i] is None else self.mb.ai[i].__name__
for i in range(2)]
timestr = datetime.now().strftime("%Y年%m月%d日 %H時%M分%S秒")
fname = f"{name[0]} VS {name[1]} {timestr}"
path = filedialog.asksaveasfilename(filetypes=[("〇×ゲーム", "*.mbsav")],
initialdir="save", initialfile=fname,
defaultextension="mbsav")
if path != "":
with open(path, "wb") as f:
data = {
"records": self.mb.records,
"move_count": self.mb.move_count,
"ai": self.mb.ai,
"seed": self.inttext.value if self.checkbox.value else None
}
pickle.dump(data, f)
def on_help_button_clicked(b=None):
self.output.clear_output()
with self.output:
print("""操作説明
マスの上でクリックすることで着手を行う。
下記の GUI で操作を行うことができる。
()が記載されているものは、キー入力で同じ操作を行うことができることを意味する。
なお、キー入力の操作は、ゲーム盤をクリックして選択状態にする必要がある。
乱数の種\tチェックボックスを ON にすると、右のテキストボックスの乱数の種が適用される
開く(-,L)\tファイルから対戦データを読み込む
保存(+,S)\tファイルに対戦データを保存する
?(*,H)\t\tこの操作説明を表示する
手番の担当\tメニューからそれぞれの手番の担当を選択する
\t\tメニューから選択しただけでは担当は変更されず、変更またはリセットボタンによって担当が変更される
変更\t\tゲームの途中で手番の担当を変更する
リセット\t手番の担当を変更してゲームをリセットする
待った(0)\t1つ前の自分の着手をキャンセルする
<<(↑)\t\t最初の局面に移動する
<(←)\t\t1手前の局面に移動する
>(→)\t\t1手後の局面に移動する
>>(↓)\t\t最後の着手が行われた局面に移動する
スライダー\t現在の手数を表す。ドラッグすることで任意の手数へ移動する
手数を移動した場合に、最後の着手が行われた局面でなければ、リプレイモードになる。
リプレイモード中に着手を行うと、リプレイモードが解除され、その着手が最後の着手になる。""")
self.load_button.on_click(on_load_button_clicked)
self.save_button.on_click(on_save_button_clicked)
self.help_button.on_click(on_help_button_clicked)
# 変更ボタンのイベントハンドラを定義する
def on_change_button_clicked(b):
for i in range(2):
self.mb.ai[i] = None if self.dropdown_list[i].value == "人間" else self.dropdown_list[i].value
self.mb.play_loop(self)
# リセットボタンのイベントハンドラを定義する
def on_reset_button_clicked(b=None):
# 乱数の種のチェックボックスが ON の場合に、乱数の種の処理を行う
if self.checkbox.value:
random.seed(self.inttext.value)
self.mb.restart()
self.output.clear_output()
on_change_button_clicked(b)
# 待ったボタンのイベントハンドラを定義する
def on_undo_button_clicked(b=None):
if self.mb.move_count >= 2 and self.mb.move_count == len(self.mb.records) - 1:
self.mb.move_count -= 2
self.mb.records = self.mb.records[0:self.mb.move_count+1]
self.mb.change_step(self.mb.move_count)
self.update_gui()
# イベントハンドラをボタンに結びつける
self.change_button.on_click(on_change_button_clicked)
self.reset_button.on_click(on_reset_button_clicked)
self.undo_button.on_click(on_undo_button_clicked)
# step 手目の局面に移動する
def change_step(step):
self.mb.change_step(step)
# 描画を更新する
self.update_gui()
def on_first_button_clicked(b=None):
change_step(0)
def on_prev_button_clicked(b=None):
change_step(self.mb.move_count - 1)
def on_next_button_clicked(b=None):
change_step(self.mb.move_count + 1)
def on_last_button_clicked(b=None):
change_step(len(self.mb.records) - 1)
def on_slider_changed(changed):
if self.mb.move_count != changed["new"]:
change_step(changed["new"])
self.first_button.on_click(on_first_button_clicked)
self.prev_button.on_click(on_prev_button_clicked)
self.next_button.on_click(on_next_button_clicked)
self.last_button.on_click(on_last_button_clicked)
self.slider.observe(on_slider_changed, names="value")
# ゲーム盤の上でマウスを押した場合のイベントハンドラ
def on_mouse_down(event):
# Axes の上でマウスを押していた場合のみ処理を行う
if event.inaxes and self.mb.status == Marubatsu.PLAYING:
x = math.floor(event.xdata)
y = math.floor(event.ydata)
with self.output:
self.mb.move(x, y)
# 次の手番の処理を行うメソッドを呼び出す
self.mb.play_loop(self)
# ゲーム盤を選択した状態でキーを押した場合のイベントハンドラ
def on_key_press(event):
keymap = {
"up": on_first_button_clicked,
"left": on_prev_button_clicked,
"right": on_next_button_clicked,
"down": on_last_button_clicked,
"0": on_undo_button_clicked,
"enter": on_reset_button_clicked,
"-": on_load_button_clicked,
"l": on_load_button_clicked,
"+": on_save_button_clicked,
"s": on_save_button_clicked,
"*": on_help_button_clicked,
"h": on_help_button_clicked,
}
if event.key in keymap:
keymap[event.key]()
else:
try:
num = int(event.key) - 1
event.inaxes = True
event.xdata = num % 3
event.ydata = 2 - (num // 3)
on_mouse_down(event)
except:
pass
# fig の画像イベントハンドラを結び付ける
self.fig.canvas.mpl_connect("button_press_event", on_mouse_down)
self.fig.canvas.mpl_connect("key_press_event", on_key_press)
Marubatsu_GUI.create_event_handler = create_event_handler
修正箇所
import math
from datetime import datetime
from tkinter import Tk, filedialog
import pickle
def create_event_handler(self):
元と同じなので省略
# 待ったボタンのイベントハンドラを定義する
def on_undo_button_clicked(b=None):
if self.mb.move_count >= 2 and self.mb.move_count == len(self.mb.records) - 1:
self.mb.move_count -= 2
self.mb.records = self.mb.records[0:self.mb.move_count+1]
self.mb.change_step(self.mb.move_count)
- self.draw_board()
+ self.update_gui()
元と同じなので省略
# step 手目の局面に移動する
def change_step(step):
self.mb.change_step(step)
# 描画を更新する
- self.draw_board()
+ self.update_gui()
元と同じなので省略
Marubatsu_GUI.create_event_handler = create_event_handler
実行結果は省略しますが、上記の修正後に、下記のプログラムで gui_play を実行し、プログラムが正しく動作することを確認して下さい。
from util import gui_play
gui_play()
今回の記事のまとめ
今回の記事では、ゲーム木と木構造の説明をし、ノードの作成と子ノードの計算、親ノードと子ノードの関係を視覚化するプログラムを実装しました。
なお、ノードなどの、ゲーム木に関連するプログラムは、tree.py というファイルに保存することにします。
本記事で入力したプログラム
以下のリンクから、本記事で入力して実行した JupyterLab のファイルを見ることができます。
以下のリンクは、今回の記事で更新した marubatsu.py です。
以下のリンクは、今回の記事で作成した tree.py です。
次回の記事
