シリーズ構成
1. スカラー移流方程式
1.1 輸送速度が正の場合
1.2 輸送速度の符号が不明の時の線形問題
1.3 数値流束を利用した方法
1.4 輸送速度が未知量であるとき(Burgers方程式)
1.5 多次元への拡張(2次元スカラー移流方程式)
1.6 実践的な計算法(TVD方程式)
2. 移流方程式の時間積分法
2.1 時間陽解法について
2.2 時間陰解法について(Crank-Nicholson法、近似LDU分解)
3. 2階偏微分方程式
3.1 1次元熱伝導方程式の数値計算法
3.2 楕円方程式の数値計算法
4. 圧縮性流れの数値計算法
4.1 オイラー方程式の数値計算法
はじめに
今回から,圧縮性流体の数値計算について扱っていきます.まずは,圧縮性オイラー方程式を題材として,1980年代以前に用いられていた計算方法を紹介し,圧縮性流体においてしばしば用いられる衝撃波管問題を計算してみます.
圧縮性オイラー方程式
1次元圧縮性の非粘性流れにおける支配方程式は,以下の圧縮性オイラー方程式です.
\frac{\partial \rho}{\partial t}+\frac{\partial(\rho u)}{\partial x}=0\tag{1}
\frac{\partial}{\partial t}(\rho u)+\frac{\partial}{\partial x}(p+\rho u^2)=0\tag{2}
\frac{\partial e}{\partial t}+\frac{\partial}{\partial x}((e+p)u)=0\tag{3}
ここで,$\rho$は気体の密度,$u$は速度,$p$は圧力,$e$は気体の全エネルギーを表しています.式(1)~(3)を合わせて圧縮性オイラー方程式といいます.未知数が$\rho,u,p,e$の4種類であることから,もう一つ補助的な方程式として気体の状態方程式があります.
p=(\gamma-1)\Big(e-\frac{1}{2}\rho u^2\Big)\tag{4}
式(1)~(3)をまとめて,
\frac{\partial \mathbf{Q}}{\partial t}+\frac{\partial \mathbf{E}}{\partial x}=\mathbf{0}\tag{5}
\mathbf{Q}=
\left[
\begin{array}{ccc}
\rho \\
\rho u \\
e \\
\end{array}
\right],
\mathbf{E}=
\left[
\begin{array}{ccc}
\rho u\\
p + \rho u^2 \\
(e+p)u \\
\end{array}
\right]
\tag{6}
式(5)を保存型で書くと,
\frac{\partial \mathbf{Q}}{\partial t}+\mathbf{A}\frac{\partial \mathbf{Q}}{\partial x}=\mathbf{0}\tag{7}
ここで,流束ヤコビアンマトリックス$\mathbf{A}$が定義でき,
\mathbf{A}=\frac{\partial \mathbf{E}}{\partial \mathbf{Q}}=
\left[
\begin{array}{ccc}
0 & 1 & 0 \\
-\displaystyle\frac{3-\gamma}{2}u^2 & (3-\gamma)u & \gamma-1 \\
\displaystyle\Big(\frac{\gamma-1}{2}u^2-H\Big)u & H-(\gamma-1)u^2 & \gamma u \\
\end{array}
\right]
\tag{8}
です.ここで,$H=(e+p)/\rho$はエンタルピーです.
圧縮性オイラー方程式の数値計算法
まずは,スカラー移流方程式のときにも扱ったLax-Wendroff法から始めます.
Lax-Wendroff法
\mathbf{Q}^{n+1}_j=\mathbf{Q}^n_j-\frac{1}{2}\Big(\frac{\Delta t}{\Delta x}\Big)(\mathbf{E}^n_{j+1}-\mathbf{E}^n_{j-1})+\frac{1}{2}\Big(\frac{\Delta t}{\Delta x}\Big)^2(\mathbf{A}_{j+1/2}(\mathbf{E}^n_{j+1}-\mathbf{E}^n_j)-\mathbf{A}_{j-1/2}(\mathbf{E}^n_j-\mathbf{E}^n_{j-1})\tag{9}
プログラミングをする際に,流束ヤコビアンマトリックス$\mathbf{A}$をかけるという演算が出てきてしまい,計算コストが高くなってしまいます.そこで,以下に簡素化手法を紹介します.
2段階Lax-Wendroff法
\left\{
\begin{array}{l}
\mathbf{Q}^{n+1/2}_{j+1/2}=\displaystyle\frac{1}{2}(\mathbf{Q}^n_{j+1}+\mathbf{Q}^n_j)-\displaystyle\frac{1}{2}\Big(\frac{\Delta t}{\Delta x}\Big)(\mathbf{E}^n_{j+1}-\mathbf{E}^n_j) \\ \\
\mathbf{Q}^{n+1}_j=\mathbf{Q}^n_j-\displaystyle\Big(\frac{\Delta t}{\Delta x}\Big)(\mathbf{E}^{n+1/2}_{j+1/2}-\mathbf{E}^{n+1/2}_{j-1})
\end{array}
\right.
\tag{10}
MacCormack法
\left\{
\begin{array}{l}
\mathbf{Q}^*_j=\mathbf{Q}^n_j-\displaystyle\Big(\frac{\Delta t}{\Delta x}\Big)(\mathbf{E}^n_j-\mathbf{E}^n_{j-1}) \\ \\
\mathbf{Q}^{n+1}_{j}=\displaystyle\frac{1}{2}(\mathbf{Q}^n_j+\mathbf{Q}^*_j)-\displaystyle\frac{1}{2}\Big(\frac{\Delta t}{\Delta x}\Big)(\mathbf{E}^*_{j+1}-\mathbf{E}^*_j)
\end{array}
\right.
\tag{11}
衝撃波管問題への応用
衝撃波管とは,膜を隔てて左右に圧力が異なる気体を入れた管のことです.衝撃波管の膜を破断すると,低圧側には圧縮波が,高圧側には膨張波が伝播します.最初にあった密度の境界面は,衝撃波よりも遅い速度で低圧側に移動します.
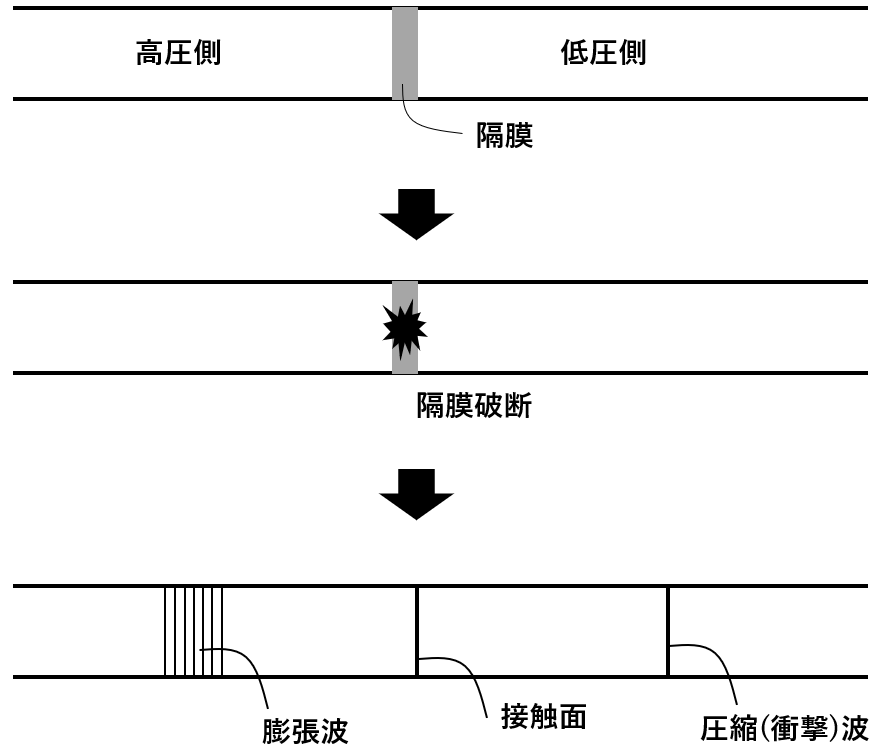
この衝撃波管問題をMacCormack法を用いて計算します.数値計算の都合上,発散を抑えるために高次の粘性項を加えます.
\mathbf{Q}^{n+1}_j=\overline{\mathbf{Q}}^{n+1}_j+\kappa(\overline{\mathbf{Q}}^{n+1}_{j-1}-2\overline{\mathbf{Q}}^{n+1}_j+\overline{\mathbf{Q}}^{n+1}_{j+1})\tag{12}
\kappa=\varepsilon_c\frac{|\overline{\mathbf{Q}}^{n+1}_{j-1}-2\overline{\mathbf{Q}}^{n+1}_j+\overline{\mathbf{Q}}^{n+1}_{j+1}|}{|\overline{\mathbf{Q}}^{n+1}_{j-1}+2\overline{\mathbf{Q}}^{n+1}_j+\overline{\mathbf{Q}}^{n+1}_{j+1}|}\tag{13}
これは4次の拡散項であるので,2次近似のMacCormack法には影響を及ぼしません.また,$\varepsilon_c$は任意に定められますが,問題ごとに吟味する必要があります.
本計算のモデルは以下の図のようになります.低圧側と高圧側の圧力比を$1:10$とします.
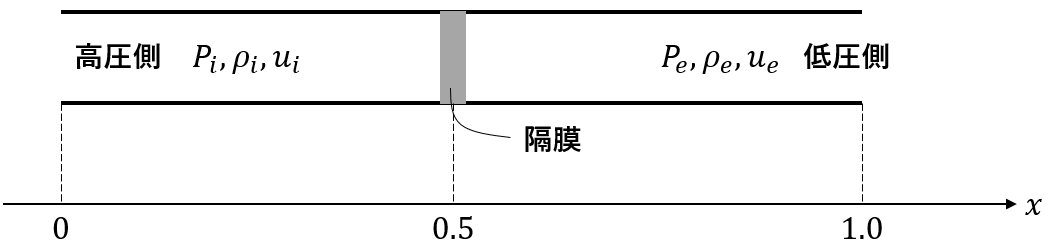
それでは実際に計算を行います.
import numpy as np
import matplotlib.pyplot as plt
jmax = 101
dt = 0.002
gamma = 1.4
PI = 1.0
RHOI = 1.0
UI = 0.0
PE = 0.1
RHOE = 0.1
UE = 0.0
xmin, xmid, xmax = 0.0, 0.5, 1.0
x = np.linspace(xmin, xmax, jmax)
dx = (xmax - xmin) / (jmax - 1)
dtdx = dt / dx
def init():
Q = np.zeros([jmax, 3])
Q[x <= xmid, 0] = RHOI
Q[x <= xmid, 1] = RHOI * UI
Q[x <= xmid, 2] = (PI / (gamma - 1.0) + 0.5 * RHOI * UI ** 2)
Q[x > xmid, 0] = RHOE
Q[x > xmid, 1] = RHOE * UE
Q[x > xmid, 2] = (PE / (gamma - 1.0) + 0.5 * RHOE * UE ** 2)
return Q
def calc_CFL(Q):
rho, rhou, e = Q[:, 0], Q[:, 1], Q[:, 2]
u = rhou / rho
p = (gamma - 1.0) * (e - 0.5 * rho * u ** 2)
c = np.sqrt(gamma * p / rho)
sp = c + np.abs(u)
return max(sp) * dtdx
def E_flux(Q, E):
rho, rhou, e = Q[:, 0], Q[:, 1], Q[:, 2]
u = rhou / rho
p = (gamma - 1.0) * (e - 0.5 * rho * u ** 2 )
E[:, 0] = rhou
E[:, 1] = p + rhou * u
E[:, 2] = (e + p) * u
def MacCormack(Q, eps_c, nmax, interval = 2):
E = np.zeros([jmax, 3])
for n in range(nmax):
if n % interval == 0:
print(f'n = {n : 4d} : CFL = {calc_CFL(Q) : .4f}')
Qs = Q.copy()
E_flux(Q, E)
for j in range(1, jmax - 1):
Qs[j] = Q[j] - dtdx * (E[j] - E[j-1])
E_flux(Qs, E)
for j in range(1, jmax - 2):
Q[j] = 0.5 * (Q[j] + Qs[j]) - 0.5 * dtdx * (E[j + 1] - E[j])
Qb = Q.copy()
for j in range(1, jmax - 1):
D1 = Qb[j - 1] - 2.0 * Qb[j] + Qb[j + 1]
D2 = Qb[j - 1] + 2.0 * Qb[j] + Qb[j + 1]
k = eps_c * np.linalg.norm(D1) / np.linalg.norm(D2)
Q[j] += k * D1 # 式(6.11)
esp_c = 0.15
nmax = 100
print_interval = 4
Q = init()
MacCormack(Q, esp_c, nmax, print_interval)
# 厳密解の計算
Pext = np.zeros([jmax, 3])
Qext = np.zeros([jmax, 3])
GUESS = 1.0
FINC = 0.01
itemax1 = 5000
itemax2 = 500
CI = np.sqrt(gamma * PI / RHOI)
CE = np.sqrt(gamma * PE / RHOE)
P1P5 = PI / PE
GAMI = 1.0 / gamma
GAMF = (gamma - 1.0) / (2.0 * gamma)
GAMF2 = (gamma + 1.0) / (gamma - 1.0)
GAMFI = 1.0 / GAMF
for it1 in range(itemax1):
for it2 in range(itemax2):
SQRT1 = (gamma - 1.0) * (CE / CI) * (GUESS - 1.0)
SQRT2 = np.sqrt(2.0 * gamma * (2.0 * gamma + (gamma + 1.0) * (GUESS - 1.0)))
FUN = GUESS * (1.0 - (SQRT1 / SQRT2)) ** (-GAMFI)
DIF = P1P5 - FUN
if np.abs(DIF) <= 0.000002:
break
if DIF >= 0.0:
GUESS += FINC
else:
GUESS -= FINC
FINC = 0.5 * FINC
else:
continue
break
P4P5 = GUESS
P4 = PE * P4P5
P3P1 = P4P5 / P1P5
P3 = P3P1 * PI
R4R5 = (1.0 + GAMF2 * P4P5) / (GAMF2 + P4P5)
RHO4 = RHOE * R4R5
U4 = CE * (P4P5 - 1.0) * np.sqrt(2.0 * GAMI / ((gamma + 1.0) * P4P5 + (gamma - 1.0)))
C4 = np.sqrt(gamma * P4 / RHO4)
R3R1 = P3P1 ** GAMI
RHO3 = RHOI * R3R1
U3 = 2.0 * CI / (gamma - 1.0) * (1.0 - P3P1 ** GAMF)
C3 = np.sqrt(gamma * P3 / RHO3)
CS = CE * np.sqrt(0.5 * ((gamma - 1.0) * GAMI + (gamma + 1.0) * GAMI * P4 / PE))
TOT = 0.0
EPST = 1.0e-14
for n in range(nmax):
TOT = TOT + dt
rad = dt / dx
x1 = xmid - CI * TOT
x2 = xmid - (CI - 0.5 * (gamma + 1.0) * U3) * TOT
x3 = xmid + U3 * TOT
x4 = xmid + CS * TOT
for j in range(jmax):
xx = x[j]
if xx <= x1:
Qext[j, 0] = RHOI
Qext[j, 1] = RHOI * UI
Qext[j, 2] = PI / (gamma - 1.0) + 0.5 * UI * Qext[j, 1]
Pext[j] = PI
elif xx <= x2:
UT = UI + (U3 - UI) / ((x2 - x1) + EPST) * ((xx - x1) + EPST)
RTRI = (1.0 - 0.5 * (gamma - 1.0) * UT / CI) ** (2.0 / (gamma - 1.0))
RT = RHOI * RTRI
PT = RTRI ** gamma * PI
Qext[j, 0] = RT
Qext[j, 1] = RT * UT
Qext[j, 2] = PT / (gamma - 1.0) + 0.5 * UT * Qext[j, 1]
Pext[j] = PT
elif xx <= x3:
Qext[j, 0] = RHO3
Qext[j, 1] = RHO3 * U3
Qext[j, 2] = P3 / (gamma - 1.0) + 0.5 * U3 * Qext[j, 1]
Pext[j] = P3
elif xx <= x4:
Qext[j, 0] = RHO4
Qext[j, 1] = RHO4 * U4
Qext[j, 2] = P4 / (gamma - 1.0) + 0.5 * U4 * Qext[j, 1]
Pext[j] = P4
else:
Qext[j, 0] = RHOE
Qext[j, 1] = RHOE * UE
Qext[j, 2] = PE / (gamma - 1.0) + 0.5 * UE * Qext[j, 1]
Pext[j] = PE
plt.figure(figsize=(7,7), dpi=100) # グラフのサイズ
plt.rcParams["font.size"] = 22 # グラフの文字サイズ
plt.plot(x, Qext[:,0], color='black', linewidth = 1.0, linestyle = 'dashed', label = 'Analytical')
plt.plot(x, Q[:,0], color='red', linewidth = 1.5, label = 'Numerical')
plt.grid(color='black', linestyle='dotted', linewidth=0.5)
plt.xlabel('x')
plt.ylabel(r'$\rho$')
# plt.legend()
plt.show()
plt.figure(figsize=(7,7), dpi=100) # グラフのサイズ
plt.rcParams["font.size"] = 22 # グラフの文字サイズ
plt.plot(x, Qext[:,1]/Qext[:,0], color='black', linewidth = 1.0, linestyle = 'dashed', label = 'Analitical')
plt.plot(x, Q[:,1]/Q[:,0], color='red', linewidth = 1.5, label = 'Numerical')
plt.grid(color='black', linestyle='dotted', linewidth=0.5)
plt.xlabel('x')
plt.ylabel('u')
# plt.legend()
plt.show()
plt.figure(figsize=(7,7), dpi=100) # グラフのサイズ
plt.rcParams["font.size"] = 22 # グラフの文字サイズ
yext = (gamma - 1.0) * (Qext[:,2] - 0.5 * Qext[:,1] ** 2 / Qext[:,0])
y = (gamma - 1.0) * (Q[:,2] - 0.5 * Q[:,1] ** 2 / Q[:,0])
plt.plot(x, yext, color='black', linewidth = 1.0, linestyle = 'dashed',label = 'Analytical')
plt.plot(x, y, color='red', linewidth = 1.5, label = 'Numerical')
plt.grid(color='black', linestyle='dotted', linewidth=0.5)
plt.xlabel('x')
plt.ylabel('p')
plt.legend()
plt.show()
実行結果は以下のようになります.
(a)密度

(b)速度

(c)圧力

多少の数値振動をしているもののよく計算できていることがわかります.
まとめ
今回は,圧縮性流体の数値計算のはじめとして,いくつかの手法を紹介し,1次元の衝撃波問題を解きました.
参考文献
藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20