シリーズ構成
1. スカラー移流方程式
1.1 輸送速度が正の場合
1.2 輸送速度の符号が不明の時の線形問題
1.3 数値流束を利用した方法
1.4 輸送速度が未知量であるとき(Burgers方程式)
1.5 多次元への拡張(2次元スカラー移流方程式)
1.6 実践的な計算法(TVD方程式)
2. 移流方程式の時間積分法
2.1 時間陽解法について
2.2 時間陰解法について(Crank-Nicholson法、近似LDU分解)
3. 2階偏微分方程式
3.1 1次元熱伝導方程式の数値計算法
3.2 楕円方程式の数値計算法
4. 圧縮性流れの数値計算法
4.1 オイラー方程式の数値計算法
4.2 MacCormack法による数値計算法
4.3 TVD法による数値計算法
はじめに
今回は,ポアソン方程式に代表される楕円方程式の数値計算法を扱っていきます.最終的には,二次元モデルにおける翼周りの数値計算をすることを目的とします.
楕円方程式の数値計算法
楕円方程式は,
\frac{\partial^2 q}{\partial x^2}+\frac{\partial^2 q}{\partial y^2}=0\tag{1}
であり,空間二階微分項を中心差分で近似すると,
\frac{q_{j-1,k}-2q_{j,k}+q_{j+1,k}}{\Delta x^2}+\frac{q_{j,k-1}-2q_{j,k}+q_{j,k+1}}{\Delta y^2}=0\tag{2}
となる.ある点$(j,k)$での物理量での物理量$q$を求めようとすると,周りの点が必要になります.その周りの点を求めるにはまた更にその周りの点が必要になります.といった形で,楕円方程式はすべての点が互いにつながりあっている方程式であるともいえます.
簡単のため式(2)で,$\Delta x=\Delta y$とすると,
q_{j,k}=\frac{1}{4}\Big (q_{j-1,k}+q_{j+1,k}+q_{j,k-1}+q_{j,k+1}\Big )\tag{3}
行列形式で書き直すと,
\left[
\begin{array}{ccc}
-4 & 1 & \cdots & \cdots & 0 \\
1 & \ddots & & & \vdots \\
\vdots & &\ddots & &\vdots \\
\vdots & & &\ddots & 1\\
0 & \cdots &\cdots & 1 & -4
\end{array}
\right]
\left[
\begin{array}{ccc}
\vdots \\
q_{j-1,k} \\
q_{j,k} \\
q_{j+1,k} \\
\vdots
\end{array}
\right]
=
\left[
\begin{array}{ccc}
\\
\\
\\
RHS \\
\\
\\
\\
\end{array}
\right]
\tag{4}
式(4)の左辺の係数行列を反転することにより解くことはできますが,現在の数値計算では格子数が多いため,これは難しいです.そこで,いくつかの計算法について紹介します.
Point Jacobi法
q^{n+1}_{j,k}=\frac{1}{4}\Big (q^n_{j-1,k}+q^n_{j+1,k}+q^n_{j,k-1}+q^n_{j,k+1}\Big)\tag{5}
Point Jacobi法では,$n=1$における初期値を設定することによって,式(5)を用いて繰り返し計算を行っていく手法です.すべての点$j,k$において$n$ステップ目と$n+1$ステップ目の物理量の差が十分小さければ式(5)は式(3)に帰着されます.この考え方を緩和法といいます.しかし,このPoint Jacobi法は収束が非常に遅いことが知られています.
Gauss-Seidel法
q^{n+1}_{j,k}=\frac{1}{4}\Big (q^{n+1}_{j-1,k}+q^n_{j+1,k}+q^{n+1}_{j,k-1}+q^n_{j,k+1}\Big)\tag{6}
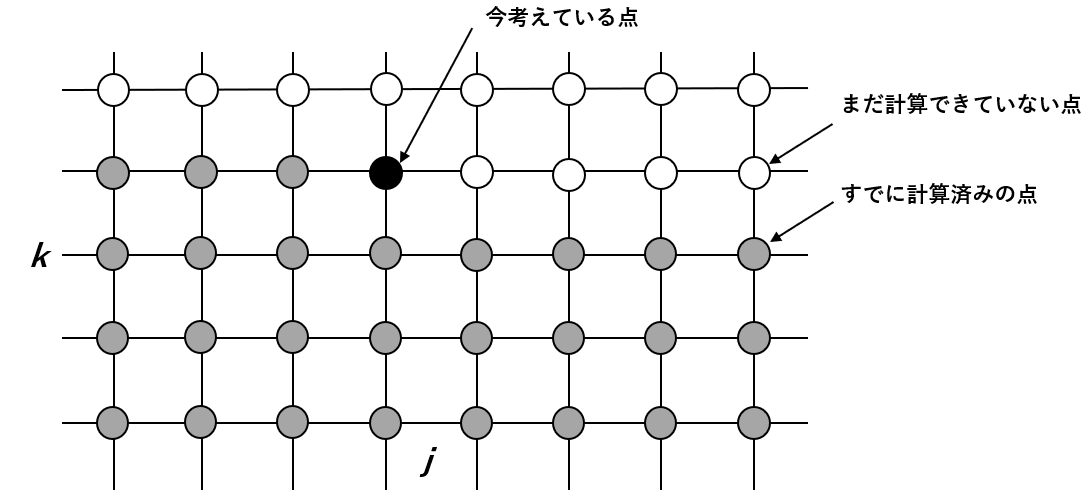
上図の格子点分布を用いて,$(j,k)$の小さいほうから順に計算していきます.ある点$(j,k)$を求める際,それまでのすべての格子点が計算済みのはずであるので,多次元LU分解のように計算可能です.
一部の離散点に新しい時間ステップでの値を利用することによって収束性がPoint Jacobi法よりもかなり向上します.
SOR法
q^{n+1}_{j,k}=q^n_{j,k}+\frac{1}{4}\omega\Big (q^{n+1}_{j-1,k}+q^n_{j+1,k}-4q^n_{j,k}+q^{n+1}_{j,k-1}+q^n_{j,k+1}\Big)\tag{7}
ここで,$\omega$は緩和係数と呼ばれ,$1<\omega<2$に設定します.$\omega=1$にときは,Gauss-Seidel法に帰着します.適切に$\omega$を設定すれば,より収束性を速めた計算ができます.
楕円方程式の応用例(翼周りの流れ計算)
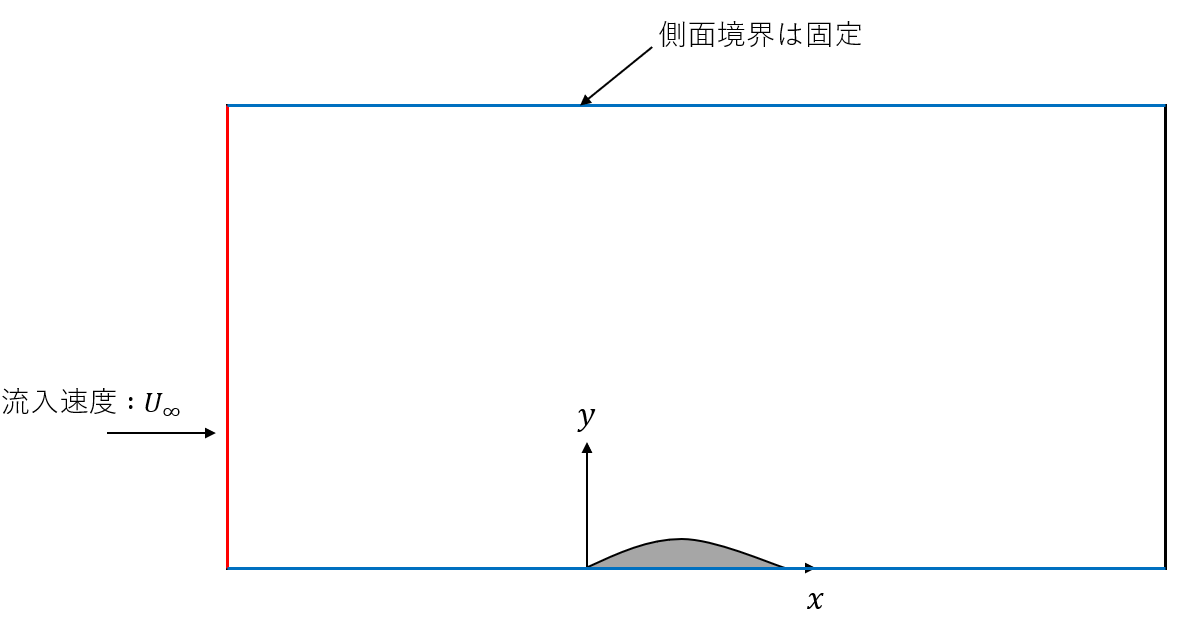
亜音速の非粘性渦なし流れでは,一様流からの微小な速度変化により微小擾乱が生じます.今回の数値計算では,以下のモデルを設定します.
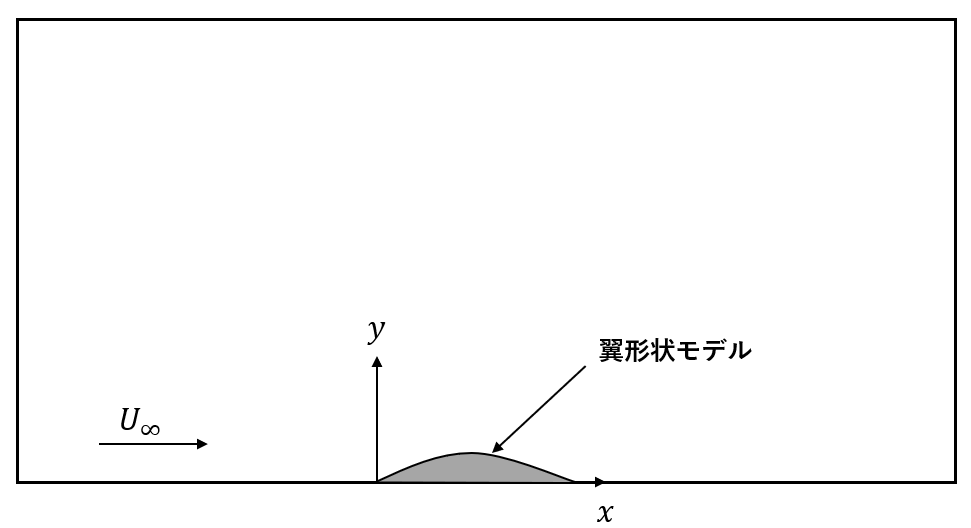
ここで,$U_{\infty}$は一様流の速度です.このような微小擾乱のみを有する流れでは,速度擾乱ポテンシャル$\phi$を用いて,擾乱速度$\bar{u},\bar{v}$は,
\bar{u}=\frac{\partial{\phi}}{\partial{x}}\tag{8}
\bar{v}=\frac{\partial{\phi}}{\partial{y}}\tag{9}
と表せます.本現象における支配方程式は,
(1-{M_{\infty}}^2)\frac{\partial^2{\phi}}{\partial{x^2}}+\frac{\partial^2{\phi}}{\partial{y^2}}=0\tag{10}
で表せます.詳しい導出は参考文献[2]を参照ください.
式(10)をGauss-Seidel法で離散化します.
\Big\{\frac{2(1-{M_{\infty}}^2)}{\Delta{x^2}}+\frac{2}{\Delta{y^2}}\Big \}\phi^{n+1}_{j,k}=\frac{1-{M_{\infty}}^2}{\Delta{x^2}}(\phi^{n+1}_{j-1,k}+\phi^n_{j+1,k})+\frac{1}{\Delta{y^2}}(\phi^{n+1}_{j,k-1}+\phi^n_{j,k+1})\tag{11}
ここで簡単のために$\Delta x=\Delta y$とすると,
\phi_{j,k}=\frac{1}{2+2(1-{M_{\infty}}^2)}\Big\{(1-{M_{\infty}}^2)(\phi_{j-1,k}+\phi_{j+1,k})+(\phi_{j,k-1}+\phi_{j,k+1})\Big\}\tag{12}
となります.翼の形状は以下の関数によってあらわします.
y=0.2x(1-x)\tag{13}
以上の条件の下,数値計算を行っていきます.
from turtle import color
import numpy as np
import matplotlib.pyplot as plt
nmax = 400
M = 0.8
alpha2 = 1 - M**2
Uinf = 0.1
dx = dy = 0.05
xs, xe = -1.0, 2.0
ys, ye = 0.0, 1.0
x_le, x_te = 0.0, 1.0
jmax = int((xe - xs) / dx) + 1
kmax = int((ye - ys) / dy) + 1
j_le = int((x_le - xs) / dx)
j_te = int((x_te - xs) / dx) + 1
x = np.linspace(xs, xe, jmax)
y = np.linspace(ys, ye, kmax)
phi = np.zeros([jmax, kmax])
u = np.zeros([jmax, kmax])
v = np.zeros([jmax, kmax])
dydx = np.array([0.2 * (1.0 - 2.0*x[j]) if j_le <= j < j_te else 0.0 for j in range(jmax)])
X, Y = np.meshgrid(x,y)
residual = np.zeros(nmax)
for n in range(nmax):
phiold = phi.copy()
#境界条件
phi[0,:] = 0.0
phi[jmax-1,:] = 0.0
phi[:,kmax-1] = 0.0
for j in range(jmax):
phi[j, 0] = phi[j, 1] - dydx[j]*dy
#Gauss-Seidel法
for k in range(1, kmax-1):
for j in range(1, jmax-1):
phi[j,k] = 1.0 / (2.0 * alpha2 + 2.0) * (alpha2 * (phi[j-1, k] + phi[j+1, k]) + phi[j, k-1] + phi[j, k+1])
residual[n] = np.sqrt(((phi-phiold) ** 2).sum() / (jmax * kmax))
for j in range(1, jmax-1):
u[j, :] = Uinf * (1.0 + (phi[j+1,:] - phi[j-1,:]) / (2*dx))
u[0,:] = Uinf * (1.0 + (phi[1, :] - phi[0, :]) / dx)
u[-1,:] = Uinf * (1.0 + (phi[-1, :] - phi[-2, :]) / dx)
for k in range(1, kmax-1):
v[:, k] = Uinf * (phi[:,k+1] - phi[:, k-1]) / (2*dy)
v[:,0] = Uinf * (phi[:, 1] - phi[:, 0]) / dy
v[:,-1] = Uinf * (phi[:, -1] - phi[:, -2]) / dy
va = np.sqrt(u ** 2 + v ** 2)
# 可視化
fig, ax1 = plt.subplots(figsize=(9,3), dpi=100)
plt.rcParams["font.size"] = 25
cnt = plt.contourf(X,Y,va.transpose(1,0),cmap='viridis',levels=100)
sty = np.arange(0.02, ye, 0.05)
stx = np.full(len(sty), -1.0)
xf = np.linspace(0,1,100)
f = 0.2*xf*(1-xf)
plt.fill_between(xf, f, color='gray')
plt.plot(xf,f,color='gray')
startpoints = np.array([stx, sty]).transpose(1,0)
plt.streamplot(X,Y,u.transpose(1,0), v.transpose(1,0), color='white',start_points=startpoints,linewidth=0.5,arrowstyle='-')
plt.xlabel('x',fontsize=25)
plt.ylabel('y',fontsize=25)
plt.xticks(fontsize = 25)
plt.yticks(fontsize = 25)
plt.xticks([xs,0,1,xe])
plt.subplots_adjust(left=0.17)
plt.colorbar(orientation='horizontal')
plt.show()
実行すると,
①$M_{\infty}=0.1$
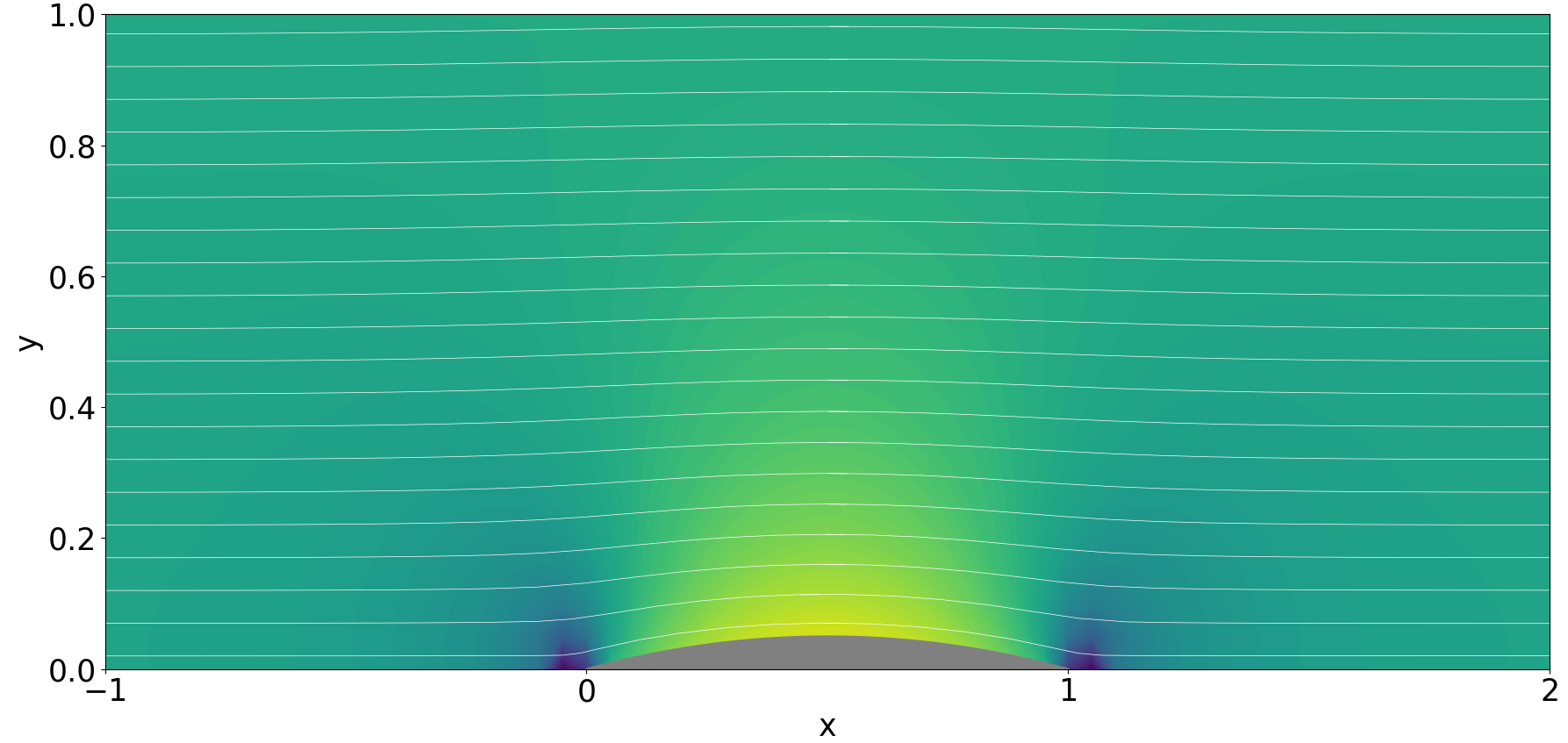
②$M_{\infty}=0.5$
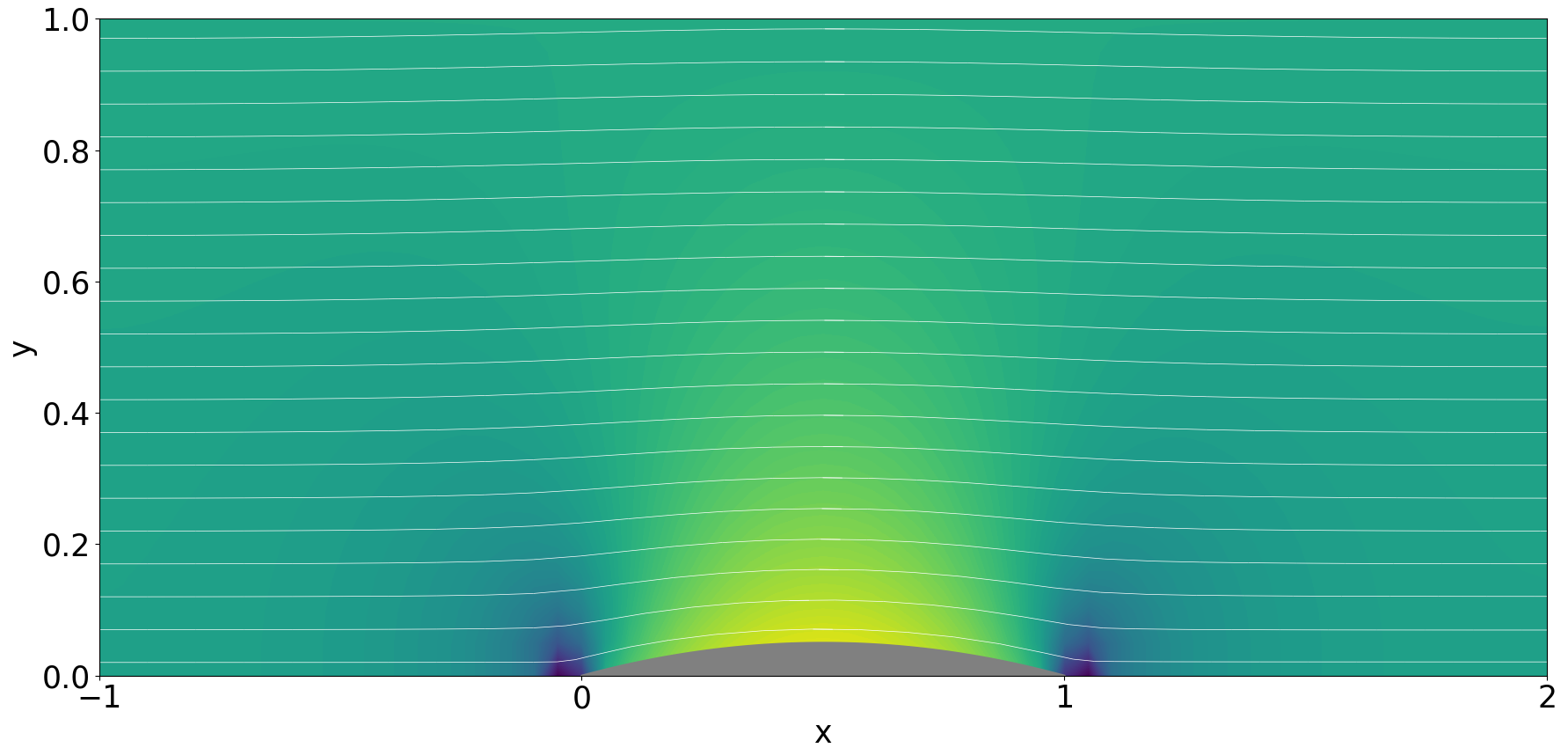
③$M_{\infty}=0.8$
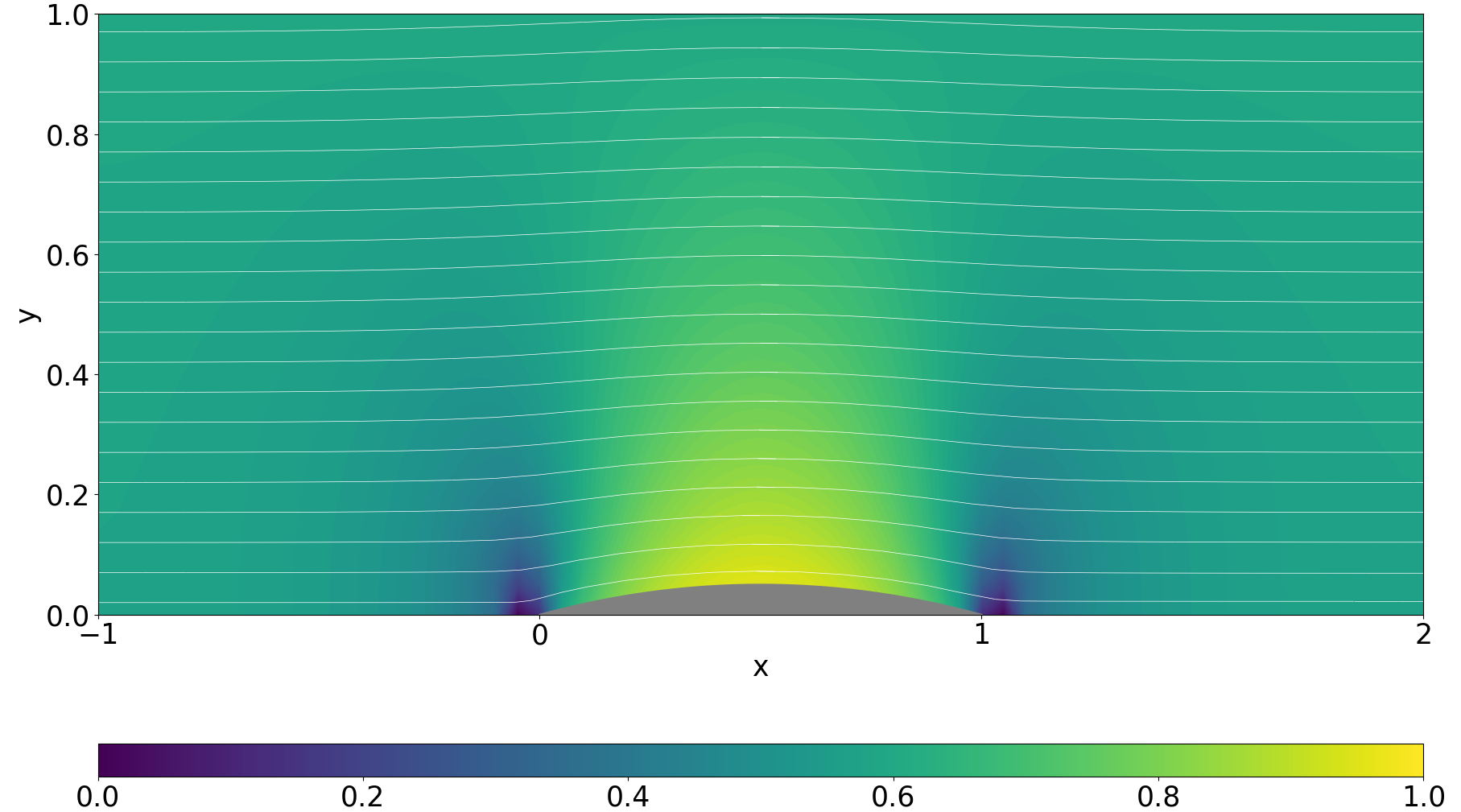
等高線は,その地点の流速を最大流速に対する比として色付けしています.白の実線は,流線を表しています.
この解析結果から,マッハ数が大きくなるほど翼形状によるy方向の擾乱がより遠くまで伝播していることがわかります.
まとめ
今回は楕円方程式に対しての数値計算法を紹介しました.応用例として,翼形状周りの流体解析を行いました.次回からは,圧縮性流れの数値計算法について扱っていきます.
参考文献
[1] 藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20
[2] 林圭佐,2 次元無限領域における圧縮性亜音速流れの領域分割法,https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1198-6.pdf