はじめに
今回は、数値流体力学シリーズの第3回です。移流方程式を数値流束という考え方によって数値計算していきます。
何か間違いなどありましたら気軽にコメントしてください!
シリーズ構成
1. スカラー移流方程式
1.1 輸送速度が正の場合
1.2 輸送速度の符号が不明の時の線形問題
1.3 数値流束を利用した方法
1.4 輸送速度が未知量であるとき(Burgers方程式)
1.5 多次元への拡張(2次元スカラー移流方程式)
1.6 実践的な計算法(TVD方程式)
2. 移流方程式の時間積分法
2.1 時間陽解法について
2.2 時間陰解法について(Crank-Nicholson法、近似LU分解)
3. 2階偏微分方程式
3.1 1次元熱伝導方程式の数値計算法
3.2 楕円方程式の数値計算法
4. 圧縮性流れの数値計算法
4.1 オイラー方程式の数値計算法
4.2 MacCormack法による数値計算法
4.3 TVD法による数値計算法
今回扱う内容
今回は、数値流束がテーマとなっています。まず、数値流束のアイデアを考えたのち、それを第1回、第2回で扱った、移流方程式の数値計算法に適用していきます。最後にスカラー移流方程式の数値計算では有名なGodunovの定理について考えてます。
数値流束とは?
流束$f$を$f=cq$と定義して、スカラー移流方程式を考えると、
$$\frac{\partial{q}}{\partial{t}}+\frac{\partial{f}}{\partial{x}}=0\tag{1}$$
となります。

上図のように空間格子の間に仮想的に境界を考えてみましょう。さて、時間$n$ステップでの格子点$j$と格子点$j+1$との間には、仮想的な境界$j+1/2$があることになります。このような境界面を考えることによって、式(1)は
q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta{t}}{\Delta{x}}\Big(\tilde{f}^{n}_{j+1/2}-\tilde{f}^{n}_{j-1/2}\Big)\tag{2}
のように離散化できます。ここで、$\tilde{f}^{n}_{j+1/2}$などを数値流束といいます。数値流束には、構成の任意性がある(空間格子の半分のところでなくてもいいわけですね)ので、定義点(空間格子点)での流束と区別して一般的にチルダ「~」をつけることが慣習となっています。
数値流束を数値計算法に適用してみる
第1回、第2回で考えた移流方程式の数値計算法に対して、$j+1/2$における数値流束の評価方法を考えてみましょう。
FTCS法
$j+1/2$における数値流束を評価するとき、左右の平均を利用するとFTCS法となります。
\tilde{f}^{n}_{j+1/2}=\frac{f^{n}_{j+1}+f^{n}_{j}}{2}\tag{3}
1次精度風上法
$j+1/2$における数値流束を流れの風上方向、つまり格子点$j$の流束で評価すると1次精度風上法となります。
\tilde{f}^{n}_{j+1/2}=f^{n}_{j}\tag{4}
Lax法
\tilde{f}^{n}_{j+1/2}=\frac{1}{2}\Big\{\Big(1-\frac{1}{\nu}\Big)f^{n}_{j+1}+\Big(1+\frac{1}{\nu}\Big)f^{n}_{j}\Big\}\tag{5}
Lax-Wendroff法
\tilde{f}^{n}_{j+1/2}=\frac{1}{2}\Big\{(1-\nu)f^{n}_{j+1}+(1+\nu)f^{n}_{j}\Big\}\tag{6}
輸送速度cの符号が不明のとき
FTCS法、Lax法、Lax-Wendroff法は離散点に対して対称な評価式であるから、$c$の符号に依存しません。1次精度風上法を考えてみましょう。$f=cq$と定義したことにより、
\tilde{f}^{n}_{j+1/2}=\frac{c+|c|}{2}q^n_j+\frac{c-|c|}{2}q^n_{j+1}=\frac{1}{2}\Big\{\Big(f^{n}_{j+1}+f^{n}_{j}\Big)-|c|\Big(q^n_{j+1}-q^n_{j}\Big)\Big\}\tag{7}
これは、圧縮性流体解析にも出てくる重要な考え方になります。
数値流束を用いた高精度化(Godunovの定理)
これまでは移流方程式を1次精度で評価してきました。1次精度であっても格子点の数を増やすことによって、それなりに正確な解を得られることができるということは分かったと思います。しかし、実際の数値計算では格子点の数が限られている場合があり、2次精度以上の計算を利用することが必要になってきます。
輸送速度が正のとき
スカラー移流方程式は、
$$\frac{\partial{q}}{\partial{t}}+c\frac{\partial{q}}{\partial{x}}=0\tag{7}$$
である。ここで、格子点$j-1$と$j-2$でのテイラー展開を考えてみましょう。
q_{j-1}=q_{j}-\left.\frac{\partial{q}}{\partial{x}}\right|_{j}\Delta{x}+\frac{1}{2}\left.\frac{\partial^2{q}}{\partial^2{x}}\right|_{j}\Delta{x^2}-\frac{1}{3!}\left.\frac{\partial^3{q}}{\partial^3{x}}\right|_{j}\Delta{x^3}+・・・\tag{8}
q_{j-2}=q_{j}-\left.\frac{\partial{q}}{\partial{x}}\right|_{j}(2\Delta{x})+\frac{1}{2}\left.\frac{\partial^2{q}}{\partial^2{x}}\right|_{j}(2\Delta{x})^2-\frac{1}{3!}\left.\frac{\partial^3{q}}{\partial^3{x}}\right|_{j}(2\Delta{x})^3+・・・\tag{9}
式(8)の4倍から式(9)を引くと、
\left.\frac{\partial{q}}{\partial{x}}\right|_{j}=\frac{3q_{j}-4q_{j-1}+q_{j-2}}{2\Delta{x}}+O(\Delta{x^2})\tag{10}
この式は、2次精度であることがわかります。つまり、これを移流方程式に適用することで、空間微分項を1次精度から2次精度へと高精度化することができますね。
では、式(10)を式(7)に適用してみましょう。
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{3q^n_{j}-4q^n_{j-1}+q^n_{j-2}}{2\Delta{x}}\tag{11}
これを変形すると、
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{\Big(\frac{3}{2}q^n_{j}-\frac{1}{2}q^n_{j-1}\Big)-\Big(\frac{3}{2}q^n_{j-1}-\frac{1}{2}q^n_{j-2}\Big)}{\Delta{x}}\tag{12}
ここからわかるように、1次精度の離散化における$q^n_j$を$\frac{3}{2}q^n_{j}-\frac{1}{2}q^n_{j-1}$に置き換えることにより2次精度になることがわかります。
数値流束としては、
\left \{
\begin{array}{l}
\tilde{f}^{n}_{j+1/2}=f^{n}_{j} (1次精度) \tag{13} \\
\tilde{f}^{n}_{j+1/2}=\frac{3}{2}f^n_{j}-\frac{1}{2}f^n_{j-1} (2次精度)
\end{array}
\right.
と書けることになります。
さて、この2次精度化を使ってスカラー移流方程式を数値計算してみましょう。プログラムは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
def init(q1, q2, dx, jmax):
x = np.linspace(0, dx * (jmax-1), jmax)
q = np.array([(float(q1) if i < 0.5 * jmax else float(q2)) for i in range(jmax)])
return (x, q)
def UPWIND1(q, c, dt, dx, j):
ur = q[j+1]
ul = q[j]
fr = c * ur
fl = c * ul
return 0.5 * (fr + fl - abs(c) * (ur - ul))
def UPWIND2(q, c, dt, dx, j):
ur = 1.5 * q[j+1] - 0.5 * q[j+2]
ul = 1.5 * q[j] - 0.5 * q[j-1]
fr = c * ur
fl = c * ul
return 0.5 * (fr + fl - abs(c) * (ur - ul))
def do_computing(x, q, c, dt, dx, nmax, ff, order = 1, interval = 2, ylim = None, yticks = None):
plt.figure(figsize=(7,7), dpi=100)
plt.rcParams["font.size"] = 22
plt.plot(x, q, marker='o', lw=2, label='n=0')
for n in range(1, nmax+1):
qold = q.copy()
for j in range(order, jmax-order):
ff1 = ff(qold, c, dt, dx, j)
ff2 = ff(qold, c, dt, dx, j-1)
q[j] = qold[j] - dt/dx * (ff1 - ff2)
if n % interval == 0:
plt.plot(x, q, marker='o', lw=2, label=f'n={n}')
plt.grid(color='black', linestyle='dashed', linewidth=0.5)
plt.xlabel('x')
plt.ylabel('q')
plt.legend()
if ylim is not None:
plt.ylim(ylim)
if yticks is not None:
plt.yticks(yticks)
plt.show()
c = 1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 6
q1 = 1
q2 = 0
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, c, dt, dx, nmax, UPWIND1, order = 1, interval = 2)
c = -1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 6
q1 = 0
q2 = 1
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, c, dt, dx, nmax, UPWIND1, order = 1, interval = 2)
c = 1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 6
q1 = 1
q2 = 0
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, c, dt, dx, nmax, UPWIND2, order = 2, interval = 2, \
ylim = [-1, 1.1], \
yticks = np.arange(-1, 1.1, 0.2))
c = -1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 6
q1 = 0
q2 = 1
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, c, dt, dx, nmax, UPWIND2, order = 2, interval = 2, \
ylim = [-1, 1.1], \
yticks = np.arange(-1, 1.1, 0.2))
実行すると、
①1次精度かつ$c>0$のとき
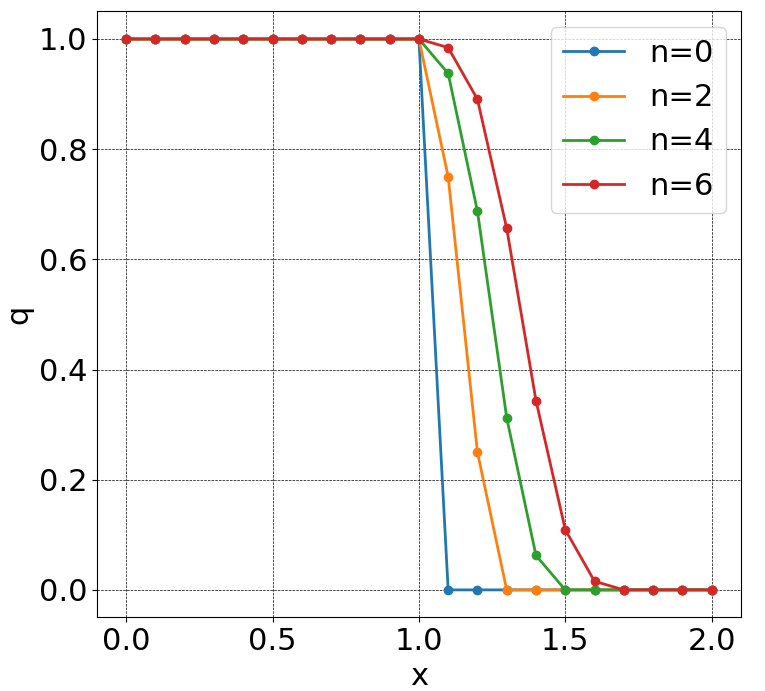
②1次精度かつ$c<0$のとき
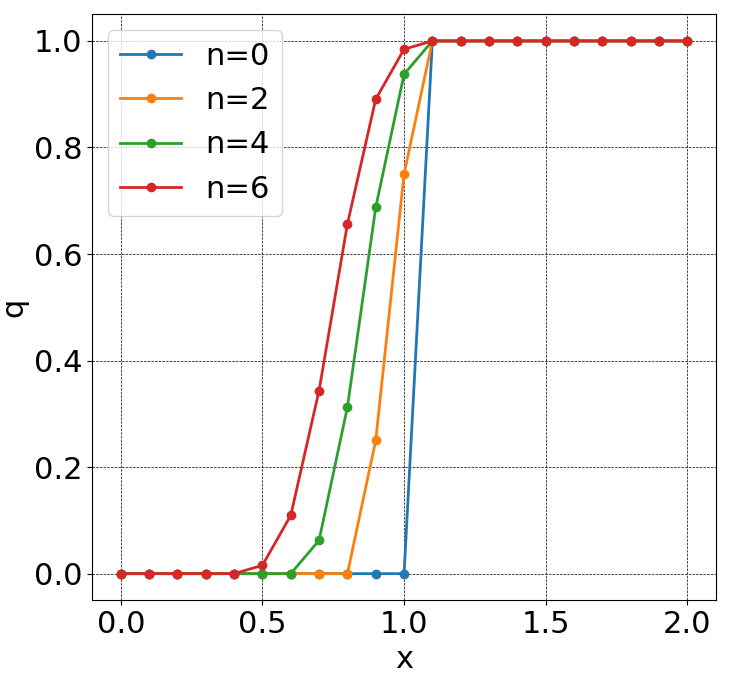
③2次精度かつ$c>0$のとき

④1次精度かつ$c<0$のとき
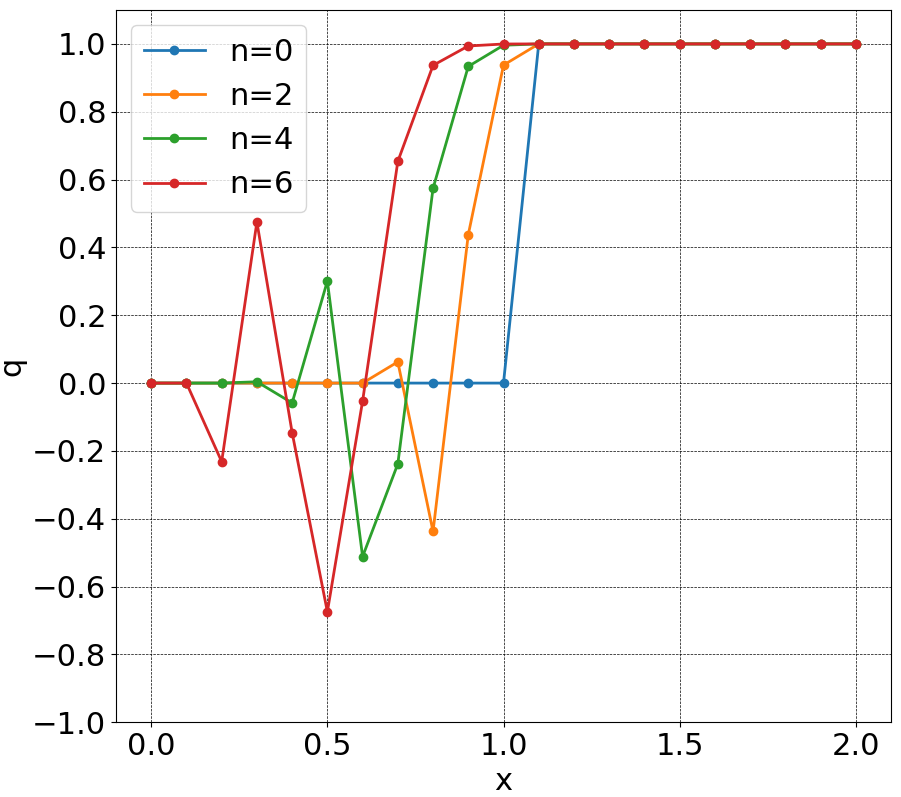
この結果からもわかる通り、スカラー移流方程式に対しては、以下の形の2次以上の精度をもつスキームを使用すると解の単調性が保てないことが知られています。これをGodunovの定理といいます。
q^{n+1}_{j}=\displaystyle\sum_{k}c_kq^{n}_{j+k} \tag{14}
**解の単調性を保つためには係数$c_k$のすべてが正でなければならないのです。**具体的にこれまで見てきた計算法で確認してみましょう。それぞれの方法について$q^{n}_{k}$の係数を抜き出してその正負についてみていきましょう。
1次精度風上法
$$c_j=1-\nu \tag{15}$$
$$c_{j-1}=\nu \tag{16}$$
1次精度風上法では安定な時間積分のためにCFL条件があるので、これらの係数は常に正です。つまり、単調性が維持できることになります。
2次精度風上法
$$
c_j=1-\frac{3}{2}\nu \tag{17}$$
$$c_{j-1}=2\nu \tag{18}$$
$$c_{j-2}=-\frac{1}{2}\nu \tag{19}$$
係数$c_{j-2}$は必ず負の値をとってしまうから、単調性が維持できないことがわかります。
Lax-Wendroff法
$$c_j=1-\nu^2 \tag{20}$$
$$c_{j-1}=\frac{1}{2}\nu(1+\nu)\tag{21} $$
$$c_{j-2}=-\frac{1}{2}\nu(1-\nu)\tag{22}$$
こちらも、係数$c_{j-2}$は必ず負の値をとってしまうから、単調性が維持できないことがわかります。
このように、各係数を見ることによってその計算法の数値振動の有無を調べることができます。
まとめ
今回は数値流束を用いて、移流方程式の評価式を考えてみました。そのあと、評価式の高精度化を図り、数値解析を行いました。それを通して、Godunovの定理の確認をしました。
参考文献
藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20