##はじめに
今回からシリーズとして、数値流体解析(CFD)の基礎をまとめる記事を書こうと思います。1次元移流方程式から始まり、拡散方程式、ポアソン方程式等順を追って、最終的には圧縮性のNavier-Stokes方程式を解くことを目的とします。数値計算にはPythonを使用していきます。
このシリーズを通して基本的な数値計算法がさらえるように構成していきます。
なお、参考文献は「Pythonで学ぶ流体力学の数値計算法」です。
何か間違いなどありましたら気軽にコメントしてください！
##シリーズ構成
####1. スカラー移流方程式
1.1 輸送速度が正の場合←本記事
1.2 輸送速度の符号が不明の時の線形問題
1.3 数値流束を利用した方法
1.4 輸送速度が未知量であるとき(Burgers方程式)
1.5 多次元への拡張(2次元スカラー移流方程式)
1.6 実践的な計算法(TVD方程式)
####2. 移流方程式の時間積分法
2.1 時間陽解法について
2.2 時間陰解法について(Crank-Nicholson法、近似LU分解)
####3. 2階偏微分方程式
3.1 1次元熱伝導方程式の数値計算法
3.2 楕円方程式の数値計算法
####4. 圧縮性流れの数値計算法
4.1 オイラー方程式の数値計算法
4.2 MacCormack法による数値計算法
4.3 TVD法による数値計算法
##今回扱う内容
今回は、1次元移流方程式についてです。移流方程式の性質を考えたのち、輸送速度が正のときについて、FTCS法、一次精度風上法、Lax法、Lax-Wendroff法を用いて数値計算します。この4つを比較してそれぞれの方法の特徴について考えていきます。
最後に、時間陽解法の弱点でもある安定化条件について、von Neumannの解析を用いて厳密にやってみようと思います。とりあえず、安定化条件の細かいところはいったん無視したうえで数値計算の流れをさらった後、最後に厳密に見てみようというわけです。
##移流方程式の性質
さて、今回から考える移流方程式は、
$$\frac{\partial{q}}{\partial{t}}+c\frac{\partial{q}}{\partial{x}}=0\tag{1}$$
です。$q$は状態量を表していて、温度、密度、圧力などがこれに当たります。$c$を輸送速度といいます。状態量$q$は時空間の関数であるので、
$$q=q(x,t)\tag{2}$$
と表せるはずです。式(1)には下のような一般解が知られています。
$$q=f(x-ct)\tag{3}$$
式(3)から、$x-ct$が同じところでは、状態量$q$の値が同じになることがわかります。つまり、時空図上で$x=ct$に沿って$q$が一定となります。この直線$x=ct$を特性線と呼びます。
この性質は、後々圧縮性流体を考えるときに非常に重要になります。
##輸送速度が正の場合の移流方程式
それでは、移流方程式の数値計算を行っていきましょう。今回は、輸送速度が正のときを考えてみます。初期条件は以下のように定めるとしましょう。
\left \{
\begin{array}{l}
q=1.0 (x\leqq1) \\
q=0.0 (x>1)
\end{array}
\right.
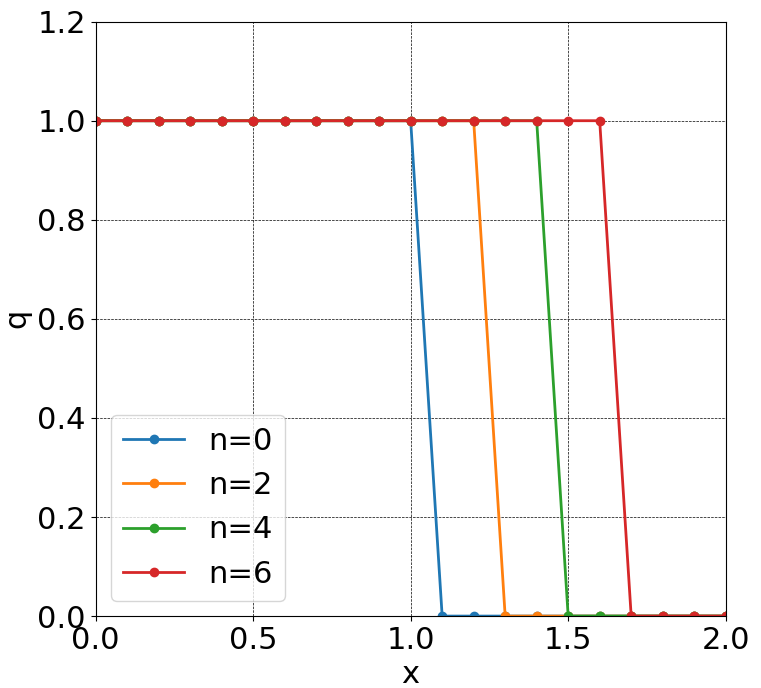
解析結果は以下のようになるはずです。
$t=0$のときの分布が時間とともに輸送速度$c$で移動する様子が得られれば完ぺきというわけです。
###FTCS法
では、実際に式(1)の評価方法について考えてみましょう。時間微分項を前進差分で、空間微分項を中心差分で評価すると、
\frac{q^{n+1}_{j}-q^{n}_{j}}{\Delta{t}}+c\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}=0\tag{5}
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}\tag{6}
このように時間微分項を前進差分で、空間微分項を中心差分で評価する方法をFTCS法(Forward in Time and Centered in Space scheme)といいます。また、一般に、時間微分項を前進差分で評価し、空間微分項を時間nステップで評価することで、時間n+1ステップでのqの値を求める方法を時間陽解法といいます。
では、このスキームを用いて移流方程式を解いてみましょう。
import numpy as np
import matplotlib.pyplot as plt
#初期値の設定、空間初期分布の設定
c = 1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 6
x = np.linspace(0, dx*(jmax-1), jmax)
q = np.zeros(jmax)
for j in range(jmax):
if (j < jmax/2):
q[j] = 1
else:
q[j] = 0
def do_computing(x, q, c, dt, namax, dx):
plt.figure(figsize=(7,7), dpi=100)
plt.rcParams["font.size"] = 22
#初期分布の可視化
plt.plot(x, q, marker='o', lw=2, label='n=0')
for n in range(1, nmax+1):
qold = q.copy()
for j in range(1, jmax-1):
q[j] = qold[j] - c * dt * (qold[j+1] - qold[j-1])/(2*dx)
#各ステップの可視化
if n % 2 == 0:
plt.plot(x, q, marker='o', lw=2, label=f'n={n}')
#グラフの後処理
plt.grid(color="black", linestyle='dashed', linewidth='0.5')
plt.xlim([0,2.0])
plt.ylim([0,2.5])
plt.xlabel('x')
plt.ylabel('q')
plt.legend()
plt.show()
do_computing(x, q, c, dt, nmax, dx)
実行結果はこのようになります。
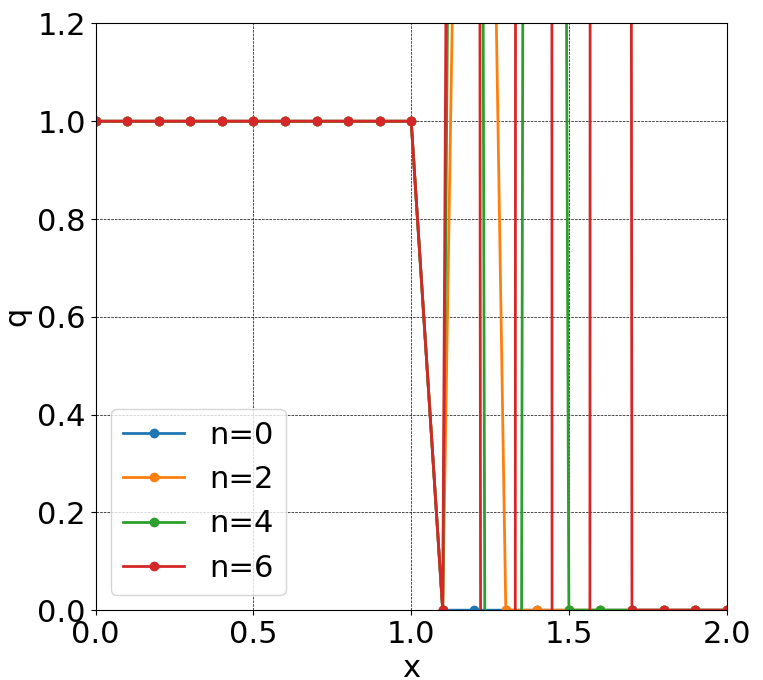
**！？！？期待される結果とは程遠いものが得られてしまいました。。**この原因について考えてみましょう。後述するCFL条件を満たしているのはプログラムを参照すればわかると思います。これは、初期条件と離散化式(6)を見てみるとすぐにわかります。試しにqの値が1から0に変わる直前の離散点を考えてみましょう。すると、j+1ではq=0.0となり、j-1ではq=1.0となります。つまり、式(6)の右辺第2項が
-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}>0
となり、**結果的に$q^{n}_{j+1}$の値が1よりも大きくなってしまうのです。**その影響が空間ステップが大きくなるにつれ伝播していくため、このような結果となってしまいました。
つまり、FTCS法は非常に不安定な計算方法であるといえます。
この不安定性の厳密な考察は、本記事の最後にやってみようと思います。
###1次精度風上法
次は、FTCS法とは違い、空間微分項に後退差分を適用して評価してみましょう。
\frac{q^{n+1}_{j}-q^{n}_{j}}{\Delta{t}}+c\frac{q^{n}_{j}-q^{n}_{j-1}}{\Delta{x}}=0\tag{7}
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j}-q^{n}_{j-1}}{\Delta{x}}\tag{8}
このような方法を、流れの情報がやってくる方向に差分をとることから由来して、1次精度風上法といいます。この方法であれば、FTCS法のような振動は起こらなさそうですね。
では、このスキームを用いて移流方程式を解いてみましょう。先ほどの計算の部分を式(8)のようにするだけです。
q[j] = qold[j] - c * dt * (qold[j] - qold[j-1])/dx
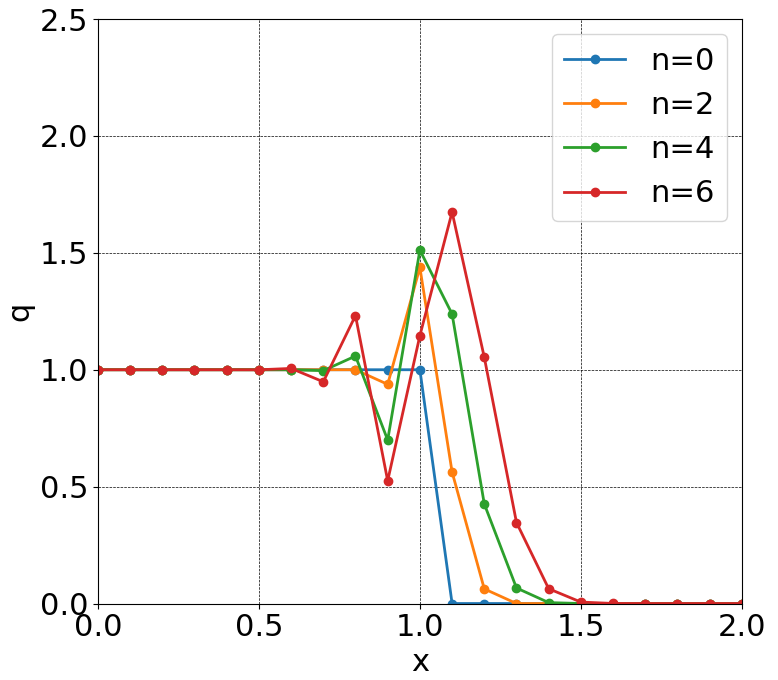
いい感じの計算結果になりました。が、期待される結果と比べると時間がたつにつれてグラフがなだらかになってしまっています。
時間の刻み幅を色々変えてプログラムを回してみましょう。
\left \{
\begin{array}{l}
① \Delta{x}=0.1,\Delta{t}=0.05 (上の結果) \\
② \Delta{x}=0.1,\Delta{t}=0.1 \\
③ \Delta{x}=0.1,\Delta{t}=0.2 \\
\end{array}
\right.
②の結果
期待していた結果と同じものが得られました！
③の結果
結果が振動してしまっていることがわかります。
①～③の結果から、この計算結果を決めるのは$\Delta{x}$や$\Delta{t}$単体ではなくて、それらの比であると考えることができます。このように、時間陽解法では一般的にクーラン数と呼ばれる$c\frac{\Delta{t}}{\Delta{x}}$についての安定化条件があり、これをCFL条件(Courant-Friedrichs-Lewy condition)と呼びます。CFL条件は、
$$c\frac{\Delta{t}}{\Delta{x}}<1.0\tag{9}$$
というものです。式(9)の条件が満たされていれば、計算が安定に進むことになります。つまり、時間陽解法を用いるときは常にCFL条件を考えなければいけないのです。
###Lax法
Lax法は、FTCS法の式(6)の右辺第1項をj+1とj-1の平均と考えて書き換えたものです。
q^{n+1}_{j}=\frac{q^{n}_{j+1}+q^{n}_{j-1}}{2}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}\tag{10}
では、このスキームを用いて移流方程式を解いてみましょう。FTCS法のプログラムの計算の部分を式(10)のようにするだけです。
q[j] = (qold[j+1] + qold[j-1])/2 - c * dt * (qold[j+1] - qold[j-1])/(2*dx)
段々があるような結果となってしまいました。期待していた結果とはかけ離れてしまっています。
###Lax-Wendroff法
$q^{n+1}_{j}$の時間ステップtでのテイラー展開を考えてみましょう。
q^{n+1}_{j}=q^{n}_{j}+\Delta{t}\left.\frac{\partial{q}}{\partial{t}}\right|_{t}+\frac{1}{2}\Delta{t^2}\left.\frac{\partial^2{q}}{\partial{t^2}}\right|_{t}+O(\Delta{t^3})\tag{11}
今、移流方程式を考えているから、
$$\frac{\partial{q}}{\partial{t}}=-c\frac{\partial{q}}{\partial{x}}\tag{12}$$
$$\frac{\partial^2{q}}{\partial{t^2}}=c^2\frac{\partial^2{q}}{\partial{x^2}}\tag{13}$$
であるので、代入すると、
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{\partial{q}}{\partial{x}}+\frac{1}{2}c^2\Delta{t^2}\frac{\partial^2{q}}{\partial{x^2}}+O(\Delta{t^3})\tag{14}
微分項をそれぞれ中心差分で近似して、
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}+\frac{1}{2}c^2\Delta{t^2}\frac{q^{n}_{j+1}-2q^{n}_{j}+q^{n}_{j-1}}{\Delta{x^2}}\tag{15}
これが、Lax-Wendroff法です。
では、このスキームを用いて移流方程式を解いてみましょう。FTCS法のプログラムの計算の部分を式(15)のようにするだけです。
q[j] = qold[j] - 0.5 * c * dt / dx * (qold[j+1] - qold[j-1]) + 0.5 * (c * dt / dx)**2 * (qold[j+1] - 2*qold[j] + qold[j-1])
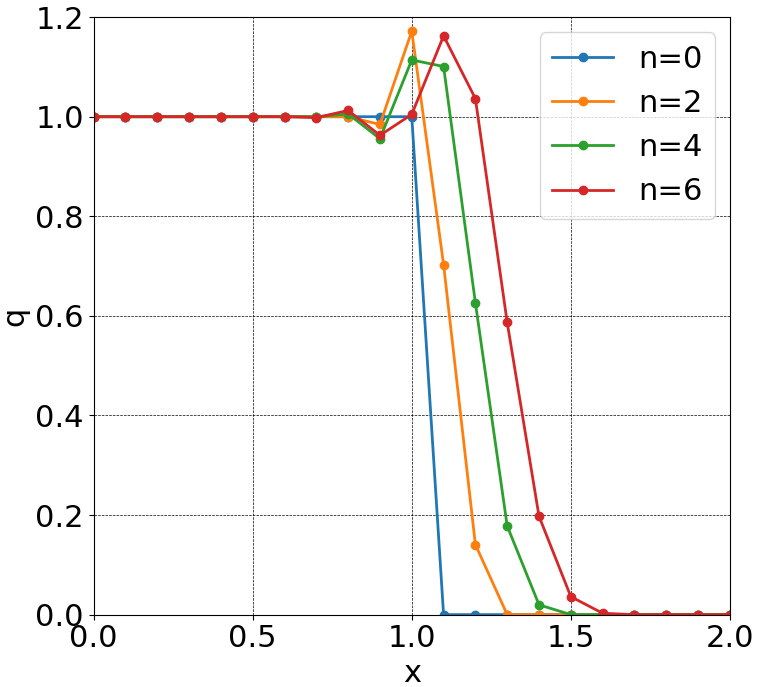状態量が0から1に変わるところで、若干の振動が生じてしまっています。
##4つのスキームの比較
最後に、今回用いた4つのスキームについて、(空間中心差分)+(拡散項)という形で書いてみましょう。
####FTCS法
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}\tag{16}
####1次精度風上法
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}+\frac{c}{2}\frac{\Delta{t}}{\Delta{x}}\Delta{x^2}\frac{q^{n}_{j+1}-2q^{n}_{j}+q^{n}_{j-1}}{\Delta{x^2}}\tag{17}
####Lax法
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}+\frac{1}{2}\Delta{x^2}\frac{q^{n}_{j+1}-2q^{n}_{j}+q^{n}_{j-1}}{\Delta{x^2}}\tag{18}
####Lax-Wendroff法
q^{n+1}_{j}=q^{n}_{j}-c\Delta{t}\frac{q^{n}_{j+1}-q^{n}_{j-1}}{2\Delta{x}}+\frac{c^2}{2}\Big(\frac{\Delta{t}}{\Delta{x}}\Big)^2\Delta{x^2}\frac{q^{n}_{j+1}-2q^{n}_{j}+q^{n}_{j-1}}{\Delta{x^2}}\tag{19}
FTCS法は不安定な方法であることはすでに述べたとおりです。これを除く3つの方法で、拡散項に注目してみるとLax法が一番数値拡散の効果が大きいことがわかります。結果的に、Lax法は安定な方法である一方で勾配が鈍ってしまいます。また、Lax-Wendroff法は非線形問題を扱うときに安定性の問題が出てきます。
##安定性の厳密な解析(von Neumann解析)
本記事ではここまで、数値計算の結果から各スキームについての安定性を考えてきました。最後に、von Neumann解析を用いて、厳密に考えてみましょう。
ここまで扱ってきた離散化式が以下の形の厳密解をもつと考えます。
q^n_j=g^n exp(i(j\theta))\tag{20}
ここで、$i$は虚数単位、$j$は格子点の位置を表します(今まで離散化式で出てきた$j$と同じ意味です)。当然、$q^n_j$は複素数であるので、実部、虚部どちらも離散化式を満たさなければいけません。$g$が複素振幅率と呼ばれ、時間ステップごとの振幅の増加率を表します。つまり、この$g$が数値振動に効いてきます。$exp(i(j\theta))$は振動を表していますが、実際の解はフーリエ分解された解の重ね合わせとして理解されています。ここでは、その1つ成分について考えていきます。
さて、von Neumann解析を各スキームに適用してみましょう。
####FTCS法
式(20)を式(16)に代入してみましょう。また、表記を簡単にするために、クーラン数を$\nu$としています。
g^{n+1}e^{ij\theta}=g^{n}e^{ij\theta}-\frac{1}{2}\nu(g^{n}e^{i(j+1)\theta}-g^{n}e^{i(j-1)\theta})\tag{21}
\Leftrightarrow g=1-\frac{1}{2}\nu(e^{i\theta}-e^{-i\theta})\tag{22}
オイラーの公式を適用すると、
g=1-\nu sin\theta \tag{23}
式(23)から、ある成分がクーラン数$\nu$で1ステップ後にどれだけ増幅するかがわかります。詳しくこの$g$を見ていくために、式(23)を振幅と位相に分けてみましょう。
g=|g|e^{i\phi}\tag{24}
式(23)(24)から、
\left \{
\begin{array}{l}
|g|^2=1+\nu^2sin^2\theta \\
\tag{25}
\phi=-tan^{-1}(\nu sin\theta)
\end{array}
\right.
ここで、解析解からして正しい解は、時間ステップが増幅しない、つまり$|g|=1$であり、位相差が$-\nu\theta$であることです。
\left \{
\begin{array}{l}
|g|=1 \\
\tag{26}
\phi=-\nu\theta
\end{array}
\right.
式(25)と(26)を比較してみると、FTCS法は振幅増加率、位相差がともに満たされていないことがわかります。なかでも、振幅増加率は常に1を上回るため振幅が際限なく増加されていしまいます。
改めて、FTCS法が不安定な方法であることが確認できました。
####1次精度風上法
FTCS法と同様に、式(21)に式(24)を代入することで、
\left \{
\begin{array}{l}
|g|=\Big[(1-\nu+\nu cos\theta)^2+(-\nu sin\theta)^2\Big]^\frac{1}{2} \\
\tag{27}
\phi=-tan^{-1}\frac{\nu sin\theta}{1-\nu+\nu cos\theta}
\end{array}
\right.
これらの式を見ることで、高周波は減衰しやすものの、拡散項による効果を除けばおおむね波の移動が正しくとらえられるだろうことがわかると思います。
####Lax法
\left \{
\begin{array}{l}
|g|^2=cos^2\theta+\nu^2sin^2\theta \\
\tag{28}
\phi=-tan^{-1}(\nu tan\theta)
\end{array}
\right.
この式を見ると、$\nu^2 \leqq 1$のときに限り、$|g| \leqq 1$となることがすぐにわかります。つまり、CFL条件の範囲内で安定した計算をすることができます。
####Lax-Wendroff法
\left \{
\begin{array}{l}
|g|^2=\{1-\nu^2(1-cos^2\theta)^2\}+\nu^2sin^2\theta \\
\tag{29}
\phi=-tan^{-1}\frac{\nu sin\theta}{1-\nu^2(1-cos\theta)}
\end{array}
\right.
##まとめ
今回は4つのスキームを使ってスカラー移流方程式を解いてみました。それぞれの方法について安定性の問題、数値解の滑らかさに問題があったことが分かったと思います。その後、安定化条件について、von Neumann解析により議論しました。
では、次回は、輸送速度の符号が正か負かわからないときの解決方法について考えていきたいと思います。
##参考文献
藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20