はじめに
これまでは、輸送速度が定数であるような移流方程式を扱ってきました。今回は、輸送速度が未知数からなる非線形の移流方程式を扱います。その中でも有名なBurgers方程式の数値計算を通じて、輸送速度が未知数からなる非線形の移流方程式の数値計算の理解を深めていきましょう。
シリーズ構成
1. スカラー移流方程式
1.1 輸送速度が正の場合
1.2 輸送速度の符号が不明の時の線形問題
1.3 数値流束を利用した方法
1.4 輸送速度が未知量であるとき(Burgers方程式)
1.5 多次元への拡張(2次元スカラー移流方程式)
1.6 実践的な計算法(TVD方程式)
2. 移流方程式の時間積分法
2.1 時間陽解法について
2.2 時間陰解法について(Crank-Nicholson法、近似LU分解)
3. 2階偏微分方程式
3.1 1次元熱伝導方程式の数値計算法
3.2 楕円方程式の数値計算法
4. 圧縮性流れの数値計算法
4.1 オイラー方程式の数値計算法
4.2 MacCormack法による数値計算法
4.3 TVD法による数値計算法
今回扱う内容
Burgers方程式の数値計算に関して、Murman-Cole法とGodunov法の2種類で行っていきます。その中で、衝撃波や方程式の弱解の概念について触れていきたいと思います。
Murman-Cole法
今回扱うBurgers方程式は、
$$\frac{\partial{q}}{\partial{t}}+q\frac{\partial{q}}{\partial{x}}=0\tag{1}$$
$q$の符号がわからないから、第2回で考えたように絶対値を用いて書き直すと、
q^{n+1}_{j}=q^{n}_{j}-\Delta{t}\Big(\frac{q^{n}_{j}+|q^{n}_{j}|}{2}\frac{q^{n}_{j}-q^{n}_{j-1}}{\Delta{x}}+\frac{q^{n}_{j}-|q^{n}_{j}|}{2}\frac{q^{n}_{j+1}-q^{n}_{j}}{\Delta{x}}\Big)\tag{2}
初期条件を、
\left \{
\begin{array}{l}
q=1.0 (x<0) \\
q=0.0 (x>0)
\end{array}
\right.
と設定しましょう。すると、$x>0$で$q$が0になると、式(2)の左辺が以降0となり、$q^{n+1}_j=q^n_j$となってしまい、どれだけ時間を進めても情報が進まないことがわかります。
そこで、式(1)を以下のように変形します。
$$\frac{\partial{q}}{\partial{t}}+\frac{\partial}{\partial{x}}\Big(\frac{1}{2}q^2\Big)=0\tag{3}$$
これを、数値流束を用いた離散化式に適用すると、
q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta{t}}{\Delta{x}}\Big(\tilde{f}^{n}_{j+1/2}-\tilde{f}^{n}_{j-1/2}\Big) \\
\Leftrightarrow q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta{t}}{2\Delta{x}}\Big((q^{n}_{j})^2-(q^{n}_{j-1})^2\Big) \\
\Leftrightarrow q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta{t}}{\Delta{x}}\frac{q^{n}_{j}+q^{n}_{j-1}}{2}\Big(q^{n}_{j}-q^{n}_{j-1}\Big)\tag{4}
式(4)は$c>0$の時のみ適用可能なので、$c<0$の場合は、
q^{n+1}_{j}=q^{n}_{j}-\frac{\Delta{t}}{\Delta{x}}\frac{q^{n}_{j+1}+q^{n}_{j}}{2}\Big(q^{n}_{j+1}-q^{n}_{j}\Big)\tag{5}
を適用すればよいです。式(4)と(5)を合わせてMurman-Cole法と呼びます。
では、Murman-Cole法をBurgers方程式に適用して数値計算してみましょう。計算条件は今までと同じです。
import numpy as np
import matplotlib.pyplot as plt
def init(q1, q2, dx, jmax):
xs = -1.0
x = np.linspace(xs, xs+dx*(jmax-1), jmax)
q = np.array([(float(q1) if i<0.0 else float(q2)) for i in x])
return (x, q)
def do_computing(x, q, dt, dx, nmax, ff, order=1, interval=2):
plt.figure(figsize=(7,7), dpi=100)
plt.rcParams["font.size"] = 22
plt.plot(x, q, marker='o', lw=2, label='n=0')
for n in range(1, nmax+1):
qold = q.copy()
for j in range(order, jmax-order):
ff1 = ff(qold, qold[j], dt, dx, j)
ff2 = ff(qold, qold[j], dt, dx, j-1)
q[j] = qold[j] - dt/dx * (ff1 - ff2)
if n % interval == 0:
plt.plot(x, q, marker='o', lw=2, label=f'n={n}')
plt.grid(color='black', linestyle='dashed', linewidth=0.5)
plt.xlabel('x')
plt.ylabel('q')
plt.legend()
plt.show()
def MC(q, c, dt, dx, j):
ur = q[j+1]
ul = q[j]
fr = 0.5 * ur**2
fl = 0.5 * ul**2
c = 0.5 * (ur + ul)
return 0.5 * (fr + fl - np.sign(c) * (fr - fl))
c = 1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 10
q1 = -1
q2 = 1
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, dt, dx, nmax, MC, interval=2)
特性速度$q$を色々変えて考察してみましょう。
\left \{
\begin{array}{l}
① q=2.0 (x<0), q=1.0(x>0) \\
② q=1.0 (x<0), q=2.0(x>0) \\
③ q=1.0 (x<0), q=-1.0(x>0) \\
④ q=-1.0 (x<0), q=1.0(x>0)
\end{array}
\right.
①のとき

②のとき

③のとき

④のとき

③と④は速度の平均が0となってしまうため、波面が移動していないことがわかります。このように、流速を利用して移流方程式を保存型にすることで非線形問題でも計算できることがわかります。
①と③は左から右に値が下がっているので流れの圧縮に相当します。不連続な降下は、いわゆる衝撃波です。一方、②と④は流れの膨張に相当します。
Godunov法
数学的には、Burgers方程式の解は一つではなくて多数存在します。これを弱解といいます。例えば、50℃のお湯を作るのには0℃の水100mlと100℃のお湯100mlを混ぜればよいですが、そのような組み合わせは無限にあります。
このような、多数の弱解から、実際に起こる現象に対応する解を見つけ出さなければいけません。Burgers方程式では、膨張衝撃波を排除することで、流れの膨張現象を正しく記述することができます。Godunov法ではMurman-Cole法を以下のように変更することでこれを実現しました。
\tilde{f}^{n}_{j+1/2}=
\left \{
\begin{array}{l}
\frac{1}{2}q^2_{j+1} (q_j,q_{j+1}<0) \\
\frac{1}{2}q^2_{j} (q_j,q_{j+1}>0)
\end{array}
\right.
\tilde{f}^{n}_{j+1/2}=
\left \{
\begin{array}{l}
\frac{1}{2}q^2_{j+1} (q_j>0>q_{j+1}かつc_{j+1/2}=\frac{q_j+q_{j+1}}{2}<0) \\
\frac{1}{2}q^2_{j} (q_j>0>q_{j+1}かつc_{j+1/2}=\frac{q_j+q_{j+1}}{2}>0) \\
0 (q_j<0<q_{j+1}(膨張波))
\end{array}
\right.
これは、MUrman-Cole法に膨張波を考慮した分岐を入れたものになります。
では、これをBurgers方程式に適用してみましょう。
import numpy as np
import matplotlib.pyplot as plt
def init(q1, q2, dx, jmax):
xs = -1.0
x = np.linspace(xs, xs+dx*(jmax-1), jmax)
q = np.array([(float(q1) if i<0.0 else float(q2)) for i in x])
return (x, q)
def do_computing(x, q, dt, dx, nmax, ff, order=1, interval=2):
plt.figure(figsize=(7,7), dpi=100)
plt.rcParams["font.size"] = 22
plt.plot(x, q, marker='o', lw=2, label='n=0')
for n in range(1, nmax+1):
qold = q.copy()
for j in range(order, jmax-order):
ff1 = ff(qold, qold[j], dt, dx, j)
ff2 = ff(qold, qold[j], dt, dx, j-1)
q[j] = qold[j] - dt/dx * (ff1 - ff2)
if n % interval == 0:
plt.plot(x, q, marker='o', lw=2, label=f'n={n}')
plt.grid(color='black', linestyle='dashed', linewidth=0.5)
plt.xlabel('x')
plt.ylabel('q')
plt.legend()
plt.show()
def GORNOV(q, c, dt, dx, j):
#分岐あり
ur = q[j+1]
ul = q[j]
fr = 0.5 * ur ** 2
fl = 0.5 * ul ** 2
c = 0.5 * (ur + ul)
if q[j] <= 0 and q[j+1] <= 0:
return fr
elif q[j] >= 0 and q[j+1] >= 0:
return fl
elif q[j] > 0 >q[j+1]:
if c < 0:
return fr
else:
return fl
else:
return 0
def GORNOV2(q, c, dt, dx, j):
#分岐なし
qm = 0.5 * (q[j] + np.abs(q[j]))
qp = 0.5 * (q[j+1] - np.abs(q[j+1]))
return np.max([0.5 * qm **2, 0.5 * qp **2])
c = 1
dt = 0.05
dx = 0.1
jmax = 21
nmax = 10
q1 = -1
q2 = 1
x, q = init(q1, q2, dx, jmax)
do_computing(x, q, dt, dx, nmax, GORNOV2, interval=2)
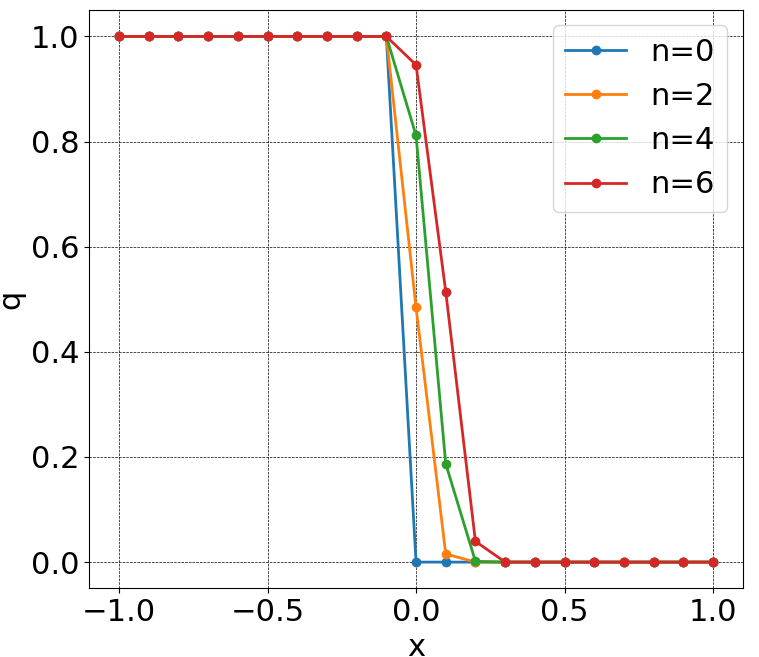
Murman-Cole法で、膨張波を表した④について実行してみましょう。

Godunov法によって、正しく計算できていることがわかると思います。
まとめ
今回は、移流方程式の輸送速度が未知数のとき(Burgers方程式)について、Murman-Cole法とGodunov法の2種類を用いて数値計算してみました。Murman-Cole法から、膨張衝撃波の影響を修正したのがGodunov法でした。
参考文献
藤井孝蔵、立川智章、Pythonで学ぶ流体力学の数値計算法、2020/10/20