お知らせ
Deep Metric Learning（深層距離学習）を使った打突音による異常検知 その2 を公開しました。
はじめに
深層学習、および、深層距離学習を使った各手法で、打突音による異常検知を比較してみました。
参考にさせて頂いた記事の寄せ集めみたいな記事になってしまいました。あしからず。
参考にさせて頂いた記事の著者の皆様に深謝致します。
比較した手法
- オートエンコーダー (AutoEncorder)
- 変分オートエンコーダー (Variational AutoEncorder)
- CNN(浅いNN）
- CNN(Resnet18)
- MetricLearning TripletLoss(浅いNN）
- MetricLearning TripletLoss(Resnet18）
- ArcFace(浅いNN）
- ArcFac(Resnet18）
#手順・概要
手順 1. 正常、及び、異常の木板を打突棒で打突
手順 2. USB接続されたマイクで録音
手順 3. 前処理
手順 4. 各種深層学習手法による訓練
手順 5. 学習したモデルを使って、推論の結果を確認
手順 1. 正常、及び、異常の木板を打突棒で打突
正常と異常の木板を数枚用意します。
木板は、適当なものを近所のホームセンターで購入してカットしてもらいました。
異常な木板には、意図的にヒビや切り込みを入れています。
また、木板のサイズは、少し（数cm程度）ばらつきを持たせています。
正常木板
 |
 |
|---|---|
| 正常木板1（13cm x 20cm) | 正常木板3（13cm x 21.5cm) |
異常木板
 |
 |
|---|---|
| 異常木板5,6（13cm x 19cm) | 異常木板7,8（13cm x 20cm) |
類似正常木板
正常木板、異常木板 その1 とは、材質が少し異なります。（ただし、類似した材質です。）
 |
|
|---|---|
| 類似正常木板11,12（13cm x 19cm) | 類似正常木板（13cm x 20cm) |
打突棒
打突棒は、Amazonで適当なものを購入しました。
https://www.amazon.co.jp/gp/product/B00QQ2J70K/ref=ppx_yo_dt_b_asin_title_o09_s00?ie=UTF8&psc=1
手順 2. USB接続されたマイクで録音
木板の端を打突棒で叩いた音をUSBマイクで録音します。
板によっては、左右の差があるかどうかを見るために、左右それぞれを打突して録音します。
USBマイクもは、Amazonで適当なものを購入しました。
https://www.amazon.co.jp/gp/product/B075PJ7V3V/ref=ppx_yo_dt_b_asin_title_o09_s00?ie=UTF8&psc=1
特に性能で選んだわけでもなく、自立するマイクで、高価でなく、ユーザー評価の高いもの適当に選びました。
録音は、３秒の長さで実施し、wavで保存しています。
録音時には、モノラルになるよう（ステレオにならないよう）注意しています。
（マイクや打突の位置が一定ではないため、ステレオにすると位置に敏感になりすぎて、余計な情報が含まれてしまうため。）
手順 3. 前処理
このままでは、データに余分なものが多く、効率的に学習できないので、前処理をします。
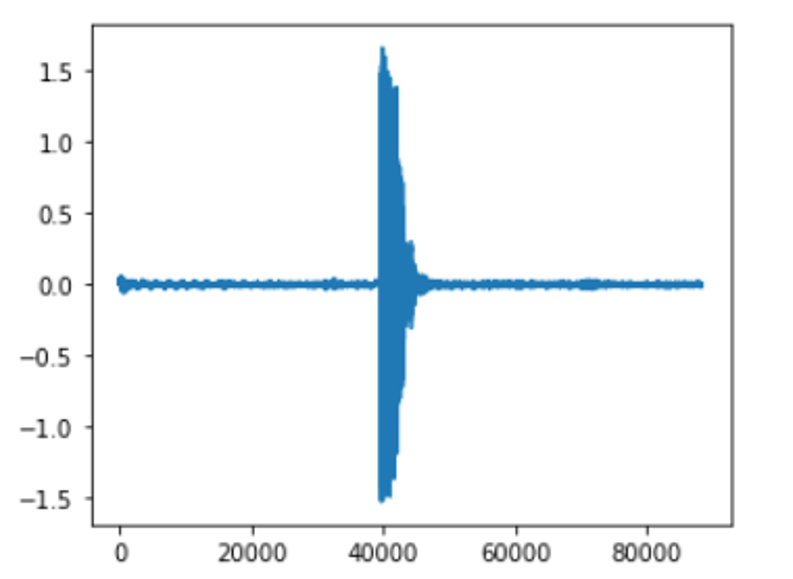上図は、wavをサンプリングして、プロットしただけのものです。（元データだと思って下さい。）
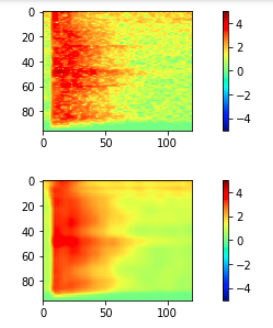
wavをスペクトラム＆対数変換します
x, fs = librosa.load(wavファイルのパス, sr=44100)
stft = np.abs(librosa.stft(x, n_fft=1024, hop_length=128))**2
log_stft = librosa.power_to_db(stft)
plt.figure(figsize=(5,4))
plt.plot(x)
plt.show()
plt.figure(figsize=(20,4))
plt.imshow(log_stft, interpolation='nearest',vmin=-5,vmax=5,cmap='jet')
plt.colorbar()
plt.show()
この時点で、下記のような 1 x 512 x 690 の配列データになります。
（512は周波数領域方向を表し、690は時間方向表します。（つまり、3秒=690列です。） ）
メルスペクトログラムではなく、スペクトログラムを使っています。
（両方試してみましたが、スペクトログラムの方が良い結果が出ました。メルスペクトログラムの性質を考えると、今回のような機械音にはスペクトログラムがいいというのは納得できる結果です。）
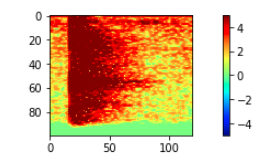
上記の画像を見ると分かる通り、赤枠以外のほとんどの部分は余分なだけでなく、モデルが学習する際に、データのどこに着目して特徴を捉えたらいいかを把握する上での邪魔になるので、必要な部分を残して削除します。
これにより、処理が軽くなる ＋ 訓練精度があがります。
（特徴として捉えて欲しいのは、赤枠の部分です。しかし、この処理をしない場合、赤枠の中が異なっていても、モデルがそれ以外に着目した場合、その部分には違いがないので、違いがないデータとして認識されてしまいやすくなります。）
赤枠の部分だけを切り出し(1 x 512 x 690 => 1 x 100 x 120)、データに正規化（標準化）の処理をします。
正規化には、最小値を0、最大値を1として、すべてを0〜1の範囲に収める正規化と、平均と分散を使って、標準正規分布に変換する標準化がありますが、打突時の強さや、マイクの位置などが一定でないため、音の大きさが毎回変わることや、外れ値の影響を考慮して、標準化にしました。（ちなみに、正規化、標準化といった言葉は、厳密には定義・共通認識化されていないようで、みなさん、かなり色々な意味で使われていますので、上記の正規化、標準化はここだけの定義と思って下さい。）
https://books.google.co.jp/books?id=siB0DwAAQBAJ&pg=PT208&lpg=PT208&dq=%E6%AD%A3%E8%A6%8F%E5%8C%96+%E6%A8%99%E6%BA%96%E5%8C%96+%E7%99%BD%E8%89%B2%E5%8C%96&source=bl&ots=Hd2DPcvZuy&sig=ACfU3U23Mx8jTKlAjvbafZLp0YTvDLMLIQ&hl=ja&sa=X&ved=2ahUKEwiTv-7KpJHoAhXTzIsBHRChCm84ChDoATAAegQICRAB#v=onepage&q=%E6%AD%A3%E8%A6%8F%E5%8C%96%20%E6%A8%99%E6%BA%96%E5%8C%96%20%E7%99%BD%E8%89%B2%E5%8C%96&f=false
https://ja.wikipedia.org/wiki/%E6%A8%99%E6%BA%96%E5%BE%97%E7%82%B9
さらに、切り出す位置を横方向（時間方法）に少しだけずらしたものを別に作り、学習データの数を増やします。（ひとつのwavから、2つずつの学習データを作ります。）
（※3月23日追記）
| 上記と同じ | 左と同じデータで切り出し方を変えたもの |
|---|---|
 |
 |
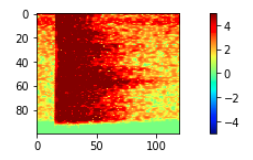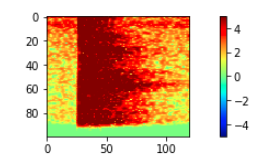（※3月23日追記）
ちなみにに、異常木板のデータは下記のような感じです。
| 異常木板5 | 異常木板6 |
|---|---|
 |
 |
わずかですが、異常木板のデータは、右下のあたりが欠けて、より矢印型のように見えます。
ここまできたら、あとは訓練させるだけです。
手順.4 訓練、および、手順.5 推論
まずは、オートエンコーダーで訓練させてみます。
1. オートエンコーダー
オートエンコーダーとは、入力データから、Encoderと呼ばれるニューラルネットワークを通して、次元数の少ない潜在変数zに変換し、それをDecoderと呼ばれるニューラルネットワークを通して、入力データと同じデータを出力するように訓練させるものです。（出力データが、入力データを再現するよう訓練されたものと言える。）
学習済みのモデルは、訓練データに最適化されているため、訓練データ（正常データ）と異なるデータ（異常データ）が入力された場合は、出力データが、入力データを再現できないという性質を利用して、異常データを検知します。
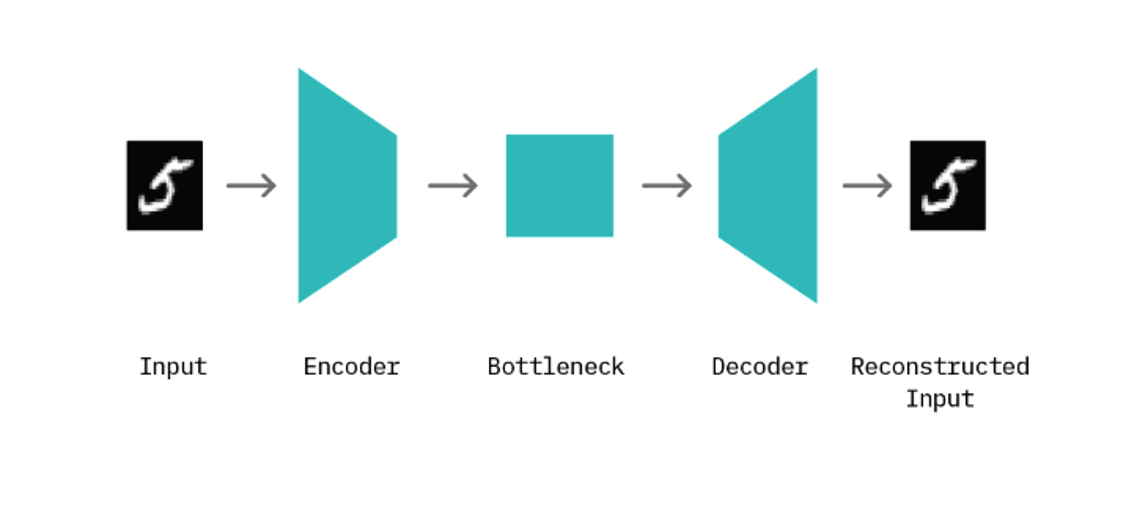
こちらに解説があります。
https://deepage.net/deep_learning/2016/10/09/deeplearning_autoencoder.html
また、実装については、下記を参考にしています。
（というか、そのまま使ってます。）
https://blog.keras.io/building-autoencoders-in-keras.html
####結果
| lr=0.00001, Epc=50 | 同左 |
|---|---|
 |
 |
| 0:正常木板3 1:正常木板3 2:異常木板7 3:異常木板7 紫:異常木板8 |
0:正常木板3 1:正常木板3 その他すべて類似木板 |
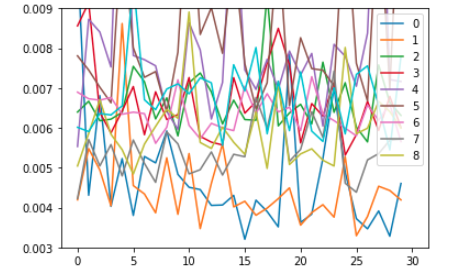
（補足）
同じ木板について、１セット30回の録音（各3秒）を行なっています。
上記の各折れ線グラフ１本が、１セットを表しています。
上記の図では、入力データと出力データの差が、MSEでスカラーとして表現されています。
水平方向は、実施回数を表しており、左端が1回目で右端が３０回目です。
####考察
lrやEpoch数を変えても、ほとんど変化はありませんでした。
正常木板と異常木板の分離がまったくできていません。
（同じ正常木板３同士の差と、正常木板と異常木板の差がほとんど変わりません。）
類似木板についても同様です。
入力データ（下図上）と出力データ（下図下）をみると、出力データはぼやけた感じになっており、細部がまったく再現できていないことが分かります。
2. 変分オートエンコーダー
変分オートエンコーダーは、Encoder、潜在変数z、Decoderを通して、入力データと同じデータを出力するように訓練させるもの、という点ではオートエンコーダーと同じですが、変分オートエンコーダー（VAE）では、潜在変数zが確率分布に従うように訓練していきます。
こちらに素晴らしい解説があります。
https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
また、実装については、下記を参考にしています。
https://qiita.com/fukuit/items/1a9760821b1166aba90c
####結果
| lr=0.00001, Epc=100 | 同左 |
|---|---|
 |
 |
| 0:正常木板3 1:正常木板3 2:異常木板7 3:異常木板7 紫:異常木板8 |
0:正常木板3 1:正常木板3 その他すべて類似木板 |
####考察
lrやEpoch数を変えても、ほとんど変化はありませんでした。
オートエンコーダーと同様に、正常木板と異常木板の分離がまったくできていません。
（同じ正常木板３同士の差と、正常木板と異常木板の差がほとんど変わりません。）
類似木板についても同様です。
こちらも、入力データ（下図上）と出力データ（下図下）をみると、出力データはぼやけた感じになっており、細部がまったく再現できていないことが分かります。
3. CNN(浅いNN）
次は、浅いNNを使った通常のCNNで訓練させてみます。
ここからは、pytorch を使います。
モデルは下記の通りです。
50クラスの分類にしているので、最終層は50次元になっています。
（たくさんの枚数の木板を、さらにたたく場所を変えて試しているので、手っ取り早く50クラスの分類にしてしまいました。。。）
可視化のために出力層の手前で2次元にしたあとで、分類のために50次元にしています。
（ちなみに、2次元を50次元に変えて、ボトルネックを作らないやり方も試しましたが、精度は上がりませんでした。）
ClassificationNet(
(embedding_net): EmbeddingNet(
(convnet): Sequential(
(0): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1))
(1): PReLU(num_parameters=1)
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(32, 32, kernel_size=(3, 3), stride=(1, 1))
(4): PReLU(num_parameters=1)
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1))
(7): PReLU(num_parameters=1)
(8): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(9): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1))
(10): PReLU(num_parameters=1)
(11): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(12): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1))
(13): PReLU(num_parameters=1)
(14): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(fc): Sequential(
(0): Linear(in_features=64, out_features=64, bias=True)
(1): PReLU(num_parameters=1)
(2): Linear(in_features=64, out_features=32, bias=True)
(3): PReLU(num_parameters=1)
(4): Linear(in_features=32, out_features=2, bias=True)
)
)
(nonlinear): PReLU(num_parameters=1)
(fc1): Linear(in_features=2, out_features=50, bias=True)
)
####結果
| Lr = 0.01, Epc = 30 | Lr = 0.01, Epc = 100 | Lr = 0.01, Epc = 200 |
|---|---|---|
 |
 |
 |
|Lr = 0.001, Epc = 100|Lr = 0.1, Epc = 200|
|---|---|---|
|
|
|
（補足）
同じ木板について、１セット30回の録音（各3秒）を行なっています。
ただし、オートエンコーダーのときと違い、２次元空間での表現となっており、また、入力データと出力データの誤差を表しているわけでもありません。（小さいからいいというわけではないし、そもそも出力が入力を再現しようとしているわけではない。）
単純に入力データを特徴ベクトル化して表示しているだけです。
各点が、それぞれの録音回を表しており、各セットについて、30個の点があります。
同じ木板を複数セット録音しているものは、セット数 x 30個の点があります。
####考察
水色が正常木板１と正常木板３で、茶色が異常木板５（左端）、黄土色が異常木板５（右端）です。
エポック100ぐらいで収束するが、たいして精度がいいとは言えない。（クラス間の分離ができていない）
学習率を変えてもたいして変化なし。optimizer は Adam です。
4. CNN(Resnet18）
次は、Resnet18ベースの（通常の）CNNで訓練させてみます。
同じく、pytorch を使います。
モデルは下記の通りです。
50クラスの分類なので、最終層は50次元になっています。
tSNEで２次元にして、可視化しています。
（入力データのは、他と同じく 1 x 100 x 120 です。）
ResNetWood(
(conv1): Conv2d(1, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(layer1): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(64, 64, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer2): Sequential(
(0): BasicBlock(
(conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer3): Sequential(
(0): BasicBlock(
(conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(layer4): Sequential(
(0): BasicBlock(
(conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): BasicBlock(
(conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(fc5): Linear(in_features=28672, out_features=512, bias=True)
(fc6): Linear(in_features=512, out_features=50, bias=True)
)
####結果
（tSNEで次元削減して可視化しているので、実行のたびに形が変わります。）
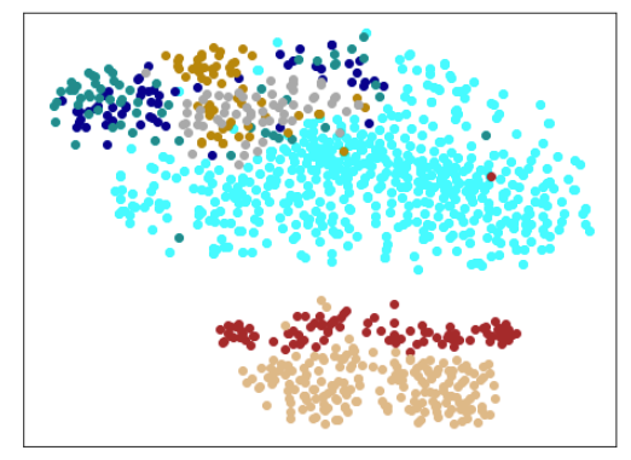
| Lr = 0.001, Epc = 300, SGD, CrossEntropyLoss | 同左 | 同左 |
|---|---|---|
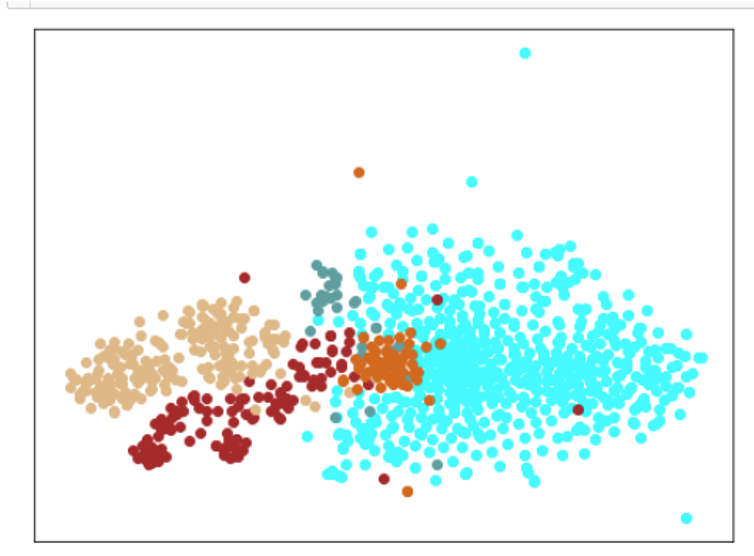
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
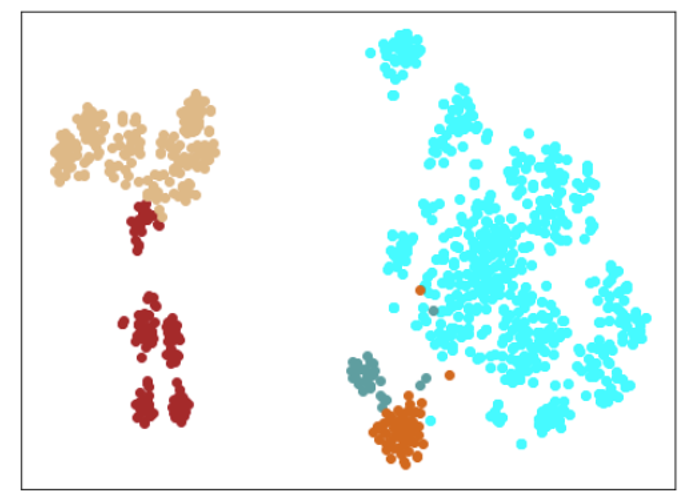
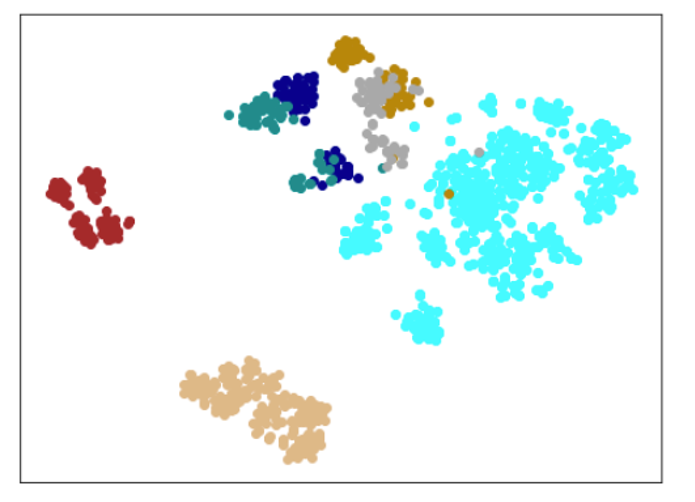
| Lr = 0.01, Epc = 100, SGD, CrossEntropyLoss | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
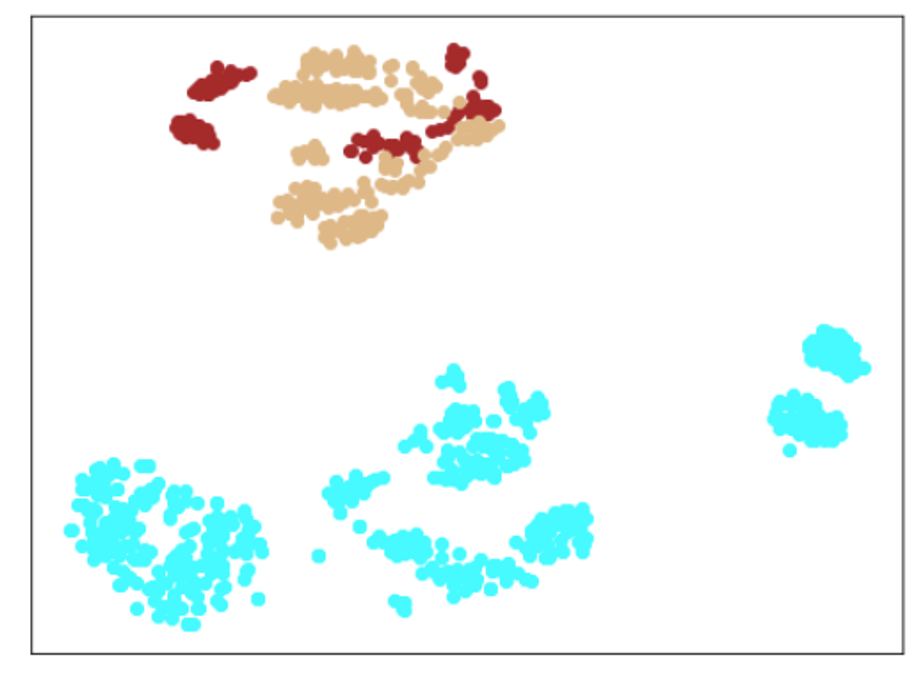
| Lr = 0.01, Epc = 100, SGD, FacalLoss | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
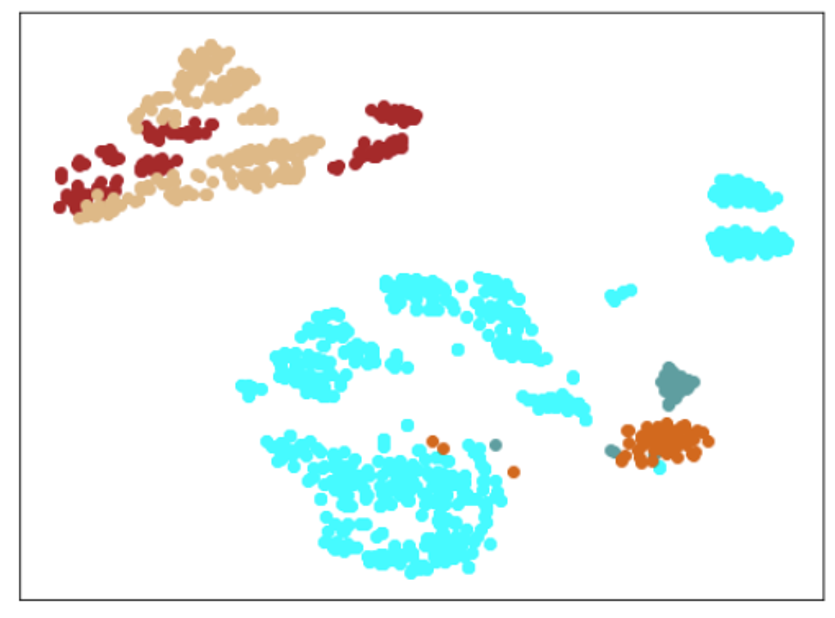| 学習データ | 異常木板7,8 | 類似木板 |
|---|---|---|
| 水色 - 正常木板１と正常木板３ 茶色 - 異常木板５（左端） 黄土色 - 異常木板6（右端） |
灰青色 - 異常木板7 明るい茶色 - 異常木板8 |
上記以外の色全て |
####考察
学習率(lr)は、0.001では小さすぎる。0.01ぐらいが良さそうだ。（ちなみに、0.1にすると収束しない。）
損失関数は、CrossEntropyLossでも、FacalLossでも大きな違いは見られなかった。
すべてのクラスを分離できているが、すべての木板をそれぞれ個別に別のものと認識しているだけで、期待するような正常、異常の特徴を捉えているとは言い難い。入力データがそれほど大きくないことや、NNの大きさを考えると過剰適応（過剰学習）しているように思える。
5. TripletLoss(浅いNN）
ここからいよいよメトリックラーニングになります。
メトリックラーニングは、同じラベルを持つもの（類似しているもの）が、ニューラルネットワークを通して生成される特徴次元空間（埋め込み空間）において、距離（ユークリッド、マハラノビス）や角度が近く配置されるように訓練するものです。
（特徴次元空間において、意味の近いデータは近く、意味の遠いデータは遠くなるよう学習されたモデル）
下記に素晴らしい解説があります。
https://copypaste-ds.hatenablog.com/entry/2019/03/01/164155
https://cpp-learning.com/metric-learning/
出典： https://vision.cornell.edu/se3/embeddings-and-metric-learning/
その中でも、ここでは、TripletLossを使います。
TripletLossの特徴は、特徴次元空間にマッピングされたデータに対し、同じラベルのデータは近くに、異なるラベルのデータは遠くになるよう学習していくことです。
具体的には、Anchorと呼ばれるデータに対し、同一ラベルのpositiveなデータと、異なるラベルのnegativeなデータを選択し、positiveなデータはAnchorに対し近くに、negativeなデータは遠くになるように学習するという処理を繰り返し行なっていきます。
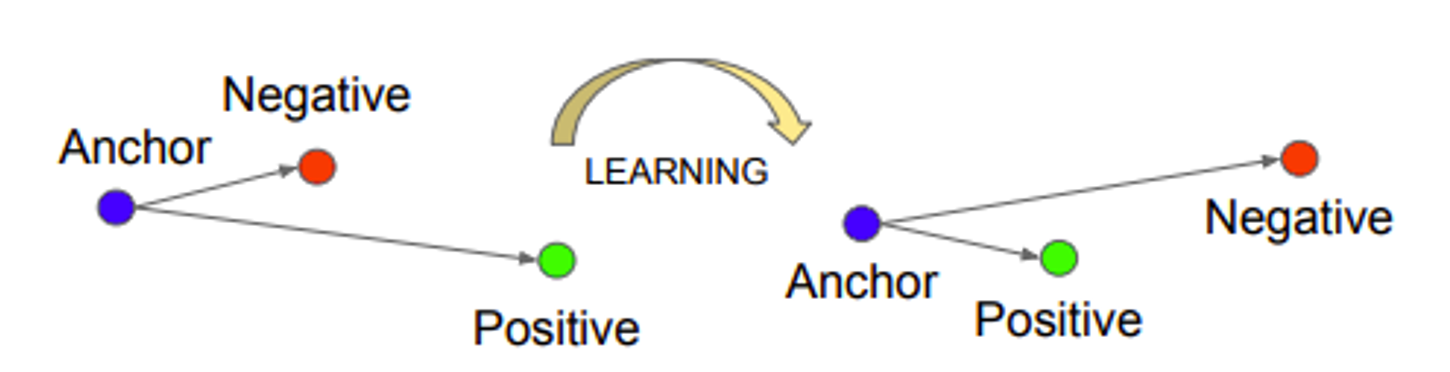
ここに素晴らしい解説があります。
https://qiita.com/tancoro/items/35d0925de74f21bfff14
実装については、pytorchで、下記を参考にさせて頂きました。
（というより、ほとんどそのまま使っています。）
https://github.com/adambielski/siamese-triplet
では、まずは、TripletLoss(浅いNN）で訓練させてみます。
（浅いNNは、上記のものとほとんど同じですが、最後の２次元を50次元に変換する層を削除しています。）
####結果
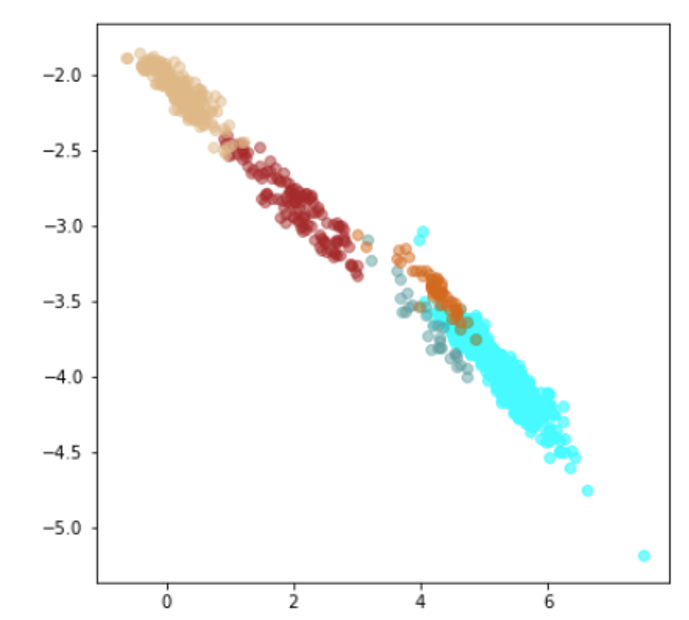
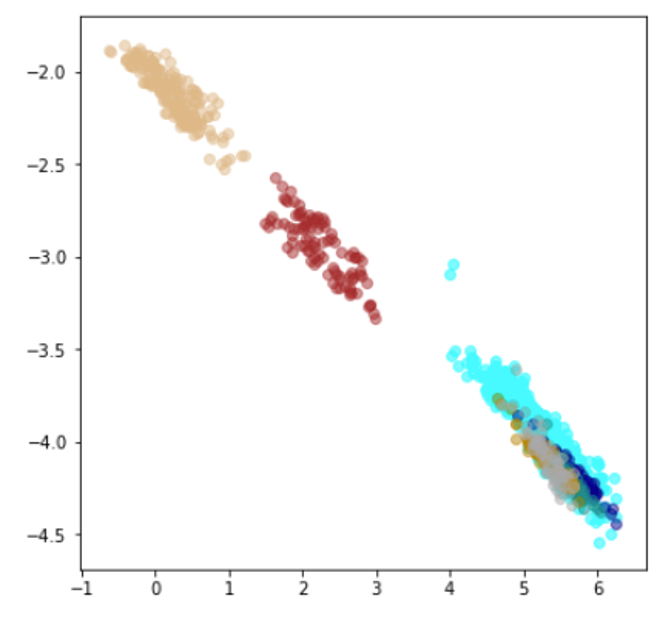
| Lr = 0.01, Epc = 100, Adam, MSE | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
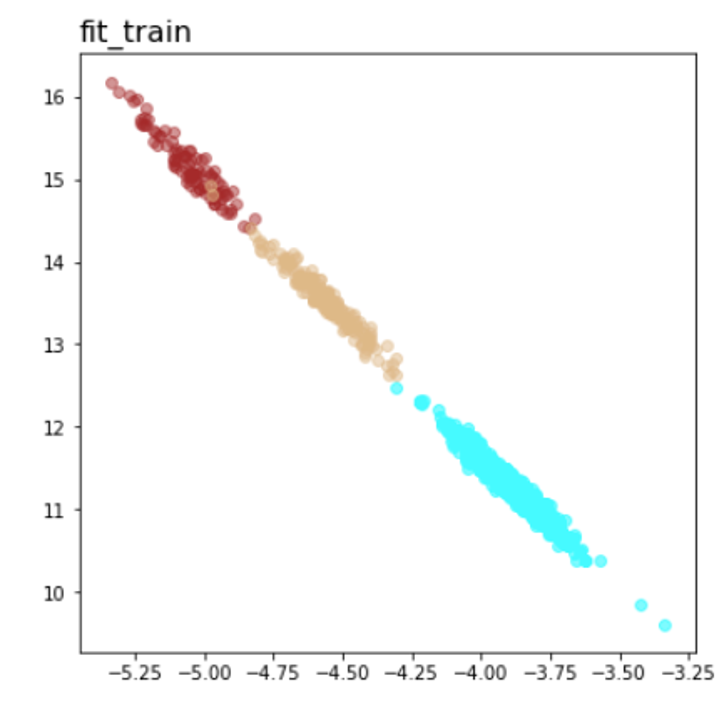
| Lr = 0.001, Epc = 100, Adam, MSE | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
| 学習データ | 異常木板7,8 | 類似木板 |
|---|---|---|
| 水色 - 正常木板１と正常木板３ 茶色 - 異常木板５（左端） 黄土色 - 異常木板6（右端） |
灰青色 - 異常木板7 明るい茶色 - 異常木板8 |
上記以外の色全て |
####考察
学習データの分離はよくできています。
訓練に使用していない異常木板7、8を推論にかけた際に、正常より少しはずれているという認識はしているものの、異常と判定するのは難しい程度の違いしか認識できていない（正常の一部に見える）。ただ、異常木板7の異常度は、異常木板8より小さい（異常木板7はほぼ正常）と判定している点が面白い。異常木板7と8は一枚の木板の左端と右端で叩く位置を変えているだけですが、切り込みが板の右側（異常木板8側）のみにあることを考えると、その違いを認識しているように見えます。
さらに、材質がわずかに異なる木板（ヒビや切り込みはなし）については、正常と判断しており、さらに、（正常の中でも）異常から離れた位置に配置されています。
かなり、期待通りの結果となっています。
6. TripletLoss(Resnet18）
では、Resnet18をベースにした TripletLossで訓練させてみます。
（上記のResnet18の最終層を２次元にしています。）
####結果
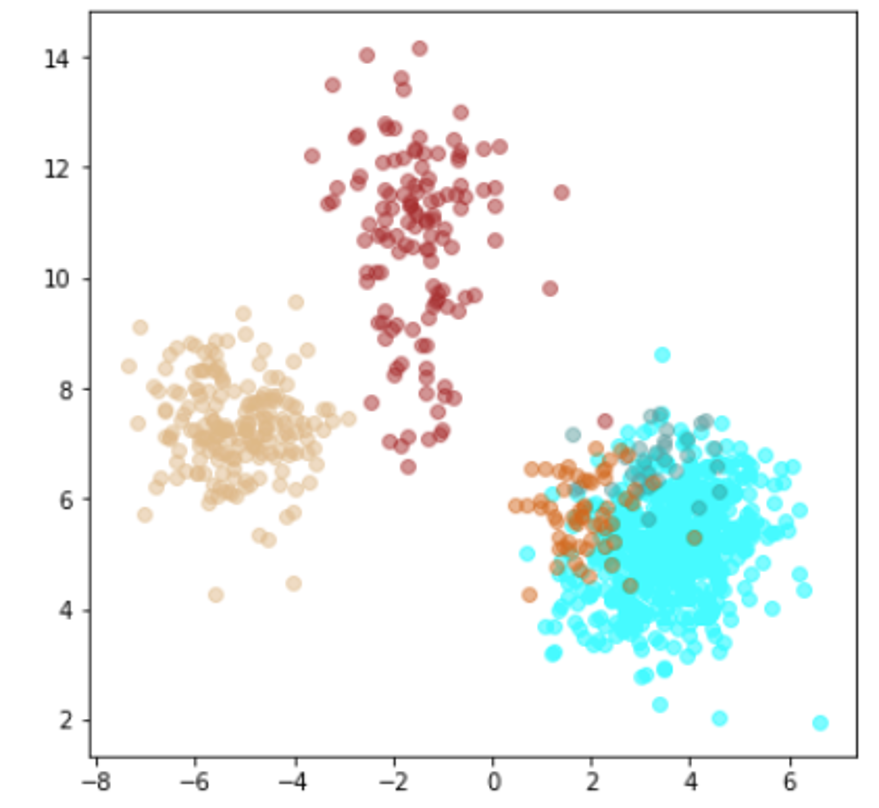
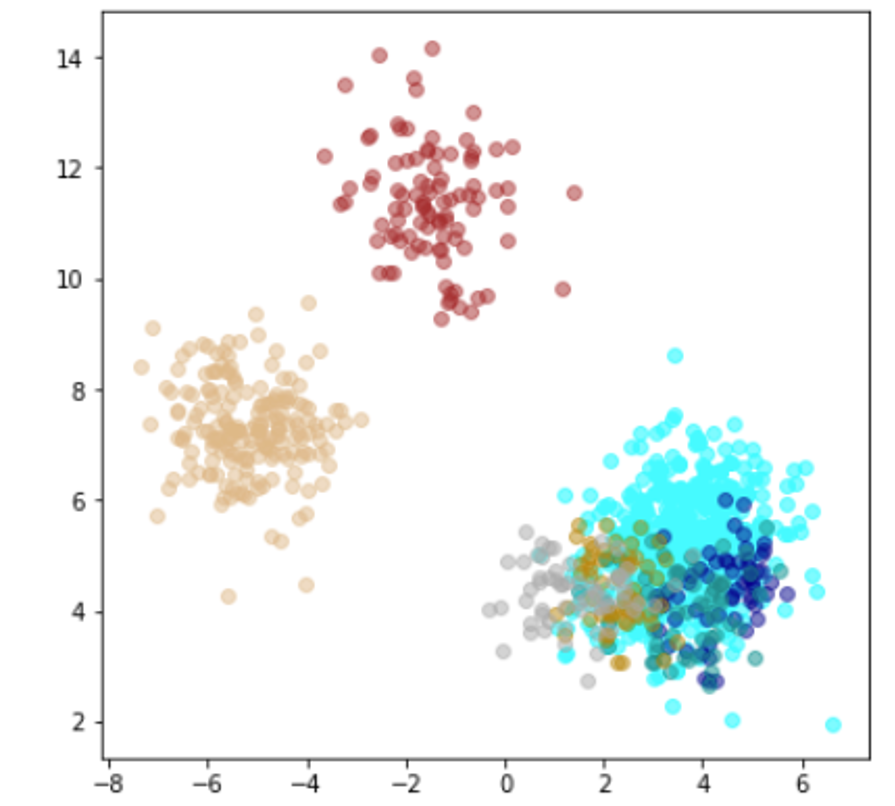
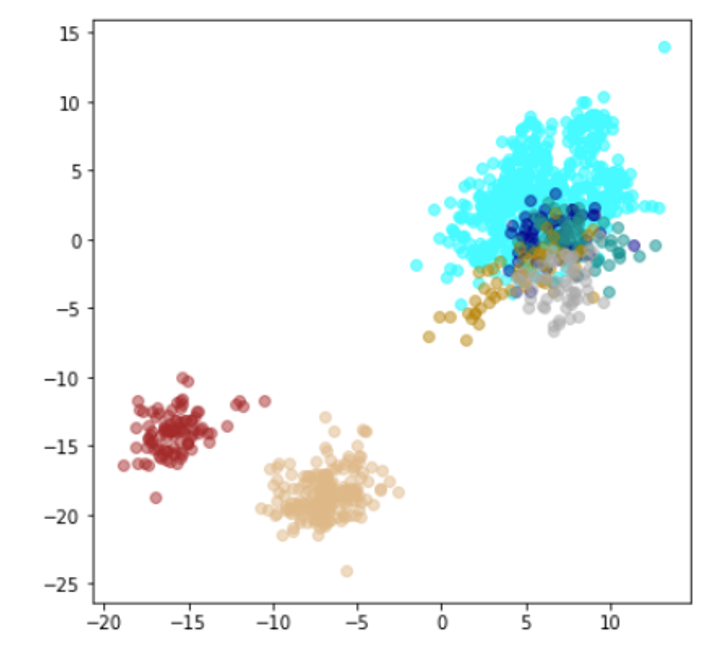
| Lr = 0.0005, Epc = 15, Adam, MSE | 同左 |
|---|---|
| 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
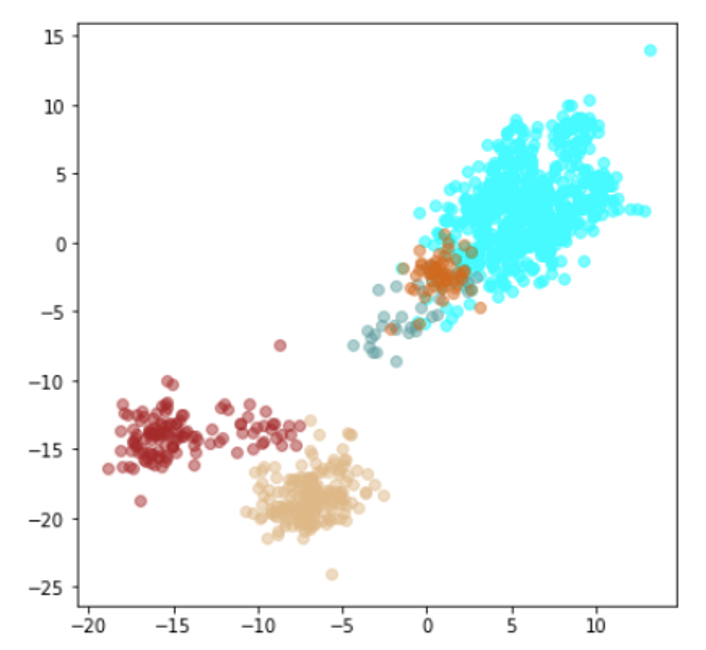
| Lr = 0.001, Epc = 20, Adam, MSE | 同左 |
|---|---|
| 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
| Lr = 0.003, Epc = 20, Adam, MSE | 同左 |
|---|---|
| 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
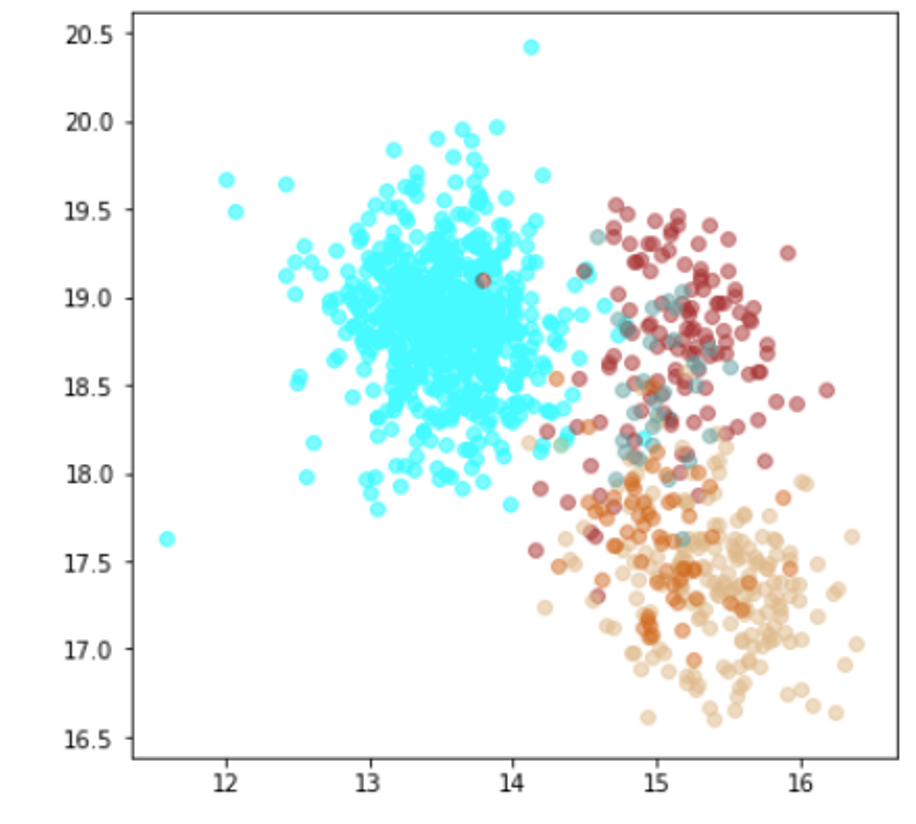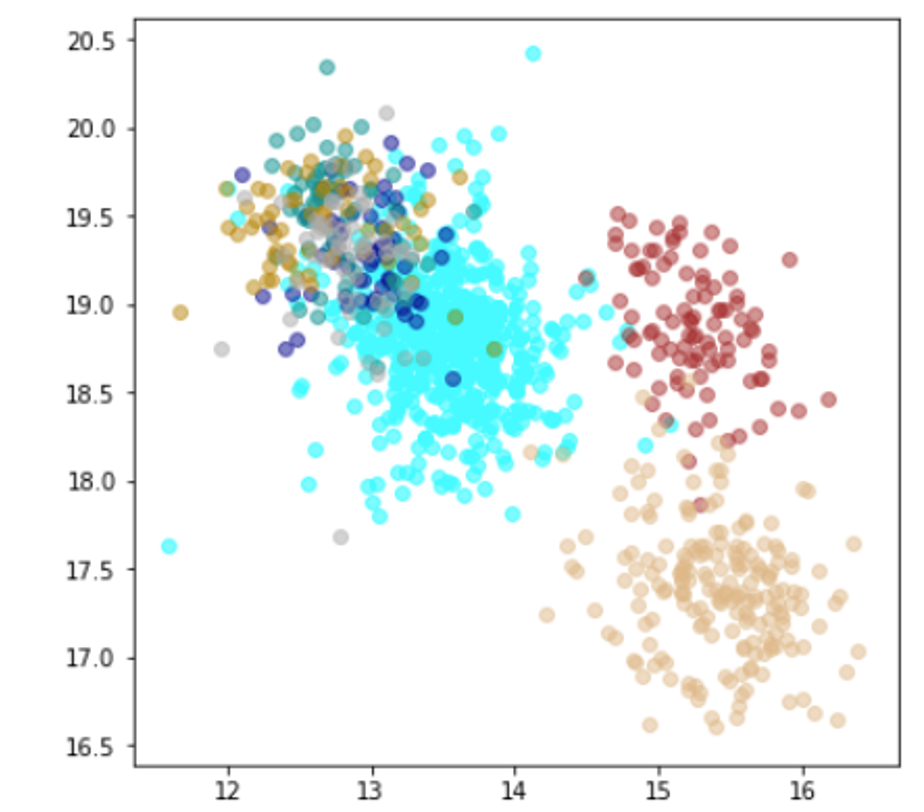| 学習データ | 異常木板7,8 | 類似木板 |
|---|---|---|
| 水色 - 正常木板１と正常木板３ 茶色 - 異常木板５（左端） 黄土色 - 異常木板6（右端） |
灰青色 - 異常木板7 明るい茶色 - 異常木板8 |
上記以外の色全て |
####考察
学習データの分離はよくできてます。
ただ、訓練に使用していない異常木板7、8の推論では、異常であることをまったく識別できていません。
材質がわずかに異なる類似木板（ヒビや切り込みはなし）については、正常と判断していますが、異常木板7、8も同じような位置に配置されているため、意味のある推論になっているかが不明です。
ただし、Resnet18とTripletLossの相性が悪いのか、私の実装力不足なのかが分かりません。（後者のような気が、強くします。）
そのため、このモデルについては、判断を保留とします。
7. ArcFace(浅いNN）
次は、ArcFaceを使います。
ArcFaceの特徴は、CNNからの特徴ベクトルxが、L2正規化されることで、一様分布に近い出力を出そうとすることを防ぎ、さらに、全結合層の重みWについても、列ごとにL2正規化されることで、角度を使って類似度を算出しています。また、ペナルティマージンにも独特の工夫があります。
下図を見ると、他の手法とのペナルティマージンの考え方の違いがよく分かります。
下記にすばらしい解説があります。
https://qiita.com/yu4u/items/078054dfb5592cbb80cc
では、まずは、ArcFace(浅いNN）で訓練させてみます。
実装は、pytorchで、下記を参考にさせて頂きました。
（これまた、ほとんどそのまま使っています。）
https://github.com/ronghuaiyang/arcface-pytorch
（ちなみに、上記のResnet18も、ここの実装をほとんどそのまま使っています。）
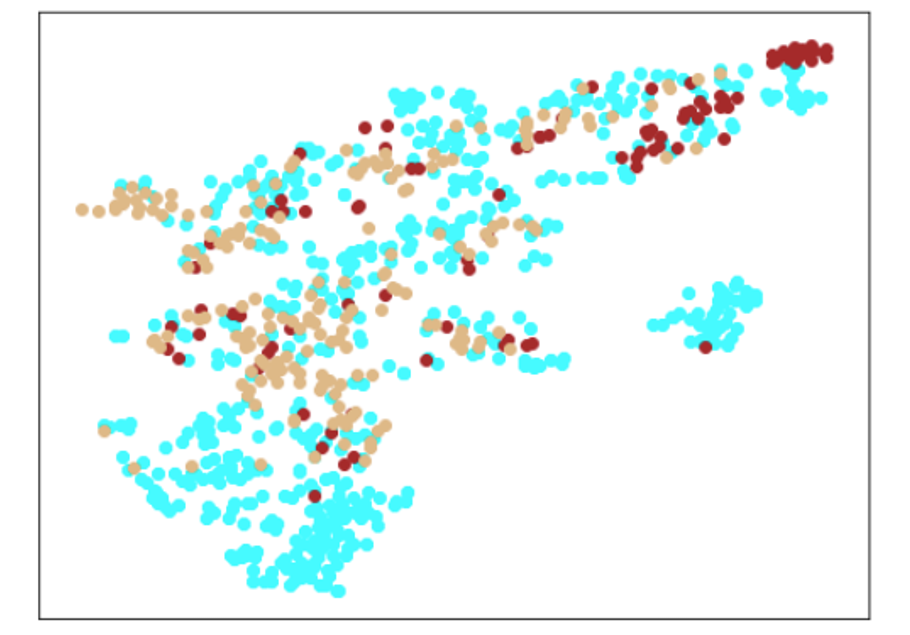
####結果
|Lr = 0.001, Epc = 100, SGD, CrossEntropyLoss|Lr = 0.001, Epc = 200, SGD, CrossEntropyLoss|
|---|---|---|
|学習データのみ|学習データのみ|
|
|
|
| Lr = 0.003, Epc = 10, SGD, CrossEntropyLoss | Lr = 0.005, Epc = 100, SGD, CrossEntropyLoss |
|---|---|
| 学習データのみ | 学習データのみ |
 |
 |
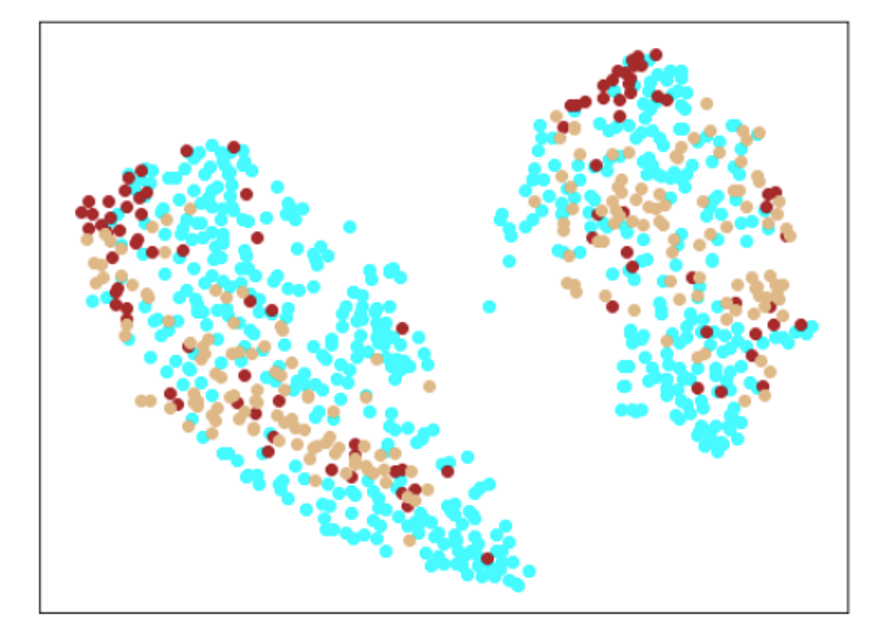|学習データ|
|---|---|
|水色 - 正常木板１と正常木板３
茶色 - 異常木板５（左端）
黄土色 - 異常木板6（右端）|
####考察
学習率は、0.001が良さそうです。学習率0.003（または、0.005）でエポック数10以上や、それ以上の学習率だと収束しません。
学習データのみを見ても分離もまったくできておらず、あまりいいモデルではないようです。
8. ArcFace(Resnet18）
続いて、ArcFace(Resnet18）で訓練させてみます。
実装は、pytorchで、同じく下記を参考にさせて頂きました。
（ますます、ほとんどそのまま使っています。）
https://github.com/ronghuaiyang/arcface-pytorch
####結果
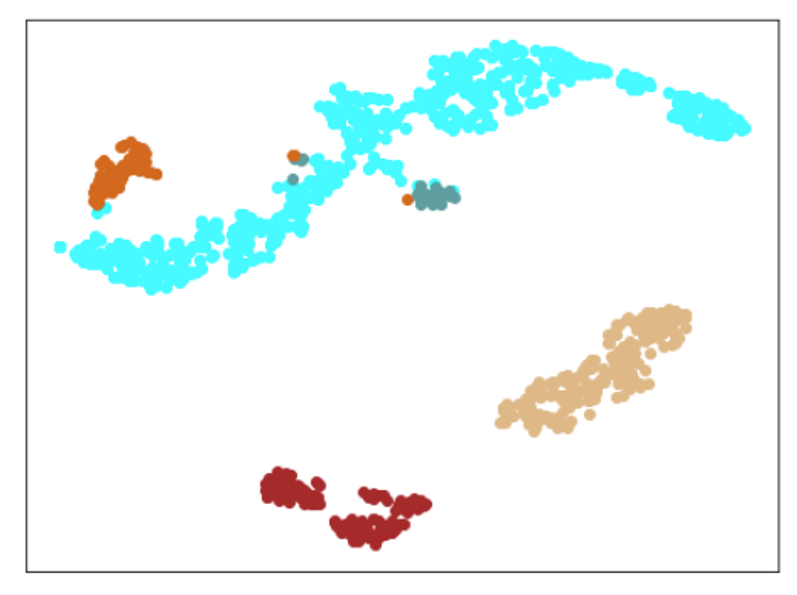
| Lr = 0.01, Epc = 100, SGD, CrossEntropyLoss | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
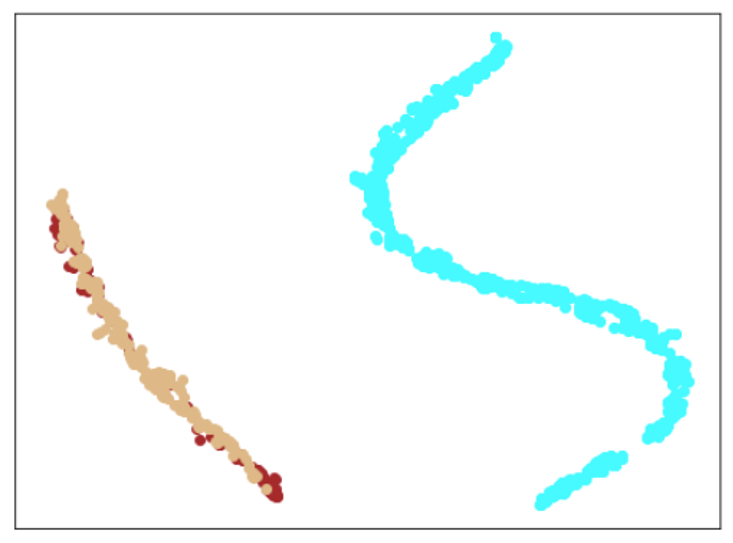
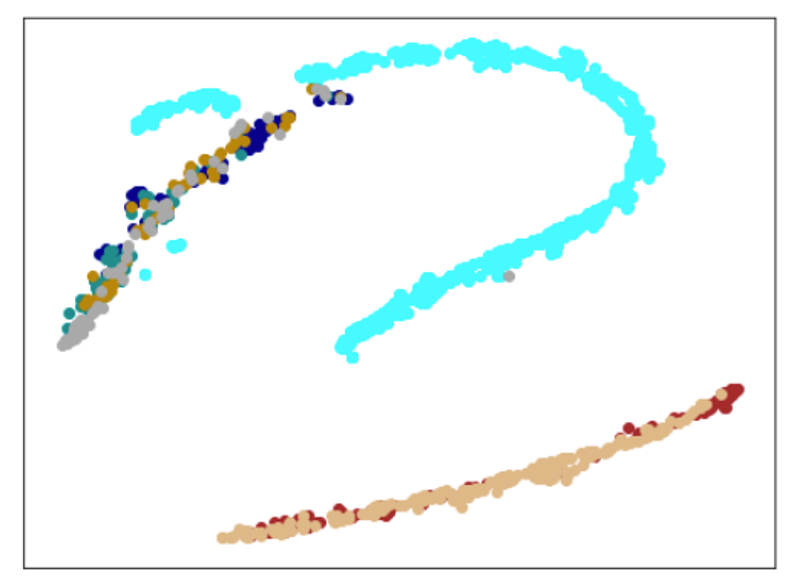
| Lr = 0.05, Epc = 100, SGD, CrossEntropyLoss | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
| Lr = 0.01, Epc = 100, SGD, FacalLoss | 同左 | 同左 |
|---|---|---|
| 学習データのみ | 学習データ+異常木板7,8 | 学習データ+類似木板 |
 |
 |
 |
| 学習データ | 異常木板7,8 | 類似木板 |
|---|---|---|
| 水色 - 正常木板１と正常木板３ 茶色 - 異常木板５（左端） 黄土色 - 異常木板6（右端） |
灰青色 - 異常木板7 明るい茶色 - 異常木板8 |
上記以外の色全て |
####考察
ここで驚くべきことが起きました。
学習データで、正常と異常をきちんと分離できたのはもちろんですが、訓練に使用していない異常木板7、8を推論にかけた際に、正常とは異なることを認識しているものの、異常木板7の異常度は、異常木板8より小さい（異常木板7は正常に近い）と判定しているように見えます。
異常木板7と8は一枚の木板の左端と右端で叩く位置を変えているだけですが、切り込みが板の右側（異常木板8側）のみにあることを考えると、その違いを認識しているように見えます。
さらに、材質がわずかに異なる類似木板（ヒビや切り込みはなし）については、正常と判断しています。
ある意味、理想としていた結果となっています。
（本当にそのように解釈できるのかは、これからさらに検証する必要があります。）
##総論
Resnet18単体の性能が非常によかったのが驚きでした。
現時点では、Resnet18ベースのArcFaceが最も性能が良さそうです。
その次は、浅いNNベースのTripletLossでした。
ただ、TripletLossは、学習データでは、しっかり認識できていても、非常に類似したテストデータでは、学習データと異なる（期待と異なる）結果になることが度々ありました。
その点、Resnet18ベースのArcFaceは非常に安定していて、学習データで認識したものは、テストデータでもしっかり認識しているような印象を受けました。（あくまで、根拠のない勝手な印象ですが。。。）
角度ベースで行なっていることや、TripletLossのように個々のデータに対し個別の処理を行なっているわけではないことなどが影響しているのかも知れません。
まだまだ、勉強が必要です。
ここまでお読み頂き有り難うございました。
（参考URL）
https://deepage.net/deep_learning/2016/10/09/deeplearning_autoencoder.html
https://blog.keras.io/building-autoencoders-in-keras.html
https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
https://qiita.com/fukuit/items/1a9760821b1166aba90c
https://copypaste-ds.hatenablog.com/entry/2019/03/01/164155
https://cpp-learning.com/metric-learning/
https://vision.cornell.edu/se3/embeddings-and-metric-learning/
https://qiita.com/tancoro/items/35d0925de74f21bfff14
https://github.com/adambielski/siamese-triplet
https://qiita.com/yu4u/items/078054dfb5592cbb80cc
https://github.com/ronghuaiyang/arcface-pytorch
https://qiita.com/cvusk/items/61cdbce80785eaf28349
https://qiita.com/shinmura0/items/858214154f889c05e4f4
https://qiita.com/gesogeso/items/547079f967d9bbf9aca8
参考URLの著者の皆様、本当に有り難うございます。