Go to Qiita Advent Calendar 2024 Top
LoginSignup
238
230

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@cvusk

ディープラーニングで音声分類

Last updated at Posted at 2018-05-13

ディープラーニングで音声分類

勉強がてらディープラーニングで環境音・自然音の分類をやってみました。
データセットはESC-50を使用します。

コード全文。

やったこと

環境音・自然音をConvolutional neural networkで分類します。
対象は動物の鳴き声や雨の音、人間の咳、時計のアラーム、エンジン音のような声（言葉）のない音です。

これらの音を使って、以下の手順で分類器をつくりました。

  1. 音声データの前処理
    2. データの入手
    3. Augmentation
    4. メルスペクトログラム
    5. データの用意
  2. CNNで分類
    1. CNNの定義
    2. 最適化関数にAmsgradを採用
    3. 学習データにmixupを採用

音声データの前処理

ESC-50は環境音を50クラス、2,000ファイル集めたデータセットです。
クラスには以下があります。

0.PNG

50クラスで各クラスのデータが40ファイルずつ用意されており、合計2,000ファイルです。
1ファイルの長さは5秒、サンプリングレートは44,100です。

データの入手

データは以下からダウンロードできます。
https://github.com/karoldvl/ESC-50

中身は音声データ（.wav）とメタデータ（.csv）です。
メタデータにはファイル名とクラス（0-49）、クラス名（上記テーブル参照）が入っています。

音声データ（.wav）はlibrosaというライブラリでロードすることでnumpy.arrayとして扱えるようになります。

以下でメタデータをロードし、データセットの一覧を取得します。


import os
import random
import numpy as np
import pandas as pd
import librosa
import librosa.display
import matplotlib.pyplot as plt
import seaborn as sn
from sklearn import model_selection
from sklearn import preprocessing
import IPython.display as ipd

# define directories
base_dir = "./"
esc_dir = os.path.join(base_dir, "ESC-50-master")
meta_file = os.path.join(esc_dir, "meta/esc50.csv")
audio_dir = os.path.join(esc_dir, "audio/")

# load metadata
meta_data = pd.read_csv(meta_file)

# get data size
data_size = meta_data.shape
print(data_size)

# arrange target label and its name
class_dict = {}
for i in range(data_size[0]):
    if meta_data.loc[i,"target"] not in class_dict.keys():
        class_dict[meta_data.loc[i,"target"]] = meta_data.loc[i,"category"]

次はwavデータをロードして波形データおよびメルスペクトログラムを描画します。

# load a wave data
def load_wave_data(audio_dir, file_name):
    file_path = os.path.join(audio_dir, file_name)
    x, fs = librosa.load(file_path, sr=44100)
    return x,fs

# change wave data to mel-stft
def calculate_melsp(x, n_fft=1024, hop_length=128):
    stft = np.abs(librosa.stft(x, n_fft=n_fft, hop_length=hop_length))**2
    log_stft = librosa.power_to_db(stft)
    melsp = librosa.feature.melspectrogram(S=log_stft,n_mels=128)
    return melsp

# display wave in plots
def show_wave(x):
    plt.plot(x)
    plt.show()

# display wave in heatmap
def show_melsp(melsp, fs):
    librosa.display.specshow(melsp, sr=fs)
    plt.colorbar()
    plt.show()

# example data
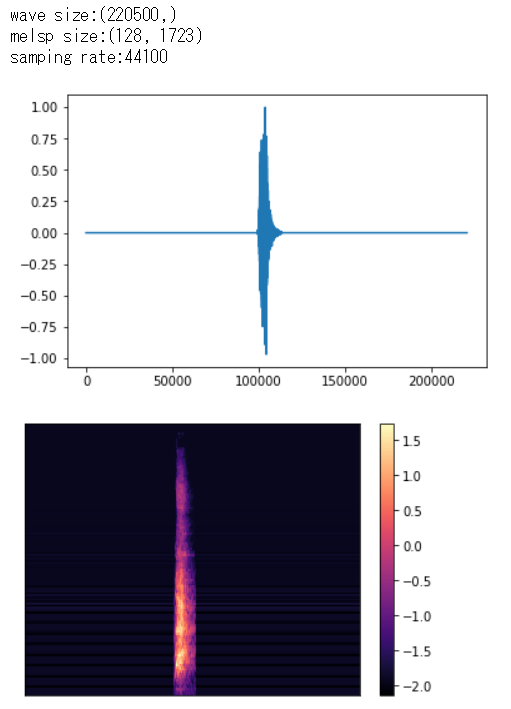
x, fs = load_wave_data(audio_dir, meta_data.loc[0,"filename"])
melsp = calculate_melsp(x)
print("wave size:{0}\nmelsp size:{1}\nsamping rate:{2}".format(x.shape, melsp.shape, fs))
show_wave(x)
show_melsp(melsp, fs)

以下のように出力されます。

7.PNG

Augmentation

画像分類同様、音声データもAugmentationして水増しします。
Augmentation手法はここを参考にしています。

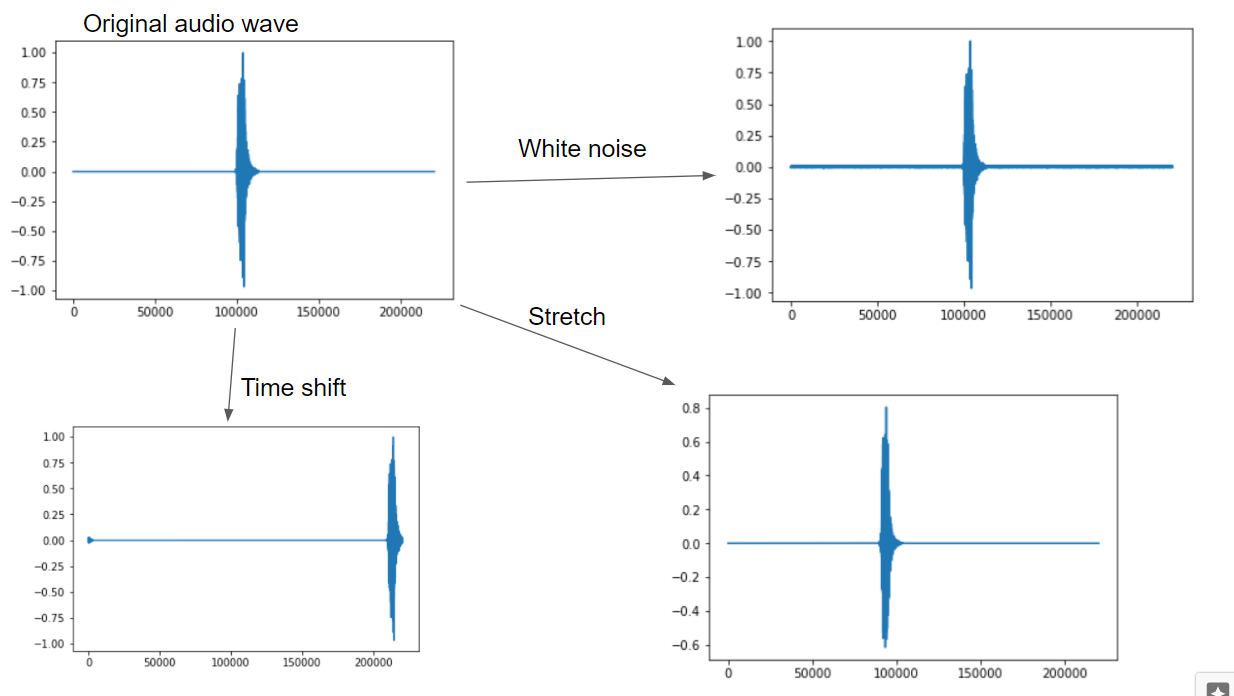
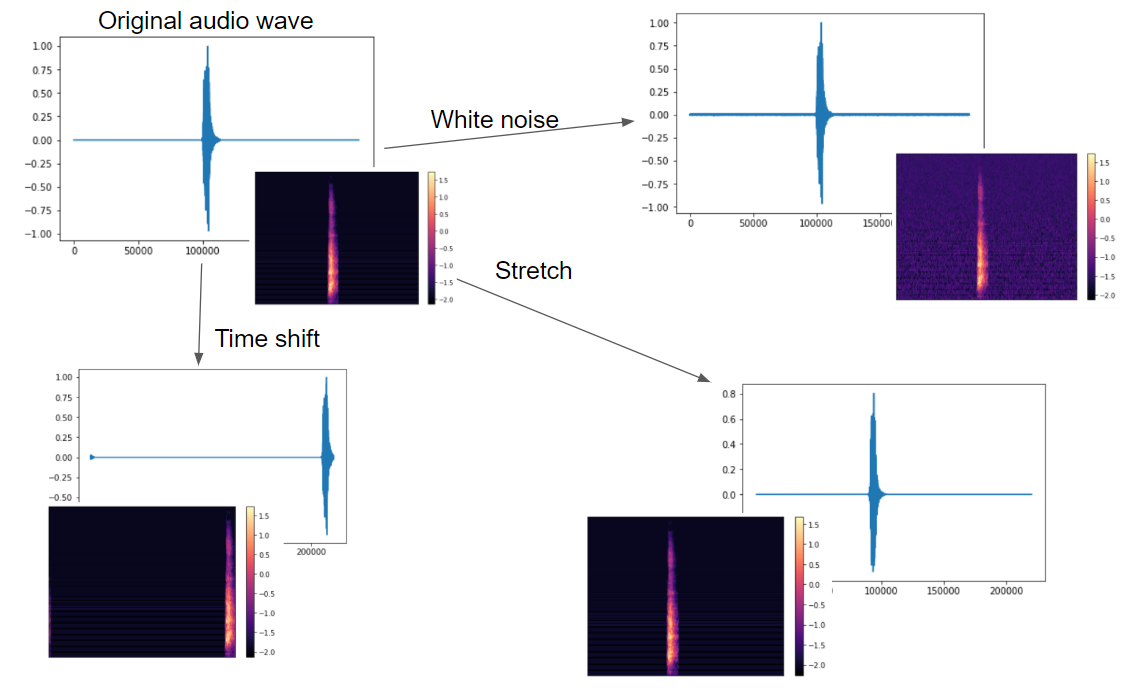
今回は音声データにホワイトノイズ、シフト、ストレッチを加えています。

以下は犬の鳴き声をもとに、Augmentationをかけた波データです。

1.PNG

Augmentationのコードです。


# data augmentation: add white noise
def add_white_noise(x, rate=0.002):
    return x + rate*np.random.randn(len(x))

# data augmentation: shift sound in timeframe
def shift_sound(x, rate=2):
    return np.roll(x, int(len(x)//rate))

# data augmentation: stretch sound
def stretch_sound(x, rate=1.1):
    input_length = len(x)
    x = librosa.effects.time_stretch(x, rate)
    if len(x)>input_length:
        return x[:input_length]
    else:
        return np.pad(x, (0, max(0, input_length - len(x))), "constant")

メルスペクトログラム

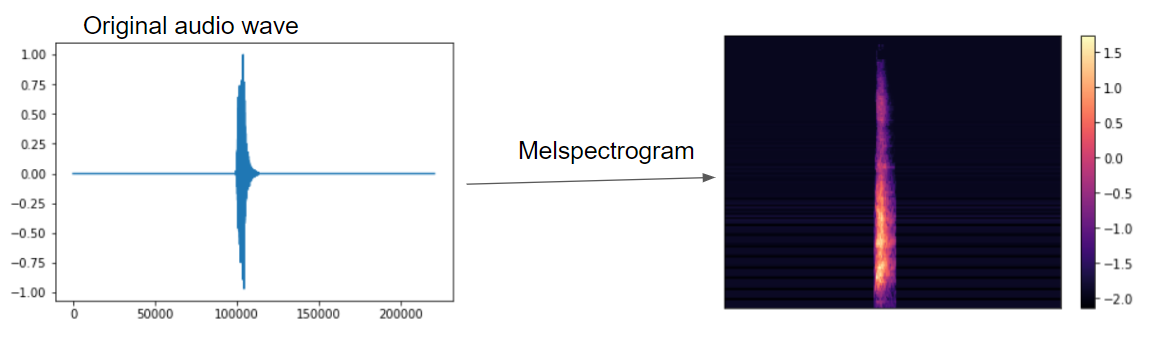
wavデータ自体は1次元の時系列データです。
これをメル周波数のフィルタバンクをかけてメルスペクトログラムを得ます。
これはlibrosa.feature.melspectrogramで取得できます。


import librosa
import librosa.display

# change wave data to mel-stft
def calculate_melsp(x, n_fft=1024, hop_length=128):
    stft = np.abs(librosa.stft(x, n_fft=n_fft, hop_length=hop_length))**2
    log_stft = librosa.power_to_db(stft)
    melsp = librosa.feature.melspectrogram(S=log_stft,n_mels=128)
    return melsp

上記同様、犬の鳴き声にメル周波数をかけたメルスペクトログラムは以下になります。

2.PNG

波データのAugmentationとメルスペクトログラムをそれぞれ並べると以下になります。

3.PNG

参考

https://qiita.com/martin-d28jp-love/items/34161f2facb80edd999f
http://r9y9.github.io/blog/2013/11/16/mel-spectrogram/
http://blog.brainpad.co.jp/entry/2018/04/17/143000#%E3%83%A1%E3%83%AB%E5%B0%BA%E5%BA%A6%E5%91%A8%E6%B3%A2%E6%95%B0

データの用意

というわけで、wavデータをAugmentationしてメルスペクトログラムにしたものを分類器の入力データとします。
前処理として全wavファイルをAugmentation、メルスペクトログラムにしたものを用意しておきます。

まずは学習データとテストデータを分割します。
テストデータは25％とし、stratify=yとすることで各クラスを均等に分割します。


# get training dataset and target dataset
x = list(meta_data.loc[:,"filename"])
y = list(meta_data.loc[:, "target"])

x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.25, stratify=y)
print("x train:{0}\ny train:{1}\nx test:{2}\ny test:{3}".format(len(x_train),
                                                                len(y_train), 
                                                                len(x_test), 
                                                                len(y_test)))

"""output
x train:1500
y train:1500
x test:500
y test:500
"""

# showing the classes are equally splitted
a = np.zeros(50)
for c in y_test:
    a[c] += 1
print(a)

"""output
[10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10.
 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10.
 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10.]
"""

学習データ、テストデータともにまとめてnpzにして保存おきます。
学習データはさらにホワイトノイズ、シフト、ストレッチ、それらの組合せをかけて、別に保存します。
結果として以下のデータがnpz形式で用意されます。

  • テストデータのメルスペクトログラム（500点）
  • 学習データのメルスペクトログラム（1,500点）
  • ホワイトノイズののった学習データのメルスペクトログラム（1,500点）
  • シフトされた学習データのメルスペクトログラム（1,500点）
  • ストレッチされた学習データのメルスペクトログラム（1,500点）
  • ホワイトノイズ、シフト、ストレッチがランダムに組み合わさった学習データのメルスペクトログラム（1,500点）

freq = 128
time = 1723

# save wave data in npz, with augmentation
def save_np_data(filename, x, y, aug=None, rates=None):
    np_data = np.zeros(freq*time*len(x)).reshape(len(x), freq, time)
    np_targets = np.zeros(len(y))
    for i in range(len(y)):
        _x, fs = load_wave_data(audio_dir, x[i])
        if aug is not None:
            _x = aug(x=_x, rate=rates[i])
        _x = calculate_melsp(_x)
        np_data[i] = _x
        np_targets[i] = y[i]
    np.savez(filename, x=np_data, y=np_targets)  

# save test dataset
if not os.path.exists("esc_melsp_test.npz"):
    save_np_data("esc_melsp_test.npz", x_test,  y_test)

# save raw training dataset
if not os.path.exists("esc_melsp_train_raw.npz"):
    save_np_data("esc_melsp_train_raw.npz", x_train,  y_train)

# save training dataset with white noise
if not os.path.exists("esc_melsp_train_wn.npz"):
    rates = np.random.randint(1,50,len(x_train))/10000
    save_np_data("esc_melsp_train_wn.npz", x_train,  y_train, aug=add_white_noise, rates=rates)

# save training dataset with sound shift
if not os.path.exists("esc_melsp_train_ss.npz"):
    rates = np.random.choice(np.arange(2,6),len(y_train))
    save_np_data("esc_melsp_train_ss.npz", x_train,  y_train, aug=shift_sound, rates=rates)

# save training dataset with stretch
if not os.path.exists("esc_melsp_train_st.npz"):
    rates = np.random.choice(np.arange(80,120),len(y_train))/100
    save_np_data("esc_melsp_train_st.npz", x_train,  y_train, aug=stretch_sound, rates=rates)

# save training dataset with combination of white noise and shift or stretch
if not os.path.exists("esc_melsp_train_com.npz"):
    np_data = np.zeros(freq*time*len(x_train)).reshape(len(x_train), freq, time)
    np_targets = np.zeros(len(y_train))
    for i in range(len(y_train)):
        x, fs = load_wave_data(audio_dir, x_train[i])
        x = add_white_noise(x=x, rate=np.random.randint(1,50)/1000)
        if np.random.choice((True,False)):
            x = shift_sound(x=x, rate=np.random.choice(np.arange(2,6)))
        else:
            x = stretch_sound(x=x, rate=np.random.choice(np.arange(80,120))/100)
        x = calculate_melsp(x)
        np_data[i] = x
        np_targets[i] = y_train[i]
    np.savez("esc_melsp_train_com.npz", x=np_data, y=np_targets)

結果として、テストデータ500点、学習データ7,500点が用意されます。

ディープラーニングによる環境音分類

環境音をConvolutional neural networkで分類します。

CNNの定義

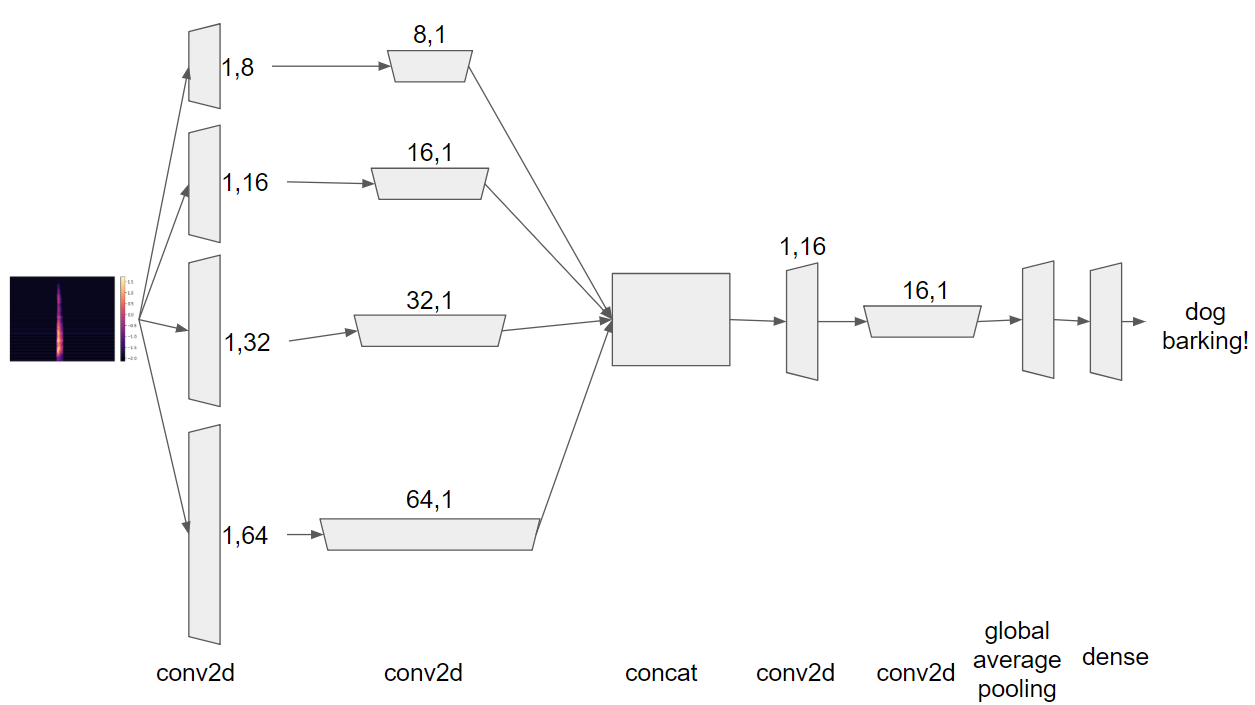
ニューラルネットワークは以下のような構造にします。


import keras
from keras.models import Model
from keras.layers import Input, Dense, Dropout, Activation
from keras.layers import Conv2D, GlobalAveragePooling2D
from keras.layers import BatchNormalization, Add
from keras.callbacks import EarlyStopping, ModelCheckpoint

# redefine target data into one hot vector
classes = 50
y_train = keras.utils.to_categorical(y_train, classes)
y_test = keras.utils.to_categorical(y_test, classes)

def cba(inputs, filters, kernel_size, strides):
    x = Conv2D(filters, kernel_size=kernel_size, strides=strides, padding='same')(inputs)
    x = BatchNormalization()(x)
    x = Activation("relu")(x)
    return x

# define CNN
inputs = Input(shape=(x_train.shape[1:]))

x_1 = cba(inputs, filters=32, kernel_size=(1,8), strides=(1,2))
x_1 = cba(x_1, filters=32, kernel_size=(8,1), strides=(2,1))
x_1 = cba(x_1, filters=64, kernel_size=(1,8), strides=(1,2))
x_1 = cba(x_1, filters=64, kernel_size=(8,1), strides=(2,1))

x_2 = cba(inputs, filters=32, kernel_size=(1,16), strides=(1,2))
x_2 = cba(x_2, filters=32, kernel_size=(16,1), strides=(2,1))
x_2 = cba(x_2, filters=64, kernel_size=(1,16), strides=(1,2))
x_2 = cba(x_2, filters=64, kernel_size=(16,1), strides=(2,1))

x_3 = cba(inputs, filters=32, kernel_size=(1,32), strides=(1,2))
x_3 = cba(x_3, filters=32, kernel_size=(32,1), strides=(2,1))
x_3 = cba(x_3, filters=64, kernel_size=(1,32), strides=(1,2))
x_3 = cba(x_3, filters=64, kernel_size=(32,1), strides=(2,1))

x_4 = cba(inputs, filters=32, kernel_size=(1,64), strides=(1,2))
x_4 = cba(x_4, filters=32, kernel_size=(64,1), strides=(2,1))
x_4 = cba(x_4, filters=64, kernel_size=(1,64), strides=(1,2))
x_4 = cba(x_4, filters=64, kernel_size=(64,1), strides=(2,1))

x = Add()([x_1, x_2, x_3, x_4])

x = cba(x, filters=128, kernel_size=(1,16), strides=(1,2))
x = cba(x, filters=128, kernel_size=(16,1), strides=(2,1))

x = GlobalAveragePooling2D()(x)
x = Dense(classes)(x)
x = Activation("softmax")(x)

model = Model(inputs, x)

# initiate Adam optimizer
opt = keras.optimizers.adam(lr=0.00001, decay=1e-6, amsgrad=True)

# Let's train the model using Adam with amsgrad
model.compile(loss='categorical_crossentropy',
              optimizer=opt,
              metrics=['accuracy'])

model.summary()

長さの違う複数のフィルタで畳み込んだ（cba）後、結合（Add）して更に畳み込み、GlobalAveragePoolingして分類します。
長さの違うフィルタは音域の畳み込みと時間軸の畳み込みに長短をつけるためです。
例えば以下では、音域方向に長さ8のフィルタで畳み込んだのち、時間軸方向に長さ8のフィルタで畳み込みます。


x_1 = cba(inputs, filters=32, kernel_size=(1,8), strides=(1,2))
x_1 = cba(x_1, filters=32, kernel_size=(8,1), strides=(2,1))

フィルタの長さを8、16、32、64と用意することで、畳み込む長さにバラエティを与えています。

分類層にはGlobalAveragePoolingを使います。
GlobalAveragePoolingにより、パラメータ数を削減する狙いです。

8.PNG

最適化関数にAmsgradを採用

最適化関数にはAdamにamsgradオプションをつけます。
Amsgradは2017年末に論文が公開された最適化関数で、Adamの改良版です。
学習率を充分に小さくすることでAdamより良いAccuracyと過学習防止が見込めるそうです。
数式的には以下になります。

Adam

\begin{aligned}
    v &\leftarrow \beta v + (1 - \beta) g_{w} \\
    r &\leftarrow \gamma r + (1 - \gamma) g_{w}^{2} \\
    w &\leftarrow w - \alpha \frac{\sqrt{1 - \gamma^{t}}}{1 - \beta^{t}} \frac{v}{\sqrt{r} + \epsilon}
\end{aligned}

Amsgrad

\begin{aligned}
    v &\leftarrow \beta v + (1 - \beta) g_{w} \\
    r &\leftarrow \gamma r + (1 - \gamma) g_{w}^{2} \\
    s &\leftarrow \max\{s, r\} \\
    w &\leftarrow w - \alpha \frac{\sqrt{1 - \gamma^{t}}}{1 - \beta^{t}} \frac{v}{\sqrt{s} + \epsilon}
\end{aligned}

詳しくは論文と以下の実験をご参照ください。
https://openreview.net/forum?id=ryQu7f-RZ
https://fdlm.github.io/post/amsgrad/

学習データにmixupを採用

学習データにはmixupを採用します。
Mixupは学習データを2つペアで混合するというものです。
こうすることで、クラス間の特徴空間をより明確に分離していくことが可能になるそうです。

同様の手法でBetween class examplesというものもあります。
こちらは東大の研究室から発表された手法です。

なお、Mixupのコードはこちらを参照しました。
ありがとうございます。

学習結果

テストデータ（500点）に対する成績は正答率82％です。
人の耳だと正答率81％になるそうなので、意外と良い線いっています。

サイズの大きなデータに対して学習率を低くした分、学習時間はだいぶかかりました。

感想

音声データを扱うのは初めてですが、案外うまくいきました。
今度はもうちょい時間短縮できるよう、メルスペクトログラムのサイズと学習率に配慮します。
今回はNvidia GPU K80で30時間学習しても完走せず、だいぶ時間がかかりました。

238
230
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
238
230

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?