Go to Qiita Advent Calendar 2024 Top
LoginSignup
240
206

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@martin-d28jp-love

音楽と機械学習 前処理編 MFCC ~ メル周波数ケプストラム係数

Posted at

最近音楽を機械学習で扱うことに興味があって色々と調べているのですが、せっかくなので備忘録と理解促進を兼ねて記事にしてみます。

機械学習に限らず、音楽をデジタル情報として扱う際には楽譜や調、歌詞など、メタな情報を扱う方法と、オーディオデータそのものを扱う方法とに大別されますが、今回はオーディオデータそのものを扱う方法の一つとして、MFCCについてまとめます。

お急ぎの方向け

mp3 を wav にして MFCC して現実的に扱えそうな次元に落とす

# ffmpegのインストール
$ brew install ffmpeg
# ffmpegで mp3 を サンプリングレート 44.1kHz wavに変換
$ ffmpeg -i hoge.mp3 -ar 44100 hoge.wav
# 必要なPythonパッケージのインストール
$ pip install --upgrade sklearn librosa

# python
import librosa
x, fs = librosa.load('./hoge.wav', sr=44100)
mfccs = librosa.feature.mfcc(x, sr=fs)
print mfccs.shape
# (n_mfcc, sr*duration/hop_length)
# DCT したあとで取得する係数の次元(デフォルト20) , サンプリングレートxオーディオファイルの長さ（=全フレーム数）/ STFTスライドサイズ(デフォルト512)

mfccs がいい感じの次元の ndarray になります。

お急ぎでない方向け

冒頭で述べたように、オーディオのデータを機械学習のロジックで扱いたいというモチベーションがあるわけですが、例えば俗に "CD音質" と呼ばれる音質で、リニアPCMという非圧縮の形式で1秒間録音した場合のデータサイズは

CD音質 - サンプリングレート 44.1kHz, ビット深度 16bit, ステレオ
44,100(Hz) x 16(bit) x 2(ch/ステレオ) ~ 1,411(kbps)

となり、10秒のデータでは一つ1.2MBぐらいのサイズになってしまいます。
モノラルにして1フレームをfloatで表現するとしても、10秒で 4.4 x 10^5 次元です。きっつー。
そこで音声としての情報をできるだけ損なわずに、Googleのような潤沢な計算リソースがなくても現実的に扱える次元にまで落とす方法が必要となるわけですが、代表的な手法として MFCC (Mel-Frequency Cepstrum Coefficients/メル周波数ケプストラム係数) を紹介します。

メル周波数ケプストラム係数とは

「メル周波数」の「ケプストラム」の係数、です。まだなんのこっちゃわからないので、それぞれ見ていきます。

メル（尺度）周波数とは

メル尺度（メルしゃくど、英語: mel scale）は、音高の知覚的尺度である。メル尺度の差が同じであれば、人間が感じる音高の差が同じになることを意図している。

というわけで、人間の音高知覚が考慮された尺度、です。人間の音高知覚についてはわかっていないところも多いそうなのですが、可聴域の下限に近い音は高め、上限に近い音は低めに聞こえるそうです。
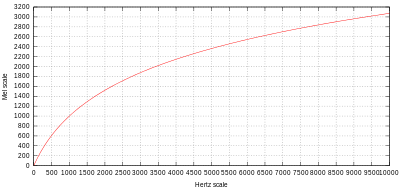
メル尺度は1000 mel = 1000 Hz を基準とし、以下の式で計算されます。

$$ m = m_0 \ln{(\frac{f}{f_0}+1)} $$

高音域で緩慢に増加していますね。

$f_0$ は $1000 mel = 1000 Hz$ という制約から導かれる式
$$ m_0 = \frac{ 1000 }{ \ln { \frac{1000}{f_0} + 1 }} $$

で算出されるパラメータです。
一例として、メル尺度への変換は以下のように計算されます。

$$ m = 1125 \ln{(\frac{f}{700} + 1)} $$

1000 mel から高さが２倍に「感じる」音が2000 mel, 半分に「感じる」音が500 melになります。上記の式より、周波数領域でのオクターブ（周波数２倍）とは異なる点に注意です。

ケプストラムとは

ケプストラムとは、（信号の）フーリエ変換の対数（位相アンラッピングを施したもの）をフーリエ変換したものである。スペクトルのスペクトルとも呼ばれる。
処理過程を FT → log → IFT（フーリエ逆変換）として説明しているものがよく見受けられる。すなわち、ケプストラムを「スペクトルの対数のフーリエ逆変換」と定義しているのである。これはオリジナルの論文にある定義ではないが、広く用いられている。

ちょっとむずかしいのですが、波形データとしての音声信号をフーリエ変換して周波数スペクトルに変換した後、その対数を取ったものを逆フーリエ変換して時間空間に戻す、と。
[ケプストラム分析 - 人工知能に関する断創録] (http://aidiary.hatenablog.com/entry/20120211/1328964624) ここに詳しいのですが、対数スペクトル領域で見るとスペクトル微細構造（細かい動き）と包絡構造（なだらかな変化）が分離できる、のが嬉しいみたいですね。

変換手順

MFCC は 「メル周波数領域」で「ケプストラム」を求めるであろうことがなんとなく想像がつきましたので、音声信号からMFCCを求める具体的な手順を見てみたいと思います。
（MFCCは "メル周波数ケプストラム係数" ですから、名称的には変換処理後の値のことを指すような気がするのですが、論文等見ても変換処理そのものとしてこの名称が使われるように思いますので、ここでも適宜文脈に応じて変換処理そのものと解釈していただければと思います。）

MFCCの計算方法自体様々亜流あるみたいですが、今回は以下を参考にしました。

Beth Logan(2000), Mel Frequency Cepstral Coefficients for Music Modeling

音声認識の特徴量として利用されるMFCCの音楽モデリングへの適応について書かれています。

また、具体的な計算方法については

あたりにも詳しいです。

論文に記載の手順は以下です。

  1. 音声データを適当な長さのフレームに分割する
  2. Window関数を適応し、離散フーリエ変換して周波数スペクトルを得る
  3. 対数をとる
  4. メル周波数で均等になるようBINを集めてスムージングする
  5. 離散コサイン変換する

少し詳しく見ていきます。

1,2. フレーム分割 ~ Window関数適応 ~ 離散フーリエ変換

これは STFT (Short-term Furier transform、短時間フーリエ変換)ですね。

短時間フーリエ変換（たんじかんフーリエへんかん、short-time Fourier transform、short-term Fourier transform、STFT）とは、関数に窓関数をずらしながら掛けて、それにフーリエ変換すること。
[短時間フーリエ変換 - Wikipedia] (https://ja.wikipedia.org/wiki/%E7%9F%AD%E6%99%82%E9%96%93%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E5%A4%89%E6%8F%9B)

離散時間でのSTFTは

$$ STFT_{x,w} [n,\omega]=\sum_{m=-\infty}^{\infty} x[n+m]w[m]e^{-i \omega m} $$

ここで$w[m]$が窓関数であり、中央が１付近の値で、範囲外で０に収束する関数です。
両端をスムーズにする目的で対象の関数にかけ合わせます。
この論文でも使われており、よく使われるHammingWindowは以下のような形です。


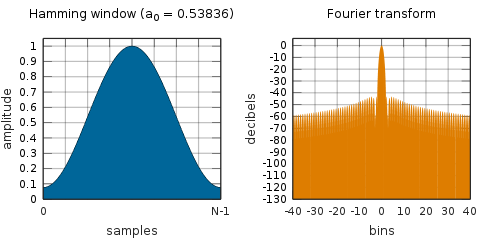
[窓関数 - Wikipedia] (https://ja.wikipedia.org/wiki/%E7%AA%93%E9%96%A2%E6%95%B0)

通常絶対値を２乗して、パワースペクトルを得ます（分割したフレームすべてに適応するので、時間変化が得られます）。位相情報が落ちますが、論文にもあるように振幅情報のほうが位相情報よりも重要とこのことですので良しとしましょう。

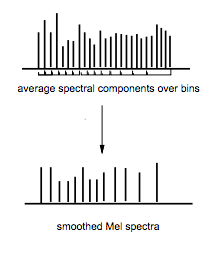
3, 4. メル周波数帯でのスムージング

イメージはこんな感じです。

logan_paper_pdf.png

論文中には明記ありませんでしたが、これは通常、「メルフィルタバンク」を適応することで計算します。
メルフィルタバンクとは、メル周波数領域で等間隔なバンドパスフィルタ（特定周波数帯のみを抽出するフィルタ）で、以下のような形をしています。

MFCC_worksheet_pdf.png
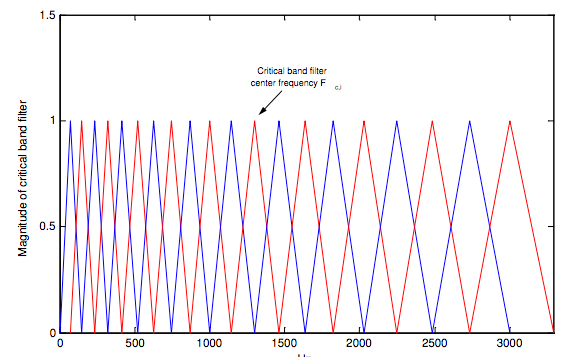
The mel frequency scale and coefficients

メルフィルタバンクの作り方は以下に詳しいです。

例として、300Hz ~ 8000Hzまでの周波数帯を10個のサブバンドに分けるメルフィルタバンクは、以下の手順で作成します。

  1. 下限・上限周波数300Hz, 8000Hzをメル周波数に変換する
    $$ (300Hz, 8000Hz) = (401.25 Mel, 2834.99 Mel) $$
    1. 上記領域を (10+2) 分割する
      $$ m(i) = [401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74,
      1949.99, 2171.24, 2392.49, 2613.74, 2834.99]Mel $$
    1. を周波数に戻す
      $$ h(i) = [300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33,
      3261.62, 4122.63, 5170.76, 6446.70, 8000]Hz $$
  4. m番目のフィルタを以下で定義する
H_m(k)=\begin{cases}
    0 & k < h(m-1) \\
    \frac{ k - h(m-1) }{ h(m) - h(m-1) } & h(m-1) \leq k \leq h(m) \\
    \frac{ h(m+1) - k }{ h(m+1) - h(m) } & h(m) \leq k \leq h(m+1) \\
    0 & k > h(m+1) \\
  \end{cases}

それぞれのフレームで、このフィルタを対数を取ったBINパワーに適応して、それぞれのサブバンドmで和を取ったものを次のステップの入力信号にします。

5. 離散コサイン変換（discrete cosine transform/DCT）

DCTは、有限数列を、余弦関数数列 cos(nk) を基底とする一次結合（つまり、適切な周波数と振幅のコサインカーブの和）の係数に変換する。
DCTでは、係数が実数になる上、特定の成分への集中度があがる。JPEGなどの画像圧縮、AACやMP3、ATRACといった音声圧縮、デジタルフィルタ等広い範囲で用いられている。
離散コサイン変換 - Wikipedia

要するに、とある信号列をいろんな振幅・位相のコサイン波の足し合わせで表現しましょうということですね。
それだけ聞くとDFTと何が違うのかと思うのですが、↑にもあるように $e^{-iω}$ と違い虚部がないので、実数を入れると必ず実数が得られるのが嬉しい、と。

基底関数が色々あるようなのですが、Wikipediaにもよく使われるとあるDCT-Ⅱを例に取ると、N個のデータをもつ $f_i$ に対して、基底関数

\phi_k[i] = \begin{cases}
  \frac{ 1 }{ \sqrt[]{N} } & k=0 \\
  \sqrt[]\frac{ 2 }{ N } \cos \frac{ (2i + 1)kπ }{ 2N } & k=1,2,...,N-1 \\
  \end{cases}

を用いて、

$$ C[k] = \sum_{i=0}^{N-1}f_i\phi_k[i] $$

として求めます。
DCTの特徴として、情報が少数の低周波数成分に集中するため、低次項から適当な数で打ち切ってしまうことで情報をなるべく残した状態で次元圧縮できるという寸法です。
というわけで、先程までの計算で求めた離散信号をDCTして低次項を取ると、めでたくMFCCが取得できます！

librosa での実装例

冒頭で見たように、librosaを使うとwavファイルを開いてたった一行で(!)MFCCが取得できてしまいます。
せっかくなので、実装を覗きつつ、計算経過を可視化してみたいと思います。

コードは以下を参考にしています。Jupyterで実行しました。

Notes on Music Information Retrieval

セットアップ

以下のコードを実行するには、事前準備としてpython と jupyter をインストールする必要があります。Macの方はanyenv経由でpyenvからanacondaをインストールするのがおすすめです。また、

のPackage Installationにあるコマンドを実行し、必要なライブラリをインストールして下さい。無心で以下のコマンドを叩くとセットアップ完了するはずです。なおPythonは2.7です。

$ brew install anyenv
$ anyenv install pyenv
$ pyenv install anaconda2-4.3.0
$ pip install --upgrade sklearn librosa seaborn mir_eval matplotlib
$ ipython notebook

実装

では実装コードです。
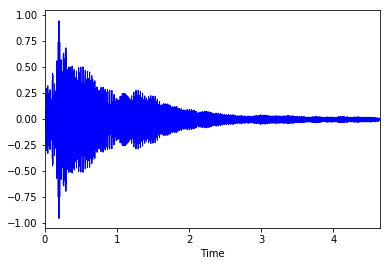
まず、サンプルのwavファイルをダウンロードして波形をプロットします。

%matplotlib inline
import matplotlib.pyplot as plt, librosa, librosa.display, urllib

# サンプルファイルをダウンロード
urllib.urlretrieve('http://audio.musicinformationretrieval.com/c_strum.wav', './c_strum.wav')
x, fs = librosa.load('./c_strum.wav', sr=44100)
librosa.display.waveplot(x, sr=fs, color='blue')

output_0_1.png

MFCCを得る関数が準備されていますので、冒頭で紹介したように以下のコードだけで変換できます。

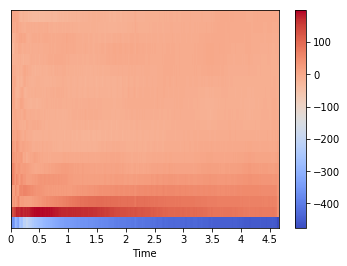
# mfccしてプロット
mfccs = librosa.feature.mfcc(x, sr=fs)

librosa.display.specshow(mfccs, sr=fs, x_axis='time')
plt.colorbar()

output_1_1.png

本当に簡単ですね。では librosa.feature.mfcc の実装を覗いてみます。

# spectral.py
def mfcc(y=None, sr=22050, S=None, n_mfcc=20, **kwargs):
    '''    
    Parameters
    ----------
    y     : np.ndarray [shape=(n,)] or None
        audio time series

    sr    : number > 0 [scalar]
        sampling rate of `y`

    S     : np.ndarray [shape=(d, t)] or None
        log-power Mel spectrogram

    n_mfcc: int > 0 [scalar]
        number of MFCCs to return
    '''
    if S is None:
        S = power_to_db(melspectrogram(y=y, sr=sr, **kwargs))

    return np.dot(filters.dct(n_mfcc, S.shape[0]), S)

audio データ(y)にmelspectrogarm関数を適応して求めた mel周波数のbinpower(振幅の２乗)を、power_to_dbでdecibel単位に変換し、その行列とDCTフィルタを作成して内積を取ることでDCTを行っています。エレガントですね。
なおデシベルは対数表現であるベルの1/10の意味ですので、おそらくこれが 3.対数をとる に該当すると思います。
n_mfccが取得するDCT低次項の数＝変換後のBinの数（画像縦軸の次元）、になります。
また、計算済みのメルスペクトログラムSを利用することもできます。この場合はdctを実行するだけですね。

melspectrogramの実装も見てみましょう。

# spectral.py
def melspectrogram(y=None, sr=22050, S=None, n_fft=2048, hop_length=512,
                   power=2.0, **kwargs):
    '''
    y : np.ndarray [shape=(n,)] or None
        audio time-series

    sr : number > 0 [scalar]
        sampling rate of `y`

    S : np.ndarray [shape=(d, t)]
        spectrogram

    n_fft : int > 0 [scalar]
        length of the FFT window

    hop_length : int > 0 [scalar]
        number of samples between successive frames.
        See `librosa.core.stft`

    power : float > 0 [scalar]
        Exponent for the magnitude melspectrogram.
        e.g., 1 for energy, 2 for power, etc.
    '''
    S, n_fft = _spectrogram(y=y, S=S, n_fft=n_fft, hop_length=hop_length,
                            power=power)

    # Build a Mel filter
    mel_basis = filters.mel(sr, n_fft, **kwargs)

    return np.dot(mel_basis, S)

渡されたyまたはSのspectrogramを計算したものに、メルフィルターバンクを適応して返します。
n_fftでwindowの幅、hop_lengthでスライドサイズを制御します。 全体のフレーム数/hop_length が（だいたい）画像横軸の次元になります。
こちらもフィルタと信号の内積で表現されており、エレガントです。

さらに _spectrogram　も見てみます。

def _spectrogram(y=None, S=None, n_fft=2048, hop_length=512, power=1):

    if S is not None:
        # Infer n_fft from spectrogram shape
        n_fft = 2 * (S.shape[0] - 1)
    else:
        # Otherwise, compute a magnitude spectrogram from input
        S = np.abs(stft(y, n_fft=n_fft, hop_length=hop_length))**power

    return S, n_fft

こちらは短時間フーリエ変換を実行してbinパワーを計算しているだけですね。
というわけで、実装からも変換手順が確認できました。

実装を掘りながら確認したせいで、変換手順を逆順で追いかけてしまいました。
最後に、手順に沿って変換を実行しながら、途中経過を可視化してみます。

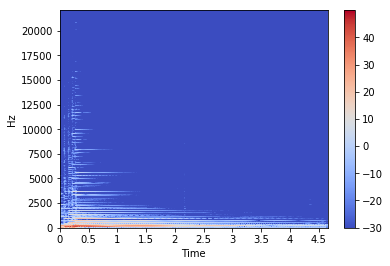
#1. 音声データを適当な長さのフレームに分割する
#2. Window関数を適応し、離散フーリエ変換して周波数スペクトルを得る
#   - STFT
#3. 対数をとる
import numpy as np

stft = np.abs(librosa.stft(x, n_fft=2048, hop_length=512))**2
log_stft = librosa.power_to_db(stft)

librosa.display.specshow(log_stft, sr=fs, x_axis='time', y_axis='hz')
plt.colorbar()

output_9_1.png

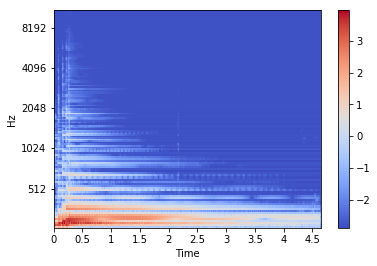
# 4. メル周波数で均等になるようBINを集めてスムージングする
#   - binパワー計算済みのSを利用して、メルフィルタバンクをあてる
melsp = librosa.feature.melspectrogram(S=log_stft)
librosa.display.specshow(melsp, sr=fs, x_axis='time', y_axis='mel')
plt.colorbar()

output_10_1.png

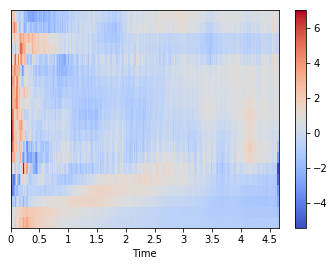
# 5. 離散コサイン変換する（低次項を取る）
# デフォルト 20bin
mfccs = librosa.feature.mfcc(S=melsp)

# 標準化して可視化
import sklearn
mfccs = sklearn.preprocessing.scale(mfccs, axis=1)
librosa.display.specshow(mfccs, sr=fs, x_axis='time')
plt.colorbar()

output_11_1.png

まとめ

音楽、特にオーディオデータを利用して機械学習するための特徴量として MFCC を紹介し、その計算手順についてまとめました。
DL系の論文では、離散コサイン変換を行わず、メル周波数のスペクトラムを直接扱っている場合もあるようです。

前提知識があまりなかったので長くなってしまいました。。ともあれこれで準備ができましたので、次はいよいよこの素性を利用して音楽を機械学習にかけてみたいと思います。

参考

240
206
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
240
206

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?