Deep Metric Learning の定番⁈ Triplet Lossを徹底解説

はじめに

Deep Learningを使った距離学習（Metric Learning）は、人物同定（Person Re-Identification）をはじめ、顔認識、細かい画像の分類、および画像検索など多くのコンピュータビジョンタスクにおいて広く利用されています。その中でも損失関数にTriplet Lossを用いたMetiric Learningは比較的ポピュラーなやり方で、関連論文もこれまでたくさん発表されています。本稿では、まず画像分類（Classification）タスクとMetric Learningの違いを考察し、次にTriplet Lossがどのように改良されてきたのか、その変遷をまとめています。

画像分類タスクとしてのPerson Re-Identification

Person Re-Identificationとは同一人物を認識するタスクです。これを一般的な画像分類タスクで解く方法を考えてみたいと思います。

画像分類ネットワークをそのまま利用する場合

下記は一般的な画像分類タスクの図です。入力画像はCNNによって畳み込まれた後、最後にSoftmaxされ、猫と予測しています。

この構造のまま、人物画像に関して学習したネットワークが下図になります。Bさんの画像を入力するとBさんと予測しています。

このネットワークにBさんの別の画像を入力した場合です。これもBさんと予測しています。

このように一見画像分類ネットワークを使って、同一人物の認識に成功していそうですが、以下はどうでしょうか。

実は、AでもBでもCでもDでもなく、Eさんの画像を入力しています。しかし、ネットワークはBさんと間違って予測をしています。画像分類ネットワークは、答えの中からもっともスコアの高いものを選ぶ事しかできないため、結局のところ、知っているものしか識別する事はできないということになります。したがって、知らない人物も判別する必要のあるPerson Re-Identificationにおいては、この構造だとまずいわけです。

また、画像分類ではClassあたりのデータ数が少ないとOverfittingしてしまう可能性が高くなるため、各Class毎に多くの学習データを用意して、汎化性能を高めるのが一般的です。しかし、Person Re-Identificationの学習データは、Class数（人物の数）が多く、Class毎のデータ数は少ない場合がほとんどであり、この点においても画像分類でPerson Re-Identificationする事は不利となります。

画像分類とMetric Learningを組み合わせた場合

画像分類ネットワークをダイレクトに使ってPerson Re-Identificationを解くのではなく、出力層近くの特徴量を抽出するためだけに利用する方法を考えてみます。抽出した特徴量は、マハラノビス距離学習やKISSME、およびXQDA¹などのMetricLearning手法によって、Embedding空間に配置されます。

また、画像分類とMetric Learningを組み合わせた別の形として、下図のような構成も考えられます。

これは、画像分類ネットワークの中間層から特徴量を抽出してきて、２つの特徴量をConcatし、それをサブネットワークの入力にして、類似度をMetric Learningするといった形です。画像分類ネットワーク部分の損失関数（Softmax Cross Entropy）とサブネットワーク部分の損失関数の２つがあるので、両者をうまくバランシングしながらネットワーク全体を学習していきます。

これらの画像分類とMetric Learningを組合わせたやり方は、一見うまくいきそうにも見えます。しかし、以下の点で疑問が残ります。

• 画像分類は「そのオブジェクトは何であるか」というIdentificationはしているが、２つ以上の画像の類似性を直接説明しているわけではない。したがって、画像分類器から抽出した中間特徴量をMetric Learningする事によって、そこに相乗的もしくは相補的な効果が得られているのかは不明である。
• 画像分類器は学習データに存在しているオブジェクト（知っているオブジェクト）は認識できるが、存在しないオブジェクトは認識できない。そのため、画像分類器から抽出する中間特徴量は、学習データに存在しているものと、そうでないもので、情報量に大きな差があっても不思議ではない。したがって、後続のMetric Learning部分で、学習データに存在したものと、そうでないものを、同等の精度で識別できるかは不明である。

こういった理由を鑑みた結果かどうかはわかりませんが、Person Re-Identificationでは、いわゆる一般的な画像分類の延長線上ではなく、Contrastive LossやTriplet LossといったMetric Learningに特化した損失関数を使った学習が、現在の主流となっているようです。

ただ、最近はClassificationを学習しながらMetric Learningを行える手法も提案されているようです。SphereFaceやCosFaceやArcFaceといった手法がそれに当たります。こちらの記事で詳しく説明されています。私自身、目からウロコだったので、まだ知らない方は一読をオススメします。

Triplet Lossとは

TripletLossは改良を加えられたりして、形が微妙に違った亜種も多く存在してますが、下図のような形が一般的な気がします。

学習は、基準となるAnchor画像 $x_a$、Anchorと同じIDのPositive画像 $x_p$、Anchorと違うIDのNegative画像 $x_n$の３つを１組として行われます。各入力画像は、CNN（変換 $f$ ）によって、Embedding空間のベクトルとして配置されます。Embedding空間ではAnchor-Positive間の距離 $d_p$ 、Anchor-Negative間の距離 $d_n$ を関数 $d$ で計測します。関数 $d$ はユークリッド距離を使う場合が多いですが、Embedding空間の２つのベクトル間の距離を計測できる関数であれば、どのようなものでも問題ありません。

上図に示す通り、最終的には $d_p + \alpha \leqq d_n$ を満たすようにCNN（変換 $f$ ）を最適化したいので、損失関数を $L_{triplet} = [d_p- d_n + \alpha]_+$ と定義します。このような損失関数をTripletLossといいます。 （ただし、$\alpha$ はマージンを表すハイパーパラメータです。）

Triplet Lossの登場

Triplet Lossは、2014年4月にarxivで発表された論文²で、画像検索における順位付けを学習するために提案されたのが最初のようです。画像検索のためのアノテーション作業において、何十枚もの画像を、似ている順番に人手で並べてラベル付けするのは、誤りはかなり多くでてしまいます。しかし、下図のように３枚の画像を１セットにし、その中の一つの画像（Query）と似ている方をPositive、似ていない方をNegative、という風に３枚毎にラベル付けを行っていけばミスもかなり減ります。

このような３枚１組みのデータセットに対して、Query-Negative間がQuery-Positive間よりもユークリッド距離が大きくなるように、繰り返し最適化していく事により、画像間の類似性が学習されていきます。画像の検索時は、Embedding空間内で近傍探査して、ユークリッド距離の近い順を、そのまま検索結果の順位とする事ができます。

Triplet Network

2014年12月にarxivに上げられた論文³で、文献²の画像検索における順位付けといった限られた用途だけではなく、Triplet LossはMetric Learningを必要とするタスクに対して広く有効な手法であると紹介されています。損失関数は、PositiveとNegativeのユークリッド距離をSoftmaxしている点が文献²と異なっています。

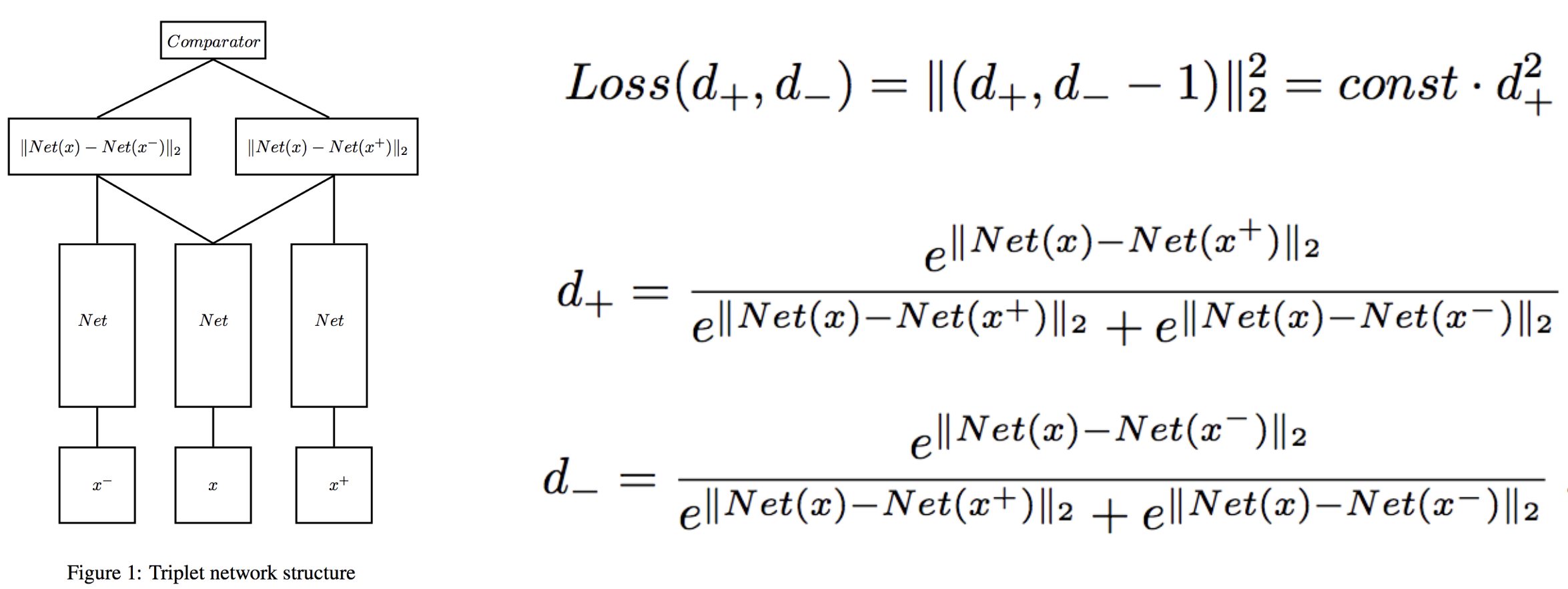
また、SiameseNetを引き合いに出しており、Triplet Networkはその欠点を改善した手法である事に関して言及しています。

SiameseNetとは

SiameseNetが提案されたのはTripletLossよりも前で、一般的に下記のような構成となっています。損失関数のContrastive Lossとセットで利用される事が多いです。

学習は２つの画像を１組みとして行われます。各入力画像は、CNN（変換 $f$ ）によって、Embedding空間のベクトルとして配置され、ベクトル間の距離を関数 $d$ で計測します。Triplet Lossの場合と同様に、$d$ はユークリッド距離を使う事が多いですが、Embedding空間の２つのベクトル間の距離を計測できる関数であれば、どのようなものでも問題ありません。Contrastive Loss関数の$\alpha$はマージンを表しています。$y_{ab}$は２つの入力画像 $x_a$と $x_b$のラベルが同じ場合は$1$、違う場合は $0$となります。したがって、$d_{ab}$は同じラベル間では小さく、違うラベル間では大きくなるように、CNN（変換 $f$ ）が学習されていきます。

SiameseNetの欠点とTripletLossによる改善

SiameseNetで学習する際、２つの画像を近づけたいのか、遠ざけたいのかはコンテキストを考慮する必要があります。例えば、性別と名前といったマルチクラスのラベル付きデータセットをMetric Learningする場合を考えてみます。男性・Aさんと男性・Bさんの２つの画像データは、近づけるべきなのか遠ざけるべきなのかはこれだけでは判断できません。Person Re-Identificationタスクのように、同一人物を見分ける用途であれば、この２つは遠ざけるべきで、性別を識別するための用途であれば、近づけるべきです。

TripletLossの場合は、基準となる画像に対して、類似度が低い方を、もう一方よりも相対的に遠ざける形となるため、コンテキストの考慮は必要ありません。

FaceNet

2015年3月に顔認識に有効な手法⁴としてGoogle Inc.から発表されました。Triplet Loss関数やネットワークの大枠の構成は、文献²のものとほとんど同じですが、顔の情報（Embedding空間でのベクトルの次元数）を128次元までに圧縮した事や、Tripletのマイニング方法の工夫により、学習効率を大幅に上げた事に対して言及しています。当時の顔認証のSOTAを記録した事もあり、この論文発表以降にTriplet Loss関数がMetric Learningにおけるメジャーな損失関数の１つとして知れ渡った感はあります。

Triplet Selection

データセットが $k$ 個のClassと、1Classあたり $c$ 個の画像がある場合、Anchorの選び方は $kc$ 個、Positiveの選び方は $c-1$ 個、Negativeの選び方は $c(k-1)$ 個となるため、可能なTripletの組み合わせは $k(k-1)c^2(c-1)$ パターンあります。学習データが多い場合、Tripletの組合せは膨大になり、全てを学習に利用していくのは非効率です。FaceNetでは、mini-batchの中だけでTripletを構築して、Semi-hard Negativeの条件 $d_p \leqq d_n < d_p + \alpha$ を満たすもののみをランダムに利用していく方法を取っています。

下図は、FaceNetの実験で利用されたTriplet Selectionの具体的な流れになります。

Hard Negativeを使わない理由

Easy Negativeに関しては、Lossがないので学習に利用する意味がないのはわかります。では、Hard Negativeを使わない理由はなぜかを、少し考えてみました。まず、Semi-Hard NegativeのLoss値を減らそうとする場合ですが、現時点よりもLoss値を減らすための最適化は、相対的にNegativeが長くなるか、Positiveが短くなるかしかありません。

しかし、Hard NegativeのLoss値を減らすための最適化は、それに加えてどちらも短くなるという選択肢があります。これはLoss値がマージンである $\alpha$ よりも大きいためです。これは、最終的に $d_p = 0$、$d_n = 0$で Loss値が$\alpha$ となる良くない局所解を目指しながら、最適化されてしまう可能性を示唆しています。

Improved Triplet Loss

Triplet Lossは、最適化の過程において、Positiveを短くするのか、Negativeを長くするのかは指定していません。あくまで、相対的な関係値のみを記述しています。したがって、$d_p + \alpha \leqq d_n$を満たした後は、それ以上の最適化は行われません。この問題を解決するために、文献⁵にてTriplet Lossの改良版が提案されました。

L_{improved\_triplet} = [d_p - d_n + \alpha]_+ + [d_p - \beta]_+

従来のTriplet Lossの項に加えて、Positiveを一定の大きさ $\beta$ よりも小さくする項が追加されています。これにより相対的な位置とは無関係に、クラス内の距離が$\beta$より小さくなるように働きます。

Positive単体でMetric Learningされるので、Contrastive Lossの要素が加わったと考える事もできます。

距離関数のDeep化

Embedding空間での距離の計測は、ユークリッド距離など、あらかじめ定義しておいた距離関数 $d$ を使うのが通例ですが、この距離計測自体をDeep Learningでやってしまうような手法が文献⁶で提案されています。ユークリッド距離ではなくDeep Learningを使う事で、２つの画像間の複雑な関係が適切にモデル化されるため、カメラ間の外観の変化や視点の違いなどに対してもよりロバストにすることができます。
ネットワークは、Shared sub-networkとsingle-image representation（SIR）、およびcross-image representation (CIR)という３つの要素で構成されています。

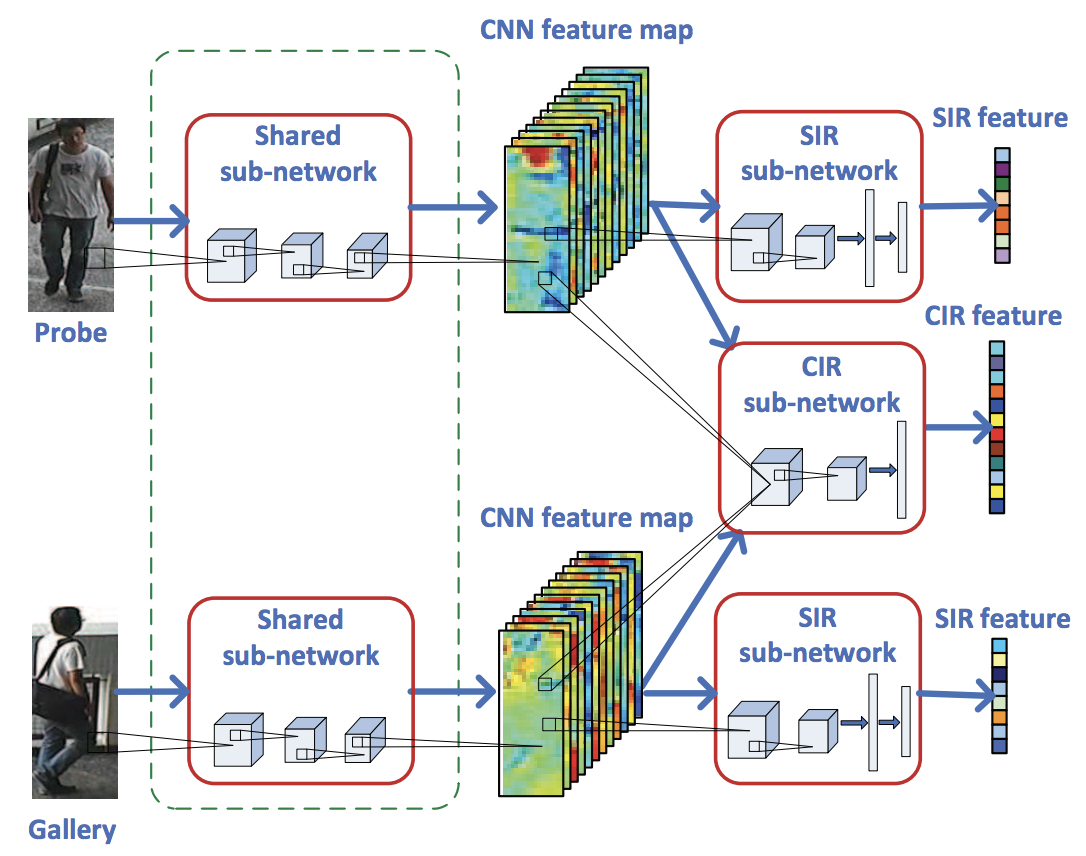
下図はネットワーク全体像で、青色の部分がShared sub-network、緑色の部分がsingle-image representation（SIR）、赤色の部分がcross-image representation(CIR)となっており、それぞれTriplet Networkの要素に当てはめると、Shared sub-networkはEmbedding部分、SIRは従来のTriplet Lossの部分、そしてCIRがDeep Learningを使ってMetric Learningしている部分になります。

CIRの最終層は1000次元のベクトルとなっていますが、CIRは２つの間の距離なのでスカラ値になっている必要があります。この部分は、CIRの損失関数内で ベクトル $w$ （学習されるパラメータ）と内積をとってスカラ値に変換しています。

SIRの損失関数はユークリッド距離を使ったマージン1のTriplet Loss となっており、SIRとCIRの損失関数を定数 $\eta$ でバランシングしたものを、最終的な損失関数としています。

Quadruplet Loss

Triplet Lossによって繰り返し学習される事により、可能な全てのTripletの組みに対し、以下の条件が満たされるように最適化されます。

d_p < d_n

下図はEmbedding空間の様子を表した例で、A, B, C ３つのClassが存在しています。今AnchorをA3、PositiveをA1、NegativeをC1とした場合、前述の条件は満たしています。

AnchorをC1、PositiveをC2、NegativeをB1とした場合も条件は満たしています。

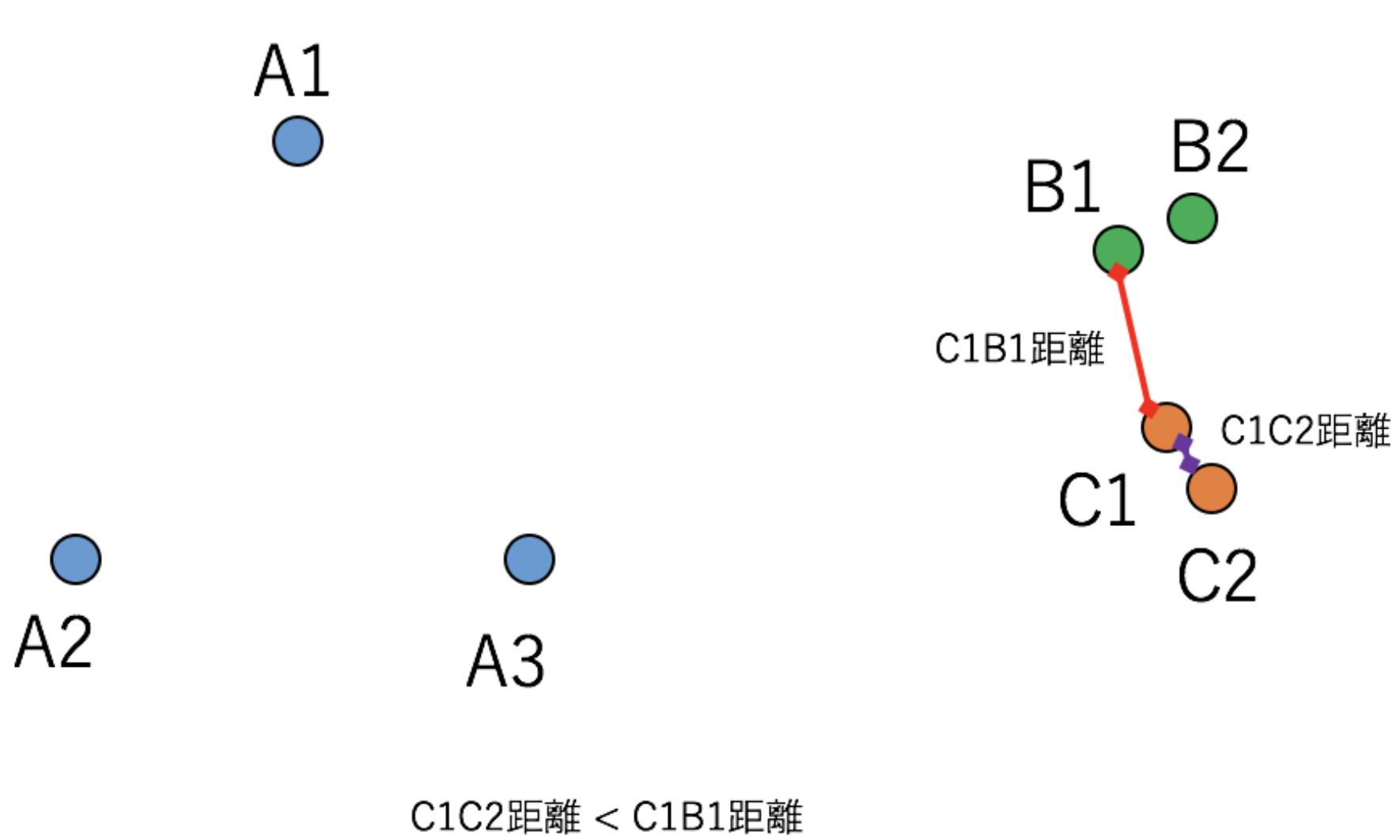
実はこの図、全てのTripletの組みに対して条件を満たしています。つまり、Triplet Lossによって十分学習されきった後のEmbedding空間の状態を表しているわけです。しかし、次のように、Aのクラス内距離がBCのクラス間距離よりも大きいといった状況が起きています。

これは、Triplet Lossはクラス内距離がクラス間距離よりも小さくなる事は保証しないという事を意味しています。このような状況になると、例えば閾値を使った同一Classの判定を行おうとした時に、問題がおきてしまう場合があります。

この課題への解決策として、文献⁷でQuadruplet Lossが提案されました。これはその名前の通りで、３つではなく４つの要素で損失関数が定義されています。

L_{quadruplet} = [d_p- d_{n1} + \alpha]_+ + [d_p - d_{n2} + \beta]_+

最初の項はTriplet Lossと同じです。２つめの項もTriplet Lossと似ていますが、別のAnchorを持つNegativeが指定されています。これにより、任意のクラス間の距離は、任意のクラス内の距離よりも大きくなるように働くため、十分に学習が進めば、クラス間最小距離はクラス内最大距離よりも大きい事が保証されます。

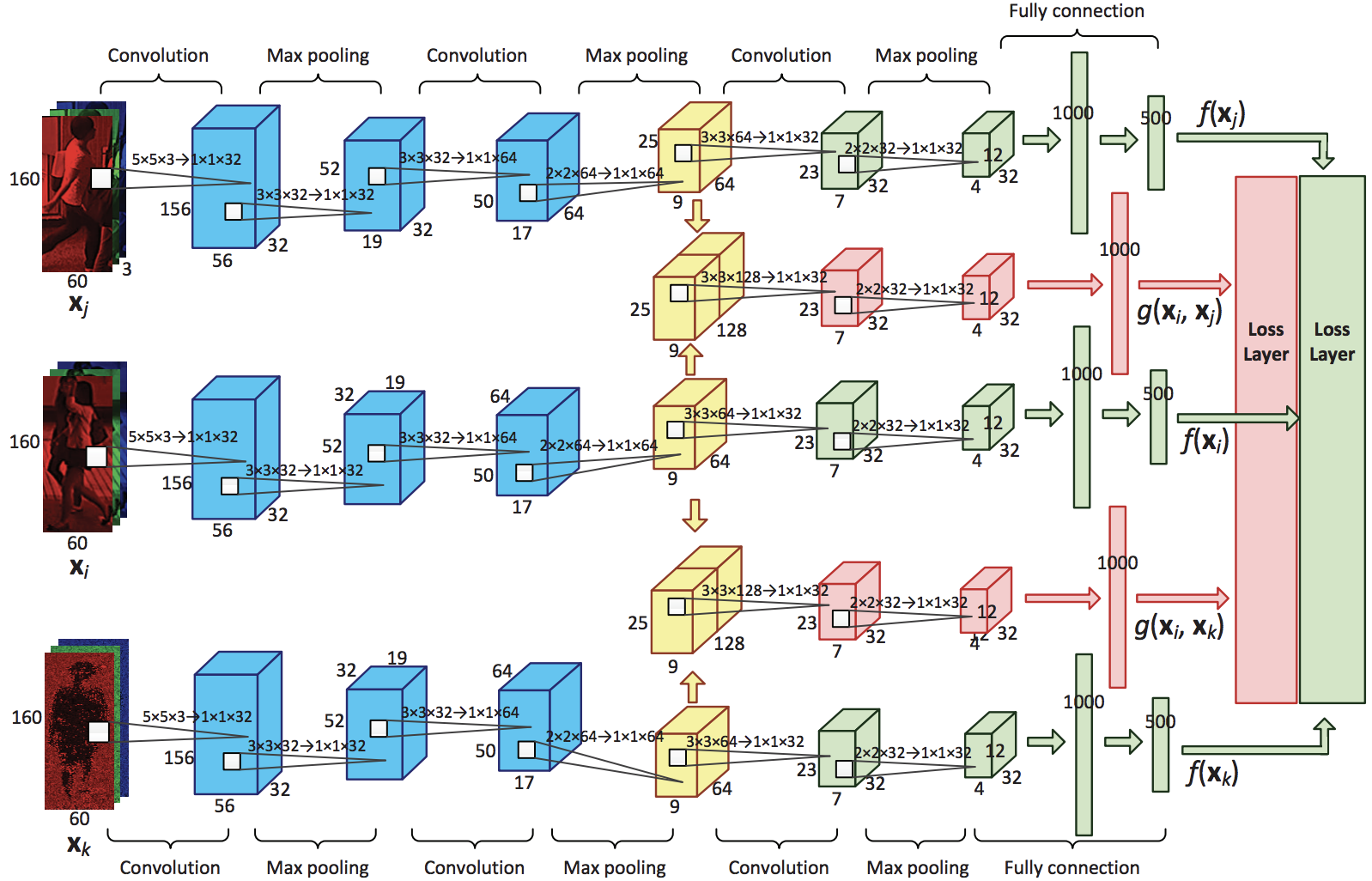
下図はネットワークの全体像になります。赤色のエリアが新たに加えられた４つ目の要素に関する部分です。

最初のConvolution1,2によりEmbeddingが行われ、Embedding空間内の距離は文献⁶と同様に、ユークリッド距離ではなくDeep Metric Learningを使っています。この距離は２つの画像が違うほど大きくなれば良いので、ネットワーク最終層をSoftmaxして、２つの画像が同じである確率と、違う確率の２つを出力し、違う確率の出力値をそのまま距離の値として利用しています。Softmaxによって距離 $d_p$、$d_{n1}$、および $d_{n2}$の値の範囲は $[0,1]$と正規化されているため、損失関数のマージン $\alpha$ や $\beta$ の値の範囲も決めやすくなっています。

Adapted Triplet Loss

Triplet Lossの性能は、学習時のTripletの選択方法に強く依存します。そのため、確実な素早い収束を得るためには何かしらの工夫が必要です。Triplet Selectionでは一定の範囲にあるHard Exampleを選択する事が重要でしたし、それ以外のApplicationでも、様々なTriplet選択方法が提案されてきました。何れも全てのTripletの組合せではなく、一部のTripletを使う事によって学習性能を向上させています。しかし、部分的なデータしか使わない学習は、本来の分布とは異なるため、データの偏りによるバイアスが生じる危険性があります。下図の $D_T$ は可能な全てのTripletの組み、$\hat D_T$ はそのTripletを構成しているデータ、$D_S$ は学習で利用するTripletの組み、 $\hat D_S$ はそのTripletを構成しているデータを表しており、$\hat D_T$ と $\hat D_S$の間には分布のズレがあります。

本来適応させたいのは $\hat D_T$ ですが、実際には $\hat D_S$ を使った学習となっているので、これはDomain Adaptationなどの転移学習と捉える事もできます。文献⁸では、この点に着目し、$\hat D_S$（ソースドメイン）の分布を $\hat D_T$（ターゲットドメイン）に近づけながら学習する手法を提案しています。

Embedding空間での分布を考える

$\hat D_T$ と $\hat D_S$ 内のデータの分布の違いは、学習方法の都合上ある意味仕方がない部分なので、Embedding空間での分布の違いをなくす方向で考えます。つまり、$\hat D_T$ および、$\hat D_S$ 内のデータの分布を表す確率密度関数をそれぞれ $P^T(x)$ と $P^S(x)$ とし、各データを $X$、Classを $Y$、Embedding空間への変換を $f(x)$ とした場合、

P^T(f(X)|Y) = P^S(f(X)|Y)

となっている状態です。これはClass $Y$ に関するEmbedding空間でのベクトルの分布（確率密度）が $\hat D_T$、$\hat D_S$ で全く同じになっている事を意味しています。しかし、現実的にこれを満たすのは難しいです。そこで、文献⁸ではそれぞれのEmbedding空間でのベクトルの期待値（平均値）だけが同じになるような損失関数$L_{match}$を導入しています。

L_{match} = \sum_y||\Phi_y^S - \Phi_y^T||_2^2

ただし、$\Phi_y^S$ と $\Phi_y^T$ はそれぞれ下記になります。

\begin{align}
\Phi_y^S = \sum_{(X,Y=y)\in \hat D_S}P^S(f(X)|Y)*f(X) \\
\Phi_y^T = \sum_{(X,Y=y)\in \hat D_T}P^T(f(X)|Y)*f(X) \\
\end{align}

この２つはそれぞれ $\hat D_S$ と $\hat D_T$ のEmbedding空間でのClass $y$ に関するベクトルの期待値（平均値）です。
最終的な損失関数は次のようになります。従来のTriplet Lossにトレードオフパラメータ $\lambda$ を乗じて加えたものです。

L_{adapted} = L_{triplet} + \lambda*L_{match}

これにより、Embedding空間での各Class毎のベクトル平均値が $\hat D_S$ と $\hat D_T$ で近づきながら、従来のTriplet Lossの効果を得る事ができます。

以下は、Class $A$ と Class $B$ の２種類のClassがある $\hat D_S$ と $\hat D_T$、およびEmbedding空間の様子を表した図になります。

\begin{align}
\Phi_A^S &= \frac{A1 + A2 + A3}{3} \\
\Phi_A^T &= \frac{A1 + A2 + A3 + A4 + A5}{5} \\
\Phi_B^S &= \frac{B1 + B2}{2} \\
\Phi_B^T &= \frac{B1 + B2 + B3}{3} \\
\end{align}

1. S. Liao, Y. Hu, X. Zhu, and S. Z. Li. "Person re-identification by local maximal occurrence representation and metric learning." In CVPR, 2015. ↩

2. J. Wang, Y. Song, T. Leung, C. Rosenberg, J. Wang, J. Philbin, B. Chen, and Y. Wu. "Learning Fine-grained Image Similarity with Deep Ranking." In CVPR, 2014. ↩ ↩² ↩³ ↩⁴

3. E. Hoffer, and N. Ailon. "DEEP METRIC LEARNING USING TRIPLET NETWORK." In ICLR workshop, 2015. ↩

4. F. Schroff, D. Kalenichenko, and J. Philbin. "Facenet: A Unified Embedding for Face Recognition and Clustering." In CVPR, 2015. ↩

5. D. Cheng, Y. Gong, S. Zhou, J. Wang, and N. Zheng. "Person Re-Identification by Multi-Channel Parts-Based CNN with Improved Triplet Loss Function." In CVPR, 2016. ↩

6. F. Wang, W. Zuo, L. Lin, D. Zhang, and L. Zhang. "Joint Learning of Single-image and Cross-image Representations for Person Re-identification." In CVPR, 2016. ↩ ↩²

7. W. Chen, X. Chen, J. Zhang, and K. Huang. "Beyond triplet loss: a deep quadruplet network for person re-identification." In CVPR, 2017. ↩

8. B. Yu, T. Liu, M. Gong, C. Ding, and D. Tao. "Correcting the Triplet Selection Bias for Triplet Loss." In ECCV, 2018. ↩ ↩²