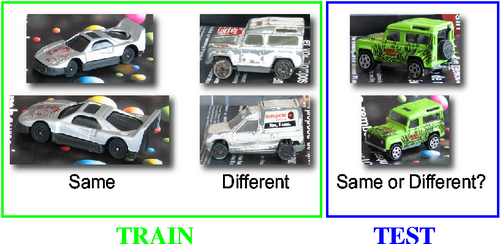
距離学習 (Metric Learning)
2つが同じモノを表しているか、それとも違うモノを表しているのか?
このような問題を解く場合、2つの間に『距離』を定義して、それが近ければ同じ、遠ければ違うと判断する方法が考えられます。ここでの『距離』は学習データを用いる事により、違うモノはより大きく、同じモノはより小さくなるように、目的に合わせて柔軟に定義する事ができます。このような操作の事を距離学習(Metric Learning)と言います。
KISSME
距離学習は、データの性質や分布の違いや目的によって、最適なやり方が変わってくる事も多いため、これまでいろいろな種類のもの(例えば、Triplet Loss を使った Metric Learning など)が提案されています。その中から、同一判定(2つのものが同じか否かを分類)するための手法として、CVPR 2012でオーストリアのグラーツ工科大から発表された 「Large Scale Metric Learning from Equivalence Constraints1」を試してみました。DeepLearning (Neural Network) を使っておらず、同一判定であれば判定対象は何でも良いので、適用範囲が広いといった特徴が挙げられます。参照される事も多く、特に人物照合(person re-identification)の研究分野における最近の論文では、実験の比較対象としてよく利用されています。また、これを応用した新しいやり方も複数発表2345されています。
この論文で提案されている距離は「Keep It Simple and Straightforward MEtric」の頭文字を取ってKISSME と呼ばれています。
考え方
人物画像を例に説明します。例えば、2つの人物画像から取得した特徴量をそれぞれ $x_i$ と $x_j$ とした場合、この組合せは必ずどちらかに分類されます。
- $\Omega_0$: $x_i$ と $x_j$ が違う人物
- $\Omega_1$: $x_i$ と $x_j$ が同じ人物
したがって、$x_i$ と $x_j$ が同じ人物である確率は、
P(\Omega_1|x_i, x_j)
です。
これはベイスの定理における事後確率なので、尤度は下記のようになります。
P(x_i, x_j|\Omega_1)
これは、2つが同一人物となるケースにおいて、その特徴量が$x_i$と$x_j$である確率 という意味になります。同様に、違う人物に関しても尤度は、$P(x_i, x_j|\Omega_0)$ と書けます。
KISSME ではこの2つの尤度の比を用いる事により、統計的推論の観点から、同一人物か否かを判定します。
つまり、仮説検定問題として、
$H0$ (帰無仮説): $x_i$ と $x_j$ は同一人物ではない
$H1$ (対立仮説): $x_i$ と $x_j$ は同一人物である
とおき、次の式
\delta(x_i, x_j) = \log \biggl( \frac{P(x_i, x_j|\Omega_0)}{P(x_i, x_j|\Omega_1)} \biggr)
がある値よりも小さい場合にはH0を棄却し、そうでない場合は採択するという尤度比検定方式による判定を行います。
ただし、この式の形だと2つの特徴量$x_i$と$x_j$を考えなければいけないので、
x_{ij} = x_i - x_j
といった差の空間で考えます。これにより2つの特徴量は1つに減り、さらに平均0の問題となるため、より単純な形に置き換える事が可能となります。ちなみに、平均が0になる理由は 各 $x_i - x_j$について必ず逆の $x_j - x_i$ が存在するからです。
\delta(x_{ij}) = \log \biggl( \frac{P(x_{ij}|\Omega_0)}{P(x_{ij}|\Omega_1)} \biggr)
上記の $P(x_{ij}|\Omega_0)$ と $P(x_{ij}|\Omega_1)$ をそれぞれ平均0のガウス分布でモデル化すると、
\delta(x_{ij}) = \log \Biggl( \frac{\mathcal{N}(x_{ij}| \, 0,\Sigma_{y_{ij}=0})}{\mathcal{N}(x_{ij}| \, 0,\Sigma_{y_{ij}=1})} \Biggr)
= \log \Biggl( \frac{\frac{1}{\sqrt{2\pi|\Sigma_{y_{ij}=0}|}}\exp(-\frac{1}{2}x_{ij}^{T}\Sigma_{y_{ij}=0}^{-1}x_{ij})}{\frac{1}{\sqrt{2\pi|\Sigma_{y_{ij}=1}|}}\exp(-\frac{1}{2}x_{ij}^{T}\Sigma_{y_{ij}=1}^{-1}x_{ij})} \Biggr)
と書け、これを展開して整理すると、
\delta(x_{ij}) = x_{ij}^{T}\Sigma_{y_{ij}=1}^{-1}x_{ij} + \log(|\Sigma_{y_{ij}=1}|) - x_{ij}^{T}\Sigma_{y_{ij}=0}^{-1}x_{ij} - \log(|\Sigma_{y_{ij}=0}|)
になります。
ここで $x_{ij}$が無い $\log(|\Sigma_{y_{ij}=1}|)$ と $\log(|\Sigma_{y_{ij}=0}|)$ の項に注目してください。この2つの項は関数の入力値である$x_{ij}$に依存しないため、オフセット値としての機能しかないただの定数項です。今の場合、ある値より小さいければ棄却、そうでなければ採択という閾値判定方式なので省いても問題ありません。定数項を省き整理すると、
\delta(x_{ij}) = x_{ij}^{T}\Bigl(\Sigma_{y_{ij}=1}^{-1} - \Sigma_{y_{ij}=0}^{-1} \Bigr) x_{ij}
となります。
最後に $(\Sigma_{y_{ij}=1}^{-1} - \Sigma_{y_{ij}=0}^{-1})$ の部分を(半)正定値化してマハラノビス距離の形にすると、
d_{M}^{2}(x_i, x_j) = (x_i - x_j)^{T}\boldsymbol{M}(x_i - x_j)
となります。
これがKISSMEの距離算出式となります。
計算方法
ガウス分布の分散共分散行列を学習データから最尤推定します。これは結局のところ、学習データの分散共分散行列がガウス分布における分散共分散行列の最尤推定量となるので、下記の計算で求める事ができます。
\begin{align}
\Sigma_{y_{ij}=1} &= \sum_{y_{ij}=1}(x_i - x_j)(x_i - x_j)^{T} \\
\Sigma_{y_{ij}=0} &= \sum_{y_{ij}=0}(x_i - x_j)(x_i - x_j)^{T} \\
\end{align}
次に、これらの逆行列を求めます。分散共分散行列は正定値行列なので、正定値行列の逆行列より、その逆行列の固有ベクトルは同じで固有値は逆数となります。つまり、$n\times n$の分散共分散行列$\Sigma$とその逆行列$\Sigma^{-1}$は下記のような関係になります。(ただし、$\boldsymbol{u}_i$は長さ$1$の固有ベクトル)
\Sigma = \sum_{i=1}^{n}\lambda_{i}\boldsymbol{u}_i\boldsymbol{u}_i^T \; \; \; \; \;
\Sigma^{-1} = \sum_{i=1}^{n}\frac{1}{\lambda_{i}}\boldsymbol{u}_i\boldsymbol{u}_i^T
これを利用すれば、分散共分散行列の逆行列$\Sigma_{y_{ij}=1}^{-1}$および $\Sigma_{y_{ij}=0}^{-1}$を求める事ができます。
次に、その差である
\hat{\boldsymbol{M}} = (\Sigma_{y_{ij}=1}^{-1} - \Sigma_{y_{ij}=0}^{-1})
を求めます。$\Sigma_{y_{ij}=1}^{-1}$および $\Sigma_{y_{ij}=0}^{-1}$のどちらも正定値行列つまり対称行列なので、$\hat{\boldsymbol{M}}$は対称行列になる事はわかります。しかし、$\hat{\boldsymbol{M}}$が正定値行列になるとは限りません。マハラノビス距離の要件を満たすためには、なんとか操作して正定値行列にする必要があります。正定値行列であることと、固有値が全て正であることは同値 となるので、以下の手順に従って固有値を全て正の実数に置換し、正定値行列$\boldsymbol{M}$を得ます。
- $\hat{\boldsymbol{M}}$ の固有値と固有ベクトルを求める。
- 固有値のうち0以下の値を(例えば0.0001などの)ごく小さい任意の正の実数に置換する。
- 置換した固有値と固有ベクトルから正定値行列$\boldsymbol{M}$を再計算する。
$\boldsymbol{M}$は対称行列なので、
\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Lambda}\boldsymbol{U^{T}}
として計算できます。$\boldsymbol{U}$は長さ1の固有ベクトルを並べた直交行列、$\boldsymbol{\Lambda}$はその固有ベクトルに対応する固有値を対角成分に順に並べた対角行列です。
実験
LEAR ToyCars6 というデータセットを使って試してみます。
このデータセットは、14種類のおもちゃの車で構成され、全部で256枚の画像があります。この中から任意の2枚の画像を選び出し、同じ車かどうかを判別します。
データセットのうち学習に利用するのは7種類の車で、同一のペア1185個と異なるペア7330個を作って学習します。残りの7種類はテスト用です。
特徴量の作成
下記の手順にしたがって画像から特徴量を作成します。
- 画像を30x30の重複しないブロックに分割する
- HSVとLabの色空間の各チャンネル毎に24binでヒストグラム化する
- LocalBinaryPatternを用いて24binでヒストグラム化する
- 2と3で抽出した特徴量をコンキャットする
- PCAを用いて50次元まで圧縮する
上記の実装部分は下記になります。
import os
import numpy as np
import cv2
from skimage import feature
from sklearn.decomposition import PCA
IMAGE_WIDTH = 540
IMAGE_HEIGHT = 150
SPLIT_WIDTH = 30
SPLIT_HEIGHT = 30
PCA_DIMENSION = 50
class ImageData():
def __init__(self, image_id, file_name):
self.image_id = image_id
self.file_name = file_name
self.bgr_img = cv2.imread(file_name)
# 30x30blockで割り切れる数に画像サイズを変更しゼロパディング.画像毎にサイズが異なるためパディングサイズは都度算出
h, w, _ = self.bgr_img.shape
sub_height = IMAGE_HEIGHT - h
sub_width = IMAGE_WIDTH - w
self.bgr_img = np.pad(self.bgr_img, [(sub_height // 2, sub_height - (sub_height // 2)), (sub_width // 2, sub_width - (sub_width // 2)), (0,0)], 'constant')
# blockに分ける
v_split = self.bgr_img.shape[0] / SPLIT_HEIGHT
h_split = self.bgr_img.shape[1] / SPLIT_WIDTH
self.bgr_images = []
for h_img in np.vsplit(self.bgr_img, v_split):
self.bgr_images.extend(np.hsplit(h_img, h_split))
# Extraction Feature
self.raw_feature = []
self.raw_feature.extend(self.hsv_hist())
self.raw_feature.extend(self.lab_hist())
self.raw_feature.extend(self.lbp_hist())
def set_feature(self, feature):
self.feature = feature
def hsv_hist(self):
hist = []
for img in self.bgr_images:
img_ch = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
# Hue 定義域は[0,180)
hist.extend(cv2.calcHist([img_ch], [0], None, [24], [0,180]))
# Saturation
hist.extend(cv2.calcHist([img_ch], [1], None, [24], [0,256]))
# Brightness
hist.extend(cv2.calcHist([img_ch], [2], None, [24], [0,256]))
return [item for sublist in hist for item in sublist]
def lab_hist(self):
hist = []
for img in self.bgr_images:
img_ch = cv2.cvtColor(img, cv2.COLOR_BGR2Lab)
# L*
hist.extend(cv2.calcHist([img_ch], [0], None, [24], [0,256]))
# a*
hist.extend(cv2.calcHist([img_ch], [1], None, [24], [0,256]))
# b*
hist.extend(cv2.calcHist([img_ch], [2], None, [24], [0,256]))
return [item for sublist in hist for item in sublist]
def lbp_hist(self):
METHOD = 'uniform'
POINTS = 22
RADIUS = 9
hist = []
for img in self.bgr_images:
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# compute the Local Binary Pattern representation of the image
lbp = feature.local_binary_pattern(gray, POINTS, RADIUS, method=METHOD)
# histogram
(block_hist, _) = np.histogram(lbp.ravel(), bins=POINTS + 2, range=(0, POINTS + 2), density=False)
hist.extend(block_hist)
return hist
def main(image_files):
# ImageDataを生成
image_list = []
for (i_id, i_file) in enumerate(image_files):
image_list.append(ImageData(i_id, i_file))
# 特徴量をまとめPCAにかける
feature_list = []
for i in image_list:
feature_list.append(i.raw_feature)
feature_numpy = np.array(feature_list, dtype=np.float)
pca = PCA(n_components=PCA_DIMENSION)
x_pca = pca.fit_transform(feature_numpy)
# PCAで50次元まで削減した値を各イメージの特徴量として設定
for i, idata in enumerate(image_list):
idata.set_feature(x_pca[i, :])
行列Mを求める
学習データの特徴量から行列$\boldsymbol{M}$を求めます。
class CarPair():
def __init__(self, image_a, image_b, is_same, is_train):
self.image_a = image_a # ImageDataのインスタンスA
self.image_b = image_b # ImageDataのインスタンスB
self.is_same = is_same
self.is_train = is_train
def get_feature_diff(self):
return self.image_a.feature - self.image_b.feature
class Mahalanobis():
def __init__(self, mat):
self.mat = mat
def distance(self, vec):
dist = vec.dot(self.mat).dot(vec.T)
dist = np.diag(dist) # vecは1次元のベクトルではなく行列を想定
return dist
class PairSpace():
def __init__(self, vec):
self.vec = vec
# 平均
def mean(self):
mean = np.mean(self.vec, axis=0)
return mean
# 分散共分散行列
def cov(self):
self.sig = np.cov(self.vec.T)
return self.sig
# 分散共分散行列の逆行列
def inv_sig(self):
# 分散共分散行列を求める
sig = self.cov()
# 分散共分散行列の固有値・固有ベクトルを求める
la, va = np.linalg.eig(sig)
# 固有値の対角行列
la_diag = np.diag(la)
# 逆行列の固有値
inv_diag = np.diag(1/la)
# 実対称行列の性質から逆行列を求める
inv_sig = va.dot(inv_diag).dot(va.T)
return inv_sig
def to_semidefinite_mat(m):
# mの固有値・固有ベクトル
lm, vm = np.linalg.eig(m)
# Mの固有値の対角行列
m_diag = np.diag(lm)
# 固有値を全て0より大きい値に変更する
lmm = np.zeros(lm.shape[0])
for i in range(lm.shape[0]):
if lm[i] > 0:
lmm[i] = lm[i]
else:
lmm[i] = 0.00000001
# 改良Mの固有値の対角行列
mm_diag = np.diag(lmm)
# 正定値行列を求める
MM = vm.dot(mm_diag).dot(vm.T)
return MM
def main(all_car_pair_list):
# CarPairのインスタンスから、同じペアの特徴量の差を取得
same_vec = np.array(list(map(lambda c: c.get_feature_diff(), filter(lambda c: c.is_same and c.is_train , all_car_pair_list))))
# CarPairのインスタンスから、違うペアの特徴量の差を取得
diff_vec = np.array(list(map(lambda c: c.get_feature_diff(), filter(lambda c: not c.is_same and c.is_train , ))))
# PairSpaceオブジェクトを生成
same_space = PairSpace(same_vec)
diff_space = PairSpace(diff_vec)
# 分散共分散行列の逆行列を取得
same_inv_sig = same_space.inv_sig()
diff_inv_sig = diff_space.inv_sig()
# 調整した半正定値行列
met = to_semidefinite_mat(same_inv_sig - diff_inv_sig)
# Mahalanobisを生成
mahalanobis = Mahalanobis(met)
実験結果
テストデータに対して距離$d_{M}^{2}(x_i, x_j)$を算出した結果になります。同一ペア(赤)1044個と異なるペア(青)6337個の分布を表しており、横軸は距離で縦軸はペアの数です。

同一ペアの距離$d_{M}^{2}(x_i, x_j)$は、0付近に集中していて、異なるペアは広範囲に分布しています。
この2つのROCカーブは下図になります。
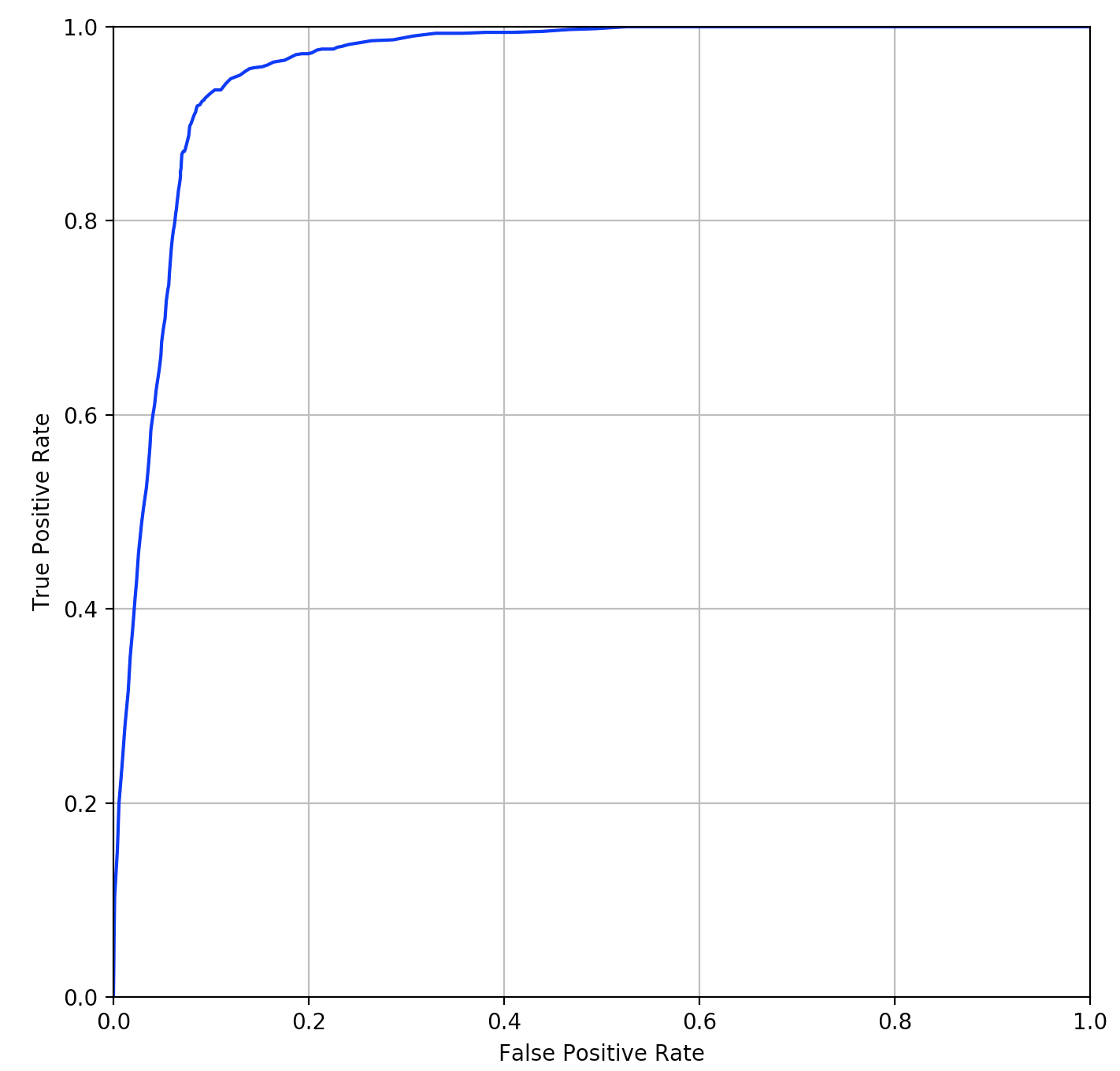
オリジナルの論文でもこのデータセットを使って実験をしていますが、それとほぼ同じぐらいの精度にはなったかと思います。この実験をやってみてわかったのは、KISSMEの距離学習の精度は、どのような特徴量を使うかで結構変わるという事です。実際に、特徴量を少し変えては精度を確認するということを繰り返しながら、手探りで進めていきました。このあたりはDeepLearningを使ってKISSMEの距離学習に合う特徴量を自動抽出するという応用も考えられそうな気がします。何か良いアイデアはないか、少し可能性を模索してみたいと思います。
正定値行列の逆行列
$\boldsymbol{A}$を正定値行列とする。固有値の定義より
$$
\boldsymbol{A}\vec{x} = \lambda\vec{x} \
$$
両辺の左から$\boldsymbol{A}$の逆行列を掛ける
\begin{align}
\boldsymbol{A}^{-1}\boldsymbol{A}\vec{x} &= \boldsymbol{A}^{-1}\lambda\vec{x} \\
\vec{x} &= \lambda \boldsymbol{A}^{-1}\vec{x} \\
\end{align}
定義より正定値行列は固有値が全て正の実数となる。つまり、$\lambda \neq 0$なので両辺を$\lambda$で割ると、
\frac{1}{\lambda}\vec{x} = \boldsymbol{A}^{-1}\vec{x} \\
これは固有値の定義に一致する。したがって、$\boldsymbol{A}^{-1}$の固有値は$\frac{1}{\lambda}$で、固有ベクトルは$\vec{x}$となる。また、全ての固有値は $\frac{1}{\lambda} > 0$ となるため、正定値行列の逆行列$\boldsymbol{A}^{-1}$も正定値行列となる。
-
M. Koestinger, M. Hirzer, P. Wohlhart, P. M. Roth, and H. Bischof. "Large scale metric learning from equivalence constraints." In CVPR, 2012. ↩
-
S. Liao, Y. Hu, X. Zhu, and S. Z. Li. "Person re-identification by local maximal occurrence representation and metric learning." In CVPR, 2015. ↩
-
Y. Yang, S. Liao, Z. Lei, and S. Z. Li. "Large scale similarity learning using similar pairs for person verification." In AAAI, 2016. ↩
-
Y. Yang, Z. Lei, S. Zhang, H. Shi, and S. Z. Li. "Metric embedded discriminative vocabulary learning for high-level person representation." In AAAI, 2016. ↩
-
S. Bak, and P. Carr. "One-Shot Metric Learning for Person Re-identification." In CVPR, 2017. ↩
-
E. Nowak and F. Jurie. "Learning Visual Similarity Measures for Comparing Never Seen Objects," In CVPR, 2007. ↩