Deep Metric Learning（深層距離学習）を使った打突音による異常検知 その2

前回の記事が、非常に反響が良かったので、調子に乗って続きを書きます。
今回は、前回やろうと思っていたけど手が回らなかったことと、前回課題として残っていたこと、ご指摘頂いたことを中心にやっていきます。（ご指摘頂いた皆様、有り難うございます！）
具体的には、AdaCosの追加と、類似木板での追加検証です。
（という書き出しで始めたのはよかったのですが、やっているうちに、どこをどういじったらどう変化したかを後日自分で見たときに思い出せるように、自分が後日見返したときに見やすいように、自分が後日見返したときに漏れがないように、という後日の自分の視点ばかりが先行して、結果、重箱の隅を突くような記事になってしまいました。あらかじめ、お詫び致します。。。）

手順・概要

基本的な手順は、前回と同じですが、おさらいも兼ねて、下記に記載します。

手順 1. 正常、及び、異常の木板を打突棒で打突
手順 2. USB接続されたマイクで録音
手順 3. 前処理
手順 4. 各種深層学習手法による訓練
手順 5. 学習したモデルを使って、推論の結果を確認

今回は、木板の種類を少し追加しました。（異常木板（材質②）です。）
また、前回と木板の呼び方を下記のように変更します。

正常木板 => 正常木板（材質①）
異常木板 => 異常木板（材質①）
類似正常木板 => 正常木板（材質②）
（今回追加） 異常木板（材質②）

正常木板（材質①）

正常木板1（13cm x 20cm)	正常木板3（13cm x 21.5cm)

異常木板（材質①）

異常木板5,6（13cm x 19cm)	異常木板7,8（13cm x 20cm)

正常木板（材質②）

正常木板（材質①）、異常木板（材質①）とは、材質が少し異なります。（ただし、類似した材質です。）

正常木板（材質②）11,12（13cm x 19cm)	正常木板（材質②）13,14（13cm x 20cm)	正常木板（材質②）15,16（13cm x 20cm)

異常木板（材質②）

正常木板（材質①）、異常木板（材質①）とは、材質が少し異なります。（ただし、類似した材質です。）

異常木板（材質②）31〜36（13cm x 19cm)	異常木板（材質②）37〜42（13cm x 20cm)

追加検証 〜 異常木板（材質②）（前回呼称：類似木板）の推論

前回は、正常のデータしかなかった木板（材質②）（前回呼称：類似木板）の異常データを推論にかけてみます。
（前回の検証では、最も結果のよかったResnet18ベースのArcFaceでの推論において、正常木板（材質②）（前回呼称：類似正常木板）は、正常木板（材質①）とほとんど同じところにプロットされました。つまり、ほとんど同じ性質のデータだという予測が出たわけです。）

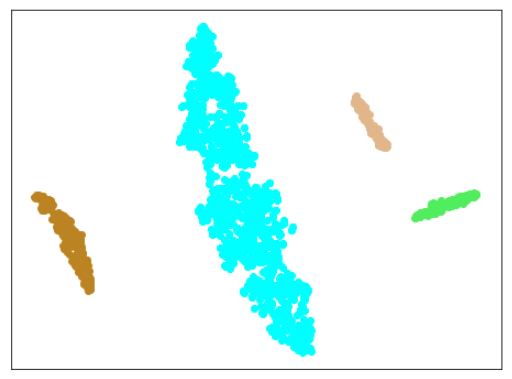
（参考）前回の結果（再出力）

※前回と同様の作業を行いましたが、今回はプロットするクラス数が多く、分かりやすくするために、番号と色の対応が前回と少し異なっています。（混乱を招くと思いますが、ご容赦下さい。。。）
下図は、新しい色配置でのプロットです。

Lr = 0.01, Epc = 100, SGD, CrossEntropyLoss	同左	同左
学習データのみ	学習データ+異常木板（材質①）7,8	学習データ+正常木板（材質②）

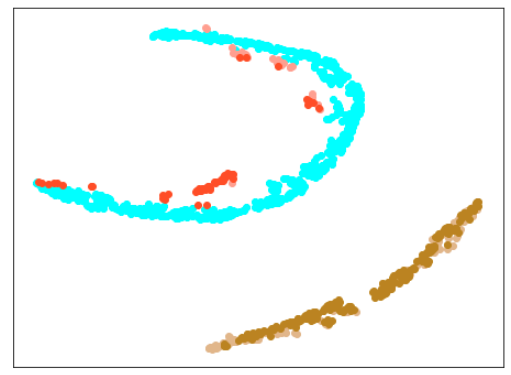学習データ	異常木板（材質①）7,8	正常木板（材質②）
水色 - 正常木板（材質①）1, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	上記以外の色全て（水色を除く青系）

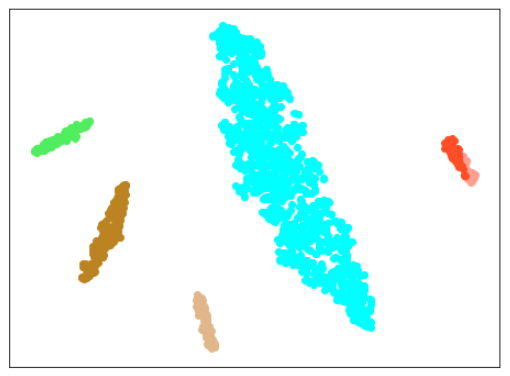
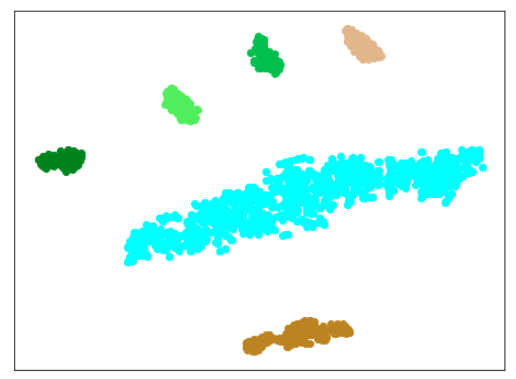
さて、今回追加した異常木板（材質②）では、どうでしょうか？

Lr = 0.01, Epc = 100, SGD, CrossEntropyLoss
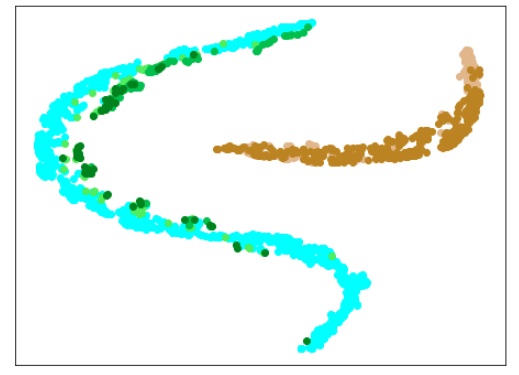薄い緑色 - 異常木板（材質②）31 緑色 - 異常木板（材質②）32 濃い緑色 - 異常木板（材質②）33

縦に切り込みを入れた異常木板（材質②）31, 32, 33のどのデータでも、異常を検出できていません。
つまり、前回の結果はぬか喜びだったということが分かりました。。。がっかりです。。。

AdaCos(Resnet18)

では、気を取り直して、精度を上げるためにいくつかの作業を実施してきます。

今回は、前回使わなかった、AdaCosを試してみます。

AdaCosの解説については、下記に素晴らしい解説があります。
https://qiita.com/ninhydrin/items/797a308c864e9238c71e
（ちなみに、難しすぎて、まだ、あまり理解していません。。。）

また、下記のサイトもおすすめです。
https://cpp-learning.com/adacos/

AdaCosのすごいところは、ハイパーパラメータを自動で設定してくれるところです。
（これは、本当にすごい！）

Metric Learningには、m（マージンパラメータ）、s（スケールパラメータ）といったハイパーパラメータが存在します。
実は、これまでの検証では、ここはほとんど無視してやってきましたが、実際には、このパラメータ次第で、結果が大きく変わります。
（つまり、これまでの検証は、ある意味、相当な手抜きで、信用できないものだったわけです。。。）
AdaCosでは、これらのハイパーパラメータを自動で決定します。

実装は、下記を参考にしています。
https://github.com/4uiiurz1/pytorch-adacos
（というより、またまた、ほとんどそのまま使っています。）

モデル

Resnet18のモデルは下記の通りです。
参考にしたサイトの実装をそのまま使っていますが、features以降が前回とは大きく異なっています。

ResNet_IR(
  (backbone): ResNet(
    (conv1): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
    (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (relu): ReLU(inplace=True)
    (maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
    (layer1): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer2): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer3): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (layer4): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
    (fc): Linear(in_features=512, out_features=1000, bias=True)
  )
  (features): Sequential(
    (0): Conv2d(1, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
    (1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
    (2): ReLU(inplace=True)
    (3): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
      (1): BasicBlock(
        (conv1): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (4): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(64, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(64, 128, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (5): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(128, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(128, 256, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
    (6): Sequential(
      (0): BasicBlock(
        (conv1): Conv2d(256, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (downsample): Sequential(
          (0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
          (1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        )
      )
      (1): BasicBlock(
        (conv1): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (relu): ReLU(inplace=True)
        (conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
        (bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
    )
  )
  (bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (dropout): Dropout2d(p=0.5, inplace=False)
  (fc): Linear(in_features=28672, out_features=50, bias=True)
  (bn2): BatchNorm1d(50, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)

AdaCos(Resnet18)を前回と同じデータ（木板（材質①）のみ）で訓練

結果

Lr = 0.1, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
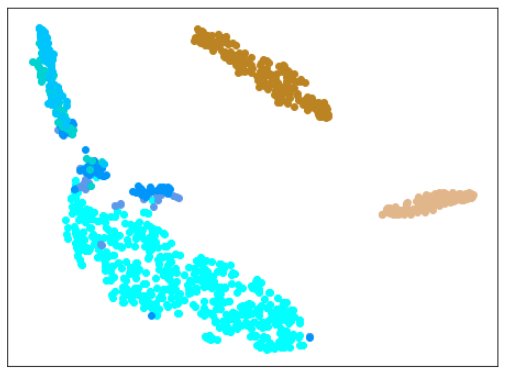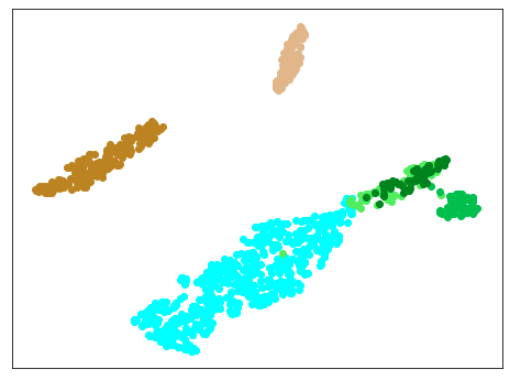学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

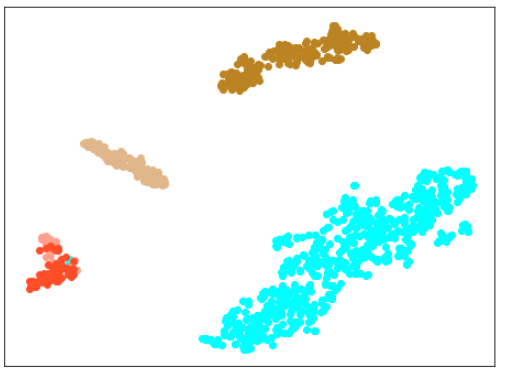
Lr = 0.3, Epc = 100, SGD, CrossEntropyLoss
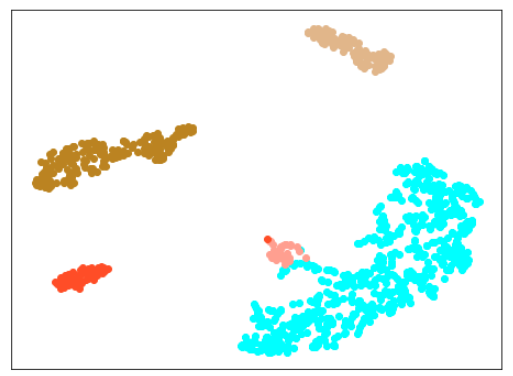学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
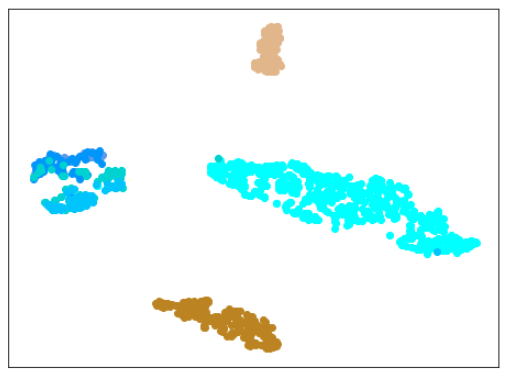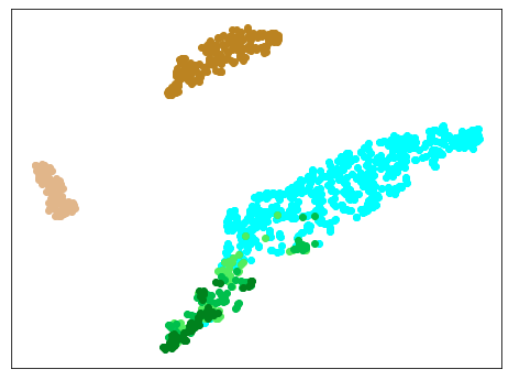学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

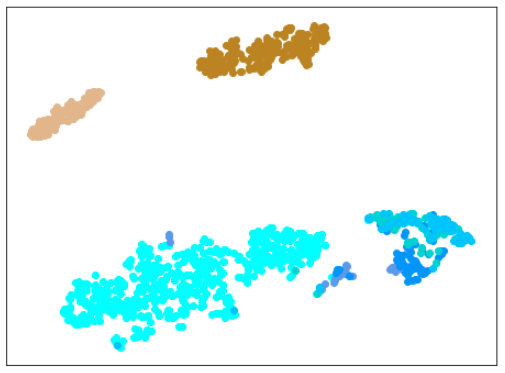
Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
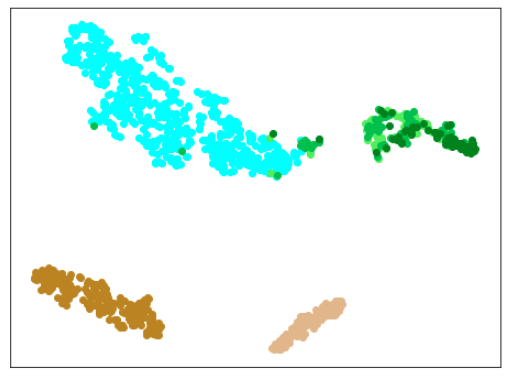学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

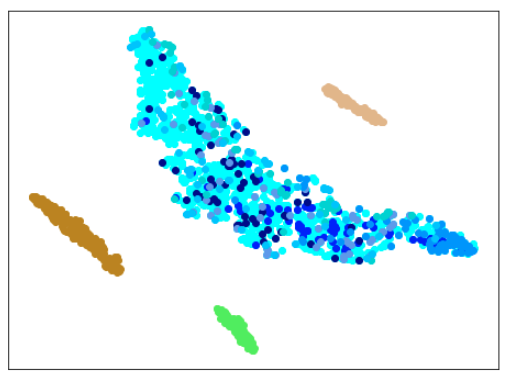
学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33

考察

学習率（lr）は、0.3か0.5がよさそうです。
（他のモデルに比べて、適した学習率が高いのは、層が厚いからか、BatchNormalizationの影響か、DropOutの影響か、AdaCosによるものかは、今後の確認が必要です。）
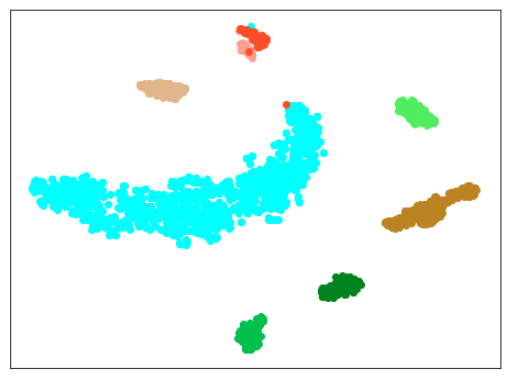
ただ、lr=0.3の場合は、正常木板（材質②）11〜16が正常だと認識できておらず、また、異常木板（材質②）31〜33も分離できていません。
また、lr=0.5の場合は、異常木板（材質②）31〜33の分離はできているものの、正常木板（材質②）11〜16が正常だと認識できていません。
結論としては、訓練に使っていない木板（材質②）については、正しく認識できていないわけです。
（エポック数を200にして試して見ましたが、結果は同じでした。）

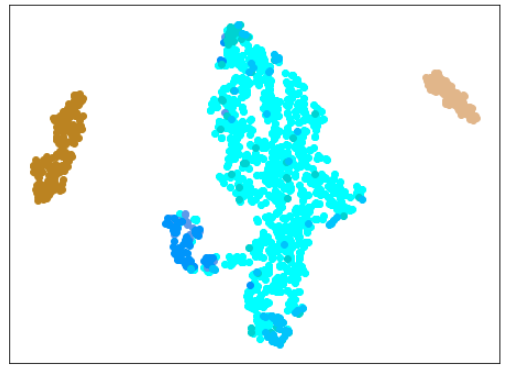
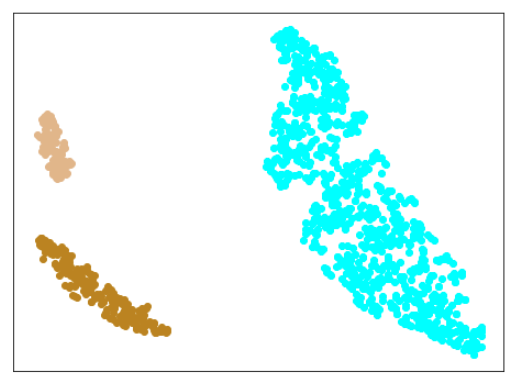
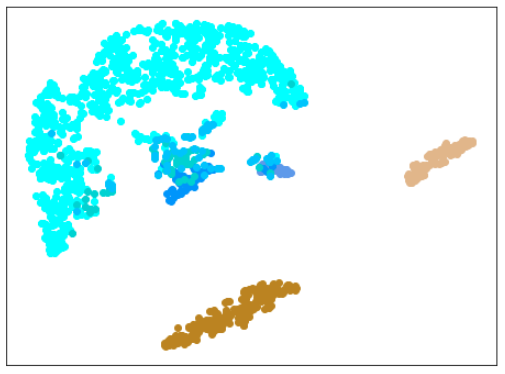
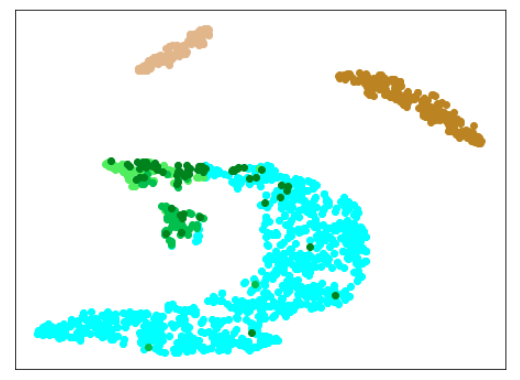
AdaCos(Resnet18) 木板（材質①）と正常木板（材質②）11,12を訓練に使用

まずは、材質②の正常木板11,12だけを訓練データに追加します。

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12

結果

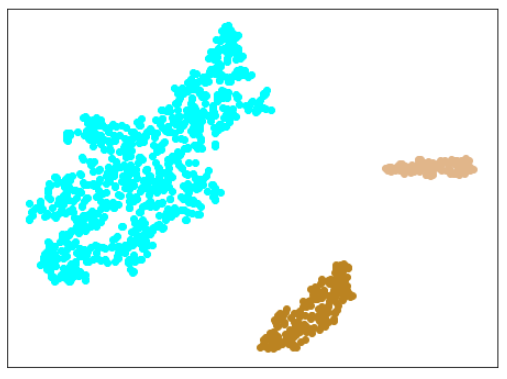
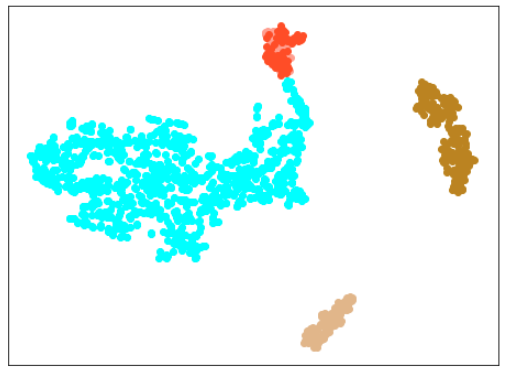
Lr = 0.3, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

やはり、木板（材質②）については、うまく分離・認識できていません。

AdaCos(Resnet18) 木板（材質①）、正常木板（材質②）11,12、異常木板（材質②）31を訓練に使用

では、次に、材質②の異常木板も訓練データに追加します。
まずは、異常木板（材質②）31のみを追加します。
また、ここからは、異常木板（材質②）37〜39をテストデータに追加します。

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12
異常木板（材質②）31

結果

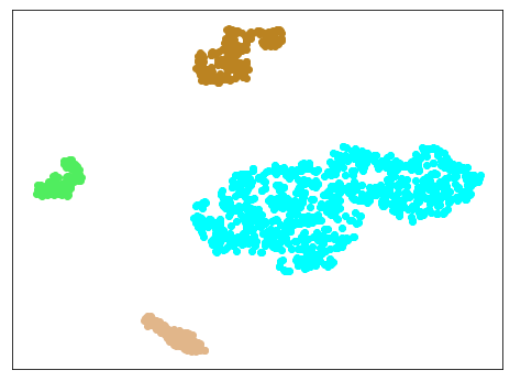
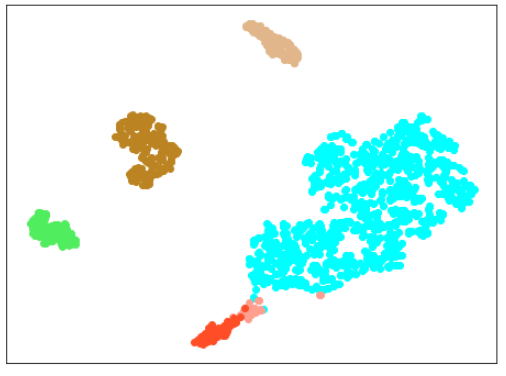
Lr = 0.5, Epc = 30, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
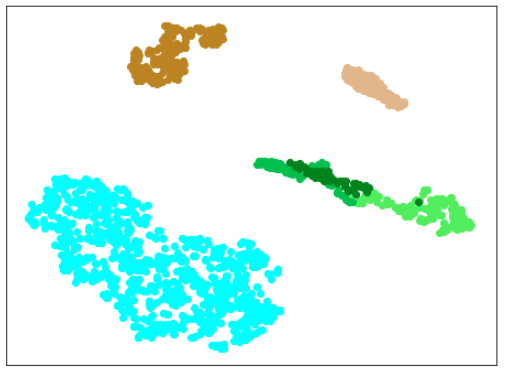学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
学習データ+異常木板（材質②）37〜39

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
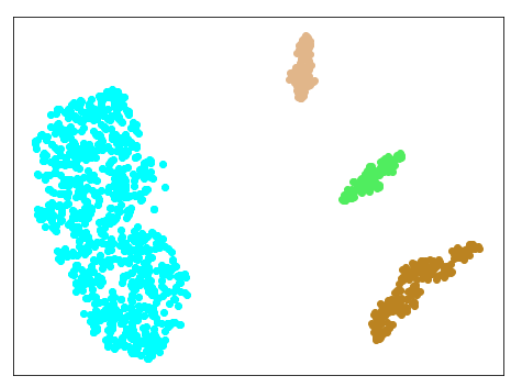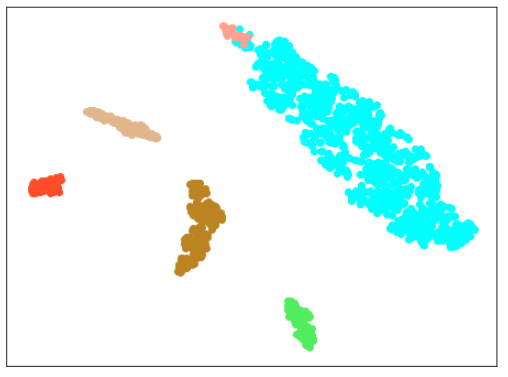学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
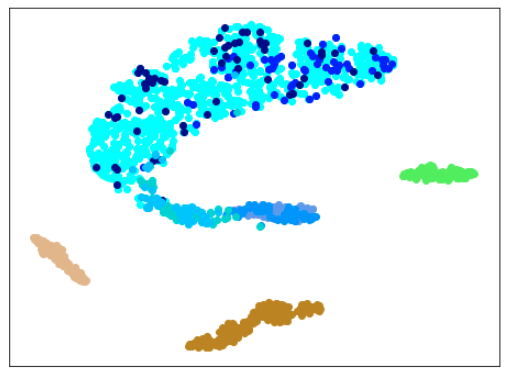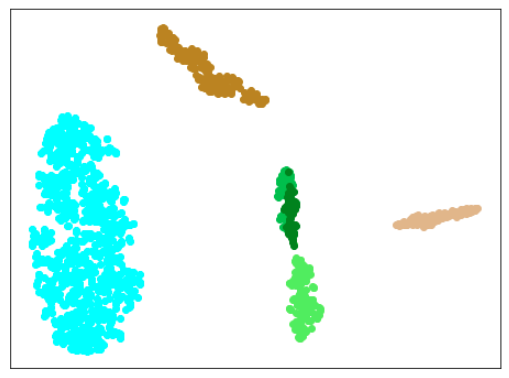学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
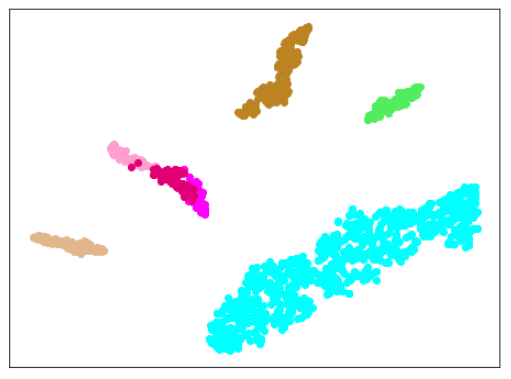学習データ+異常木板（材質②）37〜39

学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

エポック30は学習不足のようです。
エポック100では、ずいぶん良くなりましたが、（訓練に使用した正常木板（材質②）11,12以外の）正常木板（材質②）13,14,15,16が、うまく正常木板だと認識できていません。
（ちなみに、異常木板（材質①）7を正常だと認識しています。学習の度に、同じデータでも捕まえる特徴が違うので、結果が異なるのですが、異常木板（材質①）7は正常（もしくは、それに近い）と認識されることが時々あるのが面白いです。）

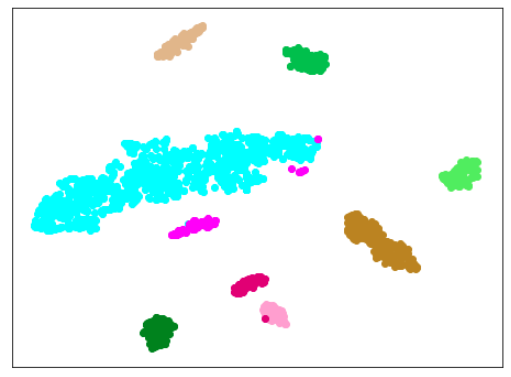
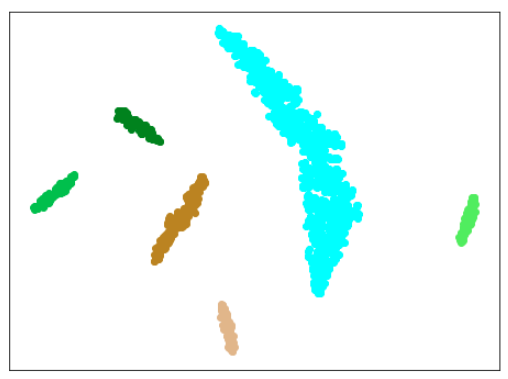
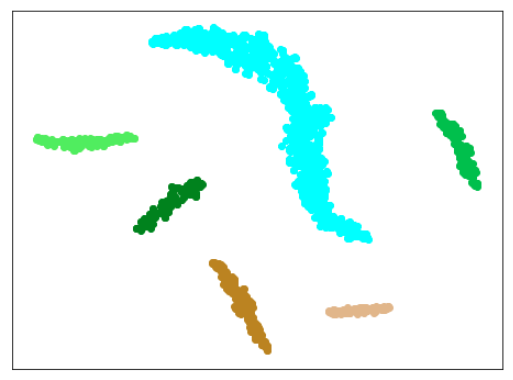
AdaCos(Resnet18) 木板（材質①）、正常木板（材質②）11,12、異常木板（材質②）31,32,33を訓練に使用

次に、異常木板（材質②）32,33も訓練データに追加します。

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12
異常木板（材質②）31,32,33

結果

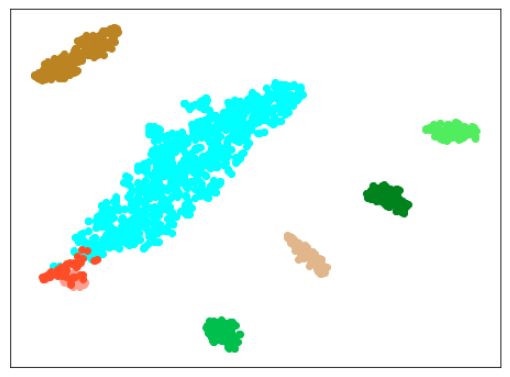
Lr = 0.5, Epc = 30, SGD, CrossEntropyLoss
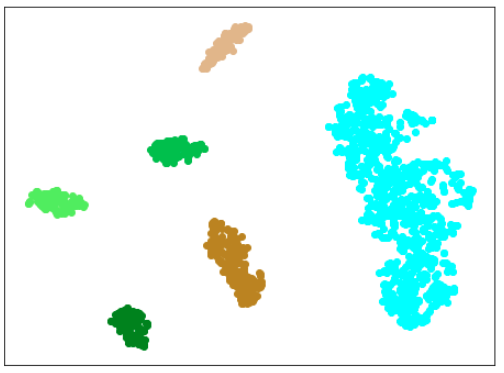学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
学習データ+異常木板（材質②）37〜39

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
学習データ+異常木板（材質②）37〜39

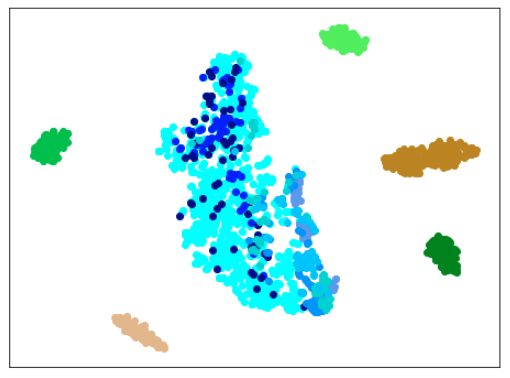
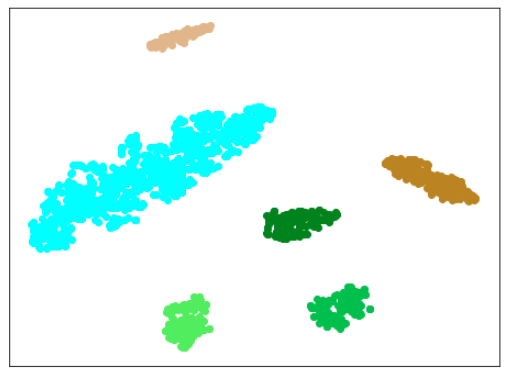
学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

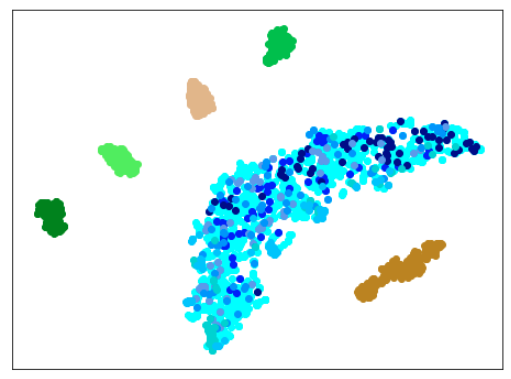
わずかですが、さらに良くなりました。
しかし、まだ、（訓練に使用した正常木板（材質②）11,12以外の）正常木板（材質②）13,14,15,16が、うまく正常木板だと認識できているとは言えません。
（ちなみに、異常木板（材質①）7を正常だと認識しています。学習の度に、同じデータでも捕まえる特徴が違うので、結果が異なるのですが、異常木板（材質①）7は正常（もしくは、それに近い）と認識されることが時々あるのが面白いです。）

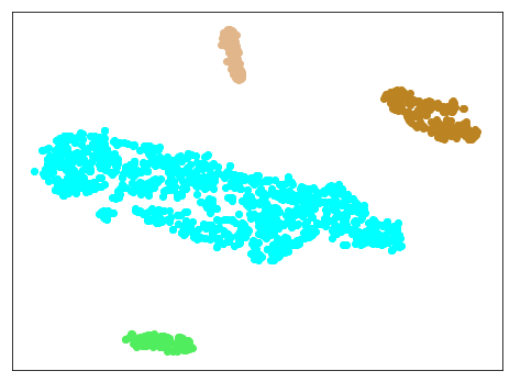
AdaCos(Resnet18) 木板（材質①）、正常木板（材質②）11,12,13,14、異常木板（材質②）31を訓練に使用

次は、異常木板（材質②）を31だけに戻して（32,33を訓練データから除外する）、さらに、正常木板（材質②）13,14を訓練データに追加します。

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12,13,14
異常木板（材質②）31

結果

Lr = 0.5, Epc = 30, SGD, CrossEntropyLoss
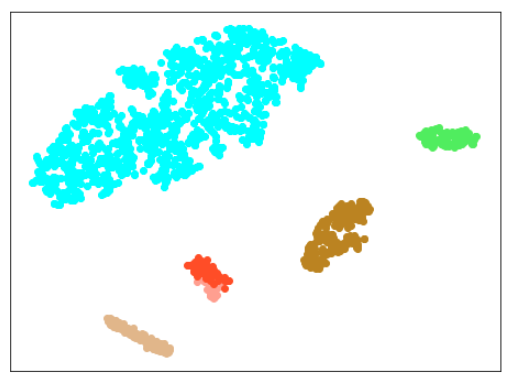学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
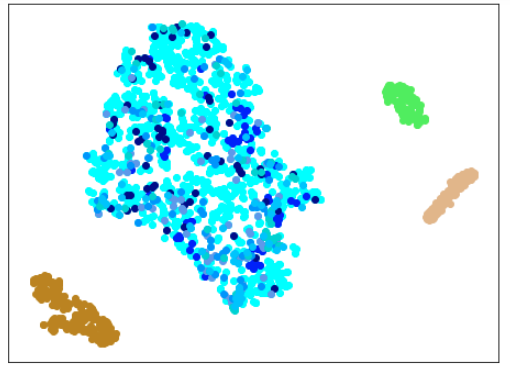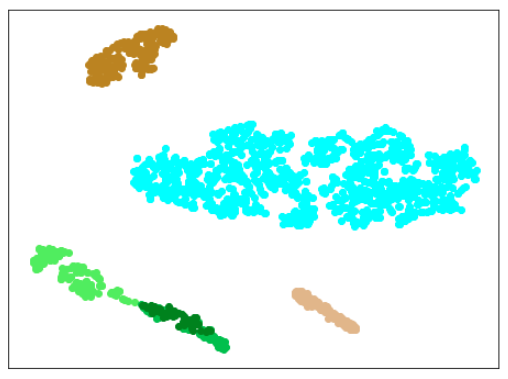学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
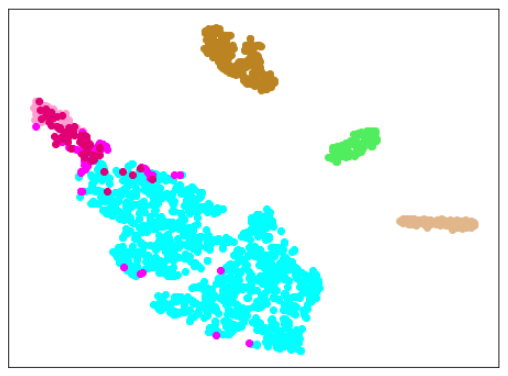学習データ+異常木板（材質②）37〜39

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33
学習データ+異常木板（材質②）37〜39

学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

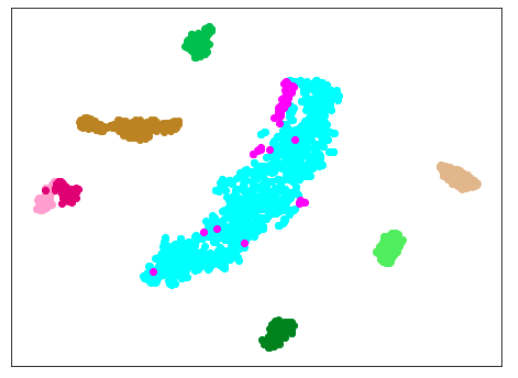
正常木板（材質②）13,14を追加したことで、正常木板（材質②）15,16をきちんと認識するようになりましたが、異常木板（材質②）32,33を削除したことで（異常木板（材質②）32,33には影響がなかったものの）、異常木板（材質②）39の一部が（なぜか4つだけ。。。）、正しく認識されなくなりました。
ただ、これなら、やりたいことが、ほぼできていると言っても問題ないかと思います。
目的は、正常とそれ以外を見分けるということなのですが、わずかな違いを見つけて、正常とは異なると認識する（違う場所にプロットする）傾向が強いので、正常の特徴をしっかり把握させるために、正常データを多めに訓練にあたえて、少量の異常データを与えるとうまくいくというのが大筋では言えるように思います。

AdaCos(Resnet18) 木板（材質①）、正常木板（材質②）11,12,13,14、異常木板（材質②）31,32,33を訓練に使用

次は、異常木板（材質②）32,33と正常木板（材質②）13,14をどちらも訓練データに含めます。

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12,13,14
異常木板（材質②）31,32,33

結果

Lr = 0.5, Epc = 30, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

エポック30では、学習不足ですが、エポック100はよさそうです。
正常木板（材質②）11,12に加え、13,14を訓練データとして使用しているので、訓練データに含まれていない正常木板（材質②）15,16が正常として認識されています。
訓練データとして使っていない異常木板（材質①）7,8もきちんと正常から離れてたところにプロットされています。
同じく、訓練データとして使っていない異常木板（材質②）37〜39もきちんと正常から離れてたところにプロットされています。

とりあえず、正常と異常を見分けるという目的は達成されました。
結論としては、やはり、ある程度の量や種類の訓練データを与える必要があるという当たり前のものでしたが、これはこれで使えそうだな、とも思いました。

さらなる追加検証

ここからは、ほとんど趣味の追加検証です。

AdaCos(Resnet18) 木板（材質①）、正常木板（材質②）11,12、異常木板（材質②）31,32,33を訓練に使用 ＋ 訓練データの水増し

先ほど追加した正常木板（材質②）13,14を取り除いて、代わりにData Augmentationっぽいことを行います。
これまでは、ひとつのwavファイルから2つの訓練データを作成してきましたが、これを４つに増やします。
また、プロットについては、先ほどはすべての訓練データをプロットにも使用していましたが、ひとつのwavファイルから4つの訓練データを作成すると訓練データが多くなり、また、バラツキも出るので、ここからは、ひとつのwavファイルからひとつの点（プロット）のみになるようにします。

これまで使用していたデータ①	これまで使用していたデータ②

ここで追加したデータ①	ここで追加したデータ②

訓練データ

正常木板（材質①）1,3
異常木板（材質①）5,6
正常木板（材質②）11,12
異常木板（材質②）31,32,33

結果

Lr = 0.5, Epc = 100, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
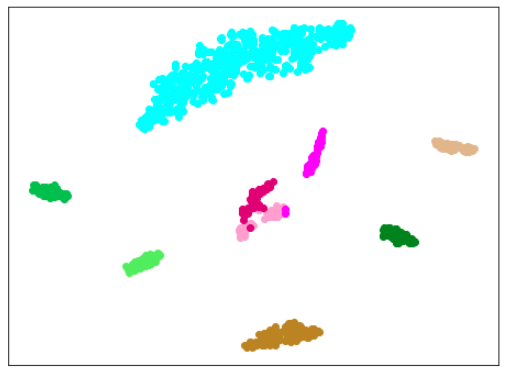学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

Lr = 0.5, Epc = 30, SGD, CrossEntropyLoss
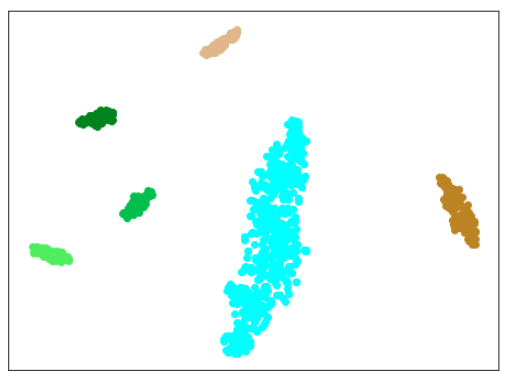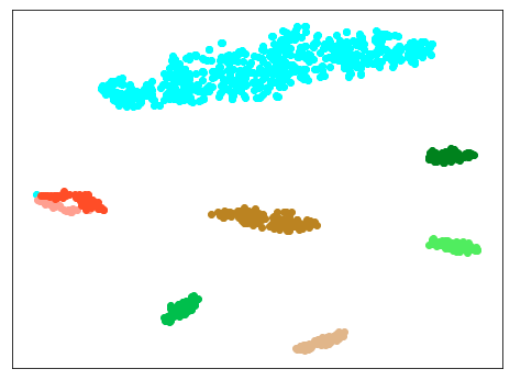学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
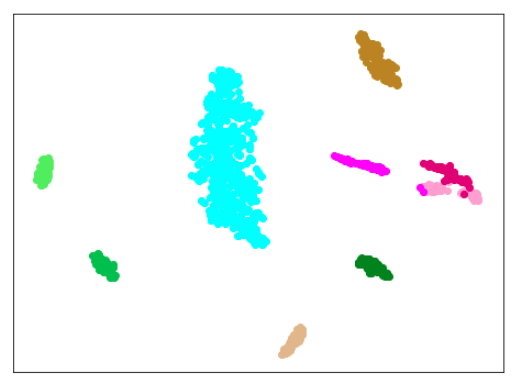学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

Lr = 0.5, Epc = 15, SGD, CrossEntropyLoss
学習データのみ 正常木板（材質①）1, 3+異常木板（材質②）5, 6	学習データ+異常木板（材質①）7, 8
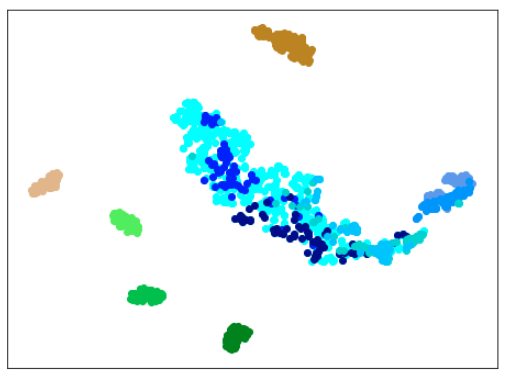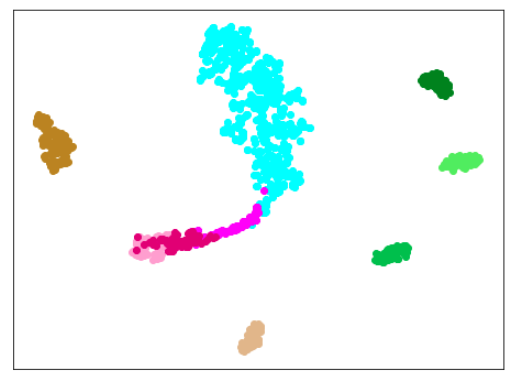学習データ+正常木板（材質②）11〜16	学習データ+異常木板（材質②）31〜33

学習データ	異常木板（材質①）7,8	正常木板（材質②）	異常木板（材質②）その1	異常木板（材質②）その2
水色 - 正常木板（材質①）１, ３ ベージュ - 異常木板（材質①）５（左端） 薄い茶色 - 異常木板（材質①）6（右端）	薄いオレンジ色 - 異常木板（材質①）7 オレンジ色 - 異常木板（材質①）8	紺 - 正常木板（材質②）11 濃紺 - 正常木板（材質②）12 水色・紺・濃紺以外の青系 - 正常木板（材質②）13〜16	薄い緑 - 異常木板（材質②）31 緑 - 異常木板（材質②）32 濃い緑 - 異常木板（材質②）33	薄いピンク - 異常木板（材質②）37 ピンク - 異常木板（材質②）38 濃いピンク - 異常木板（材質②）39

考察

思った通り、100ではエポック数が多すぎました。
（訓練データの数を２倍にしているので、当たり前かとも思いますが、ここまで影響が出るのは意外です。）
15で、すでにある程度にクラス間の分離ができており、その後は不必要に、個々のデータに適用していっているように見えます。
しかし、15では、できていない異常木板（材質②）37〜39の分離が、エポック数30ではできています。
当たり前ですが、適切なエポック数を設定することは重要ですね。

ただ、このモデルでも、正常木板（材質②）13,14,15,16を正常と認識することができておらず、正常木板（材質②）13,14を訓練データに含めたモデルには敵わないようです。

結果として、ひとつのwavファイルから4つの訓練データを作成するという作業は、あまり意味がないようでした。
同じ木板の同じ箇所を60回ずつ叩いているので、訓練データの数を増やすことには意味がないのは分かっていましたが、横方向に数パターンのシフトをすることで、うまく特徴を捉えられないかと思いましたが、今回はダメでした。
（とはいえ、この手法がいつも意味がないということではないと考えます。）

あとがき

ここで、当然のように、前回結果のよかったArcFace(Resnet18ベース）とTripletLoss（浅いNNベース）で、今回の内容を試したらどうなるんだ？という疑問が湧くわけです。
もちろん、やります。
なのですが、少し長くなりすぎたので、次回にします。

参考URL

https://qiita.com/ninhydrin/items/797a308c864e9238c71e
https://cpp-learning.com/adacos/
https://github.com/4uiiurz1/pytorch-adacos

参考にさせて頂いたサイトの作者様、本当に有り難うございます。