More than 3 years have passed since last update.

Deep Metric Learning 入門

Last updated at 2019-11-23Posted at 2019-10-16

こんにちは. Qiita初投稿です.
私は生体認証の研究をしており, 最近Deep Metric Learning(以下DML)なるものをよく目にするようになりました. いくつかの論文を読み, 自身の頭の整理という意味も込めて解説をしてみたいと思います.
それではよろしくお願いいたします.

0. 注意 & 表記

注意

本記事では基本的に画像に対するDMLを扱っています. グラフや言語に関するDMLは扱っていません.
レベルとしてはCNNによる画像の多クラス分類の原理を分かっている方であれば十分に理解できる内容だと思います.

表記

表記	意味
$\theta$	CNNの学習パラメタ
$\hat{\theta}$	学習を終えたCNNのパラメタ
$f(・;\theta)$	入力・に対するCNNの出力ベクトル
$f(・;\hat{\theta})$	入力・に対する学習を終えたCNNの出力ベクトル
$L(・;f)$	入力・に対するCNN $f(・;\theta)$のLoss値
$x_i^c$	全データの中のi番目のサンプルでcクラスに属している(添字が無いときは特に重要でない場合を表している)
$y_i$	$x_i$が属しているクラス

1. Deep Metric Learning 概要

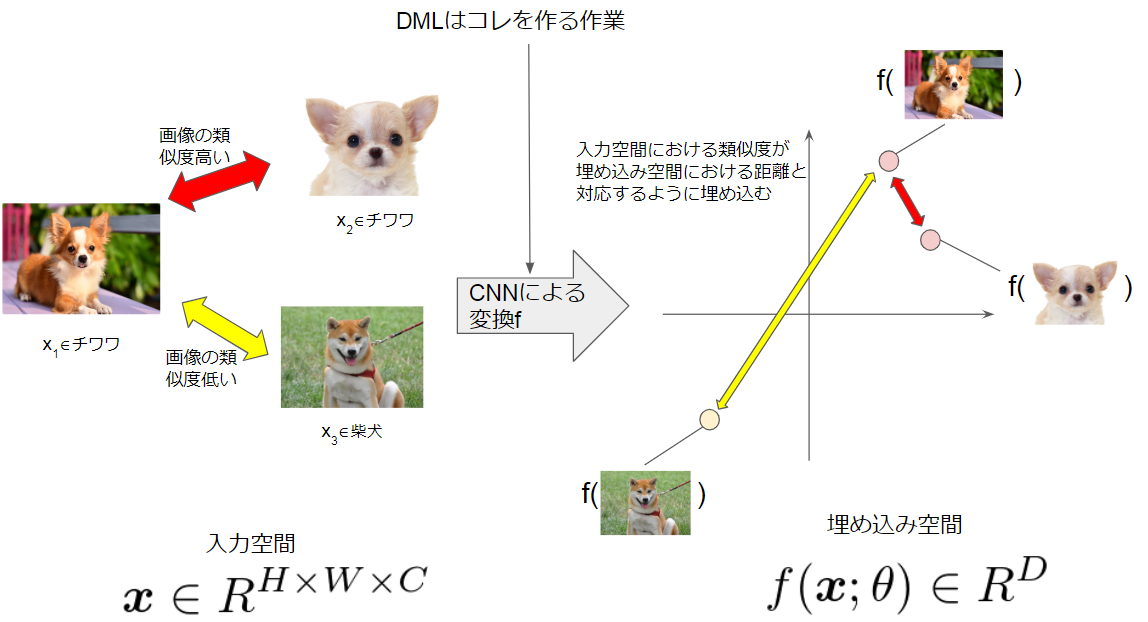
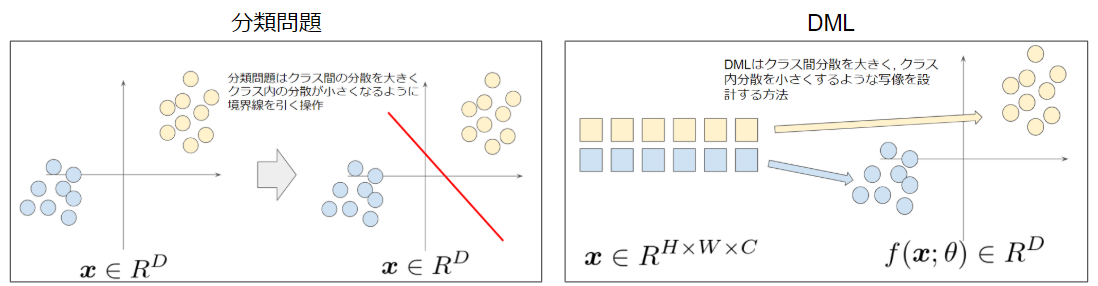
Metric Learningとは日本語で「距離学習」と呼ばれる方法で, 入力空間におけるサンプル同士の類似度が, ユークリッド距離やコサイン類似度などの尺度と対応するように別空間に埋め込むための変換を学習する方法です. この別空間のことを埋め込み空間や特徴空間といいます(以後, 埋め込み空間で統一). DMLは, この変換をDeep Neural Networkによって非線形に設計します. とりわけ入力が画像であれば, DNNとしてConvolutional Neural Networkが用いられます.

犬種を用いた例をあげます.
$x_1$, $x_2$はチワワの画像を表しており, $x_3$は柴犬の画像を表しています. $x_1$と$x_2$は同じ犬種なので画像としての類似度が高いと言えます. 一方で$x_1$と$x_3$は異なる犬種なので類似度が低いです. ここで$Similarity(画像A,画像B)$なる関数を考えてみましょう. DMLとは, 以下に示す通りSimilarity()の大きさを距離に対応させるような$f$を学習させる方法なのです.

Similarity(x_1, x_2) = ||f(x_1)- f(x_2)||^2_2\\
Similarity(x_1, x_3) = ||f(x_1)- f(x_3)||^2_2\\
Similarity(x_1, x_2) > Similarity(x_1, x_3) \Rightarrow ||f(x_1)- f(x_2)||^2_2 < ||f(x_1)- f(x_3)||^2_2

2. Deep Metric Learning の意義

DMLを研究する意義は, 様々なタスクに利用できるからです. DMLが利用されるタスクは以下のものが挙げられます.

画像検索
生体認証
- verification
- identification
クラスタリング
異常検知
zero-shot-learning

本章では画像検索と生体認証(verification, identification)について軽く説明をします.

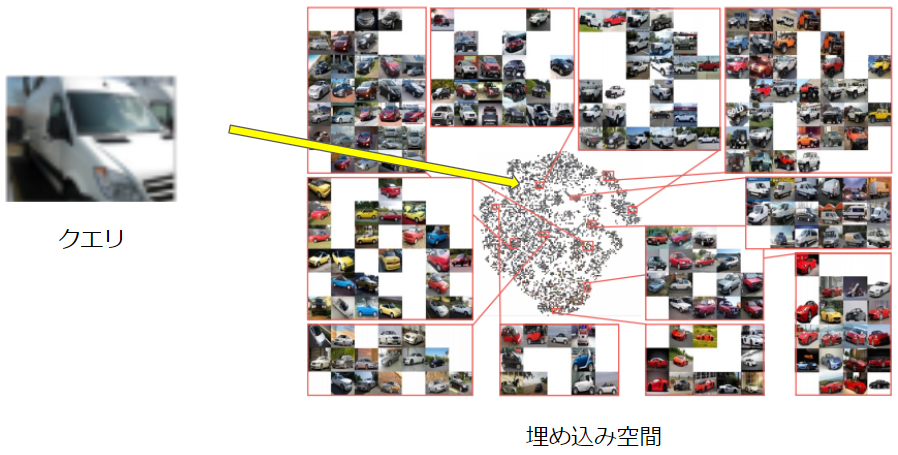
画像検索

画像検索はクエリ画像$x_{query}$に対して, データベース$\{x_i\}_{i=1,\cdots, N}$の中からクエリ画像に似ている画像$x_i$を見つけるというタスクです. 学習フェーズではデータベースの画像を用いてDMLを行い, $f(・;\hat{\theta})$ を作ります. 次に$f(・;\hat{\theta})$を用いて, データベース画像を埋め込みます. 検索フェーズでは, クエリ画像を変換$f$に入力し埋め込み空間上で$f(x_{query}; \hat{\theta})$の近傍にある点$f(x_i;\hat{\theta})$となる画像$x_i$を検索結果として提案します.

x_i = argmin_{x_i} || f(x_{query};\hat{\theta}) - f(x_i;\hat{\theta})||^2_2

生体認証(verification)

verificationとは, 1つの取得データ$x_p$と1つの登録データ$x_g$が同一人物のものか？異なる人物のものか？を判定するタスクです. スマートフォンへのログインなどに用いられます. 従来, $x_p$と$x_g$をSIFTやLBPといった特徴抽出器で特徴ベクトルを抽出し, その特徴ベクトル同士の距離や類似度を元に判定していました.

DMLは「入力空間における類似度が埋め込み空間における距離と対応するように変換を学習させる方法」なので, SIFTやLBPなどの特徴抽出器の代用となり得ます. またこれらの特徴抽出器よりもデータ分布を反映した変換を獲得することが出来ます.

||f(x_p;\hat{\theta}) - f(x_g;\hat{\theta})||^2_2 < Threshold \Rightarrow y_p = y_g

例えば, 明るい場所に設置してある認証装置と暗い場所に設置してある認証装置を考えてみます. 人間の手による特徴抽出器では明るい画像に適した前処理・特徴抽出器, 暗い画像に適した前処理・特徴抽出器を適宜選ばなければなりません. 一方でDMLであれば, データから学習してくれるため「明るい画像データセット」「暗い画像データセット」で事前学習を行えばその環境に見合った適当な変換が獲得できます.

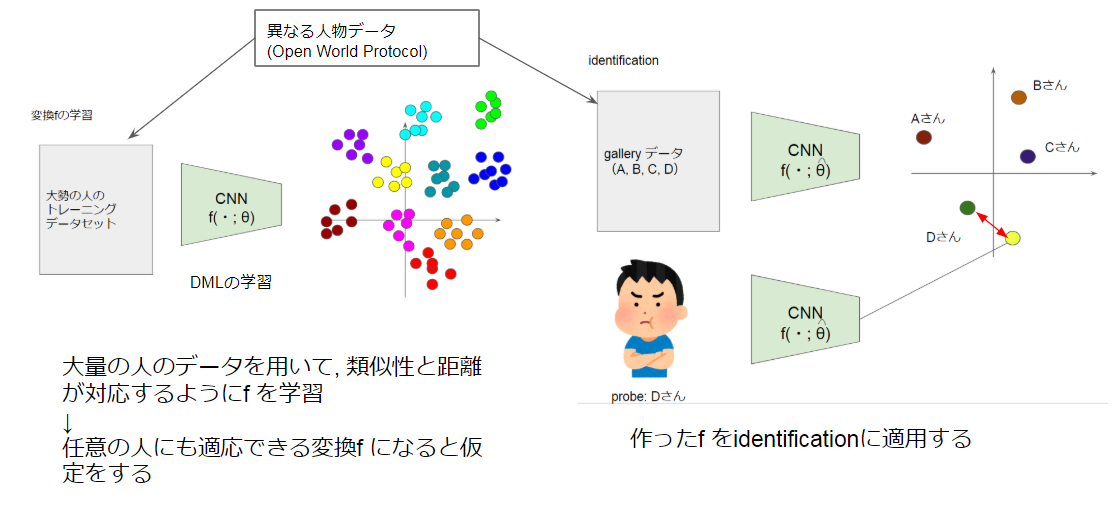
生体認証(identification)

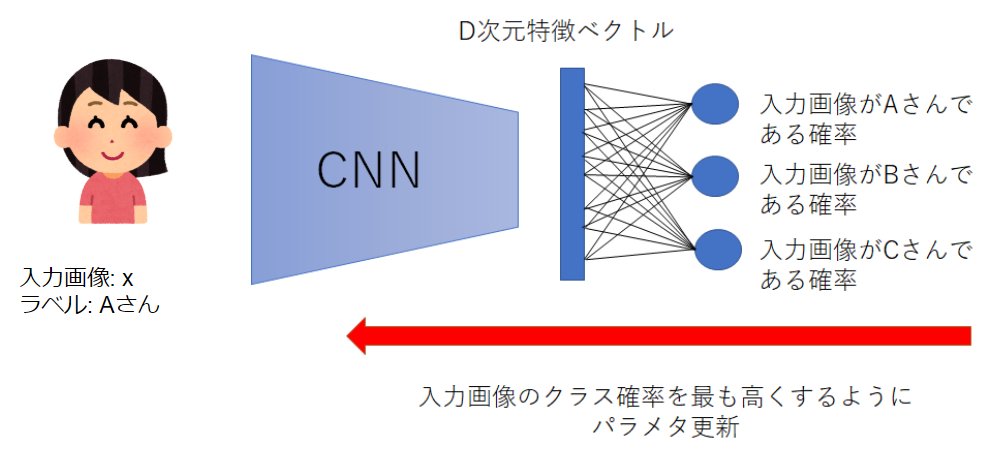
identificationは, 入力画像$x_p$がデータベースに登録されている人物の誰か？を判定する入館などに使われるタスクです. これを実現する方法として下図のようなCNNによる多クラス分類を想像した人は多いのではないでしょうか？

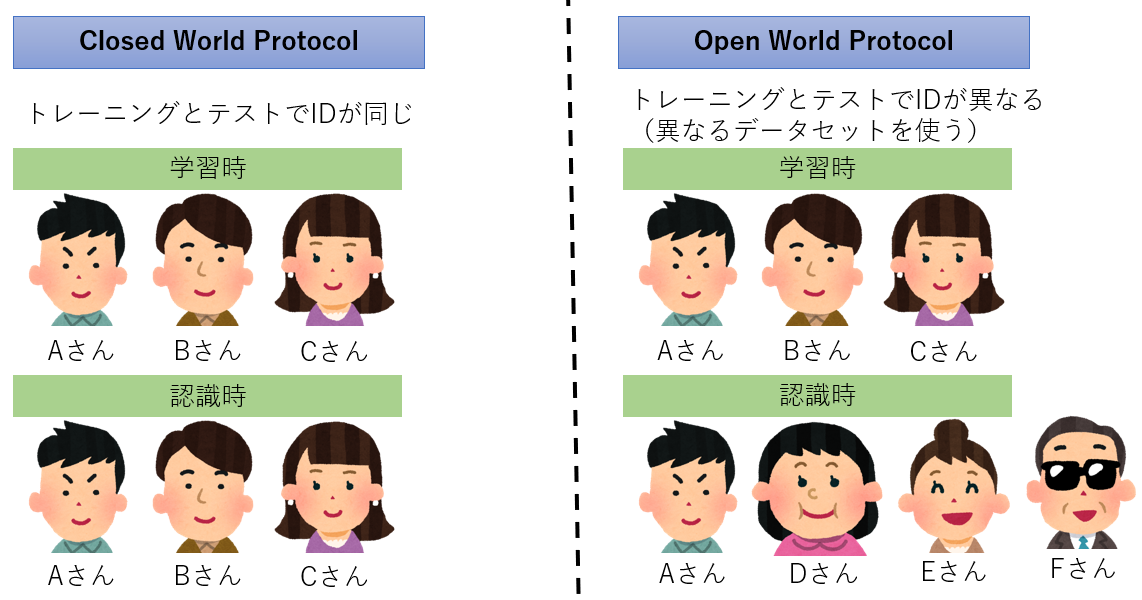
しかし, この方法だと出力層が限定されており, A, B, Cさんでしか認識できません. Dさんも認識したいと思ったときネットワークの出力層の個数を変更し, パラメタを再学習させる必要があります. この例では小規模ですが, 認識対象となる人物が100, 1千, 1万と増えていったら再学習はコストに見合いません. 上図の例のようにトレーニングとidentificationで同じ人物を使うことをある論文では"Closed World Protocol"と呼んでいました. 実世界で有用なのは, トレーニングとidentificationのデータが, 異なる人物で構成されている"Open World Protocol"の方です.

Open World Protocolで利用されるのがDMLです. 学習フェーズでは大量の人物の画像を用いてDMLで変換を学習させます. 変換$f(・;\hat{\theta})$は大量の人物の類似度を距離として反映した埋め込みを実現するため, 任意の人物に対しても適用できるという仮定のもと, identificationフェーズに適用します.

y_g = id\left\{argmin_{x_g} || f(x_{p};\hat{\theta}) - f(x_g;\hat{\theta})||^2_2\right\}

よくある誤解

よく間違えられる事項として, 「DMLはクラス分類はできないのか？」という質問が来ます. フィッシャーの線形判別分析を思い出してください. これは, 2クラスのクラス内分散が最小に, クラス間分散が最大となるような「境界線を引くアルゴリズム」です. 一方で, DMLは埋め込み空間上でクラス内分散が小さく, クラス間分散が大きくなるような「変換を学習させるアルゴリズム」です. したがって, DMLは分類問題とは根本的に異なります.

3. Deep Metric Learning の方法

では, どのように類似性が距離と対応した空間への変換を学習するのでしょうか？
大きく分けて2つの方法があります. Siames NetworkとTriplet Networkです.

Siamese Network

「シャムネットワーク」と読みます.
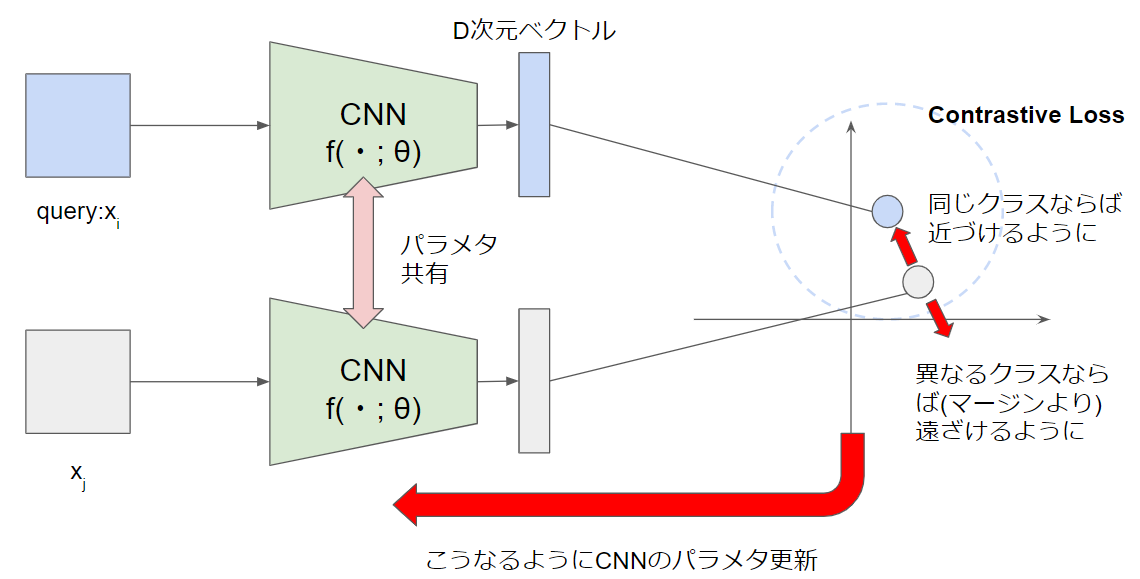
入力空間における類似性を埋め込み空間で距離として反映させるためには, 同じクラスのサンプル同士は近くに, 異なるクラスのサンプル同士は遠くに写像すればよいわけです. このような思想で生まれたのがSiamese Network/ Contrastive Lossです. これは互いに異なる任意のサンプルのペア($x_i$, $x_j$)を入力とします.

L_{Contrastive}((x_i, x_j);f) = t_{ij}d_{ij} + (1-t_{id})(m - d_{ij})\\
d_{ij} = ||f(x_i) - f(x_j) ||^2_2

です. $t_{ij}$は$x_i$と$x_j$が同じクラス(正のペア)であれば1, 異なるクラス(負のペア)であれば0を取ります. $m$は超パラメタでマージンを意味します.Contrastive Lossによる最適化は下図のようにloss値を小さくする方にCNNのパラメタを更新します.

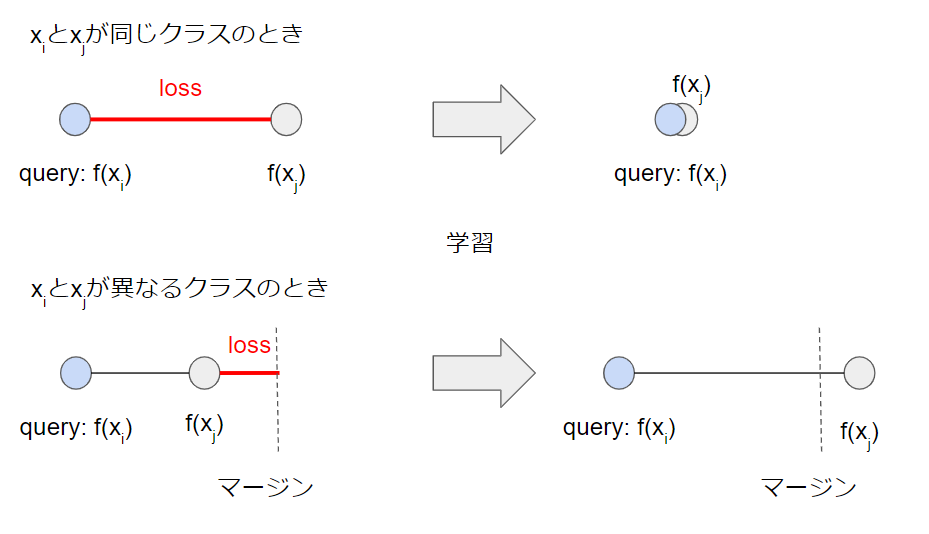
このContrastive Lossの欠点として, 負のペアはマージンを超えた時点で最適化が終了するのに対して, 正のペアは単一点に埋め込まれるまで最適化し続けてしまうことです. これによって正負で不均衡が生じ, 類似度を反映した良い埋め込み空間を得ることが困難になってしまいます. そこで考案されたのがTriplet Network/ Triplet Lossです.

Triplet Network

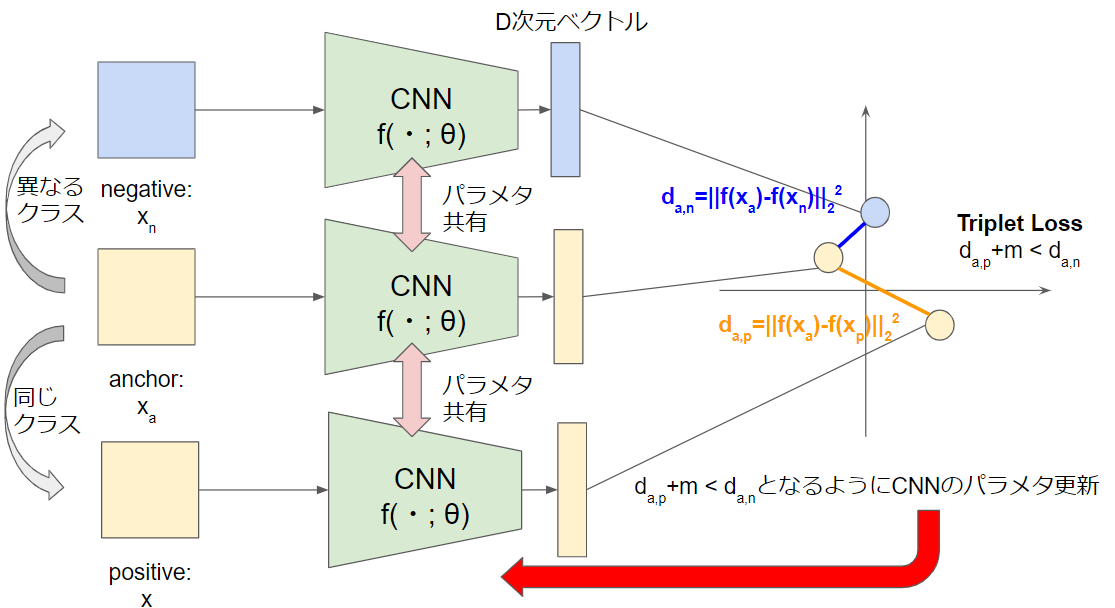
Triplet Networkでは, anchorと呼ばれる任意のサンプル, positiveと呼ばれるanchorと同じクラスでanchorと異なるサンプル, negativeと呼ばれるanchorと異なるクラスの任意のサンプルを1組としたTriplet(anchor, positive, negative)を入力とします.

L_{triplet}((x_a,x_p,x_n);f) = max(0, d_{a, p} + m - d_{a, n})\\
d_{a,p} = ||f(x_{a}) - f(x_{p})||^2_2\\
d_{a,n} = ||f(x_{a}) - f(x_{n})||^2_2

Triplet Lossでは,正ペアの距離を0にする必要はなく, 正ペアの距離と負ペアの距離を相対的に最適化することによって不均衡を解消しました. そのような理由で現在のDMLでは圧倒的にTriplet Networkの方が利用されています.

Triplet Networkのアルゴリズムは次のようになっています.
サンプル全体からバッチを取り出し, バッチ内で(anchor, positive)ペアを構成し, anchorと異なるクラスのnegativeをペアに加えることでTriplet(anchor, positive, negative)を構成し, それをLoss関数に入力しネットワークのパラメタを更新していきます.
Triplet Network Algorithm

一見Triplet Networkは非常に優れたアルゴリズムに見えますが, Siamese Networkには無かった問題点が新たに発生します. これについては次の章で説明します.

4. Deep Metric Learning の問題点

前述した通り, Triplet Networkは現在のDMLの主流になっていますが, 欠点があります.
本章では, Triplet Networkのデフォルト的な立ち位置にいるFaceNetの論文を踏まえて解説したいと思います.

Triplet Networkの欠点とは, 学習がすぐに停滞してしまうことです. なぜ, 学習が停滞してしまうのでしょうか？その答えは, 考えうる入力の組み合わせが膨大にあり,かつ学習に連れてその殆どがパラメタ更新に影響を及ぼさなくなるからです.

まず入力の組み合わせが膨大にあることについて例を挙げ説明します.
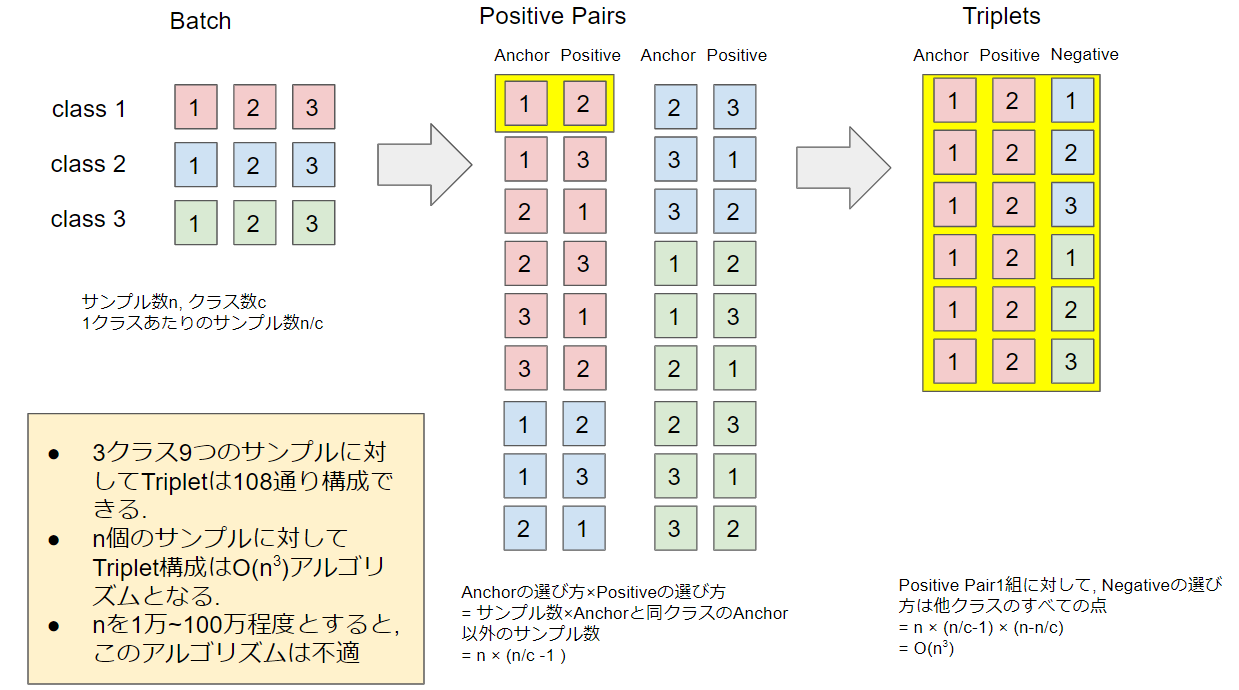
サンプル数$9$, クラス数$3$, 1クラスあたりのサンプル数$3$というバッチがあるとします.
この時,

anchorの選び方はサンプル数の$9$通り
positiveの選び方はanchorと同じクラスのanchorとは異なるサンプルの個数なので$3-1=2$通り
negativeの選び方は, anchorと異なるクラスのすべてのサンプル数なので$9-3=6$通り

したがって考えられるTripletの組合せは, $9\times 2\times 6=108$通りです.
一般にサンプル数$n$, クラス数$c$, 1クラスあたりのサンプル数$\frac{n}{c}$とすると, Tripletの組み合わせは$O(n^3)$計算量にもなってしまいます.

これらすべてのTripletを入力すると時間がかかりすぎてしまいます. したがって, 膨大なTripletの組合せのうち学習に有効なTripletのみを厳選する必要があります. 学習に有効なTripletを選ぶ操作を"Triplet Selection"と言います.

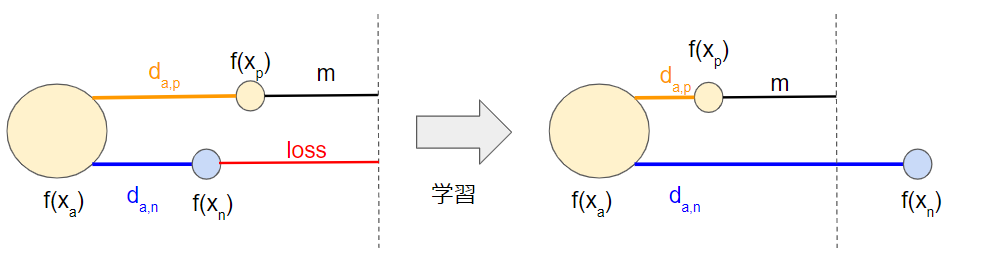
では, 学習に有効なTripletとは何でしょうか？これは, Triplet Loss値が0でないTripletと言うことができます. 下図で左の状態は$loss>0$ですが, 右の状態は$loss=0$となっています. 右のようなTripletを入力しても, loss値が0のためCNNは学習しません. したがって入力の対象として除外すべきです.

上図の左側の状態を解釈してみましょう. これは, 埋め込み空間でanchorに対して, 同じクラスのサンプル(positive)よりも他クラスのサンプル(negative)の方が近くなっているという状態です. 入力空間上では同じクラスのサンプル同士の方が異なるクラスのサンプル同士よりも類似度が高いという仮定があったため, 埋め込み空間では$f(x_a;\theta)$に対して$f(x_p;\theta)$は$f(x_n;\theta)$よりも近くにあるべきなのです. このような入力空間における類似性の仮定に反する状態のTripletこそ学習によって是正することが必要なのです.

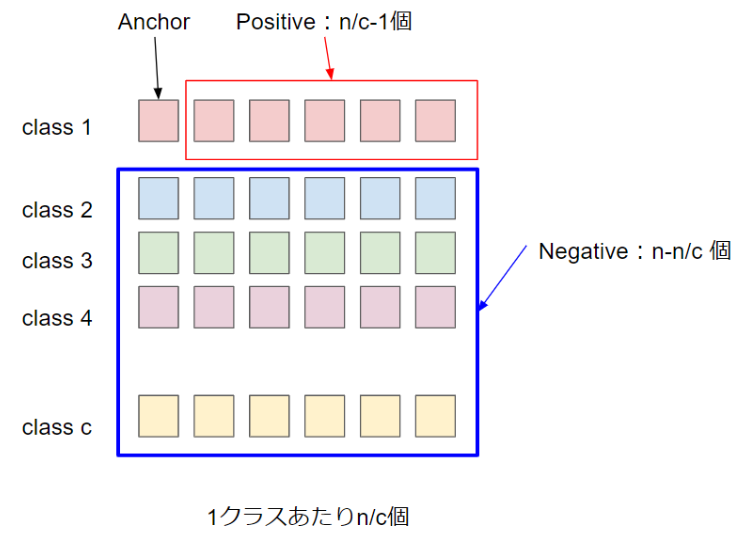
では, どうやって学習に有効なTripletを構成しましょうか？まず思いつくのが上図左のように"anchorから遠い距離にあるpositive:hard positive", "anchorに近いnegative:(semi-)hard negative"を優先的に選ぶことです. 確かにこのTriplet Slectionは学習に有効ですが, 厳選しすぎているという問題が発生します. これはpositiveとnegativeを対等に見てしまっているからです. positiveとnegativeは個数が明らかに異なるため対等に見てはいけないのです.

例を挙げて説明します. 生体認証や画像検索の文脈ではクラス数1000, 1クラスあたりのサンプル数10などで学習を行う場合があります. このとき, あるanchorに対してpositiveは9個, negativeは9,990個となります. ただでさえ少ないpositiveの中からhard positiveのみを選択してしまうと, 学習するためのTripletが絶望的に不足してしまいます.

そのため, 多くの研究ではhard positiveを厳選するのではなく, 任意のpositiveを使うという戦略をとります. 一方でnegativeの個数は莫大に多いため学習に有効な(semi-)hard negativeを厳選するということが許されます.

ところで, "anchorに近いnegative"を(semi-)hard negativeと言いましたが, 厳密には次のように定義づけられまています. (anchor, positive)ペアが決まっているときに, negativeの種類は3つあります.

easy negative: $d_{a,p}+m \leq d_{a,n}$
semi-hard negative: $d_{a,p} \leq d_{a,n} < d_{a,p} + m$
hard negative: $d_{a,n} < d_{a,p}$

semi-hard negativeや, hard-negativeを採用する"Triplet Selection"戦略をそれぞれ"semi-hard negative mining", "hard negative mining"と言います. FaceNetではsemi-hard negative miningを採用しています. なぜ, hard negative miningでは無いのかと言うと, ラベル付けに誤りがあった時のことを考慮しそれを見過ごすためとされています.

本章は非常に複雑であったためまとめを行います.

Triplet Networkに入力するためのTripletの組合せは膨大であり, すべてを入力するのは現実的に不可能である.
全Tripletの中には, $L_{Triplet}((x_{anchor},x_{positive},x_{negative});f)=0$の学習に影響を及ぼさない組合せが存在しており, 学習が進むごとにその割合は多くなる.
$Loss>0$の学習に影響のある組合せのみを選定することが重要である.
positiveの個数は, negativeの個数よりも圧倒的に少ないため, hard positive miningは難しい.
positiveは全て採用し, 学習に有効な(semi-)hard negativeを選択する.
つまり, Triplet Networkの学習には, Tripletの選定作業を伴い, 学習はその作業に大きく依存する.

5. 最新のDeep Metric Learning

この章では, 2017年あたりからの画像系会議(CVPRやICCVなど)におけるDMLをいくつか紹介します.

5.1 Improved Deep Metric Learning with Multi-class N-pair Loss Objective

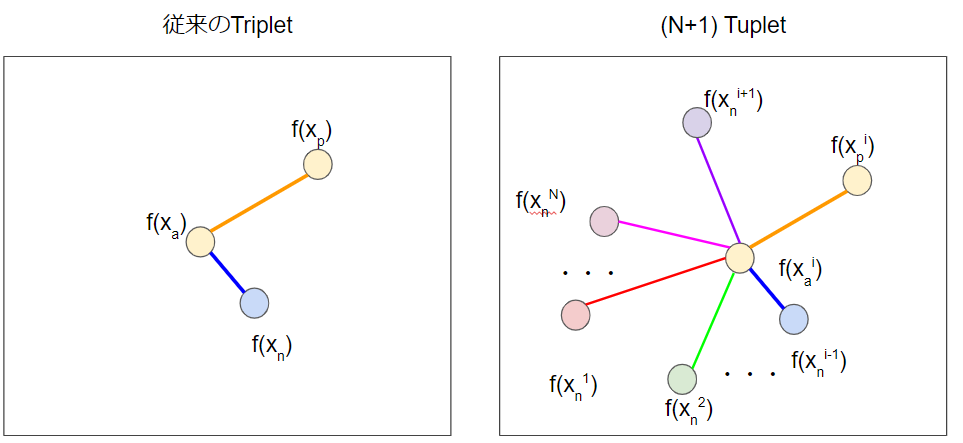
Triplet Lossを一般化した損失関数(N+1) Tuplet Lossと, それを効率良く学習させるため限定的な条件を加えたN-pair Multi Class Loss を提案した論文です.

まず, (N+1) Tuplet Lossから説明します. Nはクラス数を表しています. 従来のTriplet Lossでは, anchorが属しているクラスとnegativeが属しいるクラスの1クラス対1クラスのみを考慮していました. しかし, anchorが属するクラスに対してより多くのクラスとの相対関係を考慮した方がより安定した埋め込みができるはずです. そこで, (anchor, positive)に対するnegativeをanchorが属しているクラス以外のN-1クラスから選びます. 1つのanchor, 1つのpositive, N-1個のnegativeで(N+1)Tuplet$(x_a^i, x_p^i, x_n^1, \cdots, x_n^{i-1}, x_n^{i+1}, \cdots, x_n^{N})$を構成し入力します.(肩の数字は属しているクラスを表します.)

L_{(N+1)Tuplet}((x_a^i, x_p^i, x_n^1, \cdots, x_n^{i-1},  x_n^{i+1}, \cdots, x_n^{N});f) = \log\Bigl(1+\Sigma_{j=1,\cdots,N,j\neq i}\exp \bigl(f(x_a)^Tf(x_n^j)-f(x_a)^Tf(x_p)\bigr)\Bigr)\\

N=2のときは2クラスのみを考えている状況なので, anchorに対する負のクラス数は1となりTriplet Lossとほぼ同義になります.

L_{3-Tuplet}((x_a^i, x_p^i, x_n^j);f) = log\Bigl(1+\exp\bigl(f(x_a^i)^Tf(x_n^j)-f(x_a^i)^Tf(x_p^i)\bigr)\Bigr)

また, (N+1) Tuplet Lossは, 次のように表現することもでき, Softmax関数の考えを取り入れていることがわかります.

\begin{eqnarray}
L_{(N+1)Tuplet}((x_a^i, x_p^i, x_n^1, \cdots, x_n^{i-1},  x_n^{i+1}, \cdots, x_n^{N});f)&=&\log\Bigl(1+\Sigma_{j=1,\cdots,N,j\neq i}\exp \bigl(f(x_a^i)^Tf(x_n^j)-f(x_a^i)^Tf(x_p^i)\bigr)\Bigr)\\
&=&\log\Bigl(1+\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_n^j)\bigr)\exp\bigl(-f(x_a^i)^Tf(x_p^i)\bigr)\Bigr)\\
&=&\log\Bigl(1+\exp\bigl(-f(x_a^i)^Tf(x_p^i)\bigr)\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_n^j)\bigr)\Bigr)\\
&=&-\log\frac{1}{1+\exp\bigl(-f(x_a^i)^Tf(x_p^i)\bigr)\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_n^j)\bigr)}\\
&=&-\log\frac{\exp\bigl(f(x_a^i)^Tf(x_p^i)\bigr)}{\exp\bigl(f(x_a^i)^Tf(x_p^i)\bigr)+\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_n^j)\bigr)}\\
\end{eqnarray}

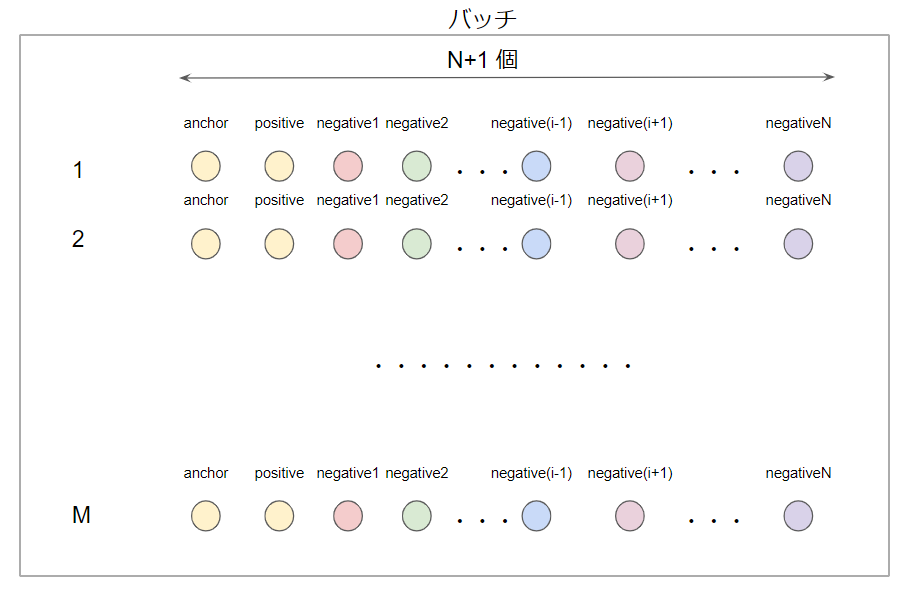
(N+1) Tuplet LossはNが大きいほど理想的な埋め込みになります. その一方で空間計算量が非常に大きくなります. 1エポックでM個のTupletを用意するとします. すると, $M\times (N+1)$個ものサンプルが必要になります.

メモリ空間を節約するため, より効率的なバッチ構成をするのがN-pair Multi Class Lossです.
まず, N個の各クラスからそれぞれpositive pairs$\bigl\{(x_a^1, x_p^1), (x_a^2, x_p^2),\cdots,(x_a^N, x_p^N)\bigr\}$を用意します. バッチで使うサンプル数はこの$2N$個のみです.他のpairにおけるpositiveは, 自pairにおけるnegativeなので, 次のようにバッチを構成することができます.

$$
\bigl\{(x_a^1, x_p^1,x_p^2,\cdots, x_p^{N-1}, x_p^N), (x_a^2, x_p^2, x_p^1, \cdots, x_p^{N-1}, x_p^N),\cdots,(x_a^N, x_p^N, x_p^1, x_p^2, \cdots, x_p^{N-1})\bigr\}
$$

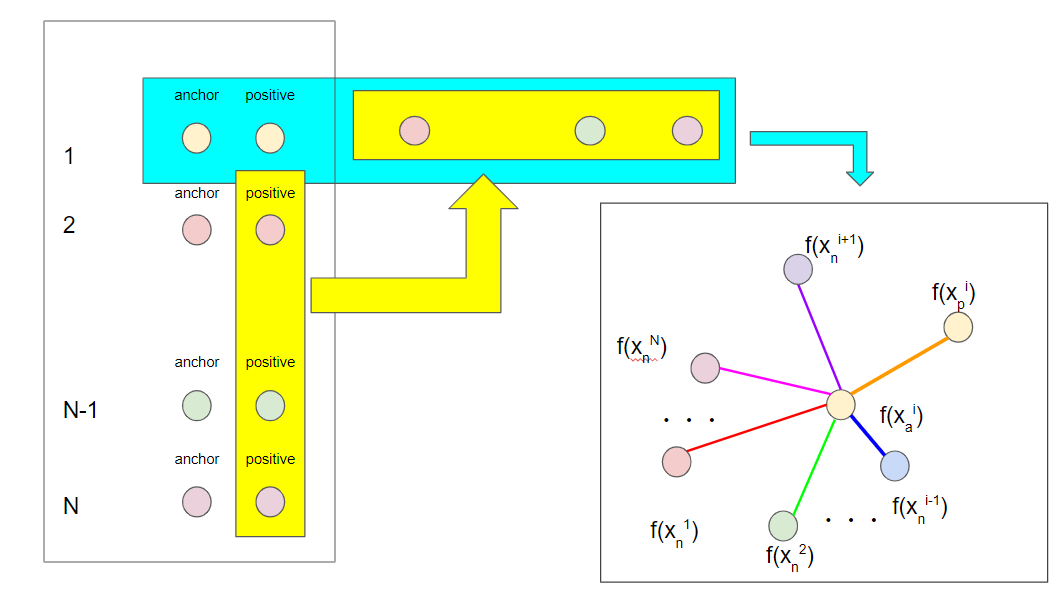
以上をまとめてN-pair Multi Class Lossを数式で表すと, 以下のようになります.

L_{N-pair MC}((x_a^i, x_p^i,x_p^1,\cdots,x_p^{i-1},x_p^{i+1},\cdots, x_p^N);f) = \log\Bigl(1+\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_p^j)-f(x_a^i)^Tf(x_p^i)\bigr)\Bigr)

N-pair Multi Class Lossは, その誕生の経緯からバッチ単位で表現する方がより適切だと思うので, バッチ単位のLoss関数も併記します.

L_{N-pair MC}(\left\{(x_a^i, x_p^i,x_p^1,\cdots,x_p^{i-1},x_p^{i+1},\cdots, x_p^N)\right\}_{i=1,\cdots,N};f) = \frac{1}{N}\Sigma_{i=1}^{N}\log\Bigl(1+\Sigma_{j\neq i}\exp\bigl(f(x_a^i)^Tf(x_p^j)-f(x_a^i)^Tf(x_p^i)\bigr)\Bigr)

5.2 Ranked List Loss for Deep Metric Learning

Siamese Networkにおける学習方法を改良した論文です. 従来のSiamese Networkは, クエリに対して1サンプルの対しか考慮していませんでした. その結果, 学習に有用なペアが無視されてしまうことがありました. また, Contrastive Lossでは正ペアを単一点に埋め込んでしまうという欠点がありました. 本手法はそれらの欠点を克服した方法になります.

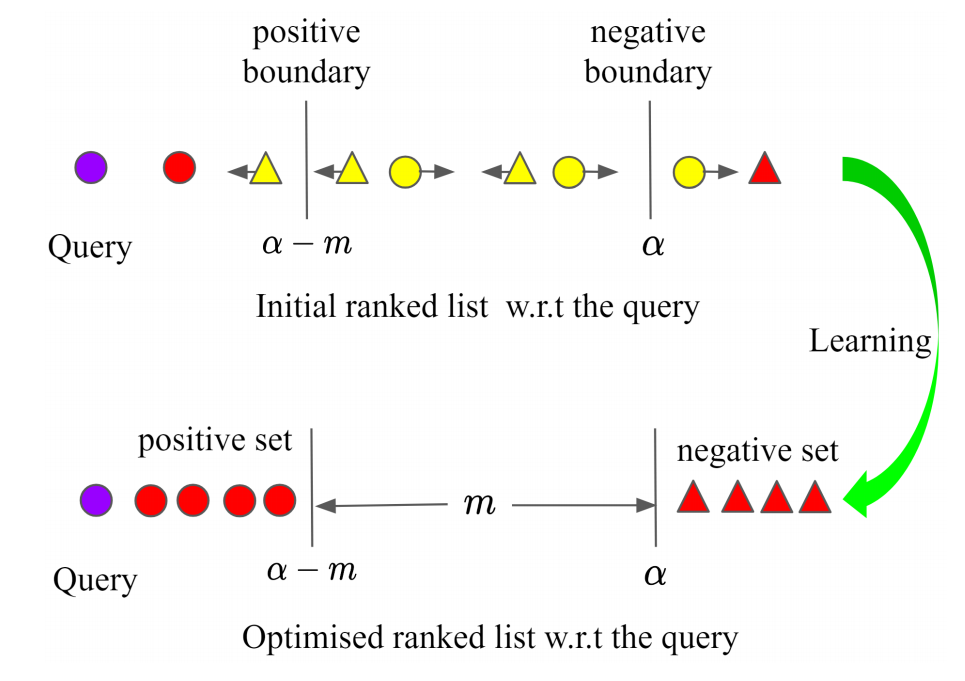
上図のようにクエリに対して, 半径$\alpha$の位置をnegative boundaryとします. そこから, クエリ方面にマージン$m$を設定します. クエリから$α-m$の位置をpositive boundaryとします. クエリに対して, positive boundaryよりも遠い全てのpositiveをnon-trivial positivesとして同時に損失を計算します. また, クエリに対して, negative boundaryよりも近くにある全てのnegativeをnon-trivial negativesとして同時に損失を計算します. non-trivial positivesは数が少ないため重みをつけず, non-trivial negativesは数が多いため重みをつけます.

L_{RLL}(x_i; f) = \frac{1}{P^*_i}\Sigma_{x_j \in P_i^*}(d_{i,j}-(\alpha-m))+\Sigma_{x_j\in N^*}\frac{w_{i,j}}{\Sigma_{x_j\in N^*}w_{i,j}}(\alpha-d_{i,j})

$P_i^{*}$は$x_i$に対するnon-trivial positivesで, $N^*_i$は$x_i$に対するnon-trivial negativesです.

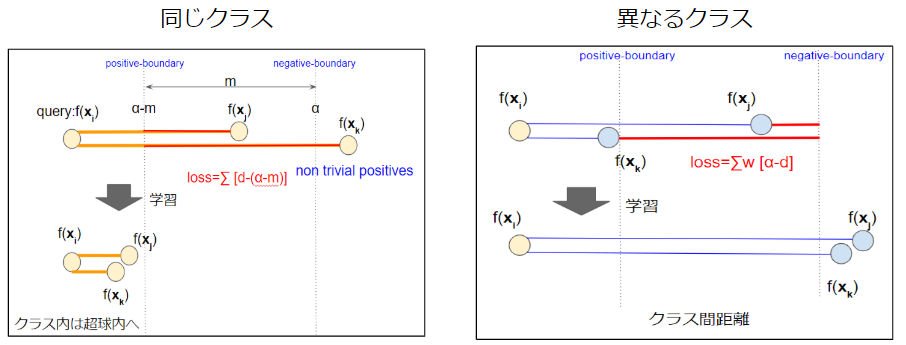
クエリに対して1対1ではなく, 1対多で考えることによって有用なサンプルが無視されるのを防ぎます. Tripletではなく, pairベースで考えているため, 組合せの問題も抑えられます. 同一クラスの最適化では, positive-boundaryよりも近くなった時点でqueryとpositiveにおける損失が無くなるためそれ以上近くなることはありません. このようにしてpositive-pairが単一点に埋め込まれてしまうのを防ぎます. 異なるクラスの最適化では, クラス間マージンmよりも離したところで最適化が終わるため, クラス間マージンを保証することができます.

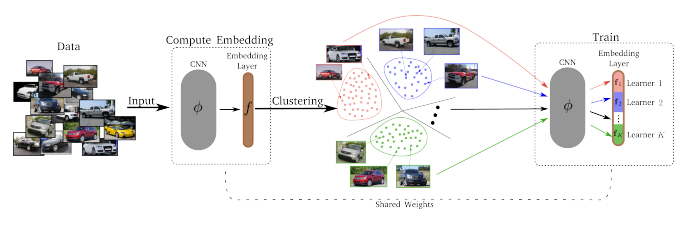
5.3 Divide and Conquer the Embedding Space for Metric Learning

DMLに分割統治法を取り入れた方法です. 埋め込み空間上でまず距離に基づくクラスタリングを行います. できあがったクラスタごとでTriplet Selectionを行います. 距離に基づくクラスタリングをしているため, クラスタ内のnegativeはかなりの確率でhard negativeとなり学習に影響のあるTripletを構成しやすくなります. このように, クラスタリングとDMLの学習を交互に行うことによって, 学習を加速させています. また分割統治法を用いることによって, DMLを並列計算できるようにもしています.

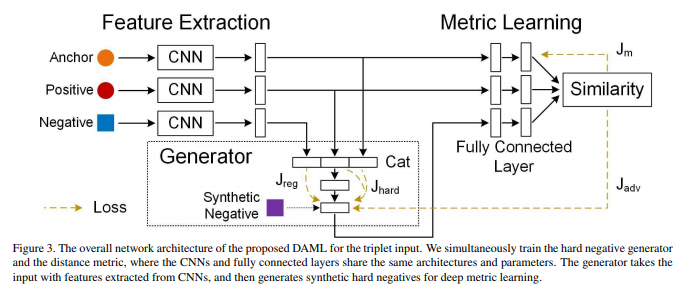
5.4 Deep Adversarial Metric Learning

従来のTriplet Networkの場合, 学習を安定させるため, Triplet構成時にhard negative, semi-hard negativeを見つけることが重要でした. その結果, 大量のeasy negativeを無駄にしてしまっていました. この論文は, 大量のeasy negativeを学習に活かせないかということがモチベーションとなっています. 主旨としては, hard negativeを選ぶのではなく, negative全体の分布をもとにhard negativeを作り出してしまおうというものです. 流れは下図の通りです.

まず, Triplet(anchor, positive, negative)を選びます. 注意して欲しいのは, 従来このTripletを選ぶ時点で, negativeとして(semi-)hard negativeを選択していました. しかし, この論文では, 任意のnegativeを用います.
次にGeneratorを用いて, synthetic negativeという架空のhard negativeを生成します.
Generatorの目的関数は以下の通りです.

\begin{eqnarray}
L_{Generator}((x_{a}, x_{p}, x_{n});g) &=& ||x_{sn}-x_{a}||^2_2 + \lambda_1 ||x_{sn}-x_{n}||^2_2 + \lambda_2 max(0,D(x_{sn},x_{a})^2-D(x_{p},x_{a})^2-\alpha)\\
&=& ||x_{sn}-x_{a}||^2_2 + \lambda_1 ||x_{sn}-x_{n}||^2_2 + \lambda_2( -L_{Triplet}((x_{a}, x_{p}, x_{sn});f))\ \ (0<\lambda_1<1)
\end{eqnarray}

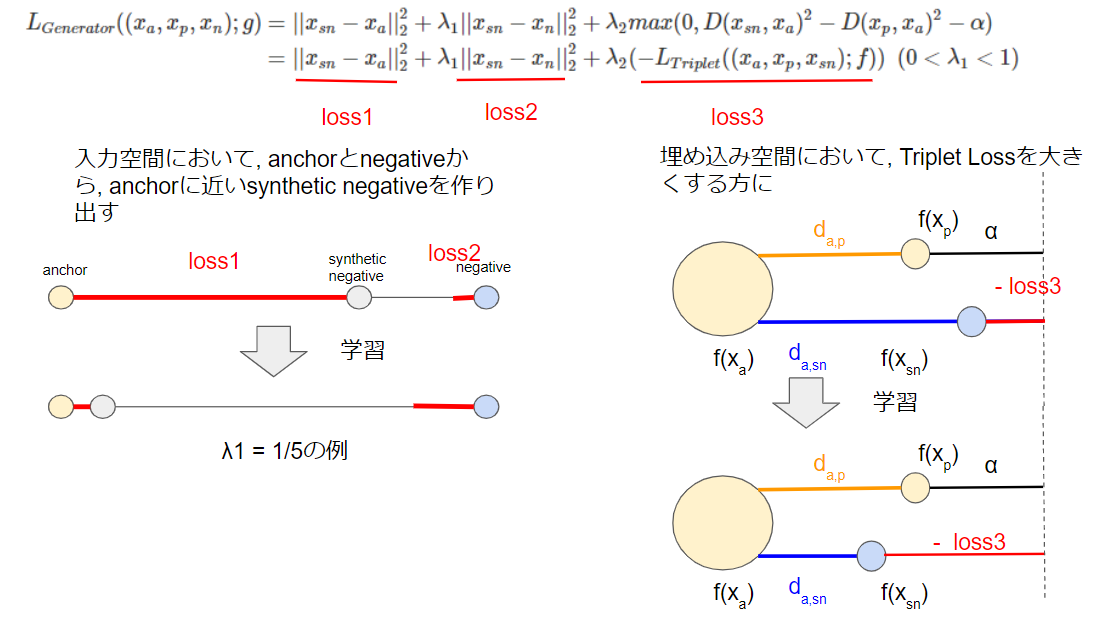
図にすると以下の通りです.

Loss1は, 入力空間においてsynthetic negativeをanchorに近づけための損失です. Loss2は, 入力空間においてsynthetic negativeとnegativeを近づけるための損失です. Loss1とLoss2はトレードオフの関係になっており, 超パラメタ$\lambda_1$の大きさによって元のデータをどの程度反映するかを設定します.
Loss3は, Triplet Lossの符号を逆にしたものです. すなわちTriplet Lossを大きくするようにsynthetic negativeを動かします. このようなGeneratorの学習と, Triplet NetworkのCNNの学習を交互に行います. 二つのネットワークパラメタを交互に学習するのは, GANの学習方法に似ていますね.

min_{\theta_g}min_{\theta_f}L = L_{Generator}((x_a, x_p, x_n);g) + \lambda L_{Triplet}((x_a, x_p, g((x_a, x_p, x_n);\theta_g)); f)

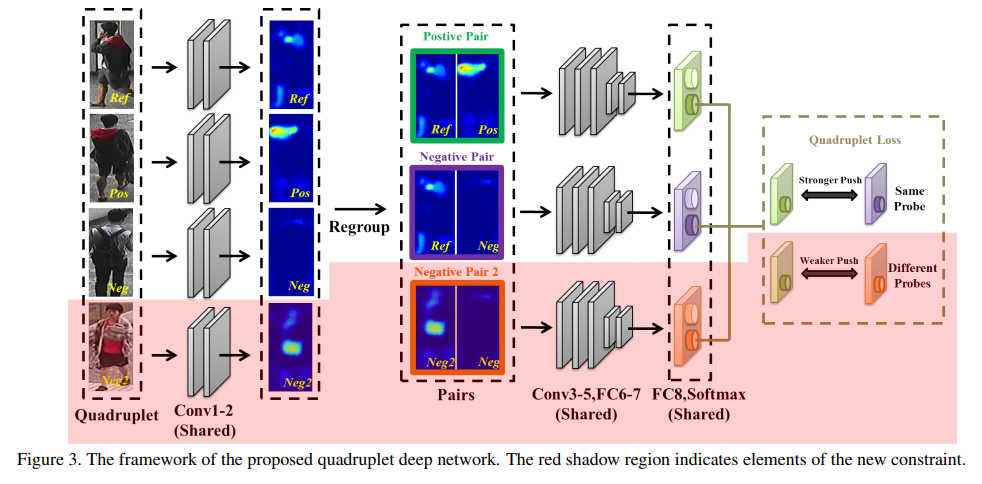
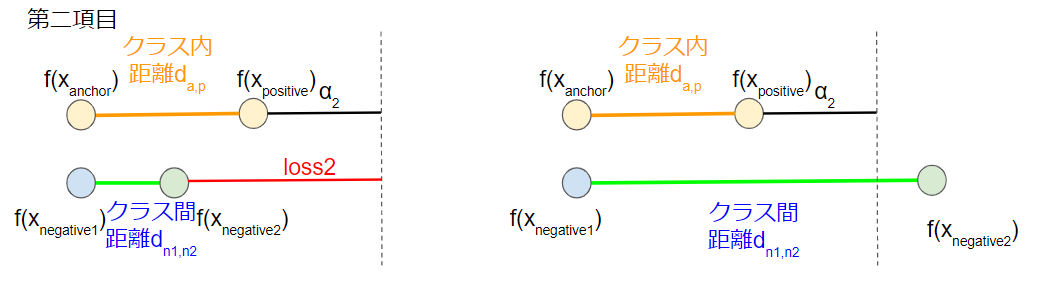
5.5 Beyond triplet loss: a deep quadruplet network for person re-identification

この論文は, 入力をTriplet(anchor, positive, negative)からQuadruplet(anchor, positive, negative1, negative2)に拡張したものです. negative2はnegative1とは異なるクラスのnegativeを指しています.

損失関数は以下の通りになっています.

\begin{eqnarray}
L_{Quadruplet}((x_a,x_p,x_{n1},x_{n2});f) &=& max(d_{a, p} - d_{a, n1} + \alpha_1, 0) + max(d_{a,p} - d_{n1,n2} + \alpha_2, 0)\\
&=& L_{Triplet}((x_a, x_p, x_{n1});f) + max(d_{a,p} - d_{n1, n2} + \alpha_2, 0)
\end{eqnarray}

第一項目は, 通常のTriplet Lossです. つまり, 正ペアの距離を負ペアの距離よりも相対的に小さくしようとする損失です.
第二項目は任意のクラス内距離を任意のクラス間距離よりも相対的に小さくしようとする損失です.

この最適化によって, 任意のクラス内距離 < 任意のクラス間距離　となるように埋め込みを実現します.

||f(x_i) - f(x_j)||^2_2 < ||f(x_k) - f(x_l)||^2_2 \ \ (y_i=y_j, y_k \neq y_l, y_i \neq y_k, y_i \neq y_l)

5.6 Deep Metric Learning Beyond Binary Supervision

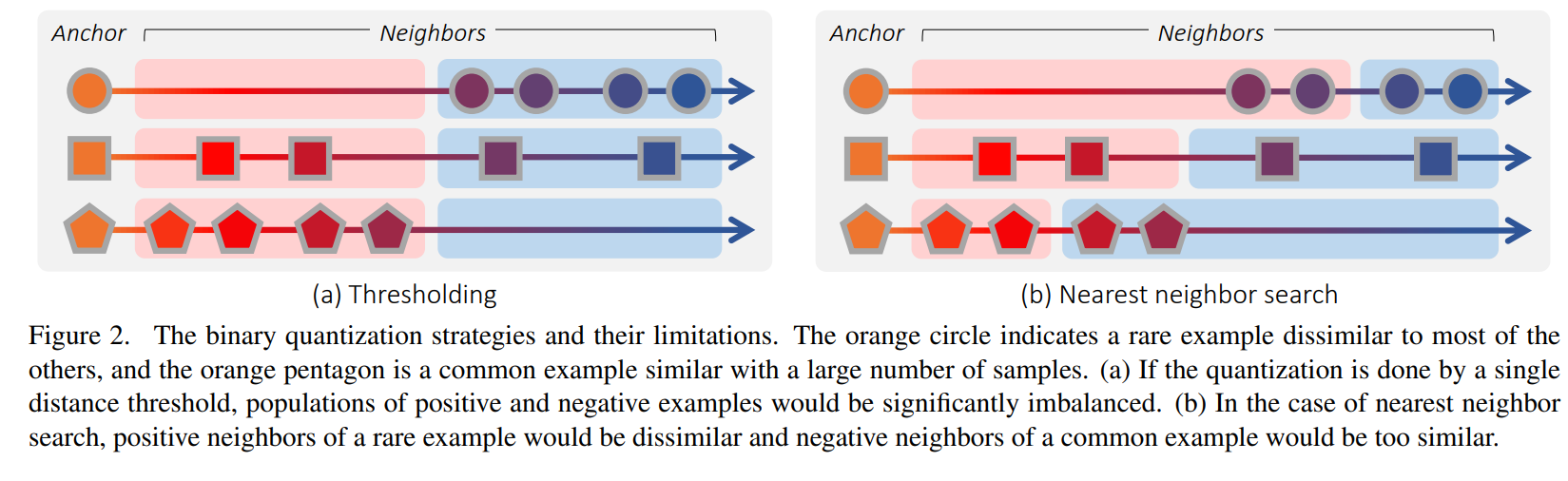
この論文は, DMLで連続ラベルを扱えるようにしたものです. 連続ラベルとは, ビデオデータのある瞬間の画像$x$に対する時刻$t$のようなものです. 従来の連続ラベルを扱うDMLは, 閾値やNearest Neighbor法によって無理矢理離散ラベルに変換することによって, Triplet Networkの枠組みに当てはめていました. しかしこの方法だと下図のような不都合が生じ柔軟な埋め込み空間を得ることができませんでした.

(a)はanchorに対して, 閾値で連続ラベルを2値離散ラベルに変換している図です. この方法を使うと, 上段や下段のようにpositiveやnegativeが存在しない場合が生じてしまいます. [](また, 類似度の高い画像同士を異なるラベルとして処理してしまう可能性があります. 10秒の動作において, anchorを時刻0, 閾値を時間5秒とすると, 時刻4.9と時刻5.1はほぼ同じ姿勢であるにも関わらず時刻4.9の画像はpositive, 時刻5.1における画像はnegativeとしてしまうため, 良質な埋め込み空間が得られません.)
(b)はanchorに対して, Nearest Neighbor法で連続ラベルから2値離散ラベルに変換している図です. 上段のように遠すぎるpositiveや下段のように近すぎるnegativeが生じる恐れがあります. [](10秒の動作において, anchorを時刻0, バッチ内に2-NN法を適応するとき, 類似度が低いはずである時刻6,7のデータがpositiveと扱われてしまう可能性があります.)

そこでこの論文では, 下のLoss関数を用いて, anchor画像に対する画像i, 画像jの埋め込み空間上の距離の比と, ラベル空間における連続ラベルの同士の距離の比を一致させるように最適化する提案がなされました.

L(a, i, j) = \Bigl( \log \frac{D(f(x_a),f(x_i))}{D(f(x_a),f(x_j))}-\log\frac{D(y_a, y_i)}{D(y_a, y_j)}\Bigr)^2

その他

この章では, 近年のDML改良案としてそれぞれ個性のある論文を用意しました. 興味を持たれた方は目的別に以下の論文にも目を通してみてください.

5.1や5.2のように損失関数やmining方法の改良に興味を持たれた方

5.3, 5.4, 5.5のように特殊な学習方法に興味を持たれた方

5.6のようにDMLタスクを拡張することに興味を持たれた方

日本語解説記事

最後に

DML, 非常に面白いですね！
本記事では, 画像に対するDMLを扱いましたが, DLの他のトピックである言語, 音, グラフにも応用でき非常に可能性のある研究だと思います. また, 既存の手法はハードウェアに大きく制約を受けておりその中でなんとか性能を出すという案が多いように感じました. 今後ハードウェア性能が上がるにつれて, DMLはさらに多く用いられると思います.

本記事を読んでいただき誠にありがとうございました.
本記事におかれまして誤字や, 私の理解不足, 解釈違い, Qiitaでの書き方のアドバイス等ありましたら, ご指摘いただけると幸いです.

参考文献

339

288

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up