「FaceNet: A Unified Embedding for Face Recognition and Clustering」の解説と実装

Siamese Network＋Triplet lossの論文として名高い「FaceNet」の論文を読んだのでその解説と実装を書いていきます。Train with 1000を使って実験もしてみました。

TL;DR

• FaceNetはある画像に対して、同一のクラス（人物）の画像、異なるクラスの画像の合計3枚の「Triplet」を作り、画像間の距離を学習する。
• 画像を特徴量のベクトルに変換し、プロットする一方で、k-Nearest Neighbor法の要領で未知の画像に対するクラスの推定もできる。またクラス数が後から追加されたり削除されたりするようなパターンでも、「画像間の距離」を学習しているため、新たに訓練する必要がなくロバストである。
• 行列の計算テクニックを使うことで、オンラインのTriplet選択が可能になり、計算量を大きく減らすことができる。
• FaceNetをTrain with 1000を使って実験したところ、同一ネットワークのSoftmaxよりも精度が良かった。

FaceNetの目的

顔認証で使うことを想定されたニューラルネットワークです。一般的な画像分類の場合、例えば10個のクラスがあるのなら、

from kera import layers
x = layers.Dense(10, activation="softmax")(some_inpit)

のようにSoftmax関数で訓練するのが直接的かつ強力な方法です¹。しかし、顔認証では、認証する人が増えたり減ったりするので、クラス数が事実上可変の（10人を分類するときもあれば、11人になったり、9人になったりする）分類問題となります。そのたびにニューラルネットワークを再訓練するのは効率が悪いです。

そこで考え出されたのが、画像の埋め込み（Embedding）という発想です。自然言語処理のWord2Vecと発想は似ていて、画像同士の近さや遠さといった「類似度」を計算できる特徴量（数値）によって画像を表現しようというものです。

これはなぜクラス数が可変の場合に使えるのかというと、例えばある人の顔画像Aがあったとしましょう。その特徴量ベクトルを$\vec{a}$とします。そして同じ人の別の顔画像Bがあり、その特徴量ベクトルを同じく$\vec{b}$とします。この2つのベクトルの「類似度」に着目します。例えば、類似度をユークリッド距離で評価するのなら、

$$d(\vec{a}, \vec{b})=||\vec{a}-\vec{b}||_2 $$

とすればよいですし、コサイン類似度で評価するのなら、

$$cos\theta = \frac{\vec{a}\cdot\vec{b}}{||\vec{a}||\cdot||\vec{b}||} $$

とすればよいです。どちらの関数（類似度の関数や距離関数）を使うかは好みなので、どちらでも良いです。FaceNetの場合はユークリッド距離を使います。もうちょっとアバウトに言うなら、「$\vec{a}$と$\vec{b}$は数値的にものすごく似てるから同一人物と考えて良いよね？」というアプローチです。これならニューラルネットワークの再訓練は要りません。

実はこの発想、k-Nearest Neighbor法の延長線上であるのかがわかるでしょうか？k-Nearest Neighbor法を知っておくと非常に理解がスムーズになります。SklearnではKNeighborsClassifierで簡単にできるので、やったことない方はIris等で動かしてみるのをおすすめします。

いま、特徴量が2次元で、潜在空間がこのように平面にプロットできるとしましょう。右下の「？」はおそらく緑色として推定するのが自然でしょう。左上の「？」はおそらく赤色として推定するのが自然でしょう。この「自然」という概念をもう少し正確に定義すると次のようになります。

「？の場所から最も近い点の色（ラベル）を、推定ラベルとしなさい」

近さを判定する距離関数は何でもいいですが、ユークリッド距離がわかりやすいでしょう。実はこれがk=1のk-Nearest Neighbor法なのです。kが増えるとどうなるかというと、近い順に見ていって最も多いラベルを採用する、とかになります。このk-Nearest Neighbor法はFaceNetを始めとしたSiamese Networkの推論時に必須になるので、k=1の場合だけでいいので、Numpyベースから書けるようにしておくと楽になります。

Siamese Network

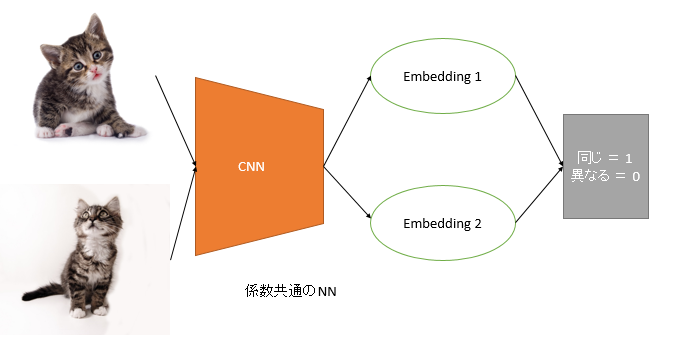
「画像が似ているかどうか」を学習するネットワークは既にあって、Siamese Networkといいます。今2つの猫が同一だということをネットワークに覚えさせたいとしましょう。

2枚の画像を同時にかつ係数を共有するニューラルネットワークに訓練させ、2つの画像の特徴量を得ます。そこから「2枚の画像が同じなら1、異なるのなら0」というラベルを使って学習させます。今回は同じなので、y_true=1ですね。あとは二値分類の要領で、出力層をsigmoidにして、損失関数をbinary_crossentropyにすれば訓練できます。

さてここでSiamese-Networkの特徴をまとめます。

1. 係数を共有するレイヤーを使う
2. どのクラスに属するのかという強いラベルを使うのではなく、画像が同一かという「弱いラベル」を使う
3. 画像を1枚1枚訓練させるのではなく、画像の「ペア」として訓練させる。

1点目は「（重み）共有レイヤー」と呼ばれるもので、例えばKerasなら、

from keras import layers
from keras.model import Model

some_layer = layers.Dense(256, activation="relu")

input1 = layers.Input((784,))
input2 = layers.Input((784,))
x1 = some_layer(input1)
x2 = some_layer(input2)

model = Model([input1, input2], [x1, x2])

のように書くと実装できます。ここではレイヤーのインスタンスが1つなので、x1とx2は同一の係数から計算されます。

2点目は、One-shot Learning特有のアイディアだと思います。通常、Softmaxで訓練する場合、1クラスあたり100枚や1000枚のように大量を画像を用意します。しかし、顔認証のように1クラス（人）あたり1枚～数枚、数十枚のようにとても少ない画像数の場合は、どれがどのクラスに属するのかを強いラベルで訓練させるのには、サンプル数が足りません。

もちろん最初に述べたように、クラス数が可変である問題に適用させたいという事情もあります。しかし、実際にSoftmaxを使い、強いラベルで訓練させるととんでもなくオーバーフィッティングします。一方でSiamese Networkでは、同一か異なるかという弱いラベルで訓練させるため、タスクが簡単になり、ニューラルネットワークが特徴量を見つけやすくなります（ただしその代償として推論の手間がかかります）。後で確認しますが、サンプル数が少ないとSoftmaxよりもかなり有利になります。

3点目はSiamese Networkは2つの画像を使っていることによるものです。しかし、これはデメリットにもなります。なぜなら計算量が爆発的に増えるからです。例えば1万枚画像があり、1クラス1000枚としましょう。同一（$y=1$）のペアは、10×1000×999÷2=499.5万、異なる（$y=0$）のペアは10×1000×9000÷2=4500万もあります。5000万近くのペアを訓練させたら1エポック何日かかるのでしょうか。もし画像が10万枚になったらもうどうしようもありませんね。これはかなりシビアな問題です。

行列での組み合わせ表現

Siamese Networkのペア数の組み合わせ爆発には対処法があります。例えば、今5サンプルあり、それぞれのラベルが

$$y=(0,1,2,1,0)$$

とします。これを縦横に配置して総当たりで組み合わせると、次のような行列ができます。

\begin{bmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 1 \end{bmatrix}

ここで0や1はラベルではなく、同一かどうかのフラグを表します。対角成分は同じサンプル同士なので常に1になります。1行目の5列目は、1番目のサンプルと5番目のサンプルが同じ0というラベルなので、同一を示す1になっています。Numpyで書くなら全然難しくなくて、

>>> import numpy as np
>>> y=np.array([0,1,2,1,0])
>>> np.expand_dims(y,axis=1)==np.expand_dims(y,axis=0)
array([[ True, False, False, False,  True],
       [False,  True, False,  True, False],
       [False, False,  True, False, False],
       [False,  True, False,  True, False],
       [ True, False, False, False,  True]])

expand_dimsとブロードキャスティングのテクニックを使って総当たりは簡単に作れます。しかし実際は総当たりではなく「組み合わせ」なので、この行列の上三角行列（必要に応じて対角成分を除外）を取ると良いでしょう。こんなイメージ

>>> np.triu(np.arange(1,26).reshape(5,5),k=1)
array([[ 0,  2,  3,  4,  5],
       [ 0,  0,  8,  9, 10],
       [ 0,  0,  0, 14, 15],
       [ 0,  0,  0,  0, 20],
       [ 0,  0,  0,  0,  0]])

分かりやすいようにforループで書くと次のコードと等価です。

for i in range(5):
    for j in range(i+1, 5):
        # array[i,j]に対する処理

これで行列による組み合わせ表現を実装することができました。

オンラインによるPair/Triplet探索、オフラインによる探索

実は今の「行列による組み合わせ表現」のところが、FaceNetのオンラインによるTriplt探索の実装のキモです。Tripletという言葉は初めて使いましたが、ペアが2つの画像に対して見るのなら、Tripletは3つの画像を見るということです。どちらもSiamese Networkの一種で、3点のほうが高度な表現ができるということです。

オンライン・オフラインというのはFaceNetの論文中に出てきた言葉で、先程説明した「ニューラルネットワークに2つの画像を同時に入れる」というのはオフラインのペア探索です。オフラインの場合は、事前にペアを計算し、それに2つ/3つの画像を食わせます。従来のSoftmaxによる画像分類とほぼ同じで実装は分かりやすいですが、計算量の面で大きなデメリットがあります。

一方でオンラインのペア探索は、同時に入力する画像は1つだけれども、行列の組み合わせ表現を使い、ミニバッチの中で自動的にペア/Tripletを作り出すということを行います。

モデルのInputの数は1つになるので、ぱっと見、通常の画像分類と同じようなモデルになります。しかし、ペア生成の部分を損失関数でやるので、損失関数がえらい複雑になります。計算量ではオフラインの場合より大きく改善しますが、実装の煩雑さが代償となります。ただ理解できれば1から全然書けます。イメージ的にはカーネル法の一種と捉えてしまうのがわかりやすいのではないでしょうか。コサイン類似度の内積計算はカーネルトリックそのものですし。

オフラインとオンラインのペア/Triplet探索についてまとめると次の通りです。

• オフライン：事前にforループなどでCPUでペア/Tripletを列挙しておく。計算の効率は悪いが、実装は簡単。
• オンライン：ニューラルネットワークの中で行列の組み合わせ表現を使って、ペア/Tripetを内生的に計算する方法。計算効率は良いが、実装が煩雑。

FaceNetではオンラインのTriplet探索を行っています。基本的にオンラインの路線で行きます。

Contrastive Loss

これはFaceNetの議論ではないのですが、2枚の画像が同一かどうかのSiamese Networkを作る際によく使われる損失関数です。

$$L_n = \frac{1}{2}(y_n d_n^2 + (1-y_n)\max(\rm{margin}-d_n, 0)^2) $$

Chainerのドキュメントにある式を使いました。ここで$y_n$は画像が同一かどうかを表すフラグです。$d_n$は距離関数で、ユークリッド距離でも、(1-コサイン類似度)のコサイン距離でもなんでもOKです。

簡単に言うと、同一の場合と異なる場合で2つの損失関数を用意して、それの和を取る（場合分けをする）ということです。以下のスライドはコサイン距離の場合ですが、このスライドを見るとよくわかると思います。

参考：https://www.slideshare.net/NicholasMcClure1/siamese-networks

マージンはサポートベクターマシンで使われるマージンと似ていて、このマージンもたせることで、Softmaxよりも決定境界にゆとりをもたせてより綺麗な分類にし、どこまでなら同一の画像とみなすかというような曖昧さをコントロールすることができます。今やっているのは分類ではなく「距離」や「類似度」の学習なので、マージンをもたせることはかなり都合が良いのです。

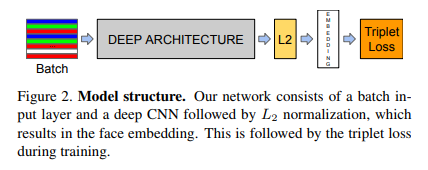
Triplet Loss

これがFaceNetで使われる損失関数です。

$$\sum_i^N\max[d(x_i^a, x_i^p)-d(x_i^a, x_i^n)+\alpha, 0] $$

ここで、$a$はアンカー（anchor）となる画像で、$p$はプラス（positive）の画像でアンカーの画像と同一のラベルの画像です。逆に$n$はマイナス（negative）の画像で、アンカーとは異なるラベルです。$d(*)$は距離関数を表し、ユークリッド距離などがこれにあたります。$\alpha$はContrastive Lossで出てきたマージンの値です。イメージ的にはこのような計算になります。

# embedding=埋め込みの行列, shape=(batch, 潜在空間の次元)
# y = ラベル, shape=(batch, )
# dist(x1, x2) = 特徴量のベクトルから距離を返す関数
# alpha マージン

n = embedding.shape[0]
loss = 0
for anc in range(n):
    for pos in range(anc+1, n):
        if y[pos] != y[anc]: continue   
        for neg in range(anc+1, n):
            if y[neg] == y[anc] : continue
            loss += max(dist(embedding[anc], embedding[pos]) - dist(embedding[anc], embedding[neg]) + alpha, 0.0)

ただこれをforで書くのは効率が悪いので、先程の「行列の組み合わせ表現」を使い頑張って実装します。TensorFlowかつGPUなら、tf.where→tf.gather_nd²を使うのがわかりやすいでしょう。

ただし、TPUの場合は現状、tf.whereによるブール配列の部分でコンパイルが失敗します。$O(N^4)$というえらく大きな計算量になりますが、「A-P」,「N-P」を総当たりで計算します。TPUの場合は、デバイスのHBMの容量が十分にあるので、バッチサイズ200程度の4乗だったら全然余裕で計算できます³。しかもそこまで速度が落ちません。

ちなみに損失関数の「max関数はどういう意味があるのか」ということですが、「訓練する意味があるTripletだけ注目するよ」という意味です。これは次に見ていきます。

Easy Triplet、Hard Triplet

TripletLossの損失関数をもう一度書きます。

$$\sum_i^N\max[d(x_i^a, x_i^p)-d(x_i^a, x_i^n)+\alpha, 0] $$

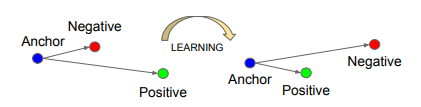
この$d(x_i^a, x_i^p)-d(x_i^a, x_i^n)$の意味を解釈すると、

「ラベルが同じ（プラス）同士のペアよりも、ラベルが違う（マイナス）同士のほうが近くにあったら、ペナルティをつけなさい。つまり、プラスのペアよりも、マイナスのペアのほうが遠くにあるようにプロットしなさい」

ということになります。これはk-Nearest Neighbor法の観点からは非常に理にかなった訓練方法です。なぜなら、k-Nearest Neighbor法は、ある画像の特徴量（アンカー）に対して「最も近い」画像のクラスを推定ラベルとするからです。

別の言い方をすれば、既に距離が「プラスのペア＜マイナスのペア」であるTripletは訓練には役立たないということになります。なぜならこのTripletの損失は、maxにより0になるからです⁴。これをEasy Triplet（簡単なTriplet）といいます。

同様に、距離が「マイナスのペア＞プラスのペア」であるTripletは、訓練に役立つということになります。これをHard Triplet（難しいTriplet）といいます。ただFaceNetではマージンがあるため、マージンを入れなければEasy Tripletなんだけれども、マージンを入れたらHard Tripletになるというケースもあります。これをSemi-hard Tripletといいます。まとめると次のようになります。

• Easy Triplet: $d(x_i^a, x_i^p)-d(x_i^a, x_i^n)+\alpha<0$
• Semi-hard Triplet : $d(x_i^a, x_i^p)-d(x_i^a, x_i^n)<0, \quad d(x_i^a, x_i^p)-d(x_i^a, x_i^n)+\alpha\geq 0$
• Hard Triplet : $d(x_i^a, x_i^p)-d(x_i^a, x_i^n)\geq 0$

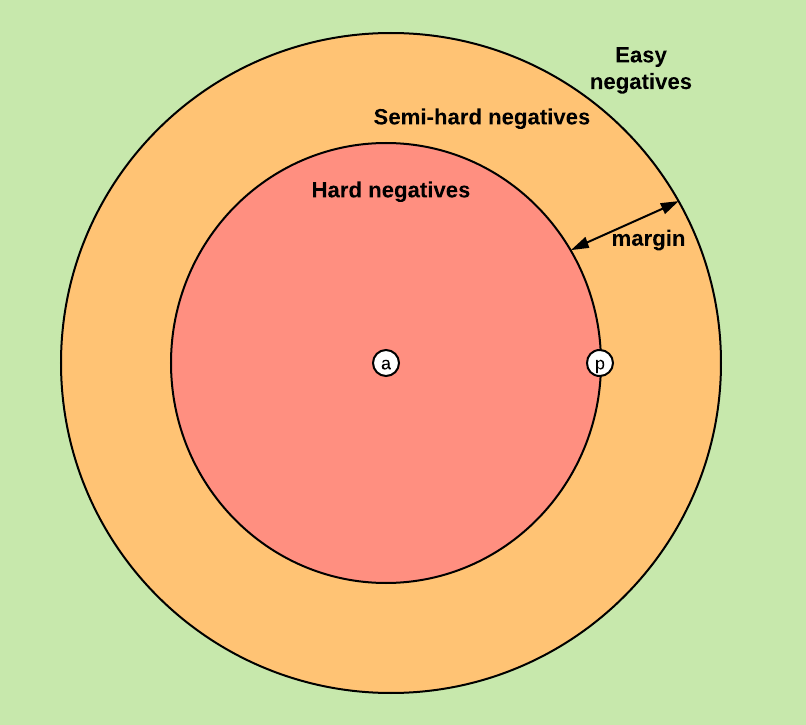
いま、anchorとpositiveの距離を固定しましょう。そうすると、negativeだけの問題になり、次のような図で表すことができます。

https://omoindrot.github.io/triplet-lossより

この図では、TripletがNegativeと表記されていますが、$d(x_i^a, x_i^p)$が固定されているため、意味は全く同じです。つまり、Easy TripletよりもHard Tripletのほうがより狭い概念で、「FaceNetではSemi-hard Triplet以上のTripletのみに注目して訓練するよ」ということです。

実際、分解して考えてみると、訓練に役立つHard Tripletよりも、訓練に役立たないEasy Tripletのほうが圧倒的に多いです。なぜなら、例えば「りんご」と「ぶどう」という2種類の埋め込みを考えた場合に、潜在空間上での距離を評価しなくても、もっと低レベルでの距離の評価（例えばピクセル値の差分）で既に十分な差分が生まれているからです。りんごは赤いし、ぶどうは紫色なので、これを潜在空間まで持っていったらほんの少し訓練すればすぐEasy Negative（Triplet）になってしまいますので。おそらくですが、「青りんごとマスカット」のように見た目の色が同じで、その画像の意味（潜在空間上での距離）を考えなければいけないケースがよりHardなNegative（Triplet）になるのだと思います。

あくまでEasy/Hardというのは相対的なもので、訓練が進んでいけばHardだったものがEasyになることもあるのに注意してください。

Tripletの選び方と悪い局所解～Batch HardとBatch All～

TripletLossではanchor, positive, negativeの3枚の画像の距離を学習することを考えました。しかし、こう考えることもできます。

「要はプラスのペアよりも、マイナスのペアが遠くになるようにしたいんだから、最も遠いプラスのペアと最も近いマイナスのペアを比較すれば、計算コストは軽くなるのでは？」

実はこの考え方は、Hardest triplet selectionやBatch Hardと呼ばれる手法です。確かにこれなら、計算量は相当軽くなりますし、精度を比較したらBatch Hardが良かったと言っている論文も確かにあります⁵。しかし、FaceNetの論文を読むと、

Selecting the hardest negatives can in practice lead to bad local minima early on in training, specifically it can result in a collapsed model (i.e. f(x) = 0)

悪い局所解に収束してしまいがちであるということが書かれています。Triplet Lossをもう一度書くと、

$$\sum_i^N\max[d(x_i^a, x_i^p)-d(x_i^a, x_i^n)+\alpha, 0] $$

ですが、もしすべての画像に対して、$d(*)=0$となるような関数があれば、この損失は簡単に収束してしまいます（=$\alpha$となる）。画像の埋め込みの場合はこのような「悪い局所解」の存在に注意しなければいけません。

自分もBatch Hardをやってみたのですが、FaceNetの論文にかかれているとおりに、モデルが崩壊しやすい、つまり「すべての画像が1つの点に集まってしまって、いかなる画像同士の距離も0になる」というケースが多発してしまいました。したがって、ここではBatch Hardではなく、すべての画像に対して総当たりでやって、行列の組み合わせ表現でオンラインでTripletを作るというBatch Allの戦略を取っていきます。もしBatch Hardでこのような局所解を回避する方法があったら教えてください。

Triplet lossのTensorFlow（Keras）での実装

さて、このオンラインでBatch AllなTriplet lossをTensorFlow（Keras）で実装すると次のようになります。このクラスになると、とてもKerasのバックエンド関数だけでは物足りないので、Kerasとして動かしているものの、バックエンドのTensorFlowの関数を直に叩くように実装しています。

import tensorflow as tf
import tensorflow.keras.backend as K

# 上三角行列から対角成分を抜いた行列
def upper_triangle(matrix):
    upper = tf.matrix_band_part(matrix, 0, -1)
    diagonal = tf.matrix_band_part(matrix, 0, 0)
    diagonal_mask = tf.sign(tf.abs(tf.matrix_band_part(diagonal, 0, 0)))
    return upper * (1.0 - diagonal_mask)

MARGIN = 0.25

def euclidean_triplet_loss(label, embeddings):
    # euclidean matrix
    x1 = tf.expand_dims(embeddings, axis=0)
    x2 = tf.expand_dims(embeddings, axis=1)
    euclidean = tf.reduce_sum((x1-x2)**2, axis=-1)

    # label equal matrix (* shape=[None, latent_dims])
    lb1 = tf.expand_dims(label[:, 0], axis=0)
    lb2 = tf.expand_dims(label[:, 0], axis=1)
    equal_mat = K.cast(tf.equal(lb1, lb2), "float32")

    # postives TPUではtf.whereが使えないので総当たりにする
    positive_flag = upper_triangle(equal_mat)
    # positive以外は0を入れる
    positive_dist = positive_flag*euclidean
    positive_dist = tf.reshape(positive_dist, [-1,1])

    # negatives
    negative_flag = upper_triangle(1.0-equal_mat)
    distance_max = tf.reduce_max(euclidean, keepdims=True)
    # negatives以外には(距離の最大値)を入れる
    negative_dist = negative_flag*euclidean + (1.0-negative_flag)*distance_max
    negative_dist = tf.reshape(negative_dist, [1,-1])

    # triplet loss
    loss = tf.maximum(positive_dist - negative_dist + MARGIN, 0.0)
    return tf.reduce_sum(loss)

TPUのコードなので$O(N^4)$を総当たりで計算していますが、GPUでしたら先程書いたようにtf.where→tf.gather_ndでpositiveとnegativeの距離行列をselectしたほうがメモリ効率は良いです。

ちなみに出力層の活性化関数は要りません。例えば、Global Average Poolingを出力層としてしまってOKです。

Triplet lossによる推定と評価

問題は埋め込みの数値からどうやってラベルを推定すれば良いのでしょうか？またどうやってモデルの精度を評価すればよいでしょうか？

最も簡単なのはk=1のNearest Neighbor、つまりある画像の特徴量が得られたら、それに最も近いアンカーのラベルの推定値とするということです。自分も確認してみたのですが、少なくともCIFAR-10とかの綺麗な（均衡データかつ明確な外れ値がない）データセットではこれが一番精度が出ました。実装も簡単です。ただ、不均衡データや外れ値があるデータセットでは、後述のスレッショルドの推定のほうが精度が出るかもしれないので、そこは試してみる価値があります。これはFaceNetの論文に出ていた手法ではないので、その点はよくわかりません。

ただし、このNearest Neighborを使う場合は、訓練と推定で同じ距離関数を使うようにしましょう。例えば、ユークリッド距離で訓練して、コサイン類似度（距離）で評価するというのはミスマッチになってしまい、精度が落ちる原因になるのではないのかな、と自分は思います。

ではFaceNetではどのように評価していたかというと、以下のようなTA（True Accept）とFA（False accept）の指標を導入します。Precision,RecallやROC曲線と発想はほぼ同じです。

VAL(d)というのは、dという距離のスレッショルド（しきい値）を変数にして、Ground Truthが同じであるペアのうち、同じであると推定できたペア数の割合を示します。これは画像が同じかどうかというRecallに等しいです。

／	真の結果が正	真の結果が負
予測結果が正	TP	FP
予測結果が負	FN	TN

という状態で、

$$VAL(d)=Recall=\frac{TP}{TP+FN} $$

であるからです。FAR(d)を同様に表すと次のようになります。

$$FAR(d)=\frac{FP}{FP+TN} $$

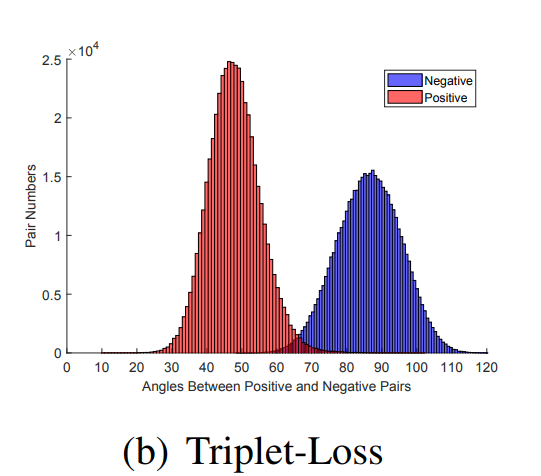
スレッショルドの直感的な理解は別の論文を見るとよりわかりやすく、

この図では横軸が角度（angle）になっていますが、マージン(d)と同じに考えて良いです。つまり、「ある横軸のマージンdで切ったときに、どれぐらいのPositiveが再現できるか」あるいは「どれぐらいのNegativeが混入してしまうか」という指標です。したがって、Positiveをすべて再現できる最小のdをスレッショルドとして選ぶのが1つの選び方となります⁶。このスレッショルドdはホールドアウトやK-Foldで求めると良いでしょう。

もし積分による表記が怖くなければ、xを確率変数としたときの、positiveとnegativeの確率密度関数を$f_p(x), f_n(x)$とし、

VAL(d)=\int_0^d f_p(x)dx \\
FAR(d)=\int_0^d f_n(x)dx \\

とも書けます。

このスレッショルドdを言い換えれば「2つの画像の距離を比較したときに距離がd以下ならば、全て同じクラスの画像と推定できる」といういうことです。これは論文に書かれていたものではなく、自分が考えたものですが、これから距離がd以下の画像をすべて選択し、(1)そのラベルを多数決で求める、(2)スレッショルド-距離でスコアを計算して近い順に重み付けてラベルを選ぶ　というようなアルゴリズムで推定できるのではないでしょうか。冒頭のk=1のNearest Neighbor法を含めると3種類の推定方法があります。

1. 最も近い画像のクラスだけを選ぶ（簡単）
2. VALやFARの指標でスレッショルドを計算し、距離がスレッショルド以下の画像について、そのラベルの多数決をとる
3. 2と同じ方法で計算したスレッショルドで、近い順に重みづけしてスコアリングしてラベルを選ぶ

後で確認しますが、自分がCIFAR-10で確認したところ1の「最も近い画像のクラスを選ぶ」が精度が良かったです。ただしこれは、外れ値が近くにくるとその影響を受けそうな気はするので、これで良いかどうかは検討の余地があると思います。

実験

ここからは自分で1からFaceNetの構造のネットワークを作り、精度を検証してみます。Train with 1000のCIFAR-10を使いました。通常CIFAR-10は訓練画像が5万枚ですが、1000枚で訓練するこのプロジェクトでは、One-shot Learningのアルゴリズムがかなり優位に機能します。

ネットワーク

何のひねりもなくVGGライクなモデルを作ります。

def create_siamese(latent_dims):
    input = layers.Input((32, 32, 3))
    x = input
    for i in range(4):
        for j in range(3):
            x = layers.Conv2D(64*(2**i), 3, padding="same")(x)
            x = layers.BatchNormalization()(x)
            x = layers.Activation("relu")(x)
        if i != 3:
            x = layers.AveragePooling2D(2)(x)
    x = layers.GlobalAveragePooling2D()(x)
    if latent_dims != 512:
        x = layers.Dense(latent_dims)(x)

    return Model(input, x)

ソフトマックスによる分類

ただのSoftmax関数による分類です。

／	精度
Data Augmentationなし	0.4806
Data Augmentationあり	0.4861

DataAugmentationはHorizontalFlip＋上下左右4ピクセルのランダムクロップを追加しました。

コードはこちら：https://gist.github.com/koshian2/9a16b0f5cc9ef7335798819126b4e2e6

Triplet lossによる分類

Data Augmentationは使わないで実験してみました。マージンは0.25とします。

コードはこちら：https://gist.github.com/koshian2/ab4595f7378e53c0586005264f46d8a2

3種類の推定方法を使います

1. Nearest Neighbor：潜在空間上で最も近い画像のクラスを推定値とする
2. Simple Threshold：VAL(d)を最大化する最も小さいスレッショルドdを求め、スレッショルド以下の画像のクラスを同じ重みで足し合わせて多数決を取る
3. Weighted Threshold:2で求めたスレッショルドdに対して、MAX(d-Distance, 0)をスコアとして、そのスコアを最大化するクラスを推定値とする

／	精度
Nearest Neighbor	0.4929
Simple Threshold	0.4822
Weighted Threshold	0.4823

Train with 1000のCIFAR-10では、Nearset Neighbor法が最も精度がよくなりました。距離関数を変えてたり、何度か試行してもNearest Neighbor法が最も良くなるので、とりあえずはNearset Neighbor法が一番良いと考えて良いと思います。精度は49.29%と、通常のソフトマックスによる分類より若干良い（1.23%）程度となりました。ただし、ソフトマックスではたまに50%を超えることもあるので、ユークリッド距離のTriplet lossでは互角かなというのが正直なところです。

ちなみにログから、内部でどういう推定をしているのか軽く説明していきたいと思います。

val_rate [0. 0. 0. ... 1. 1. 1.]
Best threshold : 0.8220000267028809, Best VAL : 1.0
Simple 1-Nearest Neighbor
Train acc:1.0, Test acc:0.4892, Best Test:0.4929
Simple thresholding
thresholded num :  100.0
[100 100 100 100 100 100 100 100 100 100]
thresholded num :  44.739
[3489  676  702  754  792  611  664  752  805  755]
Train acc:1.0, Test acc:0.4381, Best Test:0.4822
Weiged thresholding
thresholded num :  100.0
[100 100 100 100 100 100 100 100 100 100]
thresholded num :  44.739
[3489  674  702  752  794  613  664  752  805  755]
Train acc:1.0, Test acc:0.4378, Best Test:0.4823
2000/2000 [==============================] - 195s 97ms/step - loss: 0.0383

一番上の「Best threshold」というのは、VAL(d)を最大化するdの値です。この場合は、VALの最大値は1.0、つまりすべてのPositiveのペアが再現されていて、そのときのスレッショルドは0.822となります。この値はTriplet lossの損失関数の中のマージンと関係していて、マージンよりも広めの値となるはずです。

そのあとのSimple Thresholding以下の「thresholded num」は距離がスレッショルド以下であるアンカーの数の平均です。上がTrain, 下がTestです。Trainでは1クラスあたり100枚なので、100%の精度で再現されています。Test側はthresholded numが100より少なくなっていて、要はオーバーフィッティングしている状態ですね。その下の配列はクラスあたりの推定数で、Trainは完璧ですが、Test側はオーバーフィッティングしていて1番目のクラスにやたらと誤判定されるということになります。

距離関数をarccosにする

実はユークリッド距離というのは個人的にはあまり良くはないのかなと思います。なぜなら、ユークリッド距離では$(1,1)$と$(2,2)$という点同士の距離よりも、$(1,1)と(0,1)$の距離のほうが短いからです。前者はベクトルの定数倍ですが、後者はベクトルの向きが違います。それなら、ベクトルのなす角（$cos\theta$）を取ったほうが良いです。これはコサイン類似度の発想です。

実は全結合層の計算（行列の内積）と、コサイン類似度は密接に関係していて、今バイアス項を落としますが、全結合層では、

$$W^T_{y_i}x_i $$

という内積計算をしています。ここで$W_{y_i}$は係数行列の$y_i$番目の列ベクトルを、$x_i$は$i$行目の入力を表します。もし、この2つのベクトルの内積をそれぞれのノルムで割れば、

$$\cos\theta = \frac{W^T_{y_i}x_i}{||W^T_{y_i}||\cdot||x_i||}$$

コサイン類似度の式に帰着させることができます。ノルムで割るというのはL2 Normalizationと等価です。つまり、全結合層の計算において、係数と入力をそれぞれL2 Noramlization（一般的には標準化）すれば、全結合層の出力＝コサイン類似度となります。

もし潜在空間が2次元ならば、これは潜在空間上のプロットを原点を中心とした単位円にプロットしているのに他なりません。円の座標系、つまり極座標系では、角度が座標同士の距離になります（標準化しているので半径は固定です）。つまり、コサインから角度を求める、コサインの逆関数であるarccosがコサイン類似度に対応する距離関数となります。

実はこのアイディアは元ネタがあって、『ArcFace: Additive Angular Margin Loss for Deep Face Recognition』という論文からです。この論文の中でTriplet lossの距離関数にarccosを組み込んだものが検討されていました。論文によると、ユークリッド距離のTriplet lossよりも精度が出るとのことです。損失関数を数式で書くと、

$$\sum_i^N\max\biggl[\arccos\bigl(\frac{x_i^a\cdot x_i^p}{||x_i^a||\cdot ||x_i^p||}\bigr)-\arccos\bigl(\frac{x_i^a\cdot x_i^n}{||x_i^a||\cdot ||x_i^n||}\bigr)+\alpha, 0\biggr] $$

という式になります。これは距離が角度に置き換わっただけで、「Positiveのペアの角度のほうが、Negativeのペアの角度よりも小さくなるようにして、かつマージンをつける」という条件で最適化しています。

コードはこちら：https://gist.github.com/koshian2/d28a3cbdfc8f398f7d836739dbc6b5b2

これは実際に試してみると精度は結構出ます。マージンはArcFaceの論文に従って0.5としました。

／	精度
Nearest Neighbor	0.5286
Simple Threshold	0.4615
Weighted Threshold	0.4616

Data Augmentationなしで52.86%の精度を達成することができました。これはベースラインのSoftmaxから5%弱の改善になります。

なぜTriplet Lossがうまくいくのか

これはたまたまうまく行った例ですが、Softmaxよりも精度が出た理由はおそらくですが、訓練時に「サンプル間」の距離の計算をしているからだ思います。通常のSoftmaxではサンプル間の演算というのはしません。しかし、Triplet loss、もといSiamese Networkではサンプル間の関係性を見るため、より多くの情報をデータから得ているはずです。Triplet Lossなら3点の関係性を見るので、相当情報は入っているはずです。カーネルありのサポートベクターマシンが、カーネルなしのサポートベクターマシン（≒ロジスティック回帰）よりも精度が出やすいというのと似た原理だと思います。

つまり、カーネル法のアプローチから画像分類を見ていくと、より少ないサンプルで同じ精度を出すというのが可能になるのではないでしょうか。人間だって、1枚の画像を独立に見るのではなくて、複数枚の画像を見て「これとこれ似てるからこれっぽいよね」みたいなことしますよね。

参考資料

• C4W4L03 Siamese Network : https://www.youtube.com/watch?v=6jfw8MuKwpI
• C4W4L04 Triplet loss : https://www.youtube.com/watch?v=d2XB5-tuCWU
• Siamese networks : https://www.slideshare.net/NicholasMcClure1/siamese-networks
• FaceNet: A Unified Embedding for Face Recognition and Clustering : https://arxiv.org/abs/1503.03832
• ArcFace: Additive Angular Margin Loss for Deep Face Recognition : https://arxiv.org/abs/1801.07698
• In Defense of the Triplet Loss for Person Re-Identification https://arxiv.org/abs/1703.07737
• Triplet Loss and Online Triplet Mining in TensorFlow : https://omoindrot.github.io/triplet-loss

---

1. 何回か試してみたところ、Softmaxは簡単かつ安定して精度が出るので、実はとても強力な手法です。他の論文を当たってみると、このFaceNetの手法がSoftmaxより精度で劣るということも書いてあります。例えば：https://arxiv.org/pdf/1801.07698 ↩

2. こちらに書いたのでよろしければ：https://blog.shikoan.com/tensorflow-array-selecting/ ↩

3. 例えばバッチサイズが256なら、float32で256^4*4=17GBの変数になりますが、TPUのHBMは64GBあるので全然収まります。流石にバッチサイズ1024とかは無理ですね。 ↩

4. maxを入れないと意味のあるTripletによる損失を相殺してしまい、副作用があるので、maxを入れます。より正確に言えば、maxがあるから0になるというのではなく、簡単なTripletによる副作用を消したいから、maxを入れているのです。 ↩

5. In Defense of the Triplet Loss for Person Re-Identification https://arxiv.org/abs/1703.07737 ↩

6. これは絶対的な方法ではなくあくまで1つの指標でしかありません。他にも論文では書かれていませんが、F1スコア等で選ぶ方法もあっても良いでしょう。 ↩