More than 5 years have passed since last update.

Swiftで代数学入門〜 7. 代数拡大で数を作ろう！

Last updated at 2017-10-19Posted at 2016-03-23

どうも、佐野です。ついにシリーズ最終回です！これまでやってきたことの集大成として「代数拡大」を実装し、$\sqrt{2}$ や虚数単位 $i$ などがコンピュータ上で実現できることを見ていきましょう！

多項式でも「ユークリッド＆ベズー」

整数と同様に多項式についても「倍数・約数」を考えることができます。$f(x) = g(x) \cdot h(x)$ と書ける時、$f$ は $g$ の倍数、$g, h$ は $f$ の約数です。「最小公倍数・最大公約数」は整数では絶対値を見ましたが、多項式では次数を見れば同様に考えることもできます。

例えば：

\begin{eqnarray}
 f(x) &=& x^3 - 3x^2 + 2x,\\ 
 g(x) &=& x^2 - 5x + 6
\end{eqnarray}

の最大公約数は、それぞれ因数分解して：

\begin{eqnarray}
f(x) &=& x(x - 1)(x - 2), \\
g(x) &=& (x - 2)(x - 3)\end{eqnarray}

で $x - 2$ が共通因子であることから、$\gcd(f, g) = x - 2$ と分かります。
因数分解は人間にもコンピュータにも難しいので、代わりに $f, g$ に対してユークリッド互除法を使えば：

\begin{eqnarray}
f(x) &=& (x + 2) \cdot g(x) &+& 6x - 12 \\
g(x) &=& \frac{1}{6}(x - 3) \cdot (6x - 12) &+& 0
\end{eqnarray}

より、この場合 $6x - 12$ が最大公約数として求まります。

多項式の割り算では「次数」のみに注目しているので、定数倍の差は無視され $x - 2$ も $6x - 12$ も「$f, g$ の最大公約数」ということになります。最高次係数が $1$ となるものだけを取ることにすれば（このような多項式を「モニックな多項式」という）最大公約数は一つに定まります。

多項式に対してもユークリッド互除法で最大公約数が求められるのだから、整数の場合と同様にそれを逆に解けば「ベズーの等式」が得られるはずです。つまり多項式 $f(x), g(x)$ に対して多項式 $p(x), q(x)$ があって、

f(x) \cdot p(x) + g(x) \cdot q(x) = \gcd(f(x), g(x))

となります。
上の例では、

f(x) \cdot 1 - g(x) \cdot (x + 2) = 6x - 12

より $p(x) = 1,\ q(x) = -x - 2$ と求まります。

整数、多項式ともにその具体的な性質に依らず、

余りつき割り算ができる
$\Rightarrow$ ユークリッド互除法が使える
$\Rightarrow$ ベズーの等式が解ける

という構造になっていることに注目してください。いま gcd と bezout を Polynomial に対しても実装する場合、Z と別に実装するよりも「余りつき割り算ができる」という性質を protocol として切り出した上で実装を共通化したくなりますよね。

余りつき割り算ができる環のことを 「ユークリッド環」 と言います。 protocol EuclideanRing は Ring を継承し、ユークリッド除法 eucDiv を実装するものとします：

public protocol EuclideanRing: Ring {
    static func eucDiv(a: Self, _ b: Self) -> (q: Self, r: Self)
}

剰余演算 % は eucDiv の余りだけを取り出す演算なので、デフォルト実装を入れておきます：

public func %<R: EuclideanRing>(a: R, b: R) -> R {
    return R.eucDiv(a, b).r
}

まず整数環 Z については、はじめから / と % が定義されているので、それを使って EuclideanRing に適合させることができます：

extension Z: EuclideanRing {
    public static func eucDiv(a: Z, _ b: Z) -> (q: Z, r: Z) {
        return (q: a / b, r: a % b)
    }
}

デフォルト実装の % は Int に入ってる % を上書きはしないのでこれでオッケーです。次に Polynomial については前回定義した eucDiv を Polynomial の static メソッドに移し、EuclideanRing とすればいいだけです：

extension Polynomial: EuclideanRing {
    public static func eucDiv<K: Field>(f: Polynomial<K>, _ g: Polynomial<K>) -> (q: Polynomial<K>, r: Polynomial<K>) {
        ... // 前回の実装と同じ
    }
}

これで整数環 Z も多項式環 Polynomial も EuclideanRing になりました！次に Z 専用に作った gcd と bezout を EuclideanRing に一般化します。やることはほぼ関数のシグネチャを変えるだけです：

public func gcd<R: EuclideanRing>(a: R, _ b: R) -> R {
    ... // Zの場合の実装と全く同じ
}

public func bezout<R: EuclideanRing>(a: R, _ b: R) -> (x: R, y: R, r: R) {
    ... // Zの場合の実装とほぼ同じ
}

gcd も bezout も、Ring としての足し算・掛け算と EuclideanRing としての余りつき割り算しか使っていないので、このように一般化できるのです！

（さらにガウス整数環 $\mathbb{Z}[i]$ やアイゼンシュタイン整数環 $\mathbb{Z}[\omega]$ もユークリッド環なので、これらの型を定めれば自ずと gcd, bezout も定義されます。抽象化万歳）

上で計算した例で試してみましょう：

let f = Polynomial<Q>(0, 2, -3, 1)  // x^3 - 3x^2 + 2x
let g = Polynomial<Q>(6, -5, 1)     // x^2 - 5x + 6

gcd(f, g)  // 6x - 12

let (p, q, r) = bezout(f, g)

p  // 1
q  // -x - 2
r  // 6x - 12

f * p + g * q == r  // true

ちゃんと上の計算と同じ結果が得られました！

多項式の剰余環が体になる条件は？

さて、整数の剰余環 $\mathbb{Z}_n = \mathbb{Z}/n\mathbb{Z}$ が体となるのは $n$ が素数のときでした。これは任意の $a \notin n\mathbb{Z}$ に対して「ベズーの等式」より：

ax + ny = 1

となる整数 $x, y$ があり、$\bmod{n}$ では：

ax \equiv 1

より $x$ が $\mathbb{Z}_n$ における $a$ の逆元となるためです。
同様に多項式 $f, g$ が互いに素（つまり $\gcd(f, g) = 1$）ならば、

f(x) \cdot p(x) + g(x) \cdot q(x) = 1

となる多項式 $p, q$ があり、 $\bmod{g(x)}$ では、

f(x) \cdot p(x) \equiv 1

より $p(x)$ が $\bmod{g(x)}$ における $f(x)$ の逆元になります。

$g(x)$ が「素数のような多項式」であれば、$g$ の倍数でない任意の多項式 $f$ と互いに素となり、上の議論から剰余環 $K[x]/(g(x))$ は体となります（$0$ でない $f$ に対して逆元がある、というのが体の条件です）。

「素数のような多項式」とは、$g(x) = g_1(x) \cdot g_2(x)$ のように二つの定数でない多項式の積に書けないもののことです（整数の場合 $p = a \cdot b$ のように書けない数 $p$ を素数というのでした）。このような多項式のことを**「既約な」**多項式と言います。

例えば $K = \mathbb{Q}$ として、$g(x) = x^2 - 2 \in \mathbb{Q}[x]$ を考えてみます。これがもし $g(x) = (ax + b)(cx + d)$ のように分解できるとすると、展開して係数を比較すれば：

\begin{cases}
ac &=& 1 \\
ad + bc &=& 0 \\
bd &=& -2
\end{cases}

より、

\begin{cases}
c &=& \frac{1}{a} \\
d &=& -\frac{2}{b}
\end{cases}

で、

ad + bc = -\frac{2a}{b} + \frac{b}{a} = \frac{-2a^2 + b^2}{ab} = 0

より、

-2a^2 + b^2 = 0 \Leftrightarrow \left(\frac{b}{a}\right)^2 - 2 = 0

でなければなりません。しかし $a, b \in \mathbb{Q}$ なので $\frac{b}{a} \in \mathbb{Q}$ で、自乗して $2$ になる数（つまり $\mathbb{R}$ における $\sqrt{2}$ ）は $\mathbb{Q}$ の中にはないので、この等式は成り立ち得ません。

従って $g(x) = x^2 - 2$ は $\mathbb{Q}$ 上で既約で、剰余環 $L = Q[x]/(x^2 - 2)$ は体となります！…といっても、この $L$ における元（例えば $x + 1$）の逆元がどんな形をしているか、なかなか想像しづらいものがあります。

bezout を使って計算してみましょう！

let f = Polynomial<Q>(1, 1)      // x + 1
let g = Polynomial<Q>(-2, 0, 1)  // x^2 - 2

let (p, q, r) = bezout(f, g)
p  // -x + 1
q  // -x - 2
r  // -1

f * (-p)           // x^2 - 1
f * (-p) % g == 1  // true

上の計算結果から $f(x) = x + 1,\ g(x) = x^2 - 2$ に対して、

f(x)\cdot(-x + 1) + g(x)\cdot(-x - 2) = -1

で、両辺 $-1$ 倍して $\bmod{g(x)}$ で見れば：

f(x)\cdot(x - 1) \equiv 1 \pmod{g(x)}

となっているので、$L$ においては $f(x) = x + 1$ の逆元は $x - 1$ ということです！このことは直接計算でも $x^2 \equiv 2$ より $(x + 1) \cdot (x - 1) = x^2 - 1 \equiv 2 - 1 = 1$ と確かめられます。

多項式の逆元が多項式の形をしているなんて不思議ではありませんか？このことは「素数時間の時計 $\mathbb{F}_p$」で、どの数にもその中に逆元があったのと似ています。「あれ、なんでそうなるんだっけ…？」となったら「ベズーの等式」に立ち返りましょう！

まとめると：

係数体 $K$ 上の既約多項式 $g(x)$ を取ると、
剰余環 $L = K[x]/(g(x))$ は体となる。
任意の $f \in K[x]$ に対して $fp + gq = 1$ なる $p$ が $L$ における逆元。

（$\mathbb{R}$ では $g(x) = x^2 - 2 = (x - \sqrt{2})(x + \sqrt{2})$ と分解できるので「多項式が既約かどうか」は係数体に依存します。）

実装しよう！

有限体 $\mathbb{F}_p$ を作ったときと同様に、剰余環 PolynomialQuotient と同じ実装で、Field に適合させて inverse を入れれば、それで体としての剰余環の出来上がりです：

public struct PolynomialQuotientField<g: TPPolynomial>: Field {
    ...

    public var inverse: PolynomialQuotientField<g> {
        // find: f * p + g * q = r (r: const)
        // then: f^-1 = r^-1 * p (mod g)
        let (p, _, r) = bezout(f, g.value)

        if r == 0 || r.degree > 0 {
            fatalError("\(f) and \(g) aren't coprime.")
        }
        
        return PolynomialQuotientField(r[0].inverse * p)
    }
}

先ほどの計算を PolynomialQuotientField の中でやってみると…

// g(x) = x^2 - 2 を保持する型
struct g: TPPolynomial {
    typealias K = Q
    static let value: Polynomial<Q> = Polynomial<Q>(-2, 0, 1)
}

typealias L = PolynomialQuotient<g>  // L = Q[x]/(g(x))

let f = Polynomial<Q>(1, 1)          // x + 1 (mod g)
f.inverse                             // x - 1 (mod g)
f * f.inverse                         // x^2 - 1 = 1 (mod g)

問題なさそうです！

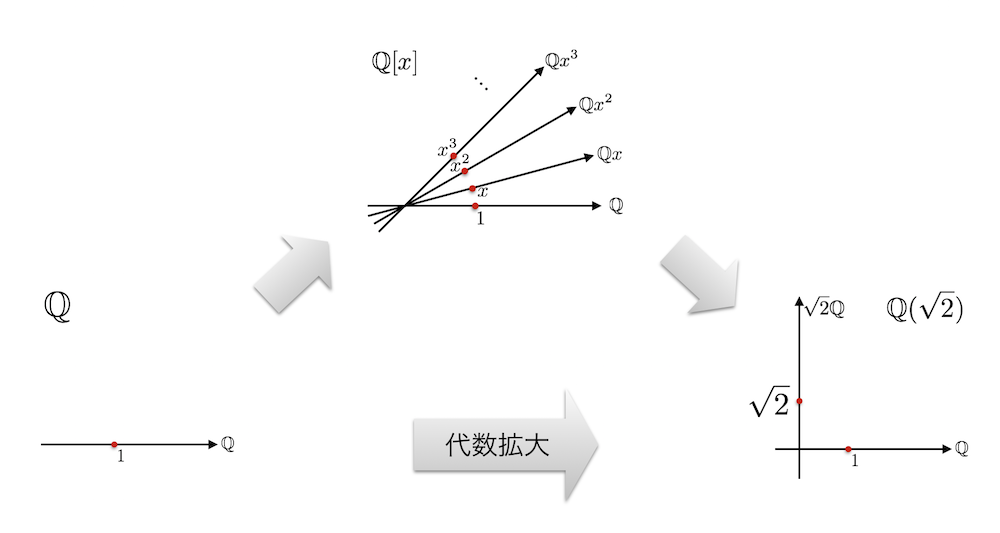
これが代数拡大だ…！

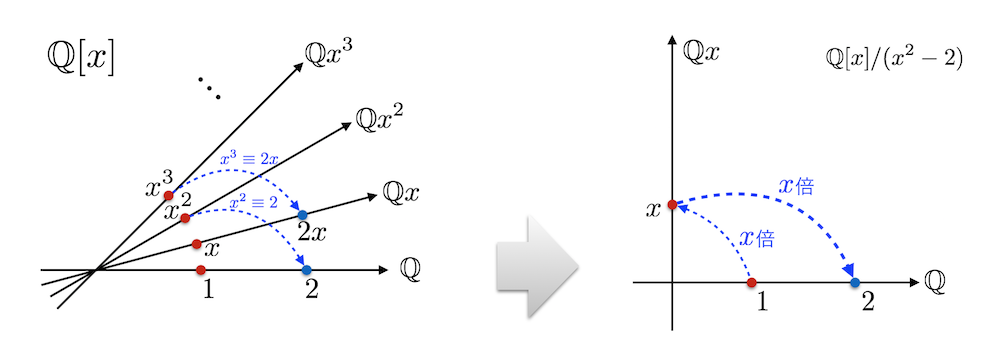
いま多項式の剰余環 $L = \mathbb{Q}[x]/(x^2 - 2)$ を作りましたが、実はこの $L$ こそ有理数体 $\mathbb{Q}$ に $\sqrt{2}$ を付け加えた体 $\mathbb{Q}(\sqrt{2})$ なのです！

$L$ と $\mathbb{R}$ の部分集合としての $\mathbb{Q}(\sqrt{2})$ は全く同じものに見えないと思います。

まず $L$ が体であることは上に示した通りです。そして $L$ は定数多項式として $\mathbb{Q}$ の元を全て含むので $\mathbb{Q} \subset L$ です。「$\sqrt{2}$ は？」というと、$1$ 次式 $x \in \mathbb{Q}[x]$ （の合同類）こそが $L$ における $\sqrt{2}$ です！

なぜなら $\bmod{g(x)}$ では $x^2 \equiv 2$ なんだから、これは $L$ において $x^2 = 2$ ということです。自乗して $2$ になるってことは、それは $\sqrt{2}$ ですよね！

誤魔化されたような気分になると思うので…

まず $\mathbb{Q}[x]$ を $\lbrace 1, x, x^2, \cdots \rbrace$ を基底とする無限次元ベクトル空間と見て、これを $x^2 \equiv 2$ というルールによって折りたたんで行ったのが $L$ です。$2$ 次以上の軸は全て折り畳まれるので、残るのは $0$次と $1$次で $L$ は $2$ 次元ベクトル空間です：

ここで $\mathbb{Q}[x]$ や $L$ はただのベクトル空間ではなく、掛け算が入ってます。$1$ を $x$ 倍すると $x$ で、また $x$倍すると $x^2$ になりますが、 $x^2$ の軸は $L$ では $2$倍されて定数軸に折り畳まれていたので $x^2 = 2$ です。

先ほど作った L = PolynomialQuotientField<g> で見てみると：

typealias L = PolynomialQuotientField<g>

let a = L(0, 1)     // √2
a * a == 2          // true

(1 + a) * (1 + a) == 3 + 2 * a  // (1 + √2)^2   = 3 + 2√2
1 / (1 + a)       == -1 + a     // 1 / (1 + √2) = -1 + √2

いま L における x の合同類（$\sqrt{2}$ だと思いたいもの）を a と置いた上で、L の中身が多項式だということを忘れます。これは自乗すると 2 になっています。1 + a の自乗を計算してみると：

(1 + \sqrt{2})^2 = 1 + 2\sqrt{2} + 2 = 3 + 2\sqrt{2}

と同じ結果になってますよね？
1 / (1 + a) についても、

\frac{1}{1 + \sqrt{2}} = \frac{1 - \sqrt{2}}{(1 + \sqrt{2})(1 - \sqrt{2})} = -1 + \sqrt{2}

と同じです。そこで $L$ の基底 $\lbrace 1, x\rbrace$ の $x$ を記号的に $\sqrt{2}$ と書くことにすれば、 $L$ 上の元は全て $a + b\sqrt{2}$ と書けて、$L$ の中では $+, -, \times, \div$ が全てできるんだから、$L$ は $\mathbb{R}$ の部分集合としての $\mathbb{Q}(\sqrt{2})$ と見なせるでしょう…！

ここでやったことを改めて見直すと、まず $\mathbb{Q}$ から $\mathbb{Q}[x]$ というめちゃくちゃ大きな環を作った上で、それをギュッとまとめて $\mathbb{Q}$ より一回り大きな体 $\mathbb{Q}(\sqrt{2})$ を作りました。これを一つの動きとしてみれば「$\mathbb{Q}$ を拡大して $\mathbb{Q}(\sqrt{2})$ という体を作った」という風に見ることができます。

「最初から $\mathbb{R}$ の中で $\sqrt{2}$ をとればいいものを、なぜこんなややこしいことをするのか…」

その答えの一つはシリーズ初回で示した通り、原理的に有限小数しか扱えないコンピュータでは $\mathbb{R}$ は近似的にしか作れません。しかし上の方法であれば「$\sqrt{2}$ そのもの」が作れてしまうのです…無理数であるにも関わらず！

複素数体を作ろう！

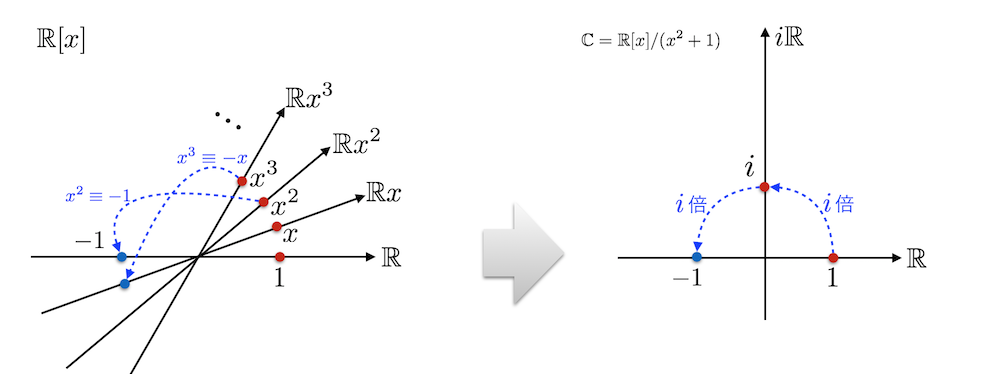
テンションを上げて今度は複素数体 $\mathbb{C}$ を作ってみましょう。$K = \mathbb{R}$ として、$\mathbb{R}$ 上の多項式環 $\mathbb{R}[x]$ を考えます。いま虚数単位 $i$ を $\mathbb{R}$ 上作りたいのですが、$i^2 = -1$ より $i$ は $g(x) = x^2 + 1$ の根（つまり $g(x) = 0$ の解）です。

$g(x)$ は $\mathbb{R}$ 上既約です（上と同様にして示されます）。従って $L = \mathbb{R}/(x^2 + 1)$ は体となり、$L$ は $\lbrace 1, x\rbrace$ を基底とする $\mathbb{R}$ 上の $2$ 次元のベクトル空間です。この $x$ を $i$ と書くことにすれば $L$ の元は $a + bi$ と書け、$\bmod{g(x)}$ では $x^2 \equiv -1$ なので $i^2 = -1$ です。

複素数体 $L = \mathbb{C}$ の出来上がりです！

右に出てくる図はまさしく「複素数平面」そのものですね！
せっかくなのでコードでも確認しておきましょう：

// g(x) = x^2 + 1 を保持する型
struct g: TPPolynomial {
    typealias K = R
    static let value: Polynomial<R> = Polynomial<R>(1, 0, 1)
}

typealias C = PolynomialQuotient<g>  // C = R[x]/(x^2 + 1)

let i = C(0, 1)        // i = √-1
i * i == -1            // true

let z = 3 + 2 * i      // z = 3 + 2i
z * z == 5 + 12 * i    // true

複素数がコンピュータ上で実現できました！

…とはいえこの R = Double は偽物の実数体なので、R の代わりに Q を取って拡大体を作れば ガウス有理数 $\mathbb{Q}(i)$ が作れます。こっちは本物です！

より一般に「円分多項式」を考えれば、$1$ の原始 $n$ 乗根（$n$ 乗してはじめて $1$ になる数）$\zeta_n$ を作ることができます（上は $n = 4$ の場合）。例えば $n = 3$ のとき $\omega = \zeta_3$ は $x^3 - 1 = (x - 1)(x^2 + x + 1)$ の根で、 $3$ 次の円分多項式 $x^2 + x + 1$ で $\mathbb{Q}[x]$ を割れば、1次式 $x$ の合同類として $\omega$ を得ます。

ガンガン拡大していこう！

体 $K$ と $K$ 上の既約多項式 $g(x)$ があれば $K$ の代数拡大体 $L = K[x]/(g(x))$ が作れるんだから、再び $L$ 上の既約多項式 $h(x)$ があればそのまた拡大体 $M = L[x]/(h(x))$ が作れます！

$\mathbb{Q}$ の2段拡大体 $\mathbb{Q}(\sqrt{2}, \sqrt{3})$ を作ってみましょう。まず $L = \mathbb{Q}[x]/(x^2 - 2)$ で $\mathbb{Q}(\sqrt{2})$ を作ります。次に $L$ 上の既約多項式 $h(x) = x^2 - 3$ を取れば、$M = L[x]/(x^2 - 3)$ によって $\mathbb{Q}(\sqrt{2}, \sqrt{3})$ が得られます。

コードでみてみましょう：

// g(x) = x^2 - 2 in Q[x]
struct g: TPPolynomial {
    static let value = Polynomial<Q>(-2, 0, 1)
}

// L = Q[x]/(x^2 - 2)
typealias L = PolynomialQuotientField<g> 

let a = L(0, 1)  // a = √2 in L
a * a == 2       // true

// h(x) = x^2 - 3 in L[x]
struct h: TPPolynomial {
    static let value = Polynomial<L>(-3, 0, 1)
}

// M = L[x]/(x^2 - 3)
typealias M = PolynomialQuotientField<h>

let b = M(a)      // b = √2 in M
let c = M(0, 1)   // c = √3 in M

b * b == 2        // true
c * c == 3        // true

先ほどと同じやり方で L を作り、その中の a （L での $\sqrt{2}$）を取っておきます。次に L の拡大体 M を作ると、先ほどの a は M の中では定数になり、M における定数多項式 b = M(a)（$M$ での $\sqrt{2}$）が取れます。もう一つ L[x] における x の合同類 c（$M$ での $\sqrt{3}$）を取ります。

すると例えば：

let d = b * c       // d = √6
let x = b + c       // x = √2 + √3
x * x == 5 + 2 * d  // true: (√2 + √3)^2 = 5 + 2√6

のように期待通り演算ができているので、 $M = \mathbb{Q}(\sqrt{2}, \sqrt{3})$ となっていることが確認できます！（ちなみに $M$ は $\mathbb{Q}$ 上 $\lbrace 1, \sqrt{2}, \sqrt{3}, \sqrt{6}\rbrace$ を基底とする $4$ 次元ベクトル空間となります）

このように、体の中で既約多項式が取れる限り代数拡大を繰り返すことができます。拡大体における $1$ 次式 $x$ の合同類はその既約多項式の根となるので、その拡大体の中では多項式は分解できます。複素数体 $\mathbb{C}$ があれば全ての多項式は $1$ 次式の積に分解できますが、特定の多項式について見るだけなら $\mathbb{Q}$ から一歩一歩やっていけばいいのです。

こうして我々はアルティンの言葉の真意を得ます：