どうも、佐野です。いよいよシリーズのゴール「代数拡大の実装」に向けて準備が整ってきました。今回は多項式環 $K[x]$ を作り、整数環 $\mathbb{Z}$ とのアナロジーで剰余環が作れることを見ていきます。
目次:
多項式の型を作る
シリーズ初回「数とは何か? 」で複素数体 $\mathbb{C}$ は「代数方程式が必ず解を持つ数体」として導入しました。代数方程式とは「多項式 $= 0$」の形でかける方程式のことで、多項式 (Polynomial) とは:
f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0
という式のことです。中学では$2$次式を習い、そのグラフが放物線となることを見たと思います。
多項式を決めるのは次数(degree) $n$ と $n + 1$ 個の係数の列 $(a_0, \cdots, a_{n-1}, a_n)$ です。先を見越してこれら係数は一般の体 $K$ の値を取ることとします。
struct Polynomial<K> を次のように定めます:
struct Polynomial<K: Field> {
private let coeffs: [K] // K型の係数リスト
init(coeffs: [K]) {
self.coeffs = coeffs
}
}
例えば $f(x) = x^2 - 3x + 2$ を作るには、
let f = Polynomial<Q>(coeffs: [2, -3, 1]) // x^2 - 3x + 2
とします。ここで係数は定数項から昇順に定めている点に注意してください(後々この方が分かりやすくなります)。Swift ではメソッドに可変長引数を与えることもできるので:
struct Polynomial<K: Field> {
...
init(_ coeffs: K...) {
self.init(coeffs: coeffs)
}
}
とすれば上の f は、
let f = Polynomial<Q>(2, -3, 1) // x^2 - 3x + 2
と少しシンプルになります。
もう一つ、次数と「係数を作る関数」を引数に取る init も作っておきます:
struct Polynomial<K: Field> {
...
init(degree: Int, gen: (Int -> K)) {
let coeffs = (0 ... degree).map(gen)
self.init(coeffs: coeffs)
}
}
こうすると例えば、
let g = Polynomial<Q>(degree: 2) { i in i + 1 } // 3x^2 + 2x + 1
と gen に { i in i + 1 } を渡され、$i$ 次の係数が $a_i = i + 1$ で定められ $g(x) = 3x^2 + 2x + 1$ が作れます。これも後々あると便利です。
多項式の次数 degree と、係数にアクセスするための subscript も定義しておきましょう:
struct Polynomial<K: Field> {
...
var degree: Int {
let n = coeffs.count - 1
for i in 0 ..< n {
if coeffs[n - i] != 0 {
return n - i
}
}
return 0
}
subscript(n: Int) -> K {
return (n <= degree) ? coeffs[n] : 0
}
}
let f = Polynomial<Q>(2, -3, 1) // f(x) = x^2 - 3x + 2
f.degree // 2
f[2] // 1
次に多項式が関数としても機能するように apply メソッドを入れます:
struct Polynomial<K: Field> {
...
func apply(x: K) -> K {
return (0 ... degree).reduce(0) { (sum, i) -> K in
sum + self[i] * (x ^ i)
}
}
}
何やら複雑なことをやっていますが、(0 ... degree).reduce(0) { sum + ... } が $\sum_{i = 0}^n$ で、self[i] * (x ^ i) が $a_i x^i$ にあたります。多項式の式の通りに x を代入した値を計算しています。
let f = Polynomial<Q>(2, -3, 1) // f(x) = x^2 - 3x + 2
f.apply(0) // 1
f.apply(1) // 0
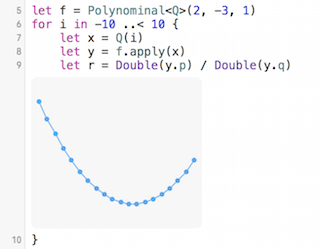
ちなみに Xcode の Playground ではループに対して値の変化を見ることができるので、ササッとこんなコードを書けば $2$次間数 f のグラフは放物線になっていることが確認できます:
これで土台はできたので、次に演算を入れて行きましょう。
多項式環に演算を入れる
多項式全体は自然な演算で環となります。ここで使う計算自体は中学校の数学でもやるものです。まず足し算は、同じ次数の係数を足すだけです:
(x^2 - 2x + 1) + (3x - 4) = x^2 + x - 3
掛け算は「式の展開」です:
(x^2 - 2x + 1)(3x - 4) = 3x^3 - 10x^2 + 11x - 4
中学でこれらの計算をやるときは、 $(3x - 4)$ などは「実体は数である文字式」と思いますが、ここでは「それ自体が多項式という実体」と思い、その演算を定めているのです。上の式で $x$ に値を代入すると、それが「体 $K$ の数」としてのイコールに変わります。つまり「代入」という操作は、多項式環 $K[x]$ から体 $K$ への環準同型である、ということです。
難しいことはさておき、 Polynomial に演算を入れていきましょう。
まずは足し算:
func +<K: Field>(f: Polynomial<K>, g: Polynomial<K>) -> Polynomial<K> {
let n = max(f.degree, g.degree)
return Polynomial<K>(degree: n) { i in f[i] + g[i] }
}
上で定義した、動的に係数を作る init がいい感じに使えてます。f + g という多項式の i 次の係数は f[i] + g[i] で定まるということが一目瞭然です。
同様に prefix - は:
prefix func -<K: Field>(f: Polynomial<K>) -> Polynomial<K> {
return Polynomial<K>(degree: f.degree) { i in -f[i] }
}
これで Polynomial は AdditiveGroup になります。
続けて掛け算:
func *<K: Field>(f: Polynomial<K>, g: Polynomial<K>) -> Polynomial<K> {
return Polynomial(degree: f.degree + g.degree) { (i: Int) in
(0 ... i).reduce(0) {
(res, j) in res + f[j] * g[i - j]
}
}
}
ちょっと複雑ですが、f * g の次数は f, g の次数の和で、i 次の係数は f, g の項から次数の和が i になるものについて和をとったもの、と定めています。例えば上の例では:
(x^2 - 2x + 1)(3x - 4) = 3x^3 - 10x^2 + 11x - 4
$x^3$ の係数は $(x^2, 3x)$ の組み合わせの積でしか作られないので係数は $1 \cdot 3 = 3$ です。$x^2$ の係数は、$(x^2, -4), (-2x, 3x)$ の組み合わせの積で作られるので係数は $1 \cdot (-4) + (-2) \cdot 3 = -10$ という具合です。
これで Polynomial<K: Field>: Ring と宣言すれば、多項式環 $K[x]$ の出来上がりです!
体K上の多項式環をベクトル空間と見る
多項式そのものを実体と見て演算を入れるという考えははじめは分かりづらいかもしれません。冒頭に書いたように $n$ 次多項式 $f$ は $n + 1$ 個の係数の列 $(a_0, \cdots, a_{n-1}, a_n)$ で決まるので、この $n + 1$ 次元のベクトルこそが $f$ であると考えてみましょう。
f(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0
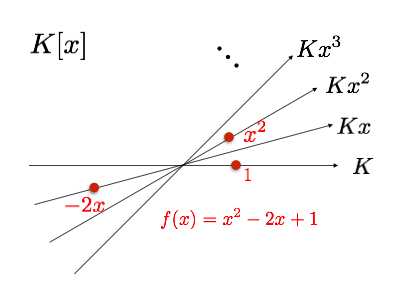
この表示は、$f$ が $\lbrace 1, x, \cdots, x^{n-1}, x^n \rbrace$ の線形結合で書けていることを表しています。これらは独立で $K[x]$ はどんな次数の多項式も入るので、$K[x]$ は無限個の $\lbrace 1, x, \cdots, x^n, \cdots \rbrace$ を基底とする(無限次元の)ベクトル空間です。
$K[x]$ という空間には $\lbrace K, Kx, Kx^2, Kx^3, \cdots \rbrace$ という無限個の独立な軸があって、そのうちの有限個の軸の上で $0$ でない値を取っているものの和が $f$ だと考えると想像しやすいかと思います。
多項式の「割り算」を考える
さて、ここから先、整数環と多項式環をパラレルに考えていきます。
整数の割り算には、$2$ 種類あります。一つは $13 \div 5 = \frac{13}{5}$ と、整数から有理数を作るものです。これは 第3回 でやった、整数環 $\mathbb{Z}$ から有理数体 $\mathbb{Q}$ を作ることに対応しています。
もう一つは $13 = 2 \cdot 5 + 3$ のように商と余りを求めるものです。この「割り算」によって出てくる商と余りは、整数の中で閉じています。除数を固定して、割った余りで整数環を分類したのが 第4回 でやった剰余環 $\mathbb{Z}_5 = \mathbb{Z} / 5\mathbb{Z}$ です。
これと同じことが多項式に対してもできます。二つの多項式 $f(x), g(x)$ に対して、$f(x) \div g(x) = \frac{f(x)}{g(x)}$ とすると、右辺は「多項式の分数」でかける 有理式 になります。有理式全体(記号では $K(x)$ と丸カッコで書く)は $\mathbb{Q}$ と全く同様にして体となります。
一方で、多項式 $f(x), g(x)$ に対して「$f$ を $g$ で割った商と余り」を考えることもできます。整数では「数の大きさ」を削りますが、多項式では「式の次数」を削ります。例えば $\ f(x) = 2x^3 + x^2 -3x + 2\ $ を $\ g(x) = x^2 + 1\ $ で割ると、
f(x) = (2x + 1) \cdot g(x) - 5x + 1
となり、商は $2x + 1$、余りは $- 5x + 1$ です。余りの次数 $1$ が $g$ の次数 $2$ より真に小さいのがポイントです。この割り算を計算する上では $x$ は不要で、係数だけ並べて整数の筆算と同様に行うことができます:
整数や多項式で定義される余り付きの割り算を「ユークリッド除法」と言います。
実装はこんな感じです:
func eucDiv<K: Field>(f: Polynomial<K>, _ g: Polynomial<K>) -> (q: Polynomial<K>, r: Polynomial<K>) {
// 0-除算はエラー
if g == 0 {
fatalError("divide by 0")
}
// 単項式で最高次だけ削る補助関数
func eucDivMonomial(f: Polynomial<K>, _ g: Polynomial<K>) -> (q: Polynomial<K>, r: Polynomial<K>) {
// 被除数と除数の次数の差
let n = f.degree - g.degree
// 除数の次数の方が大きい場合は被除数がそのまま余り
if(n < 0) {
return (0, f)
} else {
let a = f[f.degree] / g[g.degree] // 最高次係数の比
let q = Monomial(degree: n, coeff: a) // 次数 n 係数 a の単項式: a*x^n
let r = f - q * g // 最高次係数を削った余り
return (q, r) // 最高次を削る単項式と余りを返す
}
}
// 次数の高いところから順に削って商と余りを求めていく
return (0 ... max(0, f.degree - g.degree))
.reverse()
.reduce( (0, f) ) { (result: (Polynomial<K>, Polynomial<K>), degree: Int) in
let (q, r) = result
let m = eucDivMonomial(r, g)
return (q + m.q, m.r)
}
}
確認してみましょう:
let f = Polynomial<Q>(2, -3, 1, 2) // 2x^3 + x^2 - 3x + 2
let g = Polynomial<Q>(1, 0, 1) // x^2 + 1
let (q, r) = eucDiv(f, g)
q // 2x + 1
r // -5x + 1
f == g * q + r // true
バッチリですね ![]()
「余り」に注目して剰余環を作る
整数の場合と同様に、割り算の余りだけを見ることで「多項式の合同」を考えることができます。
例えば $f(x) = 2x^3 + x^2 -3x + 2\ $ を $\ g(x) = x^2 + 1\ $ で割った余りは $-5x + 1$ だったので:
f(x) \equiv -5x + 1 \pmod{g(x)}
です。
除数 $g$ を固定して $\bmod{g(x)}$ で多項式全体を分類すれば 多項式の剰余環 $K[x]/(g(x))$ ができます。
上の例だと $g(x)$ で割った余りは全て $1$ 次以下の多項式になるので、剰余環 $K[x]/(g(x))$ の元は全て $ax + b$ と表せます。「$K[x]$ をベクトル空間と見る」考え方だと、$g(x) \equiv 0 \Leftrightarrow x^2 \equiv -1$ なので、 このルールで無限次元空間 $K[x]$ を折りたたんでいくと $\lbrace 1, x \rbrace$ を基底とする $2$次元空間 $K[x]/(g(x))$ が出来上がります。
一般に $K[x]$ を $n$ 次式 $g(x)$ で割った環 $K[x]/(g(x))$ は $\lbrace 1, x, \cdots, x^{n-1} \rbrace$ を基底とする $n$ 次元ベクトル空間になります。これは $\mathbb{Z}$ を $n$ で割ると $\lbrace 0, 1, \cdots, n-1\rbrace$ という有限個の元を持つ環ができるのとよく似ていますね!
多項式の剰余環を実装する
第4回 では、整数の除数 n を保持するための型 TPInt を定義し、それを型パラメータとして受け取る整数の剰余環型 Z_<n> を作りました。多項式の場合も同じく、被除数 g: Polynomial<K> を保持できる型 TPPolynomial を定義します:
protocol TPPolynomial {
typealias K: Field
static var value: Polynomial<K> { get }
}
そしてそれを型パラメータとして受け取る多項式の剰余環型 PolynomialQuotient を定義します:
struct PolynomialQuotient<g: TPPolynomial>: Ring {
typealias K = g.K
let f: Polynomial<K>
init(_ f: Polynomial<K>) {
self.f = f
}
}
この PolynomialQuotient型に対して、以下のように剰余環の元を定められるようにしたいのです:
// g(x) = x^2 + 1 を保持する型
struct g: TPPolynomial {
typealias K = Q
static let value: Polynomial<Q> = Polynomial<Q>(1, 0, 1)
}
typealias L = PolynomialQuotient<g> // L = Q[x]/(g(x))
let f = Polynomial<Q>(2, -3, 1, 2) // 2x^3 + x^2 - 3x + 2
let fmod = L(f) // f(x) mod g(x)
L は Polynomial<Q> の g による剰余環、つまり「g で割った余り」で多項式全体を分類したものです。fmod は L において f が属するグループを表す元です。
PolynomialQuotient における演算の導入は Z_<n> の場合と全く同じです。まず PolynomialQuotient のイコールは「中の多項式の合同」で定義します:
func ==<g: TPPolynomial>(x: PolynomialQuotient<g>, y: PolynomialQuotient<g>) -> Bool {
return (x.f - y.f) % g.value == 0
}
合同類 x, y が等しいということは、その中の多項式を g で割った余りが同じ、つまりそれらの差は g で割り切れるということです。足し算や掛け算についても Z_<n> の場合と全く同じです:
func +<g: TPPolynomial>(x: PolynomialQuotient<g>, y: PolynomialQuotient<g>) -> PolynomialQuotient<g> {
return PolynomialQuotient(x.f + y.f)
}
prefix func -<g: TPPolynomial>(x: PolynomialQuotient<g>) -> PolynomialQuotient<F> {
return PolynomialQuotient(-x.f)
}
// (省略)
整数の合同類の場合と同様、この演算が「代表元の取り方によらず定まる」ことは数式で確認しないといけません(やり方は全く同じなので省略します)。こうして PolynomialQuotient は Ring となり、合同類についても多項式と同じように演算することができるようになりました!
先ほどの例で確認してみましょう。
$f = q(x) \cdot g(x) + r(x)\ $ ならば、$f \equiv r(x) \pmod{g(x)}$ のはずです:
// g(x) = x^2 + 1 を保持する型
struct g: TPPolynomial {
typealias K = Q
static let value: Polynomial<Q> = Polynomial<Q>(1, 0, 1)
}
typealias L = PolynomialQuotient<g> // L = Q[x]/(g(x))
let f = L(2, -3, 1, 2) // 2x^3 + x^2 - 3x + 2 mod g(x)
let r = L(1, -5) // -5x + 1 mod g(x)
f == r // true!
大丈夫そうです!これで多項式環 $K[x]$ とその剰余環 $K[x]/(g(x))$ が実装できました!
ところで整数環の場合は除数 $n$ が素数の場合、剰余環は体となるのでした。多項式環においても「素数のような式」があって多項式環を割ると体になりそうではありませんか…?
次回、いよいよシリーズラストです、お楽しみに!
ソースコード
GitHub: SwiftyAlgebra
宣伝
- 3/19(土) 「第6回 プログラマのための数学勉強会」
- プログラマのための数学勉強会 Facebook ページ
- 個人ブログ Imaginary & Imaginative