Swiftで代数学入門 〜 4. 時計の世界の「環」

どうも、佐野です。これまで整数環 Z: Ring や有理数体 Q: Field を作ってきましたが、環や体になるのは $\mathbb{Z}$ や $\mathbb{Q}$ のような大きなものばかりではありません。今回は「時計の世界」に住む可愛い数たちを紹介します。

目次：

1. 数とは何か？
2. 群・環・体の定義
3. 有理数を作ってみよう
4. 時計の世界の「環」 ← イマココ
5. 小さな「体」を作ろう
6. 多項式は整数によく似てる
7. 代数拡大で数を作ろう！

時計の世界の整数

今回の内容は @tsujimotter さん『時計の世界の整数論』の発表スライドを引用しながら説明させて頂きます

小学校の算数で $5 + 8 = [\ \ \ ]$ のような問題があったとして、$[\ 13\ ]$ 以外を入れたら間違いなくバツを食らうでしょう。でも時計の中で考えると「$5$時の$8$時間後は$1$時」なので $[\ 1\ ]$ でも良さそうです。あるいは曜日だと「金曜日($5$)の$8$日後は土曜日($6$)」なので $[\ 6\ ]$ でも良さそうです。

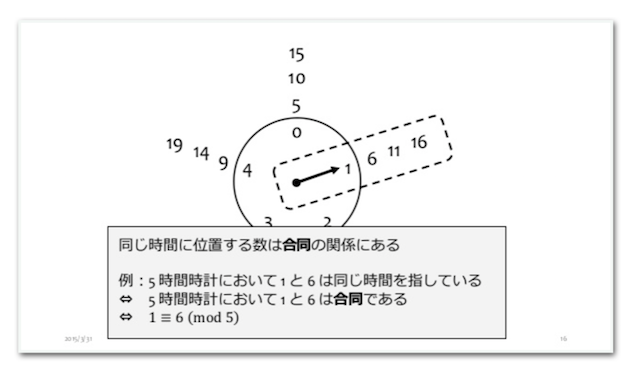
時計や曜日のような「ループする数の世界」を考えてみましょう。整数全体を「一周分の目盛りのふられた輪」にグルグルと巻きつけて、同じところに来る数を同じと見なします。「$5$ 時間時計」なら「$1, 6, 5, 16, \cdots$」は全部同じ「$1$ 時」です。

このことをより数学的に（そしてプログラム的に）扱いやすくするには、同じところに来る数の差に注目します。どの点においても、その点に来る数の差は「一周分」の何倍かになっています。「$1, 6, 5, 16, \cdots$」は全て $5$ の倍数間隔になってますよね。

この「一周分」を $n$ として、二つの数 $a, b$ の差が $n$ の倍数のとき $a, b$ は「$n$ を法として合同」といい、$a \equiv b \pmod{n}$ と書きます。整数環 $\mathbb{Z}$ を $n$ を法とする合同関係で分類したときにできるのが「$n$ 時間時計の世界」$\mathbb{Z}_n$ です。ここには「数」が $n$ 個しかありません。

（前回も有理数を作るときの「あるルールでまとめたグループを一つのものと見なす」という考え方をしました）

この「時計」に演算を入れることで「数」としての生命を帯びるようになります。
実装しながら見ていきましょう！

「法」を型に持てるようにするには？

まず n をパラメータとして $\mathbb{Z}_ n$ を表す struct Z_<n> を作りたいのですが、ここで n: Int だったら型パラメータとして渡すことはできません。Swift で型パラメータに渡せるのは「型」だけです。

「型」しか渡せないというのなら、「「Int型の値」を表す型」を大胆に作ってしまいましょう。これがその型の protocol です：

protocol TPInt {
    static var value: Int { get }
}

そして例えば 5 を表す TPInt_5 を作る場合は、こうすればいいのです：

struct TPInt_5 : TPInt {
    static let value = 5
}

あるいはペアノ式に：

struct TPInt_0 : TPInt {
    static let value = 0
}

struct TPInt_Succ<n: TPInt> : TPInt {
    static var value: Int {
        return n.value + 1
    }
}

typealias TPInt_1 = TPInt_Succ<TPInt_0>
typealias TPInt_2 = TPInt_Succ<TPInt_1>
...
typealias TPInt_5 = TPInt_Succ<TPInt_4>

としてもいいです。これで struct Z_<n: TPInt> に対して typealias Z_5 = Z_<TPInt_5> とすれば、それが $\mathbb{Z}_ 5$ です！

型レベルで n を固定することができれば演算は Z_<n> の中だけで定義できるので、別の法を持つ合同類と間違って足したりということが（コンパイラレベルで）できなくなります。まさに型安全

（「Swift で Phantom Type（幽霊型）」でやってることと本質的に同じです）

剰余類環の実装

では $\mathbb{Z}_n$ を作っていきましょう：

struct Z_<n: TPInt> {
    var mod: Int {
        return n.value
    }

    let value: Z

    init(_ value: Int) {
        self.value = value
    }
}

Z_<n> の n.value を簡単に取り出せるように mod プロパティを入れておきます。value: Z として、その合同類の中の整数を持てるようにしましょう。先にデバッグしやすいように IntegerLiteralConvertible と CustomStringConvertible を適合しておきます：

extension Z_ : IntegerLiteralConvertible {
    init(integerLiteral value: IntegerLiteralType) {
        self.init(value)
    }
}

extension Z_ : CustomStringConvertible {
    var description: String {
        return "\value mod \(mod)"
    }
}

そしたらこうできます：

typealias Z_5 = Z_<TPInt_5>
let a: Z_5 = 1               // 1 mod 5

いいですね、早くもそれっぽくなってる感じがします。

イコールの定義

Z_<n> でのイコールを定義するには、「中の数」の合同を実装すれば良いことになります。「整数の合同」の定義はなんだったか思い出すと：

a \equiv b \pmod{n}\ \Leftrightarrow \ a - b \in n \mathbb{Z}

$n \mathbb{Z}$ は「$n$ の倍数全体」です（$\mathbb{Z}$を丸ごと $n$ 倍したイメージ）。「$a$ と $b$ の差は $n$ の倍数」ということです。これをプログラムで実装するのは簡単です、剰余演算 % を使って差の余りが 0 かどうかを調べればいいのです。

Z_<n> : Equatable として == 演算を定義しましょう。

struct Z_<n: TPInt> : Equatable {
   ...
}

func ==<n: TPInt>(a: Z_<n>, b: Z_<n>) -> Bool {
    return (a.value - b.value) % n.value == 0
}

できました。== はジェネリック型 <n: TPInt> を一つだけ取っていて、引数の型はどちらも Z_<n> で固定されている点に注目してください。

確認してみましょう：

typealias Z_5 = Z_<TPInt_5>
let a: Z_5 = 2   // 2  mod 5
let b: Z_5 = 37  // 37 mod 5
a == b           // true

問題なさそうです！

四則演算の定義

次に Z_<n> : Ring として足りない演算を入れて行きましょう。

struct Z_<n: TPInt> : Ring {
   ...
}

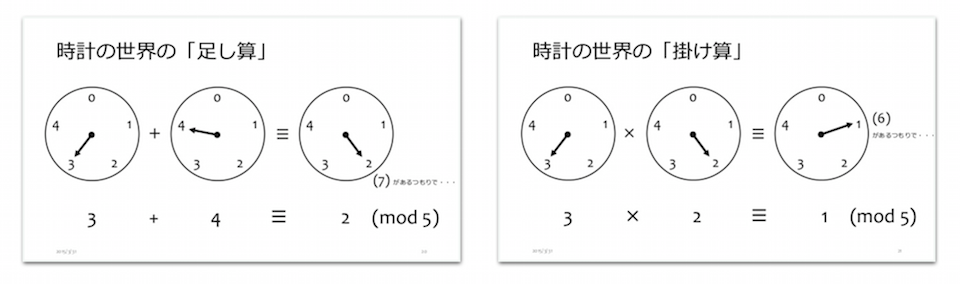
まずは足し算：

func +<n: TPInt>(a: Z_<n>, b: Z_<n>) -> Z_<n> {
    return Z_<n>(a.value + b.value)
}

…あれ、これでいいのでしょうか？ 例えば $1 \bmod 5$ は $\lbrace \cdots, 1, 6 ,11, 16, \cdots \rbrace$ を同じと見なしたもので、 value として持っているのは $1$ かもしれませんし $16$ かもしれませんし $198234191$ かもしれません。

「同じもの」ってことにしてるものを足した結果が「違うもの」になることはないのか？これを確認するには、$a \equiv b, c \equiv d$ のとき $a + c \equiv b + d$ かどうかを調べなければいけません。$a - b, c - d$ は合同の定義により $n$ の倍数なので、それぞれ $kn, ln \ (k, l \in \mathbb{Z})$ と書けるはずです。すると：

\begin{eqnarray}
(a + c) - (b + d) &=& (a - b) + (c - d) \\
&=& kn + ln \\
&=& (k + l)n
\end{eqnarray}

これは $(a + c) - (b + d)$ が $n$ の倍数だということなので、まさしく $a + c \equiv b + d$ だということです。「同じもの」ってことにしてるものが、足しても「同じもの」になることが確認できました。 $1 + 2$ と $321 + 47$ は整数としては別のものですが、$5$ を法とした合同類では同じ $1 + 2$ になってるということです。

正直この手の確認作業は全く楽しくないですが（楽しい人いたらごめんなさい）、同値類の代表元を使って演算や写像を定義する場合、それが代表元の取り方によらず定まるということは確認しなければなりません。グループの代表者として誰を選ぶかで、全然違う結論になったら困るというです（現実世界では割と起こりがちですが）。

この + がちゃんと加法群を成すかも確認しなければなりません。まずゼロ元は Z_<n>(0) で、これは Ring のデフォルト実装によって入るものです。これがゼロだということは、時計の世界では「$1$周, $2$周, $3$周, ...」は全てゼロだということです。

prefix - はこうです：

prefix func -<n: TPInt>(a: Z_<n>) -> Z_<n> {
    return Z_<n>(-a.value)
}

以上でちゃんと加法群の公理が満たされることを「群の定義」を振り返りながら確認してみてください（演習）。

次に掛け算です：

func *<n: TPInt>(a: Z_<n>, b: Z_<n>) -> Z_<n> {
    return Z_<n>(a.value * b.value)
}

まずこれが代表元の取り方によらないことは確認する必要があります。単位元は Ring のデフォルト実装で定まる Z_<n>(1) で、Z_<n> が * に関してモノイドを成すことも確認してください（演習）。

こうして Z_<n> に足し算と掛け算を入れ、環構造を定めることができました！

遊んでみよう！

Z_<n> ができたので、いろいろな n を入れて遊んでみましょう。

演算の様子を一望するには「演算表」を作るのが一番です。 printAddOpTable という関数を作って、 Z_5 の加法の演算表を見てみましょう：

let values: [Z_5] = [0, 1, 2, 3, 4]
printAddOpTable(values)

+   |   0   1   2   3   4
--------------------------
0   |   0   1   2   3   4
1   |   1   2   3   4   0
2   |   2   3   4   0   1
3   |   3   4   0   1   2
4   |   4   0   1   2   3

例えば (4, 3) 成分には 2 があり、これは $4 + 3 \equiv 2 \pmod{5}$ ということです。各行に一つだけ $0$ となる列があります。例えば 4 行を見ると、1 列と交わるところが 0 になってます。これは $-4 \equiv 1 \pmod{5}$ ということです。表が対角線に沿って対称なので、加法が可換だということも分かります。

次に乗法の演算表です：

printMulOpTable(values)

*   |   0   1   2   3   4
--------------------------
0   |   0   0   0   0   0
1   |   0   1   2   3   4
2   |   0   2   4   1   3
3   |   0   3   1   4   2
4   |   0   4   3   2   1

0 との積は常に 0 で、1 との積は不変です。加法の場合と同じく、各行に一つだけ $1$ となる列があります。例えば (3, 2) 成分が 1 になってます。これは $3 \cdot 2 \equiv 1 \pmod{5}$ というで、$3$ の逆数は $2$ だということです。

$0$ でない全ての元が掛けて $1$ になる元を持つということは…つまり $\mathbb{Z}_5$ は「体」だということです！$\mathbb{Z}_5 = \lbrace 0, 1, 2, 3, 4 \rbrace$ と数が $5$ つしかない世界が「体」になっていて、有理数や実数みたいに $+, -, \times, \div$ ができるなんて驚きませんか？

今度は n = 6 の場合を見てみましょう：

typealias Z_6 = Z_<TPInt_6>
let values: [Z_6] = [0, 1, 2, 3, 4, 5]
printAddOpTable(values)
printMulOpTable(values)

+   |   0   1   2   3   4   5
------------------------------
0   |   0   1   2   3   4   5
1   |   1   2   3   4   5   0
2   |   2   3   4   5   0   1
3   |   3   4   5   0   1   2
4   |   4   5   0   1   2   3
5   |   5   0   1   2   3   4

*   |   0   1   2   3   4   5
------------------------------
0   |   0   0   0   0   0   0
1   |   0   1   2   3   4   5
2   |   0   2   4   0   2   4
3   |   0   3   0   3   0   3
4   |   0   4   2   0   4   2
5   |   0   5   4   3   2   1

加法の演算表は Z_5 の場合とそんなに変わりませんが、乗法はかなり違います。まず各行に対して掛けて 1 になる列が必ずしもありません。また (2, 3)成分など 0 でない数同士をかけて 0 になるところがいくつかあります。1 が出てくる行と 0 が出てくる行の違いはなんでしょう…？

次回は「有限体」で、この秘密に迫ります！

（サンプルコードは追って公開するので、ぜひ手元で遊んでみてください）

参考

「時計の世界の整数論」 発表動画 / 資料 by @tsujimotter

「第2回 プログラマのための数学勉強会」での @tsujimotter さんの発表スライドを引用させて頂きました。「フェルマーの小定理」から「平方剰余の相互法則」まで分かりやすく説明してくれます。今回の記事で「時計の世界の整数」に興味を持たれた方は是非ご覧ください

ソースコード

GitHub: SwiftyAlgebra

• QuotientRing
• IntQuotientRing

宣伝

• 3/19(土) 「第6回 プログラマのための数学勉強会」
• プログラマのための数学勉強会 Facebook ページ
• 個人ブログ Imaginary & Imaginative