どうも、佐野です。前回 は「群・環・体」の定義を示し、対応する protocol として Group, Ring, Field を作りました。今回は Field 型の具体型として、有理数体 $\mathbb{Q}$ を実装しましょう。
目次:
有理数を作ろう
有理数とは「整数の分数」で表せる数のことです。分数 $\frac{p}{q}$ は 分子 $p$ と分母 $q$ からできているので、有理数型 Q は二つの整数 p: Z, q: Z を持つ struct として実現できそうです。
struct Q {
let p, q: Z
init(_ p: Z, _ q: Z) {
if q == 0 {
fatalError("denom: 0")
}
self.p = p
self.q = q
}
}
また、分母が $1$ の有理数は整数と思いたいので、分子だけ指定して有理数も作れるようにしておきます:
struct Q {
...
init(_ n: Z) {
self.init(n, 1)
}
}
これで let a = Q(2, 3), let b = Q(4)($a = \frac{2}{3}, b = 4$ のつもり)のように作れるようになりました。このままでは計算も何もできないので、演算を入れていきます。まずは Equatable です。
分数が等しいとは?
Q(p1, q2) == Q(p2, q2) を (p1 == p2) && (q1 == q2) で定義してはいけません。Q はただの数の組ではなく分数なので、「約分して等しい」ものは同じと思わなければなりません。「約分」を考えるのは面倒なので、分数のイコールの式を書き換えてみます。
\begin{eqnarray}
\frac{p}{q} = \frac{p'}{q'} \Leftrightarrow p \cdot q' = q \cdot p'
\end{eqnarray}
後の式は「整数の等号」なので定義済みです。これを使って Q を Equatable にしましょう。
struct Q: Equatable {
...
}
func ==(a: Q, b: Q) -> Bool {
return a.p * b.q == a.q * b.p
}
これでイコールが定義できました!
$\frac{2}{5} = \frac{4}{10}$ を検証してみましょう:
let a = Q(2, 5) // a = 2/5
let b = Q(4, 10) // b = 4/10
a == b // true
問題なさそうです!
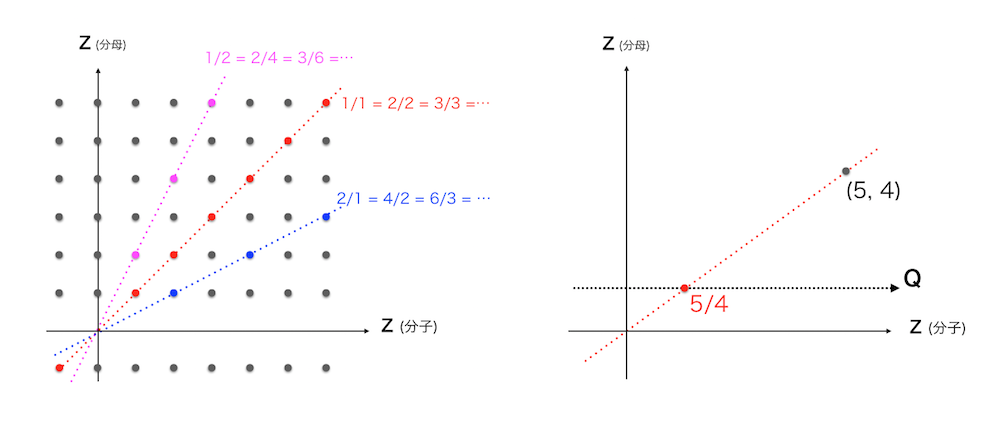
ここでやったことをより一般的な視点で見てみましょう。$\mathbb{Q}$ を構成するために二つの整数 $p, q$ を用意しましたが、これを平面上の格子点 $(p, q)$ と見ます。二つの格子点が「分数として等しい」ということは、原点から結んだ同一直線上にあるということです:
例えば $(1, 2), (2, 4), (3, 6), \cdots$ は全部同じ $\frac{1}{2}$ を表しています。
ある格子点を通る直線を定めればそれに対して一つの有理数が定まるので、「一本の直線」を「一つの有理数」だと思うことができます。するとこの直線を全て集めたものが $\mathbb{Q}$ ということになります。あるいはこの直線と $y = 1$ の交点がまさしく「その有理数」なので、格子点たちに原点から光をあててスクリーン $y = 1$ に映した「像」が $\mathbb{Q}$ だと思うこともできます。
これは数学的には、直積 $\mathbb{Z} \times \mathbb{Z}^* $ を同値関係 $(p, q) \sim (p', q') \Leftrightarrow pq' - qp' = 0$ で割った商集合として $\mathbb{Q} = (\mathbb{Z} \times \mathbb{Z}^*) / \sim$ を作ったことになります。「同値関係」というのは「グループ分けの基準」で、分けられたグループが「同値類」、その集まりが「商集合」です。
無数の格子点からなる直線が、同値関係で割った集合で見ると一つの数になっている…まるで一人の人間が無数の細胞からできているかのようです。我々は人間を見るとき「無数の細胞の集まりがある」と思わず「一人の人間がいる」と思いますよね。それと同じです。
このように「ものの集まりで作ったもの」にさらに演算を入れていくのです。実装を続けましょう!
四則演算の定義
struct Q: Field として、Field が要請する演算を入れていきましょう。まずは足し算。分数の足し算をするときは、分母が共通となるように「通分」をする必要がありました。
\frac{p}{q} + \frac{p'}{q'} = \frac{pq'}{qq'} + \frac{qp'}{qq'} = \frac{pq' + qp'}{qq'}
この式の通りに、二つの Q から一つの Q を作ればオッケーです:
func +(a: Q, b: Q) -> Q {
return Q(a.p * b.q + a.q * b.p, // 分子
a.q * b.q) // 分母
}
簡単ですね?
次にマイナスは、分子の符号を逆にするだけです:
-\left(\frac{p}{q}\right) = \frac{-p}{q}
prefix func -(a: Q) -> Q {
return Q(-a.p, a.q)
}
引き算については、protocol AdditiveGroup で 足し算 + と prefix - から自動的に定まるようにしたので、追加の実装は必要ありません(抽象化万歳 ![]() )。
)。
次は掛け算、足し算よりシンプルです。
\frac{p}{q} \cdot \frac{p'}{q'} = \frac{pp'}{qq'}
func *(a: Q, b: Q) -> Q {
return Q(a.p * b.p, a.q * b.q)
}
そして逆数、分子と分母をひっくり返すだけです:
\left(\frac{p}{q}\right)^{-1} = \frac{q}{p}
inverse プロパティは struct の中で定義しなければいけないので、中に入れます。
struct Q: Field {
...
var inverse: Q {
return Q(q, p)
}
}
ここでまた割り算 / は protocol Field で * と inverse から自動的に定まるので、追加の実装は必要ありません(抽象化万歳 ![]() )。
)。
これで有理数体 $\mathbb{Q}$ 完成です!
let a = Q( 8, 3)
let b = Q(-5, 4)
let c = Q( 3, 7)
a * b + c == Q(-61, 21) // true
追加でちょっと
Q をコードでより扱いやすくするため、 IntegerLiteralConvertible と CustomStringConvertible にも適合させておきます。
Swift は(2.* の時点では)型の暗黙キャストはサポートされていませんが、一部のリテラルからはキャストできるようになってます。その一つが IntegerLiteralConvertible で、Int 型のリテラルから値を作ることができるというものです。
Q には元々 Int 型を取る init は定義してあるので、そこに橋渡しすればいいだけです:
extension Q: IntegerLiteralConvertible {
init(integerLiteral value: IntegerLiteralType) {
self.init(value)
}
}
これで Q は整数から作ることができるようになります:
let a: Q = 3
let b: Q = Q(3, 4)
a * b == Q(9, 4) // true
これだとあまりありがたみが分かりませんが、式の中で自然に型推論してくれるので便利です:
let a: Q = Q(3, 4)
a * 4 == 3 // true
有理数 $\frac{3}{4}$ に整数 $4$ をかけたら整数 $3$ を得る、という式に見えます。
次に CustomStringConvertible ですが、これは print されたときの見た目を整えるためのものです。今のままだと、
let a = Q(3, 4)
print("a = \(a)") // a = Q(p: 3, q: 4)
となるので、
extension Q: CustomStringConvertible {
var description: String {
switch q {
case 1: return "\(p)"
case -1: return "\(-p)"
default: return "\(p)/\(q)"
}
}
}
としておけば、
let a = Q(3, 4)
print("a = \(a)") // a = 3/4
と、いよいよ有理数っぽくなりました!
ところでさきほどの計算を出力してみると…
let a = Q( 8, 3)
let b = Q(-5, 4)
let c = Q( 3, 7)
print(a * b + c) // -244/84
と、約分されない形で出力されてます(実装してないので当たり前です)。これは見づらいので、やはり約分は機能として入れておきたい。次々回に「ユークリッド互除法」で二つの数の最大公約数を求める方法を説明するので、有理数も約分できるようになります。
次回は「余りが同じなら同じと見なす」方法で、整数環や有理数体よりもずっと小さな環や体を作る方法を説明します。
お楽しみに!
ソースコード
GitHub: SwiftyAlgebra
宣伝
- 3/19(土) 「第6回 プログラマのための数学勉強会」
- プログラマのための数学勉強会 Facebook ページ
- 個人ブログ Imaginary & Imaginative