どうも、佐野です。これから数学の一分野である「代数学」の基礎を Swift で実装しながら解説するシリーズを書いてみようと思います。
目次:
動機と狙い
Swift は強い型システムを持ちながら柔軟性も高く、関数型でありながら読みやすく、変数にギリシャ文字を使えたりもして、なかなか数学と相性の良い言語だと思います。過去にも「虚数は作れる!Swift で学ぶ複素数」で発表をしたり、「Swiftで自然数を作ってみた」という記事を書いたりしました。
ある日、エミール・アルティン『ガロア理論入門
代数的な事柄の基礎づけには、「代数学の基本定理」は不要なのである。
という一文に出会い「これだ!」と奮い立ちました。興奮に任せてこれをプログラムで実装してみたところ、さらに思いもよらぬ驚きがありました。
$\sqrt{2}$ を例に見てみましょう:
let a = sqrt(2.0) // 1.414213562373095
a * a == 2.0 // false...
a = sqrt(2) は $\sqrt{2}$ なので自乗したら 2.0 になってほしいところですが == で比較すると false となります。両者の差を取ってみると…
(a * a) - 2.0 // 4.44089209850063e-16
sqrt(2)の値はあくまで Double 精度の近似値であり、自乗しても誤差 0.00000000000000044... が出て 2.0 と等しくなりません。「コンピュータなんだから仕方ないでしょ」って?
では**「代数拡大」**で作った $\sqrt{2}$ を見てみましょう:
struct f : TPPolynominal { // f(x) = x^2 - 2 in Q[x]
static let value = Polynominal<Q>(-2, 0, 1)
}
typealias K = FieldExtension<f> // K = Q[x]/(x^2 - 2)
let a = K(0, 1) // x mod (x^2 - 2)
a * a // 2 mod (x^2 - 2)
a * a == 2 // true!
これが何のことか分からなくても、最後の1行を見てください… a * a == 2 となっています! a は自乗して 2 になる数なんだから、これは $\sqrt{2}$ そのものです。同じように虚数単位 $i$ や $1$ の原始 $n$ 乗根 $\zeta_n$ も、近似ではない「その数そのもの」をプログラムで実現できてしまうのです。
このシリーズでは 「数を作る = 代数拡大」 を実装することをゴールとしつつ、その過程で代数学における「群・環・体」などの基礎的な概念についても解説していきたいと思います。
シリーズの狙い:
- 抽象的で難しい代数学を、プログラムを通して身近に感じられるようにしたい。
- 関数型やプロトコル指向に対する数学的な視点を展開してみたい。
- 「なるほど、分からん」ではなく「なるほど、すごい!」を目指す。
ちなみに僕は代数学はあまり得意ではないので、間違いなどあればご指摘下さい。またこういうことを実現するのに他の言語の方がやりやすいこともあると思うので、コメントで教えて頂けたら嬉しいです ![]() (「◯◯言語で作ってみた」は大歓迎です)
(「◯◯言語で作ってみた」は大歓迎です)
Introduction 〜数とは何か?
小さな子供に「数って何?」と聞かれたら「1, 2, 3 ... のこと」と答えるでしょう。これらは 自然数 (Natural Number) と呼ばれ、まさしく「個数を数えるの数」です。小学校で数を習った後に、足し算と引き算を習います。引き算を使うと「売り上げからコストを引いて、利益を求める」という計算ができるようになります。しかしコストが売り上げを上回ってしまった場合…これは赤字です。利益を合算するとき黒字は足して赤字は引く…というのも面倒なので「黒字と赤字をまとめた数」を考えたくなります。
こうして自然数に「ゼロ」と「マイナスの数」の数を合わせた 整数 (Integer) が得られます。自然数では $3 - 5$ のような計算をすると、その数は自然数からはみ出てしまいますが、整数ではそのようなことは起きず「整数 $-$ 整数 $=$ 整数」 となっています。このことを「演算について閉じている」と言い、「整数全体は($+$ に関して)群 (Group) を成す」と言います(正確な定義は次回以降)。
足し算と引き算のあとは、掛け算と割り算を習います。整数は $\times$ について閉じていますが、$\div$ については閉じていません($3 \div 5$ は整数になりません)。この $+, -, \times$ について閉じている性質をもって「整数全体は 環 (Ring) を成す」と言います。
そして分数を習います。分数では四則演算 $+, -, \times, \div$ を使うことができます。$2$ と $-2$ を足すと $0$ になるように、$2$ と $\frac{1}{2}$ を掛けると $1$ になります。$\times$ における $1$ は、$+$ における $0$ と同じです。ただし $\frac{1}{0}$ という数を考えることはできません。なぜなら $0 = \frac{1}{0} \times 0 = 1$ となってしまうからです。つまり $\times, \div$ は 「$0$ 以外の数」で閉じていて、群を成しています($+$ と $\times$ で二つの群構造が入っている)。整数の分数で書ける数のことを 有理数 (Rational Number) といい、四則演算ができることをもって「有理数全体は 体 (Field) を成す」と言います。
「群・環・体」は「数そのもの」ではなく「数の集まり」とその演算に対して定まる性質で、数の集合と代数的構造を指して「整数環」「有理数体」と言います。
真っ直ぐつながった数、実数
小学校では「数直線」も習います。直線上に数をプロットして使う訳ですが、実はここに「数の離散から連続への跳躍」があります。有理数は穴だらけであって、例えば円周率 $\pi$ はその穴に落ちています(そしてその穴の方が遥かに広いのです)。この穴を埋めてつなげた数のことを 実数 (Real Number) といい、有理数と同じく四則演算ができる 体 です。
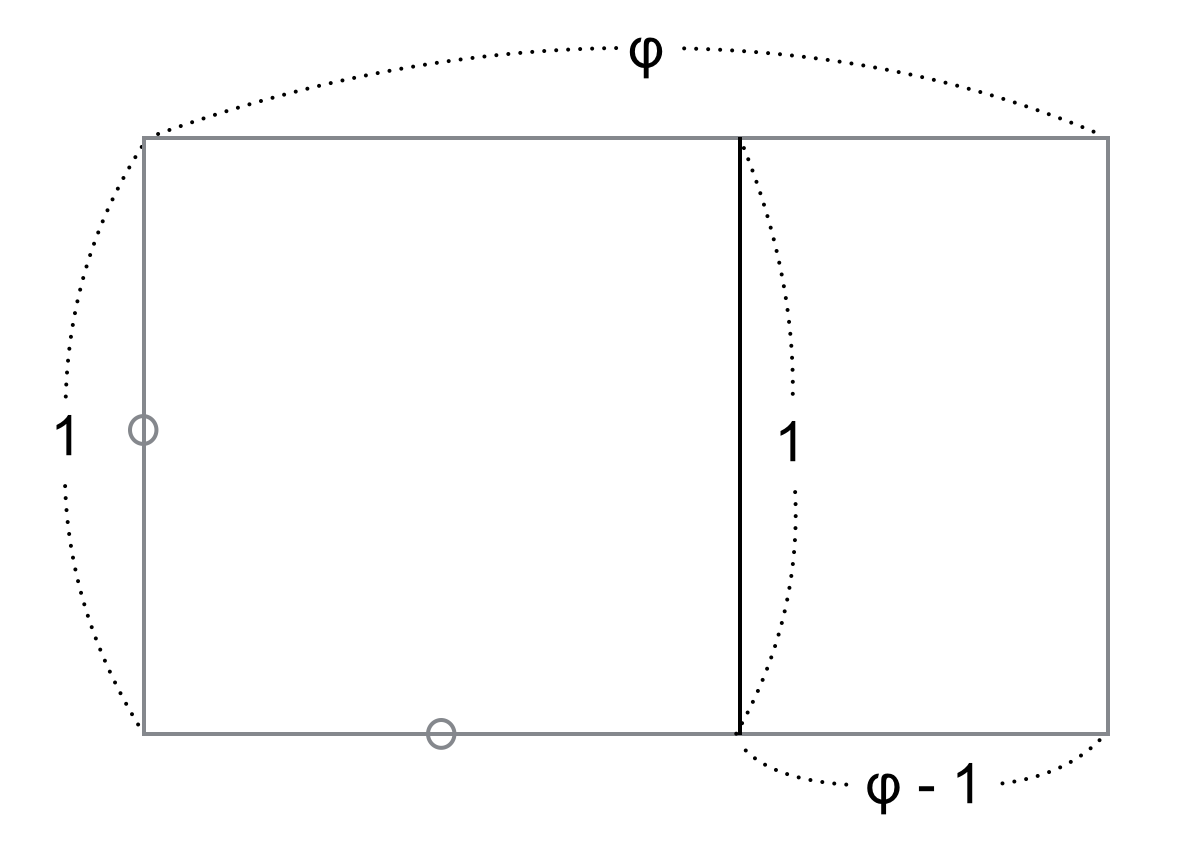
実数は長さ・大きさ・時間など「連続的に変化する量」を扱う上でなくてはならないものです。例えば底辺の長さが $1$ の直角二等辺三角形の斜辺の長さ $x$ は、ピタゴラスの定理より、$1^2 + 1^2 = x^2 \Leftrightarrow x = \pm \sqrt{2}$ のうち正の $\sqrt{2}$ で、これは 無理数(有理数でない実数)です。あるいはある長方形から正方形を切り取って、元と相似な長方形が残るような比(黄金比) $\phi$ は $1 : x = x - 1 : 1 \Leftrightarrow x^2 - x - 1 = 0$ の解で、これも無理数です。
無理数は「$x$ の多項式 = 0」の形で表される 代数方程式 を解く上で自然に出てくるもので、この点においても有理数と無理数を合わせた実数を考えた方が都合が良いということは納得できるでしょう。2次方程式については中学校で解の公式を習ったと思います:
ax^2 + bx + c = 0 \Leftrightarrow x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
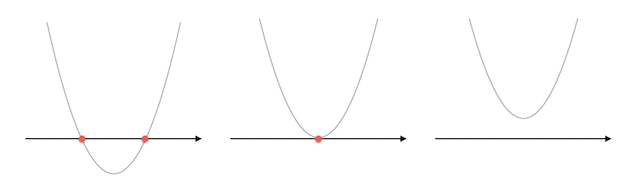
この2次方程式、解が有理数だったり無理数だったりするだけでなく、 $\sqrt{...}$ の中身によって解の個数が 2個 だったり 1個 だったり 0個 だったりします。$y = ax^2 + bx + c$ というグラフを考えれば、これはそれぞれ $x$ 軸と 2点で交わる場合、1点で接する場合、交わらない場合に対応していることが分かります。ここに虚数なんて考える必要はなさそうです(ネタバレ)。
3次・4次方程式についても解の公式があります。
3次方程式の解の公式 は文字の適当な置き換えでこんな形になります:
x' = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}} + \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}
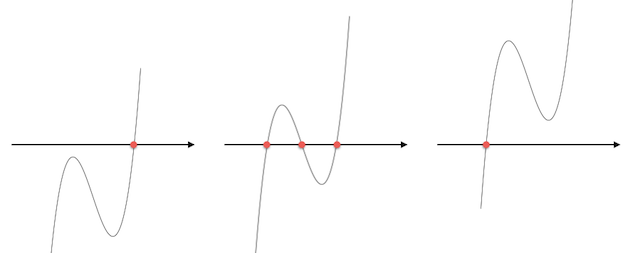
えげつない形をしてますが、式の中に $\sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}$ が2回出てきます。その中身が負の場合、2次方程式の場合と同じように解がないことになりそうです。しかし $y = ax^3 + bx^2 + cx + d$ のグラフは $x$ 軸と 少なくとも1点で 必ず交わるので、3次方程式は 少なくとも1つの実数解 を持つはずです。これはどういうことか…
とりあえず $\sqrt{-1}$ と書くことを認めて計算を進めると、結果的に1つは実数解が出てきます。この $\sqrt{-1}$ は計算のための方便に過ぎないのか、それとも…
代数的閉体、複素数
実数は「正 $\times$ 正$ = $正」「負 $\times$ 負 $=$ 正」なので $x^2 = -1$ なんて実数 $x$ はありえません。実数にはないんだから、数直線から外れたところにそういう数 $i = \sqrt{-1}$ があることにして、 $z = x + iy$ という数を考えてみます。なぜこんなものを「数」と呼んで良いんでしょう?それはその数が「体」になるからです。
$i$ を普通の定数のように扱って計算すると、以下のように演算が定まります:
\begin{eqnarray}
(a + ib) + (c + id) &=& (a + c) + i(b + d) \\\
(a + ib)(c + id) &=& (ac - bd) + i(ad + bc) \\\
\end{eqnarray}
この掛け算に関して逆数を求めてみると:
\frac{1}{a + ib} = \frac{a - ib}{a^2 + b^2}
で、これが定まる条件は分母 $a^2 + b^2 \ne 0$ 、つまり $0$ でない数には逆数があります。これがまさに「体」の条件でした。この $z = x + iy$ という数を 複素数 (Complex Number) といい、その全体を「複素数体」と言います。
代数方程式を解くために天下り的に導入した複素数ですが、複素数の範囲では $n$ 次方程式は(重解を込めて)ちょうど $n$ 個の解を持つということが示されます。2次方程式なら解が 2個 だったり 1個 だったりということではなく、必ずちょうど 2個 になります。これが**「代数学の基本定理」**で、はじめて完全に証明したのはガウスです。
ガウスは複素数を2次元平面上の点と対応させた「複素数平面(別名ガウス平面)」を考案し、複素数が「見える」ようになったことで数学者に受け入れられるようになりました。オイラーは「オイラーの公式」 $e^{i\theta} = \cos\theta + i\sin\theta$ を示したことで、それまで別のものと思われていた指数関数と三角関数が統一されます。18、19世紀に渡って複素数は微積分学にも取り入れられ「複素関数論」という一大分野が樹立します。複素数は理論・応用の両面において「完成された数」として認められていきました。
ここまで出てきた「数」をまとめるとこんな感じです: 自然数系 $\subset$ 整数環 $\subset$ 有理数体 $\subset$ 実数体 $\subset$ 複素数体
「代数学の基本定理」が不要…?
さて、ここでアルティンの言葉を振り返ってみましょう。
代数的な事柄の基礎づけには、「代数学の基本定理」は不要なのである。
これは一体?代数方程式がその範囲で必ず解を持つような「完成された数」が不要と?
3次・4次方程式には解の公式があると書きましたが、5次以上についてはありません。これは「まだ見つかっていない」ということではなく「原理的に作れない」ということです。「ガロア理論」では方程式の構造を群と対応させることでこのことが示されます。
複素数体という大きなものを考えれば代数方程式は必ず解を持つのですが、「どういう条件で方程式は具体的に解けるのか」を考える上ではむしろ大きすぎるのです。そこで改めて有理数から出発して、ある方程式が解けるような「必要最小限の数体」を考えたい。そこで出てくるのが「代数拡大」です。
有理数体 $\subset$ (代数拡大で作った体) $\subset$ 複素数体
このシリーズでガロア理論について説明することはできませんが(次シリーズでチャレンジしてみたい)、「数を作れる」というのは数学的にもプログラミング的にもとても面白いと思います。特に複素数について「虚数 $i$ は本当にあるのか?」は誰もが引っかかるところだと思いますが、大丈夫、作れます。シリーズ最終回で作ります。
まとめ
というわけでイントロがかなり長くなりましたが、まとめると…
- 有理数・実数・複素数は四則演算が自由にできる「体」である。
- 「体」という代数的構造こそ「数」の本質だと思うことにしよう。
- そういう数体はどんどん作り出せる!
「代数的構造」を protocol として、「新しい数」を struct として実装していこう、というのがこのシリーズの主旨です。お楽しみに!
宣伝
- 3/19(土) 「第6回 プログラマのための数学勉強会」
- プログラマのための数学勉強会 Facebook ページ
- 個人ブログ Imaginary & Imaginative