はじめに
ふと思い立って勉強を始めた「ゼロから作るDeep LearningーーPythonで学ぶディープラーニングの理論と実装」の5章で私がつまずいたことのメモです。
実行環境はmacOS Mojave + Anaconda 2019.10、Pythonのバージョンは3.7.4です。詳細はこのメモの1章をご参照ください。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
この記事は個人で作成したものであり、内容や意見は所属企業・部門見解を代表するものではありません。
5章 誤差逆伝播法
この章は、ニューラルネットワークの学習において重みパラメーターの算出を高速化するための、誤差逆伝播法についての説明です。
ちなみにこの「伝播」(でんぱ)という言葉はPropagetionの訳なのですが、「伝搬」(でんぱん)と訳されることもあって日本語は混沌としています。この辺りを調べたブログの記事を見つけましたので、興味のある方は 歩いたら休め > 【機械学習】"Propagation"の訳は「伝播」or「伝搬」? をどうぞ。
5.1 計算グラフ
計算グラフによる説明は、誤差逆伝播法を学ぶ上で非常に分かりやすいです。この本の人気の秘密は、この5章なのかも知れません。
ニューラルネットでは学習が必須で、そのためには重みパラメーターの勾配を求める必要があり、各パラメーターの微分の計算が必要になります。計算グラフを利用すると、その微分の計算が、後ろから前へ向かって局所的な微分を逆伝播させることにより、非常に効率良くできることが分かります。
5.2 連鎖律
合成関数の微分公式のおさらいと、それにより逆伝播が成り立つことの説明です。さらっと読み流しても困ることはないと思いますが、正しく理解したい場合は高校の微分のおさらいが必要です。
私は微分の公式なんて全く覚えていなかったので、久々におさらいすることにしました。しかし、私は本業が終わった後に勉強することが多く、本やWebサイトだと睡魔が襲ってきてなかなか頭に入りません。サラリーマンがスキマ時間で勉強するのはなかなか大変です。
そこで見つけたのが 家庭教師のトライ がやっている トライイット です。動画の授業なのですが、無料なのにすごく分かりやすく、15分程度に分割されているので移動中や休憩中のスマホを使った勉強にも最適です。学生向けのサービスなのですが、社会人のおさらい用にも非常に適していると思います。
参考までに、微分の入門部分に関する動画へのリンクを貼っておきます。なお、私的視聴に限定されていますのでご注意ください。
5.3 逆伝播
加算ノードと乗算ノードの逆伝播の説明です。加算も乗算も微分は単純なので、逆伝播の計算も簡単です。
5.4 単純なレイヤの実装
前節の加算レイヤーと乗算レイヤーの実装です。微分が単純なので実装も簡単です。
5.5 活性化関数レイヤの実装
活性化関数のレイヤーの実装です。
5.5.1 ReLUレイヤ
ReLUは微分の計算も単純なので、実装も簡単で、学習の高速化にもつながりそうです。以下、実装したコードです。
# coding: utf-8
class ReLU:
def __init__(self):
"""ReLUレイヤー
"""
self.mask = None
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値
Returns:
numpy.ndarray: 微分値
"""
dout[self.mask] = 0
dx = dout
return dx
5.5.2 Sigmoidレイヤ
シグモイド関数の微分はちょっとややこしいですが、計算グラフを使うと少しずつ計算できます。ただそれでも、最初の「/」ノードで必要な $y=\frac{1}{x}$ の微分や「$exp$」ノードの $y=exp(x)$ の微分は公式をおさらいしないと辛いです。この辺の公式は、 具体例で学ぶ数学 > 微積分 > 微分の公式全59個を重要度つきで整理 がシンプルにまとまっていてお勧めです。
計算グラフによる計算後、本の(5.12)の式へと変形するのですが、終わりから2行目を最終行へ変形する流れが最初は分かりませんでした。次のように間に1行入れると分かりやすくなります。
\begin{align}
\frac{\partial L}{\partial y}y^2exp(-x) &= \frac{\partial L}{\partial y} \frac{1}{(1+exp(-x))^2} exp(-x) \\
&=\frac{\partial L}{\partial y} \frac{1}{1+exp(-x)} \frac{exp(-x)}{1+exp(-x)} \\
&=\frac{\partial L}{\partial y} \frac{1}{1+exp(-x)} \biggl(\frac{1+exp(-x)}{1+exp(-x)} - \frac{1}{1+exp(-x)}\biggr) ←追加した行 \\
&=\frac{\partial L}{\partial y} y(1-y)
\end{align}
この結果で驚くのは、順伝播の出力である $y$ があれば非常に簡単に計算できることです。誤差逆伝播法では先に順伝播の計算をするので、その結果を持っておけば学習の高速化につながります。$ e^x $ を微分しても $ e^x $ になるという特性も重要で、シグモイド関数を考えた人はホントすごいです。
なお、シグモイドレイヤーはこの章では使わないので、コードの掲載は割愛します。
5.6 Affine/Softmaxレイヤの実装
5.6.1 Affineレイヤ
Affineレイヤーの逆伝播の式(5.13)は計算過程が省略されていますが、@yuyasat さんが Affineレイヤの逆伝播を地道に成分計算する で計算過程をまとめられていて参考になります。
5.6.2 バッチ版Affineレイヤ
以下、実装したコードです。なお、本のコードでは入力データがテンソル(4次元のデータ)の場合の考慮がありますが、まだ使い道が分かっていないので入っていません。
# coding: utf-8
import numpy as np
class Affine:
def __init__(self, W, b):
"""Affineレイヤー
Args:
W (numpy.ndarray): 重み
b (numpy.ndarray): バイアス
"""
self.W = W # 重み
self.b = b # バイアス
self.x = None # 入力
self.dW = None # 重みの微分値
self.db = None # バイアスの微分値
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
self.x = x
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値
Returns:
numpy.ndarray: 微分値
"""
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
return dx
5.6.3 Softmax-with-Lossレイヤ
ソフトマックス関数と交差エントロピー誤差をセットにしたレイヤーの逆伝播です。
計算過程は本の付録Aに詳しく記載されていますが、$ e^x $ を微分しても $ e^x $ になることや、教師ラベルの one-hot ベクトルが全部足すと1になることなどが、式をシンプルにすることに貢献しています。
最終的に求められる $ (y_1-t_1,y_2-t_2,y_3-t_3) $という結果も驚きです。確かにニューラルネットワークの出力と教師ラベルの差を示していますし、計算も高速にできます。交差エントロピー誤差は、ソフトマックス関数の損失関数として使うとこのように"キレイ"になるように設計されているそうで、交差エントロピー誤差を考えた人もホントすごいです。
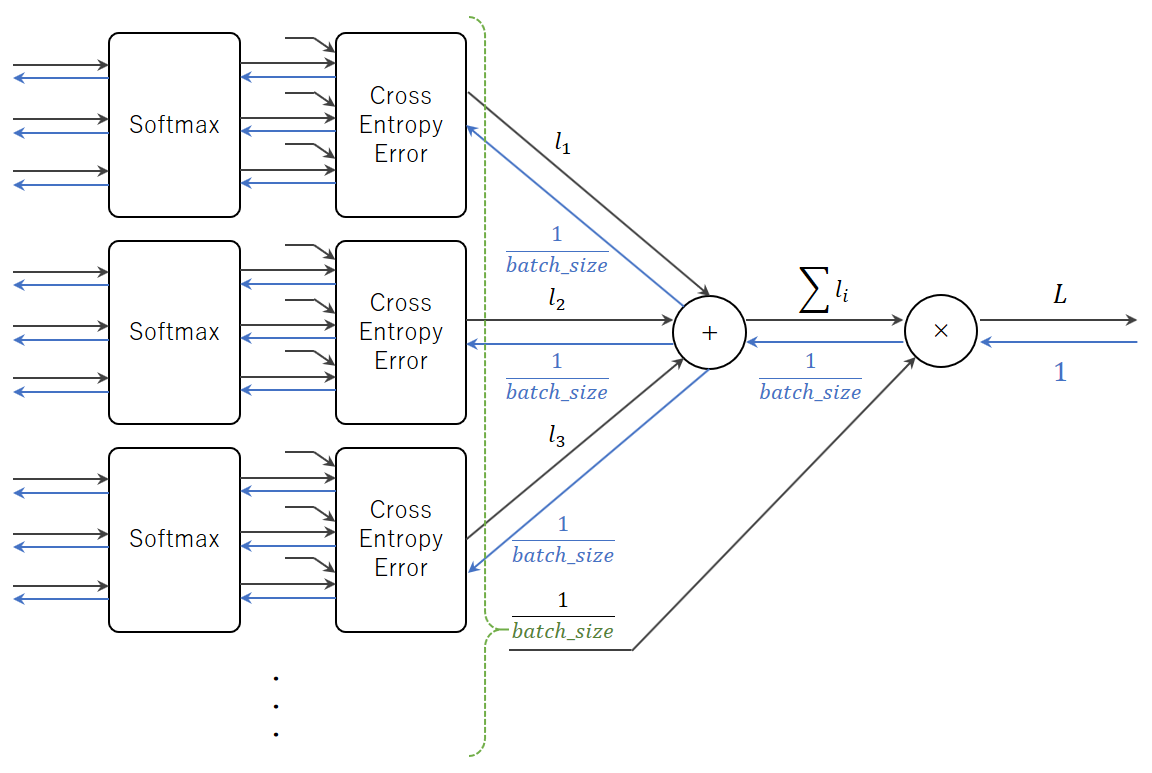
なお、バッチに対応させるには逆伝播の値をバッチの個数で割る必要があります。本では「伝播する値をバッチの個数(batch_size)で割ることで、データ1個あたりの誤差が前レイヤへ伝播する」という説明しかなく、なぜバッチの個数で割る必要があるのかピンと来なかったのですが、@Yoko303さんの ゼロから作るDeep Learning 〜Softmax-with-Lossレイヤ〜 のコードの解説で理解できました。バッチ版の順伝播では最後に交差エントロピー誤差を合計して、バッチの個数(batch_size)で割って1つの値にしています。逆伝播でもこの部分の計算が必要で、その微分値が $ \frac{1}{batch_size} $ というわけです。以下、その部分の計算グラフを書いてみました。
この理解で合っていると思いますが、もし間違いがありましたらご指摘ください。
以下、実装したコードです。
# coding: utf-8
from functions import softmax, cross_entropy_error
class SoftmaxWithLoss:
def __init__(self):
"""Softmax-with-Lossレイヤー
"""
self.loss = None # 損失
self.y = None # softmaxの出力
self.t = None # 教師データ(one-hot vector)
def forward(self, x, t):
"""順伝播
Args:
x (numpy.ndarray): 入力
t (numpy.ndarray): 教師データ
Returns:
float: 交差エントロピー誤差
"""
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
"""逆伝播
Args:
dout (float, optional): 右の層から伝わってくる微分値。デフォルトは1。
Returns:
numpy.ndarray: 微分値
"""
batch_size = self.t.shape[0] # バッチの個数
dx = (self.y - self.t) * (dout / batch_size)
return dx
なお、本のコードではbackward内でdoutが使用されていません。doutは1指定でしか使っていないので動作は問題ありませんが、おそらく間違いだと思います。
5.7 誤差逆伝播法の実装
5.7.1 ニューラルネットワークの学習の全体図
ここは実装の流れのおさらいです。とくにつまずく部分はありません。
5.7.2 誤差逆伝播法に対応したニューラルネットワークの実装
まず、汎用の関数の実装です。 前章で書いたものから必要なものだけを持ってきました。
# coding: utf-8
import numpy as np
def softmax(x):
"""ソフトマックス関数
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
# バッチ処理の場合xは(バッチの数, 10)の2次元配列になる。
# この場合、ブロードキャストを使ってうまく画像ごとに計算する必要がある。
# ここでは1次元でも2次元でも共通化できるようnp.max()やnp.sum()はaxis=-1で算出し、
# そのままブロードキャストできるようkeepdims=Trueで次元を維持する。
c = np.max(x, axis=-1, keepdims=True)
exp_a = np.exp(x - c) # オーバーフロー対策
sum_exp_a = np.sum(exp_a, axis=-1, keepdims=True)
y = exp_a / sum_exp_a
return y
def numerical_gradient(f, x):
"""勾配の算出
Args:
f (function): 損失関数
x (numpy.ndarray): 勾配を調べたい重みパラメーターの配列
Returns:
numpy.ndarray: 勾配
"""
h = 1e-4
grad = np.zeros_like(x)
# np.nditerで多次元配列の要素を列挙
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index # it.multi_indexは列挙中の要素番号
tmp_val = x[idx] # 元の値を保存
# f(x + h)の算出
x[idx] = tmp_val + h
fxh1 = f()
# f(x - h)の算出
x[idx] = tmp_val - h
fxh2 = f()
# 勾配を算出
grad[idx] = (fxh1 - fxh2) / (2 * h)
x[idx] = tmp_val # 値を戻す
it.iternext()
return grad
def cross_entropy_error(y, t):
"""交差エントロピー誤差の算出
Args:
y (numpy.ndarray): ニューラルネットワークの出力
t (numpy.ndarray): 正解のラベル
Returns:
float: 交差エントロピー誤差
"""
# データ1つ場合は形状を整形(1データ1行にする)
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 誤差を算出してバッチ数で正規化
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
そして、ニューラルネットワークのクラスです。前章のコードをベースにしているので、同じ部分も多いです。
# coding: utf-8
import numpy as np
from affine import Affine
from functions import numerical_gradient
from relu import ReLU
from softmax_with_loss import SoftmaxWithLoss
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,
weight_init_std=0.01):
"""2層のニューラルネットワーク
Args:
input_size (int): 入力層のニューロンの数
hidden_size (int): 隠れ層のニューロンの数
output_size (int): 出力層のニューロンの数
weight_init_std (float, optional): 重みの初期値の調整パラメーター。デフォルトは0.01。
"""
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# レイヤー生成
self.layers = {} # Python 3.7からは辞書の格納順が保持されるので、OrderedDictは不要
self.layers['Affine1'] = \
Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = ReLU()
self.layers['Affine2'] = \
Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
"""ニューラルネットワークによる推論
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
Returns:
numpy.ndarray: ニューラルネットワークの出力
"""
# レイヤーを順伝播
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""損失関数の値算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
float: 損失関数の値
"""
# 推論
y = self.predict(x)
# Softmax-with-Lossレイヤーの順伝播で算出
loss = self.lastLayer.forward(y, t)
return loss
def accuracy(self, x, t):
"""認識精度算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
float: 認識精度
"""
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / x.shape[0]
return accuracy
def numerical_gradient(self, x, t):
"""重みパラメーターに対する勾配を数値微分で算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
dictionary: 勾配を格納した辞書
"""
grads = {}
grads['W1'] = \
numerical_gradient(lambda: self.loss(x, t), self.params['W1'])
grads['b1'] = \
numerical_gradient(lambda: self.loss(x, t), self.params['b1'])
grads['W2'] = \
numerical_gradient(lambda: self.loss(x, t), self.params['W2'])
grads['b2'] = \
numerical_gradient(lambda: self.loss(x, t), self.params['b2'])
return grads
def gradient(self, x, t):
"""重みパラメーターに対する勾配を誤差逆伝播法で算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
dictionary: 勾配を格納した辞書
"""
# 順伝播
self.loss(x, t) # 損失値算出のために順伝播する
# 逆伝播
dout = self.lastLayer.backward()
for layer in reversed(list(self.layers.values())):
dout = layer.backward(dout)
# 各レイヤーの微分値を取り出し
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads
なお、本のコードではOrderedDictを使っていますが、ここでは通常のdictを使っています。Python 3.7からはdictオブジェクトの挿入順序が保存されるようになった1ためです。
5.7.3 誤差逆伝播法の勾配確認
誤差逆伝播法で求めた勾配と数値微分で求めた勾配を比較するコードです。
# coding: utf-8
import os
import sys
import numpy as np
from two_layer_net import TwoLayerNet
sys.path.append(os.pardir) # パスに親ディレクトリ追加
from dataset.mnist import load_mnist
# MNISTの訓練データとテストデータ読み込み
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
# 2層のニューラルワーク生成
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 検証用のデータ準備
x_batch = x_train[:3]
t_batch = t_train[:3]
# 数値微分と誤差逆伝播法で勾配算出
grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)
# 各重みの差を確認
for key in grad_numerical.keys():
# 差の絶対値の算出
diff = np.abs(grad_backprop[key] - grad_numerical[key])
# 平均と最大値を表示
print(f"{key}: [差の平均]{np.average(diff):.10f} [最大の差]{np.max(diff):.10f}")
本では絶対値の差の平均だけを確認していましたが、絶対値の差の最大値も確認してみました。
W1: [差の平均]0.0000000003 [最大の差]0.0000000080
b1: [差の平均]0.0000000021 [最大の差]0.0000000081
W2: [差の平均]0.0000000063 [最大の差]0.0000000836
b2: [差の平均]0.0000001394 [最大の差]0.0000002334
b2が小数点以下7桁くらいの値なので、本よりも少し誤差が大きい印象です。実装にマズい点があるのかも知れません。お気づきの点がありましたら、ご指摘いただけますと助かります![]()
5.7.4 誤差逆伝播法を使った学習
以下、学習のコードです。
# coding: utf-8
import os
import sys
import matplotlib.pylab as plt
import numpy as np
from two_layer_net import TwoLayerNet
sys.path.append(os.pardir) # パスに親ディレクトリ追加
from dataset.mnist import load_mnist
# MNISTの訓練データとテストデータ読み込み
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
# ハイパーパラメーター設定
iters_num = 10000 # 更新回数
batch_size = 100 # バッチサイズ
learning_rate = 0.1 # 学習率
# 結果の記録リスト
train_loss_list = [] # 損失関数の値の推移
train_acc_list = [] # 訓練データに対する認識精度
test_acc_list = [] # テストデータに対する認識精度
train_size = x_train.shape[0] # 訓練データのサイズ
iter_per_epoch = max(int(train_size / batch_size), 1) # 1エポック当たりの繰り返し数
# 2層のニューラルワーク生成
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
# 学習開始
for i in range(iters_num):
# ミニバッチ生成
batch_mask = np.random.choice(train_size, batch_size, replace=False)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 勾配の計算
grad = network.gradient(x_batch, t_batch)
# 重みパラメーター更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 損失関数の値算出
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1エポックごとに認識精度算出
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
# 経過表示
print(f'[更新数]{i:>4} [損失関数の値]{loss:.4f} '
f'[訓練データの認識精度]{train_acc:.4f} [テストデータの認識精度]{test_acc:.4f}')
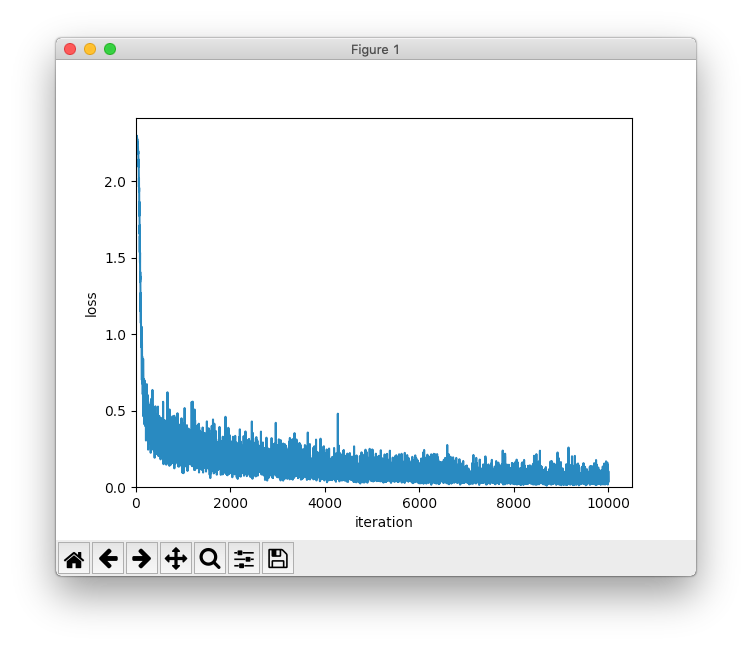
# 損失関数の値の推移を描画
x = np.arange(len(train_loss_list))
plt.plot(x, train_loss_list, label='loss')
plt.xlabel('iteration')
plt.ylabel('loss')
plt.xlim(left=0)
plt.ylim(bottom=0)
plt.show()
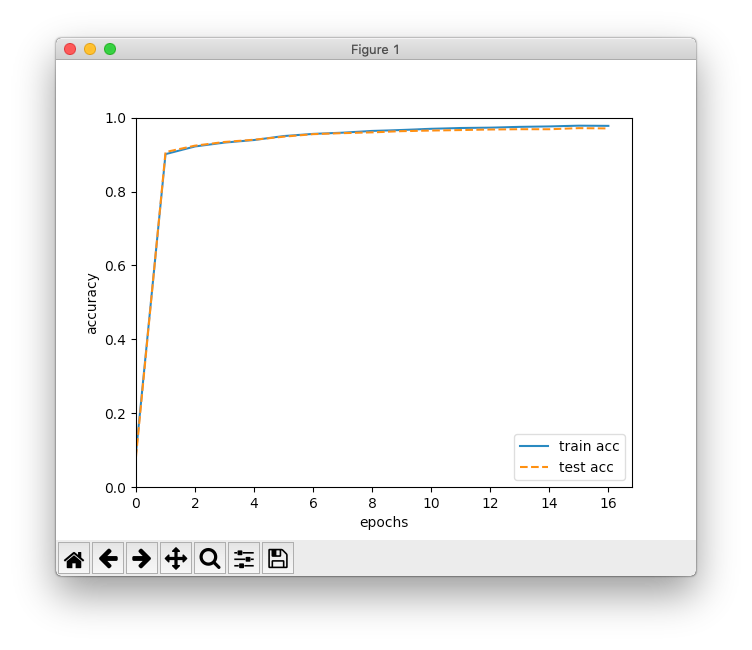
# 訓練データとテストデータの認識精度の推移を描画
x2 = np.arange(len(train_acc_list))
plt.plot(x2, train_acc_list, label='train acc')
plt.plot(x2, test_acc_list, label='test acc', linestyle='--')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.xlim(left=0)
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
そして、前章と同じ形の実行結果です。
[更新数] 0 [損失関数の値]2.3008 [訓練データの認識精度]0.0926 [テストデータの認識精度]0.0822
[更新数] 600 [損失関数の値]0.2575 [訓練データの認識精度]0.9011 [テストデータの認識精度]0.9068
[更新数]1200 [損失関数の値]0.2926 [訓練データの認識精度]0.9219 [テストデータの認識精度]0.9242
[更新数]1800 [損失関数の値]0.2627 [訓練データの認識精度]0.9324 [テストデータの認識精度]0.9341
[更新数]2400 [損失関数の値]0.0899 [訓練データの認識精度]0.9393 [テストデータの認識精度]0.9402
[更新数]3000 [損失関数の値]0.1096 [訓練データの認識精度]0.9500 [テストデータの認識精度]0.9483
[更新数]3600 [損失関数の値]0.1359 [訓練データの認識精度]0.9559 [テストデータの認識精度]0.9552
[更新数]4200 [損失関数の値]0.1037 [訓練データの認識精度]0.9592 [テストデータの認識精度]0.9579
[更新数]4800 [損失関数の値]0.1065 [訓練データの認識精度]0.9639 [テストデータの認識精度]0.9600
[更新数]5400 [損失関数の値]0.0419 [訓練データの認識精度]0.9665 [テストデータの認識精度]0.9633
[更新数]6000 [損失関数の値]0.0393 [訓練データの認識精度]0.9698 [テストデータの認識精度]0.9649
[更新数]6600 [損失関数の値]0.0575 [訓練データの認識精度]0.9718 [テストデータの認識精度]0.9663
[更新数]7200 [損失関数の値]0.0850 [訓練データの認識精度]0.9728 [テストデータの認識精度]0.9677
[更新数]7800 [損失関数の値]0.0403 [訓練データの認識精度]0.9749 [テストデータの認識精度]0.9686
[更新数]8400 [損失関数の値]0.0430 [訓練データの認識精度]0.9761 [テストデータの認識精度]0.9685
[更新数]9000 [損失関数の値]0.0513 [訓練データの認識精度]0.9782 [テストデータの認識精度]0.9715
[更新数]9600 [損失関数の値]0.0584 [訓練データの認識精度]0.9777 [テストデータの認識精度]0.9707
前章の結果と比べると、認識精度の上がり方が早くなっています。最終的に97%くらいになりました。数値微分と誤差逆伝播法の違いは勾配の計算方法だけのはずなので、シグモイド関数からReLU関数に変わったことが改善につながっているみたいです。
5.8 まとめ
計算グラフは分かりやすくて良いですね。また、出力層や損失関数が、微分値を求めやすいように設計されていることが良く分かりました。
この章は以上です。誤りなどありましたら、ご指摘いただけますとうれしいです。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
-
What's New In Python 3.7 の「Python のデータモデルの改善」をご参照ください。 ↩