ゼロから作るDeep Learningで素人がつまずいたことメモ:3章

はじめに

ふと思い立って勉強を始めた「ゼロから作るDeep LearningーーPythonで学ぶディープラーニングの理論と実装」の3章で私がつまずいたことのメモです。

実行環境はmacOS Mojave + Anaconda 2019.10です。詳細はこのメモの1章をご参照ください。

（このメモの他の章へ：1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ）

この記事は個人で作成したものであり、内容や意見は所属企業・部門見解を代表するものではありません。

3章 ニューラルネットワーク

この章はニューラルネットワークの仕組みの説明です。

3.1 パーセプトロンからニューラルネットワークへ

層の数え方の違いや、パーセプトロンとニューラルネットワークの違いなどの説明です。人によって層の数え方が違うというのはちょっと不便ですね。

3.2 活性化関数

活性化関数の種類の紹介です。登場する3種類の関数をグラフにしてみました。

# coding: utf-8
import numpy as np
import matplotlib.pylab as plt


def step_function(x):
    """入力が0を超えたら1を返すステップ関数
    
    Args:
        x (numpy.ndarray): 入力
    
    Returns:
        numpy.ndarray: 出力
    """
    return np.array(x > 0, dtype=np.int)


def sigmoid(x):
    """シグモイド関数
    
    Args:
        x (numpy.ndarray): 入力
    
    Returns:
        numpy.ndarray: 出力
    """
    return 1 / (1 + np.exp(-x))


def relu(x):
    """ReLU関数
    
    Args:
        x (numpy.ndarray)): 入力
    
    Returns:
        numpy.ndarray: 出力
    """
    return np.maximum(0, x)


# 計算
x = np.arange(-5.0, 5.0, 0.01)  # stepはステップ関数が斜めに見えないように小さめ
y_step = step_function(x)
y_sigmoid = sigmoid(x)
y_relu = relu(x)

# グラフ描画
plt.plot(x, y_step, label="step")
plt.plot(x, y_sigmoid, linestyle="--", label="sigmoid")
plt.plot(x, y_relu, linestyle=":", label="ReLU")
plt.ylim(-0.1, 5.1)
plt.legend()
plt.show()

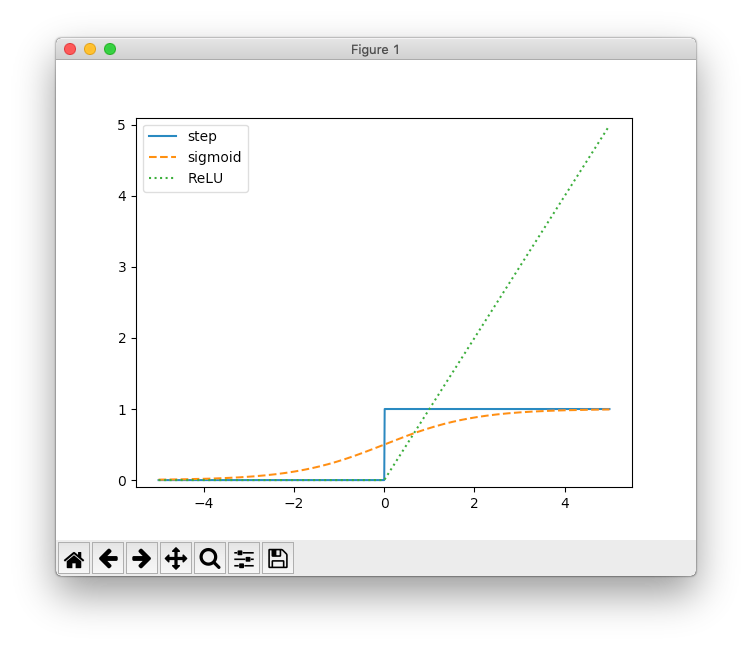
1つだけわからなかったのは、活性化関数に線形関数を用いてはならない、という部分。各層のニューロンが1つしかないのであれば、多層にしても1層で表現できてしまうということは本の解説で理解できました。でも各層にニューロンが複数あった場合でも、それが1層で表現できてしまうのでしょうか。ここはうまく理解できませんでした。

3.3 多次元配列の計算

多次元配列の計算を行列の計算に置き換えて効率化しましょうという解説です。私は3年ほど前に機械学習のオンライン講座¹を受けた時に行列計算への置き換えを勉強し、その後の言語処理100本ノックでも使った²ので、そのおさらいになりました。

3.4 3層ニューラルネットワークの実装

前節の行列計算を使って3層ニューラルネットワークを実装します。学習する機能はないので、特につまずく部分はありませんでした。

3.5 出力層の設計

ソフトマックス関数の解説です。ここも特につまずく部分はありませんでした。 つまずいていないつもりだったのですが間違いに気づきました。バッチ処理をしない場合は本の実装通りで問題ないのですが、「3.6.3 バッチ処理」を実装する際に修正が必要です。

以下、バッチ処理に対応させてみたソフトマックスのコードです。

def softmax(x):
    """ソフトマックス関数
    
    Args:
        x (numpy.ndarray): 入力
    
    Returns:
        numpy.ndarray: 出力
    """

    # バッチ処理の場合xは(バッチの数, 10)の2次元配列になる。
    # この場合、ブロードキャストを使ってうまく画像ごとに計算する必要がある。
    if x.ndim == 2:

        # 画像ごと（axis=1）の最大値を算出し、ブロードキャストできるよにreshape
        c = np.max(x, axis=1).reshape(x.shape[0], 1)

        # オーバーフロー対策で最大値を引きつつ分子を計算
        exp_a = np.exp(x - c)

        # 分母も画像ごと（axis=1）に合計し、ブロードキャストできるよにreshape
        sum_exp_a = np.sum(exp_a, axis=1).reshape(x.shape[0], 1)
        
        # 画像ごとに算出
        y = exp_a / sum_exp_a

    else:

        # バッチ処理ではない場合は本の通りに実装
        c = np.max(x)
        exp_a = np.exp(x - c)  # オーバーフロー対策
        sum_exp_a = np.sum(exp_a)
        y = exp_a / sum_exp_a

    return y

なお、この本のGitHubリポジトリhttps://github.com/oreilly-japan/deep-learning-from-scratchにあるソースでは、ブロードキャストするために転置させていました。もしかしたら速度的に有利なのかも知れませんが、パッと見だと何をやっているのか分からなかったため、私はreshapeを使うコードにしてみました。

3.6 手書き数字認識

学習済みのパラメーターを使って、実際にニューラルネットワークの推論処理を実装します。学習済みのパラメーターが保存されたsample_weight.pklが必要なので、この本のGitHubリポジトリhttps://github.com/oreilly-japan/deep-learning-from-scratchのch3フォルダーにあるファイルをカレントディレクトリーに持ってきましょう。

本に従って実装を進めると、オーバーフローのワーニングに遭遇しました。

/Users/segavvy/Documents/deep-learning-from-scratch/ch03/3.6_mnist.py:19: RuntimeWarning: overflow encountered in exp
  return 1 / (1 + np.exp(-x))

これについては、機械学習のPythonとの出会い>>ロジスティック回帰>>シグモイド関数 の解説を参考に、xの値を見てオーバーフローしないよう修正してみました。

また、最後の認識精度の計算時に、本ではaccuracy_cntをfloatに型変換していますが、python3では整数同士の割り算は浮動小数点を返すので、この変換は不要みたいです。

あと、実装のついでに、上手く推論できなかった画像がどんなものなのか気になったので、表示するようにしてみました。

以下、私の書いたコードです。

# coding: utf-8
import numpy as np
import os
import pickle
import sys
sys.path.append(os.pardir)  # パスに親ディレクトリ追加
from dataset.mnist import load_mnist
from PIL import Image


def sigmoid(x):
    """シグモイド関数
    本の実装ではオーバーフローしてしまうため、以下のサイトを参考に修正。
    http://www.kamishima.net/mlmpyja/lr/sigmoid.html

    Args:
        x (numpy.ndarray): 入力
    
    Returns:
        numpy.ndarray: 出力
    """
    # xをオーバーフローしない範囲に補正
    sigmoid_range = 34.538776394910684
    x = np.clip(x, -sigmoid_range, sigmoid_range)

    # シグモイド関数
    return 1 / (1 + np.exp(-x))


def softmax(x):
    """ソフトマックス関数
    
    Args:
        x (numpy.ndarray): 入力
    
    Returns:
        numpy.ndarray: 出力
    """

    # バッチ処理の場合xは(バッチの数, 10)の2次元配列になる。
    # この場合、ブロードキャストを使ってうまく画像ごとに計算する必要がある。
    if x.ndim == 2:

        # 画像ごと（axis=1）の最大値を算出し、ブロードキャストできるよにreshape
        c = np.max(x, axis=1).reshape(x.shape[0], 1)

        # オーバーフロー対策で最大値を引きつつ分子を計算
        exp_a = np.exp(x - c)

        # 分母も画像ごと（axis=1）に合計し、ブロードキャストできるよにreshape
        sum_exp_a = np.sum(exp_a, axis=1).reshape(x.shape[0], 1)
        
        # 画像ごとに算出
        y = exp_a / sum_exp_a

    else:

        # バッチ処理ではない場合は本の通りに実装
        c = np.max(x)
        exp_a = np.exp(x - c)  # オーバーフロー対策
        sum_exp_a = np.sum(exp_a)
        y = exp_a / sum_exp_a

    return y


def load_test_data():
    """MNISTのテスト画像とテストラベル取得
        画像の値は0.0〜1.0に正規化済み。

    Returns:
        numpy.ndarray, numpy.ndarray: テスト画像, テストラベル
    """
    (x_train, t_train), (x_test, t_test) \
        = load_mnist(flatten=True, normalize=True)
    return x_test, t_test


def load_sapmle_network():
    """サンプルの学習済み重みパラメーター取得
    
    Returns:
        dict: 重みとバイアスのパラメーター
    """
    with open("sample_weight.pkl", "rb") as f:
        network = pickle.load(f)
    return network


def predict(network, x):
    """ニューラルネットワークによる推論
    
    Args:
        network (dict): 重みとバイアスのパラメーター
        x (numpy.ndarray): ニューラルネットワークへの入力
    
    Returns:
        numpy.ndarray: ニューラルネットワークの出力
    """
    # パラメーター取り出し
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # ニューラルネットワークの計算（forward）
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)

    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)

    return y


def show_image(img):
    """イメージ表示
    
    Args:
        image (numpy.ndarray): 画像のビットマップ
    """
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()


# MNISTのテストデータの読み込み
x, t = load_test_data()

# サンプルの重みパラメーター読み込み
network = load_sapmle_network()

# 推論、認識精度算出
batch_size = 100  # バッチ処理の単位
accuracy_cnt = 0  # 正解数
error_image = None  # 認識できなかった画像
for i in range(0, len(x), batch_size):

    # バッチデータ準備
    x_batch = x[i:i + batch_size]

    # 推論
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)

    # 正解数カウント
    accuracy_cnt += np.sum(p == t[i:i + batch_size])

    # 認識できなかった画像をerror_imageに連結
    for j in range(0, batch_size):
        if p[j] != t[i + j]:
            if error_image is None:
                error_image = x_batch[j]
            else:
                error_image = np.concatenate((error_image, x_batch[j]), axis=0)

print("認識精度:" + str(accuracy_cnt / len(x)))

# 認識できなかった画像を表示
error_image *= 255  # 画像の値は0.0〜1.0に正規化されているので、表示できるように0〜255に戻す。
show_image(error_image.reshape(28 * (len(x) - accuracy_cnt), 28))

そして実行結果です。

認識精度:0.9352

失敗した 793個 648個のイメージを単純に縦に連結しているので、とんでもなく縦長の画像が表示されますが、確かに分かりにくい文字が多いです。でも、中には認識できそうな文字も混ざっていますね。

あと、本では認識精度が0.9352になると書いてあるのですが、なぜか0.9207になってしまいました。シグモイド関数をワーニングが出る状態に戻しても変わらなかったので、他にどこか間違いがあるのかも……

3.7 まとめ

3章も私にとってはおさらいの部分が多かったので、大きくつまずくことはなかったのですが、最後の認識精度の違いが気になるところです。
3章はつまずいていないつもりだったのですが、以下２点に後から気づきました。

後から気づいた問題１

@tunnel さんのご指摘で、本と認識精度が違っていた原因が分かりました！本来は画像データの値を0.0〜1.0に正規化したもの使う必要があるのですが、0〜255のままのものを流してしまっていました。@tunnel さん、ありがとうございました！
それにしても、ここまで値が違うと認識精度がボロボロになりそうなのですが、それほど悪くならなかったのは中々興味深いところです。

後から気づいた問題2

第4章でなぜか学習しても損失関数が小さくならず、原因を調べていたらソフトマックス関数がバッチ処理に対応できていないことに気づきました。上述のコードは修正済みです。
（これは3章でもう少し説明があると嬉しかったなぁ……）

（このメモの他の章へ：1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ）

1. Courseraというオンライン講座のサービスの中でStanford Universityが提供している講義Machine Learningです。有志の方が日本語字幕を付けてくれているので、英語が苦手でもなんとかなりました。配列計算を行列計算に置き換える手法は、ベクトル化（Vectorization）という名前で解説されています。 ↩

2. 言語処理100本ノック2015の第8章の問題73を解いた時に使いました。当時の学習メモを素人の言語処理100本ノック:73として投稿しています。 ↩