はじめに
ふと思い立って勉強を始めた「ゼロから作るDeep LearningーーPythonで学ぶディープラーニングの理論と実装」の6章で私がつまずいたことのメモです。
実行環境はmacOS Mojave + Anaconda 2019.10、Pythonのバージョンは3.7.4です。詳細はこのメモの1章をご参照ください。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
この記事は個人で作成したものであり、内容や意見は所属企業・部門見解を代表するものではありません。
6章 学習に関するテクニック
この章は、学習を効率化する手法や過学習の対策に関する説明です。
6.1 パラメータの更新
ニューラルネットワークの学習において、勾配を求めたあと、それを使ってどのように重みパラメーターを最適化するのか、その手法についての説明です。
最初に出てくる風変わりな冒険家の例ですが、この冒険家は地図の使用を禁止し、わざわざ目隠しまでしているのに効率重視で、しかもなぜかもっとも深い谷底を探し求めています。これではちょっと風変わりがすぎて感情移入できません![]()

ちょっとググってみたら、良い例を見つけました。ml4a さんの ニューラルネットワークの訓練 の冒頭の例です。山頂にいたら日が暮れてしまい、早くベースキャンプに戻らないといけないけど懐中電灯が貧弱で足元しか照らせない、あなたならどうします?というお話です。もしかしたら、他にも似たような例え話がたくさんあるのかも知れません。
冒険家の気持ちになれれば、SGDの欠点は非常に分かりやすいです。自分が今いる位置の勾配しかわからず周りが見渡せない状況ですから、とりあえず勾配のきつい方向へ進むしかありません。確かに行ったり来たりで非効率になることもありそうです。
この改善手法として、Momentum、AdaGrad、RMSProp、Adamが紹介されていますが、ちょっと困ったのはこれらの手法の呼び方です。最初のモーメンタムは良いのですが、後者3つの読み方が分かりません。それぞれ、「アダ・グラッド」、「アール・エム・エス・プロップ」、「アダム」でOKでしょうか。
話が脱線してしまいますが、呼び方がわからないのはなかなか切実な問題で、社内の勉強会などで誤った呼び方を使い始めると社員が外で恥をかいてしまいます。この悩みを持つ方は非常に多いらしく、@ryounagaoka さんのまとめられている IT業界で横行する恥ずかしい英語発音 のいいねの数や膨大なコメントを見ると、ホント日本語の不便さを痛感してしまいます。この業界で働くなら、やっぱり英語圏に生まれたかったものです![]()
話を戻します。本で紹介されているこれらの改善手法は、自分が今いる位置の勾配だけでなく、その地点に至った時の勢いや過去の動きも利用するように工夫されています。MomentumとAdaGradは本で詳しく解説されていることもあり、特につまずくところはありませんでした。他の手法については詳細が省略されていますが、本で紹介されていない手法も含めて、@deaikei さんの OPTIMIZER 入門 ~線形回帰からAdamからEveまで に分かりやすくまとまっています。
手法がたくさんあることからも想像できますが、万能な手法はなく、対象のニューラルネットワークの構造やハイパーパラメーターによって結果が変わってしまうとのこと。最適な手法の選択やハイパーパラメーターの調整はなかなか大変そうですね。
本では実際にMNISTデータセットで検証していますが、SGDが一番学習が遅く、Momentum、AdaGrad、Adamはいずれも同じくらい高速化されていました。なお、この検証ではいきなり5層のニューラルネットワークが出てきます。これまで2層でやってきたので、同じもので検証してくれれば分かりやすいのに!と思ったのですが、ある程度複雑なネットワークにしないと検証がやりにくくなる模様です。
6.2 重みの初期値
学習前の重みをどのような値にしておくかの説明です。
過学習を抑えるために重みの初期値を小さくしましょうという流れですが、なぜ過学習が抑えられるのかがピンときませんでした。入力値に重みを掛けるので重みが大きいと結果に及ぼす影響も大きくなりますから、確かに過学習になりそうな感じもしますが、ちょっとスッキリしない出だしです。
過学習を抑えるという話は別として、アクティベーションの分布がいい感じにバラつかないと、勾配消失や複数のニューロンが同じような出力になってしまい性能が落ちてしまうことは良く分かりました。前章のメモの 5.5.2 Sigmoidレイヤ で褒めちぎったシグモイド関数も、逆伝播の微分値は $ y(1-y) $ なので、重みが大きいと $ y $ も大きくなって微分値が小さくなり、逆伝播でかけ合わさっていくと勾配がどんどん小さくなって学習が進まなくなる問題を抱えています。勾配消失という点では、ReLUは $ x>0 $ の時の微分値が $ 1 $ なので非常に強そうです。
もしかしたら出だしでスッキリしなかった件はシグモイド関数の勾配消失を指していて、重みの初期値が大きいと学習の最初の方の入力データにより勾配が消失してしまい、後に続くデータの影響を受けにくくなって過学習が起きる、だから重みを小さくしましょう、ということなのかも知れません。
なお、説明の中でガウス分布や標準偏差やヒストグラムという言葉が出てきます。ガウス分布は正規分布のことなので、「正規分布とは」などでググるとたくさん解説がでてきます。標準偏差やヒストグラムは 映像授業 Try IT(トライイット) > 数学Ⅰ データの散らばりと相関 がすごく分かりやすいです。
あと、ここでまた、内容は理解できたのですが読み方のわからない手法が2つ出てきました。活性化関数が線形関数の場合に適しているXavierの初期値と、ReLUに適しているHeの初期値ですが、それぞれ「ザビエルの初期値」と「ヘの初期値」で良いのでしょうか![]()
6.3 Batch Normalization
重みの初期値の説明では、各層のアクティベーションの分布をいい感じにバラつかせようとしていましたが、Batch Normalization は各層の途中で強制的に分布を正規化してしまおうという手法です。具体的には、ミニバッチを1つの単位として、AffineレイヤーとReLUレイヤーの間に調整のためのレイヤーをはさみ込んで、そこで平均が0、分散が1になるように値を調整する形です。
この調整の数式が(6.7)として出てきたのですが、ここでちょっとつまずきました。
\begin{align}
&\mu _B \leftarrow \frac {1}{m} \sum _{i=1} ^{m} x_i \\
&\sigma^2 _B \leftarrow \frac {1}{m} \sum _{i=1} ^{m} (x_i - \mu_B)^2 \\
&\hat{x_i} \leftarrow \frac {x_i - \mu_B}{\sqrt{\sigma^2_B+ \epsilon}}
\end{align}
式中の$ B $ はミニバッチの入力データで、$ B = \{ x_1, x_2, \cdots,x_m \} $ という $ m $ 個の入力データです。1行目の $ \mu _B$ ($ \mu $:読み方はミュー)がミニバッチの入力データの平均で、2行目の $ \sigma^2 _B $ ($ \sigma $:シグマ)が分散というところまでは前述のトライイットのおさらい直後なのでバッチリなのですが、3行目によってなぜ平均が0、分散が1に正規化できるのかが良く分かりません。これについては、 具体例で学ぶ数学 > 確率、データ処理 > 統計における標準化の意味と目的 の解説で理解することができました。
なお、本ではこのBatch Normレイヤーの逆伝播の解説は省略されていて、詳しくは Frederik Kratzertのブログ「Understanding the backward pass through Batch Normalization Layer」 をとのことです。英語だとテンションが下がってしまう私のような方は、代わりに @t-tkd3a さんの Batch Normalization の理解 がお勧めです。
6.4 正則化
過学習を抑制する手法である、Weight decay(読み方はウェイトディケイ?)とDropout(ドロップアウト)の説明です。
見出しに「正則化」という言葉が出てきますが、本では言葉の説明がなく、「 $ \lambda $ は正則化の強さをコントロールするハイパーパラメータです」みたいに突然出てきて少し戸惑いました。Wikipedia 曰く「不良設定問題を解いたり過学習を防いだりするために、情報を追加する手法」とのことです。Weight decayのように損失関数にペナルティを与える手法全般を指しているようですね。ちなみに $ \lambda $ の読み方はラムダです。
本の内容で気になったのは、手法の検証結果です。訓練データの数を減らし、かつ層を増やして表現力を増したネットワークで過学習が起きるのを確認した後、Weight decayやDropoutによって訓練データに対する過学習が抑制できることを確認しています。しかし、肝心のテストデータに対する認識精度が改善されていません。
Weight decayの図6-20と図6-21では訓練データの認識精度は下がっているのですが、テストデータの認識精度は大差ありません。また、Dropoutの図6-23では、テストデータの認識精度まで下がってしまっていて、本末転倒な感じがしてしまいます。過学習を抑制する目的は、テストデータの認識精度を上げるためですよね?
さらに図6-23で気になるのは、最終結果の301エポックでは訓練データもテストデータも認識精度がまだ上り調子な点です。これだともう少しエポックを増やしたくなるので、本のソースコードch06/overfit_droput.pyで、図6-23に合わせてdropout_rate=0.15とし、601エポックで回してみました。
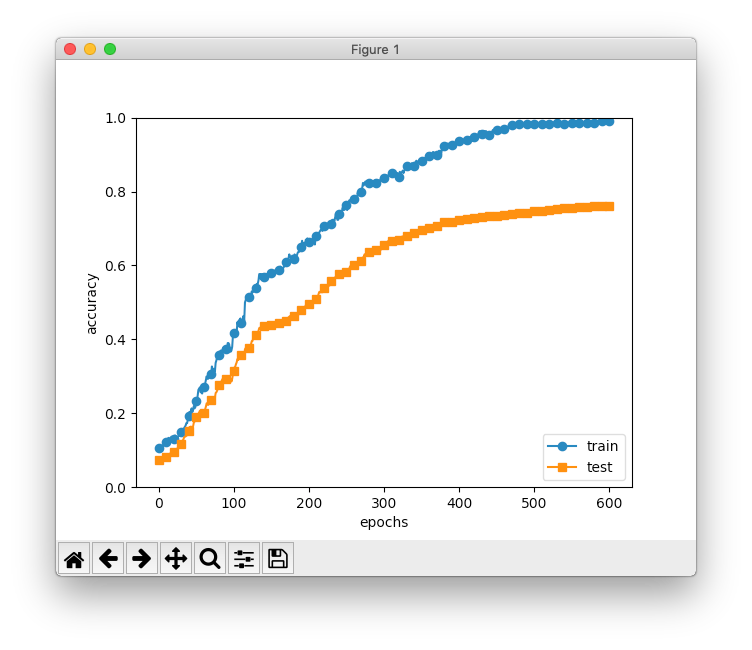
この結果を見ると、認識精度が安定した500エポック辺りの訓練データとテストデータの認識精度は、Dropoutしない場合の100エポック辺りと同じ感じなので、単に学習の時間を遅くしただけに思えてしまいます。
本の例では訓練データの数が少なすぎて、過学習を抑制してもテストデータの認識精度が上げられない状態になっているのかも知れません。
6.5 ハイパーパラメータの検証
ハイパーパラメーターの最適値を探す方法の説明です。
ランダムサーチのような泥臭いやり方が、効率的に思えるグリッドサーチよりも良い結果になるのが面白いですね。なお、もっと洗練された手法としてベイズ最適化が紹介されていますが、他にもハイパーパラメーターを自動調整する手法はいろいろあるそうです。@cvusk さんの ハイパーパラメータ自動調整いろいろ で、各手法が紹介されています。
6.6 まとめ
ニューラルネットワークの学習におけるテクニックを学ぶことができました。「6.4 正則化」の検証結果の図はモヤモヤが残っていますが、大きくつまずく点はありませんでした。
この章は以上です。誤りなどありましたら、ご指摘いただけますとうれしいです。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)