曖昧な理解だったのを、自前で実装できるくらいに理解しようと図解しました。その際の資料を公開します。
内容は、ほぼ"Understanding the backward pass through Batch Normalization Layer"の焼き直しです。
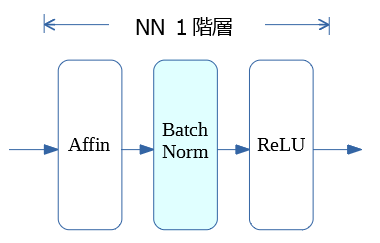
全結合NN の Batch Normalization
いつ行うの？
全結合のニューラルネットワークの場合、Affinの後、活性化(例:ReLU)の前
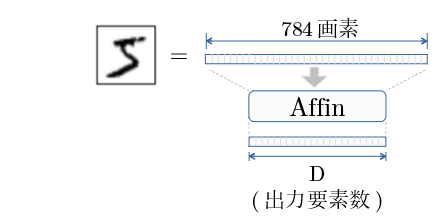
入力は？
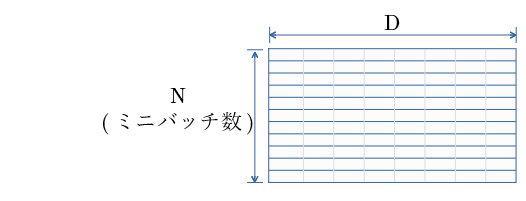
Affinの出力を 行 として、
（図は入力層→NN第一層での例）
ミニバッチ数分のAffin出力を並べた行列が入力。
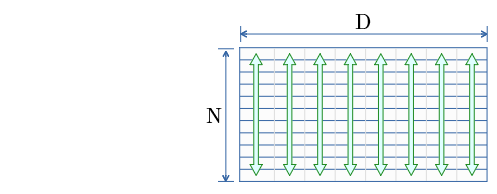
入力行列をどう演算するの？
要素毎（列内）で正規化の演算します。
演算式は？
上図の１列の演算を示す
入力:
上図の１列の値 { $x_1$ ... $x_N$ } ( $N$:ミニバッチ数)
学習値 $γ$ , $β$
出力：
y_i = BatchNorm _{γβ} ( x_i )
ミニバッチ平均:
\mu _x \leftarrow \frac {1}{N} \sum _{i=1} ^{N} x_i
ミニバッチ分散:
\sigma^2 _x \leftarrow \frac {1}{N} \sum _{i=1} ^{N} (x_i - \mu_x)^2
正規化：
\hat{x_i} \leftarrow \frac {x_i - \mu_x}{\sqrt{\sigma^2_x+ \epsilon}}
変倍・移動
y_i \leftarrow γ \hat{x_i} + β
\equiv BatchNorm _{γβ} ( x_i )
効果は？
- 学習を速く進行させることができる（学習係数を大きくすることができる）
- 初期値にそれほど依存しない（初期値に対してそこまで神経質にならなくてよい）
- 過学習を抑制する(Dropout などの必要性を減らす)
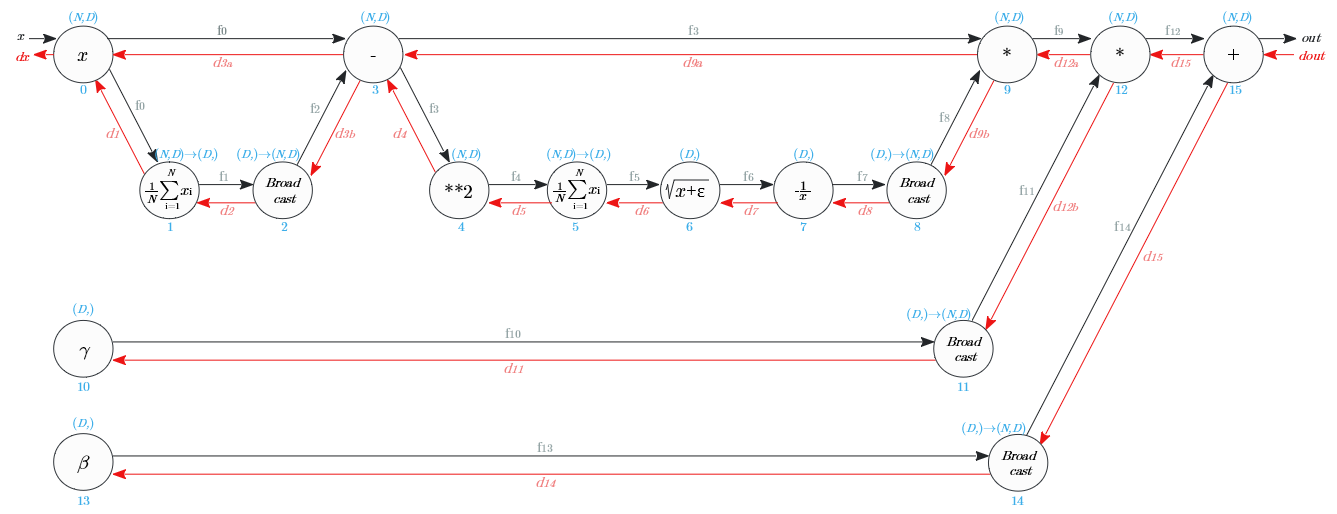
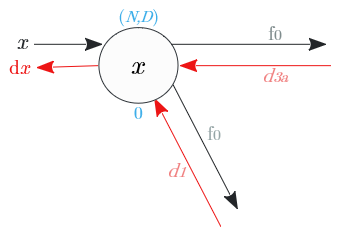
逆伝播値の求め方は？
入力
| 識別名 | 次元 | 値 |
|---|---|---|
| $d_{out}$ | $(N,D)$ | 後続層からの逆伝搬値 |
順伝播の計算時に保持した値
| 識別名 | 次元 | 値 | 備考 |
|---|---|---|---|
| $f_3$ | $(N,D)$ | $x_i-μ_x$ | |
| $f_5$ | $(D,)$ | $ \frac{1}{N} \sum_{i=1} ^{N} (x_i - \mu_x)^2$ | $=\sigma^2 _x$ |
| $f_7$ | $(D,)$ | $\frac{1}{\sqrt{\sigma^2 _x + \epsilon}}$ | $=\frac{1}{\sqrt{f_5 + \epsilon}}$ |
| $f_9$ | $(N,D)$ | $\frac{x_i - \mu_x}{\sqrt{\sigma^2 _x + \epsilon}}$ | $=\hat{x_i}$ |
計算過程値
| 識別名 | 次元 | 値 |
|---|---|---|
| $d_{12a}$ | $(N,D)$ | $d_{out}\circ γ$ |
| $d_{3a}$ | $(N,D)$ | $f_7\circ(d_{12a}-f_3\circ \frac{1}{f_5 + \epsilon} \circ \frac{1}{N}\sum ^N _{i=1}(f _3 \circ d _{12a} )) $ |
出力
| 識別名 | 次元 | 値 |
|---|---|---|
| $d_x$ | $(N,D)$ | $d_{3a} - \frac{1}{N}\sum ^N _{i=1} d _{3a}$ |
| $d_γ$ | $(D,)$ | $\sum ^N _{i=1}(\hat{x_i} \circ d _{out}$) |
| $d_β$ | $(D,)$ | $\sum ^N _{i=1} d _{out}$ |
逆伝播の式はどう求めた？
計算グラフで
$d_{out}$から、各ノードの逆伝播の出力値を辿り、$d_x$を求めます。
「誤差逆伝播法等に用いる 計算グラフ の基本パーツ」 を前提にしています。
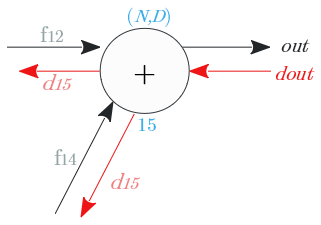
ノード⑮
加算ノードの逆伝播は、入力値をそのまま伝搬。
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_{15}$ | $(N,D)$ | $d_{out}$ |
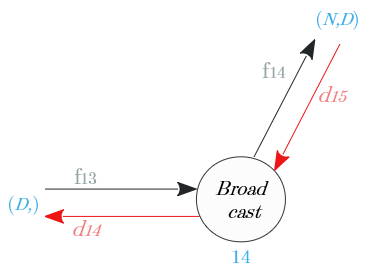
ノード⑭
Broadcastノードの逆伝播は、入力値の総和。
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_β = d_{14}$ | $(D,)$ | $\sum^N_{i=1} d_{15}$ |
ノード⑫
乗算ノードの逆伝播は、順伝播の入れ替えし伝搬
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_{12a}$ | $(N,D)$ | $f_{11} \circ d_{15}$ |
| $d_{12b}$ | $(N,D)$ | $f_9 \circ d_{15}$ |
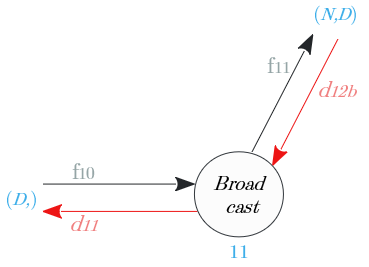
ノード⑪
Broadcastノードの逆伝播は、入力値の総和。
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_γ = d_{11}$ | $(D,)$ | $\sum^N_{i=1} d_{12b}$ |
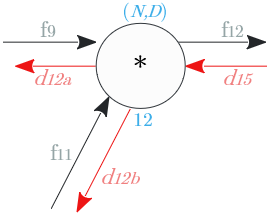
ノード⑨
乗算ノードの逆伝播は、順伝播の入れ替えし伝搬
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_{9a}$ | $(N,D)$ | $f_8 \circ d_{12a}$ |
| $d_{9b}$ | $(N,D)$ | $f_3 \circ d_{12a}$ |
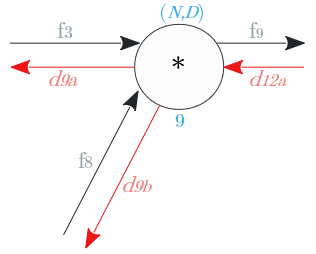
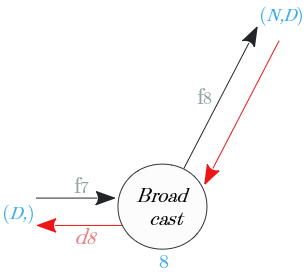
ノード⑧
Broadcastノードの逆伝播は、入力値の総和。
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_8$ | $(D,)$ | $\sum^N_{i=1} d_{9b}$ |
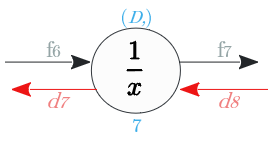
ノード⑦
逆伝播は、$\frac{1}{x}$を$x$で微分し、入力値に乗じた値
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_7$ | $(D,)$ | $- \frac{1}{(f_6) ^2} \circ d_8$ |
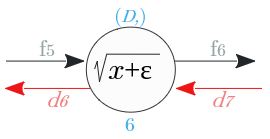
ノード⑥
逆伝播は、$\sqrt{x+\epsilon}$ を $x$ で微分し、入力値に乗じた値
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_6$ | $(D,)$ | $ \frac{1}{2\sqrt{f_5 +\epsilon} } \circ d_7$ |
(※)$\epsilon$ は 小さい値 (例：$1^{-7}$)
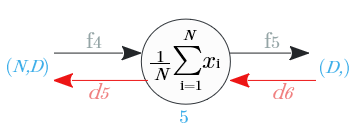
ノード⑤
総和の逆伝播は、入力値をそのままN個に分配し、次元を$(D,)$ →$(N,D)$ に変える
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_5$ | $(N,D)$ | $\frac{1}{N} d_6$ |
ノード④
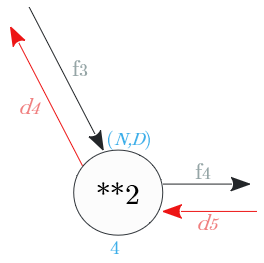
逆伝播は、$x^2$ を $x$ で微分し、入力値に乗じた値
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_4$ | $(N,D)$ | $2$ $f_3 \circ d_5$ |
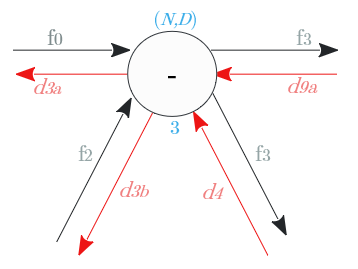
ノード③
マイナスの加算と分岐のノード
分岐の逆伝播は加算
加算の逆伝播は分岐
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_{3a}$ | $(N,D)$ | $d_{9a} + d_4$ |
| $d_{3b}$ | $(N,D)$ | $-d_{3a}$ |
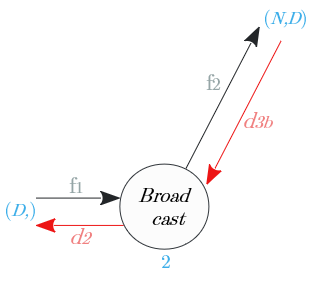
ノード②
Broadcastノードの逆伝播は、入力値の総和。
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_2$ | $(D,)$ | $\sum^N_{i=1} d_{3b}$ |
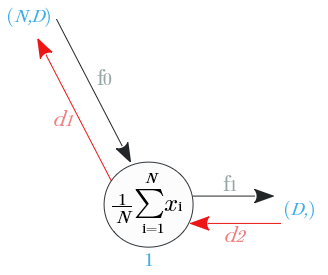
ノード①
総和の逆伝播は、入力値をそのままN個に分配し、次元を$(D,)$ →$(N,D)$ に変える
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_1$ | $(N,D)$ | $\frac{1}{N} d_2$ |
ノード⓪
分岐ノードの逆伝播は、入力の加算
| 出力識別名 | 次元 | 値 |
|---|---|---|
| $d_x$ | $(N,D)$ | $d_{3a} + d_1$ |
計算グラフから求めた逆伝播式の整理
計算過程値 $d_{12a}$
d_{15}=d_{out}\\
f_{11} = Broadcast(γ) \\
の２式を
d_{12a}=f_{11} \circ d_{15}
に代入すると
d_{12a}=γ \circ d_{out}
計算過程値 $d_{3a}$
d_{9a}= f_8 \circ d_{12a} \\
f_8 = Broadcast(f_7)\\
d_4 = 2 (f_3 \circ d_5)\\
d_5 = \frac{1}{N} d_6\\
d_6 = \frac{1}{2\sqrt{f_5 +\epsilon} } \circ d_7\\
d_7 = - \frac{1}{(f_6) ^2} \circ d_8\\
f_6 = \sqrt{f_5 +\epsilon }\\
d_8 = \sum^N_{i=1} d_{9b}\\
d_{9b} = f_3 \circ d_{12a}\\
の９式を
d_{3a}=d_{9a} + d_4
に代入すると
\begin{align}
d_3a &= f_7 \circ d_{12a} + 2 (f_3 \circ \frac{1}{N} \frac{1}{2\sqrt{f_5 +\epsilon} } \circ \frac{-1}{(\sqrt{f_5 +\epsilon }) ^2} \circ \sum^N_{i=1} (f_3 \circ d_{12a})) \\
&= f_7 \circ d_{12a} + 2 (f_3 \circ \frac{1}{N} \frac{1}{2} f_7 \circ \frac{-1}{(\sqrt{f_5 +\epsilon }) ^2} \circ \sum^N_{i=1} (f_3 \circ d_{12a})) \\
&= f_7 \circ (d_{12a} - f_3 \circ \frac{1}{f_5 +\epsilon } \circ \frac{1}{N}\sum^N_{i=1} (f_3 \circ d_{12a}))
\end{align}
出力 $dx$
d_1=\frac{1}{N} d_2\\
d_2=\sum^N _{i=1} d_{3b}\\
d_{3b}=-d_{3a}\\
の３式を
dx=d_{3a}+d_1
に代入すると
dx=d_{3a}-\frac{1}{N} \sum^N _{i=1} d_{3a}
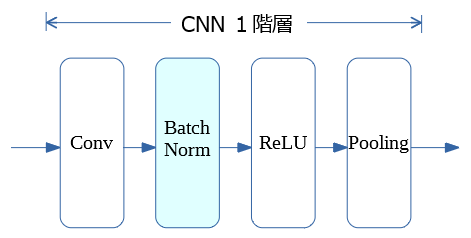
CNN の Batch Normalization
CNNの場合はいつ行うの？
CNNの場合、Convolutionの後、活性化(例:ReLU)の前
CNNの場合の入力は？
Convolution の出力の チャンネルをシリアライズし１行とし、
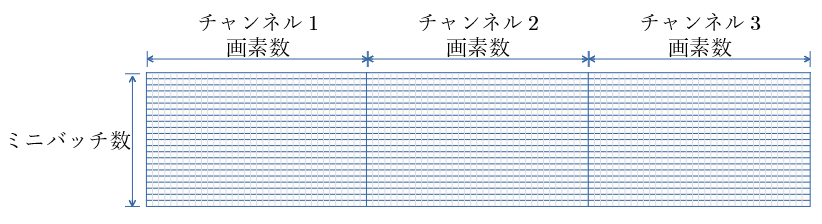
ミニバッチ数の行数とした行列。
以後の計算は、全結合のBatch Normalization と同じ。
参考文献
関連項目
Mind で Neural Network (準備編2) 順伝播・逆伝播 図解
誤差逆伝播法等に用いる 計算グラフ の基本パーツ
シンプルなNNで 学習失敗時の挙動と Batch Normalization の効果を見る