正解率が 1/クラス数 のままでロスも下がらない状況(学習失敗)になる挙動を見ました。
結果をここにまとめ公開します。参考になれば幸いです。
背景・経緯
- 深層学習の理解を深めようと、自前で実装を行っています。
- 学習開始直後に、正解率が 1/クラス数 のまま ロスも下がらない 学習失敗になる状況に遭遇しました。
バグを疑い涙目になる。- 勘で与えた 学習率の値 が大きかったのが原因。(学習率の値 を小さくすると学習が進む)
- 学習失敗と 学習が進む場合で、重みとバイアスの推移がどう違うのか関心がわき、グラフ化し、見比べました。
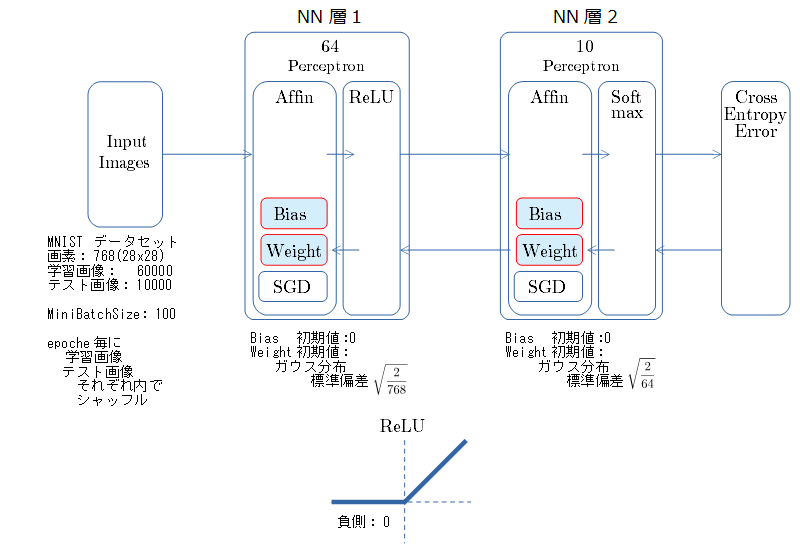
- MNIST 、隠れ層1の全結合NN のシンプルなNNで見比べました。
得た知見(結論)
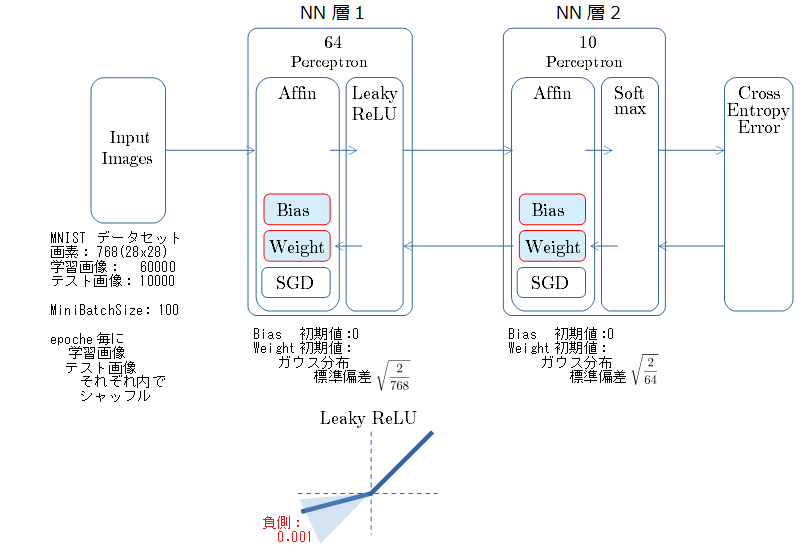
- ReLU と LeakyReLU で、異なる 学習失敗経緯 を見れた。
- ReLU にて、全てのパーセプトロンが 負の領域で反応しなくなる推移 を見れた。
- Leaky ReLUにて、正負を行き来しながら発散し無効な数値(nan)化する推移を 見れた。
- 学習率が大きいと、Bias と Weight がともにバタつき 収集つかなくなる。
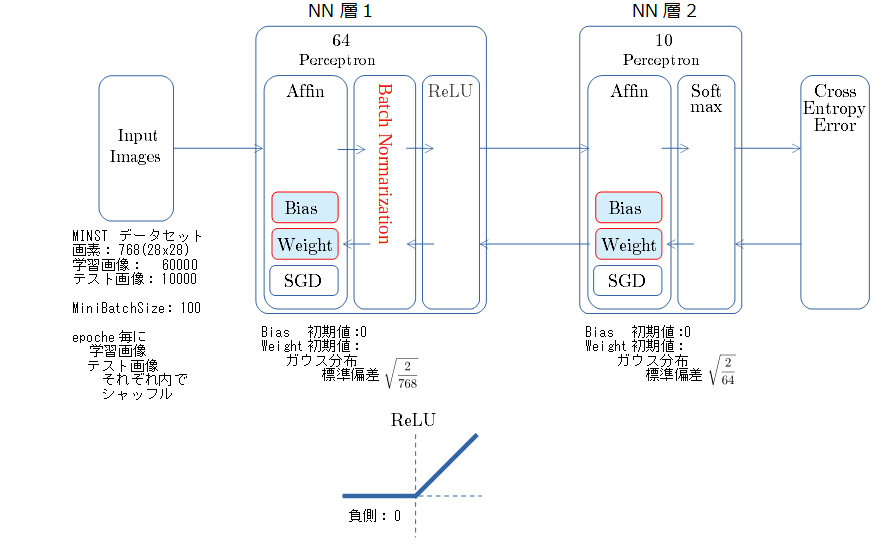
- Batch Normalization (以後 BN)すごい。
- BNなしで学習失敗した学習率より一桁大きい値でも、BNありだと学習が進む。
ReLU での挙動
NNの構成とパラメータ
- 乱数種値は 20170523 固定
- 学習率3つで比較。「学習が失敗する場合」と 「順調に進む場合」 と その中間 「なんか調子悪い」 とで比較する。
- ミニバッチ600回 (1 epoche) 期間での測定。
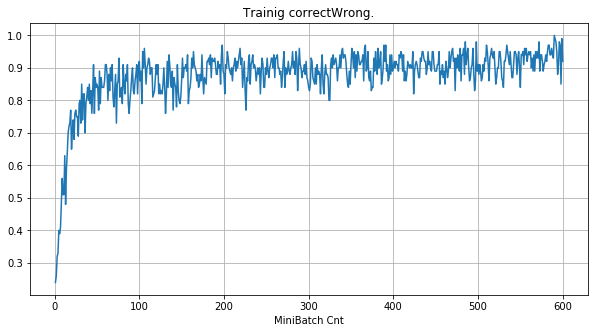
- 「①学習時正解率」は、学習時の正解率。 横軸はミニバッチ回数、縦軸は正解率。グラフは上に行くほど良く正解率が高い。
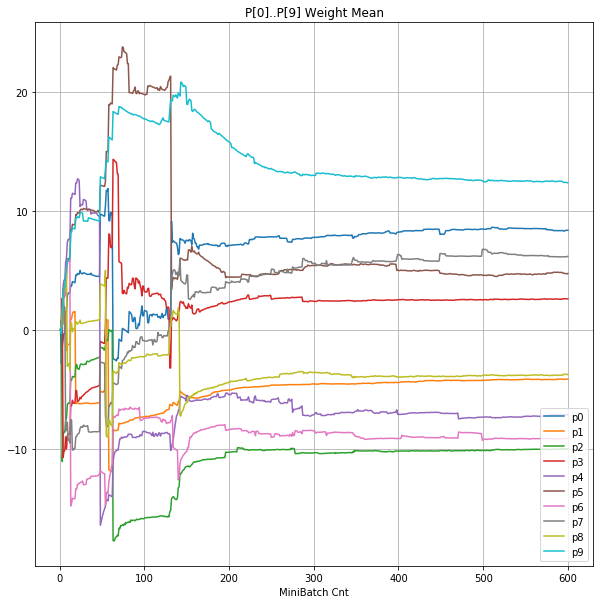
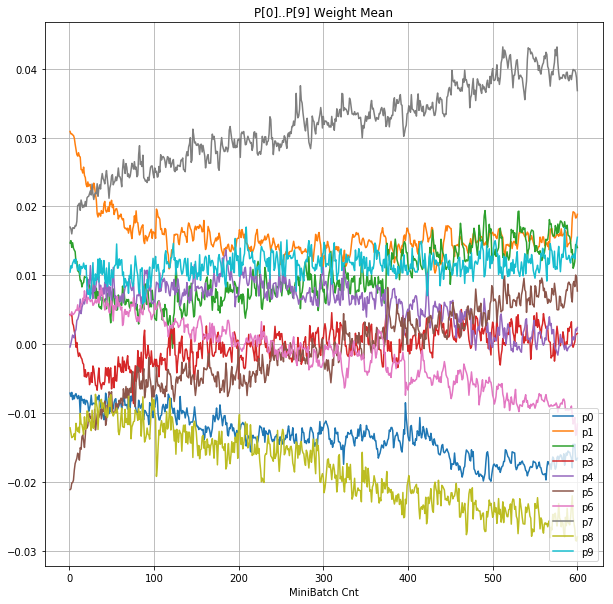
- 「②層2 Weight」は、層2の10個のパーセプトロンへのweight(10個) の平均値の推移のグラフ。横軸はミニバッチ回数、縦軸はWeight値。振動していれば学習の進行中で、横線(振動がない)状態はdying 状態。
- 「③層2 Bias」は、層2の10個のパーセプトロンへの Bias 値の推移のグラフ。横軸はミニバッチ回数、縦軸はBiasの値。
- 「④層1 Weight]は、層1の64個のパーセプトロン中の10個に注目し、各注目パーセプトロンへのWeight(768個)の平均値の推移のグラフ。横軸はミニバッチ回数、縦軸はWeight値。振動していれば学習の進行中で、横線(振動がない)状態はdying 状態。
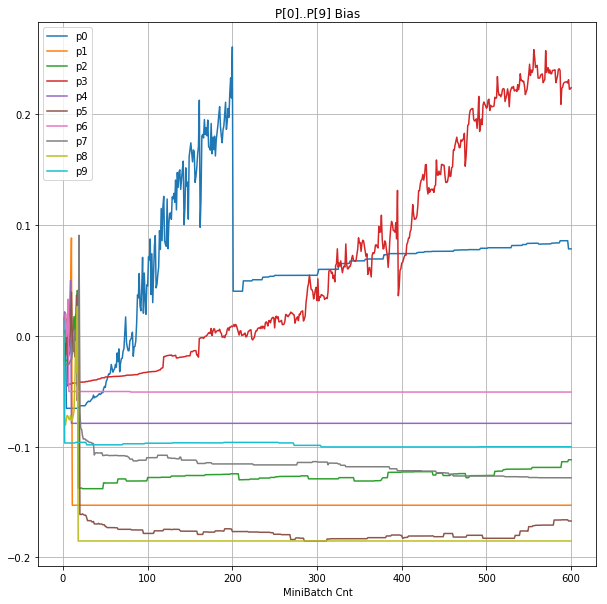
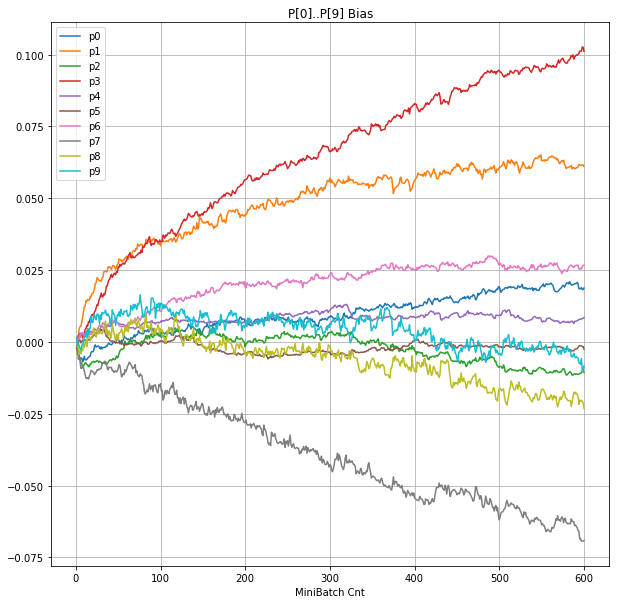
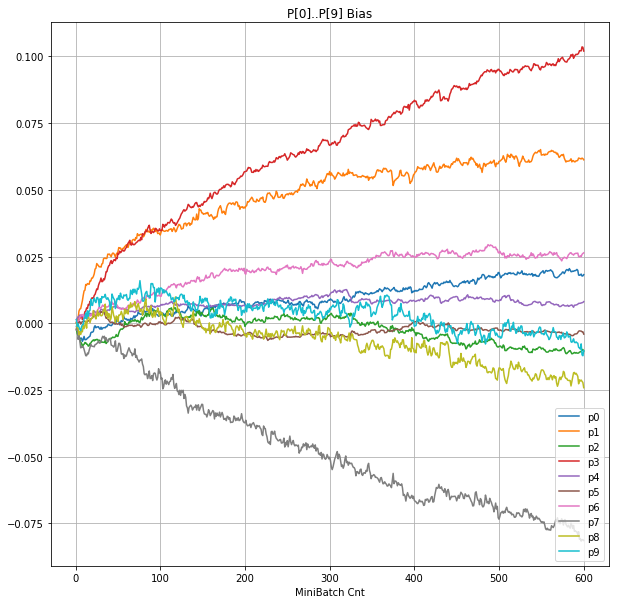
- 「⑤層1 Bias」は、④で注目したパーセプトロンへの Bias 値の推移のグラフ。横軸はミニバッチ回数、縦軸はBiasの値。
グラフ
(クリックすると拡大します)
| 学習率 | 0.05 | 0.01 | 0.001 |
|---|---|---|---|
| 備考 | 全滅 | 約半数がdying | 順調 |
| ①学習時正解率 | 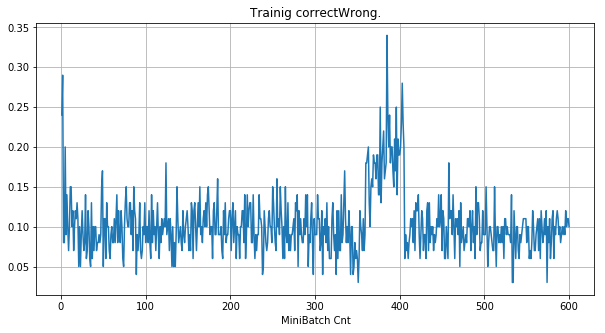 |
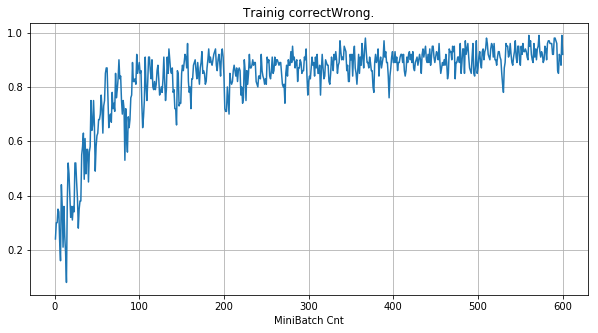 |
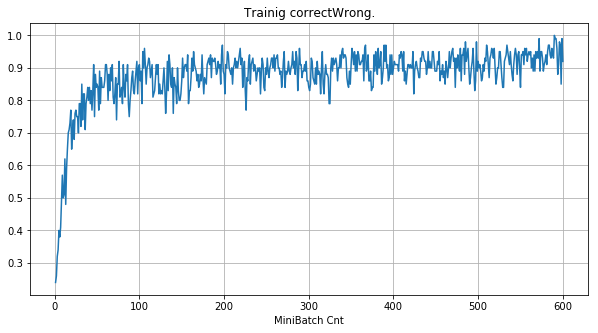 |
| ②層2 Weight | 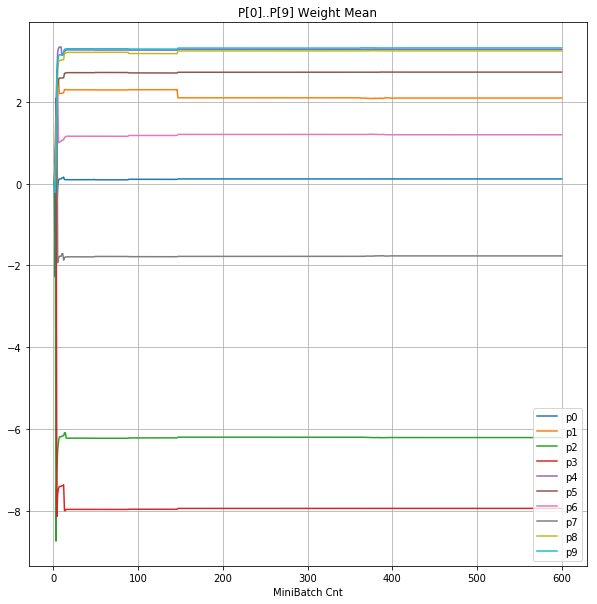 |
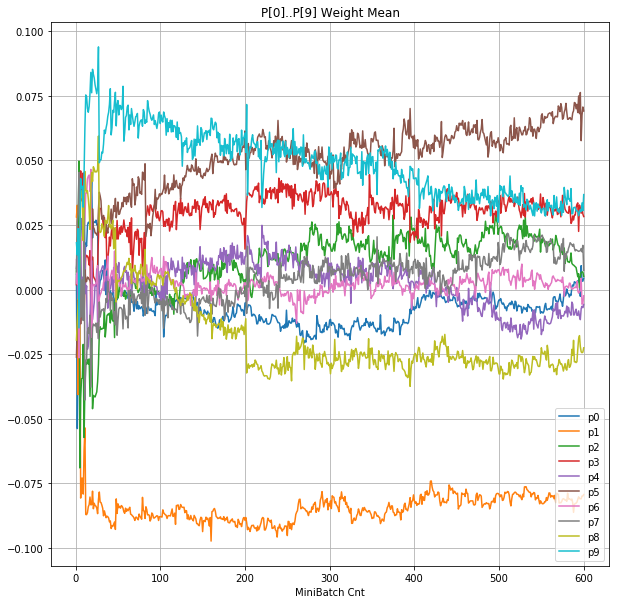 |
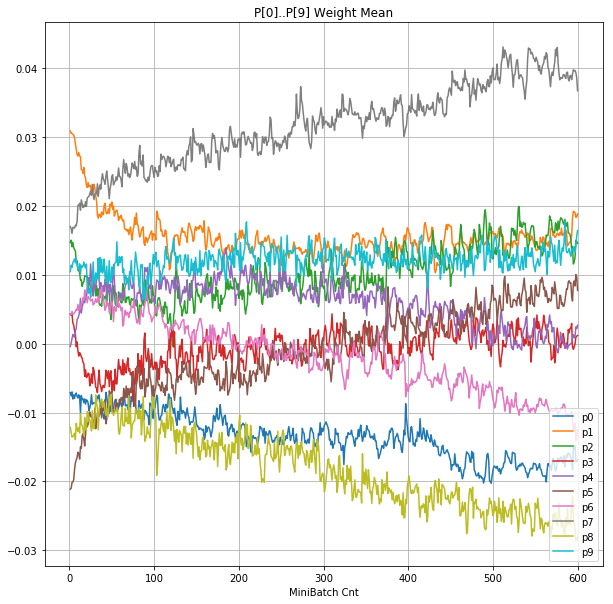 |
| ③層2 Bias | 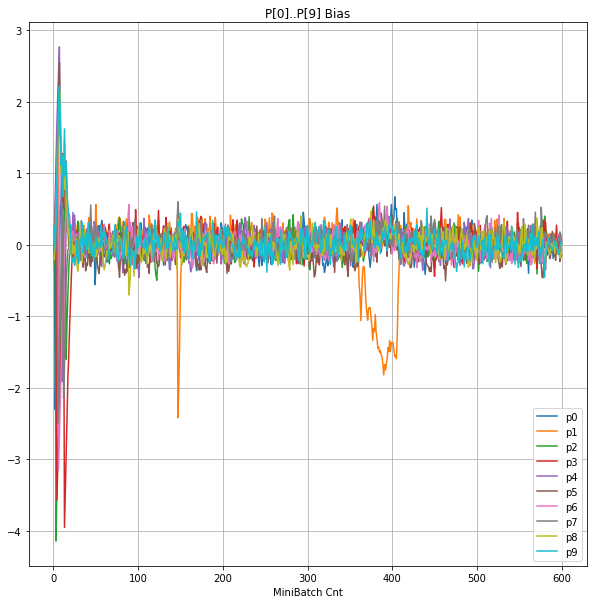 |
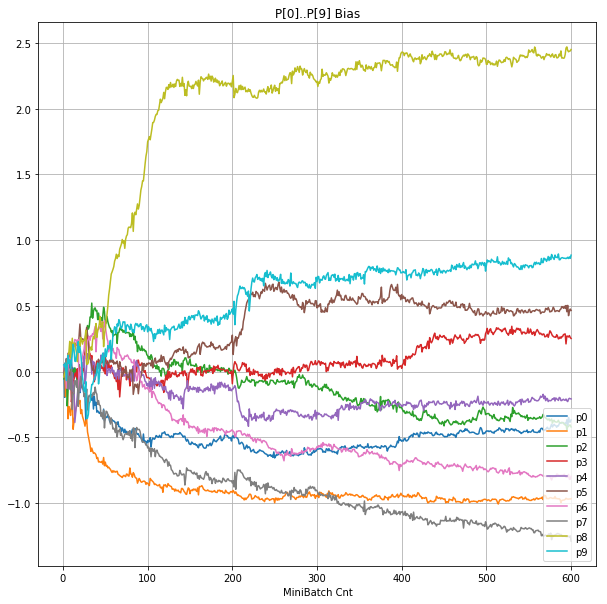 |
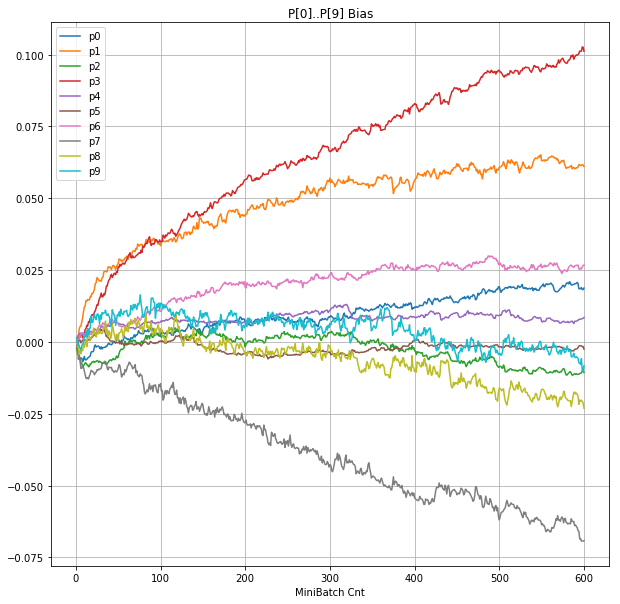 |
| ④層1 Weight | 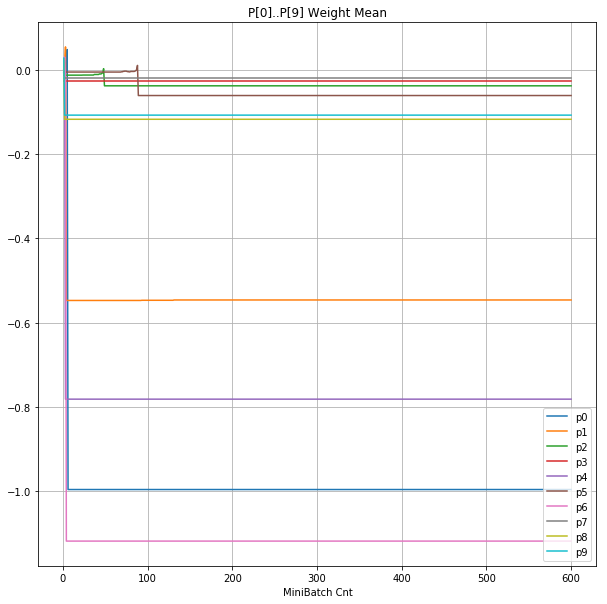 |
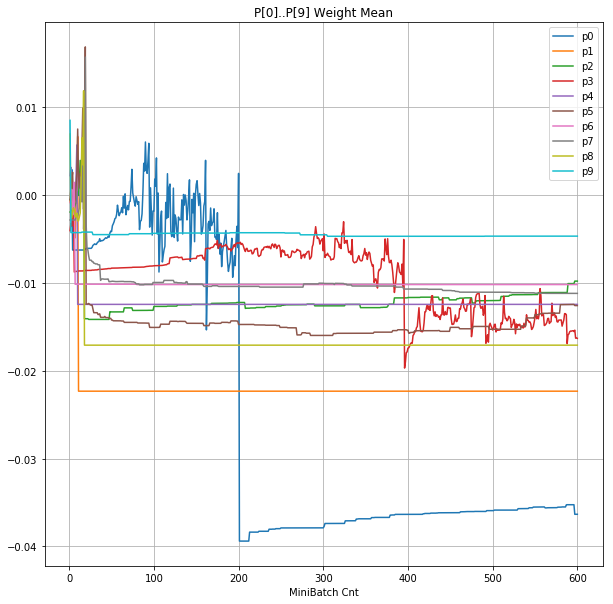 |
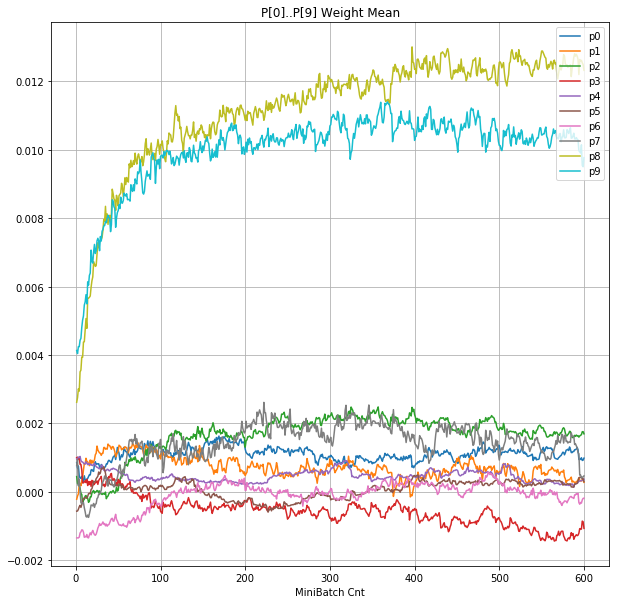 |
| ⑤層1 Bias | 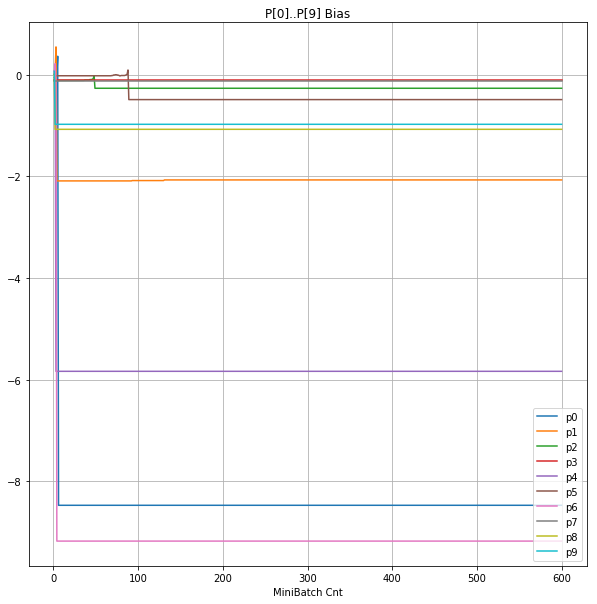 |
 |
 |
グラフから読み取ったこと
- 学習率 0.05 の時には 全数が、学習率 0.01 の時には半数が、無反応のパーセプトロン(dying ReLU)と化している。
- Bias と Weight がともに負に振れる→ReLUでの活性化がなくなる→逆伝播もなくなる→変化がなくなる(dying)。の過程が見えた。
Leaky ReLU
NNの構成とパラメータ
- 乱数種値は 20170523 固定
- 学習率3つで比較。「値が発散して失敗する場合」と その近傍で「ギリギリ発散しない値」 と 「順調に学習が進む」 とで比較する。
- ミニバッチ600回 (1 epoche) 期間での測定。
- ②と④ の 学習率 0.057 のグラフの縦軸は 対数。(対数グラフには絶対値をプロット)
- 他は ReLU の場合と同じ。
グラフ
| 学習率 | 0.057 | 0.056 | 0.001 |
|---|---|---|---|
| 備考 | 発散 | きわどい | 順調 |
| ①学習時正解率 | 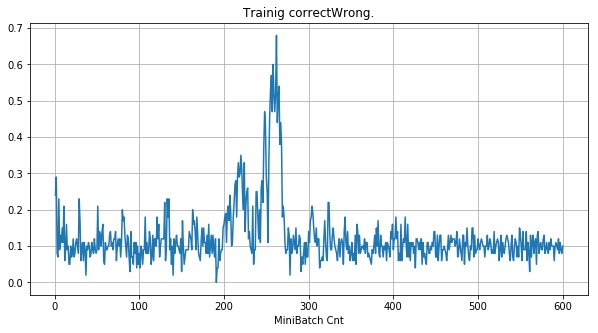 |
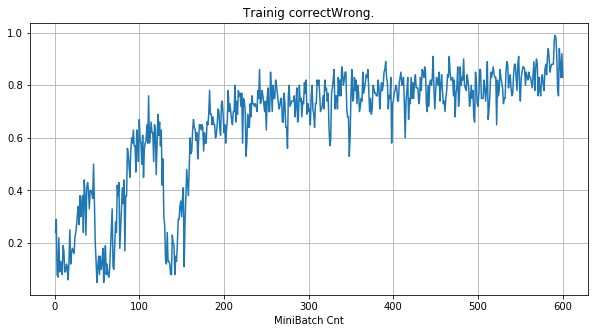 |
 |
| ②層2 Weight | 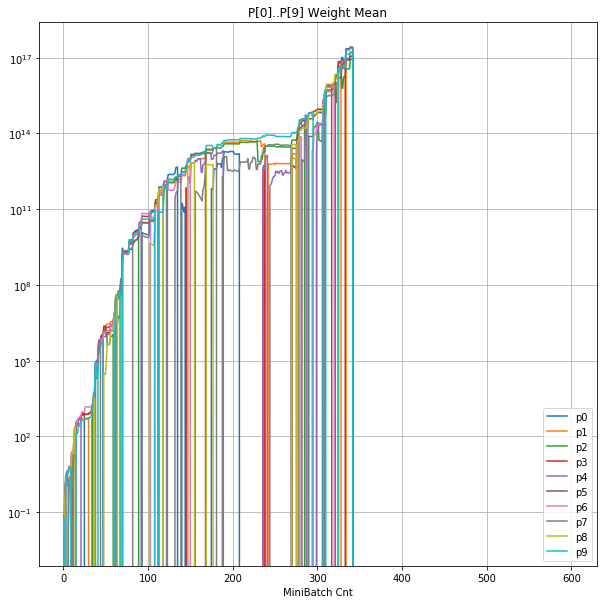 |
 |
 |
| ③層2 Bias | 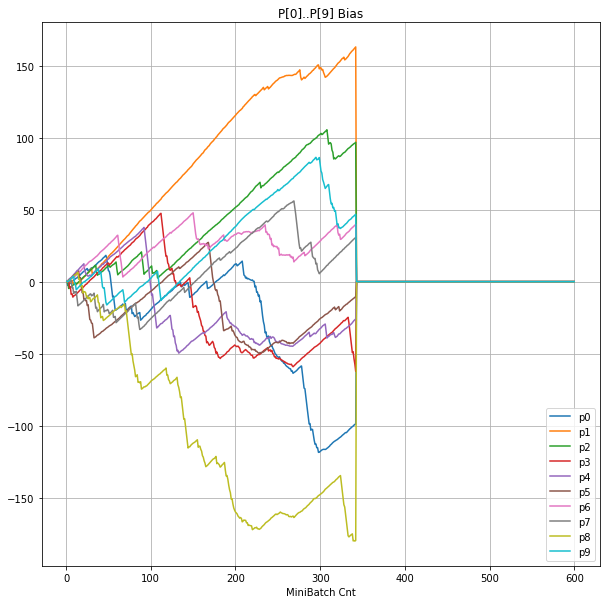 |
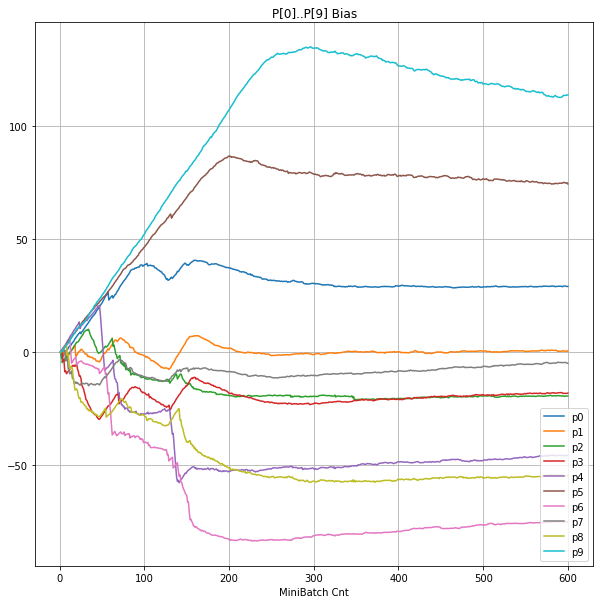 |
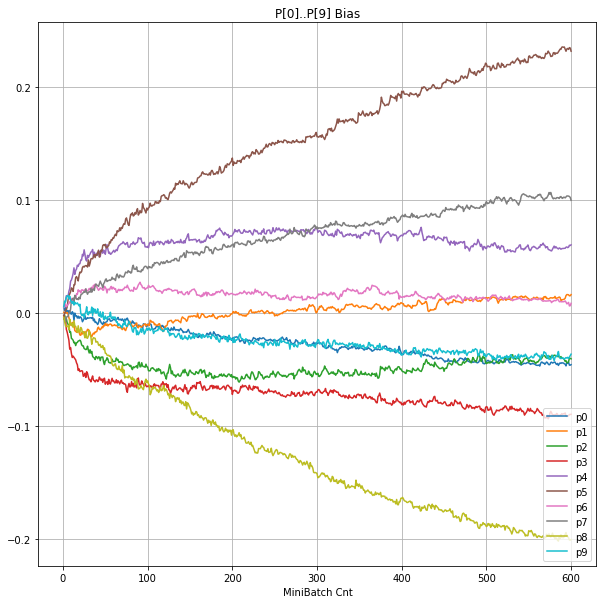 |
| ④層1 Weight | 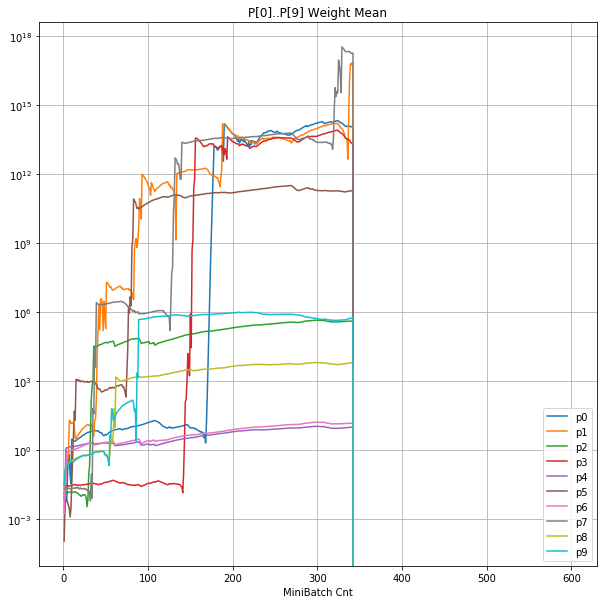 |
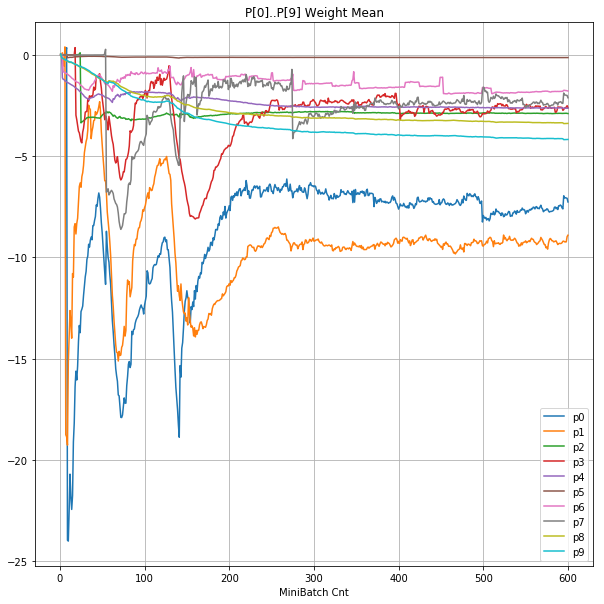 |
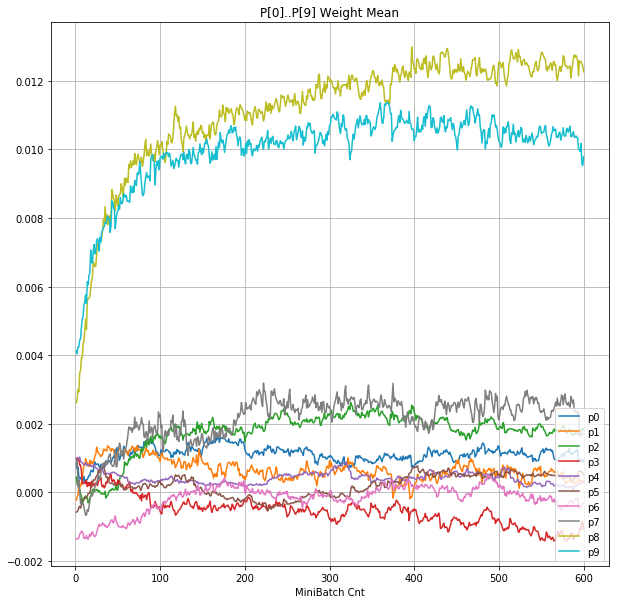 |
| ⑤層1 Bias | 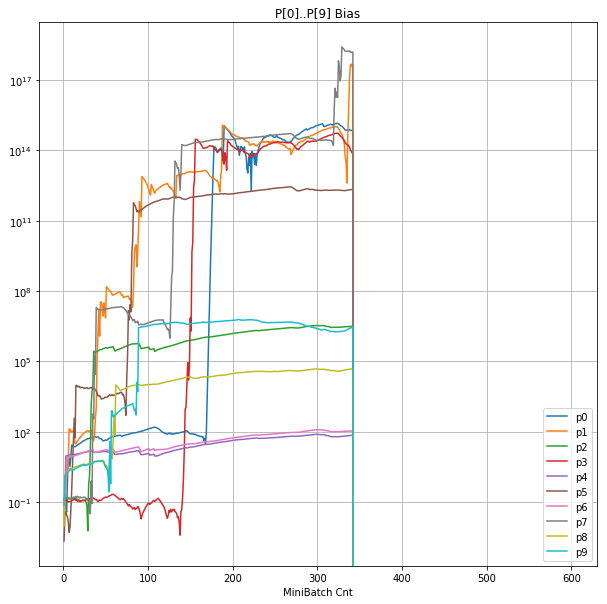 |
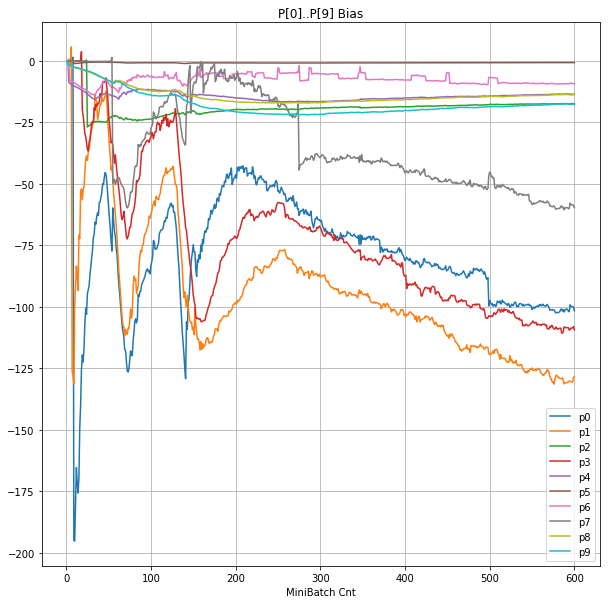 |
 |
- 学習率0.057 は、ミニバッチ回数350以降は 無効数値(nan)化し、無意味な計算をおこなっている。
グラフから読み取ったこと
- Bias と Weight が負に振れた後も、負側でも逆伝播はあり、値は変化していっている。
- 学習率0.057 の層1にて、Bias と Weight が 正負を繰り返しながら発散する状況が見れた。
- あるパーセプトロンで発散が始まると、他のパーセプトロンにも影響あたえ発散させていく。
Batch Normalization + ReLU
NNの構成とパラメータ
- 乱数種値は 20170523 固定
- 学習率3つで比較。「ReLUで学習失敗した値」と それより10倍大きい「無茶そうな値」 と 「順調に学習が進みそうな値」を用いる。
- 他は、ReLUの時と同様。
グラフ
| 学習率 | 0.5 | 0.05 | 0.01 |
|---|---|---|---|
| ①学習時正解率 | 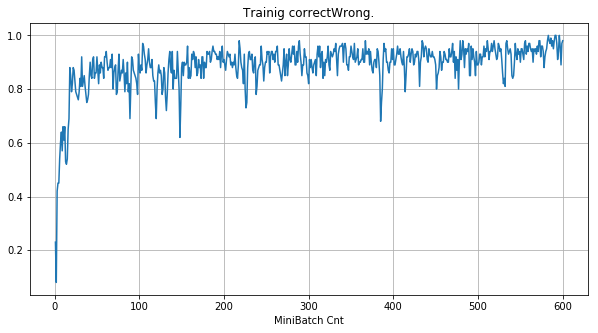 |
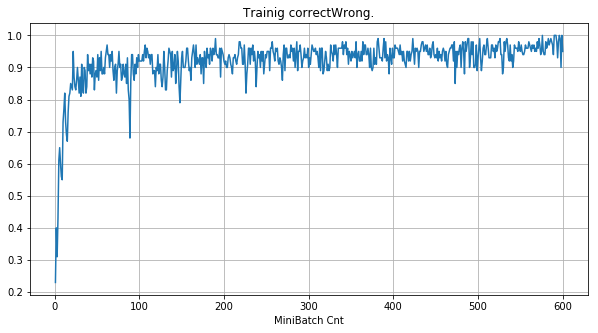 |
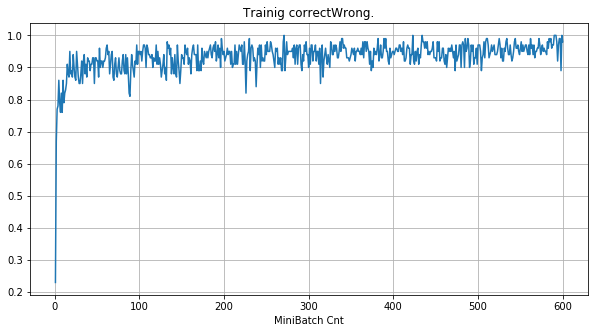 |
| ②層2 Weight | 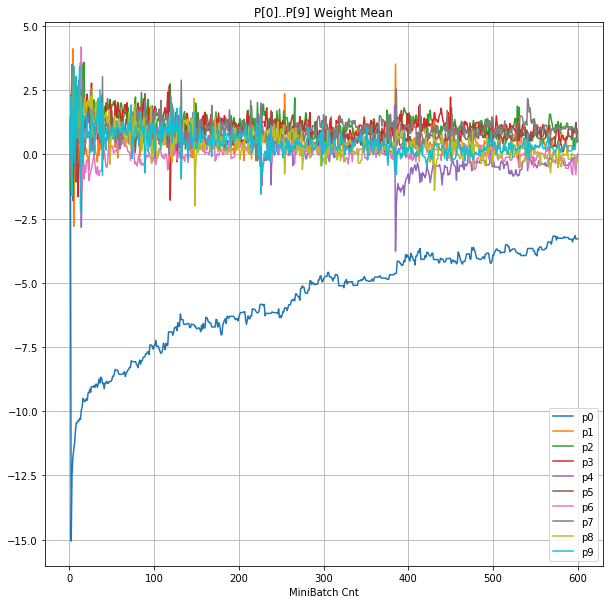 |
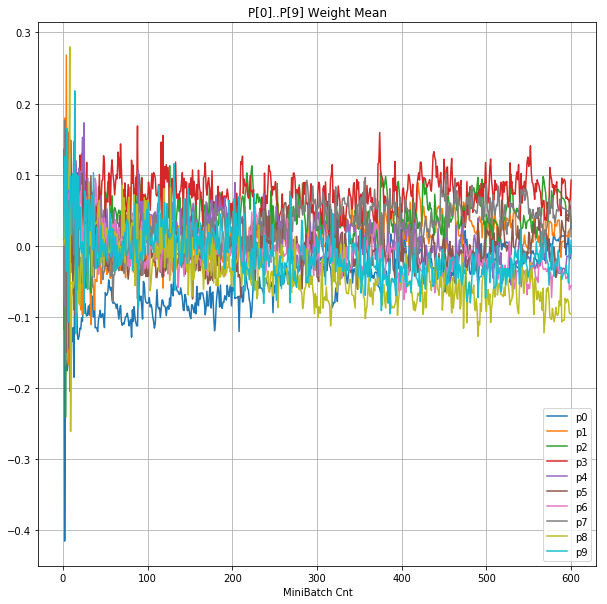 |
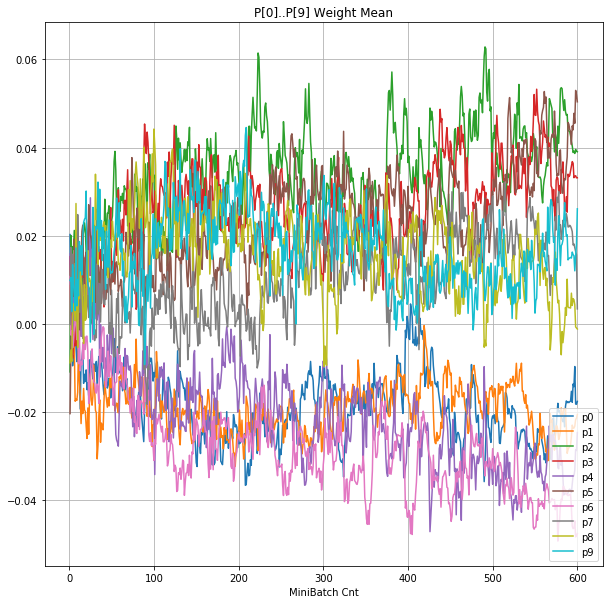 |
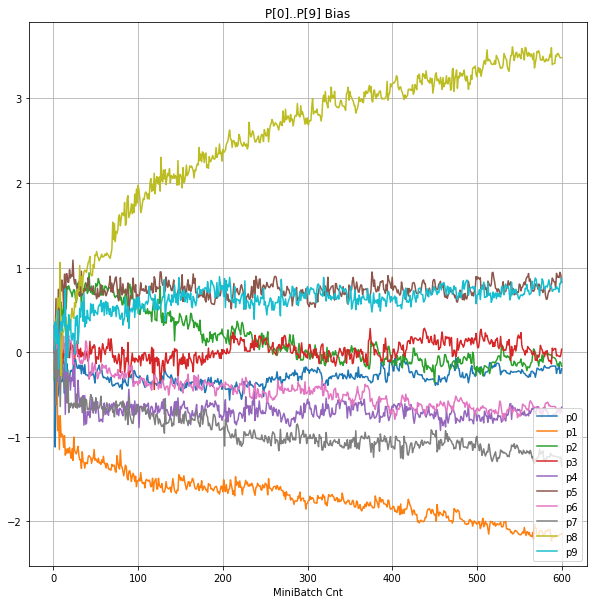
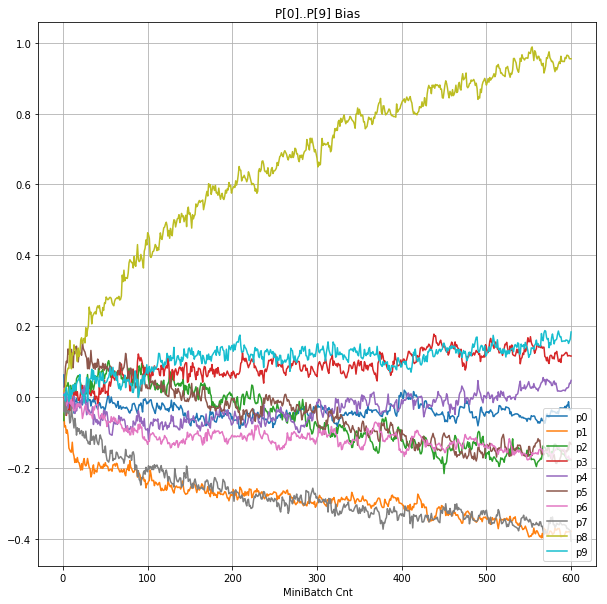
| ③層2 Bias | 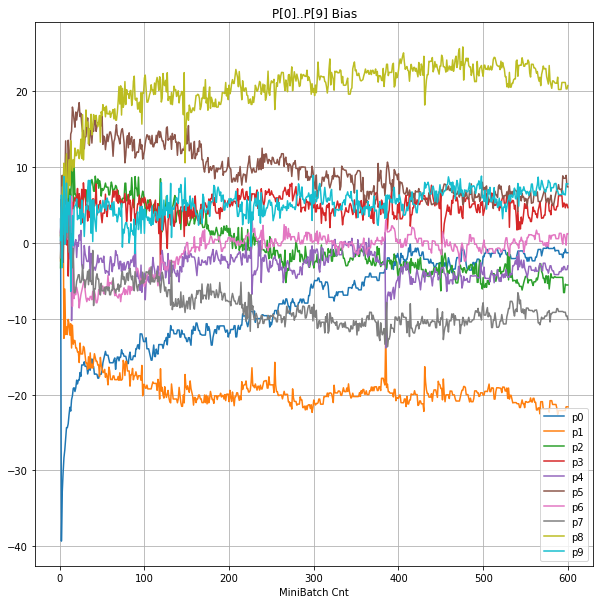 |
 |
 |
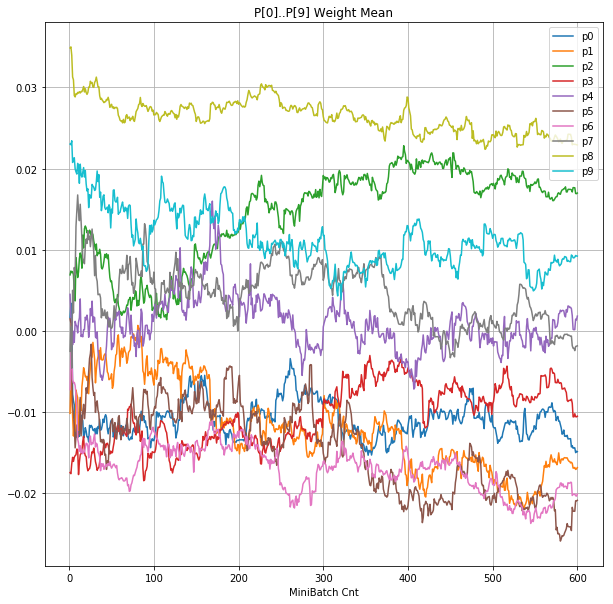
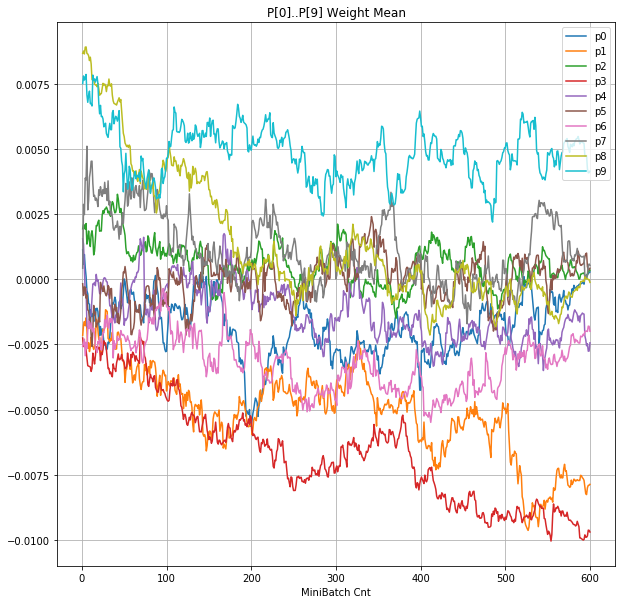
| ④層1 Weight | 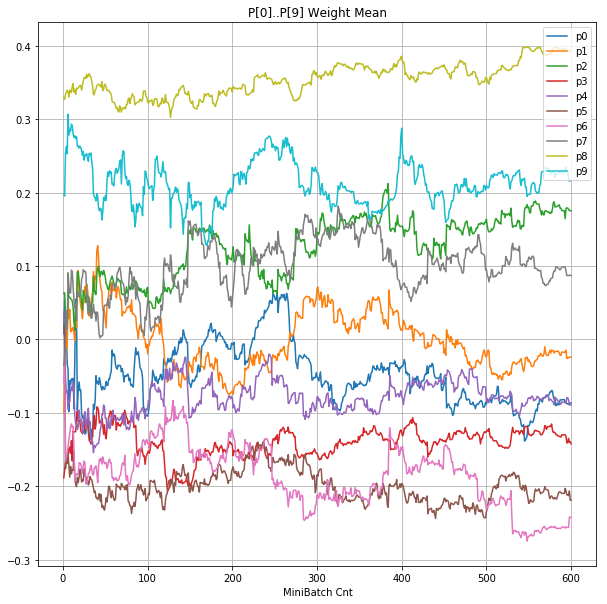 |
 |
 |
| ⑤層1 Bias | 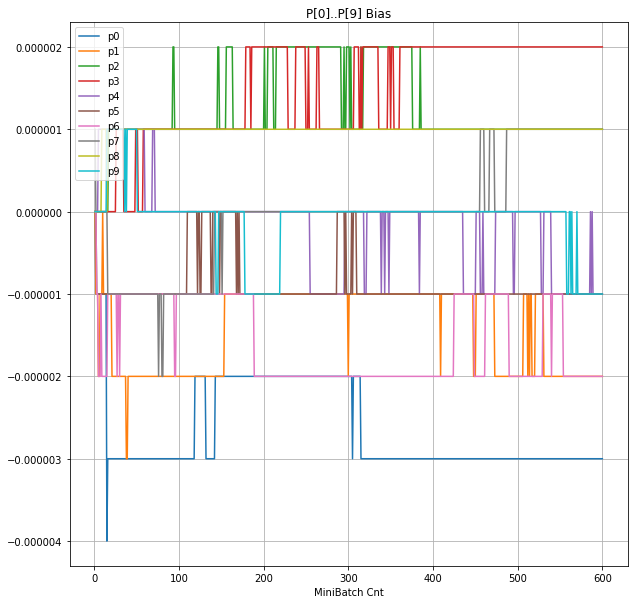 |
 |
 |
グラフから読み取ったこと
(Batch Normarizationについては このリンク先の記事も参考になれば幸いです )
- 学習率 0.5 (ReLU で 学習失敗を確認した値の10倍)でも、学習は進んでいるように見える。
- BN は順伝播時には、正規化した値を次層に伝達する。
- BNは逆伝播も平均を0にする→ ΔBiasは逆伝播の合計のため0になる → Bias 変動なし。
- ↑の特性により、発散しにくく、WeightとBiasがそろって負に偏ることもなりにくく、大きい学習率でも、学習が進むみたい。