はじめに
ふと思い立って勉強を始めた「ゼロから作るDeep LearningーーPythonで学ぶディープラーニングの理論と実装」の7章で私がつまずいたことのメモです。
実行環境はmacOS Mojave + Anaconda 2019.10、Pythonのバージョンは3.7.4です。詳細はこのメモの1章をご参照ください。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
この記事は個人で作成したものであり、内容や意見は所属企業・部門見解を代表するものではありません。
7章 畳み込みニューラルネットワーク
この章は、畳み込みニューラルネットワーク(CNN)の説明です。
7.1 全体の構造
これまでのAffineレイヤーやSoftmaxレイヤー、ReLUレイヤーに加えて、Convolution(畳み込み、コンボリューション)レイヤーとPooling(プーリング)レイヤーが出てくる説明です。
7.2 畳み込み層
畳み込み層の説明は、画像処理を少しかじっておいた方が読みやすいです。
「画像は通常、縦・横・チャンネル方向の3次元の形状です」とありますが、画像は縦・横の2Dデータですから、3次元だと奥行きまで加わった3Dデータになるのでは?と思われる方もいるも知れません。
ここでの「チャンネル」というのは、RGBなどの色ごとの情報を指しています。MNISTのようなグレースケール(白黒の濃淡のみ)のデータであれば1つの点の濃さを1つの値で表現できるので1チャンネルで済みますが、カラー画像では1つの点を赤・緑・青(RGB)の3つの値の濃さで表現するので3チャンネル必要というわけです。なお、カラー情報のチャンネルはRGBだけでなく、CMYKやHSV、さらに透明度のアルファを加えたものなどがあります。詳細は「RGB CMYK」などでググるとたくさん解説が出てきます(ちょっと印刷寄りの話が多いですが)。
あと、「フィルター」という言葉も特殊で、画像処理では画像に対して必要部分(例えば輪郭)だけを抽出したり不要な情報を除去したりする時に使う処理を指します。ピンとこない方は、画像処理における畳み込みフィルターの概要を把握すると理解しやすくなるかと思います。@t-tkd3a さんの 3x3 畳み込みフィルタ 結果画像 がイメージしやすくてお勧めです。
余談ですが、この本は「レイヤ」のように3音以上のカタカナでは長音表記を付けないルールのようです。でも「フィルター」には長音表記が付いていますので統一漏れかも知れません。そういえばマイクロソフトが2008年にカタカナの長音表記の方法を切り替えた時1、ちょうど私はWindows用のパッケージ アプリケーションの開発を担当していて、プログラムやらマニュアルやらの文言を直して回るのが大変でした。さらにその前は、Windows 98でGUIから半角カナをなくしたのにも巻き込まれたな…… この業界、ホント日本語は不便です![]()
話を戻して、先に進みます。
7.3 プーリング層
プーリング層については、特につまずくところはありませんでした。
7.4 Convolution/Pooling レイヤの実装
Convolutionレイヤー と Pooling レイヤーの実装は、コードは短いのですが、im2colやnumpy.ndarray.reshapeやnumpy.ndarray.transposeで対象データの形状がどんどん変わるので複雑です。最初は混乱しまくりでしたが、@daizutabi さんの 「ゼロから作るDeep Learning」 Convolution/Poolingレイヤの実装 を参考に理解できました。
まず、Convolutionレイヤーの実装です。形状を書いておかないと私の頭が付いていかないので、コメントはかなり多めです。
# coding: utf-8
import os
import sys
import numpy as np
sys.path.append(os.pardir) # パスに親ディレクトリ追加
from common.util import im2col, col2im
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
"""Convolutionレイヤー
Args:
W (numpy.ndarray): フィルター(重み)、形状は(FN, C, FH, FW)。
b (numpy.ndarray): バイアス、形状は(FN)。
stride (int, optional): ストライド、デフォルトは1。
pad (int, optional): パディング、デフォルトは0。
"""
self.W = W
self.b = b
self.stride = stride
self.pad = pad
self.dW = None # 重みの微分値
self.db = None # バイアスの微分値
self.x = None # 逆伝播で必要になる、順伝播時の入力
self.col_x = None # 逆伝播で必要になる、順伝播時の入力のcol展開結果
self.col_W = None # 逆伝播で必要になる、順伝播時のフィルターのcol展開結果
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力。形状は(N, C, H, W)。
Returns:
numpy.ndarray: 出力。形状は(N, FN, OH, OW)。
"""
FN, C, FH, FW = self.W.shape # FN:フィルター数、C:チャンネル数、FH:フィルターの高さ、FW:幅
N, x_C, H, W = x.shape # N:バッチサイズ、x_C:チャンネル数、H:入力データの高さ、W:幅
assert C == x_C, f'チャンネル数の不一致![C]{C}, [x_C]{x_C}'
# 出力のサイズ算出
assert (H + 2 * self.pad - FH) % self.stride == 0, 'OHが割り切れない!'
assert (W + 2 * self.pad - FW) % self.stride == 0, 'OWが割り切れない!'
OH = int((H + 2 * self.pad - FH) / self.stride + 1)
OW = int((W + 2 * self.pad - FW) / self.stride + 1)
# 入力データを展開
# (N, C, H, W) → (N * OH * OW, C * FH * FW)
col_x = im2col(x, FH, FW, self.stride, self.pad)
# フィルターを展開
# (FN, C, FH, FW) → (C * FH * FW, FN)
col_W = self.W.reshape(FN, -1).T
# 出力を算出(col_x, col_W, bに対する計算は、Affineレイヤーと全く同じ)
# (N * OH * OW, C * FH * FW)・(C * FH * FW, FN) → (N * OH * OW, FN)
out = np.dot(col_x, col_W) + self.b
# 結果の整形
# (N * OH * OW, FN) → (N, OH, OW, FN) → (N, FN, OH, OW)
out = out.reshape(N, OH, OW, FN).transpose(0, 3, 1, 2)
# 逆伝播のために保存
self.x = x
self.col_x = col_x
self.col_W = col_W
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値、形状は(N, FN, OH, OW)。
Returns:
numpy.ndarray: 微分値(勾配)、形状は(N, C, H, W)。
"""
FN, C, FH, FW = self.W.shape # 微分値の形状はWと同じ(FN, C, FH, FW)
# 右の層からの微分値を展開
# (N, FN, OH, OW) → (N, OH, OW, FN) → (N * OH * OW, FN)
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
# 微分値算出(col_x, col_W, bに対する計算は、Affineレイヤーと全く同じ)
dcol_x = np.dot(dout, self.col_W.T) # → (N * OH * OW, C * FH * FW)
self.dW = np.dot(self.col_x.T, dout) # → (C * FH * FW, FN)
self.db = np.sum(dout, axis=0) # → (FN)
# フィルター(重み)の微分値の整形
# (C * FH * FW, FN) → (FN, C * FH * FW) → (FN, C, FH, FW)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
# 結果(勾配)の整形
# (N * OH * OW, C * FH * FW) → (N, C, H, W)
dx = col2im(dcol_x, self.x.shape, FH, FW, self.stride, self.pad)
return dx
続いてPoolingレイヤーの実装です。こちらもコメントだらけです。
# coding: utf-8
import os
import sys
import numpy as np
sys.path.append(os.pardir) # パスに親ディレクトリ追加
from common.util import im2col, col2im
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
"""Poolingレイヤー
Args:
pool_h (int): プーリング領域の高さ
pool_w (int): プーリング領域の幅
stride (int, optional): ストライド、デフォルトは1。
pad (int, optional): パディング、デフォルトは0。
"""
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None # 逆伝播で必要になる、順伝播時の入力
self.arg_max = None # 逆伝播で必要になる、順伝播時に採用したcol_x各行の位置
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力、形状は(N, C, H, W)。
Returns:
numpy.ndarray: 出力、形状は(N, C, OH, OW)。
"""
N, C, H, W = x.shape # N:データ数、C:チャンネル数、H:高さ、W:幅
# 出力のサイズ算出
assert (H - self.pool_h) % self.stride == 0, 'OHが割り切れない!'
assert (W - self.pool_w) % self.stride == 0, 'OWが割り切れない!'
OH = int((H - self.pool_h) / self.stride + 1)
OW = int((W - self.pool_w) / self.stride + 1)
# 入力データを展開、整形
# (N, C, H, W) → (N * OH * OW, C * PH * PW)
col_x = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# (N * OH * OW, C * PH * PW) → (N * OH * OW * C, PH * PW)
col_x = col_x.reshape(-1, self.pool_h * self.pool_w)
# 出力を算出
# (N * OH * OW * C, PH * PW) → (N * OH * OW * C)
out = np.max(col_x, axis=1)
# 結果の整形
# (N * OH * OW * C) → (N, OH, OW, C) → (N, C, OH, OW)
out = out.reshape(N, OH, OW, C).transpose(0, 3, 1, 2)
# 逆伝播のために保存
self.x = x
self.arg_max = np.argmax(col_x, axis=1) # col_x各行の最大値の位置(インデックス)
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値、形状は(N, C, OH, OW)。
Returns:
numpy.ndarray: 微分値(勾配)、形状は(N, C, H, W)。
"""
# 右の層からの微分値を整形
# (N, C, OH, OW) → (N, OH, OW, C)
dout = dout.transpose(0, 2, 3, 1)
# 結果の微分値用のcolを0で初期化
# (N * OH * OW * C, PH * PW)
pool_size = self.pool_h * self.pool_w
dcol_x = np.zeros((dout.size, pool_size))
# 順伝播時に最大値として採用された位置にだけ、doutの微分値(=doutまんま)をセット
# 順伝播時に採用されなかった値の位置は初期化時の0のまま
# (ReLUでxが0より大きい場合およびxが0以下の場合の処理と同じ)
assert dout.size == self.arg_max.size, '順伝搬時のcol_xの行数と合わない'
dcol_x[np.arange(self.arg_max.size), self.arg_max.flatten()] = \
dout.flatten()
# 結果の微分値の整形1
# (N * OH * OW * C, PH * PW) → (N, OH, OW, C, PH * PW)
dcol_x = dcol_x.reshape(dout.shape + (pool_size,)) # 最後の','は1要素のタプルを示す
# 結果の微分値の整形2
# (N, OH, OW, C, PH * PW) → (N * OH * OW, C * PH * PW)
dcol_x = dcol_x.reshape(
dcol_x.shape[0] * dcol_x.shape[1] * dcol_x.shape[2], -1
)
# 結果の微分値の整形3
# (N * OH * OW, C * PH * PW) → (N, C, H, W)
dx = col2im(
dcol_x, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad
)
return dx
7.5 CNNの実装
これまでの実装を組み合わせてCNNを実装します。
(1)各レイヤーの実装
まず、今回のネットワークにおける入出力の整理です。
| レイヤー | 入出力の形状 | 実装時の形状 |
|---|---|---|
| $ (バッチサイズN, チャンネル数CH, 画像の高さH, 幅W) $ | $ (100, 1, 28, 28) $ | |
|
|
↓ | |
| $ (バッチサイズN, フィルター数FN, 出力の高さOH, 幅OW) $ | $ (100, 30, 24, 24) $ | |
|
|
↓ | |
| $ (バッチサイズN, フィルター数FN, 出力の高さOH, 幅OW) $ | $ (100, 30, 24, 24) $ | |
|
|
↓ | |
| $ (バッチサイズN, フィルター数FN, 出力の高さOH, 幅OW) $ | $ (100, 30, 12, 12) $ | |
|
|
↓ | |
| $ (バッチサイズN, 隠れ層のサイズ) $ | $ (100, 100) $ | |
|
|
↓ | |
| $ (バッチサイズN, 隠れ層のサイズ) $ | $ (100, 100) $ | |
|
|
↓ | |
| $ (バッチサイズN, 最終出力サイズ) $ | $ (100, 10) $ | |
|
|
↓ | |
| $ (バッチサイズN, 最終出力サイズ) $ | $ (100, 10) $ |
ConvlolutionレイヤーとPoolingレイヤーの実装は前述の通りです。
Affineレイヤーは以前の実装に少し修正が必要です。以前 5.6.2 バッチ版Affineレイヤ で実装した時は入力が2次元( $バッチサイズN$, 画像サイズ)だったのですが、今回、4番目のAffineレイヤーは入力が4次元(バッチ数 $N$ , フィルター数 $FN$ , Pooling結果の $OH$ , $OW$)になるので、その対応が必要です。本のP.152で「なお、common/layers.pyにあるAffineの実装は、入力データがテンソル(4次元のデータ)の場合も考慮した実装であり」との但し書きがあって、なんのことか分からず放置していたのですが、今回使うことを想定していたということですね。
以下、3次元以上の入力にも対応したAffineレイヤーの実装です。
# coding: utf-8
import numpy as np
class Affine:
def __init__(self, W, b):
"""Affineレイヤー
Args:
W (numpy.ndarray): 重み
b (numpy.ndarray): バイアス
"""
self.W = W # 重み
self.b = b # バイアス
self.x = None # 入力(2次元化後)
self.dW = None # 重みの微分値
self.db = None # バイアスの微分値
self.original_x_shape = None # 元の入力の形状(3次元以上の入力時用)
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
# 3次元以上(テンソル)の入力を2次元化
self.original_x_shape = x.shape # 形状を保存、逆伝播で戻す必要があるので
x = x.reshape(x.shape[0], -1)
self.x = x
# 出力を算出
out = np.dot(x, self.W) + self.b
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値
Returns:
numpy.ndarray: 微分値
"""
# 微分値算出
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
# 元の形状に戻す
dx = dx.reshape(*self.original_x_shape)
return dx
ReLUレイヤーとSoftmaxレイヤーは以前の実装と変わりませんが、再掲します。
# coding: utf-8
class ReLU:
def __init__(self):
"""ReLUレイヤー
"""
self.mask = None
def forward(self, x):
"""順伝播
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
self.mask = (x <= 0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
"""逆伝播
Args:
dout (numpy.ndarray): 右の層から伝わってくる微分値
Returns:
numpy.ndarray: 微分値
"""
dout[self.mask] = 0
dx = dout
return dx
# coding: utf-8
from functions import softmax, cross_entropy_error
class SoftmaxWithLoss:
def __init__(self):
"""Softmax-with-Lossレイヤー
"""
self.loss = None # 損失
self.y = None # softmaxの出力
self.t = None # 教師データ(one-hot vector)
def forward(self, x, t):
"""順伝播
Args:
x (numpy.ndarray): 入力
t (numpy.ndarray): 教師データ
Returns:
float: 交差エントロピー誤差
"""
self.t = t
self.y = softmax(x)
self.loss = cross_entropy_error(self.y, self.t)
return self.loss
def backward(self, dout=1):
"""逆伝播
Args:
dout (float, optional): 右の層から伝わってくる微分値。デフォルトは1。
Returns:
numpy.ndarray: 微分値
"""
batch_size = self.t.shape[0] # バッチの個数
dx = (self.y - self.t) * (dout / batch_size)
return dx
softmaxレイヤーの実装で必要な関数も、以前の通りですが再掲します。なお、今回使わない関数は削っています。
# coding: utf-8
import numpy as np
def softmax(x):
"""ソフトマックス関数
Args:
x (numpy.ndarray): 入力
Returns:
numpy.ndarray: 出力
"""
# バッチ処理の場合xは(バッチの数, 10)の2次元配列になる。
# この場合、ブロードキャストを使ってうまく画像ごとに計算する必要がある。
# ここでは1次元でも2次元でも共通化できるようnp.max()やnp.sum()はaxis=-1で算出し、
# そのままブロードキャストできるようkeepdims=Trueで次元を維持する。
c = np.max(x, axis=-1, keepdims=True)
exp_a = np.exp(x - c) # オーバーフロー対策
sum_exp_a = np.sum(exp_a, axis=-1, keepdims=True)
y = exp_a / sum_exp_a
return y
def cross_entropy_error(y, t):
"""交差エントロピー誤差の算出
Args:
y (numpy.ndarray): ニューラルネットワークの出力
t (numpy.ndarray): 正解のラベル
Returns:
float: 交差エントロピー誤差
"""
# データ1つ場合は形状を整形(1データ1行にする)
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 誤差を算出してバッチ数で正規化
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
(2)オプティマイザーの実装
パラメーターを最適化するオプティマイザーについては、6.1 パラメータの更新 を読んだだけで実装をサボっていたので、今回使うことにした AdaGrad を実装してみました。ほぼ本のコードと同じです。
# coding: utf-8
import numpy as np
class AdaGrad:
def __init__(self, lr=0.01):
"""AdaGradによるパラメーターの最適化
Args:
lr (float, optional): 学習係数、デフォルトは0.01。
"""
self.lr = lr
self.h = None # これまでの勾配の2乗和
def update(self, params, grads):
"""パラメーター更新
Args:
params (dict): 更新対象のパラメーターの辞書、keyは'W1'、'b1'など。
grads (dict): paramsに対応する勾配の辞書
"""
# hの初期化
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
# 更新
for key in params.keys():
# hの更新
self.h[key] += grads[key] ** 2
# パラメーター更新、最後の1e-7は0除算回避
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
(3)CNNの実装
CNNは、以前 5.7.2 誤差逆伝播法に対応したニューラルネットワークの実装 で作ったTwoLayerNetをベースに、本の説明に従って実装しました。
なお、本のコードではOrderedDictを使っていますが、前回同様、ここでは通常のdictを使っています。Python 3.7からはdictオブジェクトの挿入順序が保存されるようになった2ためです。あと、accuracyの実装でつまずいたので後述します。
以下、CNNの実装です。
# coding: utf-8
import numpy as np
from affine import Affine
from convolution import Convolution
from pooling import Pooling
from relu import ReLU
from softmax_with_loss import SoftmaxWithLoss
class SimpleConvNet:
def __init__(
self, input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01
):
"""シンプルな畳み込みニューラルネットワーク
Args:
input_dim (tuple, optional): 入力データの形状、デフォルトは(1, 28, 28)。
conv_param (dict, optional): 畳み込み層のハイパーパラメーター、
デフォルトは{'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1}。
hidden_size (int, optional): 隠れ層のニューロンの数、デフォルトは100。
output_size (int, optional): 出力層のニューロンの数、デフォルトは10。
weight_init_std (float, optional): 重みの初期値の調整パラメーター。デフォルトは0.01。
"""
# 畳み込み層のハイパーパラメーター取り出し
filter_num = conv_param['filter_num'] # フィルター数
filter_size = conv_param['filter_size'] # フィルターのサイズ(高さ・幅同じ)
filter_stride = conv_param['stride'] # ストライド
filter_pad = conv_param['pad'] # パディング
# プーリング層のハイパーパラメーターは固定
pool_size = 2 # サイズ(高さ・幅同じ)
pool_stride = 2 # ストライド
pool_pad = 0 # パディング
# 入力データのサイズ算出
input_ch = input_dim[0] # 入力データのチャンネル数
assert input_dim[1] == input_dim[2], '入力データは高さと幅が同じ前提!'
input_size = input_dim[1] # 入力データのサイズ
# 畳み込み層の出力サイズ算出
assert (input_size + 2 * filter_pad - filter_size) \
% filter_stride == 0, '畳み込み層の出力サイズが割り切れない!'
conv_output_size = int(
(input_size + 2 * filter_pad - filter_size) / filter_stride + 1
)
# プーリング層の出力サイズ算出
assert (conv_output_size - pool_size) % pool_stride == 0, \
'プーリング層の出力サイズが割り切れない!'
pool_output_size_one = int(
(conv_output_size - pool_size) / pool_stride + 1 # 高さ・幅のサイズ
)
pool_output_size = filter_num * \
pool_output_size_one * pool_output_size_one # 全フィルターの合計サイズ
# 重みの初期化
self.params = {}
# 畳み込み層
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_ch, filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
# Affine層1
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
# Affine層2
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤー生成
self.layers = {} # Python 3.7からは辞書の格納順が保持されるので、OrderedDictは不要
# 畳み込み層
self.layers['Conv1'] = Convolution(
self.params['W1'], self.params['b1'], filter_stride, filter_pad
)
self.layers['Relu1'] = ReLU()
self.layers['Pool1'] = Pooling(
pool_size, pool_size, pool_stride, pool_pad
)
# Affine層1
self.layers['Affine1'] = \
Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = ReLU()
# Affine層2
self.layers['Affine2'] = \
Affine(self.params['W3'], self.params['b3'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
"""ニューラルネットワークによる推論
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
Returns:
numpy.ndarray: ニューラルネットワークの出力
"""
# レイヤーを順伝播
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""損失関数の値算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
float: 損失関数の値
"""
# 推論
y = self.predict(x)
# Softmax-with-Lossレイヤーの順伝播で算出
loss = self.lastLayer.forward(y, t)
return loss
def accuracy(self, x, t, batch_size=100):
"""認識精度算出
batch_sizeは算出時のバッチサイズ。一度に大量データを算出しようとすると
im2colでメモリを食い過ぎてスラッシングが起きてしまい動かなくなるため、
その回避のためのもの。
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル(one-hot)
batch_size (int), optional): 算出時のバッチサイズ、デフォルトは100。
Returns:
float: 認識精度
"""
# 分割数算出
batch_num = max(int(x.shape[0] / batch_size), 1)
# 分割
x_list = np.array_split(x, batch_num, 0)
t_list = np.array_split(t, batch_num, 0)
# 分割した単位で処理
correct_num = 0 # 正答数の合計
for (sub_x, sub_t) in zip(x_list, t_list):
assert sub_x.shape[0] == sub_t.shape[0], '分割境界がずれた?'
y = self.predict(sub_x)
y = np.argmax(y, axis=1)
t = np.argmax(sub_t, axis=1)
correct_num += np.sum(y == t)
# 認識精度の算出
return correct_num / x.shape[0]
def gradient(self, x, t):
"""重みパラメーターに対する勾配を誤差逆伝播法で算出
Args:
x (numpy.ndarray): ニューラルネットワークへの入力
t (numpy.ndarray): 正解のラベル
Returns:
dictionary: 勾配を格納した辞書
"""
# 順伝播
self.loss(x, t) # 損失値算出のために順伝播する
# 逆伝播
dout = self.lastLayer.backward()
for layer in reversed(list(self.layers.values())):
dout = layer.backward(dout)
# 各レイヤーの微分値を取り出し
grads = {}
grads['W1'] = self.layers['Conv1'].dW
grads['b1'] = self.layers['Conv1'].db
grads['W2'] = self.layers['Affine1'].dW
grads['b2'] = self.layers['Affine1'].db
grads['W3'] = self.layers['Affine2'].dW
grads['b3'] = self.layers['Affine2'].db
return grads
この実装でつまずいたのは、本では説明が省略されているaccuracyです。
学習中に1エポック単位で認識精度の計算をするのですが、4章で書いたコードでは、訓練データ60,000枚を一気に放り込んで認識精度を求めていました。ただ今回同じことをやるとim2colの展開でメモリを大量消費するらしく、私のメモリ4GBのVMではスラッシング3で止まってしまいます![]()
でも、本のソースだとメモリ消費が少ないままで、私の環境でも普通に動きます。不思議なのでソースを追ってみたところ、内部で分割して処理されていました。というわけで私もマネして内部で分割しています。なお、分割の実装にはnumpy.array_splitを使ってみました。
(4)学習の実装
学習は、以前の5.7.4 誤差逆伝播法を使った学習 をベースに実装しました。以下、何点かポイントです。
- 前回と異なり今回の入力画像は(1, 28, 28)なので、
load_mnistでMNISTのデータを読み込む際にflatten=Falseの指定が必要です。 - ハイパーパラメーターの
learning_rateは、AdaGradのために小さくし、何回か試行して0.06にしました。 - 更新回数はテストデータの認識精度が比較的早く安定するので
6000(10エポック)にしました。 - 前回のソースは更新数の表示が1ズレていて、初回の認識精度の表示も更新前ではなく1回更新後になっていたため修正しました。
以下、学習の実装です。
# coding: utf-8
import os
import sys
import matplotlib.pylab as plt
import numpy as np
from ada_grad import AdaGrad
from simple_conv_net import SimpleConvNet
sys.path.append(os.pardir) # パスに親ディレクトリ追加
from dataset.mnist import load_mnist
# MNISTの訓練データとテストデータ読み込み
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, flatten=False, one_hot_label=True)
# ハイパーパラメーター設定
iters_num = 6000 # 更新回数
batch_size = 100 # バッチサイズ
learning_rate = 0.06 # 学習率、AdaGradを想定
train_size = x_train.shape[0] # 訓練データのサイズ
iter_per_epoch = max(int(train_size / batch_size), 1) # 1エポック当たりの繰り返し数
# シンプルな畳み込みニューラルネットワーク生成
network = SimpleConvNet(
input_dim=(1, 28, 28),
conv_param={'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01
)
# オプティマイザー生成
optimizer = AdaGrad(learning_rate) # AdaGrad
# 学習前の認識精度の確認
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_loss_list = [] # 損失関数の値の推移の格納先
train_acc_list = [train_acc] # 訓練データに対する認識精度の推移の格納先
test_acc_list = [test_acc] # テストデータに対する認識精度の推移の格納先
print(f'学習前 [訓練データの認識精度]{train_acc:.4f} [テストデータの認識精度]{test_acc:.4f}')
# 学習開始
for i in range(iters_num):
# ミニバッチ生成
batch_mask = np.random.choice(train_size, batch_size, replace=False)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 勾配の計算
grads = network.gradient(x_batch, t_batch)
# 重みパラメーター更新
optimizer.update(network.params, grads)
# 損失関数の値算出
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1エポックごとに認識精度算出
if (i + 1) % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
# 経過表示
print(
f'[エポック]{(i + 1) // iter_per_epoch:>2} '
f'[更新数]{i + 1:>5} [損失関数の値]{loss:.4f} '
f'[訓練データの認識精度]{train_acc:.4f} [テストデータの認識精度]{test_acc:.4f}'
)
# 損失関数の値の推移を描画
x = np.arange(len(train_loss_list))
plt.plot(x, train_loss_list, label='loss')
plt.xlabel('iteration')
plt.ylabel('loss')
plt.xlim(left=0)
plt.ylim(0, 2.5)
plt.show()
# 訓練データとテストデータの認識精度の推移を描画
x2 = np.arange(len(train_acc_list))
plt.plot(x2, train_acc_list, label='train acc')
plt.plot(x2, test_acc_list, label='test acc', linestyle='--')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.xlim(left=0)
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
(5)実行結果
以下、実行結果です。私の環境では1時間くらいかかりました。
学習前 [訓練データの認識精度]0.0909 [テストデータの認識精度]0.0909
[エポック] 1 [更新数] 600 [損失関数の値]0.0699 [訓練データの認識精度]0.9784 [テストデータの認識精度]0.9780
[エポック] 2 [更新数] 1200 [損失関数の値]0.0400 [訓練データの認識精度]0.9844 [テストデータの認識精度]0.9810
[エポック] 3 [更新数] 1800 [損失関数の値]0.0362 [訓練データの認識精度]0.9885 [テストデータの認識精度]0.9853
[エポック] 4 [更新数] 2400 [損失関数の値]0.0088 [訓練データの認識精度]0.9907 [テストデータの認識精度]0.9844
[エポック] 5 [更新数] 3000 [損失関数の値]0.0052 [訓練データの認識精度]0.9926 [テストデータの認識精度]0.9851
[エポック] 6 [更新数] 3600 [損失関数の値]0.0089 [訓練データの認識精度]0.9932 [テストデータの認識精度]0.9850
[エポック] 7 [更新数] 4200 [損失関数の値]0.0029 [訓練データの認識精度]0.9944 [テストデータの認識精度]0.9865
[エポック] 8 [更新数] 4800 [損失関数の値]0.0023 [訓練データの認識精度]0.9954 [テストデータの認識精度]0.9873
[エポック] 9 [更新数] 5400 [損失関数の値]0.0051 [訓練データの認識精度]0.9959 [テストデータの認識精度]0.9860
[エポック]10 [更新数] 6000 [損失関数の値]0.0037 [訓練データの認識精度]0.9972 [テストデータの認識精度]0.9860
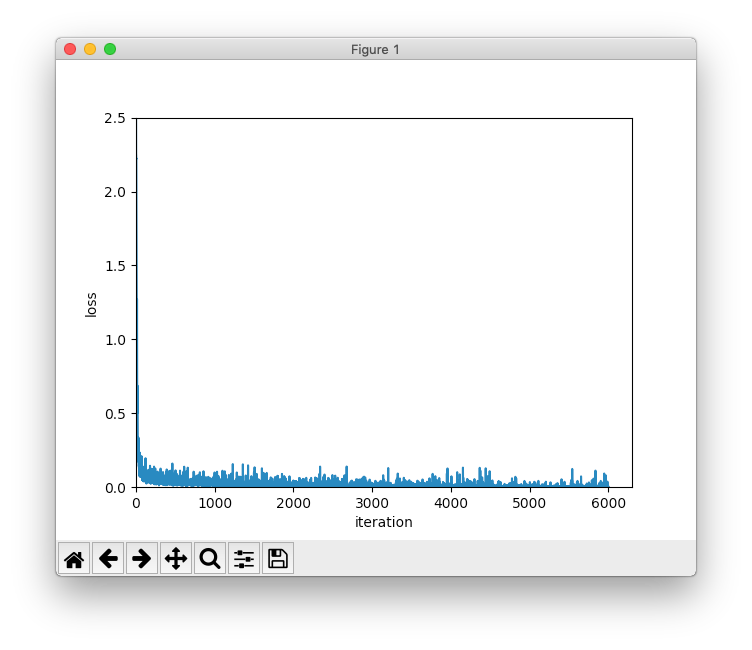
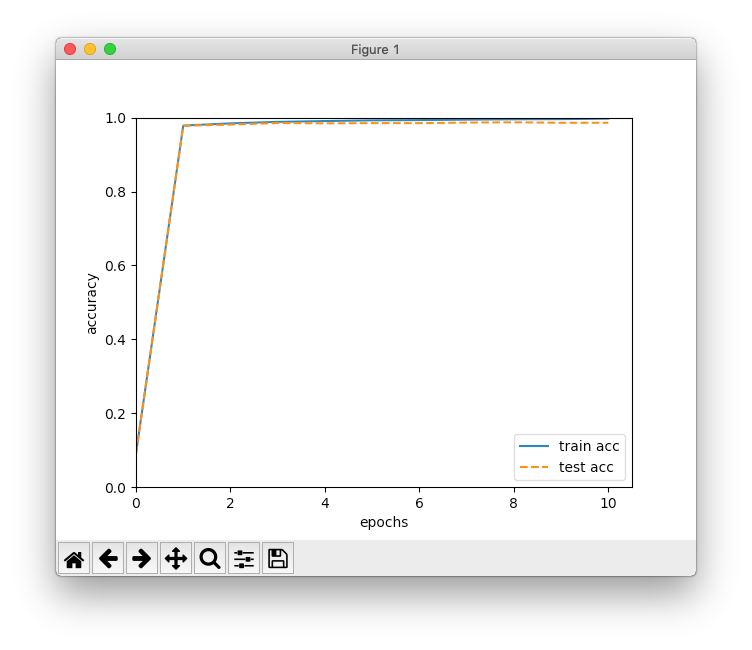
結果は、訓練データの認識精度が99.72%、テストデータの認識精度は98.60%でした。1エポックで、すでに前回の認識精度を超えています。7エポック辺りからテストデータの認識精度は変わっていないので、それ以降はただ過学習を進めるだけになっていたのかも知れません。それにしても、シンプルなCNNで98.60%という精度はすごいです。
なお、本のソースも実行してみたのですが、なぜか1エポック単位の認識精度の算出がすごく高速です。不思議に思い追ってみたところ、Trainerクラスのevaluate_sample_num_per_epochパラメーターでサンプリングできるようになっており、訓練画像もテスト画像も先頭1,000枚だけで計算するようになっていました。ズルい!![]()
7.6 CNNの可視化
エッジやブロブの抽出など、必要なフィルターが自動的に出来上がるのがすごいですね。層を重ねると抽象度が上がっていくのが非常に興味深いです。
7.7 代表的なCNN
ディープラーニングの発展においてビッグデータとGPUが大きく貢献しているとありますが、膨大なマシンリソースを安価に使えるようにしたクラウドの普及も大きなポイントだと思います。
あと、完全に余談なのですが、LeNetの提案が1998年で20年も前ですという話で、感慨深いというかなんというか、1998年はもっと最近の印象でした。歳は取りたくないものです![]()
7.8 まとめ
実装がちょっと大変でしたが、おかげでCNNが理解できました。
この章は以上です。誤りなどありましたら、ご指摘いただけますとうれしいです。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
-
マイクロソフト製品ならびにサービスにおける外来語カタカナ用語末尾の長音表記の変更について(※当時のページが残っていないので、Wikipedia > 長音符 からもリンクされている Internet Archive の Wayback Machine へのリンクです) ↩
-
What's New In Python 3.7 の「Python のデータモデルの改善」をご参照ください。 ↩
-
スラッシングはメモリ不足時に起きる現象で、OSごと操作不能に陥ることもあり厄介です。OSのメモリ管理についてご興味のある方は、以前投稿させていただいた 誰でもわかるメモリ管理入門:01 をどうぞ!
 ↩
↩