機械学習初心者でも、ニューラルネットワーク(neural network : NN)について理解しなければならない日がいつか来る。なので初心者代表の私が、ニューラルネットワークについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
本記事は、初心者の初心者による初心者のためのニューラルネットワーク#1〜理論:順伝播編〜の続きとなります。
1. なぜ人はニューラルネットワークを学ぶのか
今や日常生活の様々な場面に用いられている、機械学習のコアの部分だからです。(多分)
2. 本記事の目的
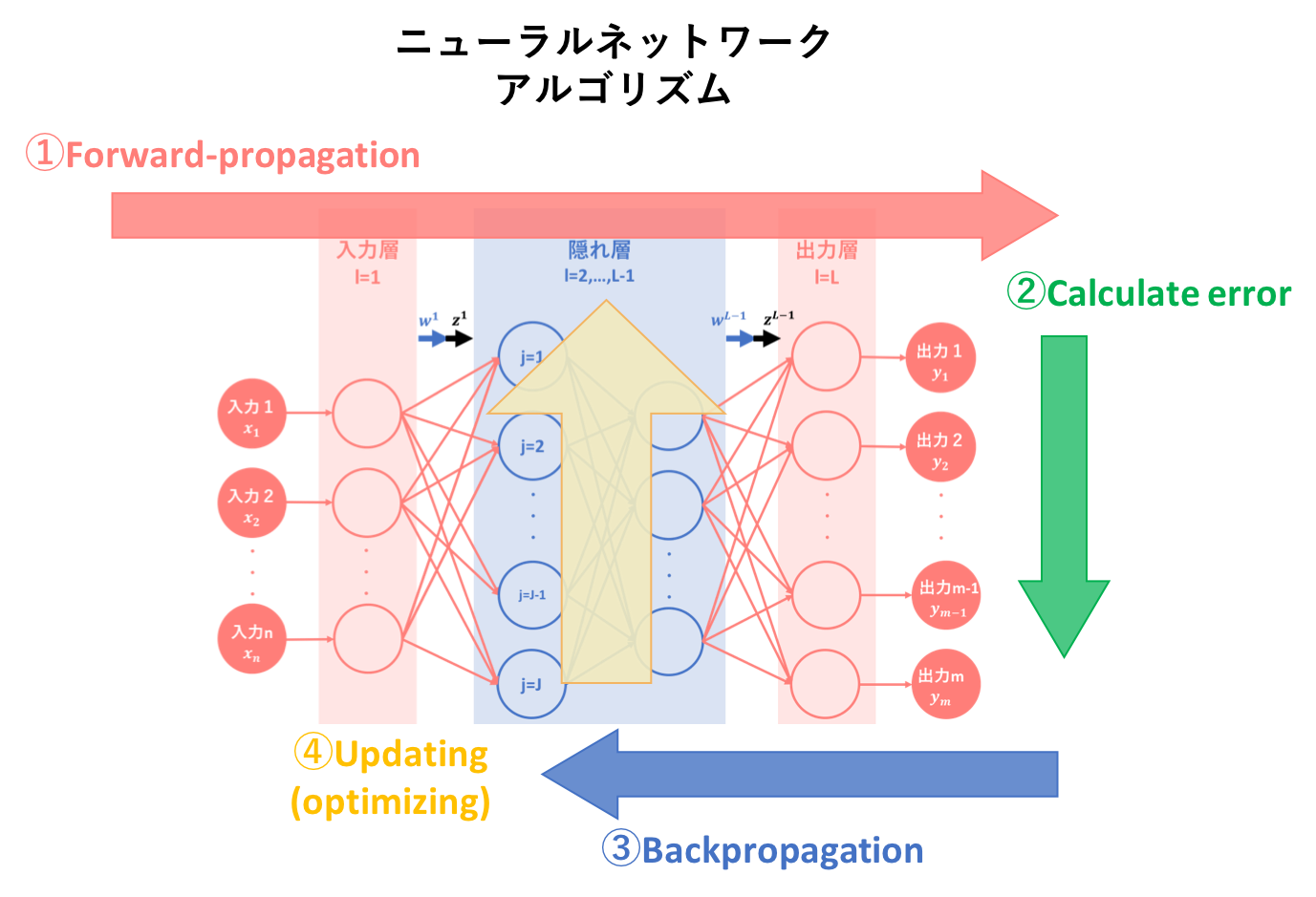
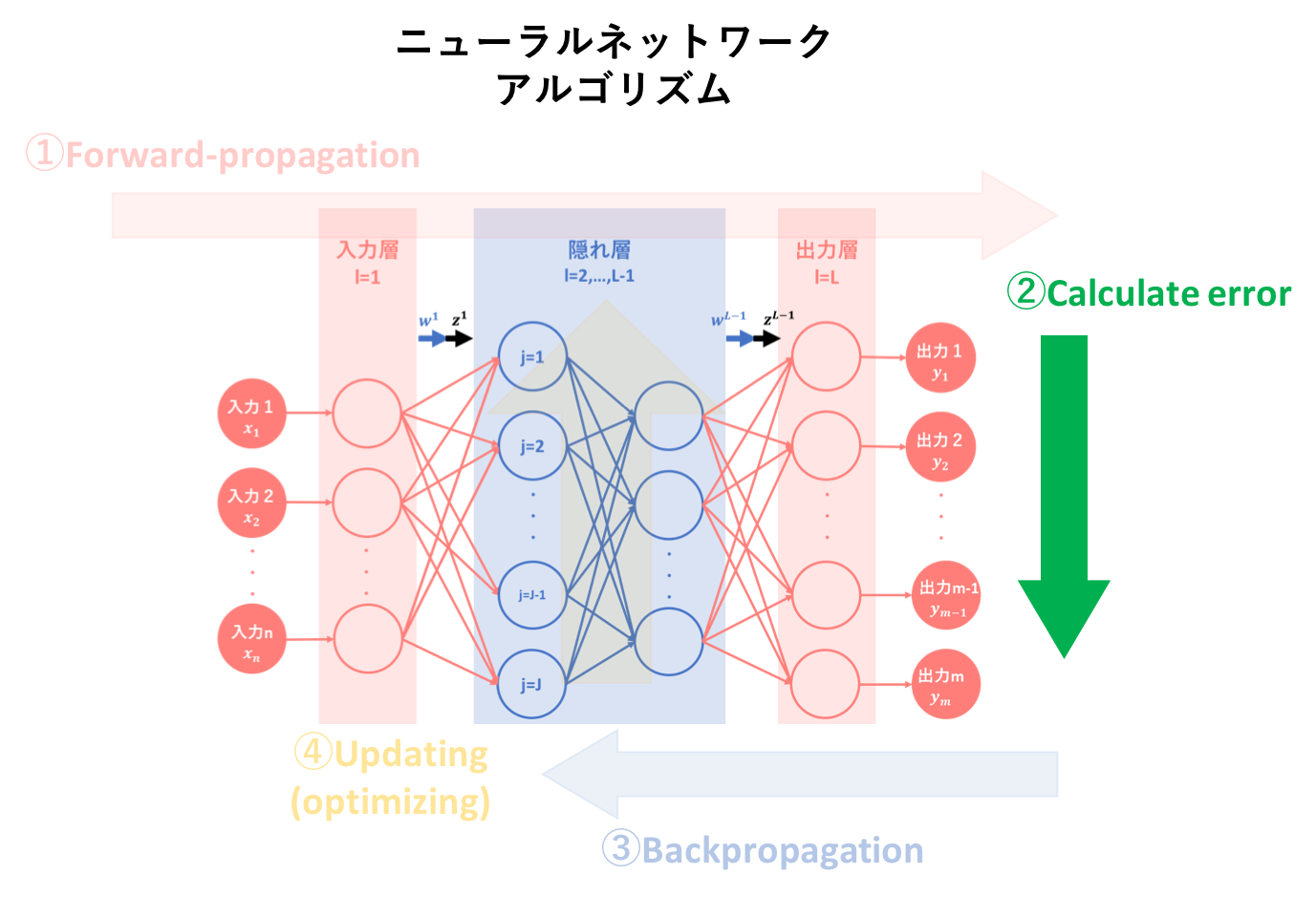
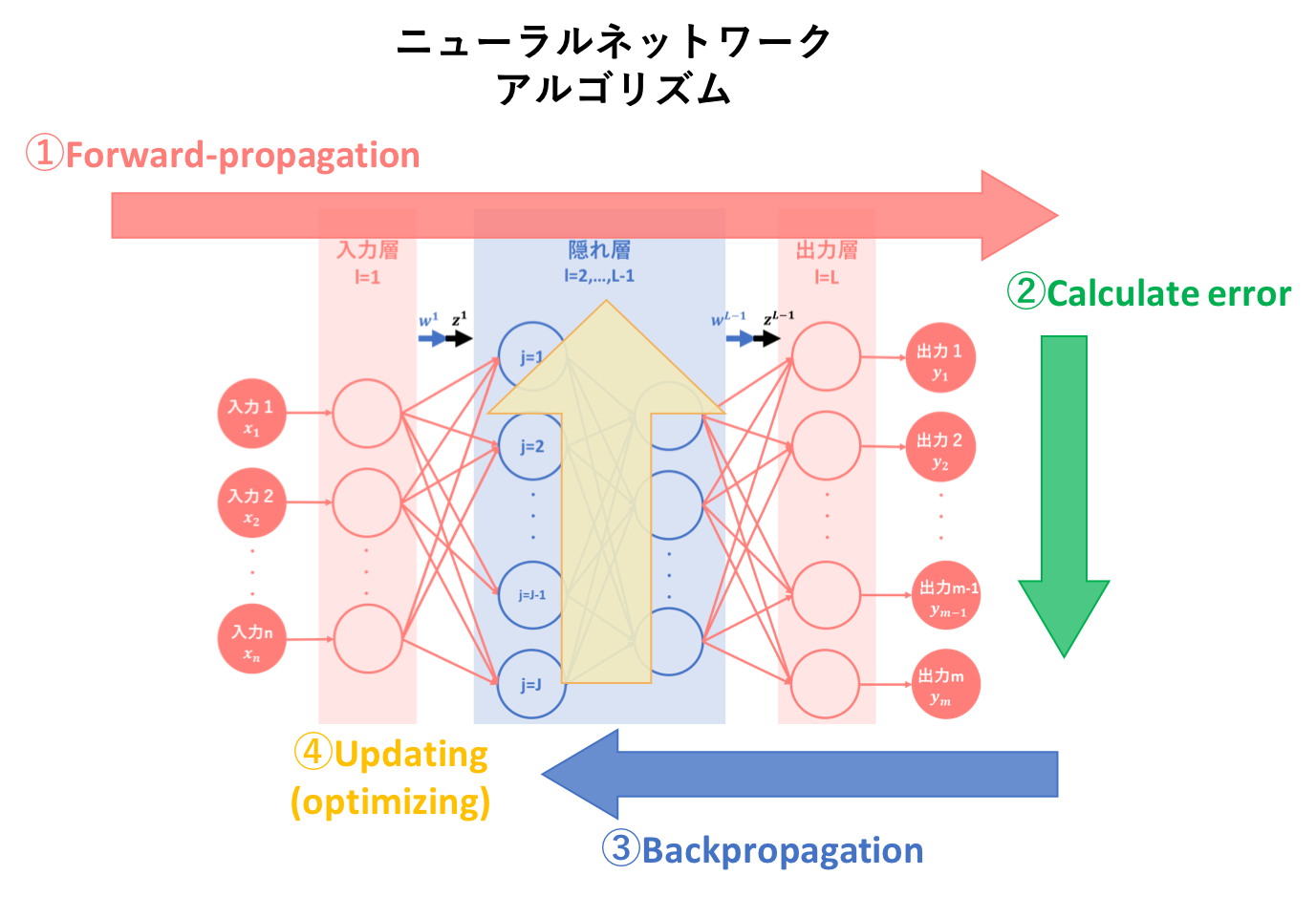
本記事では、ニューラルネットワークのアルゴリズムを簡易図式化した以下の図のうち、②誤差計算についての説明を行います。
3. 前記事の要約
初心者の初心者による初心者のためのニューラルネットワーク〜理論:順伝播編〜では、ニューラルネットワークの基本概念、基本構造そしてアルゴリズム①である順伝播(forward-propagation)について説明しました。
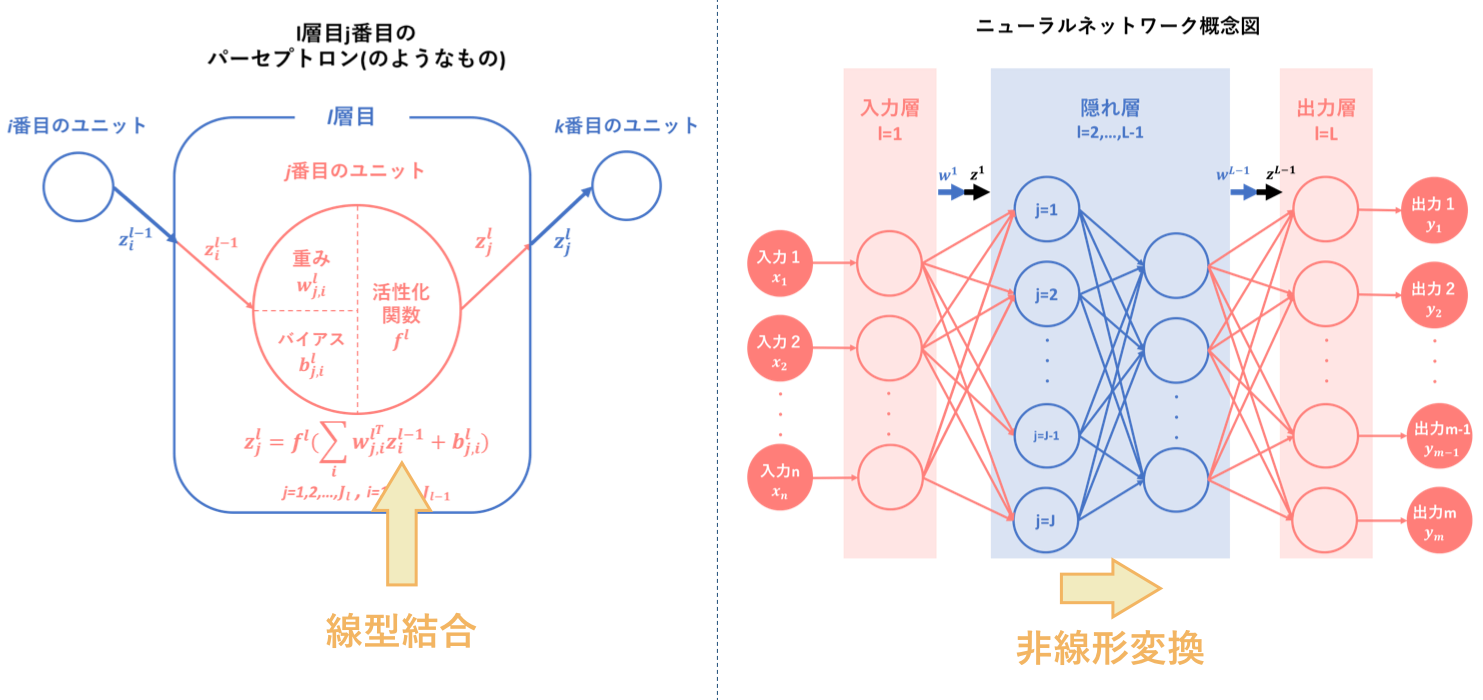
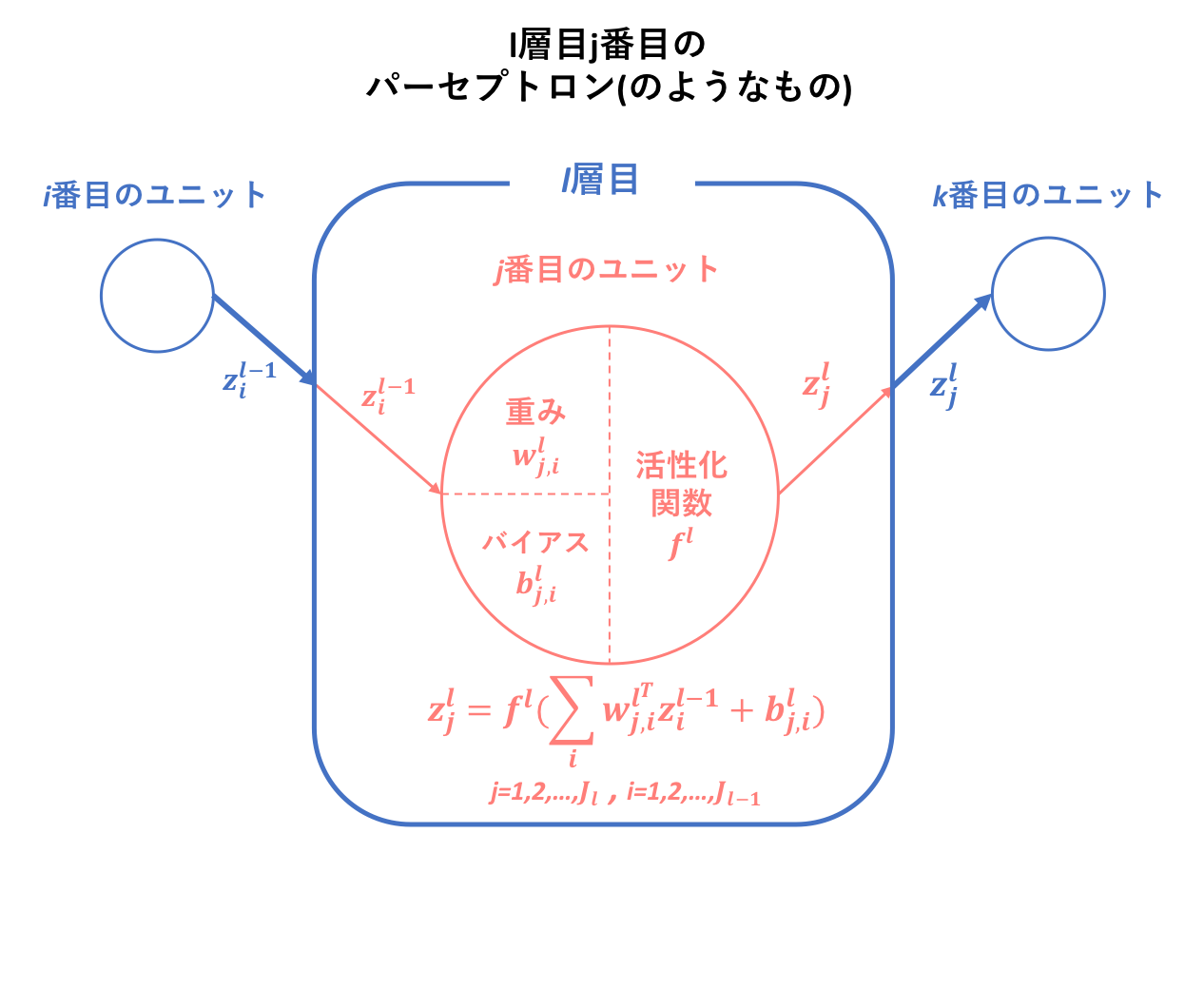
その要約として以下の図をあげます。ニューラルネットワークとは、『パーセプトロン(のようなもの)を基に人間の脳神経系のニューロンを数理モデル化したもの』のことであり、『線型結合と非線形変換を繰り返す合成関数 $f(w,x)$によって入力から出力を表すモデル』です。
そして、ニューラルネットワークの目的は最適パラメータの発見であり、そのために学習を繰り返すことによって予測出力を最適化するようなパラメータを導出します。
順伝播は、その学習アルゴリズムの一つ目でした。
4. 多層パーセプトロンの誤差関数
では、ニューラルネットワークの学習アルゴリズム②:誤差計算について説明していきます。
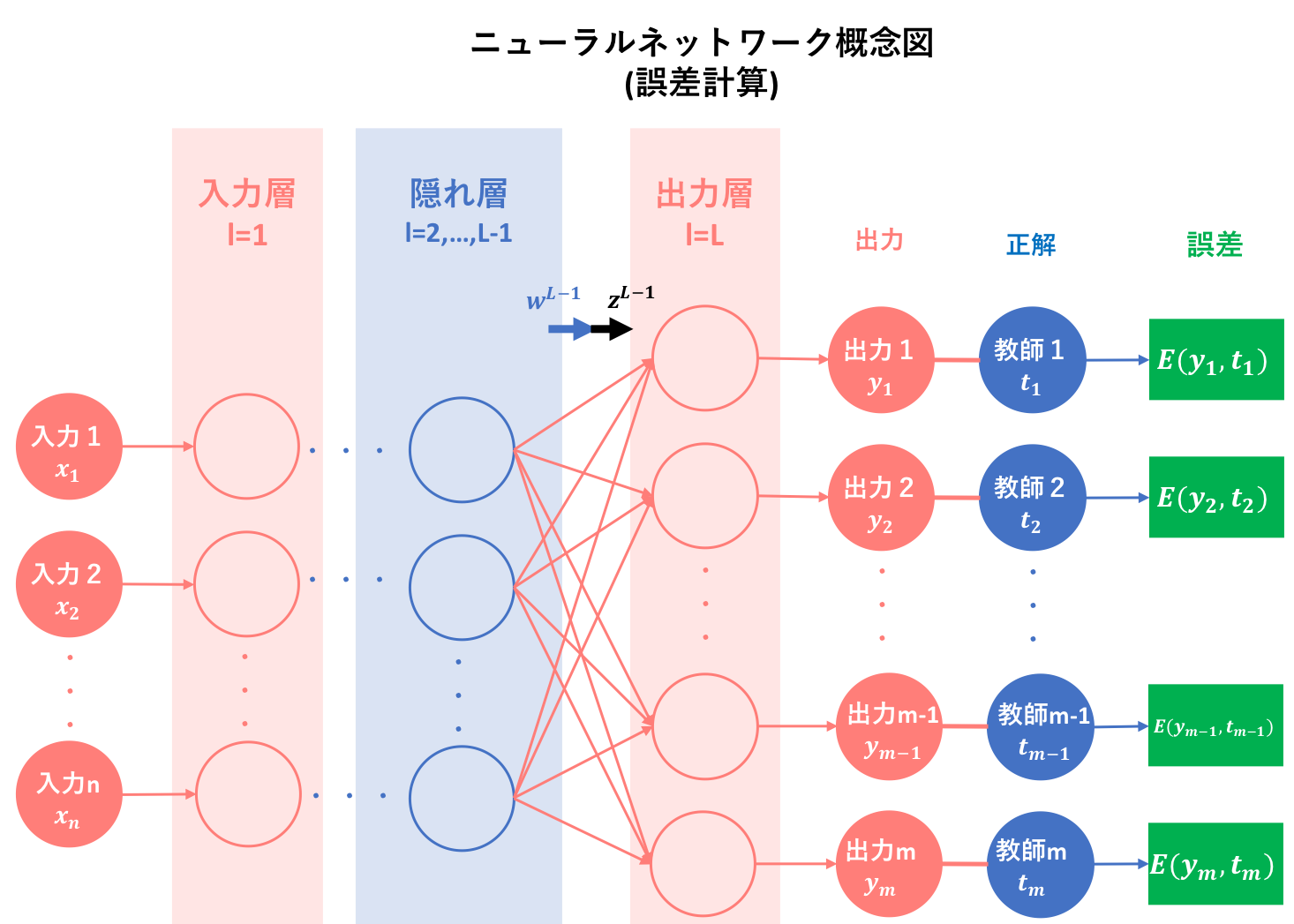
前記事で簡潔に述べましたが、学習機械としてのニューラルネットワークにおける目標は、学習を繰り返すことによって最適なモデルを構築することでした。そして、最適なモデルとは多くの場合、目標値と予測値の差が最も近くなるようなモデルのことを指します。
このとき、目標値が予測値とどれくらい近いのかを示す関数を別途定義する必要が生じます。このような目標値が予測値とどれくらい近いのかを示す関数を損失関数や誤差関数と呼び、多くの学習機械はこの関数を最小化することを目標とします。
今回、多層パーセプトロンはネットワーク全体で1つの学習機械ですから、誤差関数も全体で1つだけ定義します。しかし、その誤差関数にも様々な種類があります。以下に、代表例として取り上げられることの多い誤差関数を紹介します。
以下では、$y_k$は順伝播によって出力された予測値, $t_k$は望まれる出力値である教師信号(supervisory signal)を表しています。
4.1. 二乗誤差
$$E_{se}=\sum_{k} \frac{(y_k−t_k)^2}{2}$$
$y_k$ は出力層k番目のユニットの出力値なので、$(y_k - t_k)$はそのユニットの「理想の出力値と実際の出力値の差」となり、それを二乗します。二乗するのは後の誤差逆伝播法という勾配探索手法で都合がいいからですが、損失が負の値にならないというメリットもあります。
また、$\sum_k (y_k - t_k)^2$ は出力層の全ユニットについてその計算をして足し合わせるということです。そしてさらに $\frac{1}{2}$をかけます。これも後の計算で都合がいいからという理由です。誤差を二乗した値の和(の定数倍)なので、この$E_{se}$を2乗誤差と呼びます。
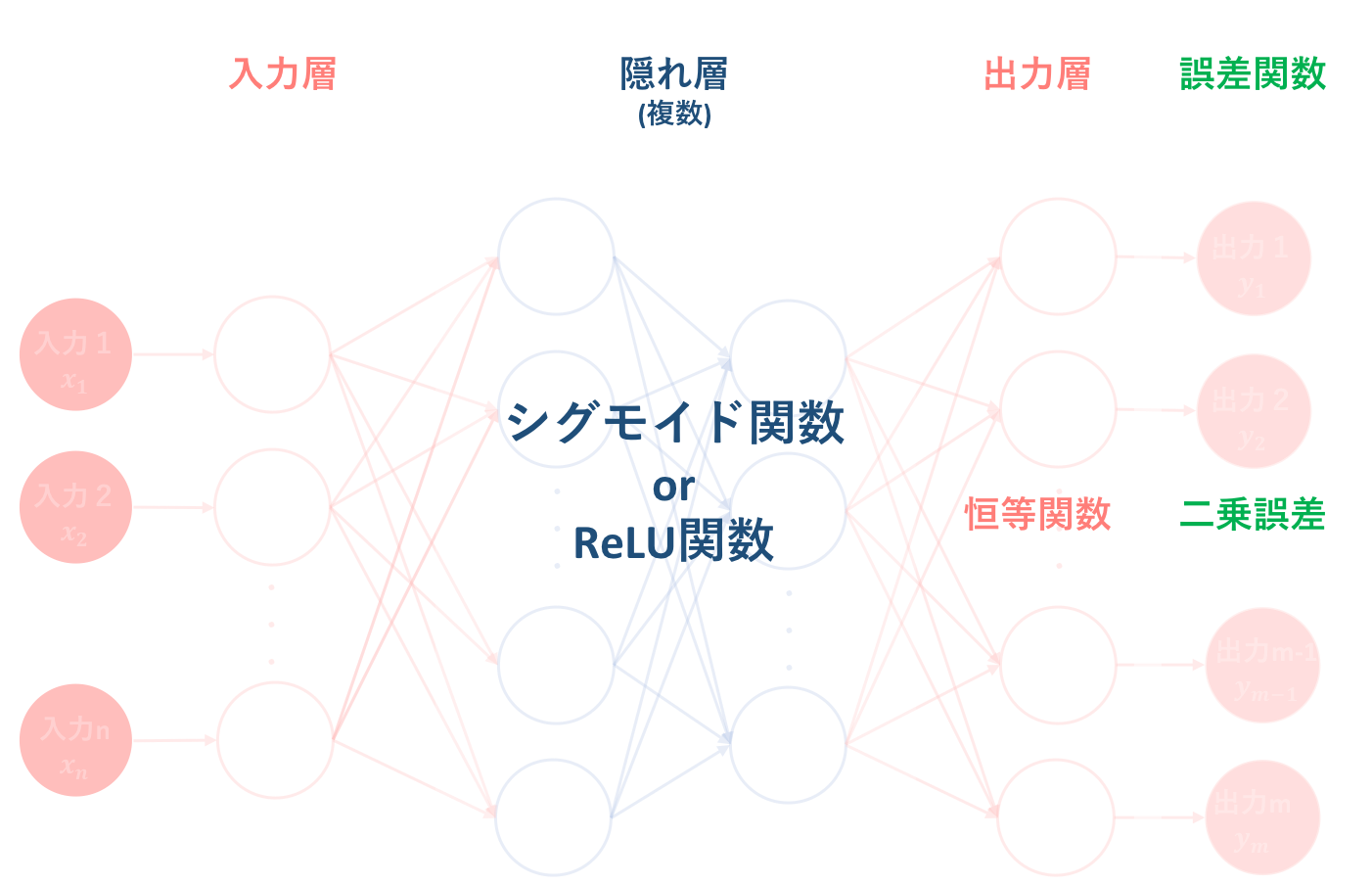
**2乗誤差関数は主に、ニューラルネットワークが連続値を出力するようなタスクに対して使われます。つまり、教師あり学習では回帰問題に対して用いられることが多いです。**また、連続値を出力とする場合、$f_k(v)=v$ として恒等関数を出力層の活性化関数にするのが常套手段となります。(5項で説明します)
4.2. 交差エントロピー
$$E_{cross}=−\sum_kt_klogy_k+(1−t_k)log(1−y_k)$$
$$or$$
$$E_{cross}=−\sum_kt_{k}logy_{k} \quad \bigr(ただし\sum_{k}t_{k}=1\bigr)$$
続いて、交差エントロピーについて説明します。本来は2つの確率分布 P、Q に対して、$−\sum_xP(x)logQ(x)$となる関数を交差エントロピーと呼びます。
p×log(p)のようにlogの中身と外側に同じ変数が使われているのが普通のエントロピー。
それに対して、t×log(y)のようにlogの中身と外側に異なる変数が使われているものを"交差"エントロピーと呼ぶらしい。ー「ゼロから作るDeep Learning」を読んだ(後編)
PもQも二値変数(ベルヌーイ分布)の場合、$P(x_1)=p, P(x_2)=1−p, Q(x_1)=q, Q(x_2)=1−q$となるので 交差エントロピーは$−plogq−(1−p)log(1−q)$ ,
またPもQも多値変数の場合、つまり$P(x_i)=p_i(i=1,…,n),$ $Q(x_i)=q_i(i=1,…,n)$のとき、交差エントロピーは$−\sum_{i=1}^np_ilogq_i$となります。(代入しただけです)
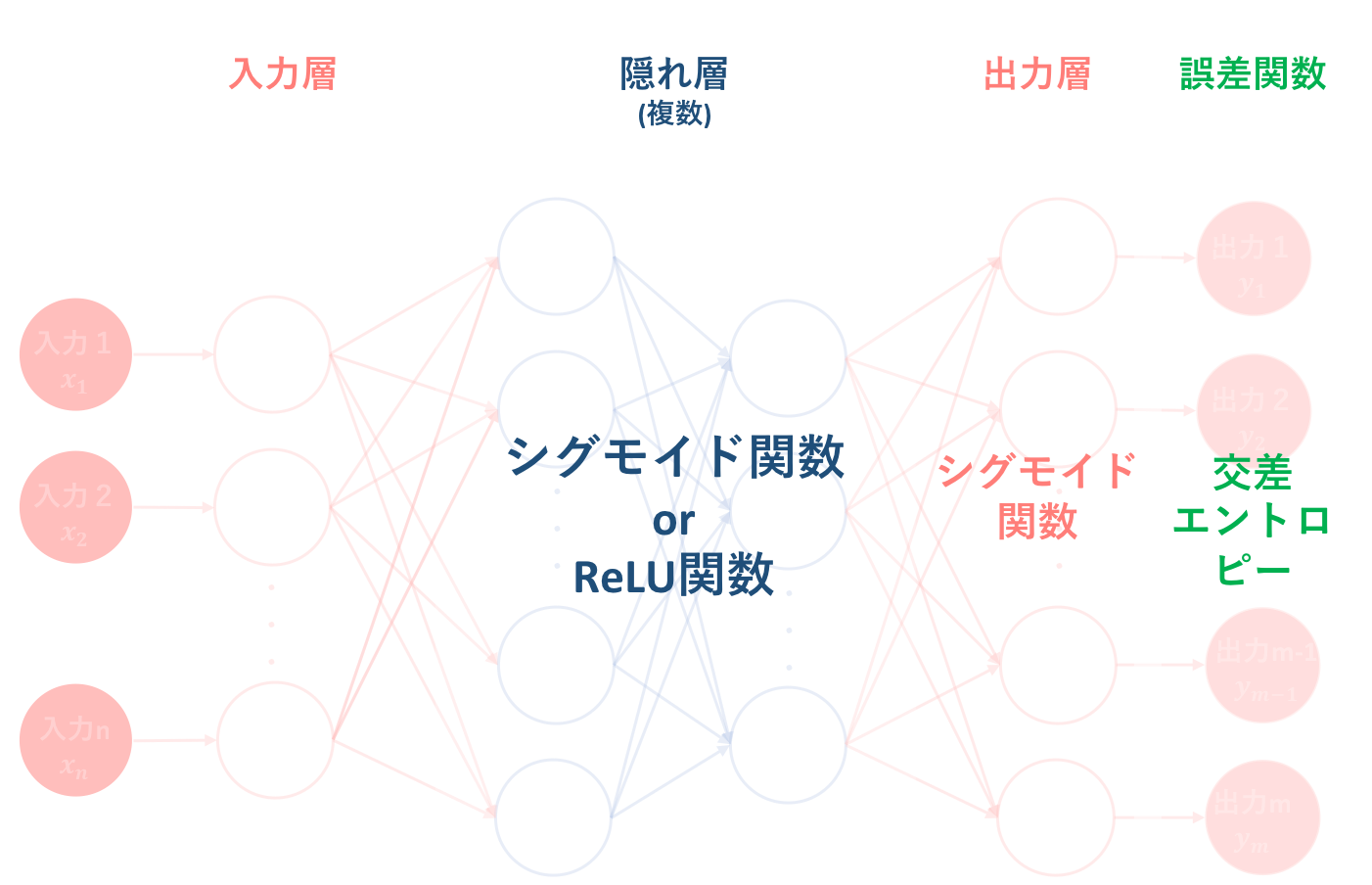
このとき、$p≒q≒0$のときと$p≒q≒1$のときは$E≒0$となり、それ以外のときはより大きい値になるので、2クラス分類問題に使えそうです。このことから、交差エントロピーは識別(分類)問題において用いられやすいことが伺えます。
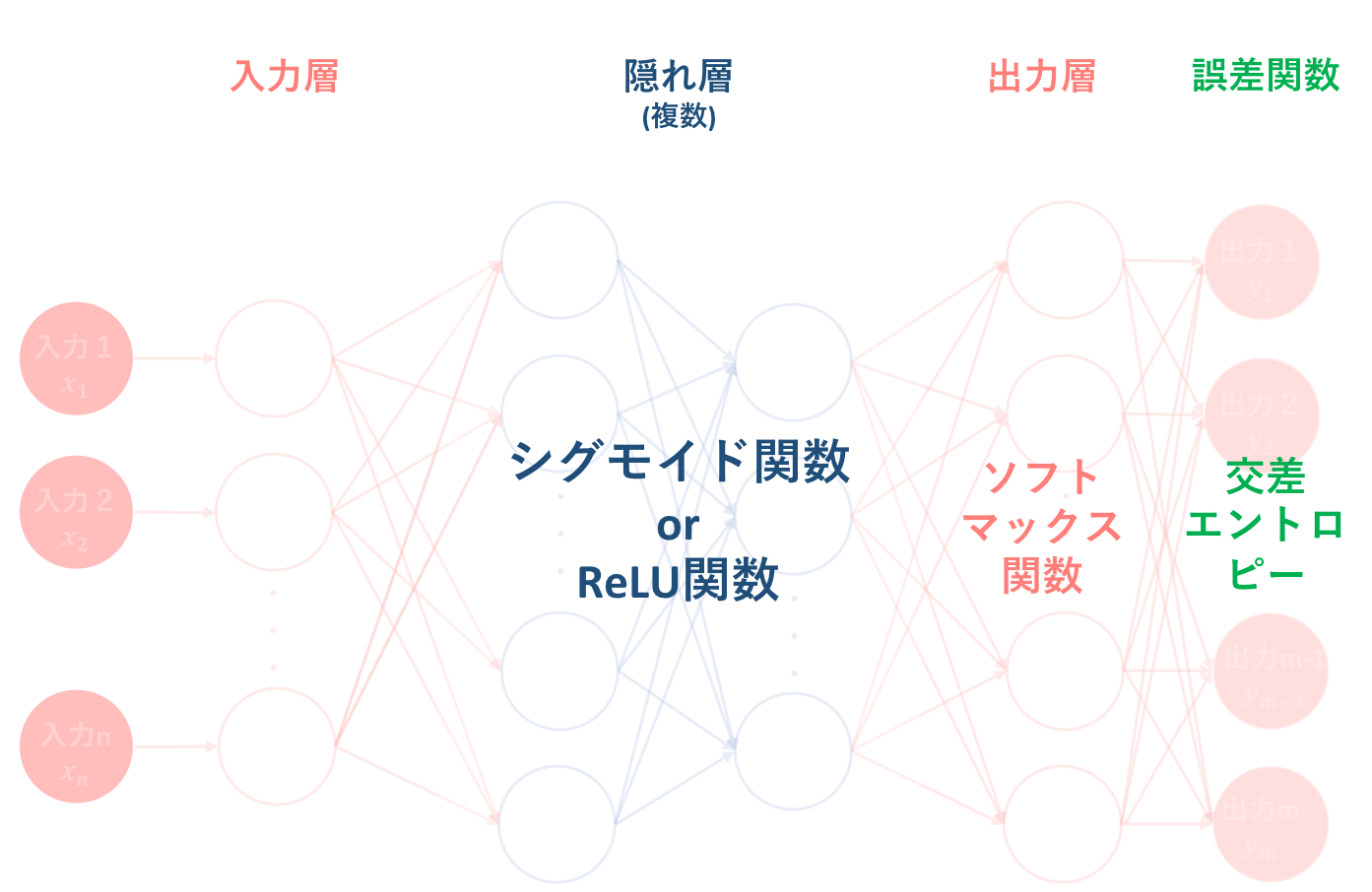
しかし、ニューラルネットワークではこれだけでは不十分です。以上はあくまで出力層の一つでの話なので、出力層が複数あるニューラルネットワークの場合はすべての層の和をとることによってそのモデルでの誤差とします。この結果が、上式のようになります。また、この場合、出力層の活性化関数はすべての出力で $y_k∈(0,1)$ かつ$\sum{y}=1$としておきたいので、そのような活性化関数としてソフトマックス関数が用いられます。(5項で説明します)
4.3. エントロピー
$$E_{entropy}=H=−\sum_ky_klogy_k+(1−y_k)log(1−y_k)$$
また、出力の活性化関数をシグモイド関数(5項で説明します)にして、その出力を確率とみなしたエントロピーを誤差関数としたときについてですが、こには教師信号(supervisory signal)が用いられることなく定式化されています。ここからは私見なのですが、この誤差関数を用いるのは教師なし学習の場合であり、その際にエントロピー(平均情報量)は少ない方が良いという前提におけるものだと考えられます。つまり、それぞれの層からの出力値が$0$or$1$に近ければ近いほど情報量が少なくなり、誤差が小さいと言えるというわけです。
以下のサイトに情報理論におけるエントロピーが説明されているので、参考にしてください。
→雑記: 交差エントロピーって何
→情報理論の基礎~情報量の定義から相対エントロピー、相互情報量まで~(より詳しい)
4.4. 多層パーセプトロンの誤差
さて、上記に代表的な誤差関数をいくつか紹介しましたが、多層パーセプトロンの誤差というのは、これらの誤差関数を用いて以下のように計算されます。
$$E_{total}=\frac{1}{N}\sum_{n=1}^NE_n$$
$E_n$は$n$番目のデータに対する誤差関数の値を示しており、このように多層パーセプトロンの誤差は誤差関数$E$を学習に使うデータの数$N$だけ足して平均した値で表されます。なぜ平均するかについては、裏で確率の話があり、PRML1章にこれに当たる内容が書かれているようなのですが、詳しくは分かりませんでした...
4.5. 誤差関数の条件
ここで、誤差関数の目的について確認します。この項の最初にも述べましたが、誤差関数とは目標値が予測値とどれくらい近いのかを示す関数であり、多くの学習機械はこの関数を最小化することを目標とします。なので、どの状態が最適かを判断するために誤差関数は必要とされ、すなわち誤差関数は原則$E≧0$となります。しかし、誤差関数はその目的を満たせば良いというわけではありません。
実は誤差関数は、すべての重みwにおいて微分可能であるような関数でなければならないのです。これは、誤差逆伝播法によると多くのWebサイトでは書いているのですが、私自身としては勾配降下法を用いることによると説明した方が分かりやすいような気がします。しかし、誤差逆伝播法はそもそも勾配降下法を用いることが前提となっているので、結局は同義です。
勾配降下法は初心者の初心者による初心者のための単純パーセプトロンでも簡単に説明していますが、目的関数(損失関数/誤差関数)の重みwにおける微分を用いてパラメータ最適を図る手法です。よってパラメータ最適にこの手法を用いるのであれば、目的関数はすべてのwで微分可能であることが必要条件となります。
5. 多層パーセプトロンの活性化関数
それでは、本来ならば本記事の目的である誤差計算の仕組み解説は達成されたのでここで終わりなのですが、実は誤差関数と多層パーセプトロン内の活性化関数は密接に関係しあっているので、誤差計算編の延長、そして逆伝播編の導入として多層パーセプトロンの活性化関数について説明します。
ここで重要なのは、必ずしも隠れ層と出力層で同じ活性化関数を用いる必要はないということです。留意して下さい。
5.1. パーセプトロン(のようなもの)
ここで一度復習パートに入りますが、私の記事の中では、多層パーセプトロンの基本構成単位をパーセプトロンではなく、パーセプトロン(のようなもの)としていました。この理由として、以下に前記事の引用を載せておきます。
ニューラルネットワークの基本原理がパーセプトロンであることに疑いの余地はありませんが、厳密にはパーセプトロンに少し変化を加えたものを構成単位としています。そしてその違いは、活性化関数にあります。
パーセプトロンの基本である形式ニューロンに立ち返ってみましょう。形式ニューロンでは、活性化関数としてステップ関数を用いることを指定していました。しかし、ニューラルネットワークでは構成原子においてステップ関数を用いずに、シグモイド関数(sigmoid function)やランプ関数(ReLU)を用います。これは、ステップ関数の微分値が常に0になってしまうことに拠ります。微分値が常に0という状態は、後に説明する誤差逆伝播法(backpropagation)という画期的な学習手法に適さないので、微分可能な関数が代用されたということです。ちょうど、0-1損失関数と代理損失関数の関係に似ていますね。-初心者の初心者による初心者のためのニューラルネットワーク〜理論:順伝播編〜
つまり、ニューラルネットワークにおける活性化関数には原則としてステップ関数は用いられず、すべての入力に対して連続である関数を用います。ここでは、あえて微分可能という表現を避けていますが、その理由はあとで説明します。
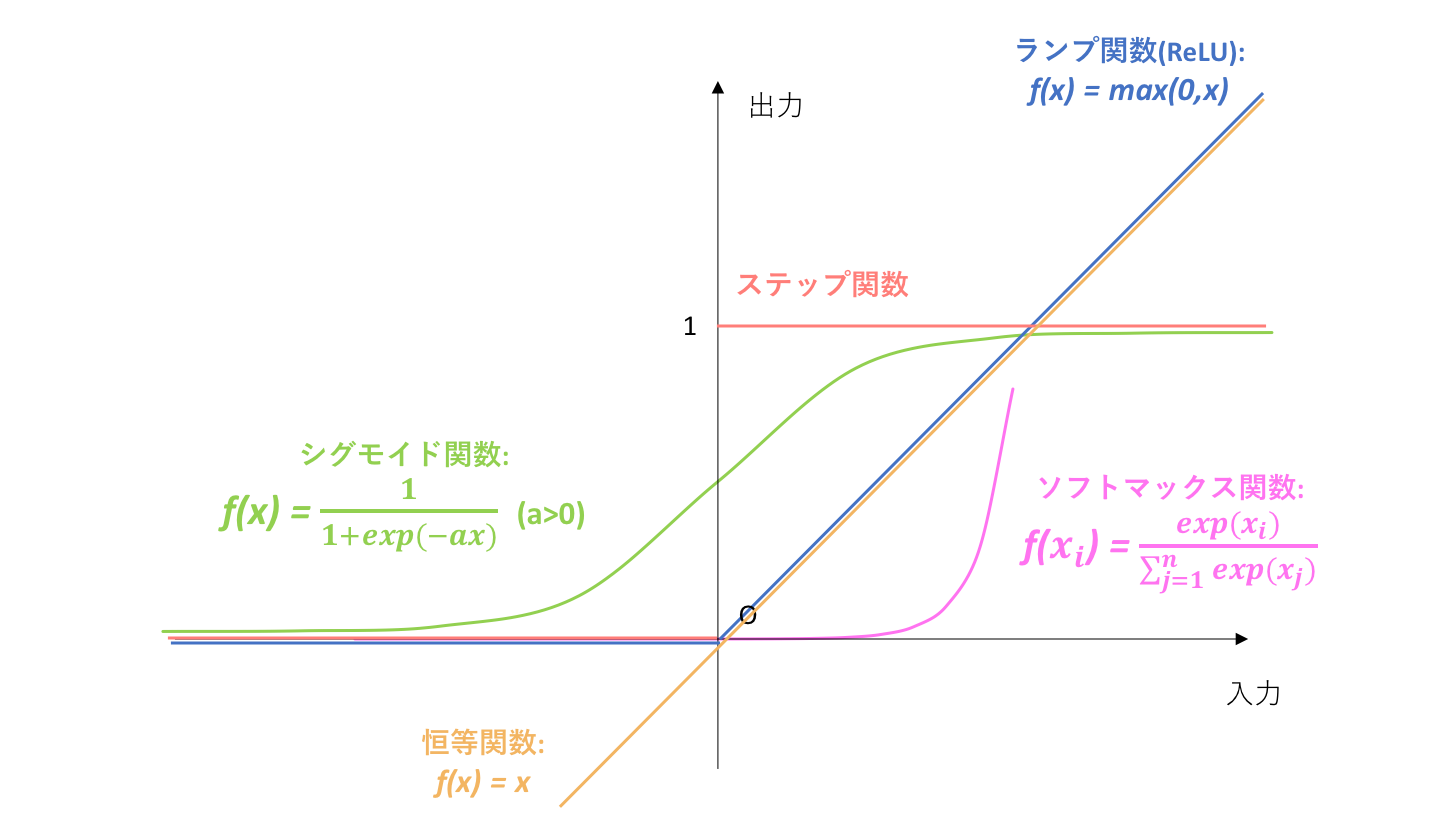
上の図は、ニューラルネットワークにおいて代表的な活性化関数をまとめたものです。以降では、それぞれについて説明していきます。(無理やり一枚の図にまとめています)
今回は上に載せた四種類の関数しか紹介しませんが、以下のサイトではより多くの活性化関数が綺麗に可視化されているので、よろしければご参考ください。
→Visualising Activation Functions in Neural Networks
5.2. シグモイド関数
シグモイド関数は$f(x)=\frac{1}{1+e^{-ax}}$で表され、一般的にニューラルネットワークでは$a=1$を代入した標準シグモイド関数をシグモイド関数と呼んでいます。シグモイド関数の特徴としては、
・必ず傾きが求まる(必ず微分可能)
・出力が0−1に収まる
・ステップ関数と比較して入力の値を反映しやすい
・誤差逆伝播法で微分する際の計算コストが軽い(次回説明します)
などが挙げられます。シグモイド関数はステップ関数を連続的に表したものであり、出力は0or1に寄ることから、二クラス分類問題において出力層の活性化関数としても用いられます。
また、活性化関数は原点を通すべきと言う考えから、標準シグモイド関数よりもそれを線形変換しである双曲線正接関数:$y=\frac{e^x−e^{−x}}{e^x+e^{−x}}$の方が良いと提案された経緯もあります。
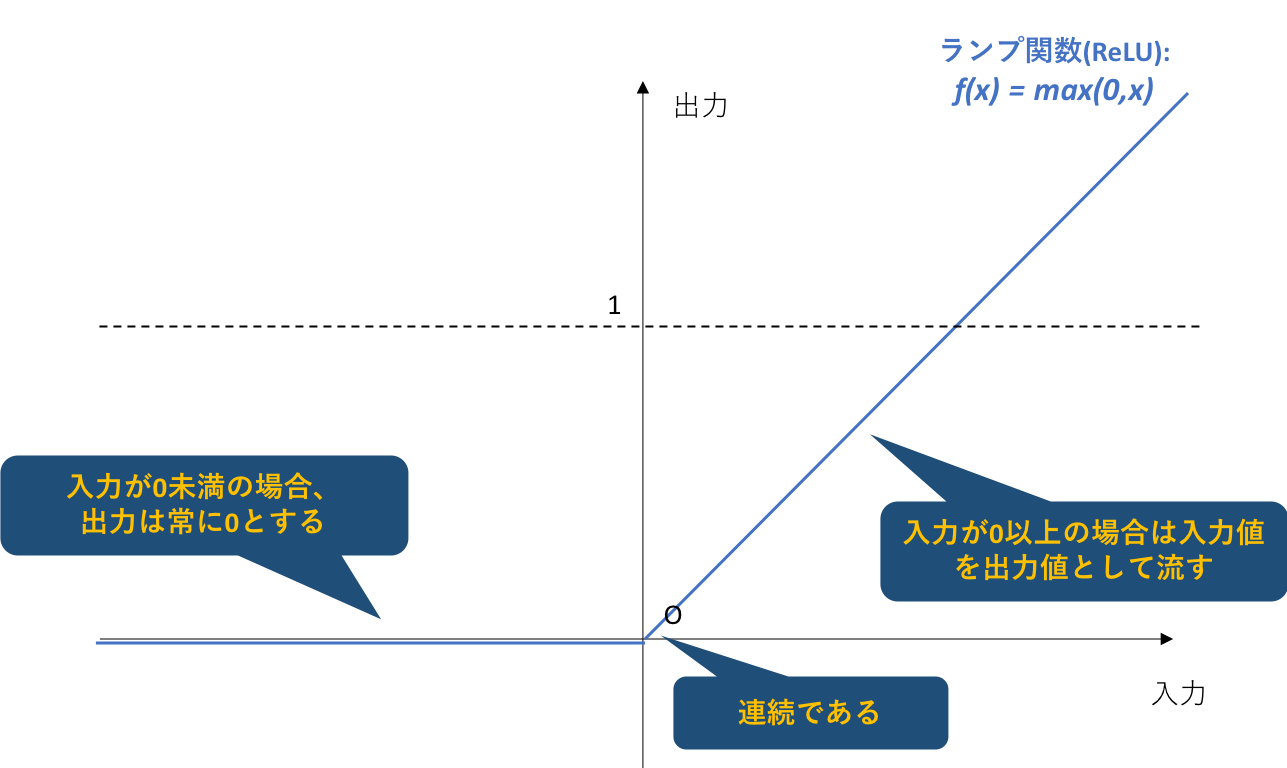
5.3. ReLU関数(ランプ関数)
**近年は、このランプ関数が活性化関数として用いられることが多いようです。**これは、ランプ関数が持つ二つの大きなメリットによるものです。以下その二つのメリットについて説明します。本節は、以下のサイトからの引用になります。
→ニューラルネットワークの線形変換と活性化関数について
メリット①:勾配消失問題の解消
シグモイド関数や双曲線正接関数は、原点から遠ざかる(値の絶対値が大きい)ほど勾配が無くなるため、一度ユニットが大きな値を持ってしまったら学習が停滞するという問題がありました。例えばシグモイド関数で、入力の値が偶然10などになった場合、微分の値が極めて小さな値を取ることが想定できます。この小さな値が学習の係数に掛かってきてしまうため、本来はまだ最適解にたどり着いていないのに学習が滞ってしまう勾配消失問題の引き金になってしまうのです。(実際には0になるわけではないのだが、多層の場合に、複数の層でこのようなことが起こると、誤差逆伝搬で誤差を伝えていくうちに、非常に小さい数の掛け算が行われていった挙句、誤差が正しく伝搬されなくなる)
しかしランプ関数では、この勾配消失問題が経験的に解消されることが知られています。
メリット②:ネットワークのスパース化
ReLUのもう1つの特徴としては、ネットワークのスパース化に貢献するという点です。ニューラルネットワークがスパースであるとは、出力が0であるユニットがたくさんある状態を指します。
仮にあるユニットへの入力が0未満になると、出力が0になります。そしてその領域においてReLUの微分は0であるため、これが学習の係数に掛かるときに、結果としてそのユニットは全く学習が行われなくなります。
そして、学習が行われなくなったユニットに対するパラメータは変化しないため、入力も変化せず(0未満のまま)、出力がその後ずっと0となります。学習は残ったユニットだけで行われるようになりますが、ニューラルネットワークは元来冗長であるため、返ってユニットを厳選していくこととなり、良い成果が得られるのだと言われています(事実上学習するパラメータを厳選していることになる)。
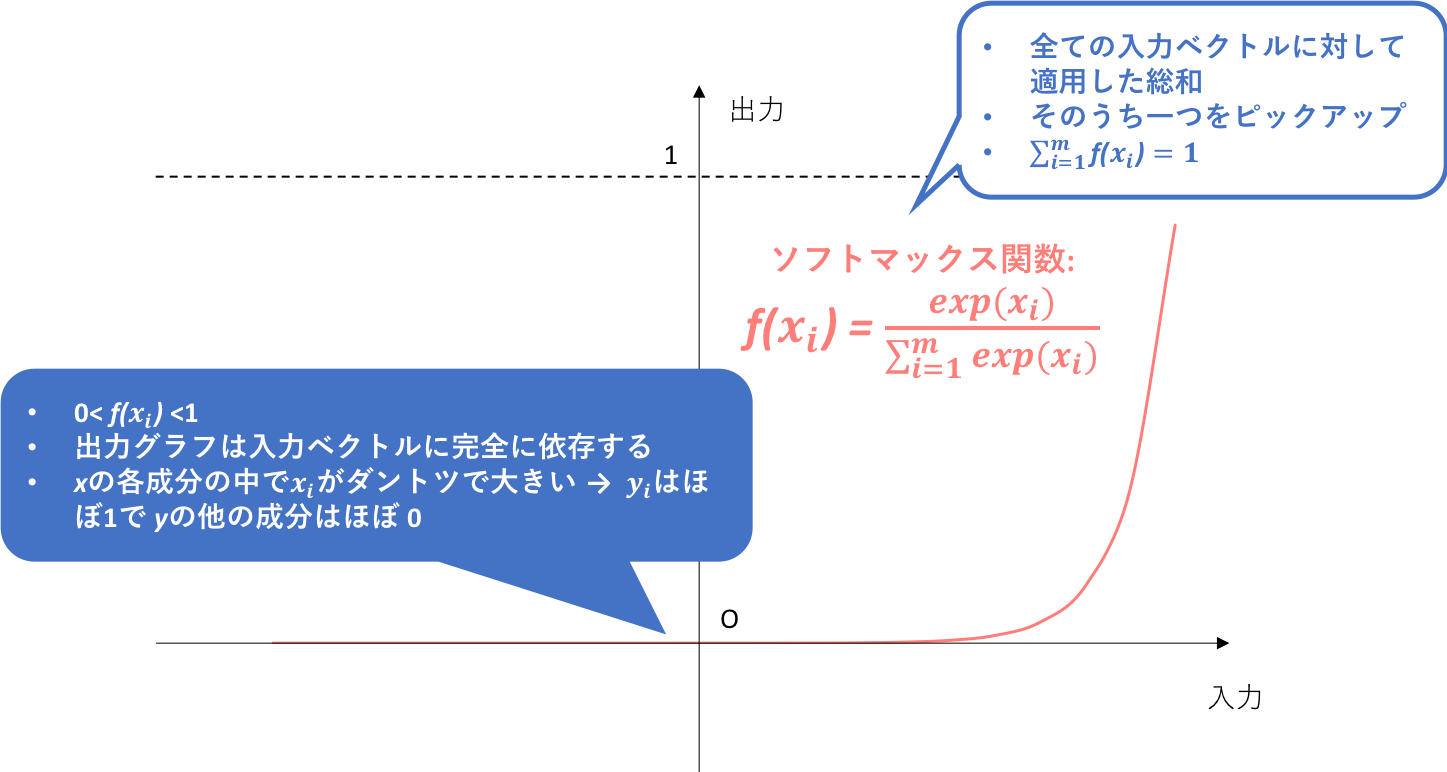
5.4. ソフトマックス関数
ソフトマックス関数は、既出の二つの活性化関数とは少し性質が異なります。関数の中身をみれば分かりやすいと思うのですが、一つのユニットからの出力が、自らのユニットへの入力だけでなく他のユニットへの入力にも依存します。よって、出力グラフも完全に入力ベクトルに依存することになります。
そして、**ソフトマックス関数は原則として多クラス分類問題において、そしてその中でも出力層のみで使われることが多いようです。**この理由について、少し深く突っ込んでいきます。
5.4.1. ソフトマックス関数の一般化
ここでは、他の関数に比べて挙動の分かりづらいソフトマックス関数が、出力層でどのように関数として機能するのかについて説明します。出力層のみで用いられることを前提とすれば、ニューラルネットワークの出力層においては、ソフトマックス関数は以下のように働きます。
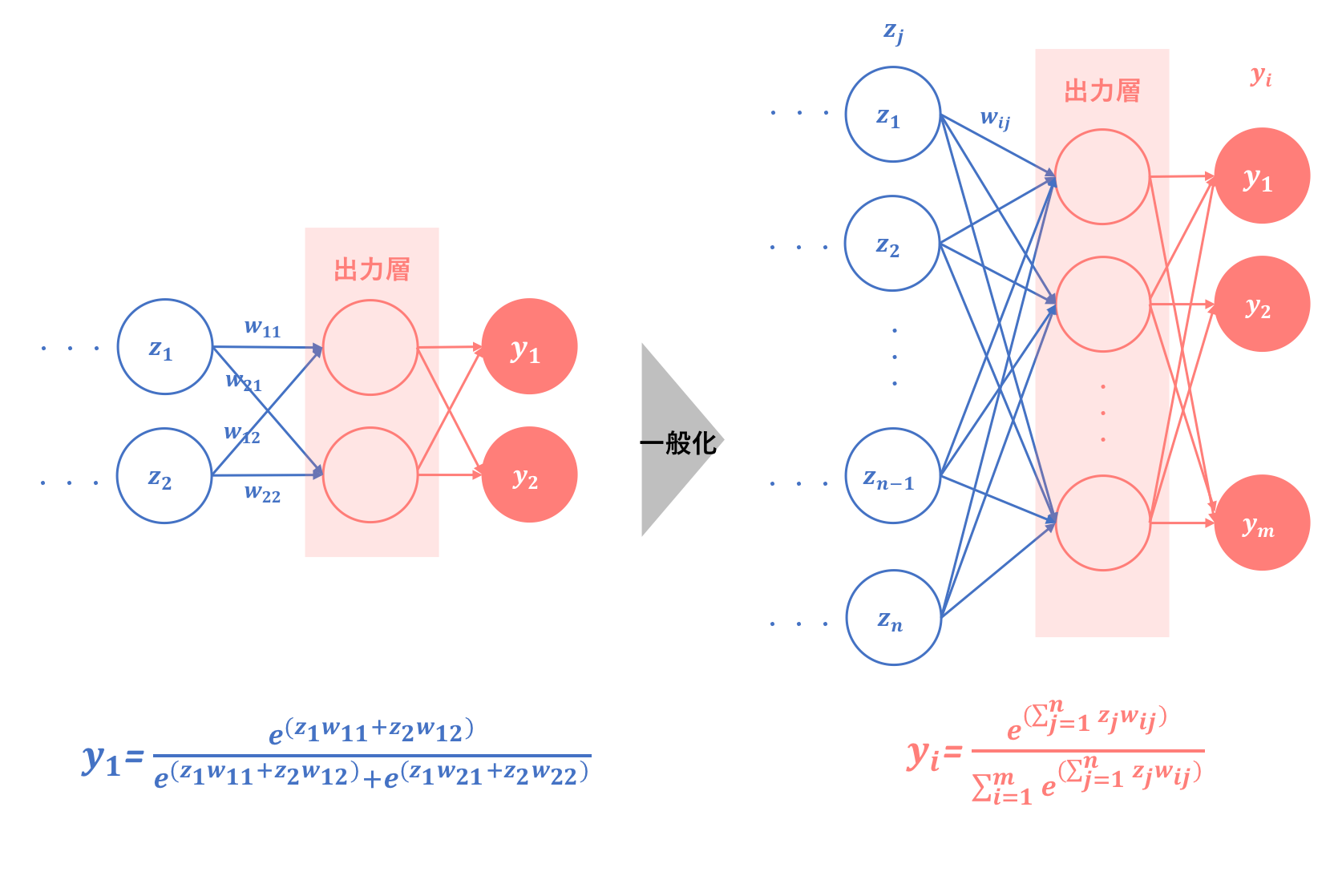
図の左部分については、まずソフトマックス関数へのイメージを持つために隠れ層出力層ともに2層だったときのソフトマックス関数出力を表しています。そしてこれを一般化すると、右部分のようになります。式は$\sum$が多用されており分かりづらいですが、2層の場合がイメージできれば解釈は難しくありません。
**しかしここで注意しなければいけないのは、これまでの出力層活性化関数と違い、ソフトマックス関数は一つの出力ユニットがすべての出力値に影響を与えるということです。**よって、従来は出力ユニットから出力への矢印はそれぞれ一本だけでしたが、それが$m$本になります。
5.4.2. 多クラス分類問題の出力層で用いられる理由
では、このように機能するソフトマックス関数が出力層においてよく用いられる理由は何なのでしょうか。**これを考えるうえで重要となるのが、ソフトマックス関数の
$$(0<y_i<1)∩(\sum_{i=1}^n{y_i}=1)$$
という性質です。**この部分についてはソフトマックス関数という記事が分かりやすく説明していたので、参考になると思います。
もう図を作る元気がないので、私なりに参考記事を言葉で要約させていただきます。
まず前提として、**分類問題においては出力層は分類したい種類(クラス)と同じ数のユニットで構成します。**そしてソフトマックス関数が分類問題において用いられるとき、教師信号の合計値は1となります。しかし、出力層において例えばランプ関数を用いた場合、出力値の合計は1とならず、教師信号との比較は非常に解釈が難しいものとなります。よって、ソフトマックス関数の$0<y_i<1$かつ$(\sum_{i=1}^n{y_i})=1$という性質は、教師信号との比較という面で非常に都合が良いです。
さらにこの性質によって、**ソフトマックス関数によって出力された値は、それぞれのクラスに属する確率を示していると解釈することができます。**よって、これも教師信号との比較において都合のいい要素だということが伺えます。
分類問題でなく回帰問題の場合は教師信号の合計値は1ではないので、ソフトマックス関数を用いるご利益が薄れてしまいます。
また、補足ですが、2クラス分類でもソフトマックス関数の利用は可能です。しかし、式変形を行えばそれはシグモイド関数を用いることと同義になるので、2クラス分類ではシグモイド関数を用いると結論づけさせて頂きます。
→参照:ソフトマックス関数
5.4.3. ソフトマックス関数の実装小ネタ
ソフトマックス関数は関数に$e^{a_i}$を使うのですが、指数関数は入力値が増えると、出力の増加率も大きいので、値によっては桁数がたりずにオーバーフローしてしまいます。よってこれを防ぐために、実装の際は変形したものである
$$f(x)=\frac{e^{ak-C1}}{\sum_{i=0}^ne^{a_i-C1}}ただしC1=max(a_i)$$
を用いることが多いようです。以下参照です。
→ソフトマックス関数についてのまとめ
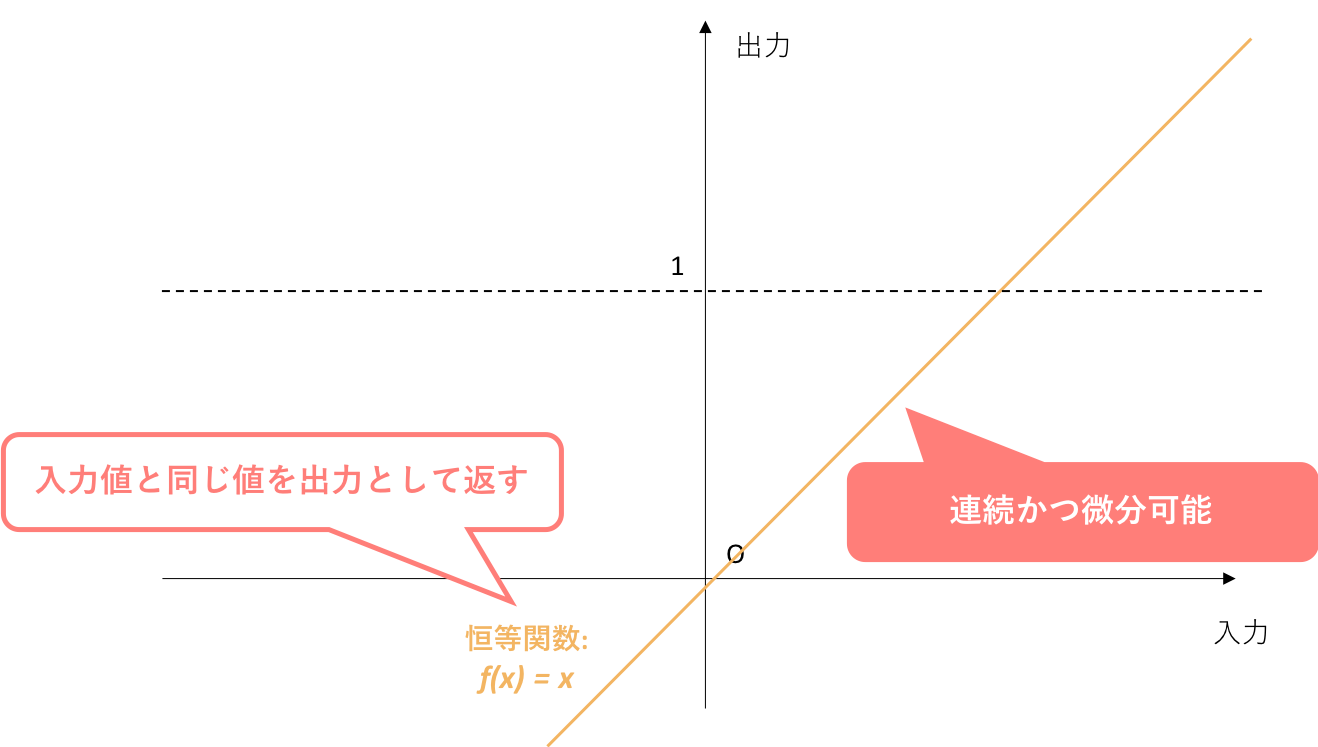
5.5. 恒等関数
恒等関数は、一般的に出力層において用いられるという面ではソフトマックス関数と同じですが、回帰問題において用いられます。
回帰問題では、出力層に与えられた値をどこかのクラスに振り分けたりする必要なくそのまま出力できるので、恒等関数が基本的に用いられます。
6. まとめ
それでは、今回の議論をまとめます。誤差計算編ということでしたが、今回は誤差関数に密接に関係する活性化関数についても説明しました。
6.1. 回帰問題
6.2. 二クラス分類問題
6.3. 多クラス分類問題
また、近年分類問題において新たな活性化関数が論文で発表されたようなので、そのことを紹介した(論文のタイトルだけですが)記事を載せておきます。
→分類問題における新たな活性化関数「Gumbel-Softmax」
7. (小話)多層パーセプトロンとニューラルネットの違い
ニューラルネットワークはシナプスの結合によりネットワークを形成した人工ニューロン(ノード)が、学習によってシナプスの結合強度を変化させ、問題解決能力を持つようなモデル全般を指す。狭義には誤差逆伝播法を用いた多層パーセプトロンを指す場合もあるが、これは誤った用法である。
-ニューラルネットワーク(Wikipedia)
それでは、次の記事はアルゴリズム③理論:逆伝播編となります。
①初心者の初心者による初心者のためのニューラルネットワーク#1〜理論:順伝播編〜
②初心者の初心者による初心者のためのニューラルネットワーク#2〜理論:誤差計算編〜(本記事)
③初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜
④初心者の初心者による初心者のためのニューラルネットワーク#4〜理論:パラメータ更新編〜
8. 参照
【数式なしで説明】なぜニューラルネットワーク分類にクロスエントロピー、シグモイド、ソフトマックスが使われがち?
「ゼロから作るDeep Learning」を読んだ(後編)
雑記: 交差エントロピーって何
ソフトマックス関数についてのまとめ
ソフトマックス関数
活性化関数のまとめ(ステップ、シグモイド、ReLU、ソフトマックス、恒等関数)
ニューラルネットワークの線形変換と活性化関数について
出力層で使うソフトマックス関数
分類問題における新たな活性化関数「Gumbel-Softmax」
初心者の初心者による初心者のためのニューラルネットワーク〜理論:順伝播編〜