活性化関数のまとめ（ステップ、シグモイド、ReLU、ソフトマックス、恒等関数）

[参考]ゼロから作るDeep Learning

活性化関数とは

活性化関数は、入力信号の総和がどのように活性化するかを決定する役割を持ちます。これは、次の層に渡す値を整えるような役割をします。

一般的に、
「単純パーセプトロン」の活性化関数では、「ステップ関数」などが使われ、
「多層パーセプトロン（ニューラルネットワーク）」の活性化関数では、「シグモイド関数、ソフトマックス関数」や恒等関数が使われます。
また、これら「ステップ関数、シグモイド関数、ソフトマックス関数」を非線形関数と呼ぶのに対し、「y=cx」のような関数を線形関数と呼びます。
一般的に、ニューラルネットワークでは線形関数は使われません。この理由は、「なぜ多層パーセプトロンで線形関数を使わないのか？」で説明します。
一般的に、ソフトマックス関数と恒等関数は出力層で使われます。

ステップ関数

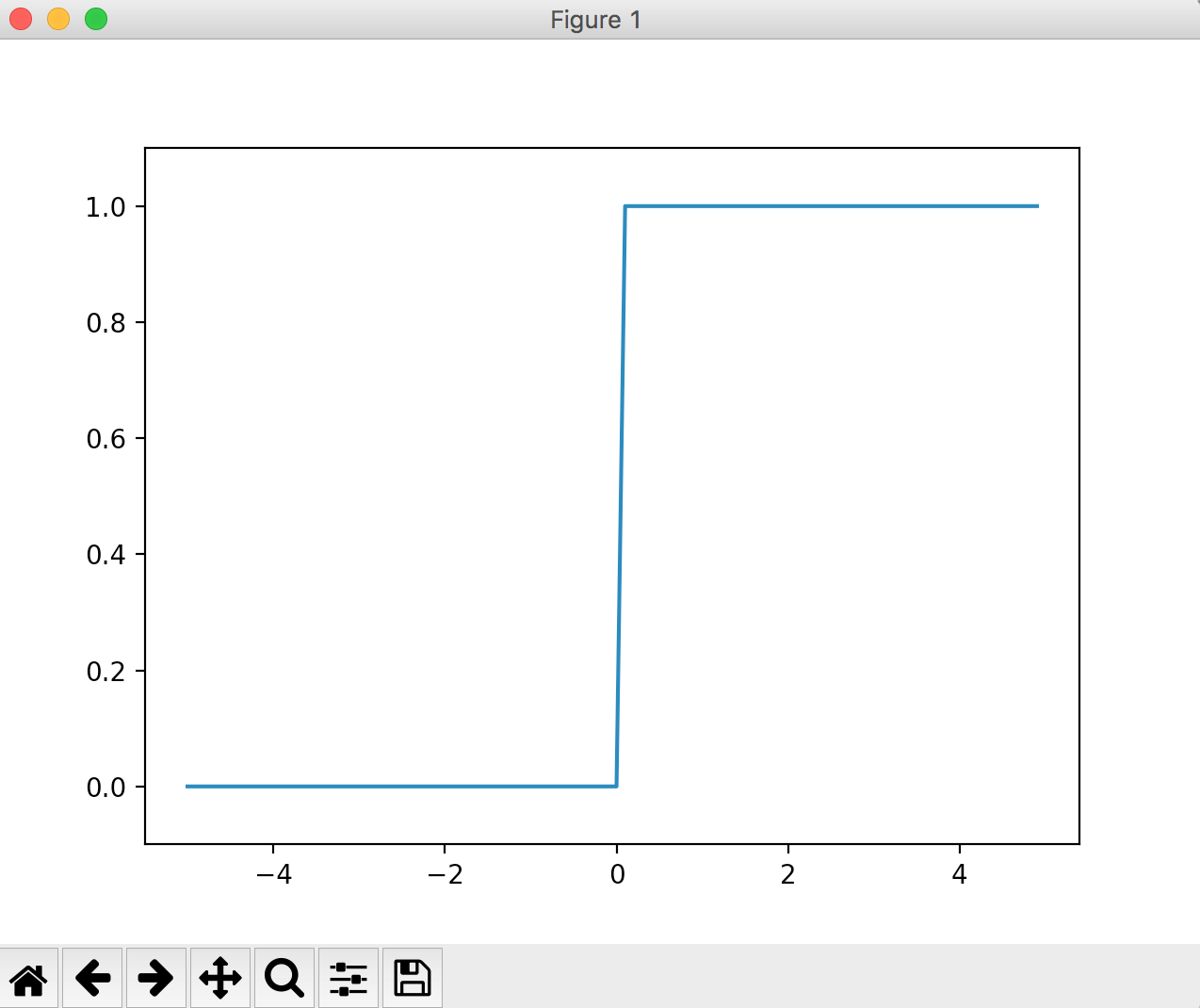
ステップ関数は、閾値を境にして出力が切り替わる関数です。「階段関数」とも呼ばれます。
一般的に、単純パーセプトロン（単層のネットワーク）で使われる関数です。

入力した値が0以下のとき0になり、0より大きいときに1になるステップ関数を例として、
実装と動作を以下に示します。

def step_function(x):
  if x>0:
    return 1
  else:
    return 0

# step_function(4) => 1
# step_function(-3) => 0

グラフは以下のように実装できます。
step_functionは配列【np.array()】を引数として扱えるように実装してありますが、
配列を扱う以外の動作は変わりません。

import numpy as np
import matplotlib.pylab as plt

def step_function(x):
  y = x > 0
  return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

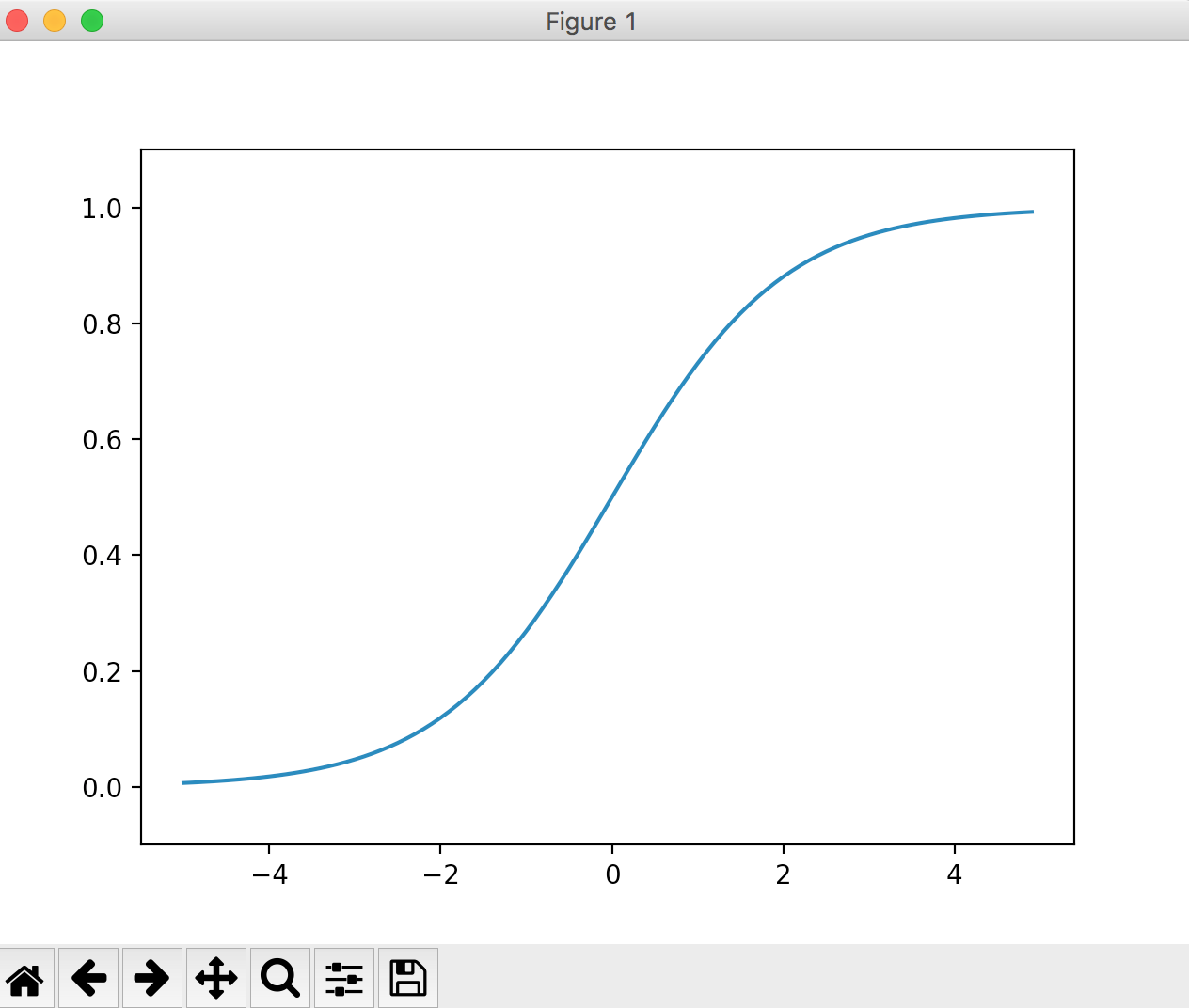
シグモイド関数

式は以下のようになります。

h(x) = \frac{1}{1+e^{-x}}\\
e^{-x}はnumpyではnp.exp(-x)と書ける。

入力した値が大きければ大きいほど1に近づき、
入力した値が小さければ小さいほど0に近づく関数です。
ステップ関数の出力は0か1であることと比較して、元の入力の値を殺しすぎないと言えるでしょう。

実装と動作が以下になります。

import numpy as np

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.array([-3.0, 1.0, 4.0])
# sigmoid(x) => [ 0.04742587  0.73105858  0.98201379]

グラフは以下のようになります。

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x):
  return 1 / (1+np.exp(-x))

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()

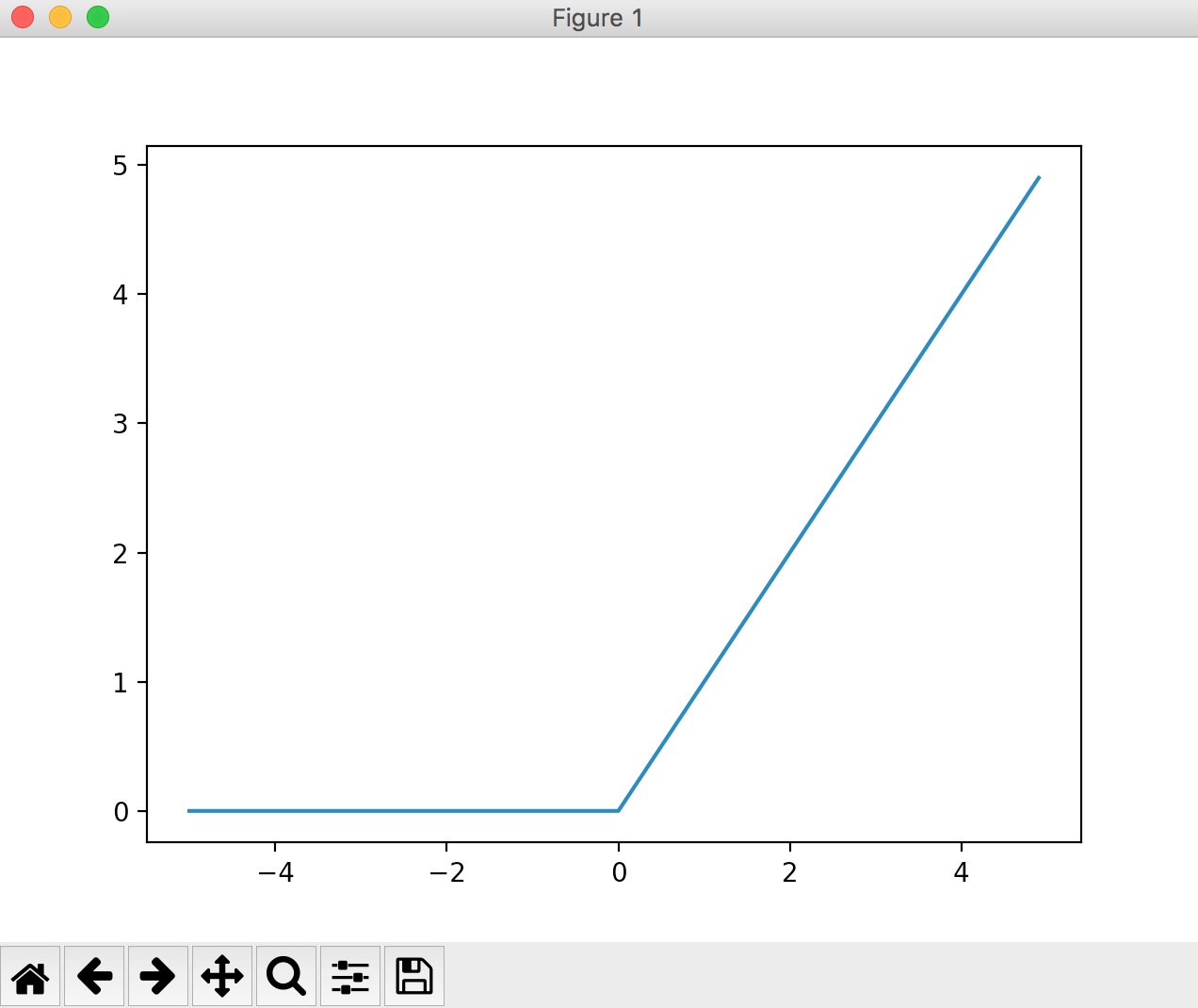
ReLU関数

入力した値が0以下のとき0になり、1より大きいとき入力をそのまま出力します。
以下のようなグラフになります。

import numpy as np
import matplotlib.pylab as plt

def relu(x):
  return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.show()

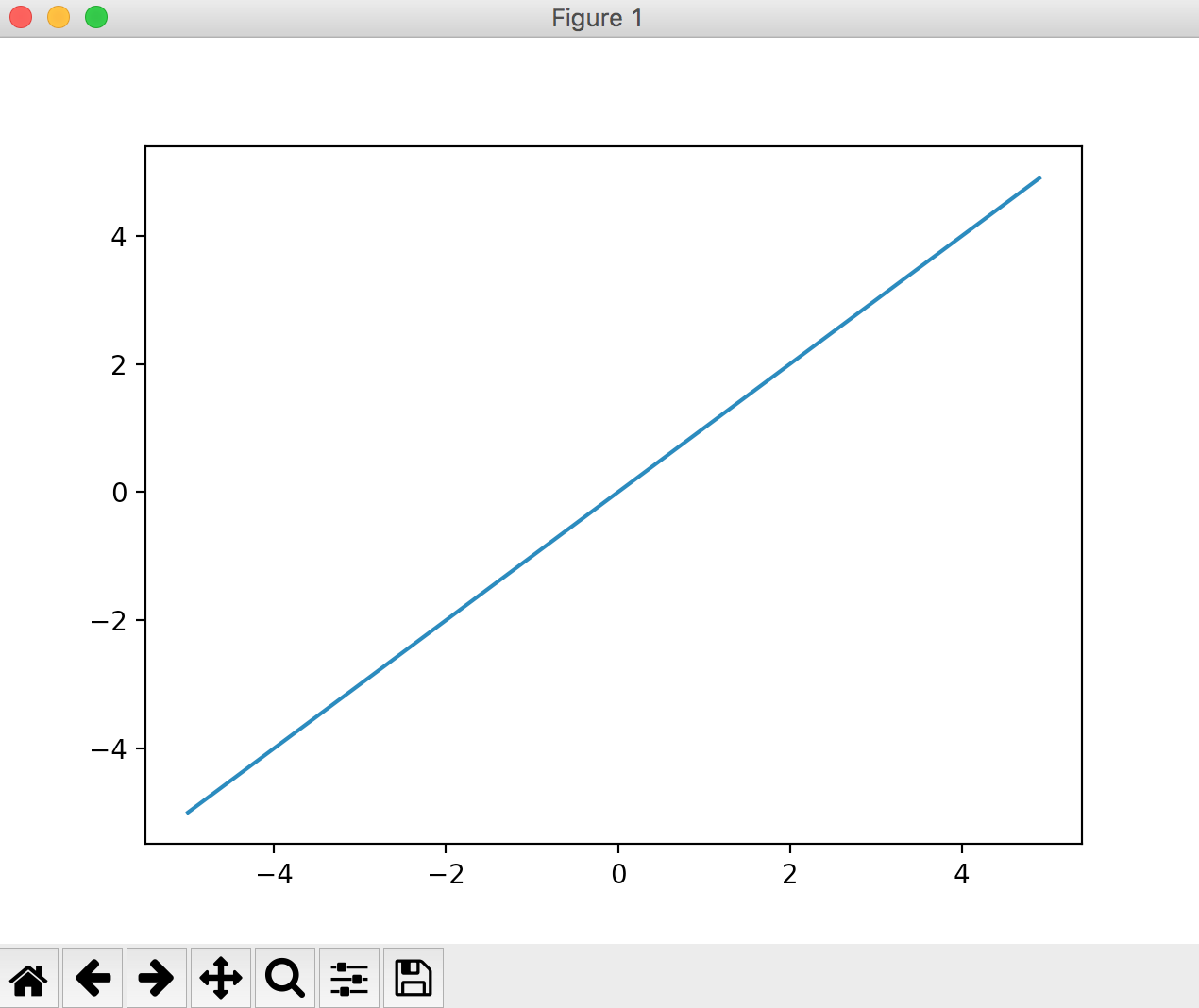
恒等関数

出力層で使われる関数です。
入力した値と同じ値を常にそのまま返す関数です。
【質問】数学：恒等関数とは

一般的に、回帰問題で使われます。

import numpy as np
import matplotlib.pylab as plt

def koutou(a):
  return a

x = np.arange(-5, 5, 0.1)
y = koutou(x)
plt.plot(x, y)
plt.show()

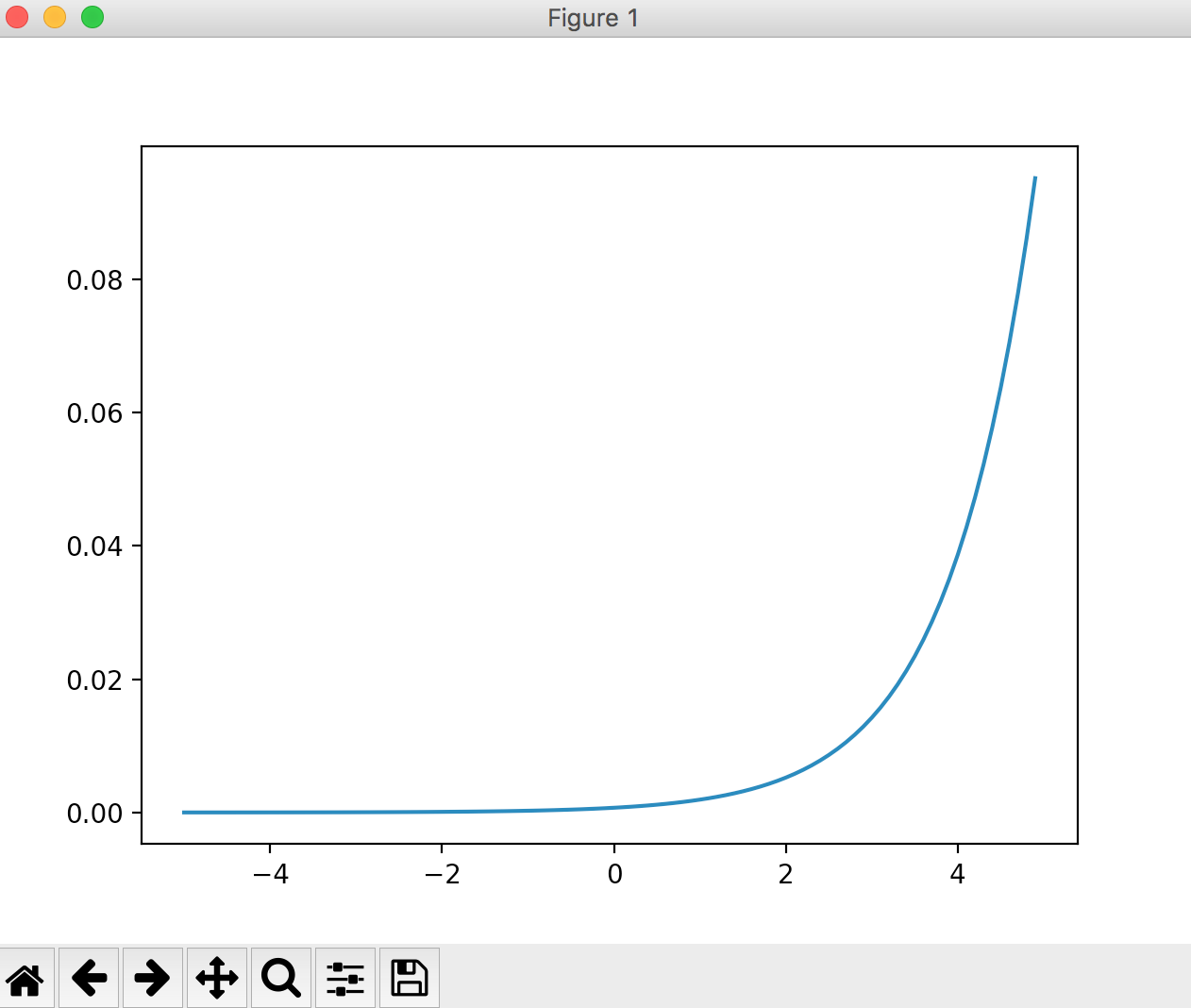
ソフトマックス関数

出力層で使われる関数です。
一般的に分類問題で使われます。

import numpy as np
import matplotlib.pylab as plt

def softmax(a):
  exp_a = np.exp(a)
  sum_exp_a = np.sum(exp_a)
  y = exp_a / sum_exp_a
  return y

x = np.arange(-5, 5, 0.1)
y = softmax(x)
plt.plot(x, y)
plt.show()

線形関数と非線形関数

線形関数は出力が入力の定数倍になるような関数を指します。
例えば、y=cx(cは定数)。グラフにするとまっすぐな１本の直線になります。

非線形関数は、線形関数ではないものを指します。

なぜ多層パーセプトロンで線形関数を使わないのか？

理由は、活性化関数に線形関数を用いるとニューラルネットワークで層を深くすることの意味がなくなるからです。
線形関数の問題点は、どんなに層を深くしても、それと同じことを行う「隠れ層のないネットワーク」が必ず存在する、という事実に起因します。
簡単な例として、線形関数h(x)=cxを活性化関数として３層重ねるとy=h(h(h(x))になります。つまりこれは、y=c*c*c*x(y=ax)というように隠れ層のないネットワークでも表現できてしまいます。

この例のように、活性化関数に線形関数を用いると多層にすることの利点を生かすことができません。
つまり、それは無駄に処理を増やすことにつながるかもしれないので、活性化関数に線形関数を用いるべきではありません。

回帰問題と分類問題

回帰問題は、ある入力データから、（連続的な）数値の予測を行う問題です。（例：人の写った画像から、その人の体重を予測する問題）

分類問題は、データがどのクラスに属するか、という問題です。（例：人の写った画像から、その人が男性か女性のどちらであるかを分類するような問題）