初心者の初心者による初心者のためのニューラルネットワーク#3〜理論：逆伝播編〜

機械学習初心者でも、ニューラルネットワーク(neural network : NN)について理解しなければならない日がいつか来る。なので初心者代表の私が、ニューラルネットワークについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
本記事は、以下の記事の続きとなります。
①初心者の初心者による初心者のためのニューラルネットワーク#1〜理論：順伝播編〜
②初心者の初心者による初心者のためのニューラルネットワーク#2〜理論：誤差計算編〜

#1. なぜ人はニューラルネットワークを学ぶのか
今や日常生活の様々な場面に用いられている、機械学習のコアの部分だからです。
#２. 本記事の目的
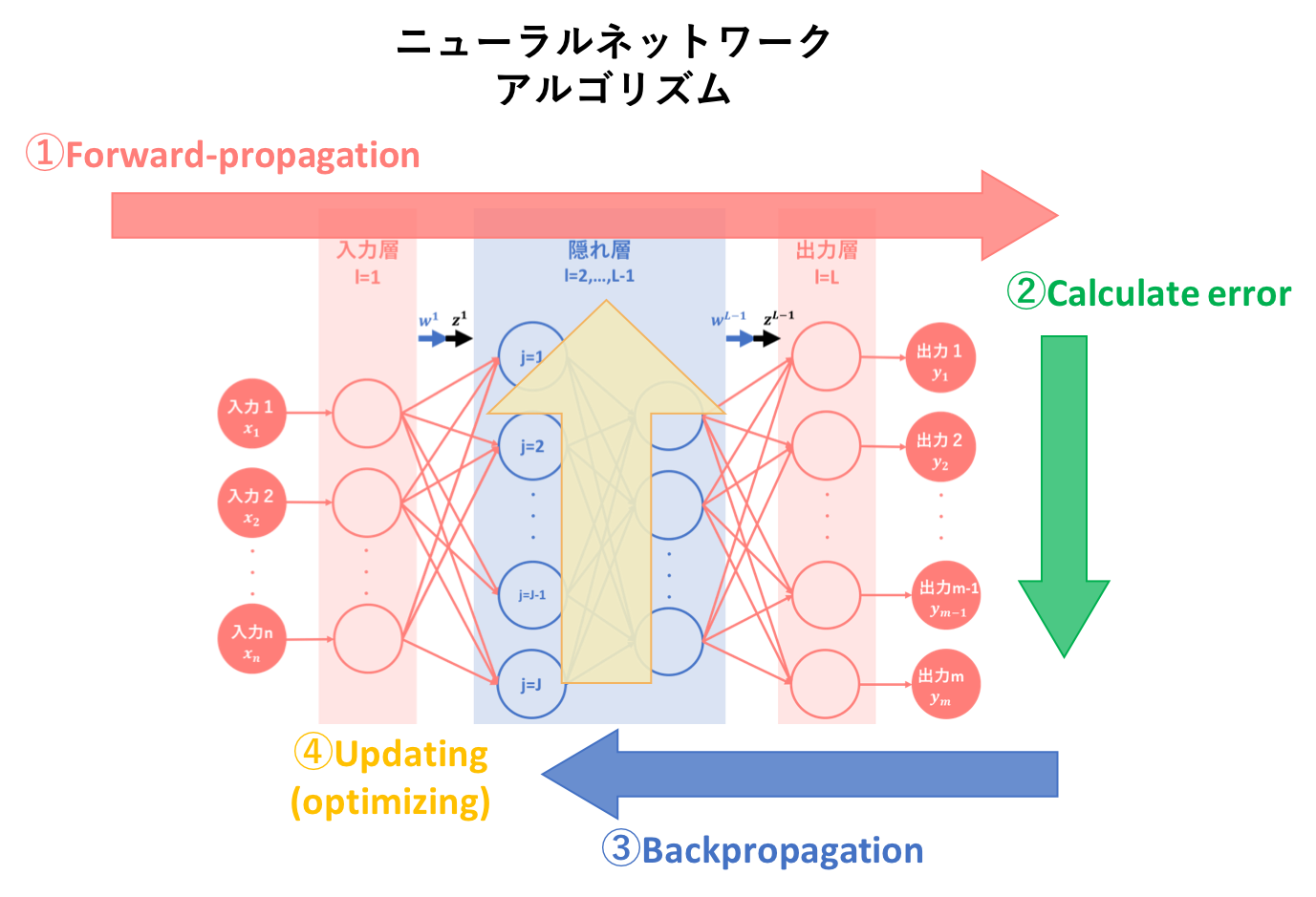
本記事では、ニューラルネットワークのアルゴリズムを簡易図式化した以下の図のうち、③逆伝播についての説明を行います。

#３. 前記事の要約
初心者の初心者による初心者のためのニューラルネットワーク〜理論：順伝播編〜では、ニューラルネットワークの基本概念、基本構造そしてアルゴリズム①である順伝播（forward-propagation）について説明しました。
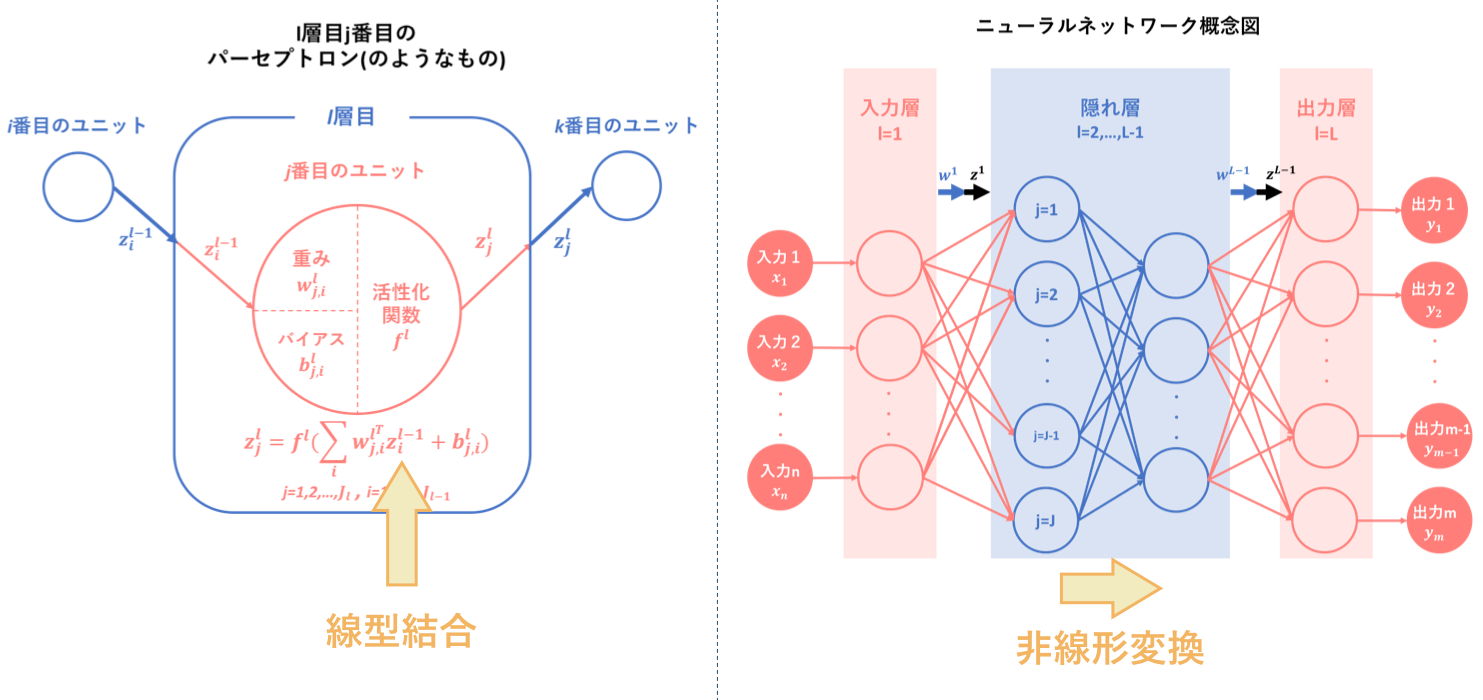
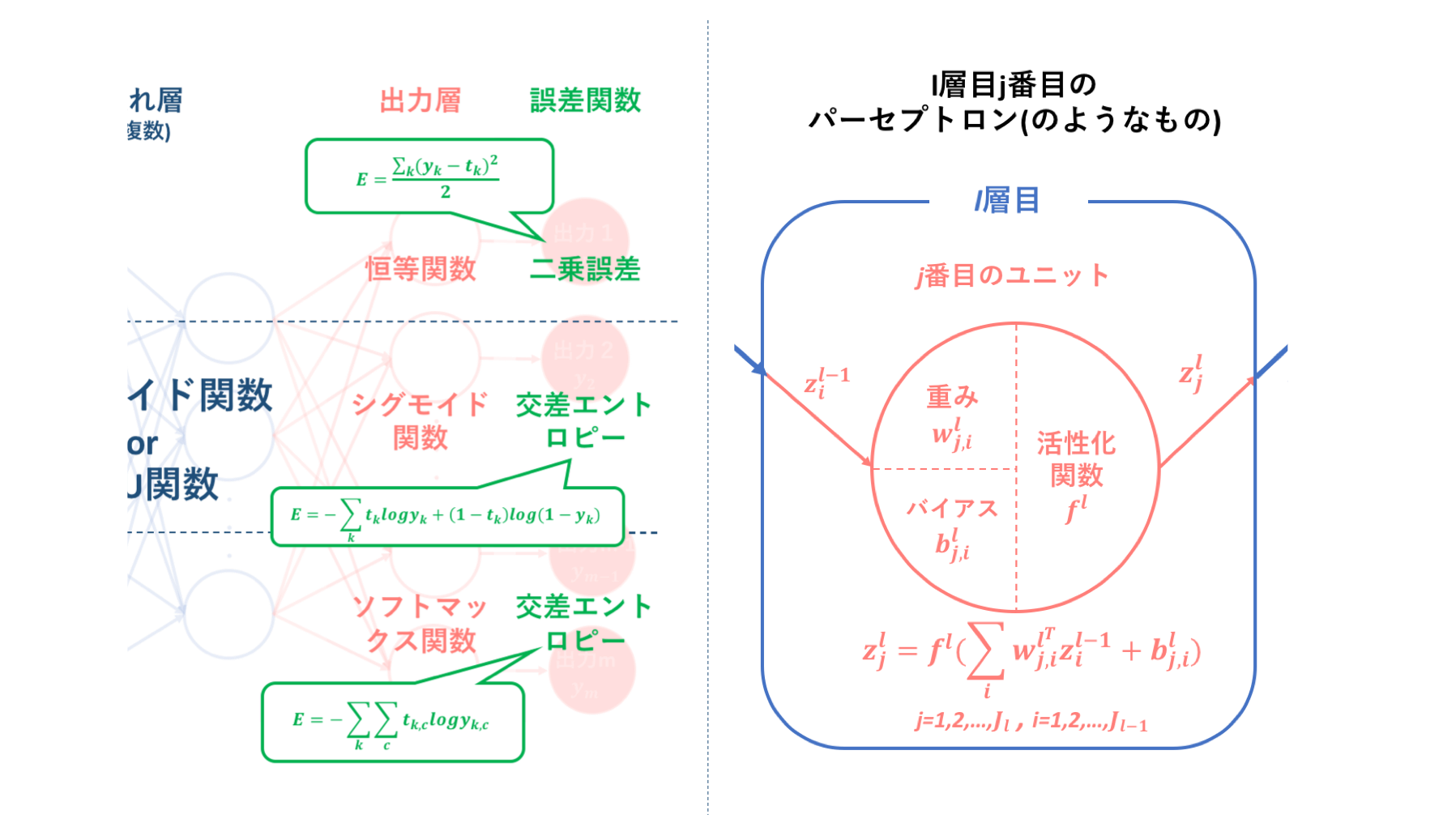
その要約として以下の図をあげます。ニューラルネットワークとは、『パーセプトロン(のようなもの)を基に人間の脳神経系のニューロンを数理モデル化したもの』のことであり、『線型結合と非線形変換を繰り返す合成関数 $f(w,x)$によって入力から出力を表すモデル』です。
そして、ニューラルネットワークの目的は最適パラメータの発見であり、そのために学習を繰り返すことによって予測出力を最適化するようなパラメータを導出します。
順伝播は、その学習アルゴリズムの一つ目でした。

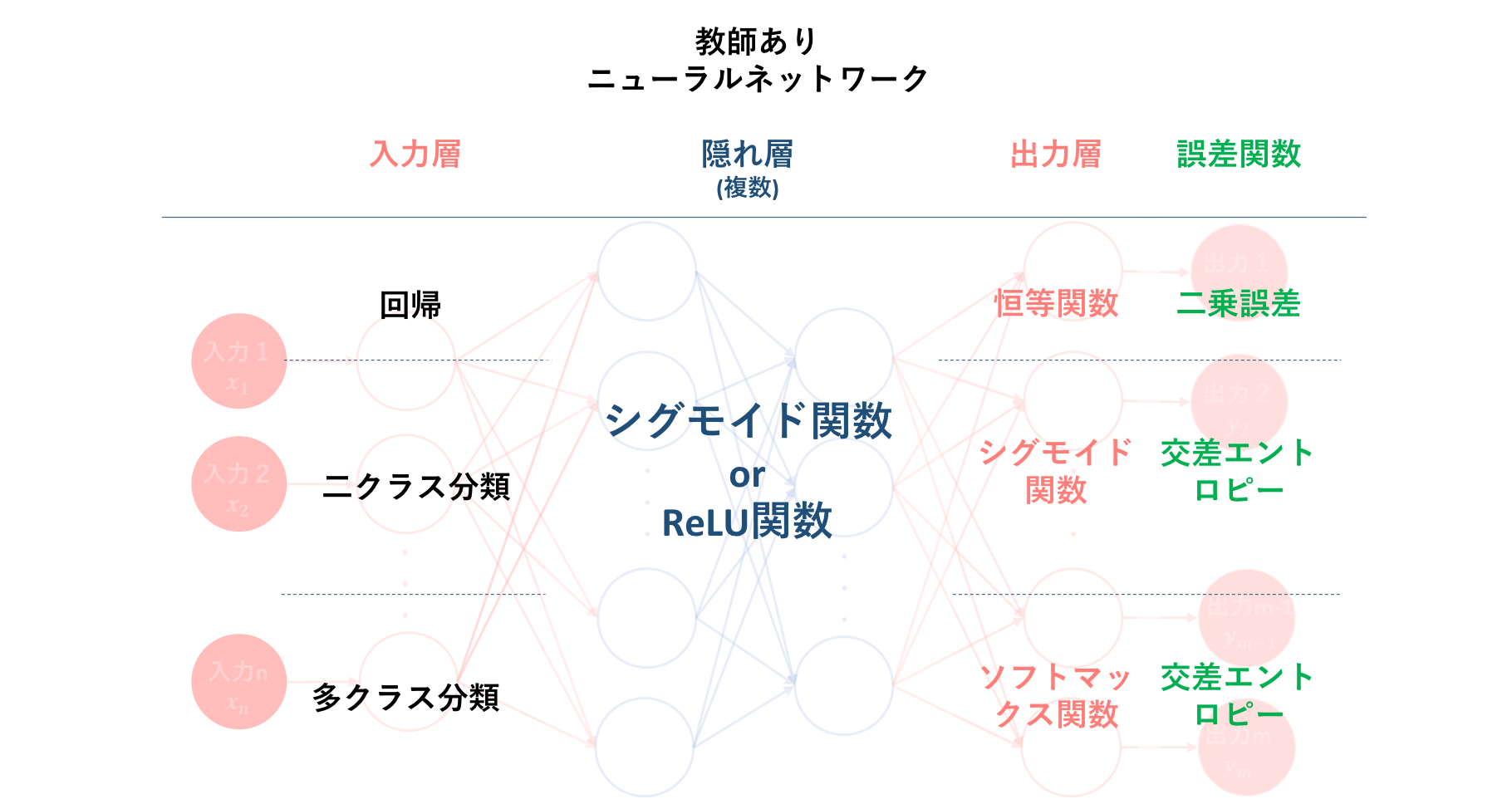
そして続く初心者の初心者による初心者のためのニューラルネットワーク〜理論：誤差計算編〜では、アルゴリズム②である出力値と教師信号のずれの程度を表すための誤差計算について説明しました。そして、こちらはアルゴリズム②には含まれない部分ですが、誤差関数と密接に関係する多層パーセプトロン内の活性化関数の種類とその使用場面についての説明も行いました。
以下の図は、それらの誤差関数および活性化関数の種類と、それぞれどのような問題に対し用いることが一般的なのかをまとめたものになります。
そしてこれに基づいた誤差計算は、学習アルゴリズムの二つ目でした。

#4. 勾配計算のアルゴリズム
ではいよいよ、ニューラルネットワークの学習アルゴリズム③：逆伝播について説明していきます。

前々記事で簡潔に述べましたが、学習機械としてのニューラルネットワークにおける目標は、学習を繰り返すことによって最適なモデルを構築することでした。そして、最適なモデルとは多くの場合、目標値と予測値の差が最も近くなるようなモデルのことを指し、そのためには最適な重み$w$を抽出する必要があります。
逆伝播では、アルゴリズム②で算出された誤差に基づいて最適な重み$w$の抽出を目指します。そしてこの抽出アルゴリズムは、誤差逆伝播法(backpropagation)という手法によって構築されています。
しかし本記事のメインテーマは誤差逆伝播法の中でも勾配計算の部分とし、それに対する説明を行います~~。また本章では、誤差逆伝播法に対しあくまで基本的なアルゴリズムの導出にとどめ、数式計算についての説明は省きます。~~以下に数式を用いて丁寧に説明している記事を紹介しますので、そちらも合わせてご参照下さい。

・高卒でもわかる機械学習 (5) 誤差逆伝播法 その1
・高卒でもわかる機械学習 (6) 誤差逆伝播法 その2
・誤差逆伝搬法（バックプロパゲーション）とは
・誤差逆伝播法のノート
・誤差逆伝播法をはじめからていねいに

##4.1. 誤差逆伝播法の基盤
さて、このようなニューラルネットワークの学習において肝の部分を担う誤差逆伝播法ですが、その考え方の基盤となっているのは、**「連鎖律」という定理と「勾配降下法」**というアルゴリズムです。
以下、それぞれについて見ていくことにしましょう。
###4.1.1. 連鎖律(chain rule)

「連鎖律」とは、複数の関数が組み合わさった合成関数を微分する際のルールのことです。
高校数学範囲内の合成関数の微分は馴染みがあるのではないでしょうか。
a が b の関数で、さらに b が c の関数とします。このとき、 a を c で微分した$\frac {da}{dc}$について、下記のような公式があります。
$$\frac {da}{dc} = \frac {da}{db} \frac {db}{dc}$$
これを大学数学の範囲では、合成関数の偏微分方程式に拡張します。
a が $b_1, b_2, \dots, b_n$ の関数（複数変数を持つ）で、$b_1, b_2, \dots, b_n$ がそれぞれ c の関数である場合、a を c で偏微分すると下記のようになります。
$$\frac {\partial a}{\partial c} = \sum_{k=1}^n \frac {\partial a}{\partial b_k} \frac {\partial b_k}{\partial c}\tag{4.1}$$
さらにこれの特殊ケースとして、$b_1, b_2, \dots, b_n$ のうち、実は m 番目のみが c の関数で、ほかは c の影響を受けない場合を考えます。
$b_k$ を表す式が c を含まないのであれば、$b_k$ を c で偏微分すると 0 になります。つまり、$\sum$の中の$\frac {\partial b_k}{\partial c}$ は、$k\neq m$ の場合はすべて 0 になるので、$k = m$の場合だけを考慮すればよくなります。
$$\frac {\partial a}{\partial c} = \frac {\partial a}{\partial b_m} \frac {\partial b_m}{\partial c}\tag{4.2}$$
イメージとしては、以下のようになります。
・変数が中継する (例えば $a_i → b_1 → c$) 場合、偏微分は各々の 積 で表す
・変数が複数に分岐する ( $b_1,b_2,…,b_n → c$) 場合、偏微分は各々の 和 で表す

###4.1.2. 勾配降下法(gradient descent)
初心者の初心者による初心者のための単純パーセプトロンでも述べていますが、ここでも再度説明します。勾配法は大きく２つあり、勾配上昇法そして勾配降下法があります。勾配降下法とは、目的関数が最小化されるようパラメータを調整し最適化するためのアルゴリズムです。損失関数を用いる多くの学習機械では損失を最小とすることを目的とするので、原則として勾配降下法が用いられます。

上の図は、この勾配降下法を分かりやすく示したものです。
縦軸のEとは損失関数(誤差関数)を指します。このEの値が極小値となる点が学習機械の目指す場所であり、そのwが最適解となります。よって、
・現在の $w_i$でグラフの傾きが正の場合 → $w_i$ を負の方向に動かす
・現在の $w_i$でグラフの傾きが負の場合 → $w_i$ を正の方向に動かす
これら２つのプロセスを繰り返し行うことにより極小点に辿り着くことができるというわけです。

そして、$w_i$が多変数、つまりベクトルになっても考え方は同じです。しかし、個々の変数を修正するためには $w_{i,1},w_{i,2},…,w_{i,n}$ それぞれの値の変化に対する$E$の増減に注目する必要が生じるため、式は偏微分になります。

##4.2. 連鎖律と勾配降下法のジョイン
さて、ここまでで誤差逆伝播法が**「連鎖律」と「勾配降下法」を基盤とするということは述べました。では一体、この定理及びアルゴリズムをどのように組み合わせれば『重み$w$の最適化』**を達成することが出来るのでしょうか。

勾配降下法を用いて重みを最適化しようとすることは比較的分かりやすいのではないかなと思います。繰り返しになりますが、多層パーセプトロンの場合、誤差関数を最小化したものが最適モデルであり、そのときの重み$w$が最適パラメーターとなります。よって、勾配降下法は収束解を求める一つの適切な手段となります。

では実際に、誤差関数$E$を$w_i$で微分してみましょう。多層パーセプトロンの構造を考えたとき、$w_i$は多変数なので、式は偏微分式となります。
$$\frac{\partial{E(w_{j,i})}}{\partial{w_{j,i}}}$$これが0になるような$w_{j,i}$を探索するわけですが、果たしてこれは簡単なことなのでしょうか。今は便宜上$E(w_{j,i})$としていますが、入力からの経路を考えれば、この誤差関数は非常に複雑な構成をしていることが伺えます。よって、この微分はいくらコンピューターでも時間がかかり過ぎてしまいます。
しかし、この式に既出の「連鎖律」という定理を適用すれば、この問題を解決することが可能になります。前記事の初心者の初心者による初心者のためのニューラルネットワーク〜理論：誤差計算編〜で、誤差関数について少し復習しましょう。

上図は、左部に誤差関数$E$を、右部に活性化関数$f$を示した（つもり）のものです。このとき、ユニットの出力は変数$z$で表されていますが、出力$y$も同様の式で表されます。
この図が示していること、それはズバリ、誤差関数$E$は出力$y$の関数であり、出力$y$はユニットの出力$z$と同等、すなわち重み$w$の関数であるということです。すなわち、この$E, y, w$の三変数に対して連鎖律が適用できることが分かります。
では、早速先程の式に連鎖律を適用してみましょう。ここで、今回は隠れ層$j$番目から出力層$i$番目への場合を考えます。

$$\frac{\partial{E(w_{k,j})}}{\partial{w_{k,j}}}=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{w_{k, j}}}$$
分かりやすくなったかどうかはさておき、どのように連鎖律と勾配降下法がジョインするか概観できたのではないでしょうか。
そして、これを各層において繰り返すと、どうやら誤差逆伝播法は最適パラメーター$w$の選定において有効な手法となるようです。本当にそうなのでしょうか。以降ではより詳しく見ていくことにしましょう。
##4.3. 出力層(L層)の勾配計算
誤差逆伝播法は誤差関数によって得られた誤差値を基準とするので、逆伝播のプロセスに沿ってみていくこととしましょう。それに従ってここではまず、L層の重み$w^L$に対する勾配を求めることを目指します。

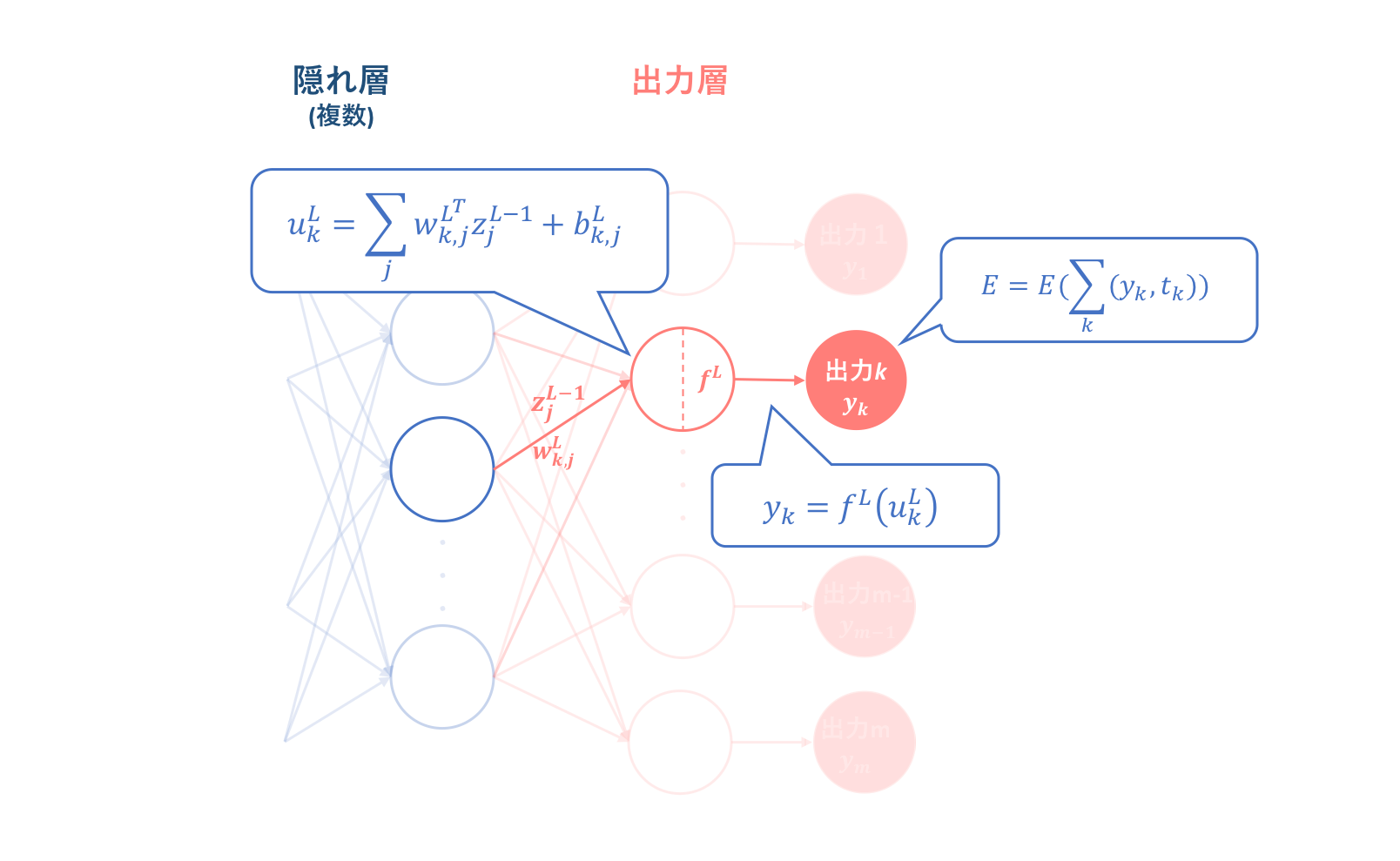
上図は出力層における順伝播をピックアップして図式化したものです。これに基づいて誤差関数の重みに対する勾配を辿ろうとすれば、前節に基づいて以下のような式変形を行うことができます。

\begin{align}
\frac{\partial{E(w_{k,j}^L)}}{\partial{w_{k,j}^L}}&=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}\frac{\partial{u_{k}^L}}{\partial{w_{k, j}^L}}\\
&=\frac{\partial{E(y_k)}}{\partial{y_{k}}}*{f^{(L)}}^{'}(u_k^{L})*z_{j}^{L-1}\\
&=\delta{_k^{L}}z_{j}^{L-1}\tag{4.3}
\end{align}

ここで、$\frac{\partial{E(y_k)}}{\partial{y_{k}}}{f^{(L)}}^{'}(u_k^{L})$は添字がすべて$k$であることから、L層k番目のユニット特有の"なにか"であることが分かります。このとき、"なにか"が何なのかというのはどうでも良いのですが、今後の計算のためにこの"なにか"を便宜上$\delta_{k}^{L}$と置くことにします。
この式$(4.3)$から分かることは、誤差関数$E$のL層の重み$w^L$に対する勾配はL-1層からの出力に大きく依存するということです。
しかしここで、非常に重要なことを気に掛けておかなければいけません。それは、$\frac{\partial{E(y_k)}}{\partial{y_{k}}}{f^{(L)}}^{'}(u_k^{L})=\delta_{k}^{L}$だという捉え方をしてしまうと、次の隠れ層の変換の際に解釈がややこしくなる場面があります。よって、$\delta_{k}^{L}=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}=\frac{\partial{E(u_{k}^L)}}{\partial{u_{k}^L}}$だと留意しておいてください。
そしてこのときの偏微分式変形において、連鎖律の式は式$(4.2)$を用いています。この理由は、変数$w_{k,j}^L$が誤差関数$E$を表す上で複数分岐せず一つの流れで表せることに拠ります。(言葉足らずの説明ですが、次との比較で感覚的理解はできると思います。)

##4.4. 隠れ層(L-1層)の勾配計算
では、出力層と同様のプロセスで、誤差関数$E$の隠れ層の重み$w_{j,i}$に対する勾配を求めていきましょう。ただし、出力層の場合と項を分けたことによってお気づきかもしれませんが、出力層の場合と完全に同様というわけにはいきません。連鎖律の観点から異なる式となるので、その点も含めて説明していきます。
今回はまず、L-1層の重み$w^{L-1}$に対する勾配をピックアップしその後一般化していきます。

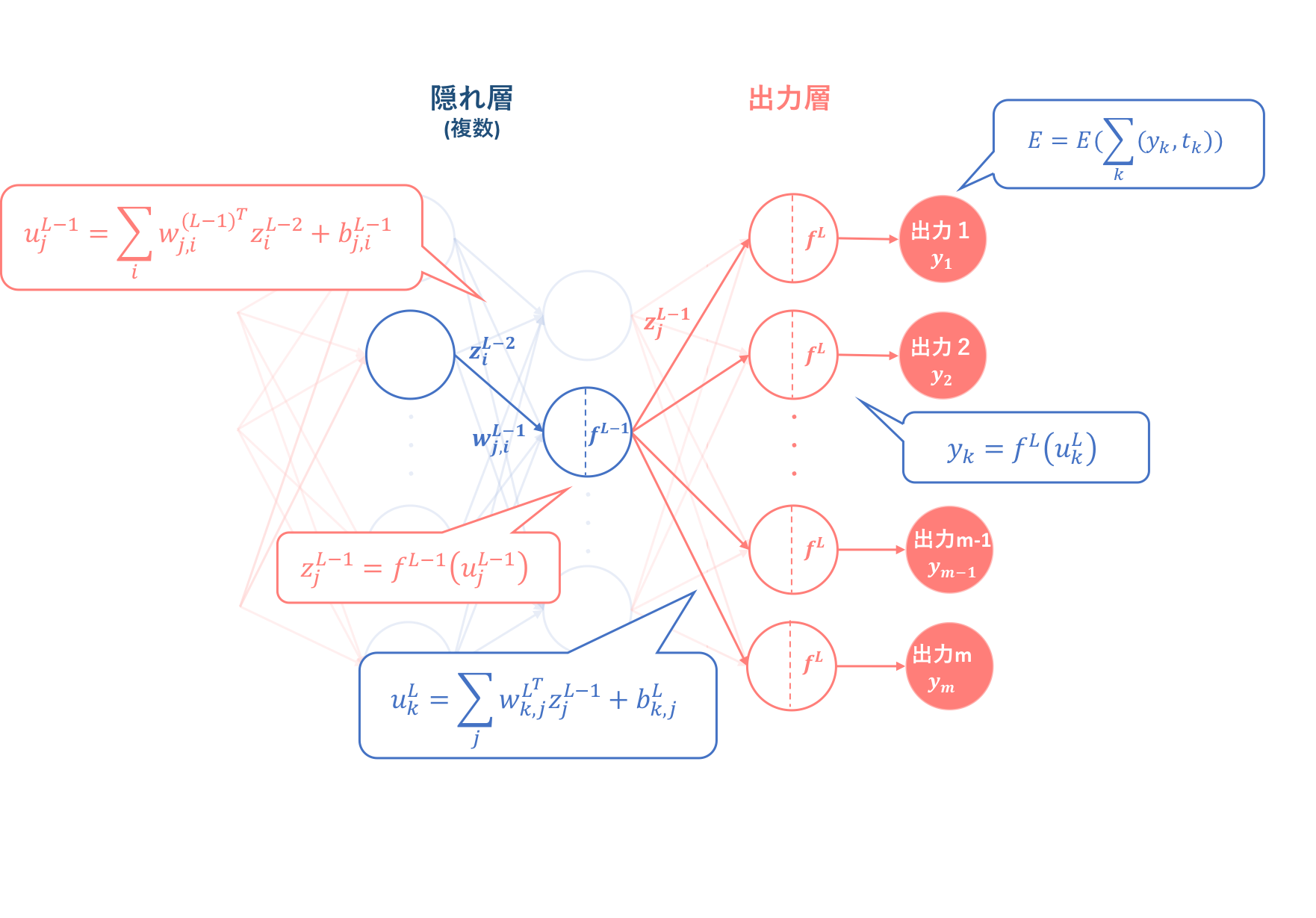
上図は出力層における順伝播をピックアップして図式化したものです。まず、出力層の場合と同様に、誤差関数$E$の隠れ層の重み$w_{j,i}^{L-1}$に対する勾配は、上図をもとに以下の式で表されます。

\begin{align}
\frac{\partial{E(w_{j,i}^{L-1})}}{\partial{w_{j,i}^{L-1}}}&=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}\frac{\partial{z_j^{L-1}}}{\partial{u_{j}^{L-1}}}\frac{\partial{u_{j}^{L-1}}}{\partial{w_{j, i}^{L-1}}}\\
&=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}*{f^{(L-1)}}^{'}(u_j^{L-1})*z_{i}^{L-2}\tag{4.4}
\end{align}

この式から、隠れ層においても誤差関数$E$のL-1層の重み$w^{L-1}$に対する勾配はL-2層からの出力に大きく依存するということが分かります。
しかしここで出力層のときと大きく異なるのは、式$(4.4)$の第一項$\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}$の部分です。出力層の場合は誤差関数$E$は出力$y_k$の関数であることは明らかであり、偏微分も簡単にできますが、式$(4.4)$では誤差関数$E$をL-1層の出力$z_j^{L-1}$で偏微分することが必要になります。
**そしてこの偏微分の際に必要となるのが、連鎖律の式$(4.1)$です。**なぜでしょうか。それは上の図を見てもらえれば分かりやすいと思うのですが、L-1層の出力$z_j^{L-1}$はL層の特定のユニットに掛けられるわけではなく、すべてのユニットに一様に掛けられています。これはつまり変数$z_j^{L-1}$が複数に分岐しているということであり、誤差関数$E$はそれらすべての出力を考慮して偏微分を行わなければいけません。
よって、隠れ層L-1の逆伝播は加えて以下の式変形が必要になります。

\begin{align}
\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}&=\sum_{k=1}^m \frac {\partial E(y_k)}{\partial y_k} \frac {\partial y_k}{\partial u_k^{L}}\frac{\partial u_k^{L}}{\partial{z_j^{L-1}}}\\
&=\sum_{k=1}^m\frac{\partial{E(y_k)}}{\partial{y_{k}}}*{f^{(L)}}^{'}(u_k^{L})*w_{k,j}^{L}\\
&=\sum_{k=1}^m\delta{_k^{L}}w_{k,j}^{L}\tag{4.5}
\end{align}

そしてこれを式$(4.4)$に代入すれば、

\begin{align}
\frac{\partial{E(w_{j,i}^{L-1})}}{\partial{w_{j,i}^{L-1}}}&=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}\frac{\partial{z_j^{L-1}}}{\partial{u_{j}^{L-1}}}\frac{\partial{u_{j}^{L-1}}}{\partial{w_{j, i}^{L-1}}}\\
&=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}*{f^{(L-1)}}^{'}(u_j^{L-1})*z_{i}^{L-2}\\
&=(\sum_{k=1}^m\delta{_k^{L}}w_{k,j}^{L})*{f^{(L-1)}}^{'}(u_j^{L-1})*z_{i}^{L-2}\\
&=\delta{_j^{L-1}}z_{i}^{L-2}\tag{4.6}
\end{align}

という式変形結果が得られます。これは先程の$(4.3)$式と非常に似ていますね。
しかしこの式変形においては、$(\sum_{k=1}^m\delta_{k}^{L}w_{k,j}^{L}){f^{(L-1)}}^{'}(u_j^{L-1})=\delta_{j}^{L-1}$というような変換を行なっています。この変換は妥当なものなのでしょうか。この変換が妥当であると言えない限りは、ただ$(4.3)$式に似せただけだという捉え方もできてしまいます。
ここで思い出して欲しいのが、$\delta_{k}^{L}=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}=\frac{\partial{E(u_{k}^L)}}{\partial{u_{k}^L}}$という仮定です。この式に基づけば、$\delta_{j}^{L-1}=\frac{\partial{E(u_{j}^{L-1})}}{\partial{u_{j}^{L-1}}}=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}\frac{\partial{z_j^{L-1}}}{\partial{u_{j}^{L-1}}}$となるため、式$(4.6)$の一行目と見比べれば、この変換には納得がいきます。
では、なぜ式$(4.6)$ではわざわざ回りくどい変換を行なったのでしょうか。実はこの回りくどい変換こそが、誤差逆伝播法というネーミングに大きく関連しているのです。これについては、ここでは一旦スキップして4.6節にて説明します。

##4.5. 隠れ層(l層)の勾配計算
先程の疑問を解決してしまう前に、隠れ層の勾配計算をL-1層だけでなくl層に一般化してしまいましょう。出力層と隠れ層で用いられる連鎖律が異なることは前節ですでに述べています。（念のため）

上図は出力層における順伝播をピックアップして図式化したものです。まず、出力層の場合と同様に、誤差関数$E$の隠れ層の重み$w_{j,i}^{L-1}$に対する勾配は、上図をもとに以下の式で表されます。

\begin{align}
\frac{\partial{E(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}&=\frac{\partial{E(z_j^{l})}}{\partial{z_j^{l}}}\frac{\partial{z_j^{l}}}{\partial{u_{j}^{l}}}\frac{\partial{u_{j}^{l}}}{\partial{w_{j, i}^{l}}}\\
&=\frac{\partial{E(u_j^{l})}}{\partial{u_j^{l}}}z_{i}^{l-1}\\
&=\delta{_j^{l}}z_{i}^{l-1}\tag{4.7}
\end{align}

この式から、隠れ層lにおいても誤差関数$E$のl層の重み$w^{l}$に対する勾配は、誤差信号$\delta^{l}$と前層の出力$z_i^{l-1}$の積で表されることが分かります。
##4.6. 誤差逆伝播の解釈(私見)
まず、4.4節で生じた疑問を整理します。
$$\delta_{k}^{L}=\frac{\partial{E(y_k)}}{\partial{y_{k}}}{f^{(L)}}^{'}(u_k^{L})\tag{4.8}$$$$\delta_{j}^{L-1}=(\sum_{k=1}^m\delta_{k}^{L}w_{k,j}^{L}){f^{(L-1)}}^{'}(u_j^{L-1})\tag{4.9}$$というような変換を行っています。この変換が適切であることは、4.4節でも述べました。

ここで思い出して欲しいのが、$\delta_{k}^{L}=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}=\frac{\partial{E(u_{k}^L)}}{\partial{u_{k}^L}}$という仮定です。この式に基づけば、$\delta_{j}^{L-1}=\frac{\partial{E(u_{j}^{L-1})}}{\partial{u_{j}^{L-1}}}=\frac{\partial{E(z_j^{L-1})}}{\partial{z_j^{L-1}}}\frac{\partial{z_j^{L-1}}}{\partial{u_{j}^{L-1}}}$となるため、式$(4.6)$の一行目と見比べればこの変換には納得がいきます。

しかし、それでは上の二式はどのように解釈を行えばいいのでしょうか。理論上は同じ誤差信号$\delta{}$を用いることが分かっても、式変形のみではいまいち腑に落ちません。
これを説明する上で、今回は隠れ層L-1と出力層Lの関係にフォーカスします。これは前節4.5において、隠れ層lでもL-1層のケースを一般化できることが分かったためです。

ではまずはじめに、式$(4.8)$を見てみましょう。ここでは「ずれ」というのをイメージしやすくするために、yの変数xでの微分値を『その値xから1ずれたときのyのずれ』と呼ぶことにします。

\begin{align}
\delta_{k}^{L}&=\frac{\partial{E(y_k)}}{\partial{y_{k}}}{f^{(L)}}^{'}(u_k^{L})\tag{4.8}\\
&=\frac{\partial{E(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}\\
&=(出力y_kがその値から1ずれたときの誤差関数Eのずれ)\\
&\qquad×(ユニット入力u_k^Lがその値から1ずれたときのy_kのずれ)
\end{align}

（ここで、${f^{(L)}}^{'}(u_k^{L})$を$\frac{\partial{y_{k}}}{\partial{u_{k}^L}}$に戻すならなんでわざわざ${f^{(L)}}^{'}(u_k^{L})$なんて出して来たんだ！と思う方がもしかするといらっしゃるかもしれません。申し訳ありませんご指摘の通りです。ですが多くのWebサイトでは${f^{(L)}}^{'}(u_k^{L})$が採用されていたので本記事でも用いたのですが、個人的な解釈としては$\frac{\partial{y_{k}}}{\partial{u_{k}^L}}$の方が分かりやすいので戻させていただきました。）

戻ります。上の式変形から、出力層における誤差信号$\delta_{k}^L$は、

\begin{align}
\delta_{k}^L&=(出力y_kがその値から1ずれたときの誤差関数Eのずれ)\\
&\quad×(ユニット入力{u_k^L}がその値から1ずれたときのy_kのずれ)\\
&\\
&=(ユニット入力{u_k^L}がその値から1ずれたときのy_kのずれ)\\
&\quad×(出力y_kがその値から1ずれたときの誤差関数Eのずれ)
\tag{4.10}
\end{align}

で解釈されることが分かりました。つまり、誤差信号$\delta_{k}^{L}$は、『出力層Lのkユニットへの入力のずれがどれだけ誤差関数に反映されるか』を示しています。これは$\delta_{k}^{L}=\frac{\partial{E(u_{k}^L)}}{\partial{u_{k}^L}}$としているので、良く考えれば当たり前のことです。では、L-1層の場合はどうでしょうか。

\begin{align}
\delta_{j}^{L-1}&=(\sum_{k=1}^m\delta_{k}^{L}w_{k,j}^{L}){f^{(L-1)}}^{'}(u_j^{L-1})\tag{4.9}\\
&=(\sum_{k=1}^m\delta_{k}^{L}w_{k,j}^{L})\frac{\partial{z_j^{L-1}}}{\partial{u_{j}^{L-1}}}\\
&\\
&=(誤差信号\delta_{k}^{L}にL層の重みをそれぞれ掛けたものの和)\\
&\qquad×(ユニット入力u_j^{L-1}がその値から1ずれたときのz_j^{L-1}のずれ)\\
&\\
&=(ユニット入力u_j^{L-1}がその値から1ずれたときのz_j^{L-1}のずれ)\\
&\qquad×\sum_{k}[(出力ユニットkへのL層の重み)\\
&\qquad\quad×(ユニット入力{u_k^L}がその値から1ずれたときのy_kのずれ)\\
&\qquad\qquad×(出力y_kがその値から1ずれたときの誤差関数Eのずれ)]\\
&\\
&=\sum_{k}[(ユニット入力u_j^{L-1}がその値から1ずれたときのz_j^{L-1}のずれ)\\
&\qquad\quad×(出力ユニットkへのL層の重み)\\
&\qquad\qquad×(ユニット入力{u_k^L}がその値から1ずれたときのy_kのずれ)\\
&\qquad\qquad\quad×(出力y_kがその値から1ずれたときの誤差関数Eのずれ)]\\
\end{align}

つまりこの誤差信号$\delta_{j}^{L-1}$は、『隠れ層L-1のjユニットへの入力のずれがどれだけ誤差関数に反映されるか』を示しています。これは$\delta_{j}^{L-1}=\frac{\partial{E(u_{j}^{L-1})}}{\partial{u_{j}^{L-1}}}$としているので、良く考えれば当たり前のことです。しかし、そこに至るまでのフローは確認できたのではないでしょうか。
ここでは隠れ層L-1を取り上げましたが、同様にして隠れ層lで一般化が可能です。よってこのことから、隠れ層と出力層の誤差信号$\delta{}$は同義であるということが感覚的にも納得できると思います。（何度も言いますがこれは当たり前のことです><）
→誤差逆伝播法のノート：この記事では隠れ層L-2層でも確認を行っています。
→高卒でもわかる機械学習 (6) 誤差逆伝播法 その2：この記事では$l$層における一般化まで述べています。
ちなみに、$l$層において一般化した誤差信号$\delta_{j}^l$は、以下のように表されます。
$$\delta_{j}^l=(\sum_{k=1}^m\delta_{k}^{l+1}w_{k,j}^{l+1})\frac{\partial{z_j^{l}}}{\partial{u_{j}^{l}}}\tag{4.11}$$

このように理論的にも感覚的にも隠れ層と出力層の誤差信号は同義であることが確認でき、式$(4.6)$を納得することができました。よって$\frac{\partial{E(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}=\delta_{j}^{l}z_{i}^{l-1}$となるため、**層$l$における誤差関数$E$のl層の重み$w^{l}$に対する勾配は誤差信号$\delta^{l}$と前層の出力$z_i^{l-1}$の積で表され、本節の議論から$l$層の誤差信号$\delta^{l}$を求めるためには$l+1$層の誤差信号$\delta^{l+1}$が必要となることが分かります。これが『誤差"逆"伝播』と呼ばれる所以になります。**ムダに長い道のりでした。

##4.7. 誤差逆伝播の目的
ここまでガチャガチャやっていると、本来の目的を忘れてしまいがちです。なのでここで今一度、誤差逆伝播法の目的について整理しましょう。

逆伝播では、アルゴリズム②で算出された誤差に基づいて最適な重み$w$の抽出を目指します。そしてこの抽出アルゴリズムは、誤差逆伝播法(backpropagation)という手法によって構築されています。

しかし今求めたのは、層$l$における誤差関数$E$のl層の重み$w^{l}$に対する勾配$\frac{\partial{E(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}$でした。なんということでしょう、これでもまだ不十分だと言うのです。
思い出せばたしかに、誤差逆伝播法の基盤は「連鎖律」と「勾配降下法」の二つでした。しかし残念ながら、本章では勾配降下法について全く触れていません…つまり今求めた勾配$\frac{\partial{E(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}$はあくまで勾配降下法適用のための下準備にすぎなかったということです。
よってこの後さらに、勾配降下法による重み最適化のためのアルゴリズムを構築する必要があるわけですが、それは次の記事で説明することにします。
##4.8. 誤差逆伝播の適用
それでは、初心者の初心者による初心者のためのニューラルネットワーク#2〜理論：誤差計算編〜で得られた結論とこれまでの議論をもとに、より具体的に逆伝播アルゴリズムを見ていくことにしましょう。

###4.8.1 回帰問題
回帰問題では、一般的に隠れ層の活性化関数にReLU関数$f(x)=max(0,x)$, 出力層の活性化関数に恒等関数$f(x)=x$, 誤差関数に二乗誤差関数$E_{se}=\sum_{k}\frac{(y_k-t_k)^2}{2}$を用います。では、それぞれ勾配計算の式に代入していきましょう。
まず出力層の勾配からみていきます。

\begin{align}
E_{se}(y_k)=\sum_{k}\frac{(y_k-t_k)^2}{2}, y_k=u_{k}^{L}&\Longrightarrow\frac{\partial{E_{se}(w_{k,j}^L)}}{\partial{w_{k,j}^L}}
=\frac{\partial{E_{se}(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}\frac{\partial{u_{k}^L}}{\partial{w_{k, j}^L}}\\
&\qquad=(y_{k}-t_{k})*1*z_{j}^{L-1}\\
&\qquad=(y_{k}-t_{k})z_{j}^{L-1}\\
&\qquad=\delta{_k^{L}}z_{j}^{L-1}
\end{align}

次に隠れ層の勾配をみていきます。

\begin{align}
E_{se}(y_k)=\sum_k\frac{(y_k-t_k)^2}{2}, z_j^{l}=max(0, u_j^{l})&\Longrightarrow\frac{\partial{E_{se}(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}
=\frac{\partial{E_{se}(z_{j}^{l})}}{\partial{z_{j}^{l}}}\frac{\partial{z_{j}^{l}}}{\partial{u_{j}^{l}}}\frac{\partial{u_{j}^{l}}}{\partial{w_{j, i}^{l}}}\\
&\qquad=\delta{_j^{l}}z_{i}^{l-1}\\
&\qquad=\left\{
\begin{array}{ll}
(\sum_{k=1}^m\delta_{k}^{l+1}w_{k, j}^{l+1})z_{i}^{l-1}&(u_j^{l}\geq 0)\\
0 & (u_j^{l} \lt 0)
\end{array}
\right.
\end{align}

###4.8.2 二クラス分類問題
二クラス分類問題では、一般的に隠れ層の活性化関数にReLU関数$f(x)=max(0,x)$, 出力層の活性化関数に標準シグモイド関数$f(x)=\frac{1}{1+e^{-x}}$, 誤差関数に交差エントロピー関数$E_{cross}=−\sum_kt_klogy_k+(1−t_k)log(1−y_k)$を用います。では、それぞれ勾配計算の式に代入していきましょう。
まず出力層の勾配からみていきます。

\begin{align}
E_{cross}&=−\sum_k[t_klogy_k+(1−t_k)log(1−y_k)], y_k=\frac{1}{1+e^{-u_{k}^{L}}}\\
&\Longrightarrow\frac{\partial{E_{cross}(w_{k,j}^L)}}{\partial{w_{k,j}^L}}
=\frac{\partial{E_{cross}(y_k)}}{\partial{y_{k}}}\frac{\partial{y_{k}}}{\partial{u_{k}^L}}\frac{\partial{u_{k}^L}}{\partial{w_{k, j}^L}}\\
&\qquad=-(\frac{t_k}{y_k}-\frac{1-t_k}{1-y_k})*(1-y_k)y_k*z_{j}^{L-1}\\
&\qquad=-\frac{y_k-t_k}{(1-y_k)y_k}*(1-y_k)y_k*z_{j}^{L-1}\\
&\qquad=(y_{k}-t_{k})z_{j}^{L-1}\\
&\qquad=\delta{_k^{L}}z_{j}^{L-1}
\end{align}

ここで、シグモイド関数の微分$\frac{\partial{y_{k}}}{\partial{u_{k}^L}}$を求める際、$y_k=\frac{1}{1+e^{-u_{k}^{L}}}$⇒$\frac{\partial{y_{k}}}{\partial{u_{k}^L}}=(1-y_k)y_k$という性質を利用しています。(証明はこちら→シグモイド関数の微分)
ここで、二クラス分類の交差エントロピーにおける出力層の勾配は、先程の二乗誤差の勾配と等しくなっていることに留意してください。
次に隠れ層の勾配をみていきます。

\begin{align}
E_{cross}&=−\sum_k[t_klogy_k+(1−t_k)log(1−y_k)], z_j^{l}=max(0, u_j^{l})\\
&\Longrightarrow\frac{\partial{E_{cross}(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}
=\frac{\partial{E_{cross}(z_{j}^{l})}}{\partial{z_{j}^{l}}}\frac{\partial{z_{j}^{l}}}{\partial{u_{j}^{l}}}\frac{\partial{u_{j}^{l}}}{\partial{w_{j, i}^{l}}}\\
&\qquad=\delta{_j^{l}}z_{i}^{l-1}\\
&\qquad=\left\{
\begin{array}{ll}
(\sum_{k=1}^m\delta_{k}^{l+1}w_{k, j}^{l+1})z_{i}^{l-1}&(u_j^{l}\geq 0)\\
0 & (u_j^{l} \lt 0)
\end{array}
\right.
\end{align}

これについては、回帰問題のときと同じ活性化関数を隠れ層に適用しているので、必然的に同じ結果が得られます。
###4.8.3 多クラス分類問題
多クラス分類問題では、一般的に隠れ層の活性化関数にReLU関数$f(x)=max(0,x)$, 出力層の活性化関数にソフトマックス関数$f(x_k)=\frac{e^{x_{k}}}{\sum_{c=1}^me^{x_{c}}}$, 誤差関数に交差エントロピー関数$E_{cross}=−\sum_lt_{l}logy_{l} \quad \bigr(ただし\sum_lt_{l}=1\bigr)$を用います。では、それぞれ勾配計算の式に代入していきましょう。
まず出力層の勾配からみていきます。ただし、今回はソフトマックス関数,　交差エントロピーがともに非常に複雑であり、添字を細かく使い分けています。それぞれの添字は以下のように設定しているので、必ず確認しながら式変形を読み解くようにして下さい。

• $c$は出力層の何番目ユニットか、$k$は出力層の何番目ユニットか、$l$は出力の何番目の要素かをそれぞれ表しています
• $c$と$k$を使い分けているのは、$c$と$k$が異なる意味合いで用いられるのに同式内に出てくるために違う変数を当てています。変数$c$にほぼ意味はありません
• 出力層のユニット数と出力の数は等しいです

\begin{align}
E_{cross}&=−\sum_{l}t_{l}logy_{l},\sum_lt_{l}=1, y_l=\frac{e^{u_{l}^{L}}}{\sum_{c}e^{u_{c}^{L}}}\\
&\Longrightarrow\frac{\partial{E_{cross}(w_{k,j}^L)}}{\partial{w_{k,j}^L}}
=(\sum_{l}\frac{\partial{E_{cross}(y_l)}}{\partial{y_{l}}}\frac{\partial{y_{l}}}{\partial{u_{k}^L}})\frac{\partial{u_{k}^L}}{\partial{w_{k, j}^L}}\\
&\qquad=\sum_l\left(-\frac{t_l}{y_l}\left\{
\begin{array}{ll}
\frac{e^{u_{l}^{L}}}{\sum_{c}e^{u_{c}^{L}}}-(\frac{e^{u_{l}^{L}}}{\sum_{c}e^{u_{c}^{L}}})^2&(l=k)\\
-\frac{e^{u_{l}^{L}}e^{u_{k}^L}}{(\sum_{c}e^{u_{c}^{L}})^2} & (l\neq k)
\end{array}
\right\}\right)z_j^{L-1}\\
&\qquad=\sum_l\left(-\frac{t_l}{y_l}\left\{
\begin{array}{ll}
y_l(1-y_l)&(l=k)\\
-y_ly_k & (l\neq k)
\end{array}
\right\}\right)z_j^{L-1}\\
&\qquad=\sum_l\left(\left\{
\begin{array}{ll}
-t_l(1-y_l)&(l=k)\\
t_ly_k & (l\neq k)
\end{array}
\right\}\right)z_j^{L-1}\\
&\qquad=\left(-t_k+y_kt_k+y_k\sum_{l\neq k}t_l\right)z_j^{L-1}\\
&\qquad=\left(-t_k+\left(y_kt_k+y_k\sum_{l\neq k}t_l\right)\right)z_j^{L-1}\\
&\qquad=\left(-t_k+y_k\sum_{l}t_l\right)z_j^{L-1}\\
&\qquad=\left(-t_k+y_k\right)z_j^{L-1}=(y_k-t_k)z_j^{L-1}\\
\end{align}

**ここで最も腑に落ちないのは、微分の際の$l=k$と$l\neq k$の場合分けです。ここでは$y_l$を$u_k$で微分しようとしており、$y_l=\frac{e^{u_{l}^{L}}}{\sum_{c}e^{u_{c}^{L}}}$という式の性質上$l=k$と$l\neq k$で場合分けが必要なことは分かりやすいと思います。しかしそれはあくまで数式上の話であり、必要であることの解釈はどのように行えばいいのでしょうか。
ソフトマックス関数が他の出力層活性化関数と大きく異なる点は、出力値を確率として解釈できるようにするために出力層からの出力$u$が自クラスだけではなく他クラスの出力$y$に影響を与えるということです。言い換えれば、出力$y$は出力層のすべてのユニット出力$u$に依存します。以下の図をみると、より分かりやすいのではないでしょうか。

上図から、同クラス出力層からの出力($l=k$)は出力$y_l$の分母・分子に共に影響を与え、他クラス出力層からの出力($l\neq k$)は分母のみにしか影響を与えないことがわかります。これが、$l=k$と$l\neq k$において場合分けを行う理由となります。
つまり、『ソフトマックス関数の出力$y_l$は同クラス($l=k$)他クラス($l\neq k$)両方に依存するけども、その影響度合い(=微分)のメインは同クラス($l=k$)からのものである』**と解釈することができます。
この場合分けについては、多くのWebサイトでは解釈が省略されていますので、気に留めておくと良いと思います。
またもう一つ重要なこととして、ソフトマックス関数はこれまでの出力層活性化関数と違い、一つの出力ユニットがすべての出力値に影響を与えるため、出力層においても式$(4.1)$の連鎖律を用います。
ここで、多クラス分類の交差エントロピーにおける出力層の勾配も、先程の二乗誤差,二クラス分類での交差エントロピーの勾配と等しくなっていることが分かりました。
次に隠れ層の勾配をみていきます。

\begin{align}
E_{cross}&=−\sum_k[t_klogy_k+(1−t_k)log(1−y_k)], z_j^{l}=max(0, u_j^{l})\\
&\Longrightarrow\frac{\partial{E_{cross}(w_{j,i}^{l})}}{\partial{w_{j,i}^{l}}}
=\frac{\partial{E_{cross}(z_{j}^{l})}}{\partial{z_{j}^{l}}}\frac{\partial{z_{j}^{l}}}{\partial{u_{j}^{l}}}\frac{\partial{u_{j}^{l}}}{\partial{w_{j, i}^{l}}}\\
&\qquad=\delta{_j^{l}}z_{i}^{l-1}\\
&\qquad=\left\{
\begin{array}{ll}
(\sum_{k=1}^m\delta_{k}^{l+1}w_{k, j}^{l+1})z_{i}^{l-1}&(u_j^{l}\geq 0)\\
0 & (u_j^{l} \lt 0)
\end{array}
\right.
\end{align}

これについては、回帰問題、二クラス分類のときと同じ活性化関数を隠れ層に適用しているので、必然的に同じ結果が得られます。
#5. まとめ
本記事では、ニューラルネットワークの学習アルゴリズムにおけるメインパート-誤差逆伝播法-を適用するために必要となる「誤差関数の重みに対する勾配」の導出方法を示しました。
以下、本記事のまとめとなります。

それでは、次回は本記事で求めた勾配を用いて重み更新を行う、アルゴリズム④理論：勾配降下編となります。

①初心者の初心者による初心者のためのニューラルネットワーク#1〜理論：順伝播編〜
②初心者の初心者による初心者のためのニューラルネットワーク#2〜理論：誤差計算編〜
③初心者の初心者による初心者のためのニューラルネットワーク#3〜理論：逆伝播編〜(本記事)
④初心者の初心者による初心者のためのニューラルネットワーク#4〜理論：パラメータ更新編〜

#6. 参照
誤差逆伝播法のノート
誤差逆伝播法をはじめからていねいに
高卒でもわかる機械学習 (5) 誤差逆伝播法 その1
高卒でもわかる機械学習 (6) 誤差逆伝播法 その2
誤差逆伝搬法（バックプロパゲーション）とは
Notes on Backpropagation
初心者の初心者による初心者のためのニューラルネットワーク〜理論：順伝播編〜
初心者の初心者による初心者のためのニューラルネットワーク〜理論：誤差計算編〜