機械学習初心者でも、ニューラルネットワーク(neural network : NN)について理解しなければならない日がいつか来る。なので初心者代表の私が、ニューラルネットワークについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
『3.1.ニューラルネットワークとは』『3.3. ニューラルネットワークによって何ができるのか』を少し軽く読んでから頭から読むとより分かりやすいかもしれません。
1. なぜ人はニューラルネットワークを学ぶのか
今や日常生活の様々な場面に用いられている、機械学習のコアの部分だからです。(多分)
2. ニューラルネットワークの概念
**『ニューラルネットワークとは、人間の脳神経系のニューロンを数理モデル化したもののこと』**だと初心者の初心者による初心者のための単純パーセプトロンでは述べられています。(述べたのは私)
人間の脳にはニューロンと呼ばれる神経細胞があり、このニューロンは、他のニューロンから信号を受け取ったり受け渡したりすることによって情報を処理しています。そしてこの仕組みをコンピューターで再現してあげれば、人間の脳と同じ能力をコンピュータがもてるのではないかという考えをベースにして生まれたのがニューラルネットワークです。
2.1. ニューロンモデル
それでは、ニューラルネットワークについて説明する前に、まずはニューロン単体を取り上げてみましょう。
先程述べたように、ニューロンは信号を受け取り、その情報を処理して受け渡します。そしてその際、ニューロンは樹状突起という部位で他の細胞から複数の入力を受け取り、入力が一定値以上に達するとそれまでとは別の信号を出力します。この状態を発火すると言います。
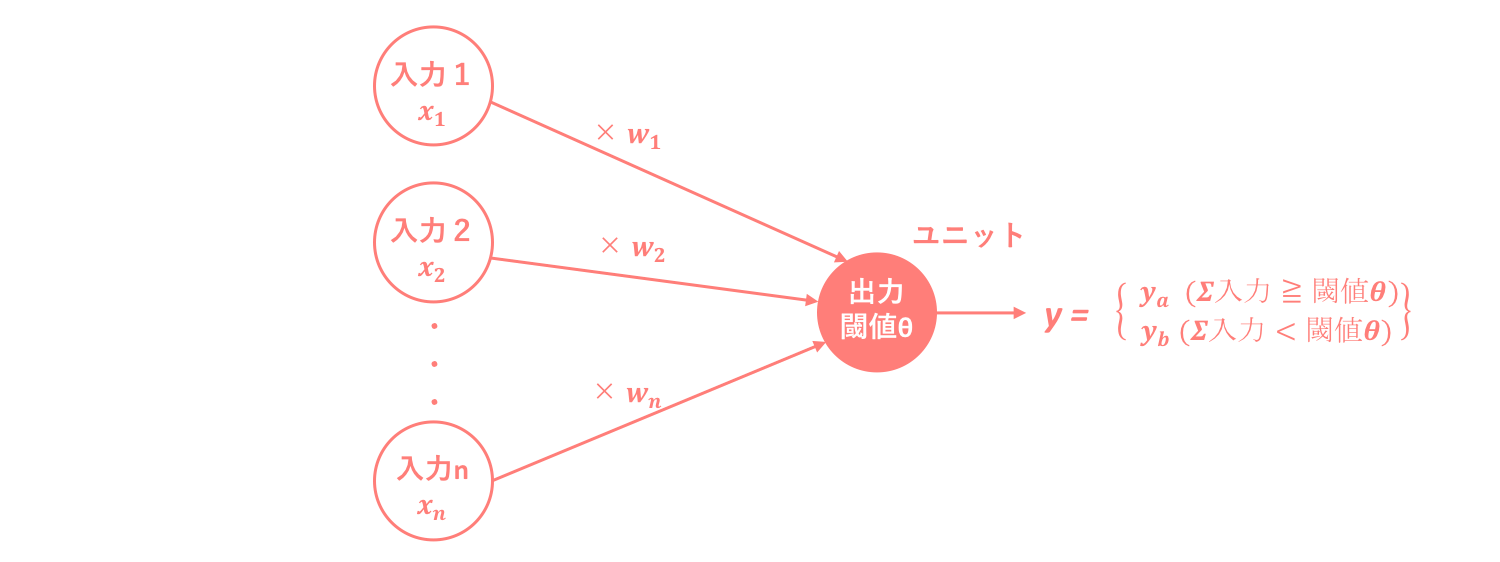
これをモデル図で表すと以下のようになります。
このような**ニューロンを簡単に表すためにステップ関数を用いてモデル化された人工ニューロンは、形式ニューロンと呼ばれます。**特徴としては、
・それぞれの入力値xに重み値wを掛けた総和が閾値θを超えたかどうかを、ユニットと呼ばれる出力機が関数を用いて判断し、超えていれば発火し出力値として1を、超えていなければ0を返す。このときの関数はステップ関数と呼ばれる。
・出力値は ∈ {1,0} でなく ∈ {1,-1} であることもあるが、常に2値である。
ステップ関数は活性化関数の一つであり、活性化関数(activation function)とは総入力を入力として出力が切り替わる関数のことを指します。
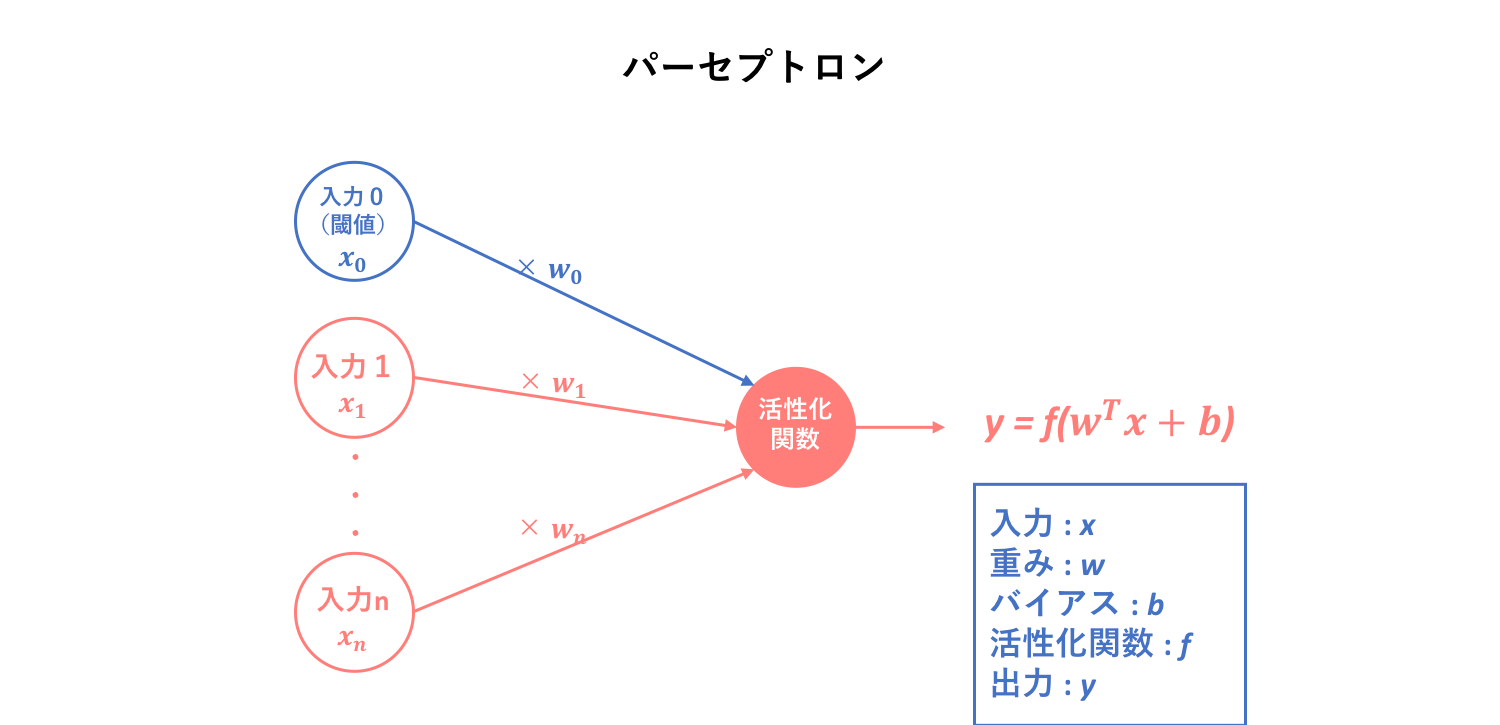
2.2. パーセプトロン(perceptron)
パーセプトロンと形式ニューロンの違いは、厳密には明らかになっていないように思います。
異なるポイントとしては、
・形式ニューロンにおいて閾値は入力に組み込まれていなかったが、パーセプトロンは閾値を入力に組み込んでいる。
ということでしょうか。なので、パーセプトロンは閾値を入力値としてモデル内に組み込んだ形式ニューロンだと言えます。そして、このパーセプトロンこそがニューラルネットワークの基本単位となります。
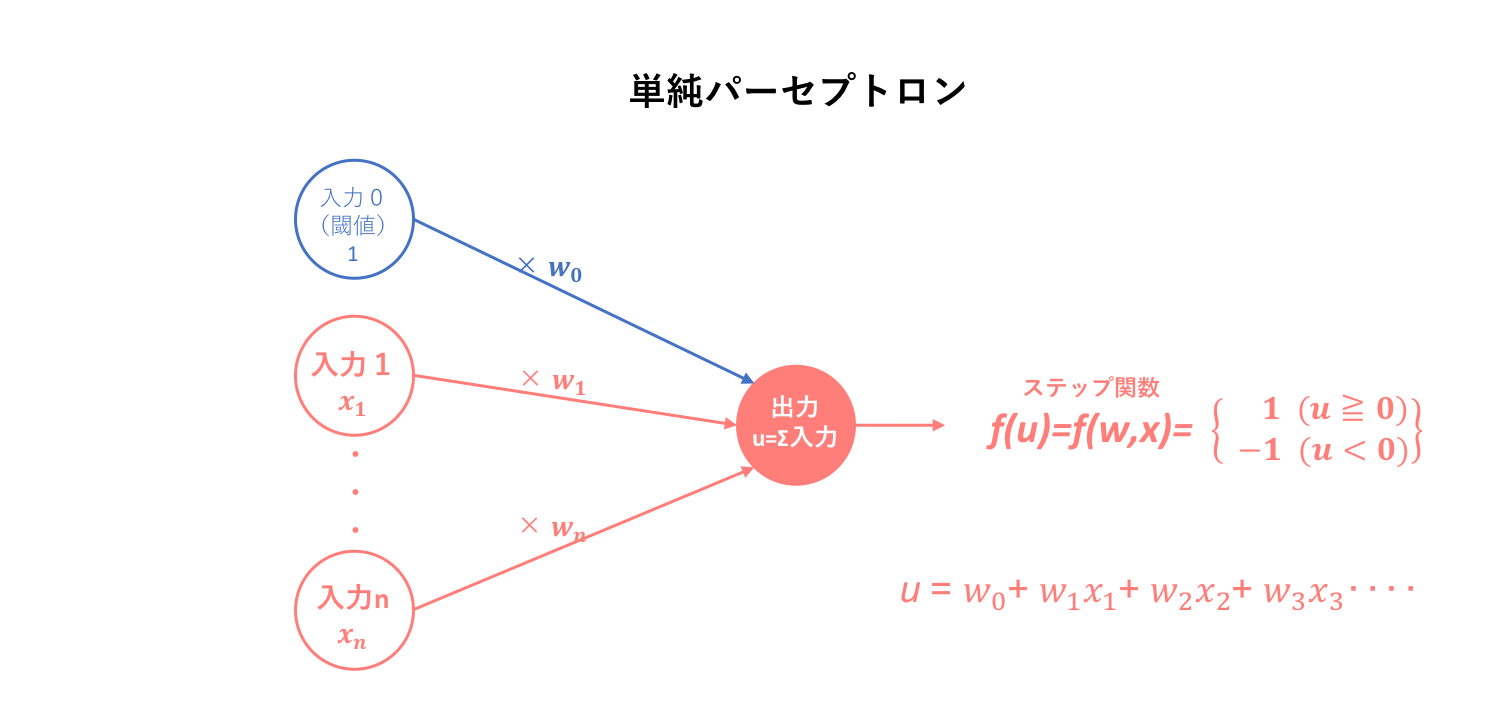
2.3. 単純パーセプトロン(simple perceptron)
ニューラルネットワークと比較を後述するために、単純パーセプトロンについても述べておきます。
単純パーセプトロンは、先に述べたパーセプトロンの中で入力そして出力の2層からなるパーセプトロンです。そして、そのモデルを用いた学習機械そのものを単純パーセプトロンと呼んでいます。
よって、単純パーセプトロンはステップ関数を用いてニューロンを数理モデル化するための学習機械と簡易的に定義できます。そしてこの単純パーセプトロンは、線形分離のための学習機械となります。この際、ステップ関数の出力を1,-1としています。(学習機械としての単純パーセプトロンアルゴリズムはこちら→初心者の初心者による初心者のための単純パーセプトロン)
2.4. ニューラルネットワークの概念
では、いよいよ本題に入っていきましょう。
人間の脳は100億から140億個のニューロンが互いにつながり、巨大なシステムを構築しています。このようなニューロンを構成素子とした回路網をニューラルネットワーク(神経回路網)と呼びます。今まで1つしかなかったニューロンモデルを複数接続することで、ニューラルネットワークを作ることができます。つまり、**ニューラルネットワークはパーセプトロン(のようなもの)を複数接続することによって構築された数理モデルです。**しかし、ただパーセプトロンを繋げればいいというものではありません。
ニューラルネットワークの基本原理がパーセプトロンであることに疑いの余地はありませんが、厳密にはパーセプトロンに少し変化を加えたものを構成単位としています。そしてその違いは、活性化関数にあります。
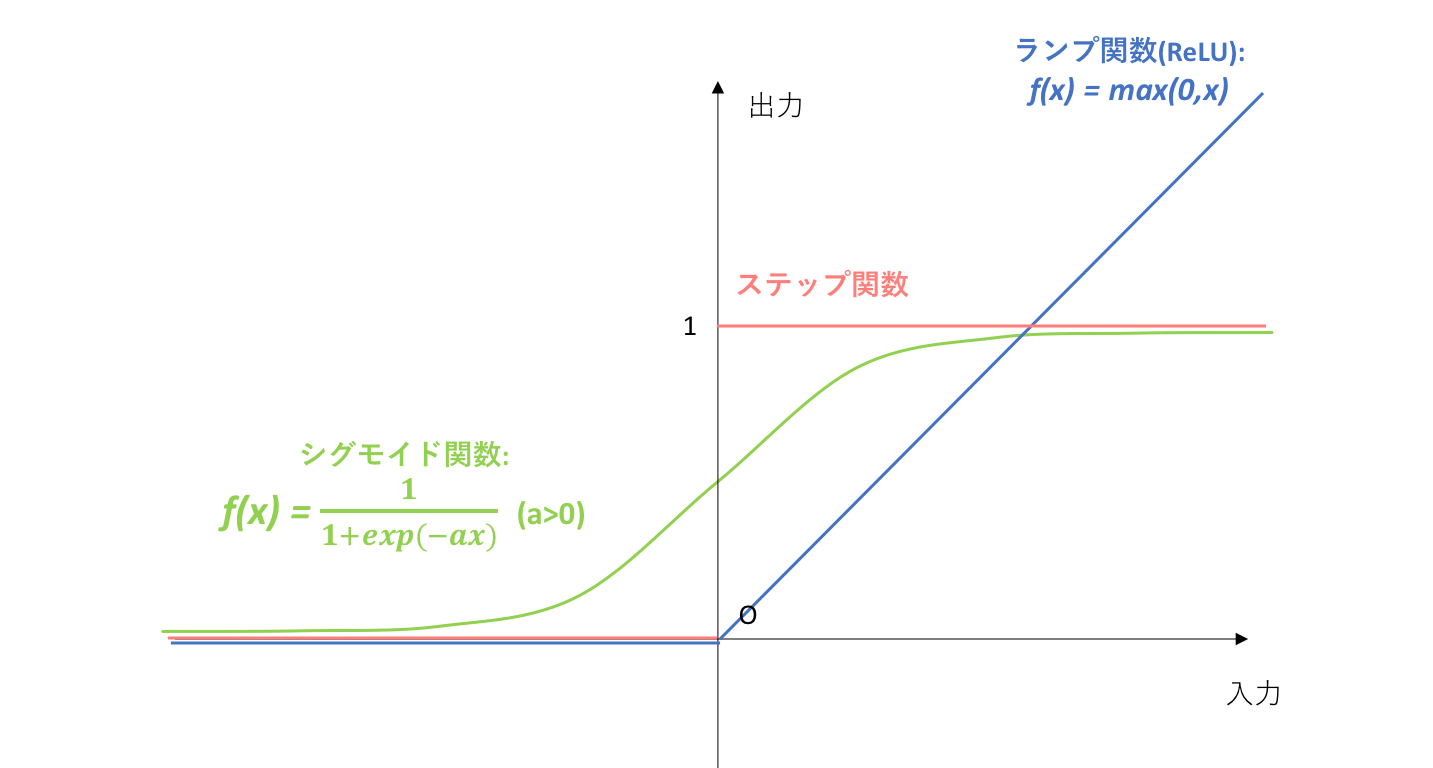
パーセプトロンの基本である形式ニューロンに立ち返ってみましょう。形式ニューロンでは、活性化関数としてステップ関数を用いることを指定していました。しかし、**ニューラルネットワークでは構成原子においてステップ関数を用いずに、シグモイド関数(sigmoid function)やランプ関数(ReLU)を用います。**これは、ステップ関数の微分値が常に0になってしまうことに拠ります。微分値が常に0という状態は、後に説明する誤差逆伝播法(backpropagation)という画期的な学習手法に適さないので、微分可能な関数が代用されたということです。ちょうど、0-1損失関数と代理損失関数の関係に似ていますね。
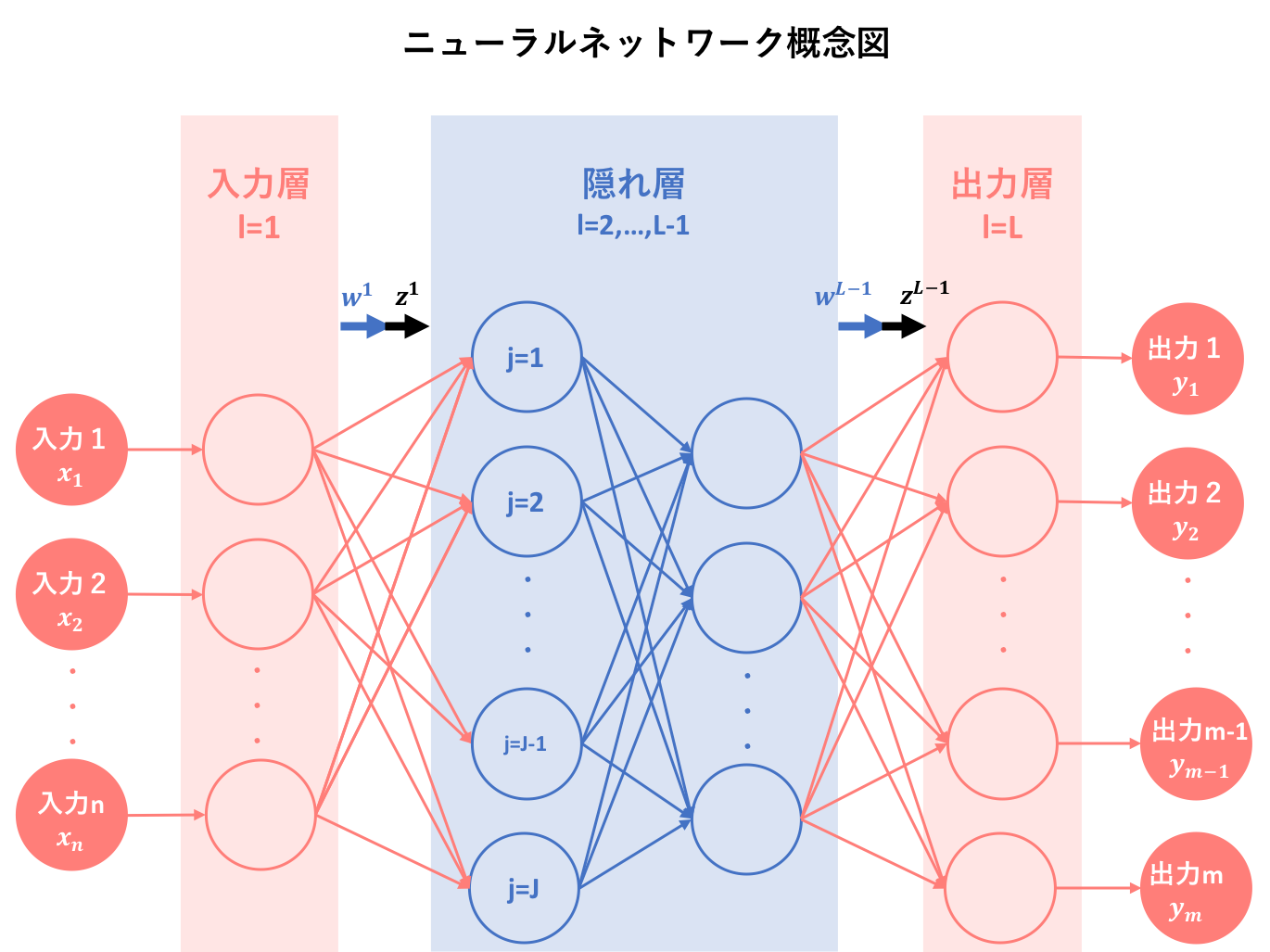
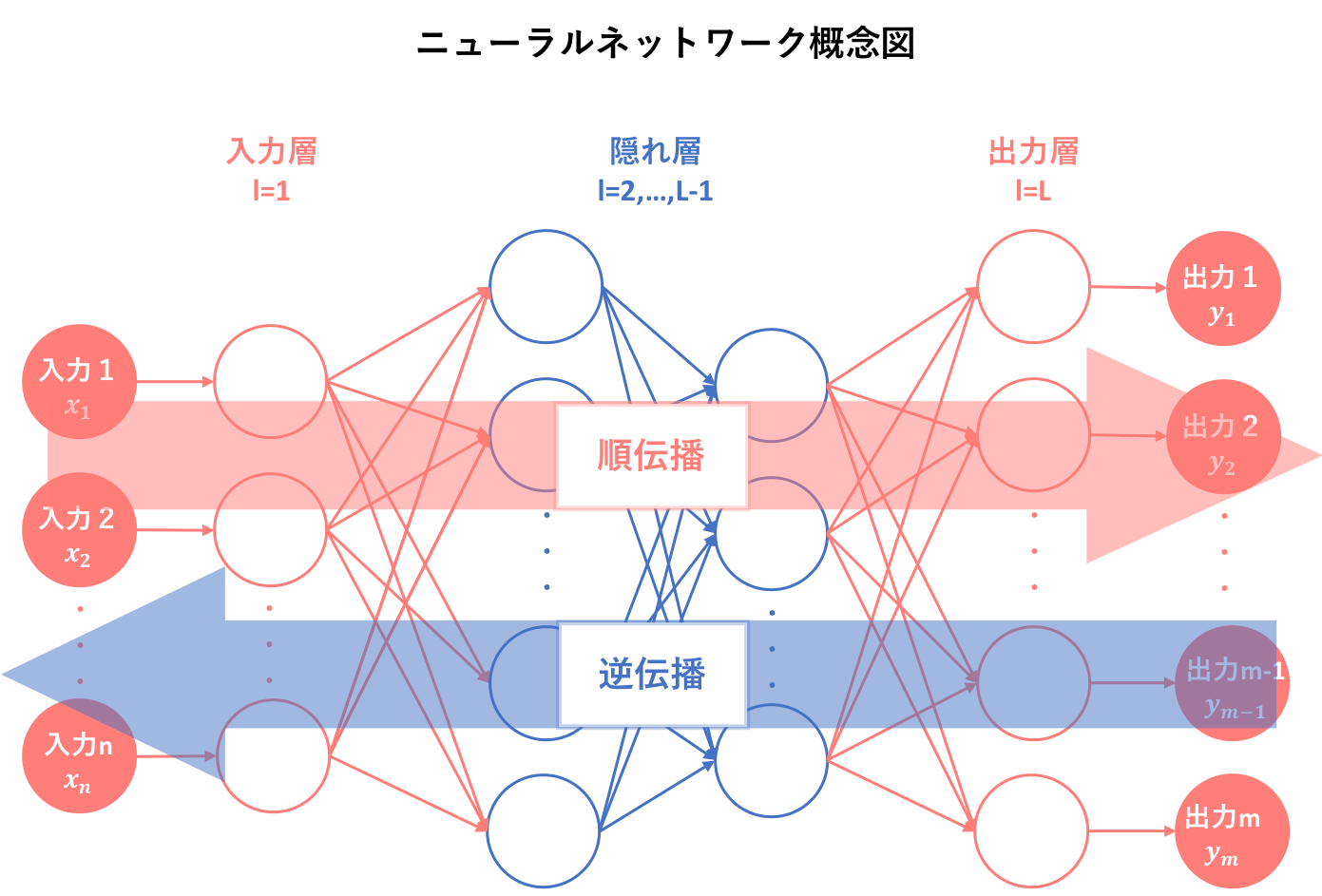
そしてニューラルネットワークでは、このパーセプトロン(のようなもの)を複数個並列接続したあと、その集合を直列に接続します。これによって、ニューラルネットワークを視覚化すると以下のようになります。
このように、**パーセプトロン(のようなもの)を複数並列に接続したものを層と呼び、その層を複数直列に接続することによってニューラルネットワークを構成します。**そしてニューラルネットワークでは入力から出力まで
入力→入力層→隠れ層1→隠れ層2→…→隠れ層(L-2)→出力層→出力
という過程を経ます。ここで隠れ層をL-2としたのは層の数をLで表すためです。深い意味はありません。
それでは、この矢印は何を意味しており、ニューラルネットワークはこのプロセスによってどのように学習していくのか、次の項で追究していくことにしましょう。
2.5. 結局ニューラルネットワークとは概念的には何なのか
ニューラルネットワークとは、『パーセプトロン(のようなもの)を基に人間の脳神経系のニューロンを数理モデル化したもの』のことであり、このモデルによって与えられたデータを基に新しい概念を学習することが可能となる。
そして、その学習を繰り返すことによって最適なモデルを構築することを目標とする。
3. ニューラルネットワーク入門(neural network : NN)
この項では、ニューラルネットワークの中身をより深く掘り下げていきます。まずニューラルネットワークの基本概念を再確認し、その構成原子のモデル化、そしてそのモデルを組み合わせることによって行われる学習の方法について説明します。
3.1. ニューラルネットワークとは
ニューラルネットワークの構造については前項で概観できました。しかし、機械学習の本質はどのように学習を行うかです。結局構成や構造が分かったところで、どのように学習が行われているのかを知らなければ、なぜそのモデルを採択するかについて明確な回答を述べることが出来ません。そしてどのように学習が行われるのかを知るためにはまず、その学習機械が置かれている環境を把握することが必要不可欠です。
3.1.1. Supervised vs Unspervised NN
ニューラルネットワークは、教師あり学習(supervised learning),教師なし学習(unsupervised learning)どちらにも適用可能な数理モデルです。ニューラルネットワークにおいて学習とは、出力層で人間が望む結果(正解)が出るようにパラメータ(重みとバイアス)を調整する作業を指します。そしてニューラルネットワークは、誤差逆伝播法(backpropagation)というアルゴリズムによって学習を行います。
🔥初心者ゾーン突入🔥
ここである疑問が生じます。ニューラルネットワークが教師あり学習において有効であることは分かりやすいですが、教師なし学習においても有効であるのはなぜでしょうか。ニューラルネットワークは、常に正解に近づけるべく重みとバイアスを調整するわけではないのでしょうか。
この疑問は、ニューラルネットワークの中間層の働き、その他脳のモデルを参照することによって解決されました。この記事によれば、やはりニューラルネットワークは本質的には教師あり学習だそうです。教師なし学習においても適用可能というのは、本来の目的である「正解ラベル」を与えていないという意味で教師がなしと言っているのであって、誤差を計算する際にニューラルネットに出力してほしい目標値が無いというわけではありません。
例えば教師なし学習のためのアルゴリズムでありニューラルネットワークの一つ、オートエンコーダ(autoencoder)では、入力値自身を目標値として設定します。つまり、正解データがないという点ではたしかに教師なし学習なのですが、入力データを目標値として設定しているという点では教師あり学習という見方もできるのです。
🔥初心者ゾーン脱出🔥
よって、ニューラルネットワークでは教師あり学習か教師なし学習かという違いは意味をなさず、どちらにおいても設定された目標値に近づけるモデルを構築することが目的となります。
3.1.2. ニューラルネットワークの利欠
では、ニューラルネットワークを用いる利点そして欠点はどのようなものなのでしょうか。時系列を交えて確認してみましょう。
①パーセプトロンは画期的ではあったが線形分離可能な問題のみにしか対応できなかった
②これに対しニューラルネットワークは隠れ層を加えることで線形分離不可能な元データを線形分離できるよう高次元に落とし込むことを可能にした
③しかし同時にニューラルネットワークには、多数のパラメータを必要とする非線形の問題に対して非常に学習が困難で、かつ膨大な時間がかかるという欠点があった
④誤差逆伝搬法の登場により、高次元への落とし込み方も学習し最適化されるようになった
⑤さらに計算機の性能が爆発的に上がり、現在よく知られているディープラーニングが可能となった
つまり大きな利点としてはやはりデータを非線形分離できるようになったこと、加えてニューラルネットワークが基盤となるディープラーニングに至っては、圧倒的な精度を誇り応用範囲も広いことが実証されいることが挙げられます。
逆に欠点は解決されたように見えますが、別途過学習の対策が必要であり、そのために事前に調節しなければならない設計変数(ハイパーパラメータ)が多いことが欠点の一つとして挙げられます。
3.2. 構成原子の数理モデル化
では、ニューラルネットワークの置かれている環境を理解したところで、学習プロセスそのものに目を向けることにしましょう。繰り返しになりますが、ニューラルネットワークの基本構成単位はパーセプトロン(のようなもの)です。そして、ニューラルネットワークはそのパーセプトロンを並列かつ直列に接続することで構成されています。
上の図は先ほど挙げたニューラルネットワーク概念図に層数l,ユニット数j,重みw,出力zとして少し手を加えたものです。この図のように、ニューラルネットワークはパーセプトロン(のようなもの)が複合的に交絡することで成り立っているわけですが、では、そもそものパーセプトロン(のようなもの)はどのように数理モデル化されているのでしょうか。
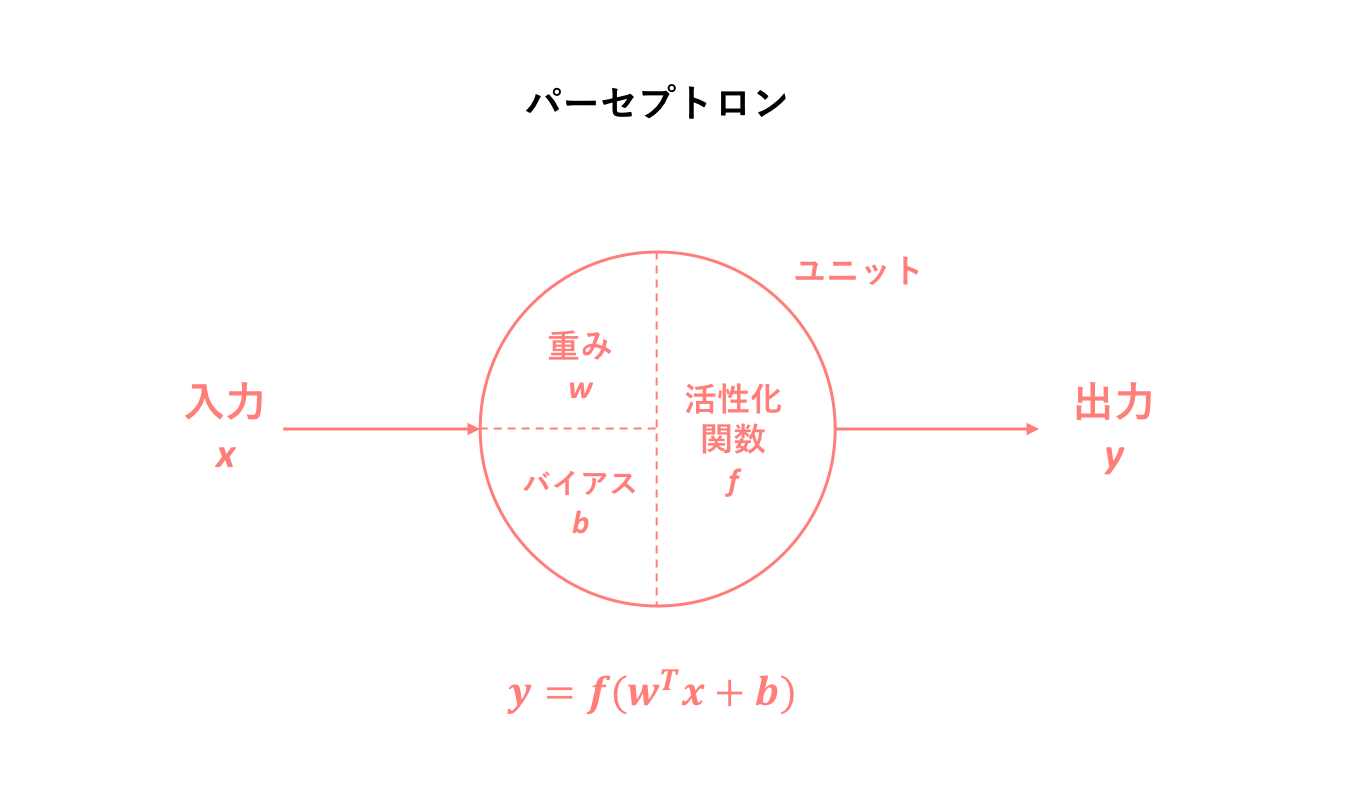
上図にはまず、パーセプトロンの仕組みを改めて簡易的に視覚化したものを示しました。
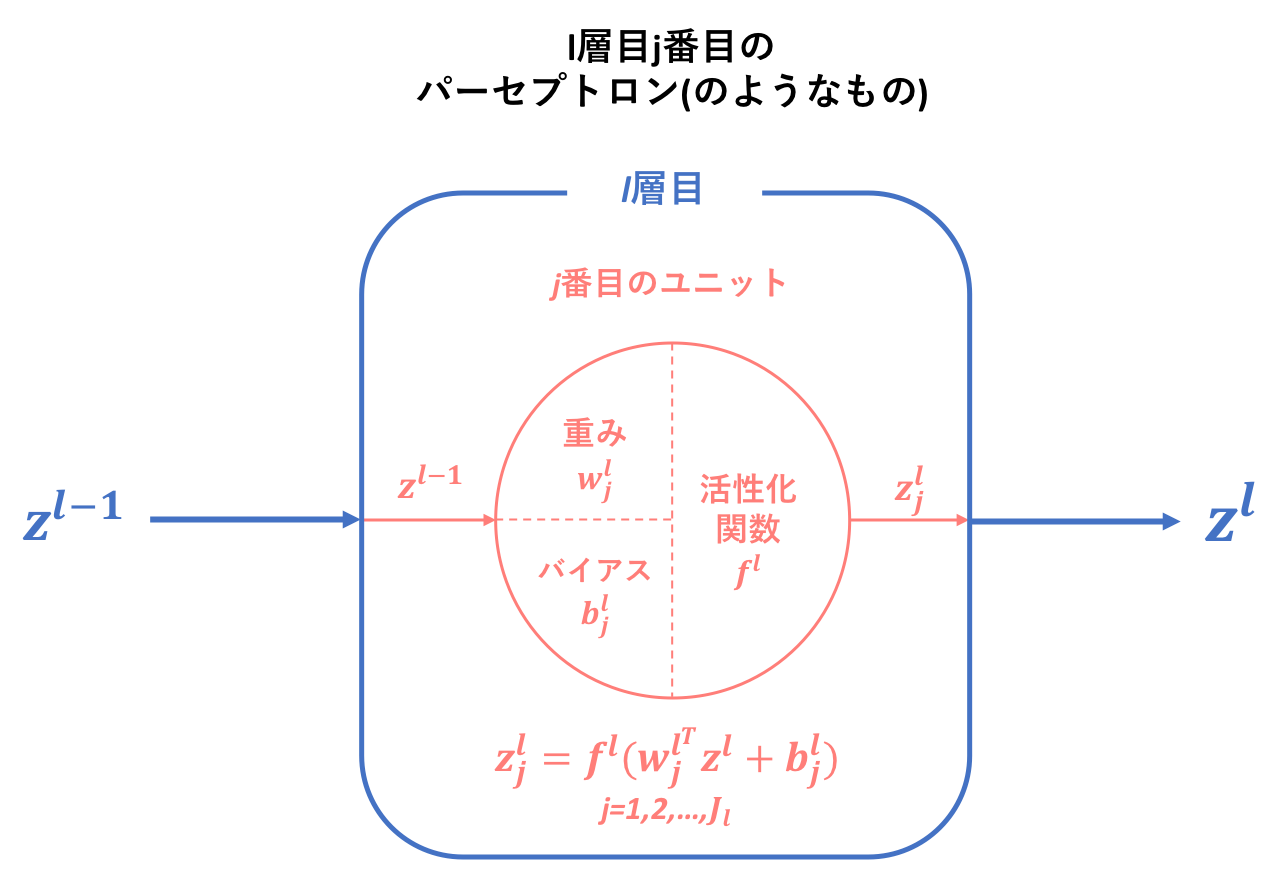
そしてこれがニューラルネットワークの一要素としてモデル内に組み込まれると、それぞれのユニットに対して独自の変数が割り当てられ固有のものとなります。以下に示すのは、ニューラルネットワークでl層目j番目に位置するパーセプトロン(のようなもの)の層間の構造です。この小モデルが重なり合うことによって、ニューラルネットワークという大モデルが構成されるのです。ユニット間の構造については、さらに下に図を示します。
🔥初心者ゾーン突入🔥
・繰り返しですがここでは層間構造を見ているので、重み,バイアスはいずれもベクトルです。
・この表記だと活性化関数が層ごとに異なるように思われますが、これは出力層は隠れ層と原則異なる活性化関数を用いることによります。しかし、すべての隠れ層で同じものを用いるかについては少々曖昧です。
🔥初心者ゾーン脱出🔥
このモデルの解釈は比較的容易ではないでしょうか。
- l-1層で出力された値がl層に伝搬する
- 伝搬された値はすべて同様にそれぞれのユニットに入力される
- ユニットごとにより入力値に対する重み,バイアスは異なるのでそれぞれのユニットがオリジナルの出力値を持つ
- それぞれのユニットによる出力値を層としての出力値にするためにベクトル化する
- l+1層に伝搬する
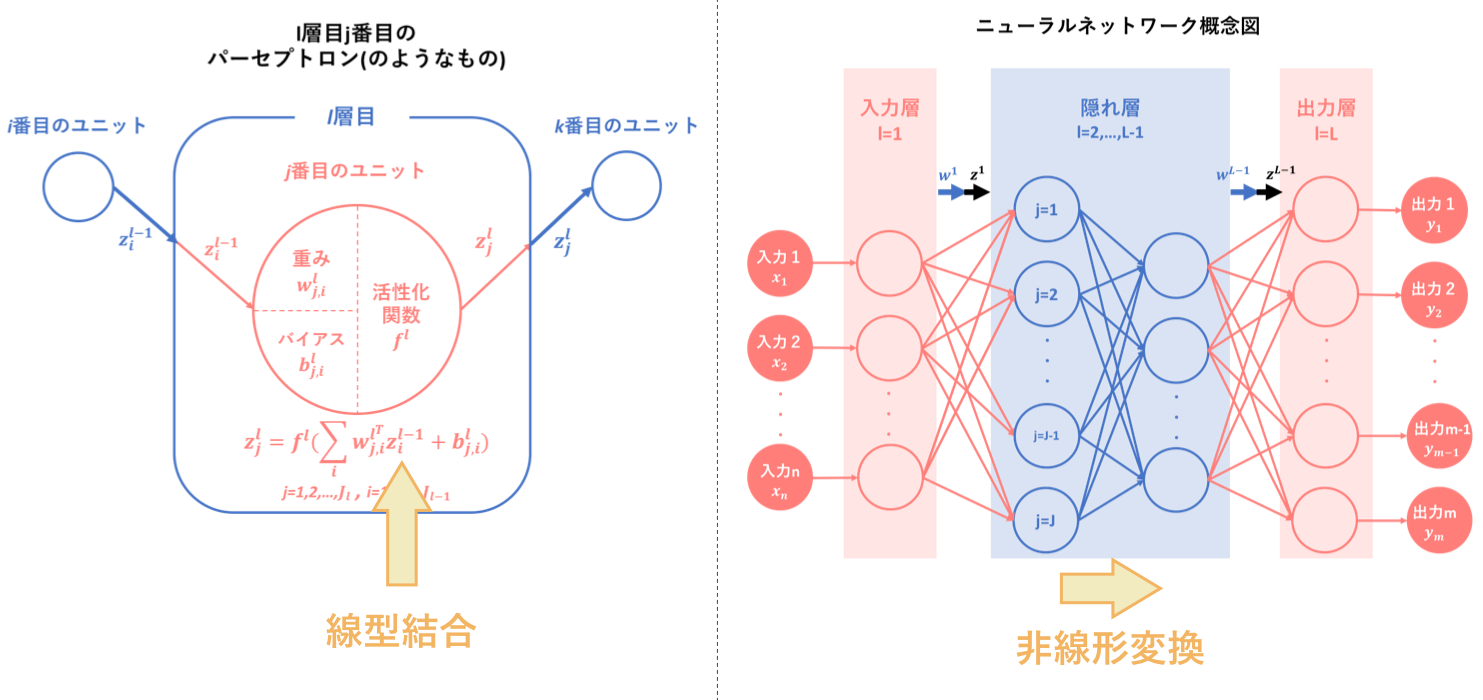
それでは、層間の関係が把握できたところで、下にさらに細かくユニット間の構造を載せておきます。基本的には層間の構造と大きな違いはないので、特に詳しい説明などは省きます。
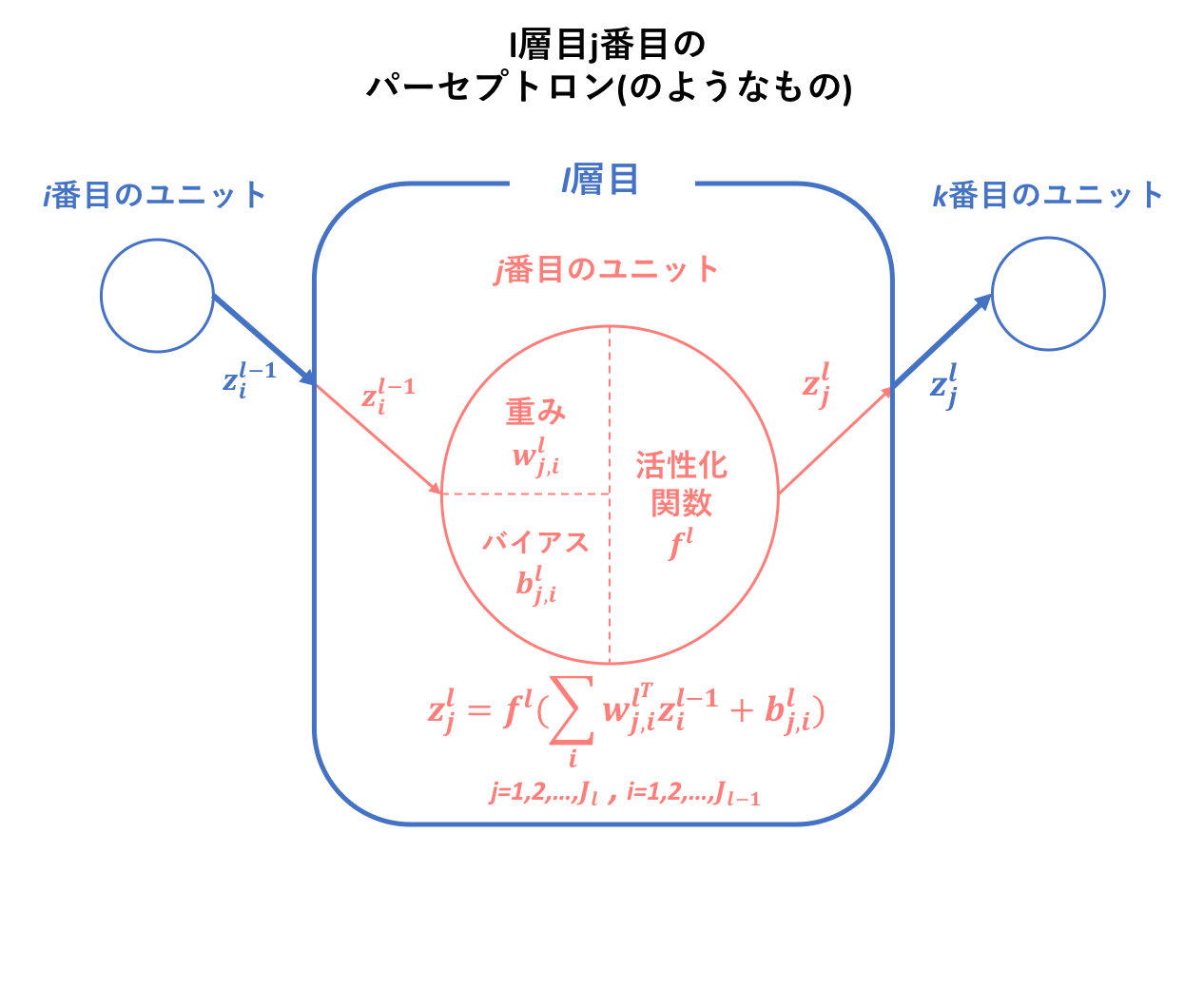
これが、ニューラルネットワーク構成原子の数理モデルとなります。
3.3. ニューラルネットワークは一体何をするものなのか
さて、この時点でニューラルネットワークの基本的な構造についての説明を終えたので、今までふれて来なかったニューラルネットワークで結局何ができるのかということについて説明してしまいましょう。本節は、ニューラルネットワークの中間層の働き、その他脳のモデルから引用しています。
**『ニューラルネットワークとは、機械学習の立場から言えば、線型結合と非線形変換を繰り返す合成関数 $f(w,x)$です。』**合成関数のパラメータwをうまいこと調整することで、入力xに対して望む出力を獲得することができます。
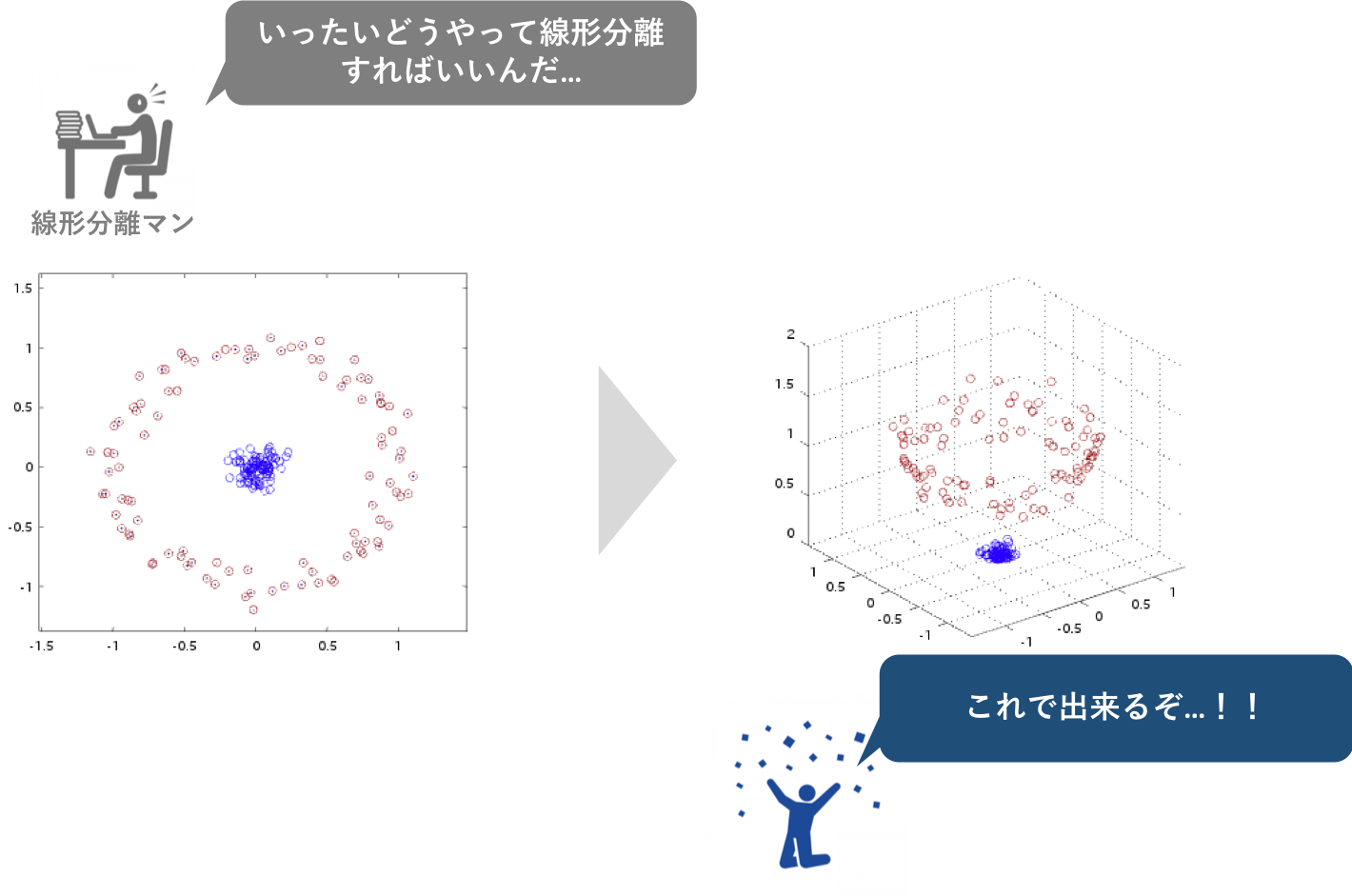
この合成関数を用いることによって、通常入力された時点ではうまく線形分離ができないような場合でも、次元をあげて非線形変換を行えば、必ず線形分離できるようになります。このような"良い"変換を行うのが、隠れ層の役割でもあります。
しかし主成分分析などの多くの統計手法は、特徴抽出において次元を削減することによって可視化できるようになったりデータの解釈を可能とします。ニューラルネットワークとは逆ですね。この相違は、ニューラルネットワークの特徴抽出が、(なんだかよくわからないが)基本的には判別に有利になるような表現を獲得することが目的であるためです。つまり、その特徴量自体が容易に解釈できるようなものではないということです。
しかし、その特徴抽出(連合層の調節)は誤差逆伝搬法により識別が上手く行くかを見ながら学習ができるため、ニューラルネットワークは非常に汎用性の高い機械学習手法となります。
4. ニューラルネットワークの全体像
ニューラルネットワークにおいて、学習を行うとは与えられた学習データに合わせて重みwの値を調整するということであり、この操作は誤差逆伝播法という手法が主となって行われます。そして学習は、この手法を用いて順伝播と逆伝播を繰り返すことによって最適パラメータを見つけることになります。よってここでは、誤差逆伝播法の説明に入る前に、順伝播と逆伝播への認識を確認することにします。(といっても超簡略にですが)
4.1. 順伝播(forward-propagation)
実はこの順伝播に関する議論はもう終わっています。順伝播とはニューラルネットワークの場合、前の層の出力を本層の入力として処理することを指します。よって、これまで述べてきた数理モデルに関する話はすべて順伝播の状況下であることが前提となっています。
4.2. 逆伝播(back-propagation)
ニューラルネットワークにおいては出力値を理想の値に近づけるためにパラメータを調節します。逆伝播とは、このときに順伝搬と全く逆方向に行われる処理のことを指します。各パーセプトロン(のようなもの)の出力値を基準にパラメータを調節しようとすることから、順伝播とは真逆の方向への処理となります。
5. まとめ
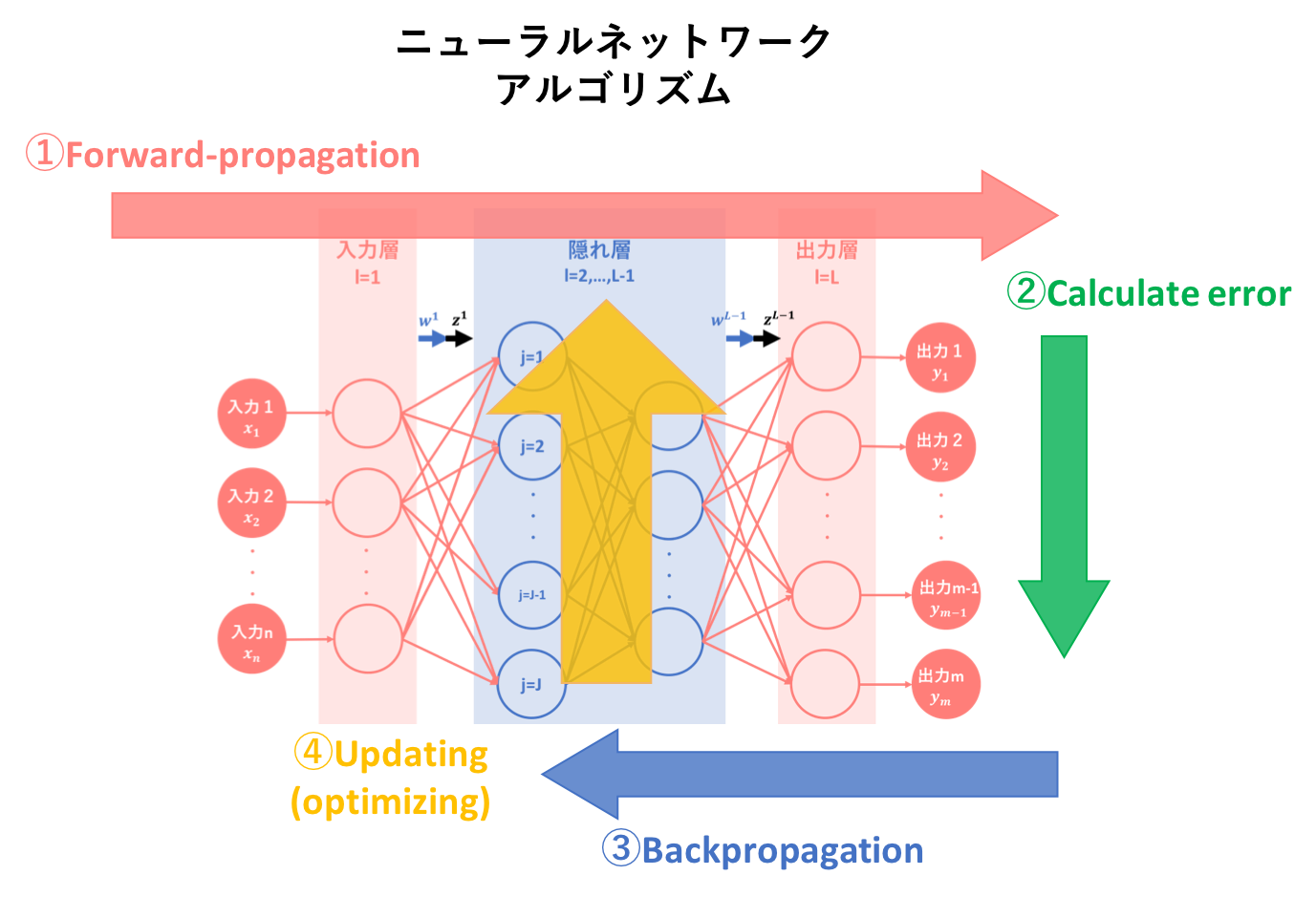
今回は、ニューラルネットワークのアルゴリズムを図式化した以下の図で①についての説明を行いました。
②〜④の説明は、それぞれ理論:誤差計算編,逆伝播編,勾配降下編で行いたいと思います。
また、その後に実装についての説明もする予定です。
①初心者の初心者による初心者のためのニューラルネットワーク#1〜理論:順伝播編〜(本記事)
②初心者の初心者による初心者のためのニューラルネットワーク#2〜理論:誤差計算編〜
③初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜
④初心者の初心者による初心者のためのニューラルネットワーク#4〜理論:パラメータ更新編〜
6. 参照
ニューラルネットワークについて学んでみた。(その1)
ニューラルネットワークについて学んでみた。(その2)
ニューラルネットワークの線形変換と活性化関数について
ニューラルネットワークの中間層の働き、その他脳のモデル
ニューラルネットワークとは?人工知能の基本を初心者向けに解説!
初心者の初心者による初心者のための単純パーセプトロン