機械学習初心者でも、単純パーセプトロンについて理解しなければならない日がいつか来る。なので初心者代表の私が、単純パーセプトロンについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
それぞれの言葉が何を指すのか、定義を明確にすることにこだわったつもりでいます。
加筆修正のコメント等あれば、遠慮なく教えてください。
1. なぜ人はパーセプトロンを学ぶのか
それはズバリ、機械学習を勉強している人には必須とも言えるサポートベクターマシン(SVM)、ニューラルネットワークの基本原理となっているからです。(だと思います)
SVM, ニューラルネットワークの理解のためには単純パーセプトロンの深い理解が必要不可欠です。(だと思います)
2. 単純パーセプトロンの定義
2.1. ニューラルネットワーク
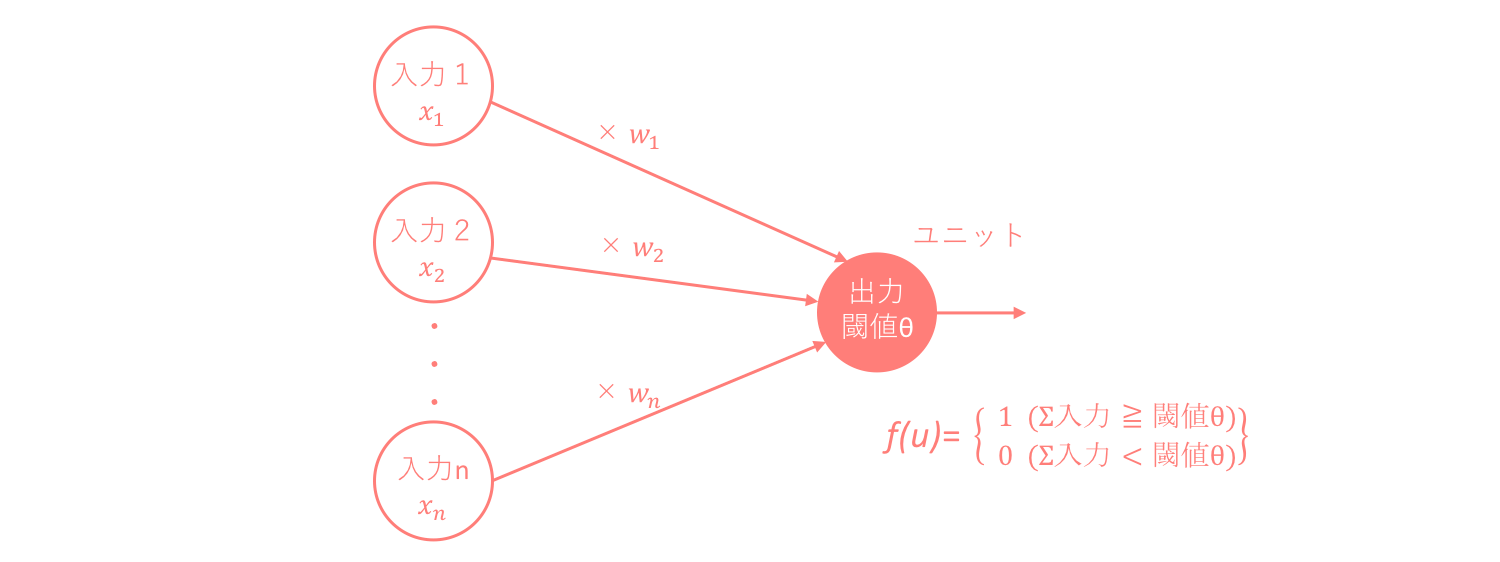
単純パーセプトロンについて調べてみると、「ニューラルネットワーク」「ニューロン(神経細胞)」「発火」という言葉がどのWebサイトでも使われていました。
ニューラルネットワークとは、人間の脳神経系のニューロンを数理モデル化したもののことです。つまり、その数理モデルを指します。これは実際に人間の脳で行われている処理を、計算機上で再現することを目的としたものです。今回はニューラルネットワークについての詳説は省略しますが、「発火する」とは、ニューロンが樹状突起という部位で他の細胞から複数の入力を受け取り、入力が一定値以上に達すると信号を出力することを指すようです。
では、これらの言葉が"単純パーセプトロン"にどのように関連するのでしょうか。
2.2. 形式ニューロン
これを説明するためには、「形式ニューロン」「パーセプトロン」という二つの言葉についても説明を加える必要があります。
形式ニューロンとはニューロンを簡単に表すためにステップ関数を用いてモデル化された人工ニューロンです。特徴としては、
・それぞれの入力値xに重み値wを掛けた総和が閾値θを超えたかどうかを、ユニットと呼ばれる出力機が関数を用いて判断し、超えていれば発火し出力値として1を、超えていなければ0を返す。このときの関数はステップ関数と呼ばれる。
・出力値は ∈ {1,0} でなく ∈ {1,-1} であることもあるが、常に2値である。
ステップ関数は活性化関数の一つであり、活性化関数とは総入力を入力として、出力が切り替わる関数のことを指します。
2.3. パーセプトロン(perceptron)
パーセプトロンと形式ニューロンの違いは、厳密には明らかになっていないように思います。
異なるポイントとしては、
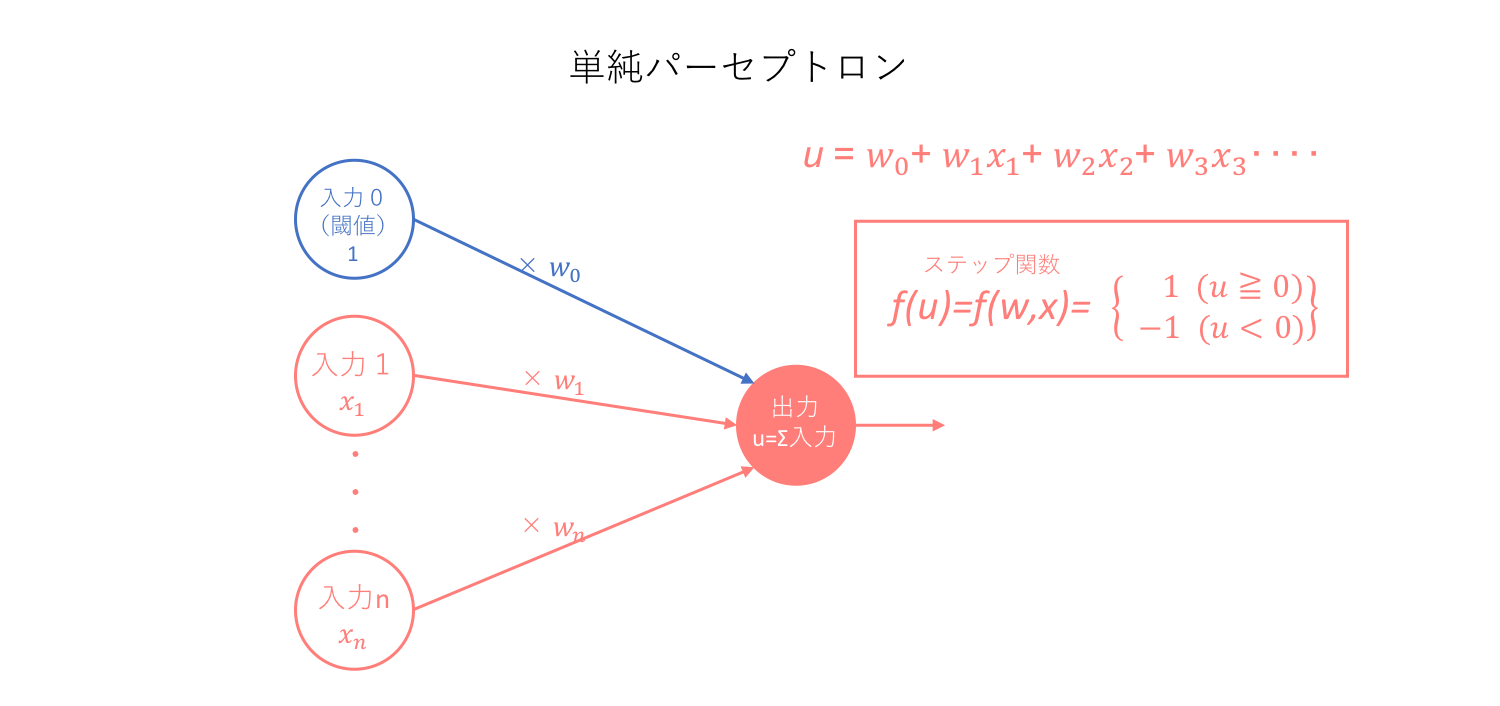
・形式ニューロンにおいて閾値は入力に組み込まれていなかったが、パーセプトロンは閾値をx0=1, w0=-θとして入力に組み込んでいる。
ということでしょうか。なので、パーセプトロンは閾値を入力値としてモデル内に組み込んだ形式ニューロンだと言えます。そしてこのように定義されたパーセプトロンこそが、ニューラルネットワークの基本単位となります。
さらにWikipediaによれば、パーセプトロンは入力そして出力の2層だけではなく、S層(入力), A層(中間), R層(出力)の3層からなるとされていました。これに基づいて、パーセプトロンは
・単純パーセプトロン
・多層パーセプトロン
の2種類に分類されます。
2.4. 単純パーセプトロン(simple perceptron)
単純パーセプトロンは、先に述べたパーセプトロンの中で入力そして出力の2層からなるパーセプトロンです。そして、そのモデルを用いた学習機械そのものを単純パーセプトロンと呼んでいます。
よって、単純パーセプトロンはステップ関数を用いてニューロンを数理モデル化するための学習機械と簡易的に定義できます。そしてこの単純パーセプトロンは、線形分離のための学習機械となります。この際、ステップ関数の出力を便宜上1,-1としています。
3. 単純パーセプトロンのアルゴリズム
3.1. 目的
単純パーセプトロンだけでなく、教師あり分類を行うための学習機械すべてに共通する目的は、教師データから最適モデルを導出しそれに基づいて未知データを"正しく"分類することです。最適モデルを導出するとは、それぞれの入力値から"正しい"出力値を推定するために必要な重み値(weight)を求めることと同義です。
つまり、未知データの正しい分類を行うためには、それぞれの入力値(x)に対して付与される重み値(w)を特定しなければなりません。
3.2. 重み値の更新
では、どのようにそれぞれの重み値を特定すればいいのでしょうか。
以下に、その重み値を特定するための簡易アルゴリズムを示します。このアルゴリズムも単純パーセプトロンに限ったものではなく、他の学習機械にも適用可能です。

このアルゴリズムによって、最適な重み値w_i,重みベクトルwを特定することが出来ます。なぜこの方法が良いのかについては、別の記事でふれようと思います。
ここで私たち初心者にとって分かりづらいのは、4, 6行目の部分です。このような書き方だと、w1~wnの重み値をw1, w2,...というように一つずつ更新していき、w2の要素値はw1に依存、w3の要素値はw2に依存...のように勘違いしてしまいがちですが、あくまで重みベクトルの更新はベクトルで行います。このtというのはあくまでそれぞれのデータを示しているのであって、説明変数の一つを示しているわけではありません。重みベクトルは説明変数、つまりデータテーブルでいう列に対応するものであって、行に対応するものではないからです。
上の単純パーセプトロンの図でのそれぞれの入力というのは、それぞれのデータではなくそれぞれの説明変数への値の入力です。一つのデータのみでの話であり、w1~wnとアルゴリズム内のwtの添え字のtは全く異なるものを指すということを頭に留めておいて下さい。←ここ分かりづらくてすいません
3.3. 損失関数(loss function)
ではここで、アルゴリズム内の2つの注釈の1つ目、損失関数に依ると記した部分について説明します。
多くのWebサイトでは、損失関数について明確な定義は特にされていませんでした。なのでここでは、分類における損失関数は予測ラベルと正解ラベルの誤差の程度を数値化するために用いられる関数と定義します。

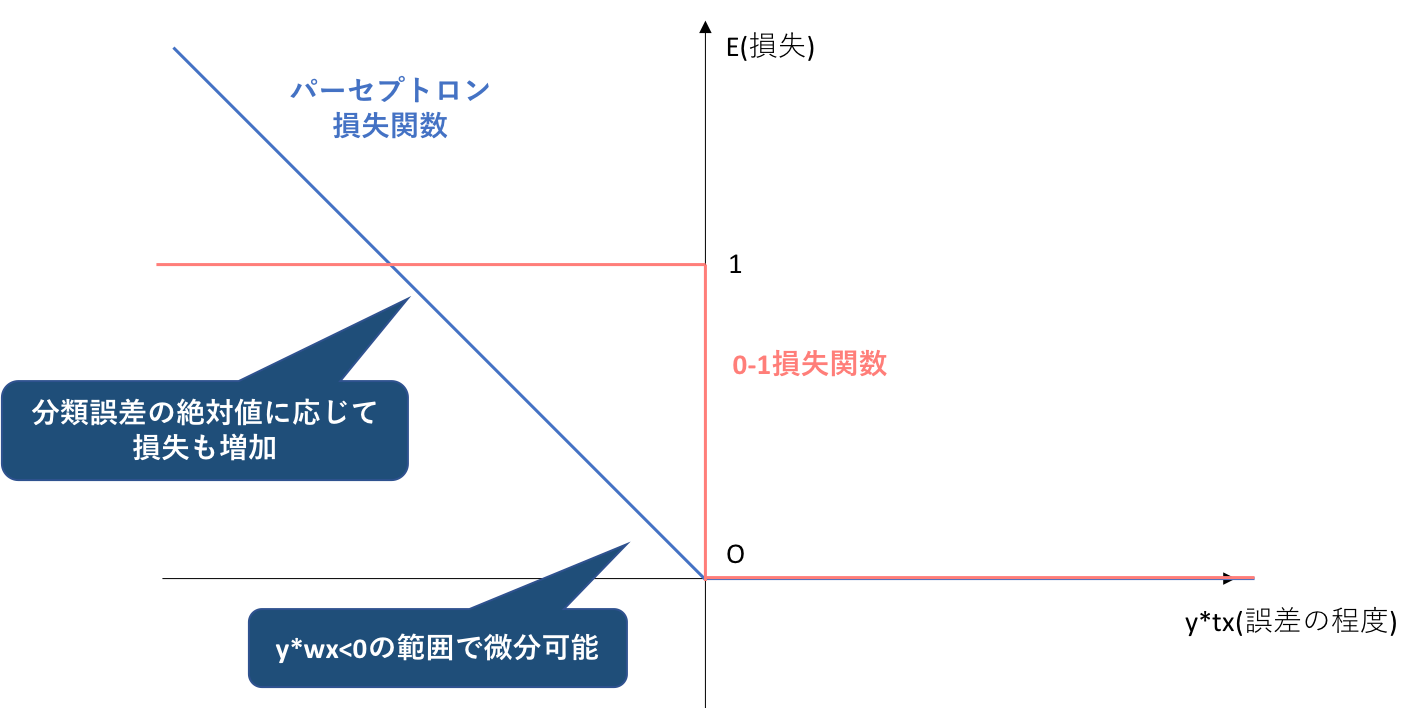
① 0-1損失関数
機械学習での分類において、最も基本となる損失関数は0-1損失関数です。0-1損失関数を定式化すると、
L(y,f(w,x))=0
if t=sign(f(w,x))
else 1
となります。この式に用いられているsignの関数は、符号関数(sign function)と呼ばれ、実数に対しその符号に応じて1、−1、0のいずれかを返す関数及びそれを拡張した関数と定義されます。ここでは、
sign(f(w,x)>0)=1
sign(f(w,x)=0)=0
sign(f(w,x)<0)=-1
となります。
0-1損失関数は、正解ラベルyと予想ラベルf(w,x)の符号が一致している(すなわち分類が成功)ならば損失は0、符号が一致していなければ損失は1として出力する関数です。ここで前提になっていることは二つあります。
・各データは識別境界(decision boundary)と呼ばれる平面によって2分割され、それぞれのデータに対し分類ラベルy=1,-1が割り当てられる
・予想ラベルは2値のみではなく、f(w,x)によって連続値として割り当てられる
0-1損失において重要なのは、y, f(w,x)それぞれの数値をみているわけではなく、符号のみをみているということです。すなわち、正解ラベルがy=-1のときに、f(w,x)=0.0000001と出力されてもf(w,x)=1000000と出力されても、0-1損失関数上の損失はどちらも1となります。
② 代理損失(surrogate loss)
しかし、これは0-1損失関数の弱点であるとも考えられます。0-1関数には弱点が大きく二つあります。
・分類がギリギリ成功するケースと余裕を持って成功するケース、あるいは同様に分類がギリギリ失敗するケースと完全に間違っているケースを区別できない
・後述する勾配法と呼ばれる手法を重み値を求める際に用いたとき、損失関数の微分が必要になります。しかし0-1損失関数は微分値が常に0になるという状態であり、勾配法に適さない
このような問題を解決するために、通常の学習では代理損失というものがそれぞれの学習機械に応じて設定され、その損失関数として代理損失関数を用います。
③ パーセプトロン損失
単純パーセプトロンでは、代理損失関数としてパーセプトロン損失関数を用います。パーセプトロン損失関数は、以下のように定式化されます。
L(y,f(w,x))=max(-yf(w,x),0)=max(−ywx,0)
∵f(u)=f(w,x)=wx
すなわち、正解ラベルtと予測ラベルwxの符号が一致(分類が成功)している場合は損失0、符号が一致していない場合は損失として|y*wx|を与えます。このとき、yは1,-1の2値しかとらないのですが、wxは連続値であり|wx|はそのデータがどれだけ識別境界から離れているかを表します。なぜ|wx|が識別境界からの距離に比例するのかについても、別の記事で説明します。
よって、y=-1のときにwx=0.0000001ならば、そのデータは識別境界にとても近いので間違って分類されやすいということから損失は0.0000001と小さく、逆に正解ラベルがy=-1のときにwx=1000000と出力されれば、そのデータは識別境界からとても遠く非常に簡単に分類されやすいのにその分類を間違えたことを示すので、損失はL=1000000と非常に大きくなります。
このことから、パーセプトロン損失関数は0-1損失関数の抱える弱点を2つとも克服していることが分かります。
④ アルゴリズム内のEについて
それでは、最後に重み特定のアルゴリズム内に記されているEという値について説明します。この値は用いる損失関数に依存すると記しましたが、パーセプトロン損失関数の場合、その値はE=0になります。これは、パーセプトロン損失は予測ラベルが不正解(y*f(u)<0)の場合に損失を与えるからです。予測ラベルが不正解の場合にのみ重みベクトルは更新されます。
3.4. 勾配法(gradient method)
続いてアルゴリズム内の2つの注釈の2つ目、更新方法に依ると記した部分について説明します。アルゴリズム図にあるように、正解ラベルと予測ラベルが間違っていた場合重みベクトルを更新するのですが、その更新の仕方は明記していませんでした。更新することによって何を目指し、そのためにはどのように更新するのが最適なのでしょうか。
今回は、その更新の仕方を勾配法と呼ばれる方法に限定します。理由としては、この方法が圧倒的に汎用されているからです。ですが私が見つけられなかっただけで、ひょっとすると他の更新方法もあるのかもしれません。

① 勾配法
勾配法とは関数の最適化手法の一つで、関数の偏導関数(勾配)を用いて最適な点を割り出す方法です。このときの関数は損失関数を指します。では、なぜ損失関数を微分することが必要なのでしょうか。これを明らかにするには、
分類学習の目的が、導出した最適モデルに基づいて未知データを"正しく"分類することであり、最適モデルは、それぞれの入力値から"正しい"出力値を推定するために必要な重み値(weight)を求めることによって導かれると述べました。しかしここではまだ、何を持って"正しい"出力値だと判断するかについては触れていません。
何を持って"正しい"出力値だと判断するか、その方法は色々ありますが、今回の場合は損失関数に大きく依存します。はっきり言えば、損失関数の値が小さければ小さいほど、そのモデルは正しいと見なされるのです。つまり、損失関数を微分するのは損失関数の大域的極小解(global optimal minimized solution)を求めるためであり、その大域的極小値をとるような重みベクトル(w)を求めるためです。
② 勾配降下法(gradient descent)
勾配法は大きく2つあり、勾配上昇法そして勾配降下法があります。勾配降下法は先述したように大域的極小解を求めるための方法でしたが、勾配上昇法は逆の大域的極大解を求めるのに用います。損失関数を用いる多くの学習機械では損失を最小とすることを目的とするので、原則として勾配降下法が用いられます。
以下の図は、この勾配降下法を非常に分かりやすく示したものです。高卒でもわかる機械学習 (2) 単純パーセプトロンから引用させていただきました。

ここに勾配降下法についても分かりやすく書かれていたのですが、繰り返し書いておきます。
まず図の内容について説明します。Eとは既出のように、損失関数を指します。このEの値が極小値となる点が単純パーセプトロンの目指す場所であり、そのwが最適解となります。よって、
・現在のw_iでグラフの傾きが正の場合 → w_i を負の方向に動かす
・現在のw_iでグラフの傾きが負の場合 → w_i を正の方向に動かす
これら2つのプロセスを繰り返し行うことにより極小点に辿り着くことができます。
そして、このグラフの傾きの正負を判断するために損失関数の微分が必要になります。よって、0-1損失関数の場合は微分値が常に0になってしまうため、この方法を用いることが出来ません。しかし代理損失関数を用いれば、このような損失関数の微分が極値を求めるために必要になった場合でも対応できます。
3.5. 単純パーセプトロンの更新式
① 一般的な更新式
では、どのように上記の2つのプロセスが繰り返されていくのでしょうか。このプロセスの繰り返しは更新と呼ばれ、重みwに対する更新式は以下のようになります。
w_i=w_i-ρf'(w_i,x)
f'(w,x)は損失関数のw_iでの微分を示しています。これにより、例えばi=1として、w1に初期値を与えます。この与えられた初期値とベクトルxをf'(w1,x)に代入していき、次々とw1の値を更新していくことになります。そして、この代入された微分値が0になったときに更新を終了します。この式に出てくる定数ρは学習率と呼ばれ、一回の更新幅をどれくらいにするかを決定します。更新するのはあくまで重みwであり、損失関数の値は重みwを更新することによって自ずと下がっていきます。
そしてこの更新は重みベクトルの要素で一つずつ行われます。ですが式では重みベクトルwを用いて、
w=w-ρf'(w,x)
とまとめられ、これが一般的な重みベクトルの更新式となります。
しかし、この方法を用いる際には、この損失関数において局所的最適解は大域的最適解と等しい、つまり凸関数であることが必要条件になっています。これについては、勾配法についての説明を別に行う予定なのでそのときに更新します。
② 単純パーセプトロンの更新式
では、単純パーセプトロンの更新式はどのようになっているのでしょうか。
上記の式に単純パーセプトロンの損失関数であるf(w,x)=max(−y*wx,0)を代入してみましょう。アルゴリズム図より正しく分類されている、つまりE=0のときは更新をする必要がないので、f(w,x)=-ywxのみを考えます。
すると、f'(w,x)=-yxとなることから、単純パーセプトロンの更新式は
w=w+ρyx
となります。
3.6. まとめ
以上をまとめると、単純パーセプトロンの学習アルゴリズムは下の図のようにまとめられます。
繰り返しになりますが、この添字は重みベクトルの要素を示すものではなくデータを示すものだと留意してください。
そしてこのアルゴリズムが、サポートベクターマシンやニューラルネットワークの基本原理となる(かな?)
もし間違っていること等あれば、是非ご指摘して頂けると幸いです。
文字量が多くなってしまったので、適宜図などは更新したいと思います。
3.7. 今回説明していない部分
・なぜ重みベクトル特定の基本アルゴリズムはあれで一般化されるのか
・なぜ|wx|が識別境界からの距離に比例するのか
・なぜ勾配降下法は局所的最適解が大域的最適解と等しいことを必要条件とするのか
4. 参照
高卒でもわかる機械学習 (2) 単純パーセプトロン
機械学習で抑えておくべき損失関数(分類編)
jubatusの分類器:前編(分類の基本・線形分類器のアルゴリズム)
パーセプトロンとは?
第4回 勾配法(最急降下法)