パーセプトロンとは?

このページは筆者がLSTM(Long short-term memory) の学習をする上で、そもそもNN(Neural Network)とはなにかについて学ぶために, 参考文献を自分のわかりやすいように書き直して理解を深めることを目的としています. 本文の主な内容は[参考文献1][ref1],[参考文献2][ref2]から引用したものです.

1 神経細胞のモデル

1-1 神経細胞(ニューロン)

　ニューロンとは脳の神経細胞のこと. 1891年にWilhelm Waldeyerによって提唱されました. ニューロンは細胞体、樹状突起、軸索、シナプスという4つの部分から構成されています.

　Fig.1-1 ニューロンの概要 (画像はこちらを[参考][ref3])

• 細胞体(部) (soma) : ニューロンの本体. Fig.1-1 の橙色の部分.
• 樹状突起 (dendrite) : 細胞体から飛び出した枝のような部分. ニューロンの入力端子にあたる.
• シナプス (synapse) : 他のニューロンと繋げる役割をする. 樹状突起はシナプスを通して他のニューロンの信号を受け取る. シナプスの伝達効率はそれぞれ異なっている.

1-2 ニューロンの信号伝達の方法

• 信号伝達は電位の変化によって起きる.
• ニューロンはその周りにある細胞外液との間に電位差を持っている.これを膜電位という.通常は-70[mV]程度.
• 入力信号によって膜電位が上がり始め、あるしきい値を超えるとニューロンは瞬間的に0[V]を超える. この状態をニューロンが発火した状態という.

1-3 ニューロンモデル

　Fig.1-1のように神経細胞をいちいち絵を書いて表すのは大変なので、ニューロンを簡単に表すためにモデル化します.モデル化されたニューロンは形式ニューロンと呼びます.

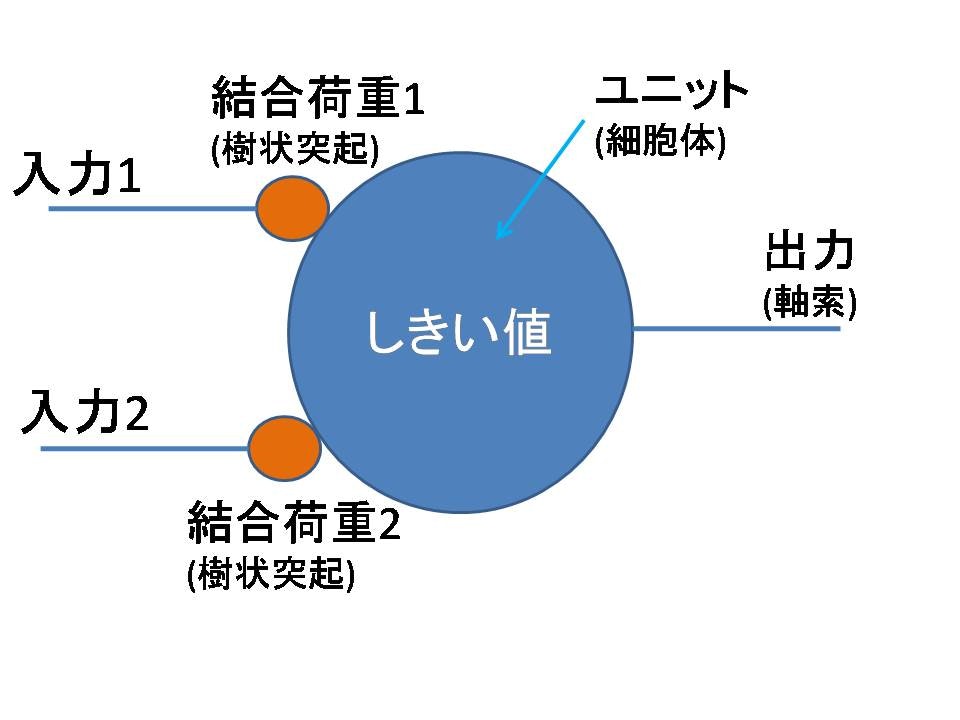
　　　　Fig.1-2 モデル化したニューロン

• 結合荷重とは樹状突起をモデル化したもの.ここには任意の実数値を入れる.これはシナプスが異なる伝達効率を持っている事を表すため.
• ユニットはニューロンの信号伝達のようにしきい値を計算するための部分. 入力に結合荷重の重みをかけた総和がしきい値を超えたかどうか判断し、超えたら"1", 超えなかったら"0"を返す.

　Fig.1-2には入力は2つしかありませんが、2つ以上の入力がユニットに入力された場合も、ニューロンが出力する値は"1(ある)"か"0(ない)"かで表すことができます. 計算機においても"0"と"1"で表したほうが処理しやすいので、出力値としてこの2つの値を使います.　(今回は"1"と"0"としていますが, "-1"と"1"だったり"-1"と"0"とすることもできます. しかし、ニューロンからの出力は常に "2値" です.)

1.3 ニューロンモデルの数式化

　次に、入力がn個あるときのニューロンモデルを数式を使って表してみます.入力がn個あるときはFig.1-2からもわかる通り結合荷重もn個存在します.ここではi番目の入力$X_i$の結合荷重を$W_i$として表します.

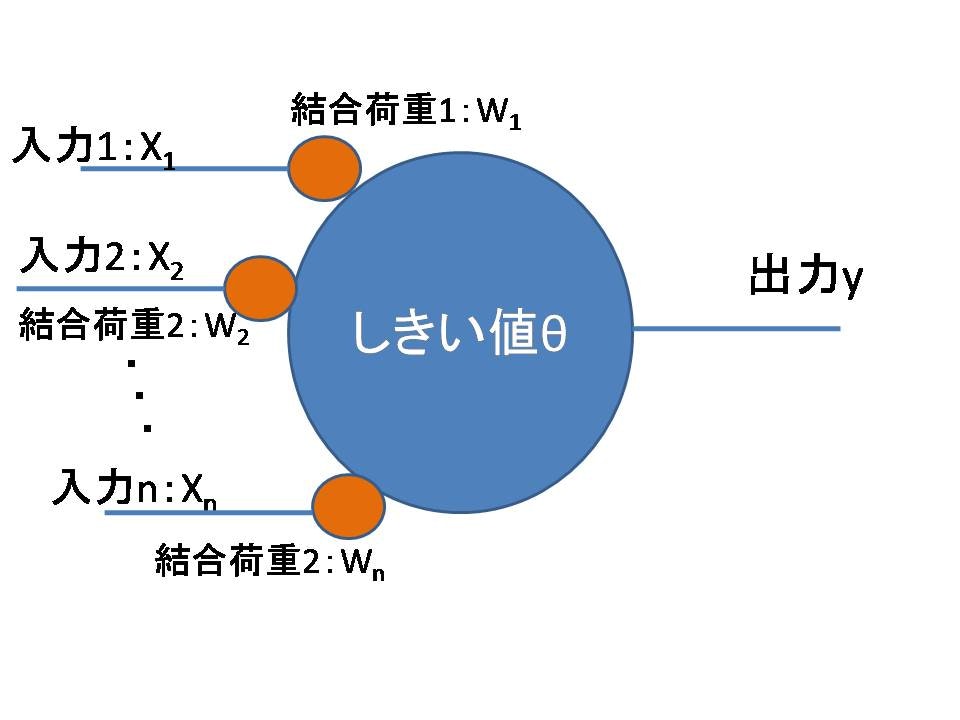
　　　Fig.1-3 ニューロンモデル(形式ニューロン)
　ニューロンには膜電位があり、膜電位は入力信号によって上昇していきます. これがあるしきい値を超えると"1",超えなければ"0"となります.これを数式で表してみます.まず、はじめにニューロンに入力される信号を考えます.

\begin{align}
u &= 入力1 × 結合荷重1 + 入力2 × 結合荷重2 + ... + 入力n × 結合荷重\\
&= X_1W_1 + X_2W_2... + X_nW_n\\
&= \sum_{i=1}^n X_iW_i \tag{1-1}
\end{align}

入力信号はそれぞれの入力Xと結合荷重Wをかけて、それらを足し合わせたものです.これをネット値 uといいます.

　ニューロンは膜電位がしきい値θを超えると発火します(出力yが"1"になる).つまり、膜電位からしきい値を引いた値が正であれば発火します.　$\Bigl( \sum_{i=1}^n X_iW_i - θ > 0 で発火 \Bigr)$
しきい値を超えていれば"1",そうでなければ"0"を出力するために次のような関数を用います(Wiki参照).
・ 階段関数(ヘビサイド関数)
・ シグモイド関数
・ 線形ランプ関数
この出力値を決定する関数を活性化関数といいます.これらの関数で、(ネット値 - θ) が正のときは"1",負の時は"0"を出力する場合には.階段関数では次のように表します.

\begin{eqnarray}
f(u)
 =
  \begin{cases}
    1 & ( u \geq 0 ) \\
    0 & ( u \lt 0 )
  \end{cases}
\end{eqnarray}

$f(u)$は0以上になったときに"1"それ以下では"0"を出力するという関数です.これは、"入力がある値を超えた時に急激に発火する"というニューロンの特性を表しています.
　$f(u)$を用いてニューロンの出力yを表すと,

\begin{align}
y &= f(\sum_{i=1}^n X_iW_i - θ) \tag{1-2}\\
y &= f(\sum_{i=0}^n X_iW_i) \tag{1-3}\\

\end{align}

式(1-2)(1-3)はどちらも同じことを表しています.ただし、式(1-3)ではi=0から始まっています. これは式(1-3)ではi=0のときの入力$X_0$を$1$, 結合荷重$W_0$を$−θ$としてしきい値も和の形として表しているためです.
　この入力の0番目$X_0$を1,結合荷重$W_0$をしきい値として入力するニューロンモデルをパーセプロトンと呼びます.このパーセプトロンがニューラルネットワークの基本単位となります.

まとめ

人間の脳にはニューロンという神経細胞があり, それを数式で表すためにニューロンモデル(形式ニューロン)が作られた. ニューロンモデルはいくつかの入力$X_n$とひとつの出力Yを持っている. 出力Yは"1"か"0"かの2つの値しか出力しない. 2つの値をどちらか決めるためにしきい値を使う. 入力$X_n$にそれぞれ結合荷重$W_n$という定数との積を足し合わせた数(ネット値)よりもしきい値が低ければ"1"そうでなければ"0"を活性化関数を使って出力する.このモデルをパーセプトロンという.

このようなモデルで表現できる機械学習を『単純パーセプトロン』と呼びます.　このページでは "パーセプトロンの入力, しきい値, 活性化関数の役割" について説明しました. 次に、このモデルを使った学習方法についてまとめます.
→ [単純・多層パーセプトロン]next

2 ニューラルネットワーク

　人間の脳は100億から140億個のニューロンが互いにつながり、巨大なシステムを構築しています. このようなニューロンを校正素子とした回路網を**ニューラルネットワーク(神経回路網)**と呼びます.今まで1つしかなかったニューロンモデルを複数接続することで、ニューラルネットワークを作ることができます.ニューラルネットワークの応用例としてはAND,XORなどの論理計算から、文字認識や連想記憶の実現などもできます.
　ニューラルネットワークはニューロンの接続の仕方でネットワークの構造と特徴が決まり,2つにわけられます.

2.1 階層型ネットワーク

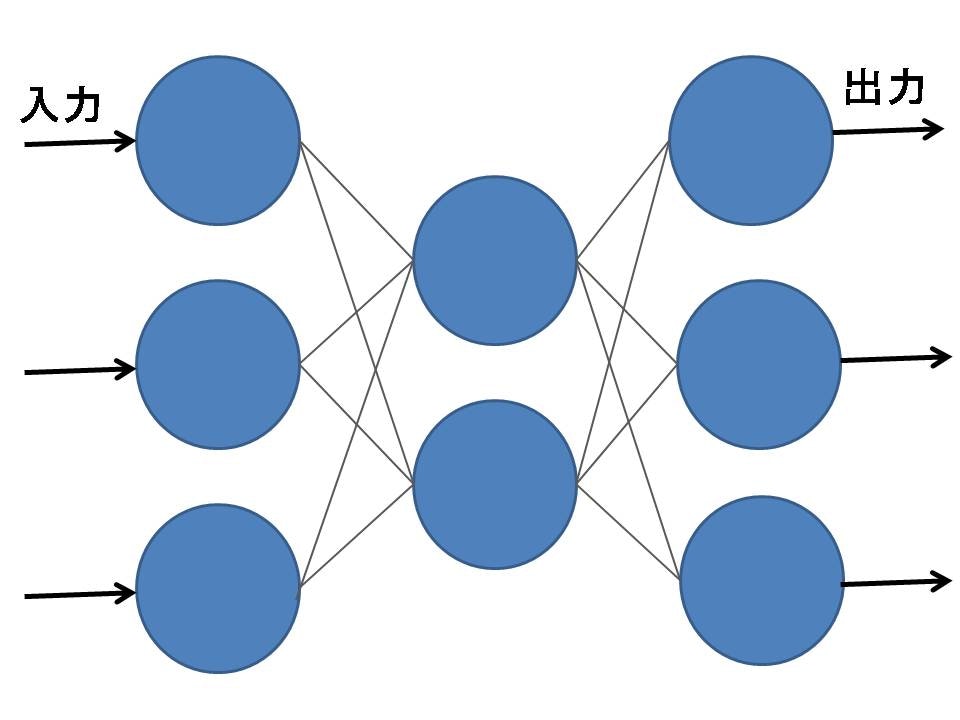　　　　**Fig.2-1 階層型ニューラルネットワーク** 　- ニューロンを層にして並べたネットワーク. 信号が伝わる方向は前の層から次の層への一方通行. 　- 入力層のニューロンに加えた信号(入力信号)に対して出力層のニューロンに加えた信号(出力信号)が一意に定まる. 　- 階層が少ないと解けない問題もある(階層型ネットワークのパーセプトロンの項で説明). しかし、最低3層あれば任意のパターンを認識させるのに十分であることが知られている.

詳しくは [単純・多層パーセプトロン][next]の説明ページで(更新予定)

2.2 相互結合型ネットワーク

　　　　　Fig.2-1 相互結合型ネットワーク 　- 階層型ネットワークと異なり、信号の流れる方向は1方向ではなく、フィードバックする. 　- 非階層型ネットワークは連想記憶モデルや音声合成、音声認識の分野に使われている.

参考文献

1. [ニューラルネットワーク入門][ref1], Iwata Laboratory Nagoya Instltute of Technology,Akira Iwata, Toshiyuki Matubara, 1996
2. [高卒でもわかる機械学習 (2) 単純パーセプトロン][ref2], hokuto shimokawa
   [ref1]:http://www-ailab.elcom.nitech.ac.jp/lecture/neuro/menu.html
   [ref2]:http://hokuts.com/2015/11/25/ml2_perceptron/
   [ref3]:http://ggsoku.com/tech/sleeping-accelarate-dendric-spine-specific-development/
   [next]:http: