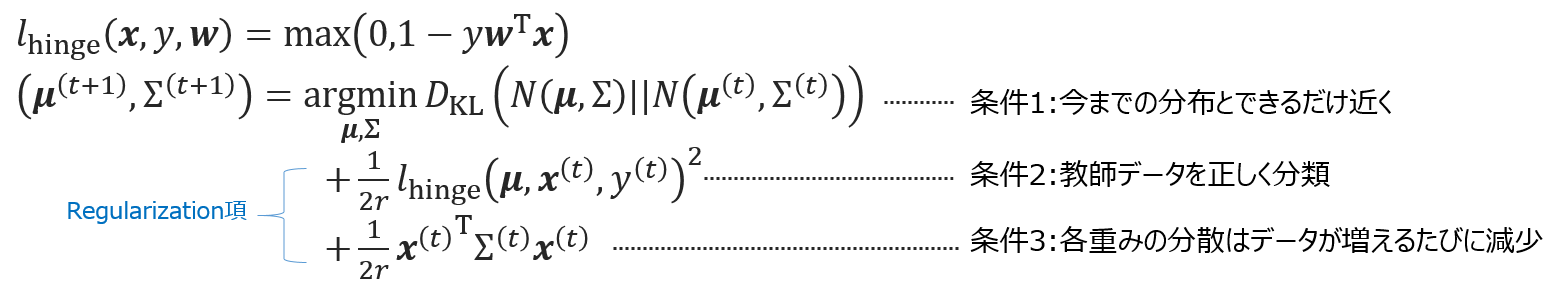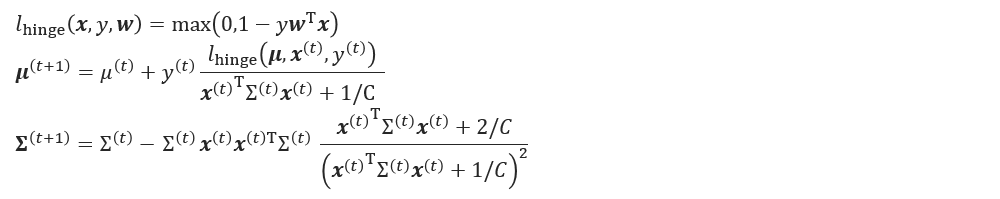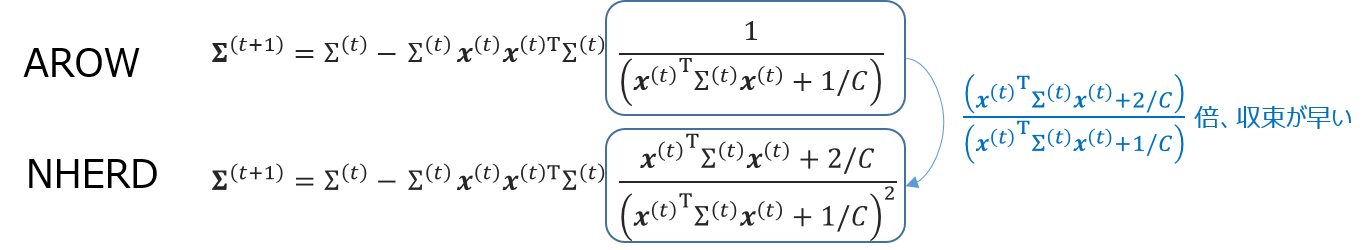More than 5 years have passed since last update.

jubatusの分類器：前編(分類の基本・線形分類器のアルゴリズム)

Last updated at 2016-12-19Posted at 2016-12-19

この記事はJubatus Advent Calendar 19日目の記事です．

こんにちは、@imaimai1125です

普段良く使う、Jubatusの分類器の中身のアルゴリズム、あまり中身が分からずに使っている方も多いのではないのでしょうか。
一応Jubatus HPにもアルゴリズム解説はあるのですが、上級者向けになっているので、少し噛み砕きながら説明します。

分類とは？

イメージとしては、ハリーポッターに出てくる組み分け帽子のようなものを想像してください。

帽子を被ると、グリフィンドール・スリザリン・ハッフルパフ・レイブンクローに分けてくれます。

機械学習的な言葉で言えば、帽子が分類器、帽子を被った人が入力、被った人の性格、才能、身長や体重といったものが特徴量になります。(実際何を基準に組み分けされているかは知りませんが。)
何らかの特徴量から判断をして、あの組み分け帽はハリーたちをクラスに分けていくのです。

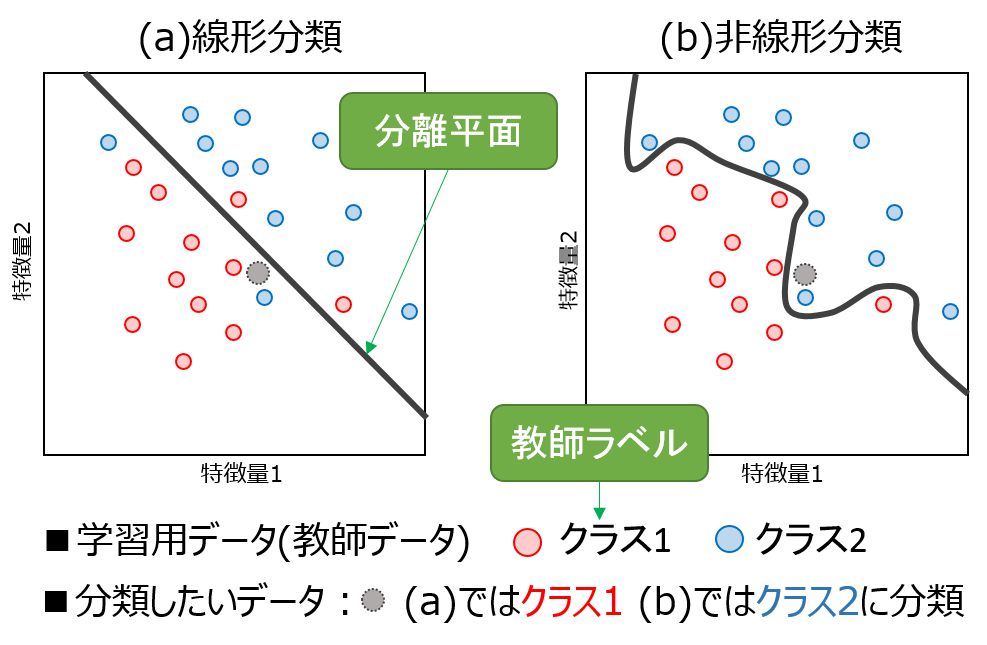
どういう感じで分類がなされているか、図にしてみました。

この図では、図示の都合上特徴量が２つですが、この特徴量は状況によって増やすことができます。
また、クラスの数も増やすことが可能です。

黒の太線が、分離平面です。先ほどの例で言えば、どのクラスになるかというギリギリの線ということになります。
この分離平面を決定するのが分類器の役割です。

青と赤の丸は、予め用意されたラベルつき教師データです。「この特徴量ならクラス1だ」というようなデータを予め用意しておいて、
それを使って分離面を作っていきます。

図のように、分離平面の作り方によって、線形分類器・非線形分類器と、大きく2種類に分かれます。

線形分類器では、まっすぐな線を引くため、分類の仕方に限界があります。なので、図のように、クラス1側が全部クラス1のデータ！というわけにはいかないこともあります。
非線形分類器では、ぐにゃぐにゃと線を引けるため、教師データの分類に関してはほぼ100%分類ができます。しかし、あまりにも教師データにあわせすぎると、ほかの新しいデータに対してうまく分けれなくなるかもしれないというような問題があります。

図では、(a)と(b)で分類結果が違うという例を挙げました。どちらを信じればいいかは機械学習の本質的に難しい問題ともいえます。興味のある人はモデル選択とか、バイアス・バリアンスという言葉で調べてみてください。

この分離平面を決めるアルゴリズムをjubaclassifierでは数種類用意しています。

jubaclassifierで使える分類アルゴリズム

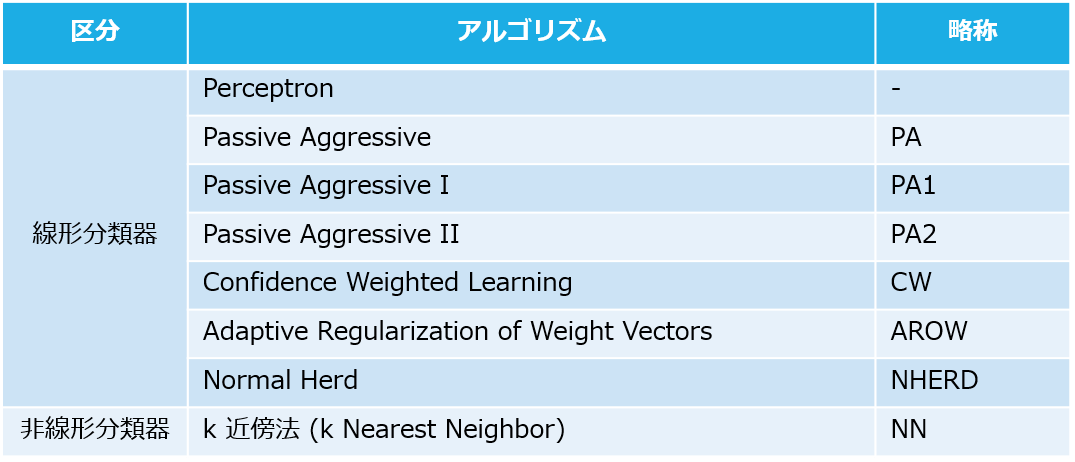
jubaclassifierでは、分類アルゴリズムとして、下記を用意しています

前編では、線形分類器について、説明します！

オンライン線形分類器

核となるアルゴリズム

Jubatusの線形分類器は様々な種類が用意されています。しかし、核となるアルゴリズムはどれも一緒です。

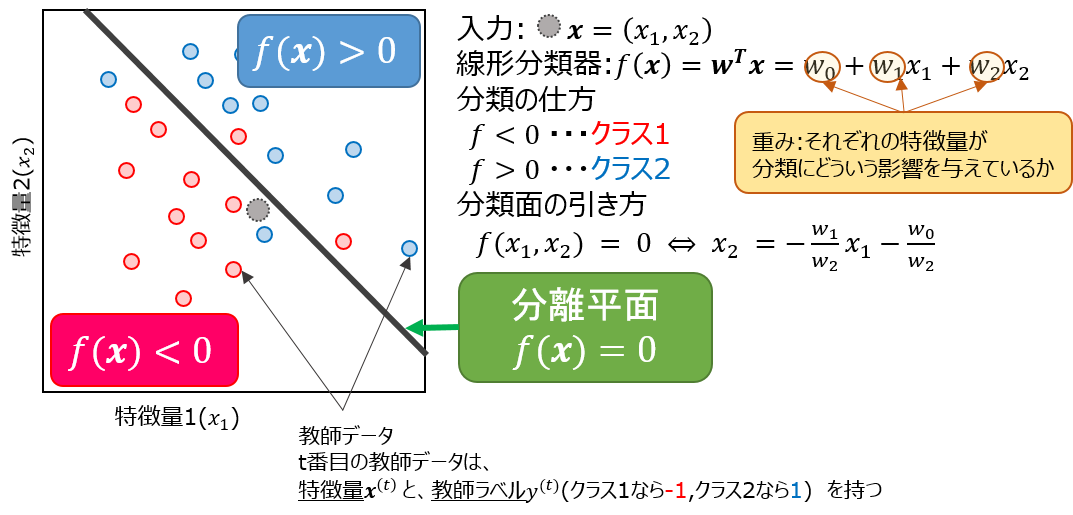
事前準備として、先ほどの図(a)について、もう少し数式を使ってみてみましょう。

この図からわかるように、**$w$**をうまく決めることが、分類器の肝となるのが、わかると思います。これを踏まえて、線形分類の核となるアルゴリズムをみていきましょう。

↓図が、核となるアルゴリズムになります。

$E$, $\alpha$と, $A$について、先ほどのアルゴリズムを見ていくと、

となります。これがjubatus線形分類器の中身です。

とはいっても、設計思想がわからないので、少し詳しく見ていきましょう

Perceptron

更新式 : $\mathbf{w^{(t+1)}}=w^{(t)}+y\mathbf{x}$

最も単純なアルゴリズムで、間違っていたらそのときの特徴量分、重みとして正解に近づくように足し合わせるようになっています

Passive Agressive

PA

サポートベクターマシン(SVM)のオンラインバージョンになっていて、

必ず正しく分類する**(Agressive)**
あまり重みを更新しすぎず、なるべく最小限に更新する**(Passive)**

という2つを考慮して重みを更新していく(更新の仕方は、ラグランジュの未定乗数法を使う)

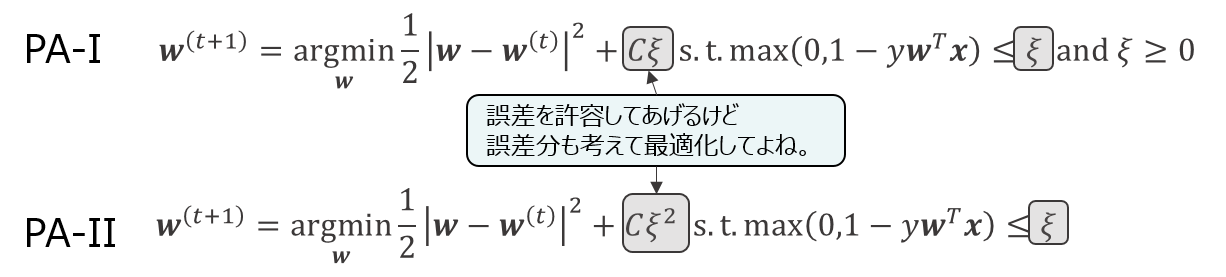
PA-I, PA-II

ただし、この絶対分類しろというのが厳しく、ひとつのミスも許されないという厳しいものになっているので、
もうちょっとマイルドにしてやろうと考えたのが、PA-IやPA-IIです。

変わったところは、ミスを許すようにした代わりに、罰則項として更新時にミスを考慮させるようにしたというところです。

このCの値は、こちら側で調節できるようになっていて、jubaclassifierでもregularization_weightをいじることで、調整ができます

{
  "method" : "PA2",
  "parameter" : {
    "regularization_weight" : 1.0
  },
  "converter" : {
    "string_filter_types" : {},
    "string_filter_rules" : [],
    "num_filter_types" : {},
    "num_filter_rules" : [],
    "string_types" : {},
    "string_rules" : [
      { "key" : "*", "type" : "str", "sample_weight" : "bin", "global_weight" : "bin" }
    ],
    "num_types" : {},
    "num_rules" : [
      { "key" : "*", "type" : "num" }
    ]
  }

Confidential Weight

思想としてはPAとほとんど同じで、「$w$を前とあまり変えすぎずに上手に分類してほしい」のですが、
CWでは、重みがガウス分布に従うという仮定が入ります。$\mathbf{w}\sim N(\mathbf{\mu},\Sigma)$、ガウス分布のパラメータである平均と分散を更新することで、重みを更新します。

$\mu$の更新式は

\begin{eqnarray}
\mu^{(t+1)}=\mu{(t)}+\alpha^{(t)}y^{(t)}\Sigma^{(t)}\mathbf{x}^{(t)}
\end{eqnarray}

となります。ここでの$\Sigma$はガウス分布の分散項で、その重みを決めたときのいわゆる自信みたいなもので、自信があれば(分散が小さければ)もうあまり$\mu$を更新しないし、自信が無ければ思い切って更新をするといったものになっています。

$\Sigma$自体、更新を繰り返すごとに0に近づいていき、そのスピードは分離できるものであればとても早いです。
弱点としては、PAと同じように分離できないものに対して弱く、データにノイズが載ったりすると著しく精度が落ちることが知られています。

jubaclassifierで設定できるパラメータとして、regularization_weightを用意しています。
厳密には$\eta$ではないのですが、上の数式の$\eta$に密接に関係する量を調節しています。

regularization_weight 大 ⇔ $\eta$ 大 : ミスは許さない.代わりに学習は早い
regularization_weight 小 ⇔ $\eta$ 小 : 多少のミスは許すが、学習は遅くなる

という特徴があります。

Adaptive Regularization of Weight Vectors

CWの弱点であるノイズに対して弱いを、正規化項を加えることで克服しようとしているものです。更新式はこちら

(細かい内容は論文を参照してください。)

CWが、何が何でも正解率$\eta$を見つけてくるような条件式になっていたのに対し、AROWはもうちょっと穏やかです.

更新式からもわかるように、3つの条件をバランスよく保ちながら、$w$を決める平均と分散を更新していきます。

jubaclassifierで設定できるパラメータとして、reguralization_weightを用意しています。
上式においてreguralization_weight$=1/r$となっているため

regularization_weight 大 ⇔ 何が何でも正しく分類しようとする。CWっぽい挙動
regularization_weight 小 ⇔ 分布の更新幅重視になる。学習は遅い

という特徴があります。

NHERD

こちらも、CWの弱点を解消しようとしたものです。

更新式としてはAROWに似たものになっているのですが、論文での導出過程をみると、更新式の裏のココロはかなり異なっているようです。
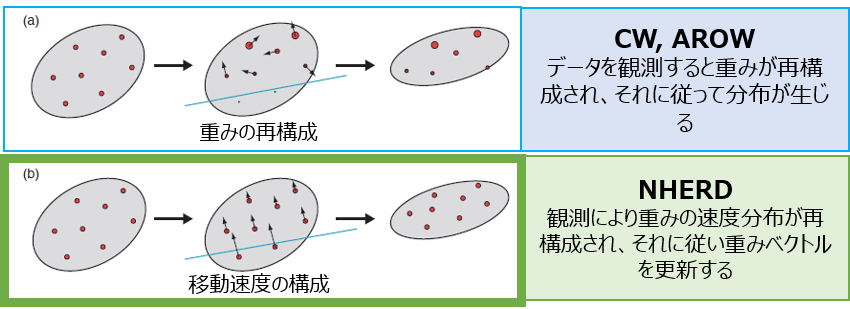
CWやAROWが、重みベクトルの分布をなるべく変えないような更新をするために、KL divergence($D_{KL}$)を最小化しようとしていたのに対して、
NHERDは重みベクトルの分布を速度だとみなして、その速度にしたがって重みベクトルを更新する。という見方をしています。

重みベクトルの更新としては

\begin{eqnarray}
w_{i+1} = Aw_i+b\end{eqnarray}

のように従って行います。このときに、wの分布の計算を、KL divergenceではなく、マハラノビス距離で計算しているところも、AROWやCWと違うところです。
ただ、更新式に($A$)は明には出てこず、結果としては下図のような更新式となります。
(細かい内容は論文のAlgorithmの章を参考にしてください)