機械学習初心者でも、ニューラルネットワーク(neural network : NN)について理解しなければならない日がいつか来る。なので初心者代表の私が、ニューラルネットワークについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
本記事は、初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜の記事の続きとなります。
1. なぜ人はニューラルネットワークを学ぶのか
今や日常生活の様々な場面に用いられている、機械学習のコアの部分だからです。(多分)
2. 本記事の目的
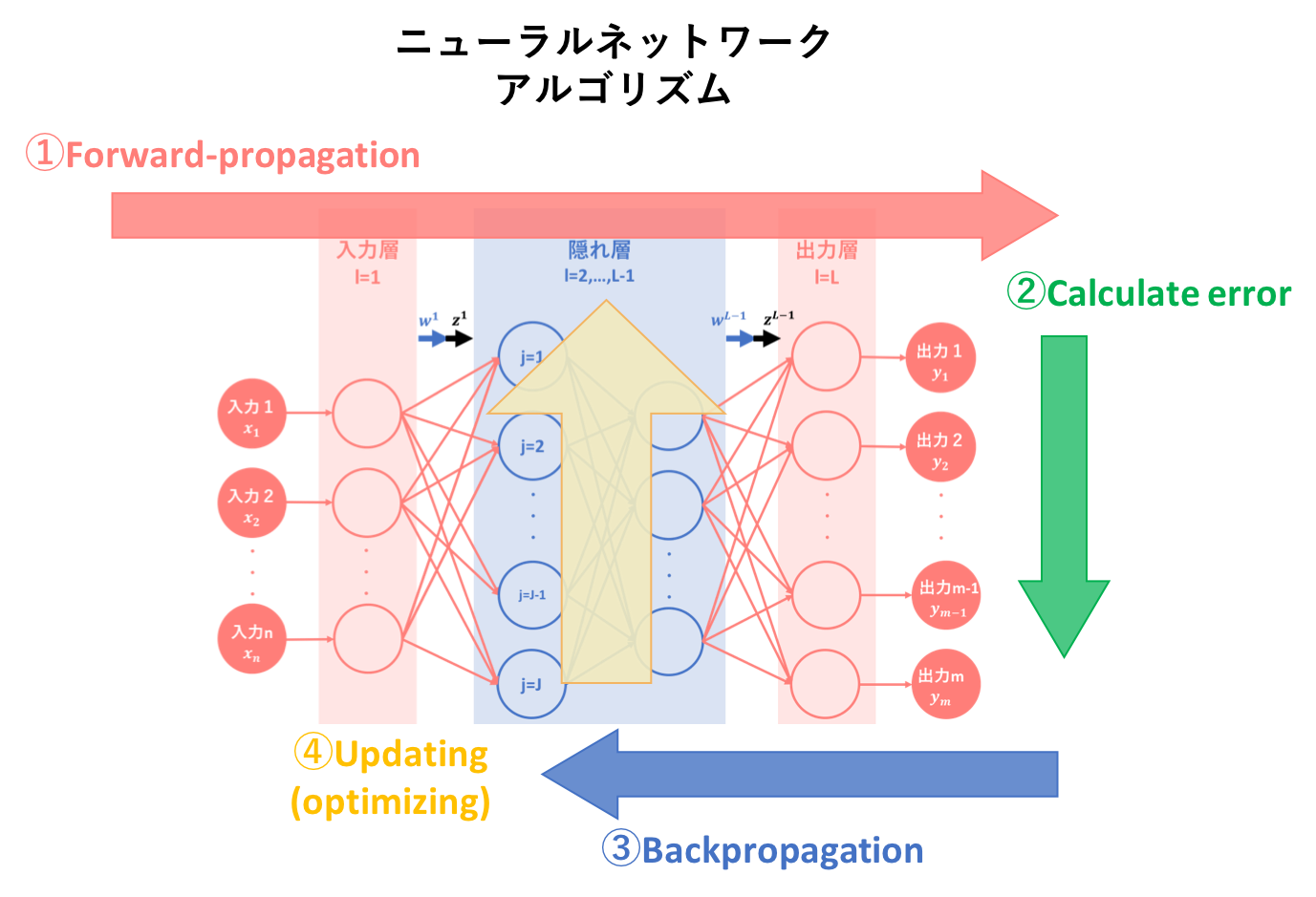
本記事では、ニューラルネットワークのアルゴリズムを簡易図式化した以下の図のうち、④パラメータ更新についての説明を行います。
3. 前記事の要約
初心者の初心者による初心者のためのニューラルネットワーク〜理論:順伝播編〜では、ニューラルネットワークの基本概念、基本構造そしてアルゴリズム①である順伝播(forward-propagation)について説明しました。
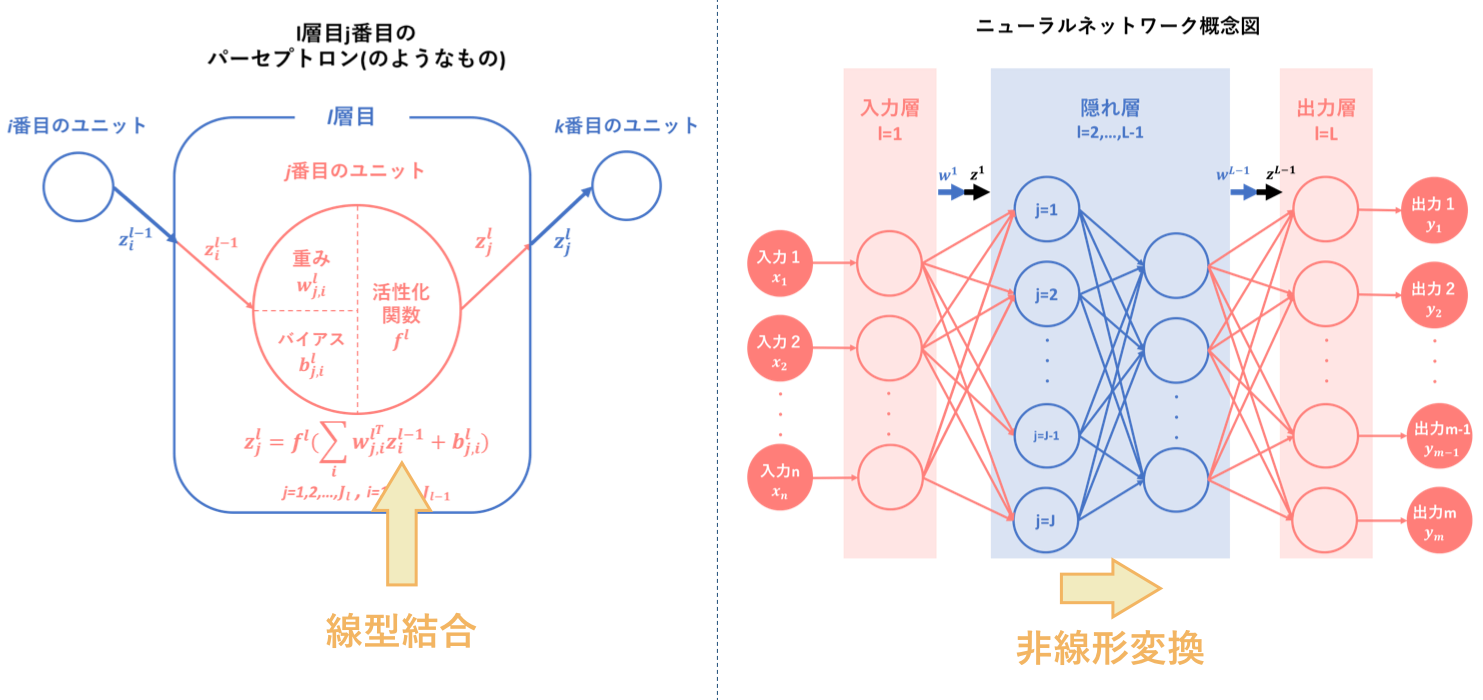
その要約として以下の図をあげます。ニューラルネットワークとは、『パーセプトロン(のようなもの)を基に人間の脳神経系のニューロンを数理モデル化したもの』のことであり、『線型結合と非線形変換を繰り返す合成関数 $f(w,x)$によって入力から出力を表すモデル』です。
そして、ニューラルネットワークの目的は最適パラメータの発見であり、そのために学習を繰り返すことによって予測出力を最適化するようなパラメータを導出します。
順伝播は、その学習アルゴリズムの一つ目でした。
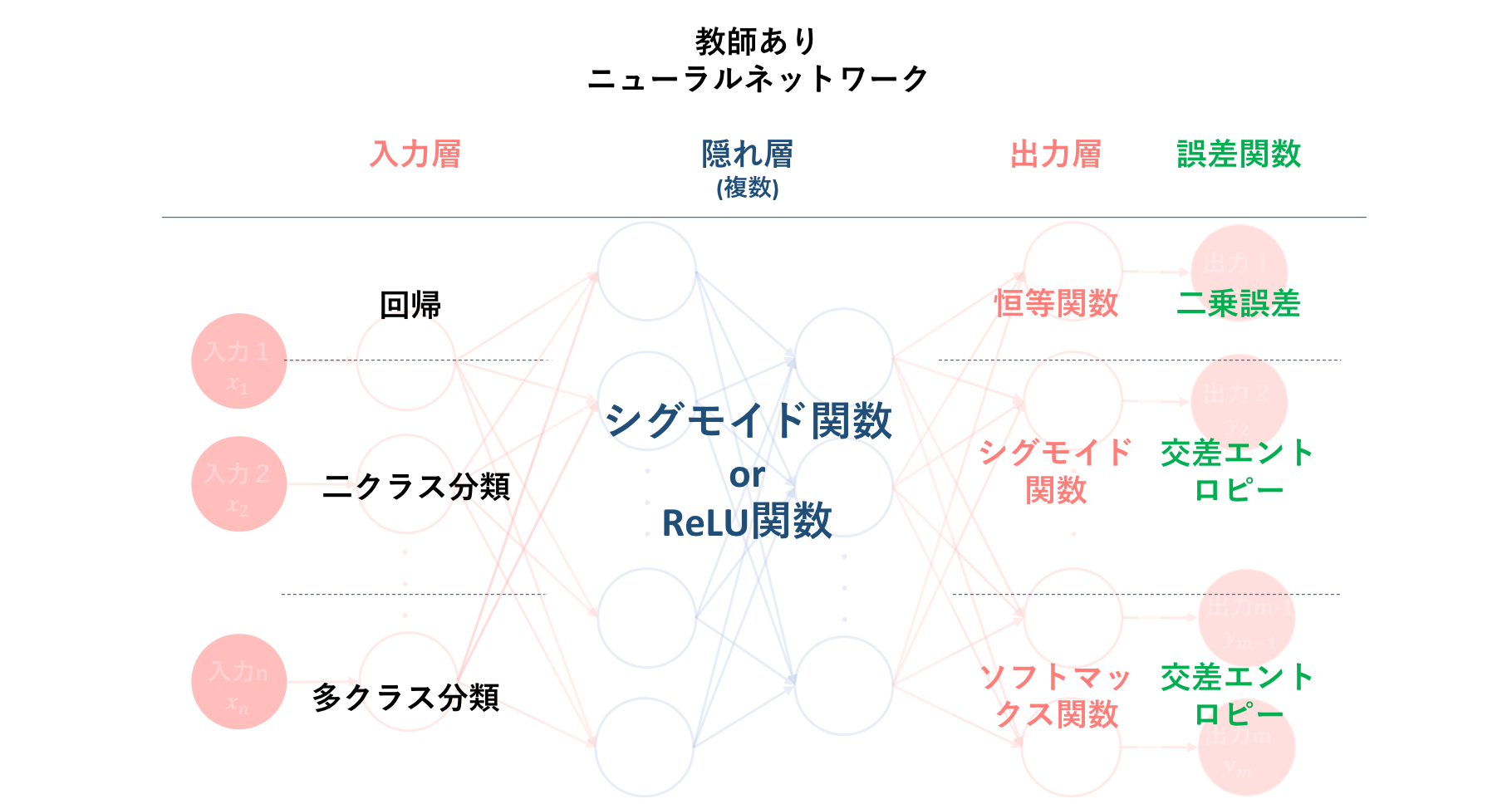
そして続く初心者の初心者による初心者のためのニューラルネットワーク〜理論:誤差計算編〜では、アルゴリズム②である出力値と教師信号のずれの程度を表すための誤差計算について説明しました。そして、こちらはアルゴリズム②には含まれない部分ですが、誤差関数と密接に関係する多層パーセプトロン内の活性化関数の種類とその使用場面についての説明も行いました。
以下の図は、それらの誤差関数および活性化関数の種類と、それぞれどのような問題に対し用いることが一般的なのかをまとめたものになります。
これに基づいた誤差計算は、学習アルゴリズムの二つ目でした。
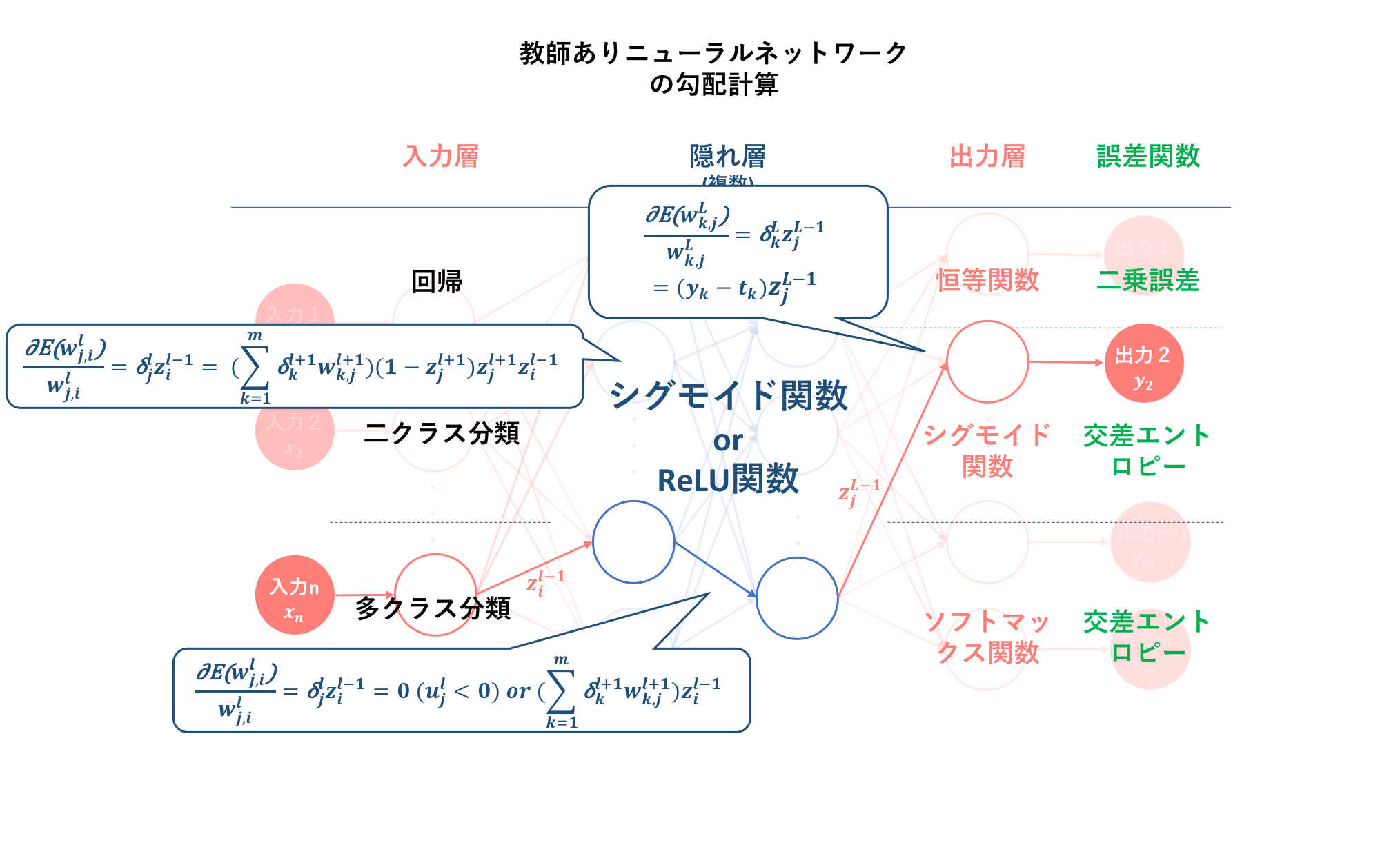
そして、初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜では、誤差を最小化するための学習方法として勾配降下法を適用するために、各層における誤差関数の重みに対する勾配の計算方法を導出しました。その結果、$l$層の勾配を算出するには$l+1$層の誤差信号及び$l$層への入力値を求める必要があることが分かりました。これによって、勾配降下法の多層パーセプトロン(この記事ではニューラルネットワークと同義)への適用には、あらかじめ
・ 順伝搬による各層の出力の算出
・ 出力値と教師信号の比較による誤差信号の算出
という二つのフェーズ、すなわち多層パーセプトロンアルゴリズムの①, ②をパスしなくてはいけないことが分かりました。
以下の図は、それぞれの活性化関数及び誤差関数を用いた場合の勾配の計算式を示したものです。なお、前記事の議論から、誤差信号は三つの出力関数には依らないということが分かっています。
この勾配の導出が、学習アルゴリズムの三つ目でした。
4. 勾配降下法によるパラメータ更新
前記事は、あくまでも勾配降下法を多層パーセプトロンに適用するための下準備のアルゴリズムについての解説でした。本記事ではいよいよ、多層パーセプトロンの基本アルゴリズムとしては最後になる、パラメータ更新について詳しく見ていきます。
4.1. 勾配降下法 (Gradient descent)
またしてもの繰り返しになりますが、本記事でも簡単に説明します。
勾配降下法とは、目的関数が最小化されるようパラメータを調整し最適化するためのアルゴリズムです。損失関数を用いる多くの学習機械では損失を最小とすることを目的とするので、原則として勾配降下法が用いられます。

上の図は、この勾配降下法を分かりやすく示したものです。
縦軸の$E$とは損失関数(誤差関数)を指します。この$E$の値が極小値となる点が学習機械の目指す場所であり、その$w$が最適解となります。よって、
・現在の $w_i$でグラフの傾きが正の場合 → $w_i$ を負の方向に動かす
・現在の $w_i$でグラフの傾きが負の場合 → $w_i$ を正の方向に動かす
これら二つのプロセスを繰り返せば、極小点に辿り着くことができるということが分かります。では、どのように繰り返せば良いのでしょうか。このプロセスの繰り返しは更新と呼ばれ、重み$w$に対する基本更新式は以下のようになります。
$$w^{(t+1)}=w^{(t)}-\eta\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$$
この式を少し掘り下げて見ていきましょう。定数$\eta$は学習率と呼ばれ、一回の更新幅をどれくらいにするかを決定します。また、添字の$t$は更新数を表しています。
この式で重要になるのは、最右項である$$\eta\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$$の部分です。これは一体、何を示しているのでしょうか。
ここで一旦、勾配降下法のゴールについて考えてみましょう。勾配降下法におけるゴールとは、誤差関数$E$の値が大域的極小値となる状態であり、それは、パラメータ誤差関数$E$の$w$に対する勾配が0となる状態($\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}=0$)です。つまり、勾配降下法によるパラメータ更新とは、$\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$の値が0となるように$w$を更新していくことだということが分かると思います。
上図は、重み$w^t$から重み$w^{t+1}$への更新を示したものです。先ほどのプロセスをもう一度確認しましょう。
・現在の $w_i$でグラフの傾きが正の場合 → $w_i$ を負の方向に動かす
・現在の $w_i$でグラフの傾きが負の場合 → $w_i$ を正の方向に動かす
このことから、$\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$の符号と$w^t$の更新方向符号はすべての$w$において逆となることが分かります。
つまり、$-\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$の符号と$w^t$の更新方向符号はすべての$w$において等しくなることが分かります。$w$の更新には、この性質を利用します。それら二つの符号がすべての$w$で等しいのであれば、あとはその更新幅を調整すればよいだけなので、その調整パラメータとして$\eta$を用います。
$$w^{(t+1)}=w^{(t)}-\eta\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}\tag{4.1}$$
しかし、だからといって**上式の最右項$\eta\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$の式の解釈で大切なのはその値ではなくその符号ということではありません。どうやらこの、$-\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$というのは、$E$の値を最も急速に降下させる方向であるからのようです。**これがなぜなのかについては、私自身理解できる部分ではありませんでした。以下の京都大学講義の資料が参考になるかもしれませんが、理解を断念...
→第 7 章 降下法
さて、不十分な理解ですがこのまま進むことにします。(すいませんw)
このような更新式で表すことのできる勾配降下法ですが、そこには細かく三種類の手法が存在します。以下でそれぞれについて説明していきます。また、この方法を用いる上では、この誤差関数において局所的最適解は大域的最適解と等しい、つまり凸関数であることが必要条件になっています。
4.1.1. 最急降下法 (Gradient descent / Steepest descent)
最急降下法のパラメータ更新式は、以下のようになります。
ここで、dはテストデータの一つ, Nはテストデータの数を表しています。
\begin{align}
w^{(t+1)}&=w^{(t)}-\eta\text{grad}E(w^{(t)})\\
&=w^{(t)}-\eta\begin{bmatrix}
\frac{\partial{E}}{\partial{w_1^{(t)}}}\\
\frac{\partial{E}}{\partial{w_2^{(t)}}}\\
\vdots\\
\frac{\partial{E}}{\partial{w_n^{(t)}}}\\
\end{bmatrix}=w^{(t)}-\eta\begin{bmatrix}
\frac{\partial(\sum_{d=1}^N{E_d})}{\partial{w_1^{(t)}}}\\
\frac{\partial(\sum_{d=1}^N{E_d})}{\partial{w_2^{(t)}}}\\
\vdots\\
\frac{\partial(\sum_{d=1}^N{E_d})}{\partial{w_n^{(t)}}}\\
\end{bmatrix}\\\tag{4.2}
\end{align}
最急降下法は、勾配降下法の中では最もオーソドックスなものです。この"最急"とは、収束速度ではなく、$-\frac{\partial{E(w^{(t)})}}{\partial{w^{(t)}}}$とが$E$の値を最も急速に降下させる方向だということに由来します。
**最急降下法は、学習データのすべての誤差の合計を取ってからパラメータを更新します。**よって、学習データが多いと計算コストがとても大きくなってしまいます。また、学習データが増えるたびに全ての学習データで再学習が必要となります。
4.1.2. 確率的勾配降下法 (Stochastic gradient descent: SGD)
確率的勾配降下法のパラメータ更新式は、以下のようになります。
ここで、dはループ(epoch)ごとにランダムに抽出されるテストデータの一つを表しています。
\begin{align}
w^{(t+1)}&=w^{(t)}-\eta\text{grad}E_d(w^{(t)})\\
&=w^{(t)}-\eta\begin{bmatrix}
\frac{\partial{E_d}}{\partial{w_1^{(t)}}}\\
\frac{\partial{E_d}}{\partial{w_2^{(t)}}}\\
\vdots\\
\frac{\partial{E_d}}{\partial{w_n^{(t)}}}\\
\end{bmatrix}\tag{4.3}
\end{align}
**確率的勾配降下法は学習データをシャッフルした上で学習データの中からランダムに1つを取り出して誤差を計算し、パラメーターを更新をします。**このとき、一つのループ(epoch)ごとにランダムに抽出します。
勾配降下法ほどの精度はありませんが、増えた分だけの学習データのみで再学習できるため再学習の計算量が圧倒的に少なくなります。このとき、重みベクトルの初期値は前回の学習結果を流用します。
4.1.3. ミニバッチ確率的勾配降下法 (Minibatch stochastic gradient descent: MSGD)
ミニバッチ確率的勾配降下法のパラメータ更新式は、以下のようになります。ここでは、重みの更新をサンプル1つ単位ではなく、少数のサンプルの集合をひとまとめにし、その単位で重みを更新します。そのひとまとめにしたサンプル集合をミニバッチと呼びます。
\begin{align}
w^{(t+1)}&=w^{(t)}-\eta\text{grad}E_{D_k}(w^{(t)})\\
&=w^{(t)}-\eta\begin{bmatrix}
\frac{\partial{E_{D^t}}}{\partial{w_1^{(t)}}}\\
\frac{\partial{E_{D^t}}}{\partial{w_2^{(t)}}}\\
\vdots\\
\frac{\partial{E_{D^t}}}{\partial{w_n^{(t)}}}\\
\end{bmatrix}=w^{(t)}-\eta\begin{bmatrix}
\frac{1}{N^t}\frac{\partial(\sum_{d\in{D^t}}{E_d})}{\partial{w_1^{(t)}}}\\
\frac{1}{N^t}\frac{\partial(\sum_{d\in{D^t}}{E_d})}{\partial{w_2^{(t)}}}\\
\vdots\\
\frac{1}{N^t}\frac{\partial(\sum_{d\in{D^t}}{E_d})}{\partial{w_n^{(t)}}}\\
\end{bmatrix}\\\tag{4.4}
\end{align}
まず上式では、t回目の更新に用いるミニバッチを$D^t$, そのサンプル数を$N^t$としています。そして$\frac{1}{N^t}$で正規化することによって、ミニバッチのサイズを変えた時に学習率を変える必要がなくなります。
ミニバッチ確率的勾配降下法は、最急降下法と確率的勾配降下法の間を取ったような形となります。 最急降下法では時間がかかりすぎ、確率的勾配降下法では一つ一つのデータにかなり揺さぶられることになるので、学習データの中からランダムにいくつかのデータを取り出して誤差を計算、パラメータを更新をします。このときの一回に取り出すデータの数をバッチサイズと呼びます。
通常ミニバッチ$D^t(t=1,2,...)$は学習前に作成し固定しておきます。ミニバッチのサイズは大体10〜100前後であり、他クラス分類の問題ではミニバッチ間の重みの更新のばらつきを平準化するために、ミニバッチそれぞれに各クラスから1つ以上のサンプルを入れるのが理想のようです。
4.1.4. GD vs SGD
では、このように学習サイズという面で対照的な関係である最急降下法と確率的勾配降下法ですが、ここでは、それぞれのメリット及びデメリットを整理したいと思います。
<確率的勾配降下法の最急降下法に対するメリット>
- 確率的勾配降下法は1つの学習データだけで更新するため、計算が早い。
- 様々な点をランダムに抽出するため、局所解に陥る可能性が低い。
- 新しいデータのみの学習(オンライン学習)が可能。
<確率的勾配降下法の最急降下法に対するデメリット>
- データをランダムに抽出するので、必ずしもその更新が最適かつ最短とは限らない。
- ランダムに抽出したデータが例外データの場合、その影響を大きく受ける。
4.2. パラメータ更新
さて、それでは下準備も終わったので、いよいよ本記事のメインである勾配降下法を用いたパラメータ更新について説明していきましょう。しかし、ここまで下準備ができていれば、あとは代入するのみです。
本節では、パラメータ更新に伴い上の図を多用します。また変数右上の添字についてですが、これ以降はその添字を何層目かを表すものとして統一します。そして、そのさらに右上の添字を更新回数とします。
$$w^{l^{(t+1)}}$$
4.2.1. l層のパラメータ更新
では、まず$\delta$を用いて$l$層のパラメータ更新式を一般化してしまいましょう。その式は、上の図から以下のようになります。
\begin{align}
w_{j, i}^{l^{(t+1)}}&=w_{j, i}^{l^{(t)}}-\eta\frac{\partial{E}}{\partial{w_{j, i}^{l}}}\\
&=w_{j, i}^{l^{(t)}}-\eta\delta_{j}^{l}z_i^{l-1}\\
&=w_{j, i}^{l^{(t)}}-\eta\left\{
\begin{array}{ll}
y_k-t_k&(\text{出力層})\\
(\sum_{k=1}^m\delta_k^{l+1}w_{k, j}^{l+1})z_j^{l+1}(1-z_j^{l+1}) & (\text{隠れ層sigmoid})\\
\sum_{k=1}^m\delta_k^{l+1}w_{k, j}^{l+1}&(\text{隠れ層relu&}u_j^l>0)\quad\\
\end{array}
\right\}z_i^{l-1}
\tag{4.5}
\end{align}
出力層及び隠れ層の活性化関数によって$\delta$の中身が異なるので、このように場合分けが必要となります。
そして、この式こそが、ニューラルネットワークの多層パーセプトロンにおけるパラメータ最適化の式となります。これをすべてのエポックで行うことによって、最適な重み$w$に近づいていくこととなります。
4.2.2. 適用するべき勾配降下法
では、この更新式に対し適用するべき勾配降下法は、先章で紹介した三つの中でどの降下法なのでしょうか。
結論から言えば、一概にどれを用いるべきというのは言えないように思います。先述したように、どの手法にもメリット・デメリットがあるので。しかし、目にしたプログラムの多くで、ミニバッチ勾配降下法が採用されていました。やはり、中間というのがどちらにも寄らず無難ということなのでしょうか。
これについては、もちろん入力データの数などにもよりますので一概には言えませんが、本記事でもミニバッチ勾配降下法をメインに使っていきたいと思います。
5. 誤差逆伝播法のアルゴリズム
さて、前記事で誤差関数$E$の重み$w$に対する勾配を求め、本記事ではそれを用いて重み$w$の更新式を導出しました。この求めた勾配を用いて次々に重み$w$の最適化を行おうとする手法こそが、誤差逆伝播法となります。
以下に、誤差逆伝播法のアルゴリズムを示します。
このアルゴリズムを繰り返し学習することによって最適なパラメータを見つけていくのが、この多層パーセプトロンの目的となります。
6. まとめ
本記事では、多層パーセプトロ
ンにおいて最適パラメータに辿り着くために必要となる、重みパラメータ$w$の更新式を導出しました。
そして、この更新式を基にしたアルゴリズムこそが、誤差逆伝播法と呼ばれる手法であり、多層パーセプトロンにおける核の部分となるものになります。
これにて、多層パーセプトロンの学習アルゴリズムについて基本的構成要素の説明は終わりとなります。
次回は、多層パーセプトロンの理論から実装への説明に入っていきたいと思います。
①初心者の初心者による初心者のためのニューラルネットワーク#1〜理論:順伝播編〜
②初心者の初心者による初心者のためのニューラルネットワーク#2〜理論:誤差計算編〜
③初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜
④初心者の初心者による初心者のためのニューラルネットワーク#4〜理論:パラメータ更新編〜(本記事)
7. 参照
確率的勾配降下法の大雑把な意味
最急降下法のイメージと例
ディープラーニング(深層学習)を理解してみる(勾配降下法:最急降下法と確率的勾配降下法)
勾配降下法ってなんだろう
深層学習(MLP) 3章 確率的勾配降下法
確率的勾配降下法とは何か、をPythonで動かして解説する
高卒でもわかる機械学習 (5) 誤差逆伝播法 その1
高卒でもわかる機械学習 (6) 誤差逆伝播法 その2