はじめに
※)「目標関数」をより一般的な名称である「損失関数(Loss Function)」表記に改めました.(2015Oct19)
誤差逆伝播法(以下,Backprop)は多層パーセプトロンを使う人にとってお馴染みのアルゴリズムですよね.
いや,これだけ有名なアルゴリズムなのでちょっとネットで探してみれば沢山解説を見つけることが出来るのですが,Backpropを予測誤差の最小化に適用する場合の説明しかみつからないんです.(とはいえ,PRMLをちゃんと読めば全部載ってるんですが). Backpropでできることは何なのか? ということがあまり明らかではありませんでした.
大学の講義や教科書でのBackpropの説明はほとんど,「教師あり学習の文脈で多層パーセプトロンを識別器あるいは関数近似器として訓練する」という文脈でなされます.そのため,初学者はBackpropは教師あり学習のためのアルゴリズムであると誤解してしまうケースが多々あるのではないかと思います.しかし後で説明する通り,Backpropは単に損失関数の微分を効率的に計算する手法の1つであって教師あり学習とか教師なし学習とかは関係ありません.
こういう誤解が時にいらぬ時間を使ってしまう場合があります.自分の場合あるとき,多層パーセプトロンでちょっと特殊な関数を目的関数中に正則化項として入れてみようかとか考えた時がありました(最終的に,それは良いパフォーマンスとならなかったのでお蔵入りとなったのですが).
このとき,なにか適当な関数を目的関数に付加して,**それが果たしてBackpropで勾配が計算できるの?**ということが判断できなかったのです.最終的な目的関数はこれまで知ってた,2乗誤差やクロスエントロピーではありませんでした.これは明らかに,Backpropに対する理解が浅かったためです.
そこで,ここはいっちょう,理解の中途半端だったBackpropをまとめて勉強すっかということでノートをまとめたので,ここにも書くことにしました.少なくとも,勾配を計算したい関数に対してBackpropが適用できるかどうかの判断なんてことに悩むような人が減ることを願います.
最近は自動微分に目的関数を放り込んだら勾配なんかすぐでてくるし,Backpropに慣れ親しんだ人なら当たり前の事実ばかりですが,知識を固定化するため,自分のためと思って書くことにします(意識高い系ということでアウトプット力を重視することにする).
ところで,webだとちゃんと先哲がいてまとめて書いてくれてます.
ニューラルネットワークと深層学習:第二章(Michael Nielsen 著)
http://nnadl-ja.github.io/nnadl_site_ja/chap2.html
実装の話も含めて考えるということであれば,こっちのほうがnotationとかもよく考えられている感じがします.じつは,Backpropで勾配が計算できる場合ってのはここにもちゃんと書いてあります.
勾配を計算できるかどうかって話だけだと同じような話を書いて終わりなので,もうちょっと例とか勾配消失の問題(Vanishing Gradient)とか書くことにしました.
誤りがありましたら,お知らせください.
多層パーセプトロン
多層パーセプトロンの基本構造
まず今回考えるニューラルネットワーク,多層パーセプトロンを導入することから始めます.
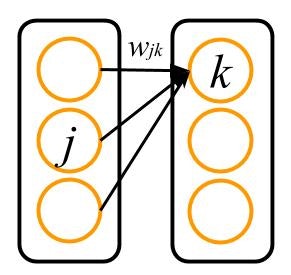
多層パーセプトロンの概要は次の図に表されるような形になっています.
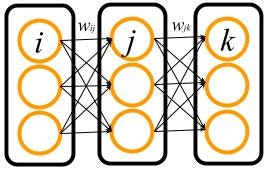
黒い四角で囲んだのは,層(layer)と呼ばれる多層パーセプトロンの構成要素を表しています.「多層」という名前の通り,多層パーセプトロンはいくつもの層が重なった形になっています.ここで $i$, $j$, $k$ はそれぞれの層内の細胞(オレンジの丸)の番号を表します.以下,それぞれの層を $i$ 層,$j$ 層などと呼びます.
ここではネットワークの最終的な出力(図では $k$ 層)を出力層,データが入力される最初の層(図では $i$ 層)を入力層,そして入力と出力の間の層(図では $j$ 層)を隠れ層と呼ぶことにします.図の例では隠れ層が1層だけですが,隠れ層の数を増やしてもそれらは全て隠れ層と呼びます.
各細胞は,自分以外ならどの細胞にもつなげることができます.この例では,$i$ 層の細胞は $j$ 層の細胞のみとつながっています.このつながりの強さは重み(weight)と呼ばれる数で決められ,たとえば細胞 $i$ と細胞 $j$ との間の重みは $w_{ij}$ というように表されます.
ところで,図のなかで細胞は常に自らの所属する層とは異なる層に属する細胞とつながっていますが,これは説明の便宜上によるものです.Backprop自体は最終的に細胞のネットワークがループのない有向グラフ(Directed Acyclic Graph; DAG)を構成していれば勾配を計算できるので,例えば $i$ 層の細胞が $j$ 層の細胞に加え,直接 $k$ 層の細胞につながっていたりしていてもokです.
ただ,この「層」という均一なまとまりで考えることで行列演算が導入できるので,実装上,より高速にBackpropで勾配計算を行うことが可能となるのです.
細胞の中身と順伝播則
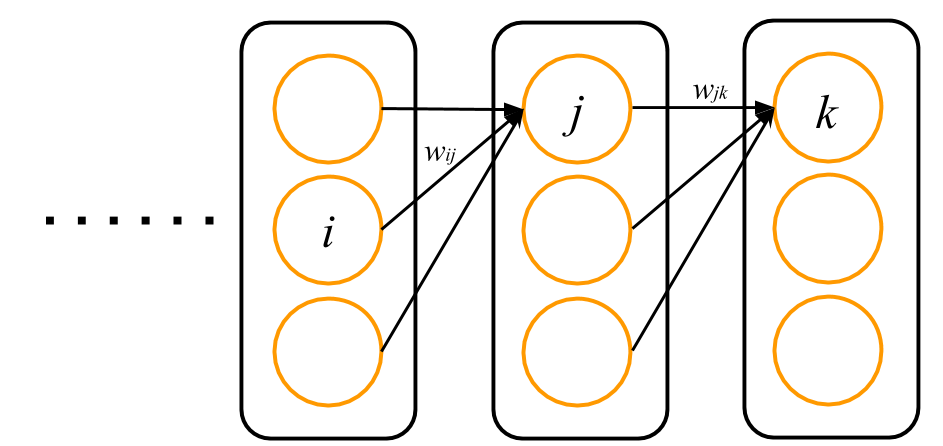
各細胞の中身は以下の図のようになっています
$j$ 層の細胞を1つ使って内容を説明しましょう.細胞はまず,つながっている矢印の根本にある細胞($i$ 層の細胞)のそれぞれから信号 $y_i$ を受け取り,それぞれの重みをかけてすべて足します.これを $v_j$ で表しましょう.
v_j = \sum_i w_{ij} y_i
これが細胞の左半分の $\Sigma$ 記号です.つぎに,この $v_j$ を入力として細胞 $j$ の出力 $y_j$ を計算します.
y_j = \phi_j(v_j)
ここで $\phi(v)$ は活性化関数(activation function)と呼ばれる関数で,各細胞ごとに定義されます($\phi$ のフォントが図と違うのはご容赦ください).この活性化関数は層ごとに同じ関数を使うのが一般的な定義のされ方です(異なる活性化関数を使う細胞は別の層を構成していると考えればいい).
多層パーセプトロンでは以上の2つの式をつかって,入力から出力を計算します.
かんたんな例題として,最初に示した多層パーセプトロンの図の出力 $y_k$ を計算してみましょう.
まず,$i$ 層に与えられる入力を $y_i$ と表します.
くりかえしになりますが,$j$ 層それぞれの $v_j$ と $y_j$ を
v_j = \sum_i w_{ij} y_i\\
y_j = \phi_j(v_j)
で得ます.続く $k$ 層の出力 $y_k$ の計算も全く同様です.
v_k = \sum_j w_{jk} y_j\\
y_k = \phi_k(v_k)
層が増えても,層同士のつながり方が変わっても,出力の計算は同様に「入力側の細胞出力の重み付き和をとって,活性化関数につっこむ」を繰り返す作業に違いはありません.
今の作業をまとめて書くと,こんな形になります.
y_k = \phi_k \Bigl(\sum_j w_{jk} \phi_j \bigl(\sum_i w_{ij} y_i \bigr) \Bigr)
活性化関数あれこれ
活性化関数は用途に応じていろいろあります.よく使われるものをpickupします.
まずはlogistic関数
\phi(v) = \frac{1}{1+e^{-v}}
またsoftmax関数
\phi(v_i) = \frac{e^{v_i}}{\sum_j e^{v_j}}
などもよく使われます.softmax関数は分母に同じ層細胞の活性(v)についての和が入っているため,出力が相互作用します.
つぎにhyperbolic tangent関数
\phi(v) = \tanh(v)
深層学習では $v$ が正のときだけ $v$ の値自体を返すRectifier Linear Unit (ReLU)
\phi(v) = \max(0,v)
がよく用いられます.以上の活性化関数は非線形関数ですが,出力層で
\phi(v) = v
とした恒等関数も活性化関数の定義として考えられます.
まあ,$v$で微分できればなんでもいいんですけどね.ただしこういう単純なことはまず先哲に学ぶことが大切です.
logistic関数とsoftmax関数は常に出力が $(0, 1)$ の領域に入るので,確率と関係させて物事を考えることができます.そのオバケがdeep belief netだったりdeep Boltzmann machineです.
hyperbolic tangent関数や恒等関数は連続値の出力を考えるときに出力層によく用いられます.ReLUは,その関数自体の表現能力は貧弱なので出力層には使われず,隠れ層に用いられます(最近はどうなのか把握していませんが).
有名な話ですが,3層(以上)の細胞層を持つ多層パーセプトロンは隠れ層の細胞が十分おおきな数だけあり,かつ隠れ層の活性化関数が非線形関数であれば任意の関数を近似することが出来る万能近似器です.
誤差逆伝播法:基礎編
前章の多層パーセプトロンの枠組みをもとに,基礎編では誤差逆伝播法(Backprop)の導出と理解を目指します.
損失関数の前提
まず,Backpropで勾配を計算したい関数をここでは 損失関数(Loss Function)と呼び,$E$ で表すことにします. この呼び方はここだけのもので,一般的な呼称ではないことに注意してください. 損失関数を導入することで,実際にBackpropを使用する時とBackpropの自体の理解との間の溝を狭めることができます.
Backpropで勾配が計算できるのは,以下の形の損失関数です.
E = E(y_1,...,y_K)
ここで $K$ は出力ユニットの総数を表し,$y_k$ は $k$ 番目のユニットの出力を表します.つまり $E$ はネットワークの出力に対して定義される関数であることが前提となります.
もう少し具体的な例を挙げると,各出力に対する教師信号を $t_k$ として2乗誤差を考えれば $E(y_1,...,y_K) = \sum_k^K (t_k - y_k)^2/2$ という形になります.各教師信号 $t_k$ は $E$ のパラメータとみなせます.2乗誤差以外の関数の例は,応用編でいろいろ紹介します.
さて,この損失関数と,Backpropを使って最終的に最小化(最大化)したい目的関数(Objective Function)との関係を説明しておかなくてはなりません.機械学習では,まず何らかの目的関数を考えることからすべての話が始まります.
たいてい,Backpropで最小化しようとする目的関数は損失関数 $E$ を学習に使うデータの数 $N$ だけ足して平均した
E_{total} = \frac{1}{N}\sum^N_{n=1} E^n
で表されます(このようにするのは裏で確率の話があるのですが,省略します.PRML1章にこれに当たる内容が書かれています).$E^n$ は $n$ 番目のデータに対する損失関数の値を示しています.
$n$ 番目のデータとして各出力に対する教師信号を $t^n_k$,ネットワークの入力を $x^n$ とおいて,$E^n$ にさっきの2乗誤差 $\sum_k (t_k^n - y_k(x^n))^2/2$ を具体的に入れてみると,はっきり見覚えのあるものが出て来ると思います.
この目的関数に対する最適化に勾配法を使い,勾配法でバッチ($N$ 個分全部計算してからパラメータを更新する)でやるかミニバッチ($N'$ 個 ($ N'< N$) 分だけ計算して更新する)でやるかといろいろあるわけですが,なんにせよ各データ $n$ に関してパラメータに関する勾配 $\partial E^n/\partial w $ をBackpropで得なければならないことには違いありません.
そのため,目的関数の勾配を計算すると呼ばずに あくまでBackpropで勾配を計算する目標の関数として損失関数 $E$ を導入したわけです.
連鎖律(Chain Rule)
誤差逆伝播法の前に,微分の連鎖律(chain rule).みなさん覚えていますでしょうか.
たしか,自分も遠き昔に解析学かなんかの講義でやった記憶があります.というか,一変数の話なら高校でもしますよね.でも多変数関数とかのはもう記憶が曖昧だったりします.
そういうことで,Backpropに必要な連鎖律を簡単に書いておきましょう.関数が $f(y)$,$y(w)$ で表される一変数関数の場合,この $f$ の $w$ に関する微分は
\frac{\partial f}{\partial w} = \frac{\partial f}{\partial y} \frac{\partial y}{\partial w}
で得られます.次に関数が $f(y_1, y_2, \dots, y_K)$ ,$y_k(w)$ ($k \in 1,2,\dots, K$)で表される多変数関数になっている場合は
\frac{\partial f}{\partial w} = \sum_{k=1}^K \frac{\partial f}{\partial y_k} \frac{\partial y_k}{\partial w}
で表されます.今は「なぜこのようになるか?」を考えずに,「とにかく,こういうルールがある」と思って使っていくことに集中しましょう.Backpropはこれら連鎖律をモリモリ使って,損失関数の勾配を全てのパラメータに関して計算します.
それでは以下,多層パーセプトロンでこの損失関数 $E$ の微分 $\partial E/\partial w$ がこの連鎖律をもとに,実際にどのようにBackpropで効率的な形で計算されるかを見て行きましょう.
出力層-隠れ層の間の重みに関する損失関数の勾配
多層パーセプトロンの出力を入力層から順に出力層まで計算していったのとは逆に,Backpropでは出力層から入力層に向かって順に勾配を計算していきます.
まず最初に,出力層とそれにつながる隠れ層との間の重みに関する損失関数の微分を計算します.今考えているのは,最初のネットワークの図のうち,以下の図のように表される部分です.
ではさっそく,損失関数 $E$ を $w_{jk}$ で微分してみましょう.これは
\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial w_{jk}}
で得られます.$w_{jk}$ につながっている細胞は $k$ だけなので,一変数関数の微分で表されます.
ここで順伝播の式を思い出してください.出力は
v_k = \sum_i w_{jk} y_j\\
y_k = \phi_k(v_k)
で計算されるのでした.なので,さっきの微分の2つめと3つめの要素は
\frac{\partial y_k}{\partial v_k} = \frac{\partial \phi_k(v)}{\partial v}|_{v=v_k} = {\phi'}_k(v_k)\\
\frac{\partial v_k}{\partial w_{jk}} = y_j
となります.これらを先ほどの微分に代入すると,
\frac{\partial E}{\partial w_{jk}} = \frac{\partial E}{\partial y_k} {\phi'}_k(v_k) y_j
で表されます.
後で理解しやすくするため,$\delta^{out}_k$ を次のように定義しておきます.
\delta^{out}_k = \frac{\partial E}{\partial v_k} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} = {\phi'}_k(v_k) \frac{\partial E}{\partial y_k}
このように定義すると,最終的に損失関数 $E$ の $w_{jk}$ に関する微分は
\frac{\partial E}{\partial w_{jk}} = \delta^{out}_k y_j
で表されることになります.このように,微分は出力側の層による要素 $ {\delta_k}^{out} $ と,1つ入力に近い側の出力( $y_j $)との積で表されます.
隠れ層-隠れ層,隠れ層-入力層の間の重みに関する損失関数の勾配
つぎに,もうひとつ入力側に近い層の間の重みに関して計算します.今度のターゲットは,以下の図の $w_{ij}$ に関して $E$ の微分を計算することです.
同じように,$E$ の微分を計算します.
今度は $k$ 層の細胞があるので多変数関数の微分となり,$k$ について和をとらなくてはいけません.いっぱい $\partial$ がでてきて大変ですが,括弧をつけたり代入しているだけなのでやってることは簡単です.
\frac{\partial E}{\partial w_{ij}} = \sum_k \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial w_{ij}}\\
= \sum_k \Bigl( \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \Bigr) \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial w_{ij}}\\
= \sum_k \Bigl( \frac{\partial E}{\partial y_k} {\phi'}_k(v_k) w_{jk} \Bigr) {\phi'}_j(v_j) y_i\\
= \sum_k \Bigl( \delta^{out}_k w_{jk} \Bigr) {\phi'}_j(v_j) y_i\\
= \Bigl( {\phi'}_j(v_j) \sum_k \delta^{out}_k w_{jk} \Bigr) y_i
ここで前の節でしたように,今度は $\delta^{hidden}_j$ を次のように定義しましょう.
\delta^{hidden}_j = {\phi'}_j(v_j) \sum_k \delta^{out}_k w_{jk}
こうすると,最終的に
\frac{\partial E}{\partial w_{ij}} = \delta^{hidden}_j y_i
とまとめることができます.結局,今回も微分は出力側の層による要素 $\delta_j^{hidden}$ と,1つ入力に近い側の出力( $y_i$ )の積で表されました.
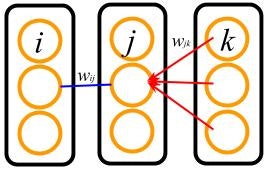
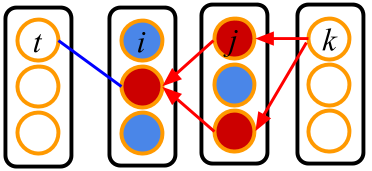
このとき,$\delta^{hidden}_j$はどういうことをしているのでしょうか?それを表すのが次の図です.
いま,$w_{ij}$ (青線)に関しての微分を考えているとすると, $\sum_k \delta_k^{out} w_{jk}$は出力層の各細胞から細胞 $j$ ($j$ 層中,真ん中の細胞) へ $\delta_k^{out}$ を,$w_{jk}$ (赤線)を伝って逆流(逆伝播)させている操作である事がわかります.
そして
\delta^{out}_k = {\phi'}_k(v_k) \frac{\partial E}{\partial y_k}
と
\delta^{hidden}_j = {\phi'}_j(v_j) \sum_k \delta^{out}_k w_{jk}
を比べると,隠れ層-隠れ層間の勾配の計算では,この逆流させて和をとった値でもって,出力層-隠れ層間で扱った $\frac{\partial E}{\partial y_k}$ に当たる擬似的な誤差信号として利用していると解釈することができます.
ではダメ押しで,$i$ 層の前に更に $t$ 層があったらどうなるでしょう?このへんになるとモリモリ計算してる感がでてきますが,やってることは同じです(texコマンドがエラいことに.).
\frac{\partial E}{\partial w_{ti}} = \sum_j \sum_k \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial y_i} \frac{\partial y_i}{\partial v_i} \frac{\partial v_i}{\partial w_{ti}}\\
= \sum_j \Bigl(\sum_k \Bigl( \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \Bigr) \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial y_i} \Bigr) \frac{\partial y_i}{\partial v_i} \frac{\partial v_i}{\partial w_{ti}}\\
= \sum_j \Bigl( \sum_k \Bigl( \frac{\partial E}{\partial y_k} {\phi'}_k(v_k) w_{jk} \Bigr) {\phi'}_j(v_j) w_{ij} \Bigr){\phi'}_i(v_i) y_t\\
= \sum_j \Bigl(\sum_k \Bigl( \delta^{out}_k w_{jk} \Bigr){\phi'}_j(v_j) w_{ij} \Bigr){\phi'}_i(v_i) y_t\\
= \Bigl({\phi'}_i(v_i) \sum_j \Bigl( {\phi'}_j(v_j) \sum_k \delta^{out}_k w_{jk} \Bigr) w_{ij} \Bigr) y_t\\
= \Bigl({\phi'}_i(v_i) \sum_j \delta^{hidden}_j w_{ij} \Bigr) y_t\\
= \delta^{hidden}_i y_t
お疲れ様でした.結局,1つ前の層を計算した時と全く同じように
\delta^{hidden}_i = {\phi'}_i(v_i) \sum_j \delta^{hidden}_j w_{ij}\\
\frac{\partial E}{\partial w_{ti}} = \delta^{hidden}_i y_t
という形で書けます.この後,入力層に至るまで全く同じ操作が続きます(書きません).入力層まで勾配が計算できたら,Backpropの作業はおしまいです.
誤差逆伝播法のまとめ
長々と書いてきましたが,Backpropの操作をまとめます.
1. 入力層から,順伝播
v_j = \sum_i w_{ij} y_i\\
y_j = \phi_j(v_j)
を計算し,全ての出力 $y_k$ を計算する.順伝播で計算したすべての層の出力 $y$ と $v$ を保存しておく.
2. 出力層から,$\delta^{out}_k$ を得る.
\delta^{out}_k = \frac{\partial E}{\partial v_k} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} = {\phi'}_k(v_k) \frac{\partial E}{\partial y_k}
3.$\delta^{out}$ を伝播させ,$\delta^{hidden}_j$ を得る.
\delta^{hidden}_j = {\phi'}_j(v_j) \sum_k \delta^{out}_k w_{jk}
4.さらに逆伝播させて,$\delta^{hidden}_i$ を得る.あとは同様に,入力層の一つ手前の層に到達するまで $\delta$ を逆伝播させる.
\delta^{hidden}_i = {\phi'}_i(v_i) \sum_j \delta^{hidden}_j w_{ij}
3.重み $w_{**}$ に関する全ての勾配を次の式で得る.
\frac{\partial E}{\partial w_{jk}} = \delta^{out}_k y_j\\
\frac{\partial E}{\partial w_{ij}} = \delta^{hidden}_j y_i
誤差逆伝播法:応用編
損失関数 $E$ が変われば
\delta^{out}_k = \frac{\partial E}{\partial v_k} = \frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k} = {\phi'}_k(v_k) \frac{\partial E}{\partial y_k}
がかわります.Backpropでいろいろな $E$ の勾配を計算する時,この最初の $\delta^{out}_k$ が代わるだけで他の操作は全て同じです.
応用編では損失関数 $E$ に色々な関数を入れてみて,Backpropによる勾配($\delta^{out}_k$)の計算がどう変わるのかを見てみることにします.
2乗誤差
2乗誤差はニューラルネットワークでBackpropを勉強するっていうときに,まず出てくる損失関数ですね.いわずもがな,教師信号 $t$ に対して,2乗誤差関数 $E_{se}$は次のように与えられます.
E_{se} = \sum_k \frac{(t_k - y_k)^2}{2}
ここで $k$ はネットワークの出力のユニット番号を表しています.2乗誤差関数は,主にニューラルネットワークが連続値を出力するようなタスクに対して使われます.
連続値を出力とするなら,$\phi_k(v) = v$ として恒等関数を活性化関数にするのが常套手段でしょう.
すると ${\phi'}_k(v) = 1$ なので
\delta^{out}_k = {\phi'}_k(v_k) \frac{\partial E_{se}}{\partial y_k} = 1 \cdot \frac{\partial }{\partial y_k} \sum_k \frac{(t_k - y_k)^2}{2} = y_k - t_k
となります.
クロスエントロピー
クロスエントロピーは物体認識などを行う識別器に対して多く用いられる関数です. 損失関数 $E_{cross}$ は次のように与えられます.
E_{cross} = -\sum_k t_k \log y_k + (1-t_k) \log(1-y_k)
この場合,出力層の活性化関数はすべての出力で $y_k \in (0,1)$ としておきたいので,logistic関数 $\phi_k(v) = \frac{1}{1+e^{-v}}$ を使えばいいなと考えます.すると ${\phi'}_k(v) = \phi_k(v) (1 - \phi_k(v))$ なので(なんで微分がこうなるかは,いい練習問題なので置いておきます.)
するとこの場合
\delta^{out}_k = {\phi'}_k(v_k) \frac{\partial E_{cross}}{\partial y_k} = \phi_k(v_k) (1 - \phi_k(v_k)) \Bigl\{ - \frac{t_k - y_k}{y_k (1 - y_k)} \Bigr\} = y_k - t_k
が得られます.最後は $y_k = \phi_k(v_k)$ を使いました.面白いことに2乗誤差と同じものが出て来ました!
ところで,おなじように $y_k \in (0,1)$ とする活性化関数,softmax関数だとどうでしょう?この場合,別の損失関数
E_{cross}^{soft} = -\sum_k t_k \log y_k
が用いられます.この場合,$\delta^{out}_k = \frac{\partial E}{\partial v_k}$ の関係で計算したほうが楽です.目的の微分を考える前に,softmax関数は出力間に依存性があるので,損失関数の微分にもこの依存性による項
\frac{\partial y_{k'}}{\partial v_k} =
\left\{ \begin{array}{ll}
y_k ( 1- y_k) & (k'=k) \\
-y_{k'} y_k & (k'\neq k)
\end{array} \right.
が出て来ます.この関係を使えば,
\delta^{out}_k = \frac{\partial E^{soft}_{cross}}{\partial v_k} = -\sum_{k'} \frac{t_{k'}}{y_{k'}} \frac{\partial y_{k'}}{\partial v_k} = - t_k(1-y_k) + \sum_{k'\neq k} t_{k'} y_k = - t_k + y_k \sum_{k'} t_{k'} = y_k - t_k
で表されます.最後の等号は教師信号の性質 $\sum_{k} t_{k} = 1$ を利用しました(正解の $k$ でのみ $t_k = 1$, それ以外は $t_k = 0$).
まとめると,logistic関数と同様に,$\delta^{out}_k = y_k - t_k$ でBackpropが計算できます.Wao!とてつもなく都合がいいですね!なんかもう,これら2乗誤差・クロスエントロピーだけ知ってれば後はどうでもいいんじゃないかとすら思えてきます.
いえいえ,Backpropはもっといろいろなことができます.もう少しお付き合いください.
エントロピー
ここでは2乗誤差やクロスエントロピーとは異なる例として,例えば出力の活性化関数をlogistic関数にして,その出力を確率とみなしたエントロピー
E_{entropy} = H = -\sum_k y_k \log y_k + (1-y_k) \log(1-y_k)
を考えてみましょう.教師信号がありませんが, Backpropの勾配計算に教師信号の有る無しは関係ありません.なので,別にBackpropは教師あり学習とか教師なし学習とかは関係ないのです.目標の関数があり,これを微分する.それが全てです.
では同じように $\delta_k^{out}$ を計算しましょう.logistic関数の微分は $\phi_k'(v) = \phi_k(v) (1 - \phi_k(v))$ なので,
\delta^{out}_k = {\phi'}_k(v_k) \frac{\partial H}{\partial y_k} = \phi_k(v_k) (1 - \phi_k(v_k)) \log \Bigl( \frac{1-y_k}{y_k} \Bigr)
で出力のエントロピーに関する微分がBackpropで計算できます.
エントロピーといえばHelmholtz自由エネルギーの片割れという印象が強いので,変分Bayes的なことを多層パーセプトロンでしようというときに何らかの形で出て来るかもしれませんね(妄想).
出力に対する勾配
他に有用そうだと思われる例(私見)は,ネットワークの出力ユニットが1つ(K=1)だけの場合において,この出力の勾配が考えられます.
E_{output} = y
簡単なのでちゃっちゃとしちゃいましょう.いまは出力が1つだけなので
\delta^{out} = \frac{\partial y}{\partial v} = {\phi'}(v)
でを得ます.出力の活性化関数に合わせてlogistic関数なり,恒等関数なりの活性化関数の微分を使えば,勾配をBackpropで計算することができます.
その他の損失関数
以上の例の他に,今のところどこで役に立つかわかりませんが
E = \prod_k y_k
E = \sum_k \sum_{k'} y_k y_{k'}
みたいな関数も全く同様の方法でモリモリ勾配の計算ができます.先の例では,たまたま何らかの関数 $f$ を導入して $\sum_k f(y_k)$ のような形が多く出てきましたが,これにとらわれる必要はありません.また,$E(y_1,\dots, y_K)$ で表される,異なる2種類以上の損失関数の和をとってもやはり $E(y_1,\dots, y_K)$ の形で表されるので,同様に計算できます.
ネットワークのJacobian
Backpropを使うわけではありませんが,Backpropと非常に似た方法で入力 $y_{in} = x$ が与えられた時の多層パーセプトロンのJacobian
\Delta_{in, out} = \frac{\partial y_{out}}{\partial y_{in}}|_{y_{in = x}}
が計算できます.$y_{out}$ は多層パーセプトロンの出力,$y_{in}$ は入力です.ここでは再び,以下の図で表される多層パーセプトロンでJacobianを計算してみることにします.
まず,出力に関して
\Delta_{kk} = \frac{\partial y_k}{\partial y_k} = 1
を得ます.
では次の層について計算してみると
\Delta_{jk} = \frac{\partial y_k}{\partial y_j} = \frac{\partial y_k}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} = \Delta_{kk} \phi_k'(v_k) w_{jk}
を得ます.$\Delta_{kk}$ が伝播して $\Delta_{jk}$ が計算されていることがわかります.では, $i$ 層について計算してみましょう.これは
\Delta_{ik} = \frac{\partial y_k}{\partial y_i} = \sum_j \Bigl( \frac{\partial y_k}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \Bigr) \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial y_i}= \sum_j \Delta_{jk} \phi_j'(v_j) w_{ij}
で得ることができます.やはり,$\Delta_{jk}$ が伝播して $\Delta_{ik}$ が計算されます.3層のこの例ではこれで計算は完了ですが,これ以降,4層でも全く同様に計算できて,$i$ 層の前に入力層 $t$ があるとすれば
\Delta_{tk} = \frac{\partial y_k}{\partial y_t}= \sum_i \Bigl( \sum_j \Bigl( \frac{\partial y_k}{\partial y_k} \frac{\partial y_k}{\partial v_k} \frac{\partial v_k}{\partial y_j} \Bigr) \frac{\partial y_j}{\partial v_j} \frac{\partial v_j}{\partial y_i} \Bigr) \frac{\partial y_i}{\partial v_i} \frac{\partial v_i}{\partial y_t} \\
= \sum_i \Bigl(\sum_j \Delta_{jk} \phi_j'(v_j) w_{ij} \Bigr) \phi_i'(v_i) w_{ti}\\
= \sum_i \Delta_{ik} \phi_i'(v_i) w_{ti}
4層以上の場合も,これと同様に逆伝播してJacobianが計算できます.このJacobianの計算には全ての細胞の $v$ が必要となるため,実際の計算では一度順伝播を計算して $v$ を全て得る必要があります.
勾配消失とRectifier Linear Unit
勾配消失(Vanishing-Gradient problem)は,古典的な多層ニューラルネットワークで層を増やしていくと,損失関数のパラメータ勾配が入力層に辿り着くまでに劇的にゼロに近づいてしまうという現象です.
この問題は深刻で,勾配消失はニューラルネットワーク業界の二度目の冬(1回目:Minsky & Papertの「Perceptrons」)をもたらした現象ではないかと思います.ここでは,この勾配消失がどのように現れてくるか,そして何故ReLUがその解決となるのかを直感的な形で理解することが目的です.
ここでは,$t$, $i$, $j$, $k$ の4つの細胞層からなる多層パーセプトロンを考えます.
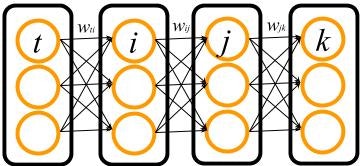
この多層パーセプトロンで $w_{ti}$ に関する損失関数 $E$ の微分を,先にBackpropの導出でしたように連鎖律で書き出します.必要な関係式を先に書いておきます.
v_j = \sum_i w_{ij} y_i\\
y_j = \phi(v_j)\\
\frac{\partial y_k}{\partial v_k} = {\phi'}(v_k)\\
\frac{\partial v_k}{\partial w_{jk}} = y_j\\
\delta^{out}_k = {\phi'}_k(v_k) \frac{\partial E}{\partial y_k}
活性関数は簡単のため,出力層($k$ 層)以外はすべて同じ $\phi(v)$ を使っていることとしましょう.すると,微分は以下のように書くことができます.
\frac{\partial E}{\partial w_{ti}} = \sum_j \sum_k
\frac{\partial E}{\partial y_k} \frac{\partial y_k}{\partial v_k}
\frac{\partial v_k}{\partial y_j} \frac{\partial y_j}{\partial v_j}
\frac{\partial v_j}{\partial y_i} \frac{\partial y_i}{\partial v_i}
\frac{\partial v_i}{\partial w_{ti}}\\
= \sum_j \sum_k
\frac{\partial E}{\partial y_k} \phi'(v_k) w_{jk} \phi'(v_j) w_{ij} \phi'(v_i) y_t\\
= \sum_j \sum_k \delta^{out}_k \Bigl( \phi'(v_j) \phi'(v_i) \Bigr) \Bigl(w_{jk} w_{ij}\Bigr)y_t
総和記号の中身をみると,「活性化関数の微分の積」で表される項と「重みの積」で表される要素が出て来ることがわかります.層が増えると,この2つの積の要素がどんどん長くなっていきます.そしてそれに $\delta_k^{out}$ と 今考えている入力層の $y_t$ が掛け合わされています.
さて,勾配消失で目に見えて問題となるのは,「活性化関数の微分の積」です.
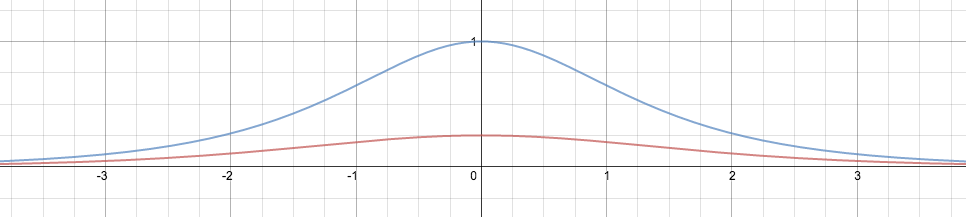
例えばlogistic関数 $\phi(v) = \frac{1}{1+e^{-v}}$ の微分は先に登場したように $\phi'(v) = \phi(v) (1-\phi(v))$ となりますが,これを横軸に $v$,縦軸に $\phi'(v)$ としてプロットしたのが以下の図の赤線になります.
logistic関数の微分は $v=0$ で最大値を取り,その値は $\phi'(0)=0.25$ です.なので,先の活性化関数の微分の積はどう頑張っても
\phi'(v_j) \phi'(v_i) \leq 0.25^2
となってしまうのは明らかです.小さな数が掛けられることになります.層が増えると,さらに指数関数的に小さくなっていきます.一方,出力層付近の勾配計算では掛けられる $\phi'$ の数が少ないので,このような小さな数をかけられることはありません.
そのため,単純に最急降下法で学習係数を大きくするようなことをすると,今度は出力層では学習係数が大きすぎてうまく動かないという泥沼にハマるのです.(とはいえ,ここでさらに総和記号があるので単純な話では無いのですが,少なくともこの例で勾配が消えていく様子は納得できます.)
LeCunたちは1998年の論文「Efficient Backprop」の中で「hyperbolic tangentの方がlogisticより良いよ」という事を言っています.hyperbolic tangent関数 $\phi(v) = \tanh(v)$ の微分$\phi(v)'$は上の図の青線で表されています.
hyperbolic tangentの微分係数はlogistic関数と同様に $v=0$ で最大値を取り, 今度は $\phi'(0) = 1$ となります. 勾配の最大値が,logistic関数とちがってより大きくなってますね.この活性化関数がより良い性能を出す理由が,少なくとも部分的に理解できます.
ただし全ての $v$ で $v=0$ というのは意味が無いので,hyperbolic tangentも $\phi'(v) < 1$ となるのが大抵の状況でしょう.非常に深いネットワークだと,やはり勾配が消失してしまう問題は残されたままです.
rectifier linear unit (ReLU)はKrizhevskyたちが導入した新しい活性化関数です.先に示したとおり,このReLUは $\phi(v) = \max(v,0)$ で定義され,$v$ がゼロ以上で $v$ 自身を返す非線形関数になっています.
ReLUの微分は $v>0$ のとき $\phi'(v) = 1$ で, $v<0$ のとき $\phi'(v) = 0$ です.$v=0$ のとき,微分は定義されません.いまは $v=0$ となった時の細かい話は置いておきましょう.このとき,Backpropによる勾配は
\frac{\partial E}{\partial w_{ti}} = \left\{ \begin{array}{ll}
\sum_{j\in\{j_{fire}\}} \sum_{k\in\{k_{fire}\}} \delta^{out}_k \Bigl(w_{jk} w_{ij} \Bigr) y_t & (v_i>0) \\
0 & (v_i<0)
\end{array} \right.
で表されます.${j_{fire}}$ は $j$ 層で発火している($v_j > 0$)細胞の集合です.ReLUを使ったBackpropで特徴的なのは,各層に発火している細胞がある限り,逆伝播において消失が起きないという点です.これは直感的には,各層が十分に広いネットワークにすれば毎回各層でどれかの細胞が発火してくれそうなもんで,そのような構造をもったネットワークは毎回入力層まで勾配消失が起こらない多層パーセプトロンになっていると考えられます.
ReLUを隠れ層に使った多層パーセプトロンで $\frac{\partial E}{\partial w_{ti}}$ を計算する様子が以下の図です.
この図では赤い細胞が発火した細胞 $v>0$,青い細胞が発火していない細胞 $v<0$ を表しています.今は青線の重み $w_{ti}$ に関する勾配を計算しているところを表しています.各出力細胞から $\delta_k^{out}$ が勾配消失なしに伝播し,発火している細胞のみを通って $w_{ti}$ につながっている細胞 $i$ に流れ込みます(赤矢印).
以上の説明が,ReLuがいかにして勾配消失を防ぐかの直感的な理解に繋がってくれていたらと思います.じつは思い出していただくと,活性化関数の微分だけではなくて,勾配は重みの積にも依存するのでした.これもまた深層学習では問題になりそうなものですが,今のところ大きな問題とはなっていないように見えます(これからわかりませんが).
将来,重みの絶対値を1付近に拘束するような必要が出てくるかもしれませんが(妄想),現在はL2ノルムでの正則化を入れておくくらいで上手くいっているようです.
参考文献
最後に,参考文献ほかおすすめを書いておきます.貧乏なのであまり専門書が買えないのが悲しいところですが,身銭を切って買ったいくつかの本や論文を紹介します.
・パターン認識と機械学習 上 (C.M.Bishop, 丸善)
言わずと知れた名著,PRML日本語訳の上巻.ニューラルネットワークについても載っていて,ネットワークのHessian(2回微分)の計算や,Hessianとベクトルの積を高速に計算する方法などがのテクニックもまとまっている.
・Neural Networks and Learning Machines(Simon S. Haykin, Pearson; 3rd)
ガッツリとニューラルネットワーク全般(多層パーセプトロン,Boltzmann machine, Hopfield network, リカレントニューラルネットワーク,強化学習+関数近似 etc.)が書かれた本.洋書.Deep Learningが流行るちょっとだけ前の本.理論とかも豊富.
・学習とニューラルネットワーク (熊沢 逸夫,森北出版)
たしか自分が大昔学部生だった頃,書店でさがして一番わかりやすそうな誤差逆伝播法の説明を書いていたと記憶する本.あくまで入門向け.
・Efficient Backprop (LeCun, et al.,1998年)
LeCun先生が誤差逆伝播法について説明している論文.入力の白色化とか,多層パーセプトロンを使うときのいろいろなトリックがまとめられている.ちょっと古いけど,おそらく今,実用上使われているものはこの時代の技術がほとんどなので参考に.
http://cseweb.ucsd.edu/classes/wi08/cse253/Handouts/lecun-98b.pdf