はじめに
強化学習はマルコフ決定過程(MDP; Markov decision process)と呼ばれるモデルを前提に学習しています。
ただ、これは現実世界をモデル化するには少し弱いモデルで、より現実に近いモデルが部分観測マルコフ決定過程(POMDP; partially observable Markov decision process)になります。
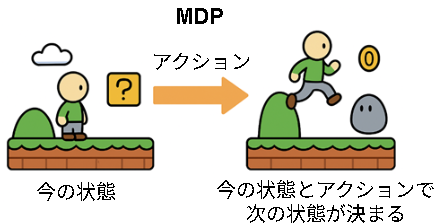
MDPをすごく簡単に言うと、今の状態とアクションで次の状態が決まるモデルです。
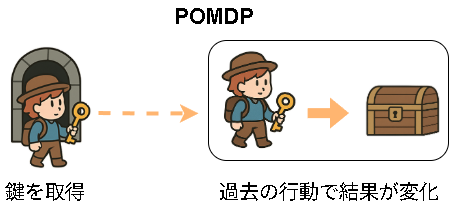
ただ、これだと例えば過去の行動(鍵の取得など)で結果が変わるような世界は学習できません。
これを学習するにはPOMDPなモデルを学習する必要があります。
MDP/POMDPの理論的な詳細については過去に書いた記事を参考にしてください。
この記事では実装に焦点を当てて書いています。
部分観測マルコフ決定過程(POMDP)
MDPでは次の状態は以下で表されます。
$$
p(s_{t+1}|s_t,a_t)
$$
これは状態 $s_t$ で行動 $a_t$ を行った後、次の状態 $s_{t+1}$ になる確率を表します。
詳細は省略しますが、POMDPは事前条件に過去の全履歴を含めればMDPとして扱うことができます。
$$
p(s_{t+1}|s_{0:t},a_{0:t})
$$
ここで $s_{0:t}$ は開始からステップ$t$までの全状態で、$a_{0:t}$ は全アクションです。
さて、深層学習でこれを実装しようとしたら最初に思いつくのがRNN(LSTM)でしょう。
歴史的に最初にLSTMを取り入れて成功したアルゴリズムはR2D2です。(ベースとしてはDRQN)
ただR2D2は分散学習やRainbowなどRNN以外のアプローチもあるので、この記事ではPOMDPだけに絞り、他の技術要素をなくして実装していきたいと思います。
- R2D2のPOMDP対策について
R2D2では状態のみを入力としているのでアクションが足りていない気がします。(昔の記憶)
Agent57ではUVFAとしてアクションも取り入れているのでPOMDPに対応しています。(POMDPを意識していたかは分かりませんが)
POMDPとRNN(LSTM)
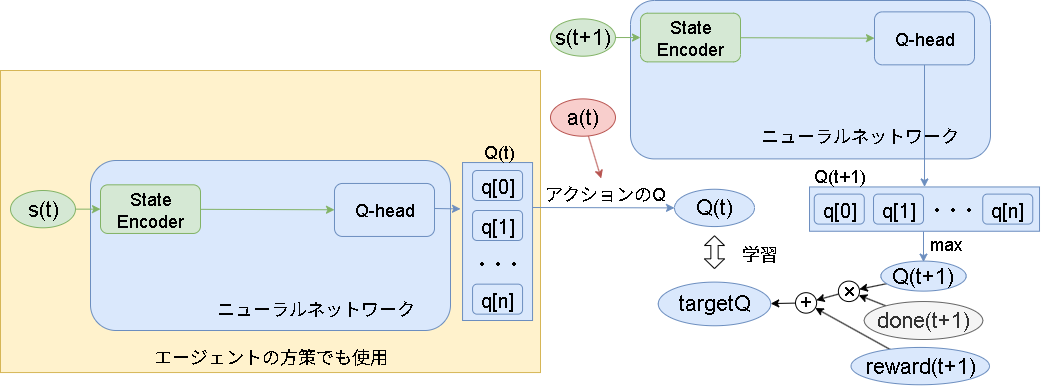
一般的なDQNの学習(MDP)は以下です。
今の状態$s_t$から"StateEncoder"と"Q-head"を通して各アクションのQ値を予測します。
学習側では次の状態 $s_{t+1}$ と報酬 $r_{t+1}$と終了フラグ $d_{t+1}$ の情報を元に、実際に選んだアクション $a_t$ のQ値が計算され、それに近づくように学習されます。
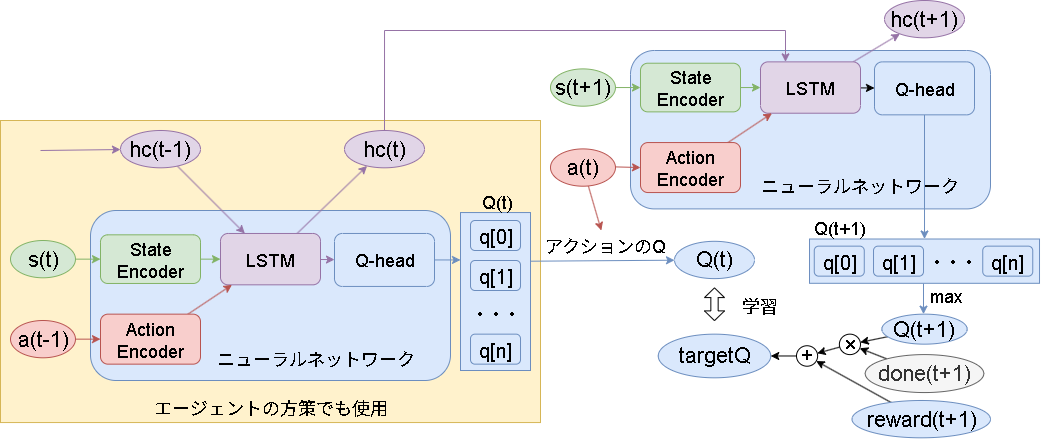
ここにLSTMを追加すると以下です。
追加した項目は "ActionEncoder" と "LSTM" です。
LSTMの目的は過去の全履歴を集約する事です。
履歴の集約として、今の状態 $s_t$ と前のアクション $a_{t-1}$ と隠れ状態 $h_{t-1}$ を入力させます。
概要としては以上ですが、これを実現するにはLSTMの隠れ状態の扱いが厄介で、時系列を保持する必要があります。
この記事では以下の2つの解決法を扱います。
- R2D2のBurn-in
- DreamerV3のエピソードをまたいだ学習手法をベースに、より実践的に実装
ベースのDQN(NoTargetDQN)
まずはLSTMを使わないDQNを実装し、これに追加する形でLSTMを実装していきます。
ベースとなるDQNは前回提案したNoTargetDQNです。
これはDQNからターゲットネットワークをなくした実装で、DQNを普通に実装するより簡単に実装でき、更に学習も安定するので採用しています。
ポイントだけ記載します。(全コードは最後に)
・Worker
まずはWorkerです。
割引報酬和を計算するためにエピソード最後まで実行した後にバッチを送っています。
(即時報酬だけの方がシンプルですが、この後LSTMで結局エピソード全て使う実装をするので、割引報酬和を使う実装にしています)
class Worker(RLWorker):
def on_reset(self, worker) -> None:
# エピソードの最初に実行、履歴を保存する配列を準備
self.episode = []
def policy(self, worker) -> int:
return ε-greedyでアクションを選択
def on_step(self, worker):
if not self.training:
return # 学習以外は何もしない
# 各ステップの情報をいったん保存
self.episode.append(
[
worker.state,
worker.next_state,
worker.action,
worker.reward,
int(not worker.terminated),
]
)
if worker.done:
# エピソード終了時、割引報酬和を計算して各stepの情報をbatchに追加する
total_reward = 0
for b in reversed(self.episode):
total_reward = b[3] + self.config.discount * total_reward
self.memory.add(b[:] + [total_reward])
・Trainer
学習です。
ターゲットネットワークの代わりに正則化項を追加しています。
ターゲットネットワークの計算や同期がなくるのでかなりすっきり実装できます。
class Trainer(RLTrainer):
def train(self) -> None:
# メモリからbatchを取得
batches = self.memory.sample()
state, n_state, action, reward, not_terminated, total_reward = バッチを変換
# 次のQ値を計算し、最大値を取得
with torch.no_grad():
n_q = self.parameter.qnet(n_state)
n_maxq = n_q.max(dim=1).values
target_q = reward + not_terminated * self.config.discount * n_maxq
# 現在のQ値を計算し、教師データに近づけるように学習
q = self.parameter.qnet(state)
q = q.gather(1, action_indices.unsqueeze(-1)).squeeze(1)
loss = self.criterion1(target_q, q) # HuberLoss
# 割引報酬和から離れすぎないようにする正則化項を追加
loss_align = self.criterion2(total_reward, q) # MSELoss
loss += self.config.loss_align_coeff * loss_align
# bp
self.opt.zero_grad()
loss.backward()
self.opt.step()
・Q-net
LSTMとの比較用でQネットも記載しておきます。
class QNetwork(nn.Module):
def __init__(self, config: Config):
super().__init__()
units = config.base_units
# state encoder: in_blockは入力が値や画像などをいい感じに整形してくれる層
self.in_block = config.input_block.create_torch_block(config)
# Q head
self.block = nn.Sequential(
nn.Linear(self.in_block.out_size, units),
nn.ReLU(),
nn.Linear(units, units),
nn.ReLU(),
nn.Linear(units, config.action_space.n),
)
def forward(self, x):
x = self.in_block(x)
return self.block(x)
1.Burn-inによる手法
LSTMを強化学習に組み込むときに厄介なのが「隠れ状態の陳腐化」です。
DQNではReplayBufferを使って過去のデータを使いまわしますが、この仕組みだと「古いデータ」が学習に混じります。
状態や行動は時間が経っても変わらないので問題ないですが、LSTMの場合は事情が違います。
LSTMは「隠れ状態」を持っていて、これはネットワークを通して毎回計算される値です。
学習が進むとネットワークが変化するので、古い隠れ状態は今のネットワークにとってはズレたものになってしまい、学習を妨げる要因になります。(陳腐化)
これを解決するためにR2D2ではBurn-inという手法が使われました。
Burn-inを簡単に言うと慣らし運転みたいなイメージで、古い隠れ状態を使うのではなく、ちょっと前のステップからLSTMを回し、最新のネットワークに合った隠れ状態に近づけてから学習する手法となります。
以下実装のポイントです。
・Q-net
アクションの変換(アクションエンコーダー)ですが、よくあるOne-hot化 + Dense層でもいいですが、より離散値に特化したEmbedding層を使いました。
LSTM層は次の手法で1step毎に特殊な処理を挟みたいのと、説明として分かりやすいので nn.LSTMCell を使って1step毎に処理しています。
(Burn-inだけならnn.LSTMで複数stepを一括処理可能です)
LSTMの詳しい扱いに関してはこの記事では扱いません。(記事の量が…)
公式や過去の記事(Tensorflowですけど)などを参考にして下さい。
class QNetwork(nn.Module):
def __init__(self, config: Config):
super().__init__()
units = config.base_units
# state encoder
self.in_block = config.input_block.create_torch_block(config)
# action encoder
self.act_encoder = nn.Embedding(
config.action_space.n,
config.act_emb_units,
)
# lstm
self.lstm_units = config.lstm_units
self.lstm = nn.LSTMCell(
self.in_block.out_size + config.act_emb_units,
self.lstm_units,
)
# Q head
self.block = nn.Sequential(
nn.Linear(self.lstm_units, units),
nn.ReLU(),
nn.Linear(units, units),
nn.ReLU(),
nn.Linear(units, config.action_space.n),
)
def forward(self, state: torch.Tensor, action_indices: torch.Tensor, hc):
ts = self.in_block(state)
ta = self.act_encoder(action_indices)
z = torch.cat([ts, ta], dim=-1)
h, c = self.lstm(z, hc)
x = self.block(h)
return x, (h, c)
def get_initial_state(self, batch_size=1):
# 初期の隠れ状態を生成する関数
return (
torch.zeros(batch_size, self.lstm_units),
torch.zeros(batch_size, self.lstm_units),
)
・バッチデータの収集
Burn-inを実装する上でここが一番厄介です。
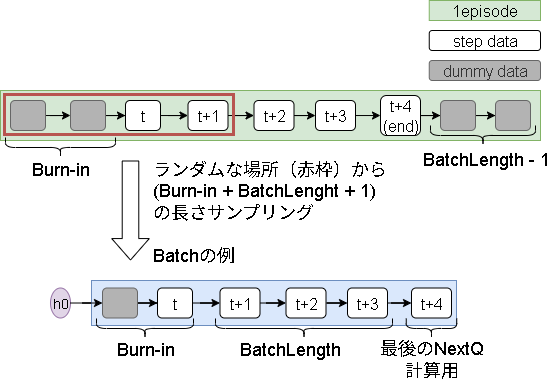
イメージは以下。
バッチデータは、Burn-inのステップ + 学習するステップ +1(NextQ用) のデータ長になります。
ランダムサンプリング時にエピソードの両端をサンプリングするとエピソード外を参照する恐れがあるので、データ収集時に補完しておきます。
具体的には以下3点を意識します。
-
Burn-inステップの追加
例えばstep0をサンプリングした場合、Burn-inのステップがエピソード外になるので最初にダミーステップを追加しておきます。 -
学習ステップの追加
同じく最後のstepをサンプリングした場合にエピソード外にいくので最後にダミーステップを追加します。
(エピソード最後の追加はサンプル時のステップの場所を調整すれば不要かもですが、サンプリングされる確率が変わるので入れています) -
Workerは毎ステップQ値の計算が必要
DQNではε-greedyでランダムアクションを引いた場合にQ値の計算は不要でした。
しかしLSTMでは隠れ状態を更新する必要があるので、毎ステップQ値を計算する必要があります。
class Worker(RLWorker):
def on_reset(self, worker) -> None:
# Worker用の初期隠れ状態
self.hc = self.parameter.qnet.get_initial_state()
self.episode = []
# Burn-inのステップを追加、ダミー状態は0、アクションは0
for _ in range(self.config.burnin):
self.episode.append(
[
np.zeros(self.config.observation_space.shape), # state
0, # action
0, # reward
1, # not terminated
0, # totel_reward用
self.hc[0],
self.hc[1],
]
)
# 0step目の情報、初期アクションは0とする
self.episode.append(
[
worker.state, # state
0, # action
0, # reward
1, # not terminated
0, # totel_reward用
self.hc[0], # hc0
self.hc[1], # hc1
]
)
# 最初のQ値を計算(隠れ状態も更新)(初期アクションは0とする)
self.q, self.hc = self.parameter.pred_q(
worker.state,
[0],
self.hc,
)
def policy(self, worker) -> int:
return ε-greedyでアクションを決定
def on_step(self, worker):
prev_hc = self.hc
# Q値を計算(隠れ状態も更新)
self.q, self.hc = self.parameter.pred_q(
worker.next_state,
[worker.action],
self.hc,
)
if not self.training:
return # 学習以外はここまで
self.episode.append(
[
worker.next_state, # state
worker.action, # action
worker.reward, # reward
int(not worker.terminated), # not terminated
0, # totel_reward用
prev_hc[0],
prev_hc[1],
]
)
if worker.done:
# batch_length分、終了後のstepを追加
# 状態は最後の状態を引き継ぎ、アクションはランダム
for _ in range(self.config.batch_length - 1):
self.episode.append(
[
worker.next_state, # state
random.randint(0, self.config.action_space.n - 1), # action
0.0, # reward
0, # not terminated
0, # totel_reward用
prev_hc[0], # 使わない
prev_hc[1], # 使わない
]
)
# 割引報酬和を計算
total_reward = 0
for b in reversed(self.episode):
total_reward = b[2] + self.config.discount * total_reward
b[4] = total_reward
# episode単位で追加
self.memory.add(self.episode)
ダミーステップをどうするかは実装側に委ねられている気がします。
ここでは以下です。
- 最初
- ダミー状態: 0固定
- アクション: 0固定
- 最後
- ダミー状態: 最後の状態継続
- アクション: ランダム
・メモリからのサンプル
エピソード内のステップからランダムで指定のエピソード長を取得します。
またエピソード単位でbufferに保存されるのでメモリサイズの計算が少し変わります。
class Memory(RLMemory):
def setup(self):
self.buffer = []
self.size = 0
def add(self, batch) -> None:
# capacityを超えないように減らす
while self.size >= self.config.memory_capacity:
b = self.buffer.pop(0)
self.size -= len(b)
self.buffer.append(batch)
self.size += len(batch)
def sample(self):
batches = []
for _ in range(self.config.batch_size):
# ランダムにエピソードを選ぶ
r1 = random.randint(0, len(self.buffer) - 1)
episode = self.buffer[r1]
# エピソードから、0~burnin+(batch_len+1) の範囲で乱数をだす
r2 = random.randint(0, len(episode) - self.config.burnin - self.config.batch_length - 1)
# エピソードから取得する範囲は r~r+burnin+(batch_len+1)
batch = episode[r2 : r2 + self.config.burnin + self.config.batch_length + 1]
batches.append(batch)
return batches
余談ですが、Prioritized Experience Replay(優先順位付けのサンプリング)の実装はこの方法だとちょっと考えたくないですね…。
参考までに、自分のフレームワークのR2D2の実装では、メモリ効率は悪いですけど、Worker側で1バッチの履歴を全て保存させて1バッチ毎に保存して実現しています。
・学習
Burn-in → 学習ステップ分学習、という流れになります。
次ステップのQ値ですが、前ステップのQ値がそのまま使えるので、2重計算を避けるために使いまわします。
class Trainer(RLTrainer):
def train(self) -> None:
# バッチを取得
batches = self.memory.sample()
states, action_indices, rewards, not_terminateds, total_rewards, hc0, hc1 = バッチを変換
# --- burnin
step = 0
hc = (hc0, hc1)
for _ in range(self.config.burnin):
_, hc = self.parameter.qnet(states[step], action_indices[step], hc)
step += 1
loss = 0
# 現在のQ値
q, hc = self.parameter.qnet(states[step], action_indices[step], hc)
for _ in range(self.config.batch_length):
# 次のQ値を計算(次の学習で使うために勾配は流す)
n_q, hc = self.parameter.qnet(states[step + 1], action_indices[step + 1], hc)
# targetQを計算、勾配は流さないようにn_qはdetachする
n_maxq = n_q.detach().max(dim=1).values
target_q = rewards[step + 1] + not_terminateds[step + 1] * self.config.discount * n_maxq
loss += ※Q値の損失と、正則化項の計算は同じなので省略
# Q値を次stepに使いまわす
q = n_q
step += 1
loss /= self.config.batch_length # mean
# bp
self.opt.zero_grad()
loss.backward()
self.opt.step()
Burn-inは以上です。
ただBurn-inは以下の問題があります。
- Burn-inの計算コストが高いしもったいない
- Burn-inの結果はどうしても近似になり真に正確ではない
分布シフト問題は発生しないのか
分布シフト問題はデータ収集時の方策と学習時の方策がずれる場合に起こる問題です。
最初は発生すると思ってretraceを入れていましたが、よくよく考えると学習は各ステップで独立しており、multistepみたいに未来のTD誤差を使うわけではないので不要でした。
2.エピソードまたぎの学習
DreamerV3の実装でひっそりあった内容です。(論文では記載なし)
隠れ状態の陳腐化が問題なら、学習時にエピソードの最初から隠れ状態を計算させればいいじゃない、という内容です。
ただし、エピソードを丸ごと学習するのは計算コストが高すぎます。
そこでエピソードを途中で区切りつつ、学習間で隠れ状態を引き継ぐ事でこれを解決するというアイデアです。
こうすることで、常に最新の隠れ状態に基づいて学習できるようになります。
考え方は簡単ですが、実装では注意しないといけないポイントが結構あります。
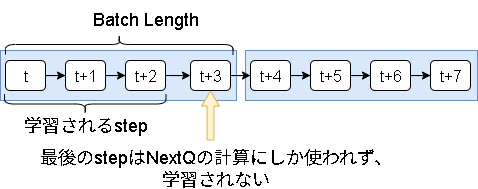
1.エピソードの流れとDQNの学習のずれ
DQNは今のQ値と次のQ値を計算して学習しますが、時系列通りに進めた場合に最後のステップが学習されません。
主な対策は以下です。
- 1stepぐらいなら影響ないと割り切り学習をあきらめる
※エピソード長とBatchLengthが噛み合うと毎回同じステップだけ学習がなくなるのでそこは注意が必要 - バッチの最後のステップだけ1step戻す
この記事では1step戻す形にしています。
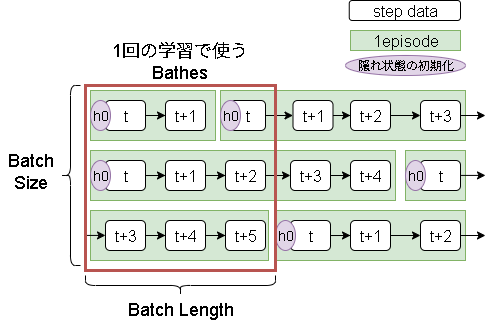
2.固定エピソードによるバッチ内の状態の偏り
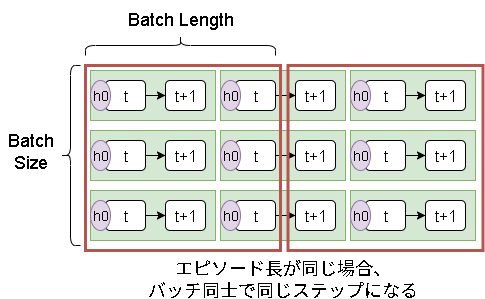
最初は各バッチで同時にエピソードが開始するのでバッチ間でも同じステップが使われます。
これはエピソード長がバラバラならばらけていくので問題ありません。
しかし、エピソード長が同じ場合はばらけないので注意が必要です。
Q-netを学習する上でバッチ内の時系列な相関がどの程度影響するかが分からず…、一応解決策は以下のアイデアがあります。
- データ収集時にダミーステップをランダム数追加し、エピソード長を変える
- バッチデータを作る際に Burn-in して開始ステップをずらす
(バッチidxに準拠し、0番目のバッチは0step Bunr-in、1番目は1step、2番目は2stepとする)
(前半stepを学習するデータが減るので注意) - バッチデータを作る際にエピソードを早めに切り上げる
(後半stepを学習するデータが減るので注意) - 諦める(相関があっても案外学習できるのでは?)
ここは改善できるかもしれませんが、この記事ではバランスを取って以下の実装をしています。
- 偶数と奇数で学習を変える
- 偶数: そのまま学習
- 奇数: batch_sizeを半分、学習ステップを+1する
(これでバッチ内の半分だけ時系列がずれる)
※バッチサイズがずれると学習率も変わるので補正する
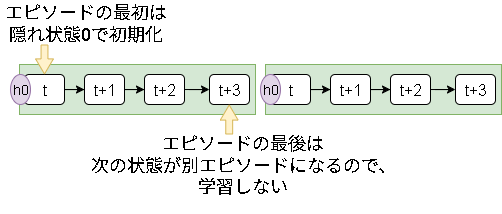
3.開始状態と終了状態
今の状態が開始状態の場合、隠れ状態を初期化する必要があります。
今の状態が終了状態の場合、次の状態は別エピソードになるために学習しないようにする必要があります。
これらをバッチ内で別々に管理する必要があります。
・Worker
Burn-inの実装とほぼ変わらず、変更点は以下です。
- 開始時のダミーステップと終了時のダミーステップがなくなった
- 同じく隠れ状態をメモリに追加する必要がなくなった
- 逆に開始状態と終了状態を表すフラグをメモリに追加
class Worker(RLWorker):
def on_reset(self, worker) -> None:
# 0step目の情報、初期アクションは0とする
self.episode = [
[
worker.state, # state
0, # action
0, # reward
1, # not terminated
0, # totel_reward用
0, # not start
True, # not done
]
]
# 最初のQ値を計算(隠れ状態も更新)(初期アクションは0とする)
self.hc = self.parameter.qnet.get_initial_state()
self.q, self.hc = self.parameter.pred_q(worker.state, [0], self.hc)
def policy(self, worker) -> int:
return ε-greedyでアクションを決定
def on_step(self, worker):
# Q値を計算(隠れ状態も更新)
self.q, self.hc = self.parameter.pred_q(
worker.next_state,
[worker.action],
self.hc,
)
if not self.training:
return # 学習以外はここまで
self.episode.append(
[
worker.next_state, # state
worker.action, # action
worker.reward, # reward
int(not worker.terminated), # not terminated
0, # totel_reward用
1, # not start
not worker.done, # not done
]
)
if worker.done:
# 割引報酬和を計算
total_reward = 0
for b in reversed(self.episode):
total_reward = b[2] + self.config.discount * total_reward
b[4] = total_reward
# episode単位で追加
self.memory.add(self.episode)
・Memory
処理のメインはTrainer側になり、ただランダムにエピソードを返すだけになります。
class Memory(RLMemory):
def sample(self):
r = random.randint(0, len(self.buffer) - 1)
return self.buffer[r]
・Trainer
ポイントは以下です。
- 偶奇で学習率が変わるのでoptimizerを2つ用意(学習率を都度変える実装でもいいと思う)
- バッチ毎に制御したい内容があるので、lossはreduction="none"とし、手動で平均をだす
- 隠れ状態を使いまわすので保持
- 同じく各バッチのエピソード情報も保持
class Trainer(RLTrainer):
def on_setup(self) -> None:
# 偶数のopt
self.opt1 = optim.Adam(self.parameter.qnet.parameters(), lr=self.config.lr)
# 奇数のopt、学習率はbatch_size/2とbatch_length+1の割合で変更
lr2 = self.config.lr * ((self.config.batch_size // 2) * (self.config.batch_length + 1)) / (self.config.batch_size * self.config.batch_length)
self.opt2 = optim.Adam(self.parameter.qnet.parameters(), lr=lr2)
# lossはreduction=noneにしてmeanは手動で実施
self.criterion1 = nn.HuberLoss(reduction="none")
self.criterion2 = nn.MSELoss(reduction="none")
# 学習間で引き継ぐ用
self.sequential_batches = [[] for _ in range(self.config.batch_size)]
self.hc = self.parameter.qnet.get_initial_state(self.config.batch_size)
def train(self) -> None:
# 偶数と奇数で学習内容を変更
if self.train_count % 2 == 0:
batch_size = self.config.batch_size
batch_length = self.config.batch_length
opt = self.opt1
else:
batch_size = self.config.batch_size // 2
batch_length = self.config.batch_length + 1
opt = self.opt2
# batch作成に足りない分をmemoryから追加
for i in range(batch_size):
while len(self.sequential_batches[i]) < batch_length + 1:
episode = self.memory.sample()
if episode is None:
return # まだmemoryがたまっていないので終了
self.sequential_batches[i].extend(episode)
# --- batchesを作成
batches = []
for i in range(batch_size):
# 学習サイズ分を取り出してバッチに追加
batch = self.sequential_batches[i][: batch_length + 1]
self.sequential_batches[i] = self.sequential_batches[i][batch_length + 1 :]
batches.append(batch)
# バッチを元に変換
states, action_indices, rewards, not_terminateds, total_rewards, not_starts, not_dones = バッチを変換
loss = 0
# batch_sizeのみ使用
hc = (self.hc[0][:batch_size], self.hc[1][:batch_size])
# 最初のqを計算、状態が開始時なら0で初期化
hc = (hc[0] * not_starts[0], hc[1] * not_starts[0])
q, hc = self.parameter.qnet(states[0], action_indices[0], hc)
for i in range(batch_length):
loss_step = 0
# 次のqを計算、状態が開始時なら0で初期化
hc = (hc[0] * not_starts[i + 1], hc[1] * not_starts[i + 1])
n_q, hc2 = self.parameter.qnet(states[i + 1], action_indices[i + 1], hc)
# 最後のstepは更新しない
if i < batch_length - 1:
hc = hc2
loss_step += ※Q値の損失と、正則化項の計算は同じなので省略
# 今が終了、次が開始の境目は学習しないようにマスクする
# meanの結果が変わるので0を掛けるのではなく要素自体を減らす
loss += loss_step[not_dones[i]].mean()
# 次のQ値を次の計算で使いまわす
q = n_q
loss /= batch_length # mean
# bp
opt.zero_grad()
loss.backward()
opt.step()
# batch_size分のhcを元に戻す、勾配は切って次に残さない
self.hc[0][:batch_size] = hc[0].detach()
self.hc[1][:batch_size] = hc[1].detach()
ちなみにLSTM以外のニューラルネットの計算は一括でforwardした方が早いです。
この記事では分かりやすさを重視して1step毎書いています。
トラ問題でPOMDPの学習を確認
POMDPの基礎問題であるトラ問題で学習を見てみます。
この問題は、扉が2つあり、片方に虎、もう片方に宝物があります。
観測者は以下の3つの行動を選ぶことができます。
- 音を聞く(報酬-0.01)
- 左の扉を開ける
- 右の扉を開ける
音を聞くでは85%の確率でトラのいる扉から声が聞こえます。
(15%でトラのいない扉から声が聞こえる)
報酬は以下です。(学習しやすいようにスケールを100分の1にしています)
- トラがいた:-1
- 宝物があった:0.1
音を何回か聞いてトラがいそうな扉を予測する必要がある問題で、MDPな環境では過去の結果を覚えることはできないので学習できない問題です。
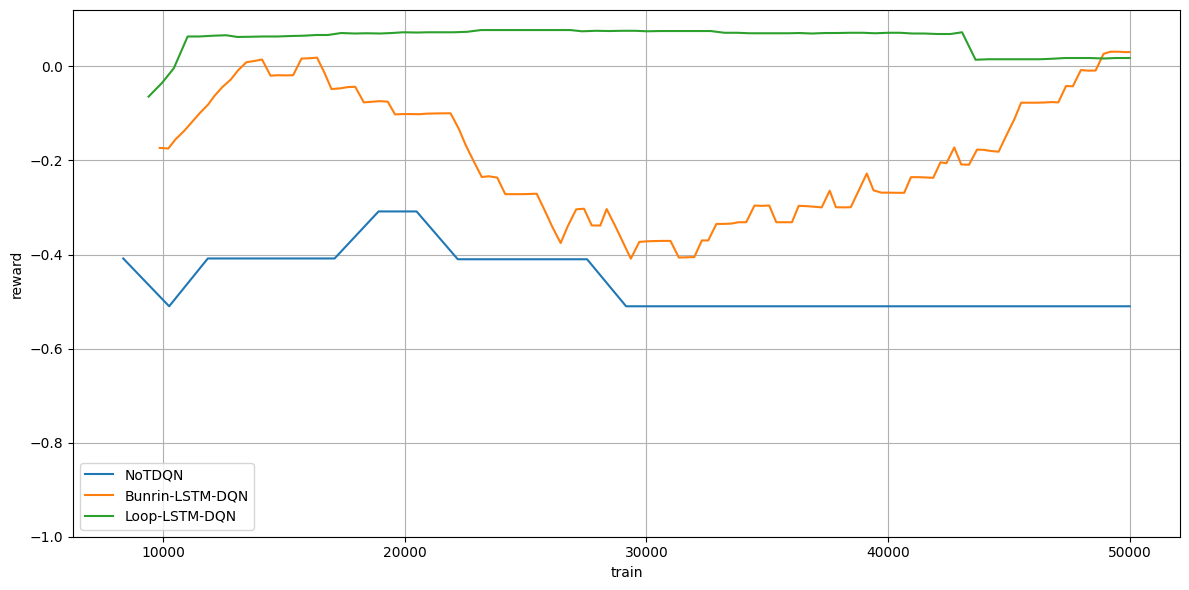
これを3種類の方法で学習した結果は以下です。
(縦軸が報酬、横時間が学習ステップです)
(5stepの移動平均)
青がベースDQNで、MDPな環境を想定しているので学習できていませんね。
(左右の扉をランダムに開けるだけなので、だいたい-0.5ぐらいの報酬になる)
オレンジと緑がLSTMによるPOMDPな環境の学習です。
ちゃんと正の報酬が手に入るように学習できていますね。
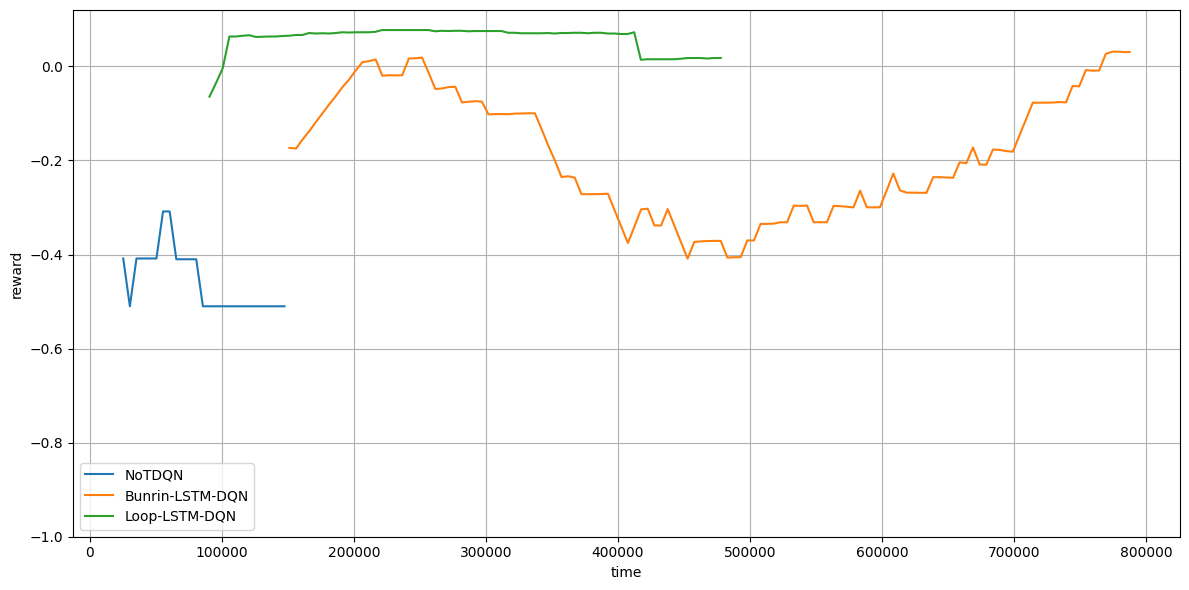
以下は横軸を時間に変えたものです。
オレンジ(Burnin)ですが、やはりBurninに時間がかかるので学習時間も長くなっていますね。
また、そもそもLSTMは計算に時間がかかるので、ベースDQNに比べて時間がかかっています。
全コード(GoogleColabo)
実際に動かしたコードは以下で公開しています。
さいごに
LSTMについて改めて基礎から振り返りたかったのでナイーブな実装をしてみました。
POMDP×深層強化学習にフォーカスした純粋な実装記事はほとんど存在しないと思います。(多分この記事が初でしょうか)
POMDPは概念は難しいですが結論は履歴を保存するだけというシンプルなものになります。
ただ、それを実装しようとするとまたいろいろと問題がでてくるという…、なかなか厄介な代物です。
また、今回はPOMDPを履歴で学習するやり方を取りましたが、ChatGPT曰く信念状態を学習するやり方もあるそうです。(よく分からないので取り上げません)
この記事が誰かの参考になれば幸いです。