この記事は自作した強化学習フレームワークであるSimpleDistributedRLの解説記事です。
概要はこちらです。
ここでは強化学習の基本的な考えについて解説します。
(フレームワークというより一般的な内容です)
1.強化学習の位置づけ
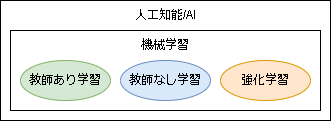
機械学習は代表的な以下の3つのカテゴリに分類でき、その中の1つが強化学習です。
各項目を簡単に言うと以下です。
- 教師あり学習:データから正解を当てるタスク(分類や回帰など)
- 教師なし学習:データから特徴を抽出(クラスタリングや次元削減など)
- 強化学習:環境から最適な行動を学習する
教師あり/なし学習と大きく違う点はデータの取得方法でしょう。
教師あり/なし学習では与えられたデータに対して学習を行いますが、強化学習では環境からどのようにデータを取得するかもタスクに含まれる事が多いです。
(模倣学習やオフライン強化学習等、データのみで学習するタスクもあります)
2.強化学習の問題設定
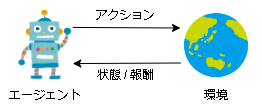
強化学習は与えられた環境に対して試行錯誤することで、最適な行動を学習します。
基本的には対話形式です。
環境はアクションを受け取った後に状態と報酬を返し、エージェントは状態と報酬を受け取った後に次のアクションを返し、とこれを繰り返します。
ここで環境がルールもなく自由に振舞いをされると考えようもないので、
一般的にはマルコフ決定過程(Markov decision process; MDP)と呼ばれるモデルを仮定して話を考えます。
参考
・機械学習スタートアップシリーズ Pythonで学ぶ強化学習 [改訂第2版] 入門から実践まで(amazonリンク)
・強化学習の基本:マルコフ決定過程ってなんぞ?
・マルコフ決定過程(wikipedia)
マルコフ決定過程(Markov decision process; MDP)
マルコフ決定過程を簡単に言うと、次の状態(正確には次の状態になる確率)は現在の状態と行動によってのみ決まる(過去の状態に依存しない)状態遷移モデルの事です。
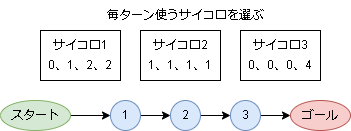
例として、以下のすごろくを考えます。
3種類のサイコロがあり、振る前に毎回選べるすごろくです。(マリ〇パーティのイメージです)
この場合、今いる位置(状態)と使うサイコロ(アクション)を決めると、次の状態(の確率)が決まります。(2つ前の状態やアクションは関係ない)
こういったモデルがマルコフ決定過程になります。
マルコフ決定過程は主に以下の要素から表されます。
\begin{align}
s &: 状態\\
a &: アクション\\
r &: 報酬\\
S = \{s_1, s_2, ..., s_N \} &: 状態の有限集合\\
A = \{a_1, a_2, ..., a_M \} &: アクションの有限集合\\
p(s'|s, a) &: sにてaを選んだ後にs'に遷移する確率\\
r(s,a,s') &: 即時報酬
\end{align}
すごろくの例だと以下です。
\begin{align}
S &= \{スタート, 1, 2, 3, ゴール \}\\
A &= \{サイコロ1, サイコロ2, サイコロ3 \}\\
\end{align}
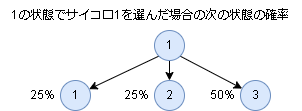
状態遷移確率と即時報酬は列挙すると多いので一部のみ載せます。
即時報酬は2のマスに止まると-1、ゴールで1とします。
\begin{align}
&p(1|1, サイコロ1) = 0.25\\
&p(2|1, サイコロ1) = 0.25\\
&p(3|1, サイコロ1) = 0.5\\
&r(1,サイコロ1,1) = 0\\
&r(1,サイコロ1,2) = -1\\
&r(3,サイコロ1,ゴール) = 1\\
\end{align}
報酬
モデルが定義できたので次に報酬について考えます。
強化学習の目的は報酬をできるだけ多く手に入れることです。
話を簡単にするために時間に制限をつけて考えます。
制限時間までの1回の試行を1エピソードとし、1エピソードの各ステップを $t(0,...,T)$ とします。
ここであるステップ $t$ からエピソード最後まで手に入れた報酬の合計は以下です。
$$
r_{t+1} + r_{t+2} + ... + r_{T}\
$$
$r$ は即時報酬で、$t=0$ の場合は1エピソードで手に入れた報酬となります。
上記が予測できれば、後はこれが最大となるように行動を選ぶだけです。
しかし、予測をする上で遠い未来の報酬は本当に手に入るかが分かりません。
ですのでその分を割り引いて計算をします。
(割引現在価値といい資産価値の計算などにも使われる一般的な手法らしいです)
計算としては割引率 $\gamma$(0~1)という係数を使って以下のように報酬の総和 $G_t$ を定義します。
\begin{align}
G_t &= r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3}... + \gamma^{T-1} r_{T}\\
G_t &= \sum_{k=0}^{T-t-1} \gamma^k r_{t+k+1} \quad (\sumでまとめたもの) \\
G_t &= r_{t+1} + \gamma G_{t+1} \quad (漸化式ver)\\
\end{align}
$G_t$ の最大化を考えますが、確率的な要素が入るため、実際には期待値を考えこれを最大化することを考えます。
\begin{align}
V_{\pi}(s_t) &= E_{\pi} [ G_t ] \\
&= E_{\pi} \Big[ r_{t+1} + \gamma G_{t+1} \Big] \\
&= E_{\pi} \Big[ r_{t+1} + \gamma V_{\pi}(s_{t+1}) \Big] \\
\end{align}
ここで $E$ は期待値を表しています。($\pi$ については後述)
またこの期待値を強化学習では ”価値” といい、かなり重要な値になります。
3.価値の推定とベルマン方程式
次にある時刻$t$における状態の価値を考えたいと思います。
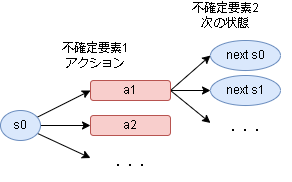
今の状態から次の状態までの不確定要素は ”アクション” と ”次の状態” です。
不確定要素は確率が分かれば期待値を計算できます。
まずはアクション1を選んだ場合の価値 $Q_{\pi}$ を考えてみます。
$$
Q_{\pi}(s0, a1) = p(s0|s0, a1) \times (報酬 + s0の価値) + p(s1|s0, a1) \times (報酬 + s1の価値) + ...
$$
期待値の求め方と同じで、全ての次の状態に対して「遷移する確率×その状態の価値」を計算して足します。
これでアクションの価値が求められたので、同様にs0の価値 $V$ を求めてみます。
$$
V_{\pi}(s0) = a1を選ぶ確率 \times Q_{\pi}(s0, a1) + a2を選ぶ確率 \times Q_{\pi}(s0, a2) + ...
$$
これで s0 の価値が求められました。
数式で書くと以下です。
\begin{align}
V_{\pi}(s) &= E_{\pi}\Big[ r(s,a,s') + \gamma V_{\pi}(s') \Big] \\
&= E_\pi \Big[ \sum_{s'}p(s'|s,a) \Big( r(s,a,s') + \gamma V_{\pi}(s') \Big) \Big] \\
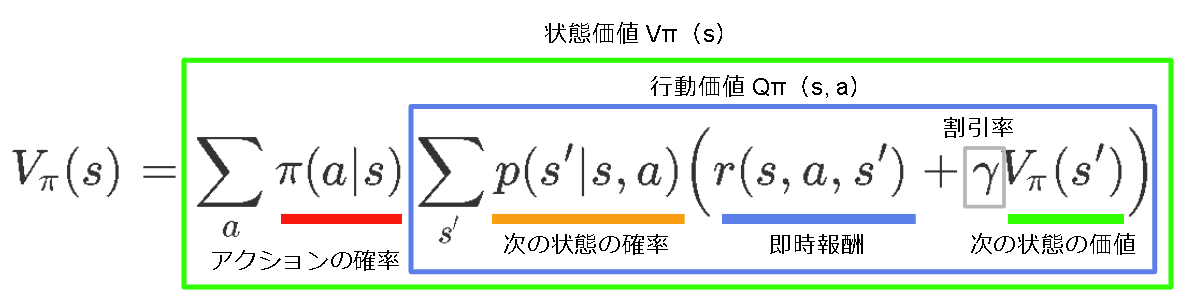
&= \sum_{a} \pi(a|s) \sum_{s'}p(s'|s,a) \Big( r(s,a,s') + \gamma V_{\pi}(s')\Big)
\end{align}
$\pi(a|s)$ はある状態 $s$ において $a$ を選ぶ確率で、方策(Policy)といいます。
この式はベルマン方程式(Bellman Equation)といい、強化学習ではこの式を最大化する事が目的となります。
また上で書いた$VQ$は名前がついており、$V$ を状態価値といい、$Q$ を行動価値といいます。
$V$ と $Q$ は相互に変形可能で、それぞれのパターンを書いておきます。
\begin{align}
Q_{\pi}(s,a) &= \sum_{s'} p(s'|s,a) \Big(r(s,a,s') + \gamma \sum_{a'} \pi(a'|s') Q_{\pi}(s', a') \Big) \\
V_{\pi}(s) &= \sum_{a} \pi(a|s) Q_{\pi}(s, a) \\
Q_{\pi}(s,a) &= \sum_{s'} p(s'|s,a) \Big(r(s,a,s') + \gamma V_{\pi}(s') \Big) \\
\end{align}
4.ベルマン方程式の解き方
ベルマン方程式が定義できたので後は解くだけですが、これが簡単ではありません。
なぜならこれは再帰構造になっているからです。
これを解く上で大きく2つの考えがあります。
価値ベース(ValueBase):価値を学習し、価値が最大になるように行動する
方策ベース(PolicyBase):価値が最大になるような方策を学習する
価値ベース
もしベルマン方程式で価値が分かっていれば次の行動を決めることは簡単です。
例えばある状態 $s$ での行動価値が以下だったとします。
\begin{align}
Q(s,a0) = -1 \\
Q(s,a1) = 1 \\
Q(s,a2) = 0 \\
\end{align}
一番価値が高い $a1$ のアクションを選べばいい事が分かりますね。
このように価値を学習し、その価値を元に行動を決める手法が価値ベースとなります。
具体的な学習方法に関しては別記事で解説予定です。
追記:記事を書きました。価値ベースアルゴリズムの基礎(Q学習)
方策ベース
マルコフ決定過程ではアクションが決まると次の状態の確率が決まりました。
という事は方策(アクションの確率)を決めてしまえば全ての不確定要素が決まるので、期待値(価値)を求めることができます。(次の状態への遷移は同じアクションなら同じ遷移確率になる)
これを利用し、価値が最も大きくなる方策を学習しようという考えが方策ベースのアルゴリズムです。
詳細は方策勾配法のページで解説予定です。
追記:記事を書きました。方策ベースアルゴリズムの基礎(方策勾配法)
最後に
各アルゴリズムに関しては少しずつ記事にしていく予定です。