記事の構成ですが、前半が過大評価問題について、後半が新手法の説明になります。
TL;DR
- 実測値の累積報酬和を正則化項として追加する事で、過大評価の抑止に成功しターゲットネットワークがいらなくなった。
- ターゲットネットワークがないので計算コストが減少(学習速度が向上)
- 最新のQネットがすぐに学習に使えるので学習効率が良くなる…はず(悪くならない事は確認)
過大評価問題
論文では過大評価バイアス(Overestimation Bias)や最大化バイアス(Maximization Bias)と主に書かれている問題です。
この記事では便宜上、過大評価問題(過小評価も含む)と言っています。
この問題はQ学習において、Q値を学習する際の最大化処理($max_a Q(s,a)$)がノイズを含んでいた場合、ノイズの上振れた値が伝播される事で起こる問題となります。
この問題について調査した結果と、思いついたアイデアを備忘録で残しておきます。
またこの記事はある程度Q学習/DQNについて知っている前提で書いていきます。
(過去に書いた記事:価値ベースアルゴリズムの基礎(Q学習)、DQN)
前:初期値の過大評価問題に対する考察
次:シンプルに方策を学習できるオフポリシー型PPOができた
コード
本記事で使ったコードはGoogleColabにあるので以下のリンクからどうぞ
また、本記事の後半で紹介する新手法は自作している強化学習フレームワークでNoT-DQNとして実装してあります。
フレームワークの記事:https://qiita.com/pocokhc/items/a2f1ba993c79fdbd4b4d
GitHub:https://github.com/pocokhc/simple_distributed_rl
現象の確認
報酬が0の環境なら割と簡単に確認できます。
パラメータは以下です。
- Env
- 状態: アクションによらず、-1~1の間をランダムに返す
- アクション: 10個
- 100ステップで終了
- DQN
- 割引率: 1.0
- ターゲットネットワークの同期: 1frame(常に同期)
- メモリのwarmup: 10_000サイズ
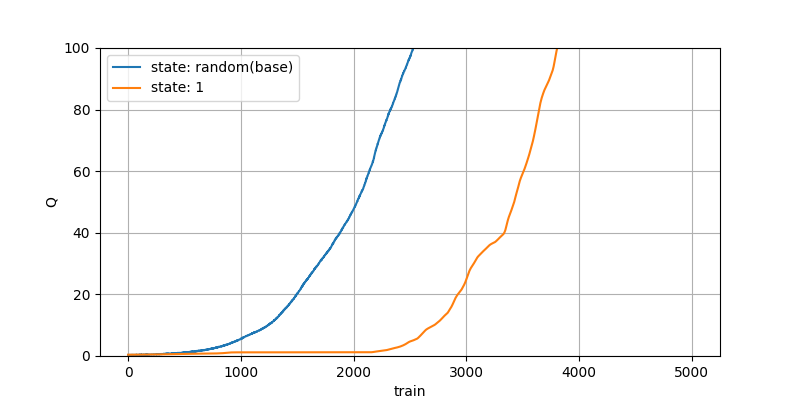
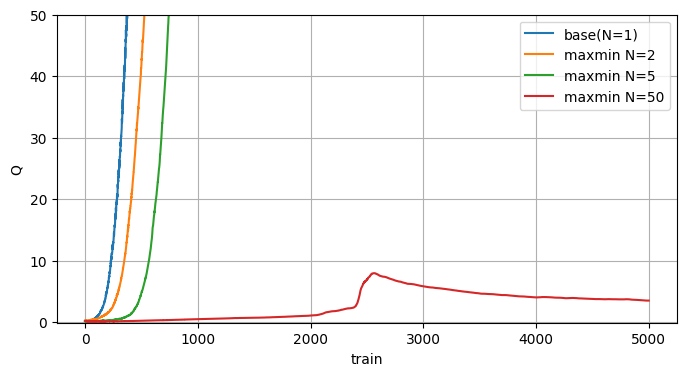
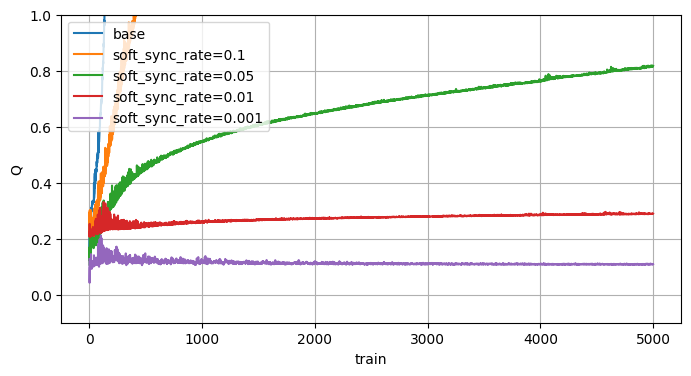
5000回学習させた結果は以下です。
横が学習回数、縦がアクション選択時のQ値です。
報酬が0の空間なので真のQ値は0になるべきですが、過大評価された値が伝播され続け学習が進むごとに増えていっています。
これがこの記事で過大評価問題と言っているものになります。
また、オレンジは状態がランダムではなく1で固定した環境です。
こちらでも過大評価問題は発生し、状態数によらず発生する問題となります。
以降はこちらの青をbeseとして他の手法を見てみます。
各手法と過大評価への影響
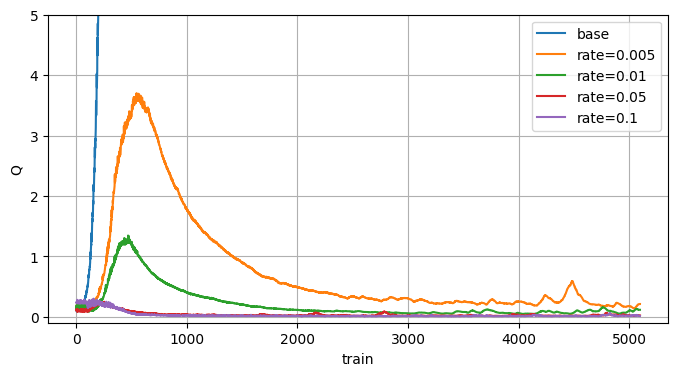
割引率
過大評価で伝播される値よりも割引率で減少する値の方が大きければ過大評価は伝播されません。
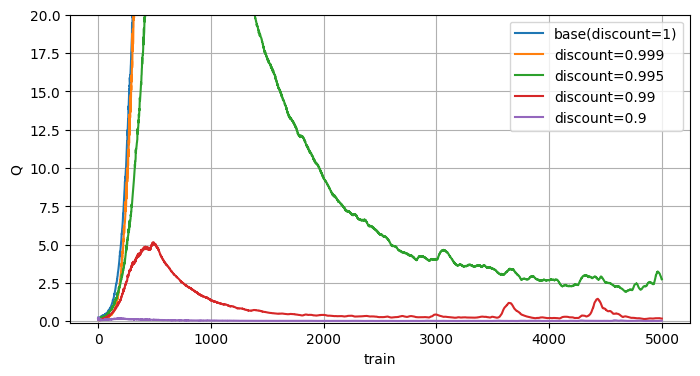
実際に割引率を変えた結果を見てみました。
割引率を下げると過大評価が抑えられます。
注目すべき点は緑や赤で、一度過大評価になったものがその後修正されていますね。
過大評価対策は抑制するだけか、過大評価後も修正されるか、といった点が重要となります。
Fixed Target Q-Network(2015; DQN)
DQNで登場した手法です。
過大評価問題を意識していたかは分かりませんが、対策としては非常に有効で、現在も主流として使われ続けています。
これはターゲットネットワークと呼ばれる同じQモデルを作成し、ターゲットネットワークから次のQ値を予測する事で学習を安定させる手法となります。
Qモデルとターゲットネットワークの同期間隔はハイパーパラメータとなり、間隔を短くすると反映が早くなって学習速度は上がるものの不安定になります。
一方、間隔を長くすると安定はする代わりに学習速度は下がります。
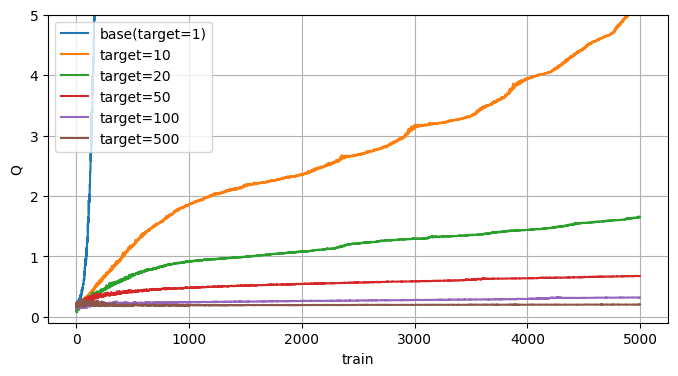
実際に同期間隔を変えて見てみました。
同期間隔を増やす毎に過大評価が抑えられていますね。
ただ抑止はされていますが、一度過剰評価された値は改善されていないように見えます。
DoubleDQN(2015)
過大評価の問題にメインに取り組んだ最初の論文だと思います。
予測するアクションの選択と評価を別モデルで行うことで過大評価の伝播を抑える手法です。
DQNでは別モデルはターゲットネットワークが担います。
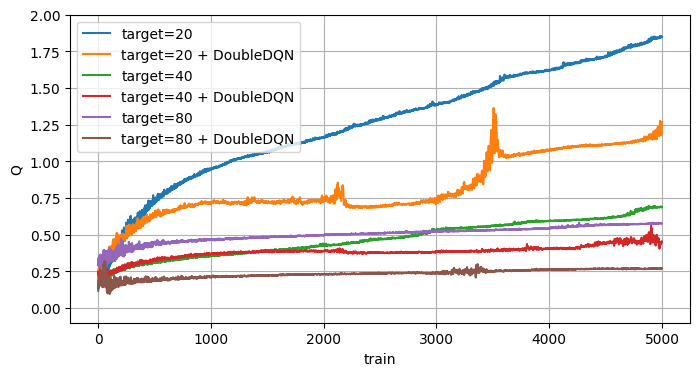
ここはターゲットネットワークと比較しました。
DoubleDQNを有効化するとターゲットネットワークの効果がより高まる感じですね。
こちらも抑止はされていますが修正はされていないように見えます。
Maxmin Q-learning
論文: https://arxiv.org/abs/2002.06487 (2021)
過大評価の対策について書かれた論文の1つです。
アンサンブル学習に分類され、ざっくり言うとたくさんのQモデルを用意し、モデル毎で最大のQ値を出し、その中から最小のQ値を採用するという手法です。
効果はあるようですけど、ターゲットネットワーク等と合わせて使う手法な気がします。
後単純に学習するモデルが増えるので計算コストが…。
ターゲットネットワークと違って過大評価を修正する効果もあるようです。
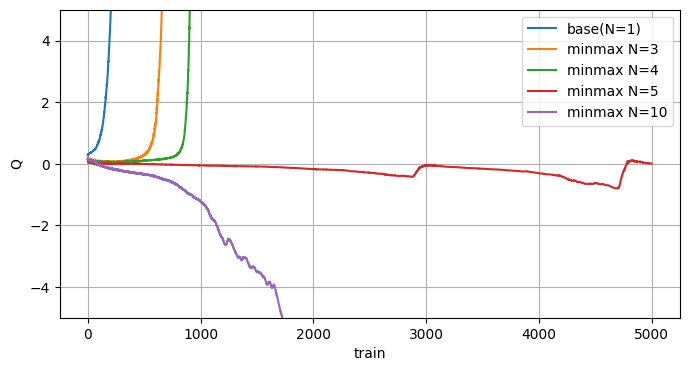
Minmax Q-learning
上記Maxmin手法の派生っぽい手法です。
Suppressing Overestimation in Q-Learning through Adversarial Behaviors(2024)の論文内で参考にされている手法です。
(この論文は過大評価として、二人零和マルコフゲームとして定式化したダミー敵対的Q学習(DAQ)という新しい手法を提案している論文です)
MinmaxはMaxminの逆で各アクション毎に全モデルの中で最小のQ値を出し、その中から最大のQ値を採用するという手法です。
面白い事にこちらはモデルを増やすと過小評価する結果になりました。
最適なNを求めるのが難しそう…。
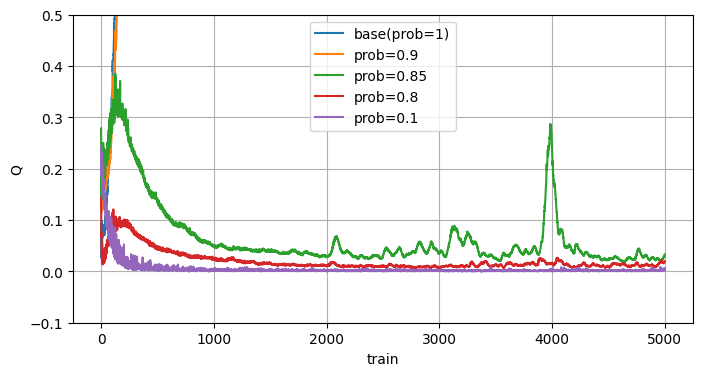
目標方策の変更
前回の初期値過大評価で行った手法で、次のQ値の予測を最大値ではなく、ε-greedyの期待値を使う手法です。(SARSAみたいな感じ)
最大値以外も伝播されるので過大評価は抑制されています。
ただ目標方策も変わるので最適な方策ではなく保守的な方策が学習される点に注意が必要ですね。
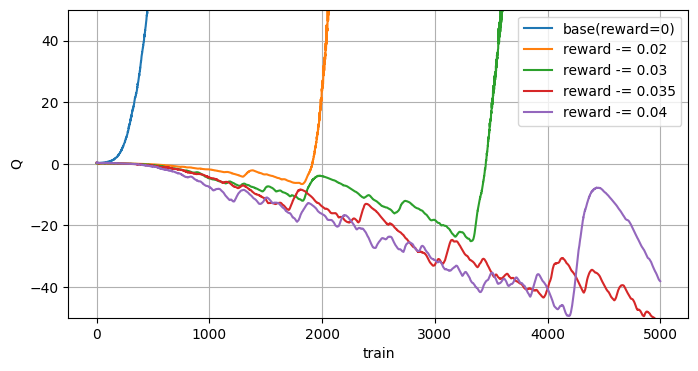
報酬シフト
過大評価を報酬で抑えようという考えです。
報酬全体をシフトするとQ値は変わりますが、方策は変わらない事を利用しています。
実装は簡単で全ての報酬に(負の)定数を加えるだけです。
報酬をシフトしすぎると過小評価するようです…。
Soft Target Q-Network
多分DDPGで提案された手法で、ターゲットネットワークの同期方法を、一気に同期するのではなく少しずつ同期する手法です。
Softに対して既存の同期はHardと言ったりします。
・Soft Target sync(毎回同期する、$\tau$は割合を示すパラメータ)
$$ \theta^{target} \leftarrow \tau \theta + (1 - \tau) \theta^{target} $$
・Hard Target sync(一定間隔で同期)
$$ \theta^{target} \leftarrow \theta$$
Hardの同期は切っています。
Softでも過大評価の抑制には効果があるようです。(Hardと同じで改善はされてなさそうですね)
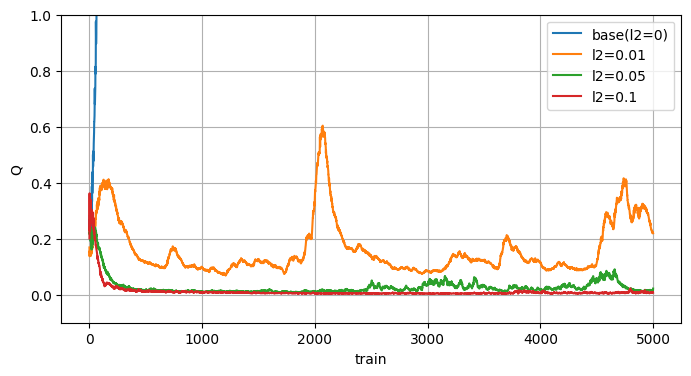
L2正則化
機械学習で一般的なL2正則化項を直接Q値に入れる方法です。
疑似コードは以下
q = q_net(state)
loss = MSE(target_q, q[action]) # Q学習
# L2正則化項
l2_rate = 0.1
loss += l2_rate * (q**2).mean()
結構効果がありますね。
ただ、これはQ値の範囲に制限を受けるので採用はできないですね(ならなぜ試したのか)
既存手法や思いついた手法については以上です。
ここからは新手法です。
No Target DQN
発想に至るまで
発想に至るまでの考えを文字にしておきます。
まずQ値は以下で更新されます。
$Q_{\theta}(s,a) \leftarrow r + \gamma Q_{\theta}(s',a')$
この時、$Q_{\theta}(s,a)$ がプラスに更新されるとニューラルネットワークの性質上、高確率で $Q_{\theta}(s',a')$ もプラスに更新されます。
$Q_{\theta}(s',a')$ が増えたので次の更新で $Q_{\theta}(s,a)$ も増加し $Q_{\theta}(s',a')$も増加、…とこのループが過大評価の根本原因と考えました。
1.増えた分を減らす
最初に思いついたのは、増加分の$Q_{\theta}(s',a')$を減らすことです。
疑似コードは以下
next_q = q_net(next_state)
target_q = r + max(next_q)
# 学習
# この時 "q_net(state)[action]" が増えると "q_net(next_state)" も高確率で増える
loss = MSE(target_q, q_net(state)[action])
# 学習後に増えた "q_net(next_state)" を学習前の値になるまで学習する
for _ in range(100):
loss_next = MSE(next_q, q_net(next_state))
ただこれは過大評価は抑えられましたが、それ以上にそもそものQ値の学習まで抑えられてしまい学習が進みませんでした。
2.差分をペナルティとする
次に実施したのは学習後のnext_stateのQ値の差分を次の学習に加える事でした。
next_q = q_net(next_state)
target_q = r + max(next_q)
# 前の学習の差分をペナルティとして加える
target_q -= prev_diff
loss = MSE(target_q, q_net(state)[action])
# 次の学習のために差分を取得
prev_diff = next_q - q_net(next_state)
まあ、これは全然うまくいきませんでした…。
3.ターゲットネットワークに近づける
次に学習時にターゲットネットワークから離れない項を追加してみました。
next_q = q_net(next_state)
target_q = r + max(next_q)
loss = MSE(target_q, q_net(state)[action])
# 次の状態のQ値はターゲットネットワークのQ値から離れすぎないようにする項を追加
next_q_target = q_target_net(next_state)
loss += MSE(next_q, next_q_target) * 0.1 # 0.1は強さのハイパラ
# 一定間隔で同期
if 一定間隔:
q_target_net.parameters() = q_net.parameters()
考え方はターゲットネットワークと同じですが、直接値を使うのではなく、学習時の抑止力として使っている点が違います。
これはうまく行きましたが、本質的にはターゲットネットワークとほぼ同じで、ターゲットネットワークの同期タイミングの問題が依然としてありました。
4.ターゲットネットワークは報酬でいいのでは?
Q値は何を基準にすればいいでしょうか?その基準をターゲットネットワークにすれば同期は不要ではないかと考えました。
一番簡単なQ値を考えます。
$Q_{\theta_{target}}(s,a) \leftarrow r$
これは割引率0の時のQ値を表しています。
乱暴ですが、これをターゲットネットワークにしてしまえばなんか行けそうな気がしました。
next_q = q_net(next_state)
target_q = r + max(next_q)
loss = MSE(target_q, q_net(state)[action])
# 次の状態のQ値がターゲットネットワークから離れすぎないようにする項
next_q_target = q_target_net(next_state)
loss += MSE(next_q, next_q_target) * 0.1 # 0.1は強さのハイパラ
#--- ターゲットネットワークの学習
target_loss = MSE(reward, q_target_net(state))
5.さすがに累積報酬和に
割引率0は流石に乖離が過ぎると思い、できる限り展開した割引累積報酬和を考えました。
ただ、これは分布シフト問題が発生するので注意が必要です。
分布シフト問題が発生しても割引率0のQ値よりは正確な値になると考えています。
$Q_{\theta_{target}}(s,a) \leftarrow r_{0} + \gamma r_{1} + \gamma^2 r_{2} + ... + \gamma^T r_{T}$
最後にQ値を使わないことが重要です。
Q値を追加すると過大評価が伝播される可能性があります。
6.次の状態である必要はある?
ターゲットネットワークの正則化項ですが、next_stateである必要はあるのでしょうか?
# 次の状態のQ値で学習
next_q = q_net(next_state)
next_q_target = q_target_net(next_state)
loss += MSE(next_q, next_q_target) * 0.1
↓
# 今の状態のQ値で学習
q = q_net(state)
q_target = q_target_net(state)
loss += MSE(q, q_target) * 0.1
感覚としてはモデル同士の差を縮めたいのでstateにしても結果は変わらないと思いました。
実際やって見てもそこまで違いはなかったです。
一旦ここまでがアイデアとなります。
7.(adv)ターゲットネットワークで近似する必要ある?
ここはさらに踏み込んだ内容です。
ターゲットネットワークは割引累積報酬和の平均値を学習するモデルとなっています。
ただ、そこまで厳密な値が欲しいわけではないので、厳密性を犠牲にして実測値をそのまま使っても許容できるのでは?というのがターゲットネットワークが消えたアイデアです。
ニューラルネットワークの計算はコストが高いので、精度を犠牲にしても速度を重視する価値があるかなと思った内容となります。
ただここはやりすぎな可能性はあるので、割引累積報酬和バージョンのターゲットネットワークを残してもいい気はします。
まとめると以下です。
# Nステップの割引累積報酬和を計算
total_reward = 0
for r in reverced(rewards):
total_reward = r + discount * total_reward
# ターゲットネットワークを使わずに、ダイレクトにQ値を更新
reward = rewards[0]
target_q = reward + discount * max(q_net(next_state))
q = q_net(state)[action]
loss = MSE(target_q, q)
# 割引累積報酬和 から離れすぎないようにするlossを正則化項として加える
loss += MSE(total_reward, q) * 0.1
割引累積報酬和の計算も気になるようなら精度は落ちますが、報酬だけでもいいと思います。(さらに計算が簡単になります)
この新手法の利点は以下です。
- 計算量削減(ターゲットネットワークの計算がまるまるなくなる)
- 学習にQ値が即時反映(ターゲットネットワークの同期待ちがなくなる)
- 過大評価が抑えられる
欠点は以下です。
- 厳密ではないQ値(実測値の割引累積報酬和)に引っ張られるので、ほんの少し真のQ値ではなくなる
- 実測値の割引累積報酬和は分布シフト問題の誤差も含まれている点に注意
報酬0の環境での過大評価の結果
ちゃんと過大評価が抑制されているだけでなく、修正されていますね。
これターゲットネットワーク使ってないんだぜ…。
(コードはColabにあります)
学習結果
比較的ナイーブなDQNとターゲット無しDQNを比較してみます。
実装はSRLフレームワークのものNoT-DQNを使っています。
(ここからのコードはColabには上げていない内容です)
FrozenLake-v1
GymにあるFrozenLake-v1です。
ただし難易度を上げるために入力をrender時に描画される画像で学習しました。
(左下のグレー画像)
学習時の主要なパラメータは以下です。
| DQN | NoT-DQN | |
|---|---|---|
| バッチサイズ | 32 | 32 |
| 学習率 | 0.0005 | 0.0005 |
| Qネット | (256) | (256) |
| 割引率 | 0.9 | 0.9 |
| epsilon | 0.1 | 0.1 |
| ターゲットネットの同期間隔 | 1000 | - |
| DoubleDQN | True | - |
| TotalRewardの正則化項率 | - | 0.1 |
コード全体
※SRLのバージョンはv1.4.1です。
import os
import mlflow
import numpy as np
import srl
from srl.utils import common
mlflow.set_tracking_uri(os.environ.get("MLFLOW_TRACKING_URI", "mlruns"))
common.logger_print()
def _train(rl_config):
env_config = srl.EnvConfig("FrozenLake-v1")
runner = srl.Runner(env_config, rl_config)
runner.set_progress(enable_eval=True)
runner.set_mlflow()
# 学習
runner.train(max_train_count=200_000)
runner.make_html_all_parameters_in_mlflow()
rewards = runner.evaluate(max_episodes=3)
print(f"[{rl_config.name}] {np.mean(rewards)}, {rewards}")
def train_dqn():
from srl.algorithms import dqn
rl_config = dqn.Config(
batch_size=32,
lr=0.0005,
epsilon=0.1,
discount=0.9,
target_model_update_interval=1000,
enable_reward_clip=False,
enable_double_dqn=True,
enable_rescale=False,
)
rl_config.memory.warmup_size = 10000
rl_config.memory.capacity = 100_000
rl_config.memory.compress = False
rl_config.hidden_block.set((256,))
rl_config.set_torch()
rl_config.observation_mode = "render_image"
_train(rl_config)
def train_notdqn():
from srl.algorithms import not_dqn
rl_config = not_dqn.Config(
batch_size=32,
lr=0.0005,
epsilon=0.1,
discount=0.9,
alignment_loss_coeff=0.1,
)
rl_config.memory.warmup_size = 10000
rl_config.memory.capacity = 100_000
rl_config.memory.compress = False
rl_config.hidden_block.set((256,))
rl_config.observation_mode = "render_image"
_train(rl_config)
if __name__ == "__main__":
train_dqn()
train_notdqn()
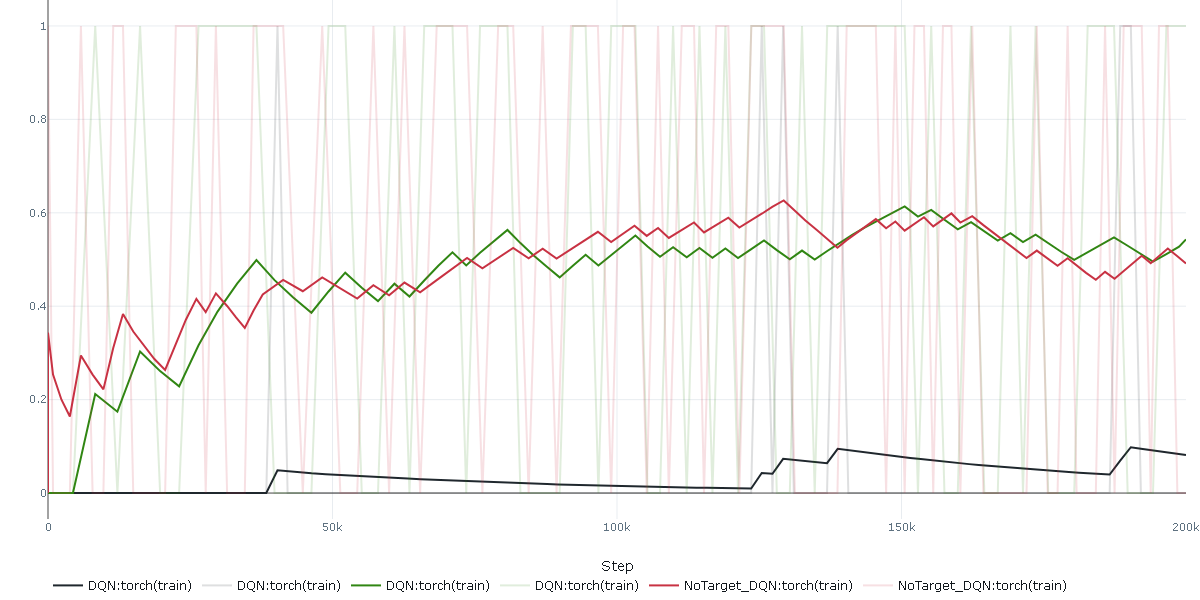
200_000回学習した結果は以下です。
横がステップ数で、縦が評価時の環境から得た総報酬です。
緑がDQN(TargetUpdate=1000)で、赤がNoTargetDQNです。
黒はDQNのTargetUpdate=1にしたもので、学習できない比較として置いています。
NoTargetDQNはターゲットネットワークがなくてもちゃんと学習出来ています。
ALE/Breakout-v5
こちらはDQN論文のパラメータをベースに学習してみました。(おまけでrainbowも)
ただそのままでは時間がかかりすぎるので、学習回数を 1_500_000 回としています。(これでも大体5時間ぐらい…)
学習時の主要なパラメータは以下です。
| DQN | Rainbow | NoT-DQN | |
|---|---|---|---|
| windows length | 4 | 4 | 4 |
| バッチサイズ | 32 | 32 | 32 |
| 学習率 | 0.00025 | 0.00025 | 0.00025 |
| Qネット | (512) | (512) | (512) |
| 割引率 | 0.99 | 0.99 | 0.99 |
| epsilon | 0.1 | 0.1 | 0.1 |
| ターゲットネットの同期間隔 | 10000 | 10000 | - |
| DoubleDQN | True | True | - |
| Multisteps | - | 1, 3 | - |
| NoisyDense | - | False | - |
| PriorityMemory | - | Proportional | - |
| DuelingNetwork | - | True | - |
| TotalRewardの正則化項率 | - | - | 0.05 |
コード全体
※SRLのバージョンはv1.4.1です。
import os
import ale_py
import mlflow
import srl
from srl.utils import common
mlflow.set_tracking_uri(os.environ.get("MLFLOW_TRACKING_URI", "mlruns"))
common.logger_print()
def _train(rl_config):
env_config = srl.EnvConfig(
"ALE/Breakout-v5",
kwargs=dict(
frameskip=4,
repeat_action_probability=0,
full_action_space=False,
obs_type="grayscale",
),
)
runner = srl.Runner(env_config, rl_config)
runner.set_progress(enable_eval=True)
runner.set_mlflow()
runner.train(max_train_count=1_500_000)
def train_dqn():
from srl.algorithms import dqn
rl_config = dqn.Config(
window_length=4,
batch_size=32,
lr=0.00025,
discount=0.99,
epsilon=0.1,
#
enable_reward_clip=False,
target_model_update_interval=10000,
enable_double_dqn=True,
)
rl_config.memory.warmup_size = 10_000
rl_config.memory.capacity = 100_000
rl_config.memory.compress = False
rl_config.input_block.image.set_dqn_block()
rl_config.hidden_block.set((512,))
rl_config.set_torch()
_train(rl_config)
def train_rainbow():
from srl.algorithms import rainbow
rl_config = rainbow.Config(
window_length=4,
batch_size=32,
lr=0.00025,
discount=0.99,
epsilon=0.1,
#
enable_reward_clip=False,
target_model_update_interval=10000,
enable_double_dqn=True,
multisteps=1,
enable_noisy_dense=False,
)
rl_config.memory.warmup_size = 10_000
rl_config.memory.capacity = 100_000
rl_config.memory.compress = False
rl_config.memory.set_proportional(
alpha=0.5,
beta_initial=0.4,
beta_steps=1_000_000,
)
rl_config.input_block.image.set_dqn_block()
rl_config.hidden_block.set_dueling_network((512,))
rl_config.set_torch()
_train(rl_config)
def train_not_dqn():
from srl.algorithms import not_dqn
rl_config = not_dqn.Config(
window_length=4,
batch_size=32,
lr=0.00025,
discount=0.99,
epsilon=0.1,
#
alignment_loss_coeff=0.05,
)
rl_config.memory.warmup_size = 10_000
rl_config.memory.capacity = 100_000
rl_config.memory.compress = False
rl_config.input_block.image.set_dqn_block()
rl_config.hidden_block.set((512,))
_train(rl_config)
if __name__ == "__main__":
train_dqn()
train_rainbow()
train_not_dqn()
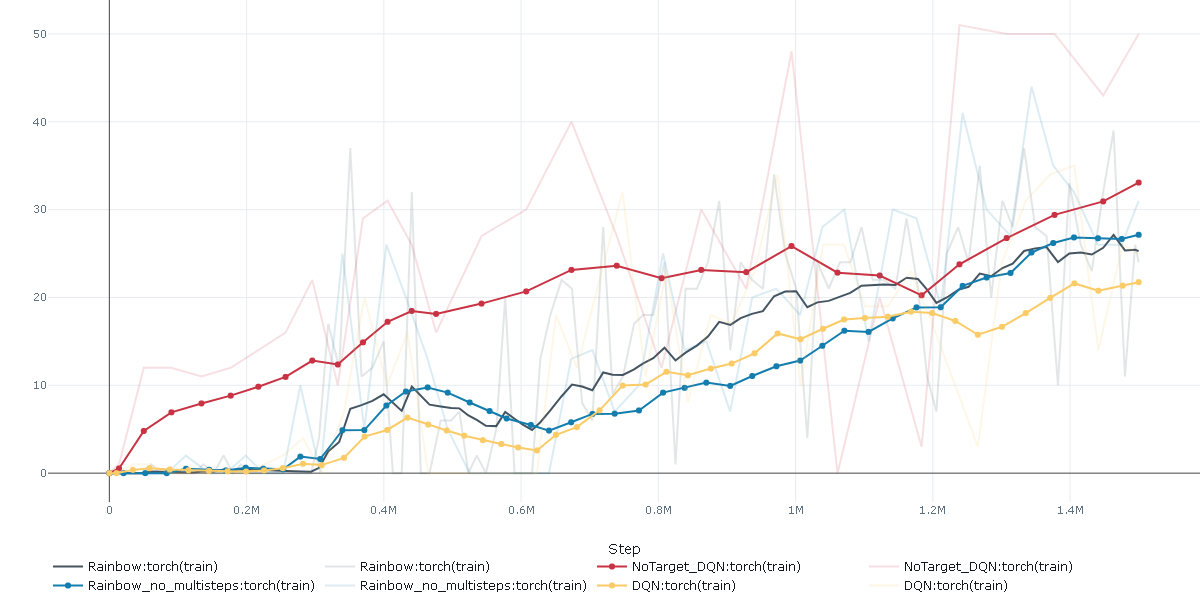
結果は以下です。
赤がNoTargetDQN、黄色がDQN、青がRainbow(Multisteps=1)、黒がRainbow(Multistesps=3+retrace)です。
(mlflowのLine smoothingで90の値にしています)
ターゲットネットワークの同期ずれがない分、NoTargetDQNは学習が早くなる結果になっています。
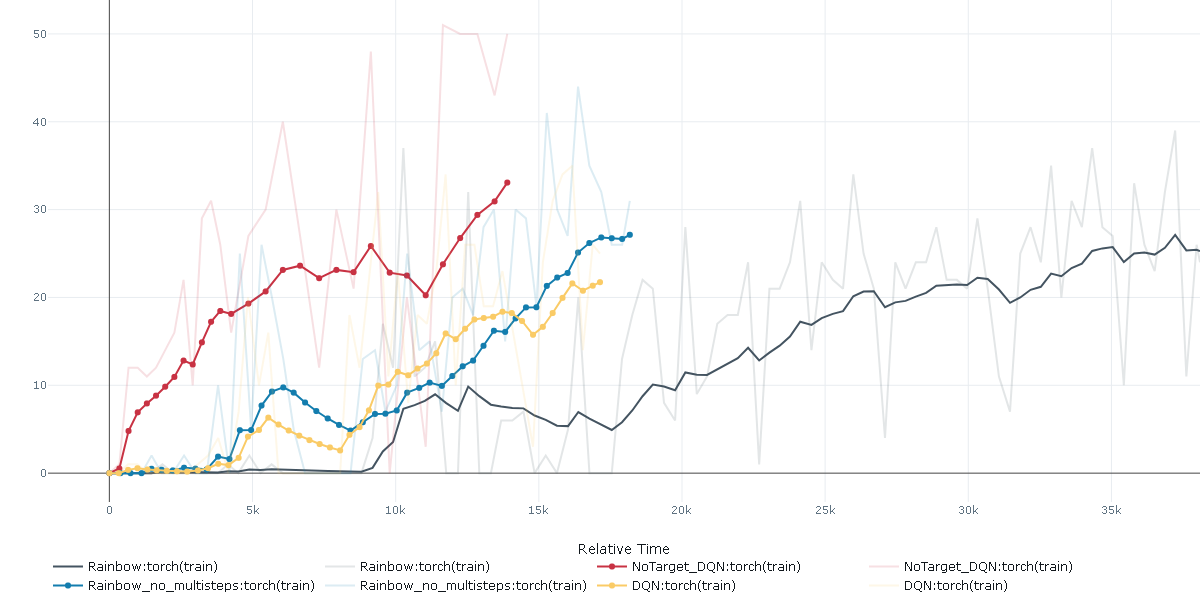
上記は横軸がstep数ですが、横軸を学習時間にした結果を見てみます。
単位は秒で、15k秒が約4.16時間です。
やはり、赤のNoTargetDQNはターゲットネットワークの計算が不要な分早いですね。
黒のRainbow(Multistesps=3+retrace)は3step分先を計算しているのでその分時間がかかります。
折角なので学習後のプレイ動画を載せておきます。
(左下のグレー画像はActorが実際に受け取っている画像、0~3の値はアクションとQ値)
おまけ
本記事の趣旨と外れますが、面白い学習結果が見れたので書いておきます。
Breakoutですが、裏技?みたいな攻略があって偶然そこに行きつくと時々すごい点数があがります。
(昔DQNが話題になった時の記事にも書いてあった気がします)
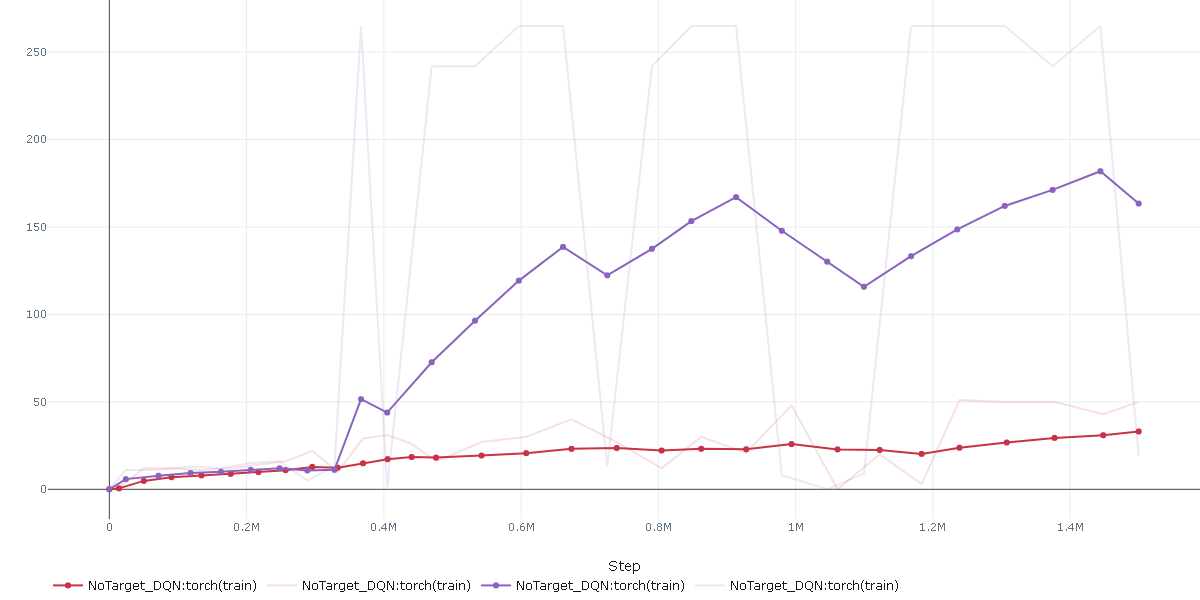
両方ともNoTargetDQNの結果です。
赤は上記比較に使った結果と同じですが、紫は赤の30~40あたりに比べて150~250と大幅にスコアを増やしています。
実際のプレイを見てみると以下です。
画面上部を開拓して一気にスコアを稼いでいますね。
さいごに
DQNに比べて早い、効率がいい、実装が簡単!といっても過言ではない結果になって満足です。
最初にChatGPTに過大評価問題の論文を調査してもらったのですが、思ったより出てこず、あまり研究されていない印象をうけました。
一応出力内容をのまとめをはっておきます。
| 論文タイトル・手法 | 対応する主な問題 | 対応手法の特徴 |
|---|---|---|
| Double Q-learning / Double DQN | 過大評価 | 二つのQ関数を分けて最大化によるバイアスを抑制 |
| Truncated Quantile Critics, Maxmin Q-learning, Meta-Debias Q-learning, TE/KE, DAQ など | 過大評価/過小評価の制御 | 自動バイアス制御、パラメータ最適化、タスク間汎化など多角的手法 |
| Dropout を使った分散制御 | 過大評価+分散 | Dropout による安定化 |
| Parameter-Free 手法 | バイアス制御(過小評価の回避含む) | パラメータ不要の理論的制御 |
対策としては、DoubleDQN以降は Maxmin Q-learning が主要かな?という感じでした。
今回の記事の手法は、DDPGやSAC等のターゲットネットワークを使っているアルゴリズムにも応用できるかと思います。
また、元のDQNよりターゲットネットワークがない分実装も簡単かと思います。(割引報酬和ではなく報酬を直接使えばさらに簡単に実装可能)
課題としては数学的な背景の考察と、正則化項と真のQ値とのずれがどこまで影響あるかですね。
ズレは今回のBreakoutレベルだとまだ問題なさそうですが、更に学習を続けるとどうなるかは少し気になります。