最近、気になる現象が起きたため色々実験した備忘録となります。
過去色々な強化学習の記事を上げていますが、この問題を正面から取り上げている記事は（私が知らないだけかもしれませんが）見たことがない内容でした。
コード
本記事で使ったコードはGoogleColabにあるので以下のリンクからどうぞ
初期値の過大評価問題
強化学習には価値を過大評価する過大評価バイアス（Overestimation bias）の問題があります。
特にオフライン強化学習では顕著に表れる問題で、過大評価を防ぐために様々な手法が提案されています。
（DoubleDQN,Conservative Q-Learning等）
初期値の過大評価問題は、この過大評価バイアスが初期値で起こる問題です。
・条件
分かっている範囲だと以下です。
- 深層強化学習（厳密には初期値が0以外の値を取る?）
- 報酬が疎でほぼ0の空間
- 状態の空間が広い
- 割引率がとても高い値
現象
自作フレームワークで事象を見てみます。（フレームワークの記事はこちら）
環境Gridは以下で、猫がゴールに向かう環境です。
ここで全ての報酬を0にし、更に状態にはエピソードをまたいで増え続けるcountを付け加えました。
（なので同じ状態はほぼこない広い空間）
ここでDQNを10000回学習させてみた結果を見てみます。
当然ですが報酬が0しかないのでQ値は0が正しい値となります。
コードはcolabを確認してください。
学習後のQ値は以下です。（0step目のみ抜粋）（ターゲットネットワークの同期周期10step、割引率0.999）
......
. G.
. . X.
.P .
......
0(←) : 7353526.00000
1(↓) : 7547071.50000
*2(→) : 7568119.50000
3(↑) : 6839872.00000
とても大きい値になっていますね…。
報酬は0なのにこの値になるのは驚きです…。
原因の考察
Q学習における行動価値（Q値）は以下で更新されます。
$$
Q(s_t, a_t) \leftarrow r_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a')
$$
Q値の更新は、得られた報酬$r_{t+1}$ + その次の状態の価値 $Q_\pi(s_{t+1}, a')$ から計算されます。
$\gamma$ は割引率です。
ここで報酬が0の空間を考えると更新の要素が最大値しかなくなります。
$$
Q(s_t, a_t) \leftarrow \max_{a'} Q(s_{t+1}, a')
$$
そしてこの最大値を下げる仕組みは存在しません。（割引率=1.0の場合）
なのでもし最大値が間違っていた場合、その値がひたすら伝播していくのが原因だと思います。
これ以降は思いついた解決策を実施してみます。
対策案1、Target-network + DoubleDQN
まずは既存手法です。
Targetネットワークは次の行動価値を別ネットワークで予測し、DoubleDQNは行動の最大値を今のQネットワークから予測する手法です。
$$
Q_{\text{online}}(s_t, a_t) \leftarrow r_{t+1} + \gamma Q_{\text{target}}(s_{t+1}, \arg\max_{a'} Q_{\text{online}}(s_{t+1}, a'))
$$
過大評価は最大値のみを伝播していたことが問題でした。
この手法では現QネットワークとTargetネットワークがずれるので、最大値ではない値が伝播されて過大評価が修正されていきます。
実際に動かした結果は以下です。
# --- ハイパーパラメータの変更箇所
# Targetネットワークの同期を大きくして、現Qネットワークとのずれを大きくする
rl_config.target_model_update_interval = 100
# DoubleDQNを有効化
rl_config.enable_double_dqn = True
......
. G.
. . X.
.P .
......
0(←) : 2.06796
*1(↓) : 2.08818
2(→) : 2.07842
3(↑) : 1.92293
かなり抑えられていますね。
まだ大きい値ですが、学習を繰り返すと0に収束していきます。
これは厳密には初期値には対応しておらず、再度同じ状態を訪れた際に過大評価を少しずつ修正していくイメージになるかと思います。
なので今回みたいに状態が違うと少し厳しい印象を受けます（ただ少しぐらいの違いはニューラルネットが学習しちゃう…）
対策案2、0報酬をなくす
多分一番簡単に思いつく方法かと思います。
0の報酬だと最大値が更新されないので、負の報酬を導入する事でQ値を減らす機構を追加しています。
下は報酬を-0.1にした結果です。
......
. G.
. . X.
.P .
......
0(←) : -0.62972
1(↓) : -0.62993
*2(→) : -0.56585
3(↑) : -0.62682
報酬を変えているのでそもそもの行動価値が変わっていますが、過大評価は修正されていますね。
対策案3、割引率を下げる
そもそも割引率を下げると過大評価が伝播されなくなります。
割引率0.9で実行すると以下です。
......
. G.
. . X.
.P .
......
0(←) : 0.00810
1(↓) : 0.00920
*2(→) : 0.01310
3(↑) : 0.01216
ただ過大評価は抑制されますが、正しい評価も伝播されにくくなっているので注意が必要です…。
対策案4、CQL手法の導入
オフライン強化学習ではオンラインで使っていた手法（DoubleDQN等）が使えないので過大評価を別の方法で修正しています。
CQL（Conservative Q-Learning）はオフライン強化学習の代表的な手法のひとつで、過大評価を抑えるために、損失関数に以下のペナルティ項を追加します。
※これはかなり簡素化した形で最低限の内容となります
\begin{align}
L &= L_{Q} + \alpha L_{CQL} \\
L_{CQL} &= \max_a Q(s_t,a) - Q(s_t, a_t) \\
\end{align}
$\alpha$はペナルティ項の反映率です。
イメージとしては、今から学習するQ値が最大値なら何もせず、違う場合は最大値のQ値を過大評価とし、それを下げるように学習させます。
疑似コードは以下です。
# Q項の計算箇所
q_all = self.q_online(state) # 全アクションのQ値
q = torch.sum(q_all * onehot_action, dim=1) # 現アクションのQ値
loss = HuberLoss(target_q, q)
# ペナルティ項の計算箇所
alpha = 0.1
loss_cql = torch.max(q_all) - q.detach()
loss += alpha * loss_cql.mean()
alpha=0.1の結果は以下。
......
. G.
. . X.
.P .
......
0(←) : -0.55537
1(↓) : -0.55961
*2(→) : -0.52483
3(↑) : -0.54271
修正されていますが、結構alphaパラメータに敏感な気がします。（まあ実装が簡素なので…）
ペナルティ項が強すぎると負の値になりますね。
対策案5、目的方策の変更
次の状態価値に対して最大値ばかり取得していたのが問題でした。
なら、最大値以外の値も利用すればいいのでは？という考えです。
ただこれをやると目的方策が変わるので注意が必要です（SARSAみたいな感じになる）
コードでは次のQ値を確率の重み割合で合計します。
# --- target q
with torch.no_grad():
n_q_online = self.parameter.q_online(n_state)
n_q_target = self.parameter.q_target(n_state)
n_act_idx = torch.argmax(n_q_online, dim=1)
if self.config.target_policy == 1.0:
# 1.0の場合は最大値
n_q = n_q_target.gather(1, n_act_idx.unsqueeze(1)).squeeze(1)
else:
# 一番良い行動に0.9、その他に(0.1 / (n - 1))の重みをつける
prob = self.config.target_policy
n_action_size = self.config.action_space.n
weight = torch.full_like(n_q_target, fill_value=0.1 / (n_action_size - 1))
weight.scatter_(1, n_act_idx.unsqueeze(1), prob)
n_q = (n_q_target * weight).sum(dim=1)
target_q = reward + not_done * self.config.discount * n_q
target_policy = 0.8 の結果は以下です。
......
. G.
. . X.
.P .
......
0(←) : 0.00710
*1(↓) : 0.00870
2(→) : 0.00545
3(↑) : 0.00732
かなり抑えられていますね。
対策案6、割引率の焼きなまし
そもそも学習していない価値を伝播しているのが問題です。
なので学習していない序盤は割引率を0にして伝播を抑えつつ、後半に向けて1にする手法となります。
target_q = reward + not_done * self.discount * n_q
# discountを少しづつ増やす
self.discount += 1 / 9_000
if self.discount > self.config.discount:
self.discount = self.config.discount
結果は以下です。
......
. G.
. . X.
.P .
......
0(←) : 1.57549
*1(↓) : 1.61760
2(→) : 1.50211
3(↑) : 1.57376
最後の1000回は割引率が元に戻るので過大評価が伝播しますが、序盤の学習でかなり抑えられていますね。
対策案7、TargetQの0化とWarmUp
ここはアイデアだけです。
そもそも初期値を0から始めれば過大評価がないのでは？という発想です。
やり方はTargetQネットワークのパラメータを全て0で初期化し、最初の一定時間、Qネットワークと同期しないという方法です。
（Qネットワークのパラメータを0で初期化してしまうとニューラルネットの特性上学習ができなくなります）
ただ、内容は割引率の焼きなまし法と見方が変わっただけで一緒なきがして試していません。
対策案8、RND+割引率の自動調整
個人的には一番効果があると思う内容です。
RND（Random Network Distillation model）は内部報酬で使われる手法で、ある状態に対して訪れた頻度を出力するネットワークです。
初めて訪れた場合に高い値、よく訪れる状態は低い値を出力します。
これを利用し、訪れ度合いに対して割引率を自動調整します。
イメージとしては割引率は信用度を表すイメージで、よく学習された状態は信用度が高い＝割引率を高く設定する、みたいなイメージです。
学習箇所のコード例は以下です。
with torch.no_grad():
target_val = self.parameter.rnd_target(n_state)
train_val = self.parameter.rnd_train(n_state)
error = ((target_val - train_val) ** 2).mean(dim=1)
# --- RNDの学習
loss_rnd = error.mean()
self.opt_rnd.zero_grad()
loss_rnd.backward()
self.opt_rnd.step()
# 最大値を保存
self.parameter.rnd_max = max(self.parameter.rnd_max, float(np.max(error.detach().cpu().numpy())))
# --- discountの計算
discount = 1 - error / self.parameter.rnd_max
正規化の方法ですが、最大値で割る事で0～1の範囲にしています。（errorはMSEの値なので必ず0以上の値）
結果は以下でちゃんと抑制されていますね。
......
. G.
. . X.
.P .
......
0(←) : 0.01638
1(↓) : 0.01708
2(→) : 0.01636
*3(↑) : 0.01967
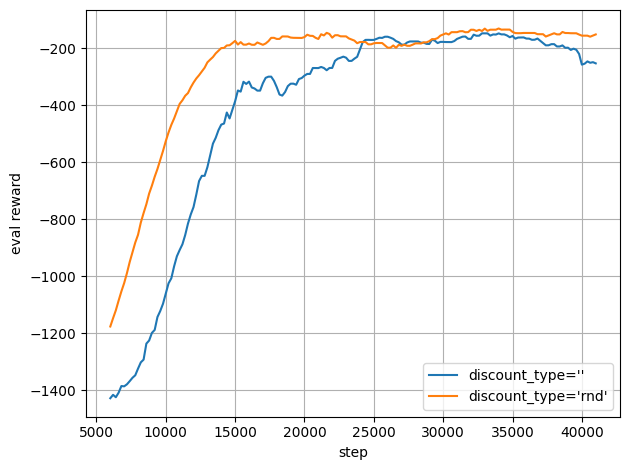
Pendulum-v1
Pendulum-v1をRNDありとなしで学習してみました。
Targetモデルの同期を100stepにしていますが、かなり安定して学習されている気がします。
終わりに
これに気づいたのはスーパーマリオブラザーズを学習させていた時でした。（ゴールにしか報酬がない）
ゴールにたどり着けていない状況でQ値を見てみたら、なぜか正の値になってたのが気付きでした。
（報酬が0と-1しかないので正になる事がありえない）
実際に試してみたら想像以上に初期値による影響が大きそうでした。
未知の状態は必ず間違った行動価値を持っているのでこの問題は結構重要な気がします。
個人的にはRND+割引率の自動調整を入れてみたら学習の速度がかなり上がった気がしました。
ただ大規模な検証はしていないのでどこまで効果があるかは分かりません。