この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。
DQNについては昔記事を書いていますが、知識も更新されているので改めて書いています。
DQN(Deep Q-Networks)
略称がネットスラングと重なったのは偶然らしいです。
また、時代背景的に初めて強化学習に深層学習(ニューラルネットワーク)の技術を採用して成果を出したことで有名になった手法となります。
Q学習の一番の問題点は、状態が離散かつ有限状態でしか表現できなかったことです。
例えば以下のマリオの位置を考えます。
マリオの座標が 1.1 と 1.11 はほぼ同じ状態とみて問題ありません。
しかし、Q学習ではこれが別の状態と認識されてしまいます。
こういう連続値は状態数が無限になるのでQ学習では学習ができません。
そこでQテーブルをニューラルネットワーク(NN)で近似して解決する事を考えます。
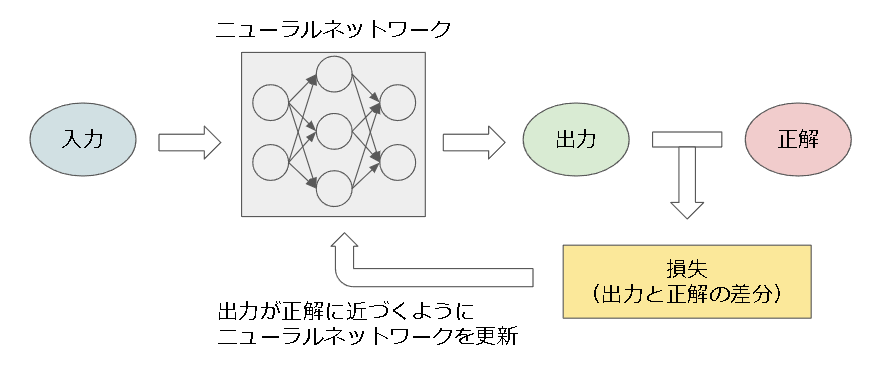
ニューラルネットワーク
ニューラルネットワークは他でもいろいろ解説があるので詳細は省いて概要だけになります。
簡単に言うと複雑なモデルを学習できる関数です。
出力結果と正解データの差を元に、正解データに出力が近づくように学習する手法がディープラーニングとなります。
行動価値Qのニューラルネットワークによる近似
Qテーブル(真の行動価値)をパラメータ $\theta$ を使って近似する事を考えます。
$$
Q_{\pi}^*(s, a) \approx Q_{\pi}(s, a; \theta)
$$
$Q_{\pi}^*$ は真の行動価値、$Q_{\pi}$ は予測した行動価値です。
近似したNNは Q-Network といいます。
Q学習の目的は予測値をサンプリング時の価値に近づける事でした。
ですので、Q-Network はサンプリング時の価値を教師データとして学習していきます。
損失を平均二乗誤差で考えた場合、損失関数は以下となります。
L_i(\theta_i) = E \Big[ \Big( Q'_{\mu}(s, a; \theta_i) - Q_{\pi}(s, a; \theta_i) \Big)^2 \Big]
$Q_{\pi}$ が予測値(NNの出力結果)、$Q_{\mu}^{'}$ はサンプリング時の価値(教師データ)で以下です。
Q_{\mu}^{'}(s, a; \theta_i) = r + \gamma \max_{a'} Q_\pi(s', a'; \theta_i)
$L_i(\theta_i)$ が最小になるようにパラメータ $\theta$ を更新(NNを学習)する手法がDQNです。
(それ以外はQ学習と同じです)
その他のテクニック
メインの部分はニューラルネットワークによる行動価値の近似ですが、それだけでは学習が安定しなく、安定させるためにいくつか細かいテクニックが使われています。
また、未来の話もすでに知っているのでさらなる改善手法がある場合はその名前も載せておきます。
1. Fixed Target Q-Network
Q-Network とは別に、全く同じ構造の Target Q-Network を用意し、
予測値はこの Target Q-Network から出力する手法です。
Target Q-Network のパラメータを $\theta^-$ と置いた場合、損失関数は以下となります。
$$
L_i(\theta_i) = E \Big[\Big( Q_{\mu}^{'}(s, a; \theta_i^-) - Q_{\pi}(s, a; \theta_i) \Big)^2 \Big]
$$
Target Q-Network は一定間隔毎に Q-Network と同期します。
これをやる理由を2つ紹介します。
-
論文に書かれている理由
$Q(s_t, a_t)$ を増加方向に更新すると多くの場合 $Q(s_{t+1}, a)$ も増加します。(パラメータを共有しているので)
その場合、予測値が増加するので $Q(s_t, a_t)$ が更に増加します。
これを繰り返すと値が発散したり、ポリシーの変動が起こる可能性があります。
そこで古いパラメータを使用して予測値を出すことで、これに遅延が発生し、発散や振動が発生する可能性がかなり低減されるとの事です。 -
私なりの解釈
更新式で更新したいのは予測値側の $Q_{\pi}$ で教師データ側である $Q_{\mu}^{'}$ は変わってほしくありません。
しかし、同じNNを使うとパラメータが共有されているので $Q_{\pi}$ が変わると $Q_{\mu}^{'}$ も変わります。
教師データがころころ変わると学習は安定しなくなるので好ましくありません。
ですので、教師データを固定させたいために別パラメータのNNを用意したのだと思います。
ただ、古いパラメータのままだとポリシーが更新されない(真の行動価値に近づかない)ので定期的に同期する必要があります。
※RainbowのDouble DQNで改良されています
2. Error clipping
損失関数を、-1から1の範囲では平均二乗誤差を使い、それ以外の範囲は平均絶対誤差を使う手法です。
平均絶対誤差は外れ値に強いというメリットがある一方で、微分値が一定なので細かい微調整ができないというデメリットがあります。
その点、平均二乗誤差は微分できるので最後の微調整が可能です。(ゆっくり近づける)
しかし平均二乗誤差は外れ値に弱い(二乗するので過敏に反応する)というデメリットがあります。
そこで、損失誤差が大きい所(-1~1の外)では平均絶対誤差を使い、その中では平均二乗誤差を使う事でいいとこ取りをしている手法となります。
また、この役割をする損失関数がすでにあり、Huber損失関数といいます。
参考
・Huber損失(wikipedia)
・損失関数のまとめ (Huber,Log-Cosh,Poisson,CustomLoss,MAE,MSE)
3. Experience Replay
学習に使う経験ですが、一度バッファに格納してその中からランダムに取り出して学習に使います。
これをやる大きな理由は以下です。
-
1、経験を使いまわせるのでサンプル効率があがる
同じ経験を学習に何回も使えるためサンプル効率が上がります。(Q学習では一度学習に使うと破棄していた) -
2、時系列の相関をなくす
経験は時系列順に入ってくるので強い相関があります。
強い相関がある(偏った)教師データでNNを学習させると汎化性能が失われます。
ですので、ランダムに選ぶことでこの相関を失わせています。 -
3、負のフィードバックループを回避する
例えば左のアクションを選ぶパラメータの場合、左側からの経験が多くなります。
次に右側にアクションが変化すると今度は右側ばかりの経験になってしまいます。
2と同様に偏った経験を教師データにすると汎化性能が失われるのでよくないです。
また、偏った経験がまだ正しいものならいいのですが、局所解など間違っている場合、その経験のみが学習されて抜け出せなくなるという負のフィードバックループが発生する可能性があります。
Experience Replay を使うとこの経験の偏りがある程度平坦化されて学習が安定します。
※Rainbow の Priority Experience Replayという手法で改良されています
4. Annealing e-greedy
探索に使用しているε-greedy法ですが、最初は探索を優先し、学習が進む毎に探索率を徐々に下げていくというものです。
具体的には探索率 $\epsilon$ をstep毎に線形に減らしていきます。
※Ape-Xにて固定値に戻されています
※Agent57のメタコントローラーでさらに改善されています
5. window length
強化学習の基礎でやりましたが、想定している環境はマルコフ決定過程で、次の状態(の確率)は現在の状態と行動によって決まるというものです。
しかし、現実は過去の状態まで見ないと次の状態が分からない場合があります。
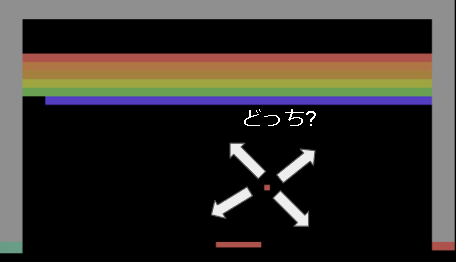
例えば玉の速さなどです。
(下の画像では次にどの方向に玉が移動するかわからない)
直近数フレームを入力状態とすることでこれを暫定的に解決しています。
※R2D2でLSTMを取り入れることで本格的に解決しています
6. Reward clipping
Atariでは報酬のスケールがゲームで大きく違います。(例えばPongは玉を入れると1点だがGalaxianは敵を倒すと30点)
そこで正を1、負を-1、0はそのままと報酬を固定する手法が Reward clipping です。
これにより全てのゲームで同じ学習率を使用できるようになったとの事です。
ただ、報酬の差(例えば1と2の違い)が区別できなくなるのでエージェントのパフォーマンスに影響が出る可能性があります。
※R2D2でRescaling関数を導入し、本格的に解決しています
7. Frame skip
Atari2600は60fpsです。(1秒間に60step)
これでは時間がかかりすぎるので1stepの時間を長くしようという考えがFrame skipです。
具体的にはそのフレームの間は同じアクションを実行しましょうというものです。
DQNの論文では 4 frame 同じアクションを実行しています。
(1秒15stepになる計算です)
8. Image preprocessor
Atariの入力は210×160×3chのカラー画像ですが、計算を簡単にするために前処理を施します。
内容はグレー化して84×84にリサイズします。
実装
関係ある個所を抜粋して書いています。
フレームワーク上の実装はgithubを見てください。
Config(ハイパーパラメータ)
ハイパーパラメータは以下です。(論文の値です)
@dataclass
class Config(DiscreteActionConfig):
discount: float = 0.99 # 割引率
lr: float = 0.00025 # 学習率
window_length: int = 4 # 状態とするフレーム数
batch_size: int = 32 # バッチサイズ
target_model_update_interval: int = 10000 # Target Q-network の同期間隔
enable_reward_clip: bool = True # 報酬のclipping
# Annealing e-greedy
initial_epsilon: float = 1.0 # 初期ε
final_epsilon: float = 0.1 # 最終ε
exploration_steps: int = 1_000_000 # 最終εになるステップ数
test_epsilon: float = 0 # テスト時のε
# Experience Replay
capacity: int = 1_000_000
memory_warmup_size: int = 50_000 # 学習を始めるまでに貯める経験数
RemoteMemory
Experience Replay を実装します。
経験を貯めておいてランダムに取り出します。
経験数は上限を決めておき、上限になったら古いものから削除していきます。
これはまんまキューのデータ構造なので collections.deque を使って実装しています。
from collections import deque
import random
class RemoteMemory(RLRemoteMemory):
def __init__(self, *args):
super().__init__(*args)
def init(self, capacity: int):
self.memory = deque(maxlen=self.config.capacity)
def length(self) -> int:
return len(self.memory)
# 経験の追加
def add(self, batch: Any):
self.memory.append(batch)
# ランダムにバッチ数サンプリング
def sample(self, batch_size: int):
return random.sample(self.memory, batch_size)
Parameter
Qネットワークを定義します。
下のサンプルコードは前処理後のAtariの画像が入力された場合となります。
(フレームワークはそれ以外の場合も対応しています)
from tensorflow.keras import layers as kl
class _QNetwork(keras.Model):
def __init__(self, config):
super().__init__()
# 入力は (window_length, width, height) の形
input_shape = (4, 84, 84)
in_state = c = kl.Input(shape=input_shape)
# 画像形式にするために (len, w, h) -> (w, h, len) に変更
c = kl.Permute((2, 3, 1))(c)
# DQNの画像処理レイヤー
c = kl.Conv2D(32, (8, 8), strides=(4, 4), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (4, 4), strides=(2, 2), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (3, 3), strides=(1, 1), padding="same", activation="relu")(c)
# flatten (w, h, ch) -> (flat_num)
c = kl.Flatten()(c)
# 隠れ層
c = kl.Dense(512, activation="relu")(c)
# 出力層、config.nb_actionsはアクション数
c = kl.Dense(config.nb_actions)(c)
self.model = keras.Model(in_state, c)
def call(self, state):
return self.model(state)
class Parameter(RLParameter):
def __init__(self, *args):
super().__init__(*args)
# Q-network と Target Q-network
self.q_online = _QNetwork(self.config)
self.q_target = _QNetwork(self.config)
Trainer
学習部分です。
optimizer ですが、論文ではRMSPropを使用しています。
ただ実装では RMSProp の改良版で現在のデファクトスタンダードになりつつある Adam を採用しました。
・【決定版】スーパーわかりやすい最適化アルゴリズム -損失関数からAdamとニュートン法-
・深層学習の最適化アルゴリズム
またモデルの更新箇所はTensorflowの公式ガイドを参照してください。
class Trainer(RLTrainer):
def __init__(self, *args):
super().__init__(*args)
# Adam optimizer
self.optimizer = keras.optimizers.Adam(learning_rate=self.config.lr)
# Huber loss
self.loss = keras.losses.Huber()
def train(self):
# 学習はある程度経験がたまった後にします
if self.remote_memory.length() < self.config.memory_warmup_size:
return {}
# メモリーからランダムにバッチ数分経験を取り出します。
batchs = self.remote_memory.sample(self.config.batch_size)
# 長くなるので学習部分は別関数にしました。
loss = self._train_on_batchs(batchs)
# 一定回数ごとに実行
if self.train_count % self.config.target_model_update_interval == 0:
# Target Q-network を Q-network に同期させる
self.parameter.q_target.set_weights(self.parameter.q_online.get_weights())
self.train_count += 1
return {"loss": loss}
def _train_on_batchs(self, batchs):
# データ整形
states = []
actions = []
n_states = []
for b in batchs:
# state は 0~3 が今の状態、1~4 が次の状態
states.append(b["states"][:-1])
n_states.append(b["states"][1:])
actions.append(b["action"])
states = np.asarray(states)
n_states = np.asarray(n_states)
# next Q を計算、結果は n_q[batch][action] という形で入っている
n_q = self.parameter.q_online(n_states).numpy()
n_q_target = self.parameter.q_target(n_states).numpy()
# 教師データ(サンプリングして得た価値)を計算
target_q = np.zeros(len(batchs))
for i, b in enumerate(batchs):
reward = b["reward"]
done = b["done"]
if done:
gain = reward
else:
# 次の状態の予測値は Target Q-network を使う
gain = reward + self.config.discount * np.max(n_q_target[i])
target_q[i] = gain
# 勾配を計算
with tf.GradientTape() as tape:
q = self.parameter.q_online(states)
# 現在選んだアクションのQ値
actions_onehot = tf.one_hot(actions, self.config.action_num)
q = tf.reduce_sum(q * actions_onehot, axis=1)
# target_q を教師データとして損失を計算
loss = self.loss(target_q, q)
# パラメータを更新
grads = tape.gradient(loss, self.parameter.q_online.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.parameter.q_online.trainable_variables))
return loss.numpy()
Worker
内容毎に抜粋して書いています。
4. Annealing e-greedy
epsilon を毎step計算する以外はQ学習のε-greedyと変わりません。
class Worker(TableWorker):
def __init__(self, *args):
super().__init__(*args)
# 最初と最後のepsilon
self.initial_epsilon = self.config.initial_epsilon
self.final_epsilon = self.config.final_epsilon
# 1stepあたりのepsilon増加数、使いやすいように事前に計算
self.epsilon_step = (
self.initial_epsilon - self.final_epsilon
) / self.config.exploration_steps
# stepの変数
self.step = 0
def call_policy(self, _state: np.ndarray) -> int:
if self.training:
# epsilonを計算する
epsilon = self.initial_epsilon - self.step * self.epsilon_step
if epsilon < self.final_epsilon:
epsilon = self.final_epsilon
else:
# テスト時は別のepsilonを使用
epsilon = self.config.test_epsilon
if random.random() < epsilon:
# epsilonより低いならランダム
action = random.choice([a for a in range(self.config.action_num) if a not in invalid_actions])
else:
# 今の状態(直近の4frameを使用)
state = self.recent_states[1:]
# Q値を出す
q = self.parameter.q_online(np.asarray([state]))[0].numpy()
# 最大値を選ぶ(複数はほぼないので無視)
action = int(np.argmax(q))
self.action = action
return action
def call_on_step(
self,
next_state: np.ndarray,
reward: float,
done: bool,
next_invalid_actions: List[int],
):
# 計算用にstepを数える
self.step += 1
5. window length & 6. Reward clipping
過去の状態を覚えておく必要があるので少しめんどくさいです。
また、予測に使う状態はどのstepでも過去4step分の状態が必要のため、ダミー状態を用意し、エピソード外の状態を表現しています。
class Worker(TableWorker):
def __init__(self, *args):
super().__init__(*args)
# エピソード外のダミー状態(ダミー状態は0.0)
self.dummy_state = np.full(self.config.observation_shape, 0.0)
def call_on_reset(self, state: np.ndarray) -> None:
# 過去の状態を保存する用の変数
# +1しているのは次の状態用(0~3が今の状態、1~4が次の状態)
self.recent_states = [self.dummy_state for _ in range(self.config.window_length + 1)]
# 初期状態を格納
self.recent_states.pop(0)
self.recent_states.append(state)
def call_policy(self, _state: np.ndarray) -> int:
# policyで使う状態
state = self.recent_states[1:]
(実際にactionを選ぶコードは 4. Annealing e-greedy を参照)
return action
def call_on_step(self, next_state: np.ndarray, reward: float, done: bool):
# 状態を格納
self.recent_states.pop(0)
self.recent_states.append(next_state)
if not self.training:
return {}
# reward clip
if self.config.enable_reward_clip:
if reward < 0:
reward = -1
elif reward > 0:
reward = 1
else:
reward = 0
# 経験を送る
batch = {
"states": self.recent_states[:],
"action": self.action,
"reward": reward,
"done": done,
}
self.remote_memory.add(batch)
return {}
7. Frame skip
アルゴリズム側ではなくフレームワーク内で実装しています。
実装ポイントを抜き出すと以下です。
# 環境側が1step実行するタイミング
def step(self, action, skip_frames: int = 0):
# 1step実行
state, reward, done, _ = self.env.step(action)
# skip frame の間は同じアクションを繰り返す
for _ in range(skip_frames):
state, skip_reward, done, _ = self.env.step(action)
# skip frame 中の報酬を加算する
reward += skip_reward
# skip frame 中に終了したら終了する
if self.done:
break
8. Image preprocessor
こちらもアルゴリズム側ではなくフレームワーク内で実装しています。
実装ポイントを抜き出すと以下です。(OpenCVで処理しています)
import cv2
# 状態を変更する関数
def process_observation(self, observation):
observation = np.asarray(observation)
# (210, 160, 3) -> (210, 160) にグレー化
observation = cv2.cvtColor(observation, cv2.COLOR_RGB2GRAY)
# (210, 160) -> (84, 84)
observation = cv2.resize(observation, self.resize)
# 0~255 -> 0~1 の範囲に正規化
observation = observation.astype(np.float32)
observation /= 255
return observation
実行
Atariは時間がかかりすぎるので(論文内だと5000万フレーム,約38日間学習してます)Open AI Gymで提供されているPendulum-v1を学習させてみました。
実行に使ったコードは github を見てください。
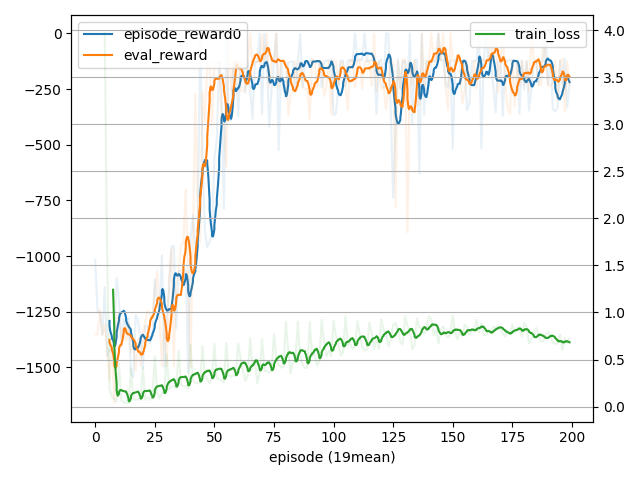
- 学習結果
- 学習過程
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 1, 3)] 0
flatten (Flatten) (None, 3) 0
dense (Dense) (None, 64) 256
dense_1 (Dense) (None, 64) 4160
dense_2 (Dense) (None, 5) 325
=================================================================
Total params: 4,741
Trainable params: 4,741
Non-trainable params: 0
_________________________________________________________________
### env: Pendulum-v1, rl: DQN, max episodes: 200, timeout: -1.00s, max steps: -1, max train: -1
22:39:44 5.01s 1011st( 5ep) 12tr 3.0m(remain), -1352.0 -1202.232 -1017.4 re(-1321.256 eval), 200.0 step, 0.93s/ep, 0.000s/tr, 1000 mem(19.2% PC)|loss 3.967|sync 1.000
22:39:54 15.03s 1514st( 7ep) 515tr 13.1m(remain), -1452.3 -1434.830 -1417.3 re(-1487.593 eval), 200.0 step, 4.09s/ep, 0.016s/tr, 1400 mem(19.0% PC)|loss 0.914|sync 1.000
22:40:14 35.04s 2492st( 12ep) 1493tr 12.8m(remain), -1429.4 -1292.861 -1098.2 re(-1395.373 eval), 200.0 step, 4.08s/ep, 0.015s/tr, 2400 mem(19.1% PC)|loss 0.152|sync 1.401
22:40:54 1.3m 4451st( 22ep) 3452tr 12.1m(remain), -1544.8 -1370.551 -1264.2 re(-1387.850 eval), 200.0 step, 4.07s/ep, 0.015s/tr, 4400 mem(19.0% PC)|loss 0.132|sync 2.901
22:42:14 2.6m 8396st( 41ep) 7397tr 10.8m(remain), -1523.0 -1183.256 -920.9 re(-1185.856 eval), 200.0 step, 4.08s/ep, 0.015s/tr, 8200 mem(19.0% PC)|loss 0.253|sync 5.791
22:44:55 5.3m 16201st( 81ep) 15202tr 8.1m(remain), -970.0 -364.134 -1.2 re(-233.645 eval), 200.0 step, 4.10s/ep, 0.016s/tr, 16200 mem(19.0% PC)|loss 0.417|sync 11.701
22:50:15 10.6m 31812st( 159ep) 30813tr 2.8m(remain), -737.6 -174.425 -0.8 re(-195.772 eval), 200.0 step, 4.10s/ep, 0.016s/tr, 31800 mem(19.2% PC)|loss 0.720|sync 23.501
22:53:02 13.4m 40000st( 200ep) 39001tr 0.00s(remain), -516.5 -186.904 -0.9 re(-167.218 eval), 200.0 step, 4.09s/ep, 0.016s/tr, 40000 mem(19.0% PC)|loss 0.775|sync 35.391
Average reward for 20 episodes: -180.68542963033252
参考文献
・Playing Atari with Deep Reinforcement Learning(論文)
・Human-level control through deep reinforcement learning(論文)