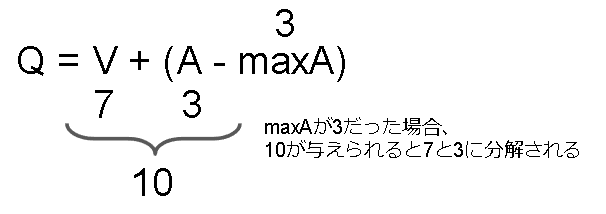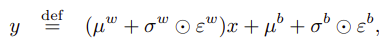この記事は自作している強化学習フレームワーク SimpleDistributedRL の解説記事です。
Rainbowについては昔記事を書いていますが、知識も更新されているので改めて書いています。
Rainbow
Rainbow は DQN 以降に登場したいろいろな改良手法を全部乗せしたアルゴリズムです。
6種類+DQN なので Rainbow とついています。
また、本記事では Multi-Step learning について Retrace を導入しています。
Rainbow: Combining Improvements in Deep Reinforcement Learning(論文)
1. Double Q-learning
参考
・Deep Reinforcement Learning with Double Q-learning (論文)
・Double Q-learning (論文)
Double Q-learning の目的は過大評価を防ぐことです。
Q学習では予測値に次の状態の最大価値を使っています。
もしこの最大価値が間違っていた場合、間違った価値(過大に評価された価値)が伝播されてしまいます。
無限回繰り返せば間違った価値は修正されるので問題ないように見えますが、過大評価による学習の遅延はかなり影響が大きいそうです。
過大評価が起こる原因は、アクションの選択と評価に同じ値を使用しているからです。
これを防ぐために選択と評価を切り離したものがDouble Q-learningとなります。
ではこれを実現するためにどうするかというと、2つのQ関数を用いて別々に学習させ、片方を選択にもう片方を評価に使用するというものです。
ここまでが Double Q-learning の前提になります。
ここからDQNに追加する場合を考えます。
DQNには Target Q-Network という別のQ関数が既に存在しているのでこれを使います。
(Target Q-Network は選択と評価を完全に分離しているわけではない点に注意)
(完全に分離しているわけではないが、自然な形で導入できるので採用しているとの事)
アクションの選択に Q-Network、評価値に Target Q-Network を用いた手法が Double Q-learning(正確には Double DQN)になります。
式としては以下となります。
\begin{align}
Q'_{\mu}(s, a; \theta_i^-) &= r + \gamma \max_{a'} Q_\pi(s', a'; \theta_i^-)\\
&↓\\
Q'_{\mu}(s, a; \theta_i^-)^{DoubleDQN} &= r + \gamma Q_\pi(s', argmax_{a'}Q_\pi(s', a'; \theta_i) ; \theta_i^-)
\end{align}
2. Prioritized Experience Replay
参考
・Prioritized Experience Replay (論文)
・Let’s make a DQN: Double Learning and Prioritized Experience Replay
・Prioritized Experience Replay
学習する経験ですが、ランダムに選ぶよりはより良い経験を何回も学習した方が効率がいいです。
そこでTD誤差を基準に優先順位付けして経験を取り出す手法を Prioritized Experience Replay といいます。
TD誤差は以下でした。
$$
\delta = Q_{\mu}^{'}(s, a; \theta_i^{-}) - Q_{\pi}(s, a; \theta_i)
$$
これを元に優先度(Priority)を決めて、優先度を元に確率で経験を取り出します。
(固定ではなく確率で取り出すのは Experience Replay の元の役割である、経験の偏りをなくすためです)
TD誤差から優先度を決める方法は2つあります。(後述します)
各経験の優先度を $p_i$ と置いた場合、確率 $P(i)$ は以下で計算されます。
$$
P(i) = \frac{p_i^\alpha}{ \sum_k p_k^\alpha}
$$
$\alpha$ は優先度の反映率で、0なら普通の Experience Replay (完全ランダム)になります。
Proportional Prioritization
TD誤差の値に比例して、優先度を決める方法です。
$$
p_i = |\delta| + \epsilon
$$
$\epsilon$ は0を回避するための小さな定数です。
優先度が大きければその分選ばれる確率が多くなる形です。
Rank-Based prioritization
順位に比例して優先度を決める方法です。
$$
p_i = \frac{1}{rank(i)}
$$
$rank(i)$ は、経験$i$の $|\delta|$ での順位を表します。
Rank-Based はTD誤差の差によらずに確率が決まるので、Proportional よりもロバストなモデルが期待できるとの事です。
(ただ論文内での比較では2つの手法にそこまで大きな差はでなかったようです)
重要度サンプリング(Importance Sampling)
期待値の計算に使うサンプリングの確率が変わった場合、これを修正しないと正しい期待値になりません。
(確率に依存した回数分、サンプリングした値にバイアスがかかってしまう)
これを修正する手法が重要度サンプリング(IS)になります。
計算式は以下です。
$$
w_i = \Big( \frac{1}{N} \frac{1}{P(i)} \Big)^{\beta}
$$
$$
w_i \leftarrow w_i \frac{1}{\max_j w_j}
$$
$N$ は今ある全経験の数です。
$\beta$ はISを反映させる割合です。(0でISなし、1で最大の反映)
またISによる急激な変化を避けるため、 $w_i$ は最大値で正規化して、必ず下方向の修正になるようにしています。
β について
ISによる修正ですが、本当に重要なのは学習の後半です。
最初の方ではそもそもQ値が定まっていないので、バイアスがかかったサンプルでも問題になりません。
ですので、$\beta$ は学習の前半では低い値からスタートして徐々に増やし、後半に1にするという手法を取っています。
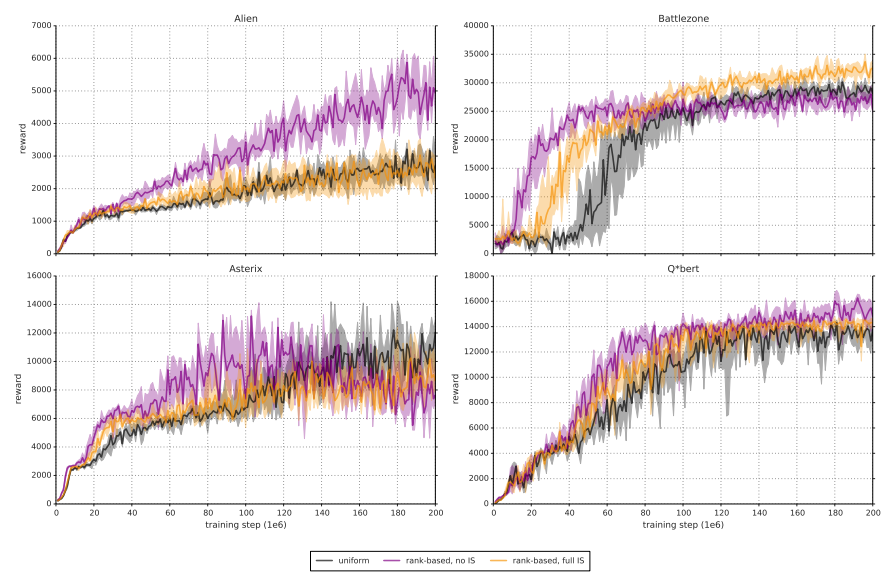
論文内の比較結果は以下です。
黒がただのメモリ、紫がISなしのRankBaseメモリ、オレンジがISありのRankBaseメモリで比較した結果です。
ISを導入すると積極的な学習が行われなくなるので学習速度が遅くなる一方、早期収束の危険性(局所解にはいってしまう)が低くなり、最終的な結果が良くなるとの事です。
(けどグラフを見るとあまり差がないような…、ゲームに依存するところが大きいような気がします)
3. Dueling networks
参考
・Dueling Network Architectures for Deep Reinforcement Learning(論文)
・Advantage Updating Applied to a Differential Game
・ADVANTAGE UPDATING
・FlappyBird で強化学習の練習 その3: DQN + Dueling network
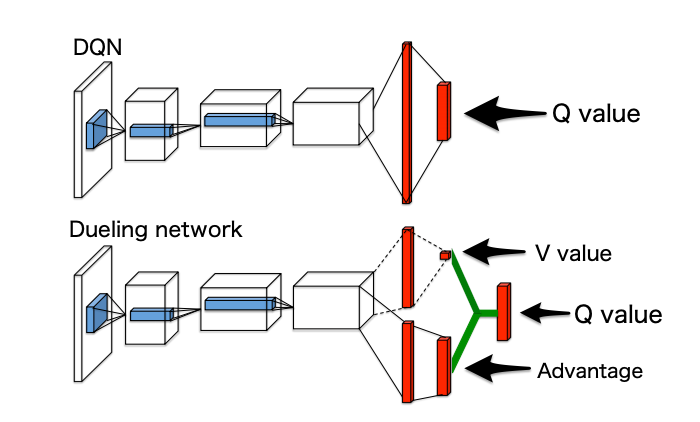
ある行動に対して行動価値から状態価値を引いたものを新しく Advantage として定義します。
$$
A_\pi(s,a) = Q_\pi(s,a) - V_\pi(s)
$$
Advantageは行動価値から状態価値を引いているので、状態によらない真に行動のみで影響する価値を表しています。
言い換えると次の行動価値について、そもそも状態価値が大きく行動は影響ないのか、状態価値は低いが特定の行動で一気に価値があがるのか、を判断できるようになります。
元の論文(Advantage Updating Algorithm)では単純にQを学習するよりもVとAに分けて学習したほうが収束が早くなる旨が記載されています。
ニューラルネットワークへの適用
Q-network をVとAに分けて学習する事を考えます。
$$
Q_\pi(s,a;\theta) = V_\pi(s;\theta) + A_\pi(s,a;\theta)
$$
ここで学習用に与えられる値はQ値になるので、VとAの見分けが付きません。
これを解決するために、選ばれた行動を最適な行動と仮定し、Advantage の推定値が 0 になるように学習させます。
$$
Q_\pi(s,a;\theta) = V_\pi(s;\theta) + \Big( A_\pi(s,a;\theta) - \max_{a'} A_\pi(s, a'; \theta) \Big)
$$
多分こういうことだと思います。
ただ実際には最大値ではなく平均値を使います。
$$
Q_\pi(s,a;\theta) = V_\pi(s;\theta) + \Big( A_\mu(s,a;\theta) - \frac{1}{N_{actions}} \sum_{a'} A_\mu(s, a'; \theta)\Big)
$$
平均値を使うと予測されるA値が最適値(Q値最大の方策: $A_\pi$)ではなく、探索に使った方策(ε-greedyの方策: $A_\mu$)になり、元の意味から外れてしまいます。
しかし、それ以上に学習が安定するという利点があるようです。
(自信はないですが、多分この解釈で合っていると思います)
学習が安定する理由は、多分平均値の方が急激な値の変化が少ないからだと思います。
Note: Advantageの期待値
ちなみにAdvantageの期待値は0になります。
\begin{align}
E_\pi \big[ A_\pi(s,a) \big] &= \sum_a \pi(s,a) A_\pi(s,a) \\
&= \sum_a \pi(s,a) Q_\pi(s,a) - \sum_a \pi(s,a) V_\pi(s) \\
&= V_\pi(s) - V_\pi(s) \\
&=0
\end{align}
2行目の左辺は $V_\pi(s) = \sum_a \pi(s,a) Q_\pi(s, a)$ です。
右辺は $\pi(s,a)$ が確率を表しており、$\sum_a \pi(s,a) = 1$ になるのでそのまま変化しません。
期待値が0という事は、あるアクションがプラスになると他のアクションがマイナスになるという事です。
Advantage という名前の通り、良いアクションを表す指標になっていますね。
4. Multi-step learning (Retrace)
参考
・Multi-step Reinforcement Learning: A Unifying Algorithm(論文)
・Safe and Efficient Off-Policy Reinforcement Learning(論文)
Multi-step learning はQ学習で書いた通り、予測値に未来の報酬を使う手法です。
2stepの例は以下です。
\begin{align}
Q_{\mu}^{'}(s_t,a_t) =& r_{t+1} + \gamma r_{t+2} + \gamma^2 \max_{a_{t+2}} Q_{\pi}(s_{t+2}, a_{t+2}) \\
\delta(s_t,a_t) =& Q_{\mu}^{'}(s_t,a_t) - Q_{\pi}(s_{t}, a_{t})
\end{align}
ただ、学習したい方策と探索に使う方策が違う(Off-Policy)場合はこの式だと問題が発生します。
詳細は前書いた記事があるのでそちらを参照してください。
やっと理解できたと思うRetraceについて丁寧に解説【強化学習】
上記数式を修正して下記の通り学習する必要があります。
\begin{align}
\delta(s_t,a_t) =& \delta'(s_t,a_t) \\
& + c_{t} \gamma \delta'(s_{t+1},a_{t+1}) \\
& + c_{t} c_{t+1} \gamma^2 \delta'(s_{t+2},a_{t+2}) \\
& + c_{t} c_{t+1} c_{t+2} \gamma^3 \delta'(s_{t+3},a_{t+3}) \\
& + \cdots \\
& + (\prod_{s=0}^{k-1} c_{t+s} ) \gamma^k \delta'(s_{t+k},a_{t+k}) \\
=& \delta'(s_t,a_t) + \sum_{s=1}^{k} \gamma^s (\prod_{s=0}^{k-1} c_{t+s}) \delta'(s_{t+k},a_{t+k}) \\
=& \delta'(s_t,a_t) + c_{t} \gamma \delta(s_{t+1},a_{t+1}) \\
\end{align}
ここで $\delta'$ は従来のTD誤差で以下となります。
$$
\delta'(s_t,a_t) = r_{t+1} + \gamma \max_{a_{t+1}} Q_{\pi}(s_{t+1}, a_{t+1}) - Q_{\pi}(s_t, a_t)
$$
また $c_t$ は以下です。
$$
c_t = \lambda \min(1, \frac{\pi(a_t|s_t)}{\mu(a_t|s_t)})
$$
$\lambda$ は任意の定数です。
コラム: なぜRainbowはRetraceを使っていないのに学習できるのか?
StackOverflow に質問があったので乗せてみました。
Answerをまとめると以下です。
-
multistep数が大きくありません(3stepです)
step数が少なければOff-policyによる影響は少なくて済みます。 -
報酬が貰えるタイミングがゲーム終了時に集中しており、影響があるタイミングが限定的です。
-
探索率が小さい
(小さいと $\pi$ と $\mu$ の差がなくなります)
(0.01~0.001あたりが使われています) -
ポリシーがゆっくりと変化する。
収束まで100万フレームもかかり、経験メモリと比べてもすごく大きい。
といった感じでした。
5. Distributional RL
これは別の記事にする予定です。
本フレームワークでは Rainbow に Distributional RL を組み込んでいません。
これは Retrace + Distributional RL の実装がかなり複雑になりそうだったからです。
そこまで時間をかけて実装する利点がなかったので別実装にしています。
6. Noisy Nets
参考
・Noisy Networks for Exploration(論文)
R2D2以降で採用されていないのでここはさらっと説明します。
Q学習において、ε-greedy法のε(探索率)は重要なハイパーパラメータにも関わらず設定が難しい問題がありました。
そこで探索率を含めてNNで学習しようという考えがNoisy Networksです。
具体的にはアクション側に含めていたノイズ(ε-greedy法だとε)を止め、NN内にノイズを発生させ、ノイズの発生頻度を含めて学習させます。
NNの線形層の1ユニットは以下で計算されました。
$$
y = wx + b
$$
$w$ と $b$ が学習されるパラメータです。
これを以下のように置き換えます。
$\mu$ と $\sigma$ が学習されるパラメータで、$\epsilon$ が標準正規分布表に従った乱数です。
$w$ と $b$ を乱数(ノイズ)に置き換える事で探索を促しています。
実装
関係ある箇所を抜粋して書いています。
フレームワーク上の実装はgithubを見てください。
Config(ハイパーパラメータ)
DQNのハイパーパラメータは省略します。
新しく増えたパラメータは以下です。
# double dqn
enable_double_dqn: bool = True
# Priority Experience Replay
capacity: int = 1_000_000
memory_name: str = "ProportionalMemory"
memory_warmup_size: int = 80_000
memory_alpha: float = 0.5
memory_beta_initial: float = 0.4
memory_beta_steps: int = 1_000_000
# DuelingNetwork
enable_dueling_network: bool = True
dueling_network_type: str = "average"
# Multi-step learning
multisteps: int = 3
retrace_h: float = 1.0
# noisy dense
enable_noisy_dense: bool = False
1. Double Q-learning
DQNのTrainerで予測値を計算していた部分を変更します。
DQNは以下でした。
# 次の状態の予測値は Target Q-network をそのまま使う
gain = reward + self.config.gamma * np.max(n_q_target[i])
Target Q-network をそのまま使うのではなく、
Q-network で使うアクションを選び、値は Target Q-network から使うように変更します。
# 予測に使うアクションは Q-network から選択
next_action_idx = np.argmax(n_q)
# 予測値は Target Q-network を使う
gain = reward + self.config.gamma * n_q_target[i][next_action_idx]
2. Prioritized Experience Replay
メモリに格納されている全経験に対して確率を計算する必要がありますが、メモリサイズNになるべく依存しない実装をする必要があります。(論文だとN=1_000_000になる)
操作としては add/sample/update が毎ステップ呼ばれます。
ですので、これらがなるべく早くなるように実装する必要があります。
呼び出し側ですが、Trainer部分は以下です。
td_error を計算してupdateに渡す必要があるので、そこを追加しています。
(後 weights を掛ける必要もあります)
class Trainer(RLTrainer):
def train(self):
# メモリに一定貯まるまで学習しない
if self.remote_memory.length() < self.config.memory_warmup_size:
return {}
# batch_size分経験を取得
# Annealing beta用に学習回数(train_countも必要)
indices, batchs, weights = self.remote_memory.sample(self.train_count, self.config.batch_size)
# 学習時にlossを計算する箇所で weights を掛ける必要あり
td_errors = (学習)
# 学習した結果を元に経験の優先度を更新
self.remote_memory.update(indices, batchs, td_errors)
self.train_count += 1
次に Worker ですが、こちらも td_error を計算させます。
これは分散学習用の処理なので逐次学習では不要です。(逐次学習では新規の経験は必ず学習されるように最大の優先度が割り当てられる)
class Worker(TableWorker):
def call_on_step(self, next_state: np.ndarray, reward: float, done: bool):
if self.config.memory_name == "ReplayMemory":
td_error = None # ReplayMemory は優先度を使わない
elif not self.distributed:
td_error = None # 逐次処理は優先度は最大
else:
q = 現ステップでのQ値を計算
target_q = 現ステップでのTargetQ値を計算
td_error = target_q - q
# 経験を送る
batch = {
"states": self.recent_states[:],
"action": self.action,
"reward": reward,
"done": done,
}
self.remote_memory.add(batch, td_error)
Proportional Prioritization
SumTreeというデータ構造を用いて実装しています。(フレームワーク上のコード)
アルゴリズムの解説は本記事では割愛いたします。
以下参考文献を見てください。
参考
・Prioritized Experience Replayのsum-treeの実装
・Sum Treeで重みにそってサンプリングする(Python実装)
・Let’s make a DQN: Double Learning and Prioritized Experience Replay
SumTreeを使った場合の速さは以下です。
| add | O(log(N)) |
| sample | O(log(N)) |
| update | O(log(N)) |
Rank-Based prioritization
あまりいい実装方法は見当たりませんでした。
論文をベースに自作しています。(フレームワーク上のコード)
ソート済み配列を用意し、それを元に確率を計算しています。
配列の追加と削除はPython公式ライブラリのbisectを使用し、サンプリングにはnp.random.choiceを使っています。(自作するより早かった…)
速さは以下です。
| add | O(N) | bisectによる挿入です。検索で O(log(N))、追加でO(N) かかります |
| sample | O(N log(N))ぐらい? + O(N) | ライブラリ実装なので正確には分かりません…、削除にO(N)かかっています |
| update | O(N) | bisectによる挿入です。 |
また経験ですが、古い経験ではなく優先度が一番小さい経験から破棄されていきます。
(ここは更新するかもしれません)
3. Dueling networks
NNの出力層を変更します。
(図はFlappyBird で強化学習の練習 その3: DQN + Dueling networkより引用)
DQNは以下でした。
# 入力層
input_shape = (config.window_length, 84, 84)
in_state = c = kl.Input(shape=input_shape)
c = kl.Permute((2, 3, 1))(c)
c = kl.Conv2D(32, (8, 8), strides=(4, 4), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (4, 4), strides=(2, 2), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (3, 3), strides=(1, 1), padding="same", activation="relu")(c)
c = kl.Flatten()(c)
# 隠れ層
c = kl.Dense(512, activation="relu")(c)
# 出力層
c = kl.Dense(config.nb_actions)(c)
# モデル
model = keras.Model(in_state, c)
隠れ層+出力層をV+Aの形に変更します。
# 入力層
input_shape = (config.window_length, 84, 84)
in_state = c = kl.Input(shape=input_shape)
c = kl.Permute((2, 3, 1))(c)
c = kl.Conv2D(32, (8, 8), strides=(4, 4), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (4, 4), strides=(2, 2), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (3, 3), strides=(1, 1), padding="same", activation="relu")(c)
c = kl.Flatten()(c)
# value
v = kl.Dense(512, activation="relu")(c)
v = kl.Dense(1)(v)
# advance
adv = kl.Dense(512, activation="relu")(c)
adv = kl.Dense(nb_actions)(adv)
# v + a - mean_a
c = v + adv - tf.reduce_mean(adv, axis=1, keepdims=True)
# モデル
model = keras.Model(in_state, c)
最後の部分ですが tf.reduce_mean ここの勾配を流すか止める(定数か)が分かっていません。
元の意味から考えると止めたほうが正しそうですが、止めても1step遅れるだけなので流しても変わらないような気がします。
止める場合は以下です。
c = v + adv - tf.stop_gradient(tf.reduce_mean(adv, axis=1, keepdims=True))
ちなみにネットの実装をいくつか見た感じは以下です。
・止めてます(https://qiita.com/omuram/items/c03a2b2266c958564a9a)
・流してます(https://horomary.hatenablog.com/entry/2021/02/06/013412)
・流してます(https://qiita.com/sugulu_Ogawa_ISID/items/6c4d34446d4878cde61a)
・流してます(https://tadaoyamaoka.hatenablog.com/entry/2019/12/18/232154)
・流してます(https://github.com/keras-rl/keras-rl/blob/master/rl/agents/dqn.py)
・流してます(https://github.com/Kaixhin/Rainbow)
簡単に両方の実行結果も見てみましたが、大きな違いはありませんでした。
フレームワーク上は流す形で実装しています。
4. Multi-step learning
TD誤差を数ステップ分計算する必要があります。
また分かりやすくするために状態はwindow length分をまとめて送っています。
(前の状態と次の状態がかぶっているので二重に送ることになりますが、バグが怖いので分かりやすさを優先しています)
class Worker(DiscreteActionWorker):
def call_on_reset(self, state: np.ndarray, invalid_actions: List[int]) -> None:
# window length用
self.recent_states = [self.dummy_state for _ in range(self.config.window_length)]
# window lengthでまとめた状態
self.recent_bundle_states = [self.recent_states[:] for _ in range(self.config.multisteps + 1)]
# multisteps で必要な履歴保存
# アクションはランダムに初期化する
self.recent_actions = [random.randint(0, self.config.nb_actions - 1) for _ in range(self.config.multisteps)]
self.recent_probs = [1.0 / self.config.nb_actions for _ in range(self.config.multisteps)]
self.recent_rewards = [0.0 for _ in range(self.config.multisteps)]
self.recent_done = [False for _ in range(self.config.multisteps)]
# 最初の状態を保存
self.recent_states.pop(0)
self.recent_states.append(state)
self.recent_bundle_states.pop(0)
self.recent_bundle_states.append(self.recent_states[:]) # window length でまとめた状態を保存する
def call_policy(self, state: np.ndarray, invalid_actions: List[int]) -> int:
# Q値を取得
state = self.recent_bundle_states[-1]
q = self.parameter.q_online(np.asarray([state]))[0].numpy()
# ε-greedyの確率を計算
probs = calc_epsilon_greedy_probs(q, epsilon, self.config.nb_actions)
# 確率に従ってアクションを出す
action = random.choices([a for a in range(self.config.nb_actions)], weights=probs)
# 学習に必要なので各情報を保存
self.action = self.action
self.prob = probs[action]
return action
def call_on_step(
self,
next_state: np.ndarray,
reward: float,
done: bool,
next_invalid_actions: List[int],
) -> Dict:
# 各状態を保存
self.recent_states.pop(0)
self.recent_states.append(next_state)
self.recent_bundle_states.pop(0)
self.recent_bundle_states.append(self.recent_states[:])
self.recent_actions.pop(0)
self.recent_actions.append(self.action)
self.recent_probs.pop(0)
self.recent_probs.append(self.prob)
self.recent_rewards.pop(0)
self.recent_rewards.append(reward)
self.recent_done.pop(0)
self.recent_done.append(done)
# メモリに追加
self._add_memory()
if done:
# multistepsとdoneの間のstepが送られないので送る
# multistepsのサイズは可変にできるので、新しい状態は追加していません
for _ in range(len(self.recent_rewards) - 1):
self.recent_bundle_states.pop(0)
self.recent_actions.pop(0)
self.recent_probs.pop(0)
self.recent_rewards.pop(0)
self.recent_done.pop(0)
self._add_memory()
return {}
def _add_memory(self):
batch = {
"states": self.recent_bundle_states[:],
"actions": self.recent_actions[:],
"probs": self.recent_probs[:],
"rewards": self.recent_rewards[:],
"dones": self.recent_done[:],
}
self.remote_memory.add(batch)
# ε-greedyの確率を計算
def calc_epsilon_greedy_probs(q, epsilon, action_num):
q_max = np.amax(q, axis=0)
q_max_num = np.count_nonzero(q == q_max)
probs = []
for a in range(action_num):
prob = epsilon / action_num
if q[a] == q_max:
prob += (1 - epsilon) / q_max_num
probs.append(prob)
return probs
ε-greedy の各アクションの確率は以下です。
ε以上とε以下で分けて考えています。
※$|A|$ : アクション数
※$|A_{max}|$ : Q値が最大のアクション数
- Q値が最大値のアクションが選ばれる確率
$$
(1-\epsilon) \times \frac{1}{|A_{max}|} + \epsilon \frac{1}{|A|}
$$
- Q値が最大値じゃないアクションが選ばれる確率
$$
(1-\epsilon) \times 0 + \epsilon \frac{1}{|A|}
$$
次に学習側です。
サンプリングの価値(教師側のデータ)の計算が変わります。
DQNでは以下でした。
# next Q
n_q = self.parameter.q_online(n_states).numpy()
n_q_target = self.parameter.q_target(n_states).numpy()
# 教師データ(サンプリングして得た価値)を計算
target_q = np.zeros(len(batchs))
for i, b in enumerate(batchs):
reward = b["reward"]
done = b["done"]
if done:
gain = reward
else:
# 次の状態の予測値は Target Q-network を使う
gain = reward + self.config.gamma * np.max(n_q_target[i])
target_q[i] = gain
これが以下に変わります。
batchs = self.remote_memory.sample(self.config.batch_size)
# NNの計算は一括でやったほうが早いので、全バッチのQ値を一括で計算。
n_states_list = []
for b in batchs:
# b["states"][0] は今の状態なので予測には不要
n_states_list.extend(b["states"][1:])
n_states_list = np.asarray(n_states_list)
n_q_list = self.q_online(n_states_list).numpy()
n_q_list_target = self.q_target(n_states_list).numpy()
# batch毎にQ値を計算、バグが怖いのでなるべく愚直に実装
target_q_list = []
n_states_idx_start = 0
for b in batchs:
target_q = 0.0
retrace = 1.0
# Q値は一括で出したので、参照用にindexを変数で扱う
n_states_idx = n_states_idx_start
# multistep分実行、rewardsを使うのは可変なので
for n in range(len(b["rewards"])):
action = b["actions"][n]
mu_prob = b["probs"][n]
reward = b["rewards"][n]
done = b["dones"][n]
# retrace cを計算、使うのは2step目以降
if n >= 1:
# greedy法の各アクション確率を計算(今の状態のアクション確率)
pi_probs = calc_epsilon_greedy_probs(
n_q_list[n_states_idx - 1]
0.0,
self.config.nb_actions,
)
pi_prob = pi_probs[action] # 現在の方策で最大を選ぶ確率
# c = h * min(1, pi/mu )
retrace *= self.config.retrace_h * np.minimum(1, pi_prob / mu_prob)
if retrace == 0:
break # 0以降は伝搬しないので切りあげる
# サンプリング時の行動価値を計算
if done:
gain = reward
else:
gain = reward + self.config.gamma * np.max(n_q_list_target[n_states_idx])
# 1step目はそのまま、2step目以降は retrace したTD誤差を伝播させる
if n == 0:
target_q += gain
else:
td_error = gain - n_q_list[n_states_idx - 1][action]
target_q += (self.config.gamma**n) * retrace * td_error
n_states_idx += 1
n_states_idx_start += len(b["rewards"])
target_q_list.append(target_q)
6. Noisy Nets
tensorflow_addons に実装されているのでそれを使います。
Dense層をNoisyDense層に置き換えるだけです。
import tensorflow_addons as tfa
# 入力層
input_shape = (config.window_length, 84, 84)
in_state = c = kl.Input(shape=input_shape)
c = kl.Permute((2, 3, 1))(c)
c = kl.Conv2D(32, (8, 8), strides=(4, 4), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (4, 4), strides=(2, 2), padding="same", activation="relu")(c)
c = kl.Conv2D(64, (3, 3), strides=(1, 1), padding="same", activation="relu")(c)
# 隠れ層:Dense → NoisyDense
c = tfa.layers.NoisyDense(512, activation="relu")(c)
# 出力層:Dense → NoisyDense
c = tfa.layers.NoisyDense(config.nb_actions)(c)
# モデル
model = keras.Model(in_state, c)
Worker側のアクションはε-greedy法を使わずそのまま出力します。
def call_policy(self, state: np.ndarray, invalid_actions: List[int]) -> int:
q = self.parameter.q_online(np.asarray([state]))[0].numpy()
action = int(np.argmax(q))
return action
実行
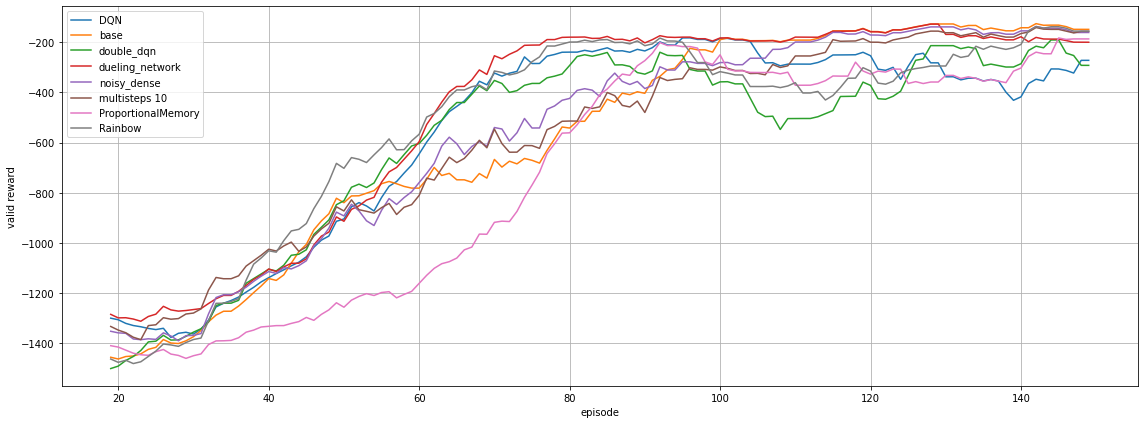
Open AI Gymで提供されているPendulum-v1の学習の様子を比較させてみました。
実行に使ったコードは github を見てください。
- 比較結果
結果は20エピソードの移動平均線をプロットしています。
ProportionalMemory の学習が遅れているのはβを1にしているので、ISの補正が聞いており、ゆっくり学習しているからです。
Multistepは10stepと大きい値を取っていますが、ちゃんと学習できているのはRetraceの成果ですね。
また、Pendulum-v1 は乱数の影響が大きく、大きく結果が変わる場合があるのであまり参考にならないかもしれません。