※2018年06月23日追記
PyTorchを使用した最新版の内容を次の書籍にまとめました。
つくりながら学ぶ! 深層強化学習 ~PyTorchによる実践プログラミング~ 18年6月28日発売
強化学習DQNの発展編である「Dueling Network」を実装・解説したので、紹介します。
概要
Open AI GymのCartPoleで、Dueling NetworkにしたDQNの実装・解説をします。
プログラムが1ファイルで完結し、学習・理解しやすいようにしています。
【対象者】
・強化学習DQNの発展版に興味がある方
・速習 強化学習: 基礎理論とアルゴリズム(書籍)を読んで、Dueling Networkを知ったが、実装方法がよく分からない方
・実装例を見たほうがアルゴリズムを理解しやすい方
【得られるもの】
ミニマム・シンプルなプログラムが実装例から、Dueling Networkを理解・使用できるようになります。
【注意】
本記事に入る前に、以下の記事で、「Open AI gymのCartPoleの使い方」と「DQNの理論と実装」をなんとなく理解しておいてください。
●CartPoleでDQN(deep Q-learning)、DDQNを実装・解説【Phythonで強化学習:第2回】
以下の記事でDueling Networkの概要をなんとなく感じておいてください。
●introduction to Dueling network(日本語)
速習 強化学習: 基礎理論とアルゴリズム(書籍)の、Dueling Networkの説明も読んでおくと、なお良いです。
Dueling Networkについて
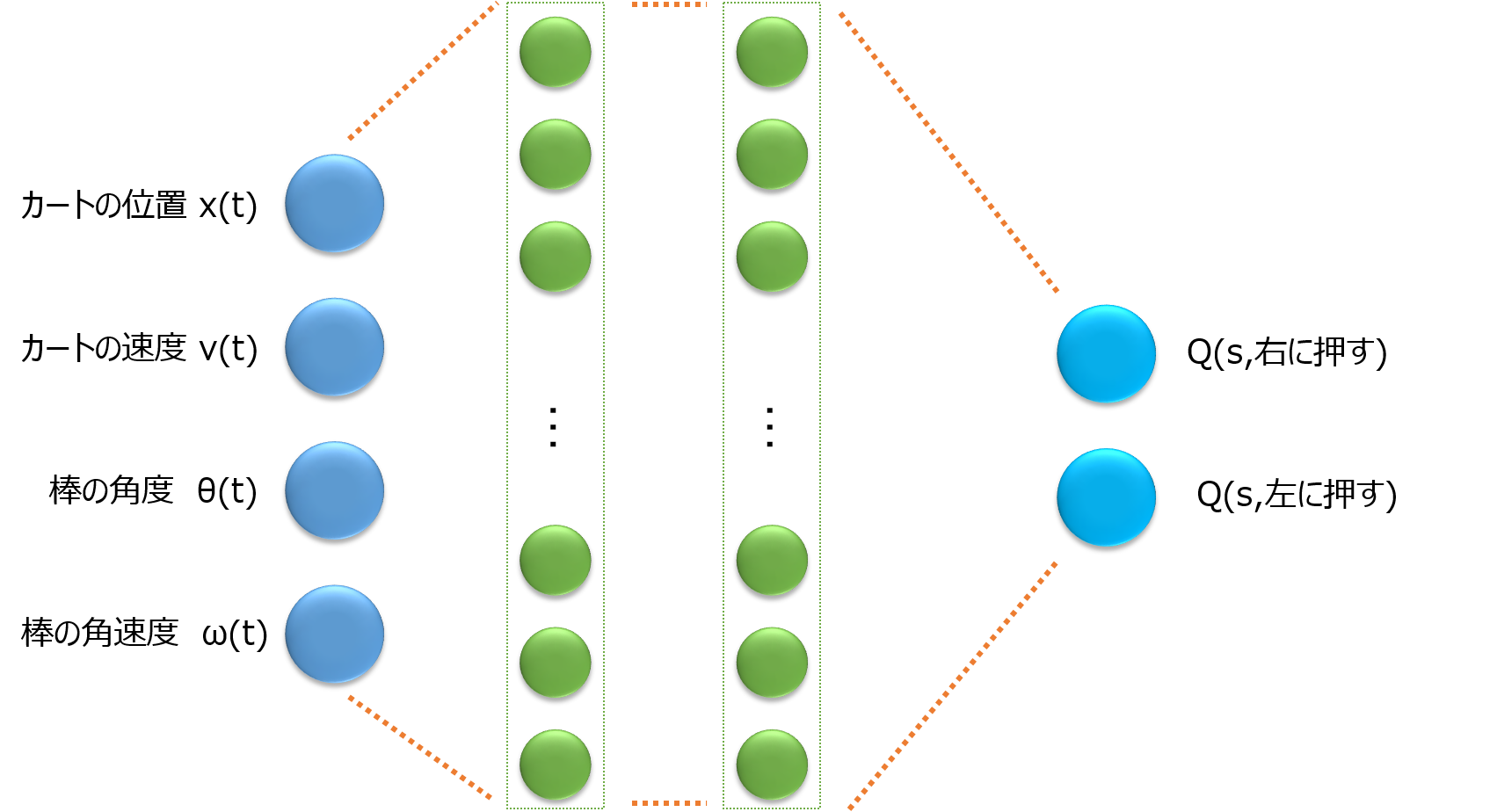
CartPole問題において、通常のDQNのネットワークを図にすると以下のようになります。
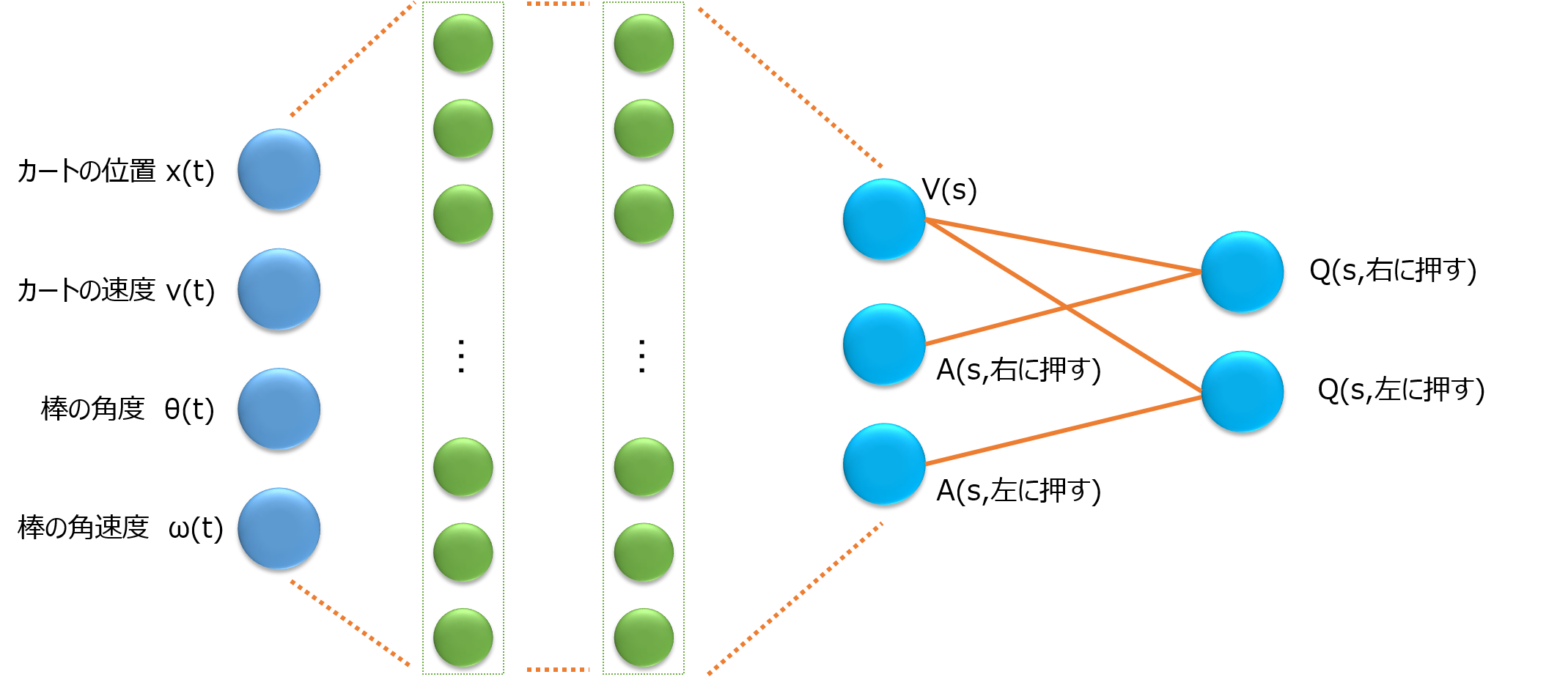
一方で、Dueling Networkは以下の図のようになります。
A(s,右に押す) は
A(s,右に押す) = Q(s,右に押す) - V(s)
のことで、Advantageと呼ばれます。
Dueling Networkが何をしたいのか説明します。
行動価値関数Qには、右に押そうが、左に押そうが、大体そのあと獲得できるであろう報酬合計が、状態sによって決まる部分があります。
例えば、もう倒れる寸前の状態sであれば、actionが右に押そうが、左に押そうが、そのあと得られるであろう報酬合計はとても少ないと予測できます。
つまり、Q関数が持つ情報は、状態sだけで決まる部分と、行動aしだいで決まる部分に分離できます。
そこでQ関数を、状態sだけで決まる部分V(s)と、行動しだいで決まる部分A(s,a)に分けて学習し、最後の出力層でV(s)とA(s,a)を足し算して、Q(s,a)を求めます。
DQNに比べた利点は、V(s)が行動aによらず毎回学習できる点です。
これは選択できる行動が増えれば増えるほど、大きな利点になります。
これを踏まえて、DQNのネットワークを書き換えてあげます。
Dueling Networkの実装
実装には以下のサイトを参考にしました。
●matthiasplappert/keras-rl
以下の実装例の
[2]Q関数をディープラーニングのduelingネットワークをクラスとして定義
の部分がDQNと異なっています。
最後の層で、V(s) と A(s,a) を足し算する部分は、KerasのLambda関数を利用して定義しています。
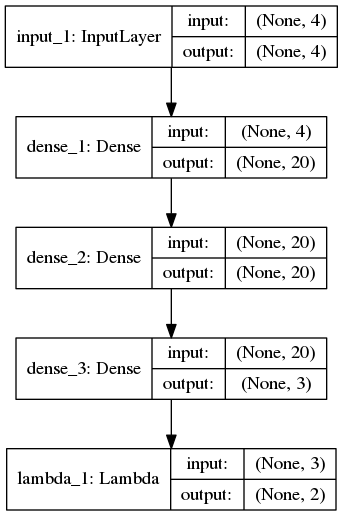
ネットワークを可視化すると以下の通りです。
Dueling NetworkではAdvantageの平均値を出力から引き算するのが一般的です。
ですが、それをすると、バックプロパゲーションするときにもマスキングの工夫が必要となり、実装が大変になります。
そこで平均値を引かないタイプのDueling Network(naive Dueling Network)を実装しています。
また、隠れ層のニューロンの数をDQNの16個から20個に増やしています。
# coding:utf-8
# [0]必要なライブラリのインポート
import gym # 倒立振子(cartpole)の実行環境
import numpy as np
import time
from keras.models import Sequential
from keras.layers import Dense, Lambda, Input # LambdaとInputを追加
import keras.models
from keras.optimizers import Adam
from keras.utils import plot_model
from collections import deque
from gym import wrappers # gymの画像保存
from keras import backend as K
import tensorflow as tf
# [1]損失関数の定義
# 損失関数にhuber関数を使用します 参考https://github.com/jaara/AI-blog/blob/master/CartPole-DQN.py
def huberloss(y_true, y_pred):
err = y_true - y_pred
cond = K.abs(err) < 1.0
L2 = 0.5 * K.square(err)
L1 = (K.abs(err) - 0.5)
loss = tf.where(cond, L2, L1) # Keras does not cover where function in tensorflow :-(
return K.mean(loss)
# [2]Q関数をディープラーニングのduelingネットワークをクラスとして定義
class QNetwork:
def __init__(self, learning_rate, state_size=(4,), action_size=2, hidden_size=10):
inputlayer = Input(shape=state_size)
middlelayer = Dense(hidden_size, activation='relu')(inputlayer)
middlelayer = Dense(hidden_size, activation='relu')(middlelayer)
# DQNの場合は以下
#y = Dense(action_size, activation='linear')(middlelayer) # 0番目がV(s), 1以降がA(s,a)
#outputlayer = Lambda(lambda a: a[:, 0:] - K.mean(a[:, 0:] * 0, keepdims=True),
# output_shape=(action_size,))(y)
# dueling network
y=Dense(action_size + 1, activation='linear')(middlelayer) # 0番目がV(s), 1以降がA(s,a), 平均値は引かないnaive型にする
outputlayer = Lambda(lambda a: K.expand_dims(a[:, 0], -1) + a[:, 1:] - 0.0*K.mean(a[:, 1:], keepdims=True),
output_shape=(action_size,))(y)
self.model=keras.models.Model(input=inputlayer, output=outputlayer)
self.optimizer = Adam(lr=learning_rate) # 誤差を減らす学習方法はAdam
self.model.compile(loss=huberloss, optimizer=self.optimizer)
#self.model.compile(loss='mse', optimizer=self.optimizer)
# 重みの学習
def replay(self, memory, batch_size, gamma, targetQN):
inputs = np.zeros((batch_size, 4))
targets = np.zeros((batch_size, 2))
mini_batch = memory.sample(batch_size)
for i, (state_b, action_b, reward_b, next_state_b) in enumerate(mini_batch):
inputs[i:i + 1] = state_b
target = reward_b
if not (next_state_b == np.zeros(state_b.shape)).all(axis=1):
# 価値計算(DDQNにも対応できるように、行動決定のQネットワークと価値観数のQネットワークは分離)
retmainQs = self.model.predict(next_state_b)[0]
next_action = np.argmax(retmainQs) # 最大の報酬を返す行動を選択する
target = reward_b + gamma * targetQN.model.predict(next_state_b)[0][next_action]
targets[i] = self.model.predict(state_b) # Qネットワークの出力
targets[i][action_b] = target # 教師信号
self.model.fit(inputs, targets, epochs=1, verbose=0) # epochsは訓練データの反復回数、verbose=0は表示なしの設定
# [3]Experience ReplayとFixed Target Q-Networkを実現するメモリクラス
class Memory:
def __init__(self, max_size=1000):
self.buffer = deque(maxlen=max_size)
def add(self, experience):
self.buffer.append(experience)
def sample(self, batch_size):
idx = np.random.choice(np.arange(len(self.buffer)), size=batch_size, replace=False)
return [self.buffer[ii] for ii in idx]
def len(self):
return len(self.buffer)
# [4]カートの状態に応じて、行動を決定するクラス
class Actor:
def get_action(self, state, episode, targetQN): # [C]t+1での行動を返す
# 徐々に最適行動のみをとる、ε-greedy法
epsilon = 0.001 + 0.9 / (1.0+episode)
if epsilon <= np.random.uniform(0, 1):
retTargetQs = targetQN.model.predict(state)[0]
action = np.argmax(retTargetQs) # 最大の報酬を返す行動を選択する
else:
action = np.random.choice([0, 1]) # ランダムに行動する
return action
# [5] メイン関数開始----------------------------------------------------
# [5.1] 初期設定--------------------------------------------------------
DQN_MODE = 1 # 1がDQN、0がDDQNです
LENDER_MODE = 1 # 0は学習後も描画なし、1は学習終了後に描画する
env = gym.make('CartPole-v0')
num_episodes = 299 # 総試行回数
max_number_of_steps = 200 # 1試行のstep数
goal_average_reward = 195 # この報酬を超えると学習終了
num_consecutive_iterations = 10 # 学習完了評価の平均計算を行う試行回数
total_reward_vec = np.zeros(num_consecutive_iterations) # 各試行の報酬を格納
gamma = 0.99 # 割引係数
islearned = 0 # 学習が終わったフラグ
isrender = 0 # 描画フラグ
# ---
hidden_size = 16+4 # Q-networkの隠れ層のニューロンの数
learning_rate = 0.00001 # Q-networkの学習係数
memory_size = 10000 # バッファーメモリの大きさ
batch_size = 32 # Q-networkを更新するバッチの大記載
# [5.2]Qネットワークとメモリ、Actorの生成--------------------------------------------------------
mainQN = QNetwork(hidden_size=hidden_size, learning_rate=learning_rate) # メインのQネットワーク
targetQN = QNetwork(hidden_size=hidden_size, learning_rate=learning_rate) # 価値を計算するQネットワーク
mainQN.model.summary()
# plot_model(mainQN.model, to_file='Qnetwork.png', show_shapes=True) # Qネットワークの可視化
memory = Memory(max_size=memory_size)
actor = Actor()
# [5.3]メインルーチン--------------------------------------------------------
for episode in range(num_episodes): # 試行数分繰り返す
env.reset() # cartPoleの環境初期化
state, reward, done, _ = env.step(env.action_space.sample()) # 1step目は適当な行動をとる
state = np.reshape(state, [1, 4]) # list型のstateを、1行4列の行列に変換
episode_reward = 0
targetQN = mainQN # 行動決定と価値計算のQネットワークをおなじにする
for t in range(max_number_of_steps + 1): # 1試行のループ
if (islearned == 1) and LENDER_MODE: # 学習終了したらcartPoleを描画する
env.render()
time.sleep(0.1)
print(state[0, 0]) # カートのx位置を出力するならコメントはずす
action = actor.get_action(state, episode, mainQN) # 時刻tでの行動を決定する
next_state, reward, done, info = env.step(action) # 行動a_tの実行による、s_{t+1}, _R{t}を計算する
next_state = np.reshape(next_state, [1, 4]) # list型のstateを、1行4列の行列に変換
# 報酬を設定し、与える
if done:
next_state = np.zeros(state.shape) # 次の状態s_{t+1}はない
if t < 195:
reward = -1 # 報酬クリッピング、報酬は1, 0, -1に固定
else:
reward = 1 # 立ったまま195step超えて終了時は報酬
else:
reward = 0 # 各ステップで立ってたら報酬追加(はじめからrewardに1が入っているが、明示的に表す)
episode_reward += 1 # reward # 合計報酬を更新
memory.add((state, action, reward, next_state)) # メモリの更新する
state = next_state # 状態更新
# Qネットワークの重みを学習・更新する replay
if (memory.len() > batch_size) and not islearned:
mainQN.replay(memory, batch_size, gamma, targetQN)
if DQN_MODE:
targetQN = mainQN # 行動決定と価値計算のQネットワークをおなじにする
# 1施行終了時の処理
if done:
total_reward_vec = np.hstack((total_reward_vec[1:], episode_reward)) # 報酬を記録
print('%d Episode finished after %f time steps / mean %f' % (episode, t + 1, total_reward_vec.mean()))
break
# 複数施行の平均報酬で終了を判断
if total_reward_vec.mean() >= goal_average_reward:
print('Episode %d train agent successfuly!' % episode)
islearned = 1
if isrender == 0: # 学習済みフラグを更新
isrender = 1
# env = wrappers.Monitor(env, './movie/cartpoleDueling') # 動画保存する場合
およそ50試行と、DQNの半分程度の試行数で学習できます。
実行結果の一例は以下の通りです。
以上、CartPoleでDueling Netwrokを実装する方法を紹介でした。
次回はディープラーニングを用いた強化学習である
prioritized experience replay
を実装する予定です。
以上、ご一読いただき、ありがとうございました。