【無限遠点を巡る数理】「半径だけの世界」から「直径もある世界」へ

オイラーの公式（Eulerian Formula）Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)、最初見つけた時点では本当に何がなんだかさっぱりだっだったのですが、最近ある種の壮大な「数学ロマン派叙事詩」じゃないかと考える様になりました。どういう事かについて、以下で説明していきたいと思います。
【Rで球面幾何学】二辺形一辺形？

NoS(Number of Sides)が2未満の世界。

とりあえず任意の観測系(Any Observation System)の極限状態、すなわち「究極の観測原点(Ultimate Observation Origin)」Od(d(imension)=0→Inf(inity)){0,0,0,…}と「究極の観測対象そのもの(Ultimate Observation Target Itself)」Td(d=0→Inf){Inf,Inf,Inf,…}のみしか存在しないN次元の原始座標系(Primitive Coordinate System)概念からから出発します。言うなれば完全なる「五里霧中」状態…
【無限遠点を巡る数理】原始座標群なる「事象の墓場」概念の設定

	Observation Origin	Observation Target
1	0	Inf
2	0	Inf
3	0	Inf
	…	…
N	0	Inf

library(xtable)
a0<-matrix(1:10,nrow=5, ncol=2)
a0[,1]<-rep(0,5)
a0[,2]<-rep(Inf,5)
a0[4,]<-rep("…",2)
rownames(a0)<-c(1,2,3,"","N")
colnames(a0)<-c("Observation Origin","Observation Target")
names(a0) <-  
print(xtable(a0), type="html")

• そういえばノルム(距離)空間はその成立条件として「N次元ベクトルXd(d=1→Inf){0,0,0,…,0}⟺X=0」なる条件を掲げている。これは任意の座標系において座標0の集合としての観測原点(Observation Origin)は(その座標系の次元展開に応じた全座標の値が0の)単なる点として扱うという事であり、この観測系もその規約には従う。
  ノルムの意味とL1，L2，L∞ノルム | 高校数学の美しい物語
• さらにこの観測系においては観測結果も全て0である状態を「(点としてのみ存在し線も面も体積も備えない)0次元」と規約する。0次元については様々な定義が試みられているが、この観測系においてはとりあえず「その座標系が観測対象を全く捉えてない状態(あるいは諸般の事情で自らの客観視が不可能な観測者の存在のみが確認されている状態)」などと見做す訳である。
  0次元 - Wikipedia

	Observation Origin	Observation Target
1	0	0
2	0	0
3	0	0
	…	…
N	0	0

library(xtable)
a0<-matrix(1:10,nrow=5, ncol=2)
a0[,1]<-rep(0,5)
a0[,2]<-rep(0,5)
a0[4,]<-rep("…",2)
rownames(a0)<-c(1,2,3,"","N")
colnames(a0)<-c("Observation Origin","Observation Target")
names(a0) <-  
print(xtable(a0), type="html")

逆をいえば、如何なる形でも(例え観測者の観測ミスや勘違いに過ぎなくても、それを確かめる手段がないので)どれかの観測結果が≠0となった時点で、その観測者は既に0次元自体からは解放されているのです。それがオイラーの公式（Eulerian Formula）Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)においては「Nosが0より大きく2より小さい」区間に該当する状態。正直この方面についてはまだまだ全然考察が足りておらず、そもそもNos=1すなわち一辺形(One Side)がどういう状態なのかすらまともに定義出来てない様な有様なので、現段階においては「語り得ない事については沈黙するほかない」を貫く事にする(要するに来年の課題)。
【Rで球面幾何学】二辺形一辺形？

• それではこの観測環境下においては観測対象そのものは観測者の目にどう映るのか。その無限次元性を保ったまま(それぞれの座標系の次元展開に応じて)無限線(Unlimited Line)/無限円(Unlimited Circle)/無限球面(Unlimited Sphere)とその見え方を転じていくのである。そして、とりあえず全ての観測結果が同じ無限遠(Inf(inity))である事からピタゴラスの定理(Pythagorean Theorem)半径r=sqrt(x^2+y^2+z^2,…)は導入(Introduce)可能と考えるなら、そこに(VRの如く観測者の視界をスッポリ包む)ある種の全球型スクリーンが現れる。
  【初心者向け】ピタゴラスの定理あるいは三平方の定理からの出発
  
  

どうやらこの意味合いにおいて原始座標系は「まだ使える距離(無限遠点Inf(inity)は使える数字にカウントされない)も角度(円の場合は円周φ、球面の場合は水平角φと垂直角θ)も備えていない極座標系(Polar Coordinates System)」とイメージするのが正しい様なのですね。
極座標系 - Wikipedia

NoS(Number of Sides)=2の世界。

ここにInf/Inf=1なる概念を導入します。距離概念が0か無限しかなかった世界に新たに1を加えると、まずは再帰処理によって自然数集合や加法整数群が使用可能となり、これを添字単位(Index Unit)や周期単位(Cycle Unit)に用いる処理が可能となります。
【初心者向け】添字化(Indexing)と単位化(Unitization)

• 自然数集合(Natulal Set)…初項(First Term)α=1,公差(Common Difference)d=1,一般項(General Term)α+(n-1)dの等差数列(Arithmetic sequence=算術数列)Nn(n=1→Inf(inity)){1+(1-1)×1=1,1+(2-1)×1=2,1+(3-1)×1=3,…,1+(Inf(inity)-1)×1=Inf(inity)}={1,2,3,…,Inf(inity)}概念から出発する。これは単純化して再帰的にNn(n=1→Inf(inity)){1,1+1=2,(1+1)+1=3,…,Inf(inity)+1=Inf(inity)}と考えても良い。
  【Rで球面幾何学】等差数列(算術数列)① 数直線概念の導入について。
• こうして成立した自然数集合に加法単位元(Additive Identity)0と逆元(Inverse Element)-Nn(n=-Inf→0){-Inf,…,-3,-2,-1,0}を射影(Projection)する事によって加法整数群(Additive Integer Group)Zn(n=-Inf→-1→0→1→Inf){-Inf,…,-3,-2,-1,0,1,2,3,…,Inf}も成立する。
  【初心者向け】群論(Group Theory)概念の根幹
  つまり従来の「半径だけの世界」と異なりプラス領域と…
  
  マイナス領域が峻別されたばかりか…
  
  連続領域として再統合されたのである。
  
• 対蹠(地球上でいうと北極と南極に該当する距離関係)が設定可能となった円/球面座標上においても(それまで区別が不可能だった)「原点からプラス方向に伸びる半径(Radius)1」概念と「原点からマイナス方向に伸びる半径1」概念が峻別されると同時に連続領域として統合され「直径(Diameter)2」なる概念が生じている。実はNoS=2で登場する二辺形(Bilateral)とは、かかる「対蹠間を結ぶ直径上の往復運動そのもの」に他ならない。
  
  

どうも全ての動きの背後に「Inf/Inf=1」なる疑念導入の副作用として同時追加となる等比数列2n(n=-Inf→0→Inf){1/(2^Inf):=0,…,1/(2^2)=1/4,1/(2^1)=1/2,2/2=1,2^1=2,1^2=4,…,2^Inf=Inf}の姿が透けて見えるのですが、まだまだ全体像は全然把握出来てません。いずれにせよその流れは思わぬ方向への展開も産む事になるのでした。

トーラス(Torus,複数形Tori）概念の追加。

実はNoS=2のタイミングで追加される立体概念は「半径1の単位球面」ばかりではありません。

同時に大半径(Major Radius)1,小半径(Minor Radius)1のトーラス(Torus,複数形Tori）もその片鱗を見せ始めるのです。

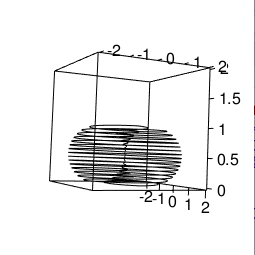
そもそもトーラスって一体何なのでしょうか？　座標系(Coordinate System)としては媒介変数t,p(0≦t≦2π,0≦p≦2π)を用いて以下の様に表します。

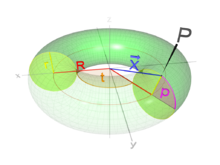
• x=大半径R×cos(t)+小半径r×cos(p)×cos(t)
• y=大半径R×cos(t)+小半径r×cos(p)×sin(t)
• z=小半径r×sin(p)

ここで重要なのが以下。

• 大半径R=0,小半径R=1の時、単位球面(Unit Sphere)を二重に描く。従って経緯度法(経度-180度~180度に対して緯度-90度~90度)や3次元極座標系(水平角φ=-π~πに対して垂直角0~π)は適用範囲を半分に減らしてなお単位球面(Unit Sphere)上の全座標を示せる訳である。
  【初心者向け】偶奇性概念と共役関係概念の連続性について。
• 逆に大半径R=1,小半径R=0の時、Z=0となってただの単位円(Unit Circle)に。

そしてこの変遷はオイラーの公式（Eulerian Formula）Cos(θ)+Sin(θ)iの一般形Cos(θ)+Cos(θ-π/NoS)i(NoS=Number of Sides)上における二辺形(Bilateral,NoS=2)すなわち「1辺がπの円弧2分割図形/1辺が2の往復線分」から円そのもの(NoS=Inf(inity))への変遷に合致するのです。
【Rで球面幾何学】二辺形と一辺形？ - Qiita

• この概念上における一辺形(One Side, NoS=1)は「1辺が2πの円弧=円そのもの」であり、ここにある種の循環性を見てとる事が出来そうである。
  一辺形(One Side)Cos(θ)-Cos(θ)i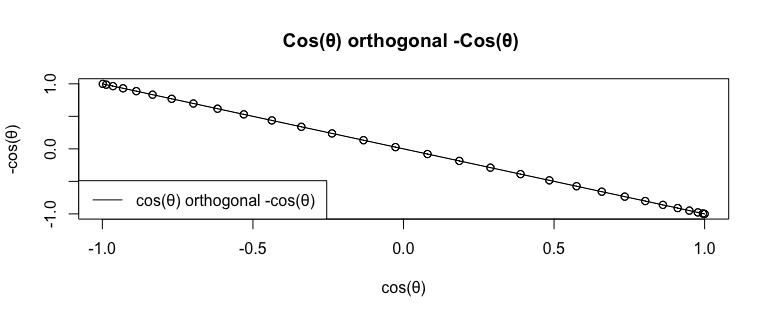
  
  二辺形(Bilateral)Cos(θ)+Sin(θ)i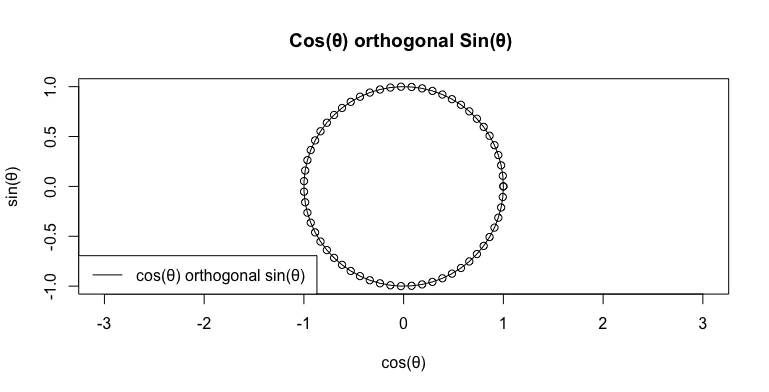
  
  円そのもの(Circle Itself)Cos(θ)+Cos(θ)i
  

以前ここに「球面に内接する正多面体と正多角形の状態遷移図」を投稿した事があります。この話はその続きでもあるんですね。
【オイラーの多面体定理と正多面体】とある「球面幾何学(Spherical Geometry)」の出発点…

立体的な動きがあるのは六角形までで、以降は「辺数が増えていくほど大半径を増大させ、小半径を減少させつつ無限遠上の円弧に向けて収束していく末期トーラス」を見守るばかりの展開となります。まさにこれこそがそれに対応する「始まりの景色」…

偶数層(Even Layer)と奇数層(Odd Layer)の分離

以下でも論じてますが、正直まだまだ不明点が多い分野です。
【初心者向け】偶奇性概念と共役関係概念の連続性について。

半径(Radius)1の二重球面たる単位球面(Unit Sphere)から出発します。偶奇性(Eveness)という時、重要なのはそこに現れてる数が偶数/奇数の関係にある事そのものより「ピッチが半周期ズレている」事なんですね。例えば同心円集合(Concentric Circle Set)半径R={0,1,2,3,4,…,Inf(inity)}から出発すると、これを偶数層(Even Layer)として奇数層(Odd Layer)が半径R={0.5,1.5,2.5,3.5,4.5,…,Inf(inity)}という形で現れるのです。
偶数層(Even Layer)0.0-1.0

奇数層(Odd Layer)0.5

偶数層(Even Layer)0.0-2.0+奇数層(Odd Layer)0.5

何かを連想しませんか？　そう、立体充填性(Space filling)における正四面体(Regular Tetrahedron)と正八面体(Regular Octahedron)の相補関係です。
【オイラーの多面体定理と正多面体】とある「球面幾何学」の出発点…

残念ながらこの問題「ピッチを2と規約する」みたいな方便で何とかなる話ではありません。射影単位(Projection Unit)が等比数列2n(n=-Inf→-0→Inf){1/(2^Inf):=0,…,1/(2^2)=1/4,1/(2^1)=1/2,2/2=1,2^1=2,2^2=4,…,2^Inf=Inf}の形でスライドするからです。
偶数系(Even System)の推移

cx<-seq(-5,5,length=11)
f0<-function(x) 2^x
cy<-f0(cx)
plot(cx,cy,type="b",xlim=c(-5,5),ylim=c(0,32),main="y=2^x(Even)")

	-5	-4	-3	-2	-1	0	1	2	3	4	5
-5	0.00	0.00	0.00	0.01	0.02	0.03	0.06	0.12	0.25	0.50	1.00
-4	0.00	0.00	0.01	0.02	0.03	0.06	0.12	0.25	0.50	1.00	2.00
-3	0.00	0.01	0.02	0.03	0.06	0.12	0.25	0.50	1.00	2.00	4.00
-2	0.01	0.02	0.03	0.06	0.12	0.25	0.50	1.00	2.00	4.00	8.00
-1	0.02	0.03	0.06	0.12	0.25	0.50	1.00	2.00	4.00	8.00	16.00
0	0.03	0.06	0.12	0.25	0.50	1.00	2.00	4.00	8.00	16.00	32.00
1	0.06	0.12	0.25	0.50	1.00	2.00	4.00	8.00	16.00	32.00	64.00
2	0.12	0.25	0.50	1.00	2.00	4.00	8.00	16.00	32.00	64.00	128.00
3	0.25	0.50	1.00	2.00	4.00	8.00	16.00	32.00	64.00	128.00	256.00
4	0.50	1.00	2.00	4.00	8.00	16.00	32.00	64.00	128.00	256.00	512.00
5	1.00	2.00	4.00	8.00	16.00	32.00	64.00	128.00	256.00	512.00	1024.00

library(xtable)
a0<-matrix(1:121,nrow=11, ncol=11)
i0<-c(1:11)
c0<-seq(-5,5,length=11)
for (i in i0){
a0[i,]<-2^(c0+(i-6))
}
rownames(a0)<-c0
colnames(a0)<-c0
names(a0) <-  
print(xtable(a0), type="html")

奇数系(Odd System)の推移

cx<-seq(-4.5,4.5,length=10)
f0<-function(x) 2^x
cy<-f0(cx)
plot(cx,cy,type="b",xlim=c(-4.5,4.5),ylim=c(0,23),main="y=2^x(Odd)")

	-4.5	-3.5	-2.5	-1.5	-0.5	0.5	1.5	2.5	3.5	4.5
-4.5	0.00	0.01	0.01	0.02	0.04	0.09	0.18	0.35	0.71	1.41
-3.5	0.01	0.01	0.02	0.04	0.09	0.18	0.35	0.71	1.41	2.83
-2.5	0.01	0.02	0.04	0.09	0.18	0.35	0.71	1.41	2.83	5.66
-1.5	0.02	0.04	0.09	0.18	0.35	0.71	1.41	2.83	5.66	11.31
-0.5	0.04	0.09	0.18	0.35	0.71	1.41	2.83	5.66	11.31	22.63
0.5	0.09	0.18	0.35	0.71	1.41	2.83	5.66	11.31	22.63	45.25
1.5	0.18	0.35	0.71	1.41	2.83	5.66	11.31	22.63	45.25	90.51
2.5	0.35	0.71	1.41	2.83	5.66	11.31	22.63	45.25	90.51	181.02
3.5	0.71	1.41	2.83	5.66	11.31	22.63	45.25	90.51	181.02	362.04
4.5	1.41	2.83	5.66	11.31	22.63	45.25	90.51	181.02	362.04	724.08

library(xtable)
a0<-matrix(1:100,nrow=10, ncol=10)
i0<-c(1:10)
c0<-seq(-4.5,4.5,length=10)
for (i in i0){
a0[i,]<-2^(c0+(i-5))
}
rownames(a0)<-c0
colnames(a0)<-c0
names(a0) <-  
print(xtable(a0), type="html")

それにしても…あえて次元表示を省略した円形尺(Circular Scale)を用いれば、こんなにスッキリして見えるのに…

f0<-function(x) 2^x
cxe<-seq(-5,5,length=11)
cye<-f0(cxe)
plot(cxe,cye,type="l",xlim=c(-5,5),ylim=c(0,32),main="y=2^x")
par(new=T)
plot(cxe,cye,type="p",xlim=c(-5,5),ylim=c(0,32),main="",xlab="",ylab="",col=rgb(0,0,1))
par(new=T)
cxo<-seq(-4.5,4.5,length=10)
cyo<-f0(cxo)
plot(cx,cy,type="p",xlim=c(-5,5),ylim=c(0,32),main="",xlab="",ylab="",col=rgb(1,0,0))
# 凡例を書き添える 。
legend("topright", legend=c("Even(2n)","Odd(2n+1)"), lty =c(1,1),col=c(rgb(0,0,1),rgb(1,0,0)))

等尺(Even Scale)表示

even_scale00<-function(inbetween){
c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy<-sin(c0)
odd<-rgb(1,0,0)
even<-rgb(0,0,1)
plot(cx*(1.0+inbetween),cy*(1.0+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="Even Scale",xlab="Cos(θ)",ylab="Sin(θ)i",col=even)
par(new=T)
#plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="Cos(θ)",ylab="",col=rgb(0,1,0))
par(new=T)
plot(cx*(0.9+inbetween),cy*(0.9+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(0.8+inbetween),cy*(0.8+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(0.7+inbetween),cy*(0.7+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(0.6+inbetween),cy*(0.6+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(0.5+inbetween),cy*(0.5+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(0.4+inbetween),cy*(0.4+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(0.3+inbetween),cy*(0.3+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(0.2+inbetween),cy*(0.2+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(0.1+inbetween),cy*(0.1+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(1.9+inbetween),cy*(1.9+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(1.8+inbetween),cy*(1.8+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(1.7+inbetween),cy*(1.7+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(1.6+inbetween),cy*(1.6+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(1.5+inbetween),cy*(1.5+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(1.4+inbetween),cy*(1.4+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(1.3+inbetween),cy*(1.3+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)
par(new=T)
plot(cx*(1.2+inbetween),cy*(1.2+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=even)
par(new=T)
plot(cx*(1.1+inbetween),cy*(1.1+inbetween),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=odd)

abline(h=0,col=rgb(0,1,0))
abline(v=0,col=rgb(0,1,0))

# 凡例を書き添える 。
legend("topright", legend=c("Even(2n)","Odd(2n+1)","x=y=0"), lty =c(1,1,1),col=c(rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))
}

#アニメーション
library("animation")
Time_Code=c(0,1/20,0,1/20,0,1/20,0,1/20,0,1/20,0,1/20)
saveGIF({
for (i in Time_Code){
　even_scale00(i)
}
}, interval = 0.1, movie.name = "even_scale04.gif")

2^x関数表示(logarithmic Scale)

logarithmic_scale00<-function(inbetween){
c0<-seq(0,pi*2,length=61)
cx<-cos(c0)
cy<-sin(c0)

c0<-rev(seq(-9,0,length=10))

for (i in c0){
plot(cx*(1-2^(i+inbetween)),cy*(1-2^(i+inbetween)),type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="",xlab="",ylab="",col=c(200,200,200,200))
par(new=T)
}

plot(cx,cy,type="l",xlim=c(-1,1),asp=1,ylim=c(-1,1),main="2^x(Logarithmic Scale)",xlab="Cos(θ)",ylab="Sin(θ)i", col=rgb(0,1,0))

abline(h=0,col=rgb(1,0,0))
abline(v=0,col=rgb(1,0,0))

# 凡例を書き添える 。
legend("topright", legend=c("Circle(Radius=2^x,Argment=θ)","x=y=0"), lty =c(1,1),col=c(rgb(0,1,0),rgb(1,0,0)))
}

#アニメーション
library("animation")
Time_Code=c(0,1/2,0,1/2,0,1/2,0,1/2,0,1/2,0,1/2)
saveGIF({
for (i in Time_Code){
　logarithmic_scale00(i)
}
}, interval = 0.1, movie.name = "logarithmic_scale04.gif")

デカルト座標系(Cartesian Coordinate System)上に強引に表示すると何と関数の曲線が4本に増えてしまうのです。

library(rgl)
#関数描画準備
cxy<-seq(-5,5,length=11)
cz<-2^cxy

#円錐描画
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
crz<-seq(-5,5,length=3000)
crze<-2^crz

f1<-function(x){x}
c0<-f1(seq(-5,5,length=3000))
crx<-Real*c0*sqrt(2)
cry<-Imaginal*c0*sqrt(2)

plot3d(crx,cry,crze,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(exp(-5),exp(5)),col=rgb(0,0,0))

#関数描画
plot3d(cxy,0,cz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(2^-5,2^5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(0,cxy,cz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(2^-5,2^5),col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)
plot3d(-cxy,0,cz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(2^-5,2^5),col=rgb(0,0,1),xlab="",ylab="",zlab="",lwd=2)
plot3d(0,-cxy,cz,type="l",xlim=c(-5,5),ylim=c(-5,5),zlim=c(2^-5,2^5),col=rgb(1,0,0),xlab="",ylab="",zlab="",lwd=2)

texts3d(0,0,0,texts="{0,0,0}",col=rgb(1,0,0),adj=1.0)

#中心線はx(y=z=0),x(y=z=0),x(y=z=0)の3本
lines3d(c(-5,5),c(0,0),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(0,0),c(2^-5,2^5),col=c(200,200,200),lwd=1)

#傍線は{x,y,z}の3通り×{x,y,z}-1の2通り×{min,max}の2通り=12通り
#傍線X
lines3d(c(-5,5),c(-5,-5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(2^-5,2^-5),col=c(200,200,200),lwd=1)
lines3d(c(-5,5),c(0,0),c(2^5,2^5),col=c(200,200,200),lwd=1)

#傍線Y
lines3d(c(-5,-5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(-5,5),c(0,0),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(2^-5,2^-5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,5),c(2^5,2^5),col=c(200,200,200),lwd=1)

#傍線Z 

lines3d(c(-5,-5),c(0,0),c(2^-5,2^5),col=c(200,200,200),lwd=1)
lines3d(c(5,5),c(0,0),c(2^-5,2^5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(-5,-5),c(2^-5,2^5),col=c(200,200,200),lwd=1)
lines3d(c(0,0),c(5,5),c(2^-5,2^5),col=c(200,200,200),lwd=1)

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test59")

• 数直線(Number line)上の直線的増減(Linear Increase Decrease)を同心円集合(Concentric Circle Set)の半径(Radius)の推移に射影(Projection)すると、周期(Cycle)毎に一周する螺旋軌道(Spiral Orbit)が現れる。
  【Rで球面幾何学】等差数列(算術数列)②数直線概念から同心円集合概念へ
  

• 偶奇性(Evenness)のピッチが2^1=2なのに対してデカルト座標系のピッチは2^2=4なのが問題の発端。それ故に円運動上の{偶数,奇数,偶数,…}の繰り返しを{偶数,奇数,-偶数,-奇数,偶数,…}の形でしか捉え得ないのである。だからこう見えてしまうのであり、この問題を回避する為には観測者側が偶数/奇数ごとに正負の符号を除去した絶対値(Absolute Value)を取って数列を4個から2個に戻さねばならない？

どうやら問題はまだまだ頻出し続ける様で…とりあえず以下続報。