LoginSignup
1
0
@ochimusha01(yasunori matuki)

【数学溢れ話】【Token】N進数から複素螺旋座標系(Complex Helix Coordinate System)へ

Last updated at Posted at 2024-02-03

【Token】実数概念の代用品としての「連続有理数集合」
上掲の投稿の内容を整理するうちに複素螺旋座標系(Complex Helix Coordinate System)とでも呼ぶべき概念に到達しました。ここではその内容をメモがてら簡単にまとめてみたいと思います。

N進数から自然指数関数へ

音階の数理表現$2^{n\frac{0-11}{12}}$から出発する。
「音階論」なる古くて新しい数理空間
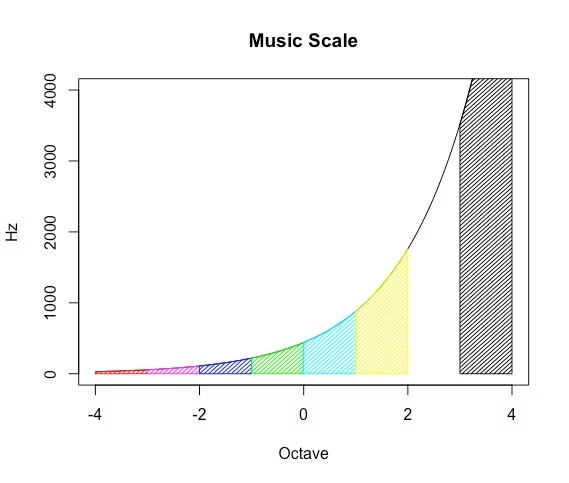
image.png
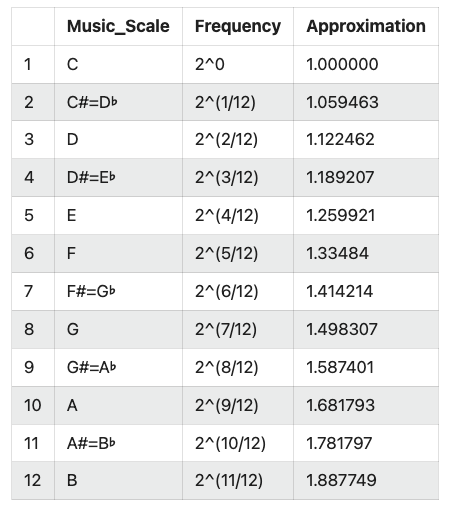
スクリーンショット 2024-02-02 21.44.39.png
この形でN進数を表現すると$N^{n\frac{m}{N}}(0≦m≦N-1,m\in\mathbb{Z})$となる。つまりに任意の数αは残差(切り捨てる端数)βを合わせ以下の形の冪級数で表される。
Wikipedia「冪級数」

α=\sum_{i=+∞}^{-∞}N^{{n_i}\frac{m_i}{N}}+β=(N^{{n_{+∞}}\frac{m_{+∞}}{N}},…,N^{{n_i}\frac{m_i}{N}},…,N^{{n_{-∞}}\frac{m_{-∞}}{N}})+β

ただしここでいう±∞はεδ論法によって定められる可算範囲の上下限とする。
ε-δ論法（イプシロンデルタ論法）を理解する

無限周期論ではさらにその先$\tilde{∞}$(符号なし無限遠点)において+∞と-∞の極限(可算範囲の外側)で交わると見做すが、ここでの計算上の残差もそちら側へ送り出す事によって集合論における閉世界仮説を成立させ、無限遠点を文字通り「座標系上における点」に収斂させる訳である。
ベン図と組み合わせ計算と確率演算(Probability Operation)
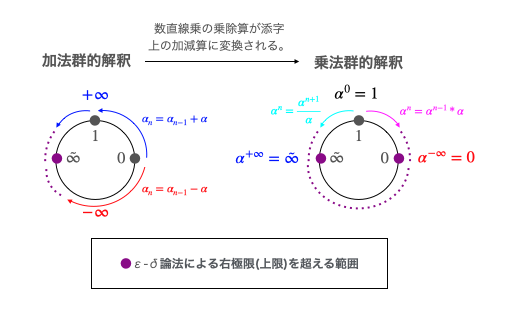
スクリーンショット 2024-02-02 23.35.50.png

この段階で群成立条件の一つである結合法則$(α_{-1}α_{±0})α_{+1}=α_{-1}(α_{±0}α_{+1})$は成立しているので、単位元として任意の(狭義には±∞からの可算範囲外の)iの位を$N^0=1$と設定すれば自明の場合としてそこを中心に逆数関係が生じ(コンピューターで扱うデータ型については浮動小数点位置の設定によっては任意の数についての逆数が存在しない)「加法群としての添字i集合」と「乗法群としての実数$α^i$集合」が成立する。
Wikipedia「群(数学)」

なお、この形で定義される加法群と乗法群と乗法群に関しては、まず指数対数関数の法則$ab=c^{log_ca+b}$が発見され、底cをとりあえず10と置いた常用対数表が普及した後に「添字と実数の増減の勾配を1とする(微積分の結果が元関数と一致する)魔法の底」ネイピア数e（2.71828182…）」が発見され、それ以外の指数関数が$α^x=e^{log(a)x}$と洗わされる様になった。逆にいうと指数関数$a^x$の接線$log(a)x+1$の傾き$log(a)$が1となるのが底aがネイピア数eの場合で、この場合のみ微分結果$e'^x=e^x$と積分結果$\int_{x=-∞}^{＋∞}e^xdx=e^x$が成立するという事である。この考え方から逆算して指数関数の微分は$a'^x=log(a)a^x$、積分は$\int_{x=-∞}^{＋∞}a^xdx=\frac{a^x}{log(a)}$とも計算される様になったという事である。
常用対数表を使った計算
【Token】ネイピア数
20211001213633.gif

巡回群、i進数系、π進数系

ところでN進数の実態は「円に内接する正多角形の描画問題」に他ならず、従ってNの極限は円周1回転分の連続表記2πラジアンとなる。

\lim_{x→\tilde{∞}}N^{n\frac{m}{N}}(0≦m≦N-1,m\in\mathbb{Z})

=2π^{n\frac{m}{2π}(0≦m≦2π)}

内接円/球面の半径と外接円/球面の半径の狭間
68747470733a2f2f71696974612d696d6167652d73746f72652e73332e61702d6e6f727468656173742d312e616d617a6f6e6177732e636f6d2f302f3539373737322f65616364383362362d303566312d366365362d323536352d6633343731326633373463612e676966 (1).gif

この様に正多角形の内接円(面)と外接円(面)が接近の末に円周(線)上でぴったりと重なり合う様子は、まさしく円の面積を求める式$πr^2$を微分して円周式$2πr$を求める過程そのもの。

f(x)'=\frac{f(x+h)-f(x)}{h}

$f(x)=πr^2,r=1$と置くと、

f(x)'=\frac{　π(r+h)^2-πr^2}{h}=\frac{　π(1+h)^2-π}{h}

=\frac{π(h^2+2h+1-1)}{h}=\frac{π(h^2+2h)}{h}

=\frac{πh(h+2)}{h}=π(h+2)

ここでhの極限を0に取ると

=\lim_{h→0}=π(h+2)=2π

ここではhを足しているので直接対応するのは以下のグラフの緑の外接多角形の振る舞いとなる。よく「微分における微少変量hは足しても引いても良い」と表現δされるが、それはこの様な「円周長は外接多角形で近似しても内接多角形で近似しても最終結果は一致する」数理に由来しているという次第。
68747470733a2f2f71696974612d696d6167652d73746f72652e73332e61702d6e6f727468656173742d312e616d617a6f6e6177732e636f6d2f302f3539373737322f38323835366661662d663565382d376561302d616264332d3763333437346238663338312e676966.gif
ところで上掲の様にコンピューターで多角形や円を描くには2πを「求める角数+1」で分割して数値集合θを構成してCos(θ)とSin(θ)を求め、前者をX軸、後者をY軸に配置して結んでいくのである。オイラーの公式$e^{θi}=Cos(θ)+Sin(θ)$を応用した考え方で、X座標とY座標は左式複素数解の実数部と虚数部に対応するばかりか「1の冪根」問題の解でもあり、全体として巡回群を構成する。
Wikipedia「1の冪根」
Wikipedia「巡回群」

その考え方の大源流はN次方程式の解法。虚数概念$i^2=-1$が三次方程式を解く鍵として導入されたのが16世紀イタリアルネサンス期、上掲の公式によって指数関数や三角関数との関係が明らかとなったのが数聖オイラー（Leonhard Euler、1707年~1783年）の時代、複素平面概念が導入されてその幾何学的意味まで周知される様になったのが「人類史上初めてコンパスと定規だけで正17角形を作図した(そして最終的にはあらゆる正多角形を作図可能とした)」数聖ガウス(Carolus Fridericus Gauss、1777年~1855年)の時代と、到達までに随分と時間を要した。
三次方程式から虚数へ
正十七角形の作図

それにつけても虚数$i^2=-1$とはどんな数字で、どうπ概念と関わってくるのであろうか？ 今度は振動関数$y=-1^x$概念から出発する。
数列の発散，収束，振動の意味と具体例

-1^x=(…,+1,-1,+1,…)= \left\{
\begin{array}{ll}
+1 & (x = 2n)\\
-1 & (x = 2n+1)
\end{array}
\right.

これを+1から-1への中心0、半径1の180度回転と見做すと‥
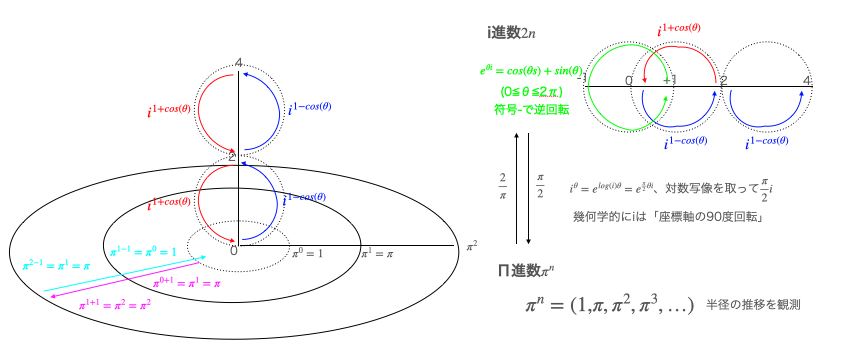
スクリーンショット 2024-02-03 5.45.00.png
指数写像
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303632372f32303231303632373132303930362e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303632372f32303231303632373132303435372e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303632372f32303231303632373132303833372e676966.gif

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation


#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="olivedrab",lw=0.5)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([0,np.pi*2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map100001.gif", writer="pillow")

対数写像
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303632372f32303231303632373132303930362e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303730392f32303231303730393136313933342e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303730392f32303231303730393136313935392e676966.gif

%matplotlib nbagg
import math as m
import cmath as c
import numpy as np
from functools import reduce
from itertools import accumulate
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#指数写像演算
def Napier_culc(ABS,n):
    RIM=ABS*m.pi*(0+1j)
    Tarm0=np.repeat(RIM/n,n)
    Tarm=np.concatenate([[(1+0j)],Tarm0])
    return accumulate(Tarm,lambda x,y:x+x*y)

#単位円データ作成
u0=np.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=np.array(u1)
uz0=np.repeat(0,61)
uz1=np.repeat(1,61)
uz2=np.repeat(2,61)

#タイムテーブル
Tcode=np.linspace(0,m.pi*2,61,endpoint =True)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def Exponential_map(n):
    plt.cla()
    #元(Element)算出
    Ed=np.array(list(Napier_culc(ABS,Time_Code[n])))-1
    #指数射影描画
    rollc0=[]
    for nm in range(len(Tcode)):
        rollxy0=[]
        for ni in range(len(Ed)):
            rollxy0.append(c.rect(Ed[ni].imag,Tcode[nm]))
        rollxy=np.array(rollxy0)
        rollc0.append(rollxy[len(rollxy)-1])
        ax.plot(rollxy.real,rollxy.imag,-Ed.real,color="gray",lw=0.5)
    rollc=np.array(rollc0)
    rollz=np.repeat(-Ed[len(Ed)-1].real,len(rollc))
    ax.plot(rollc.real,rollc.imag,rollz,color="black",lw=0.5)
    #円筒追加
    ax.plot(uc.real*np.pi,uc.imag*np.pi,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz0,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    #スポーク描画
    for num in range(len(uc)):
        ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="olivedrab",lw=0.5)
    ax.plot(uc.real,uc.imag,uz2,color="green",lw=1)
    ax.plot([0,0],[0,0],[0,1],color="black",marker='x',lw=1)
    ax.plot([0,0],[0,0],[0,2],color="black",marker='x',lw=1)
    #諸元追加
    ax.set_ylim([-np.pi,np.pi])
    ax.set_xlim([-np.pi,np.pi])
    ax.set_zlim([0,np.pi*2])
    ax.set_title("Logarithmic Projection of Exponential Map")
    ax.set_xlabel("Imaginal x")
    ax.set_ylabel("Imaginal y")
    ax.set_zlabel("Real")
    # グラフを回転(elv=45,0で水平,90で垂直)
    ax.view_init(elev=45, azim=-45)

ABS=1
Time_Code=[1,2,4,8,16,32,64,128,256]
Time_Code.reverse()

#Exponential_map(7)
#plt.show()

ani = animation.FuncAnimation(fig, Exponential_map, interval=100,frames=len(Time_Code))
ani.save("map200001.gif", writer="pillow")

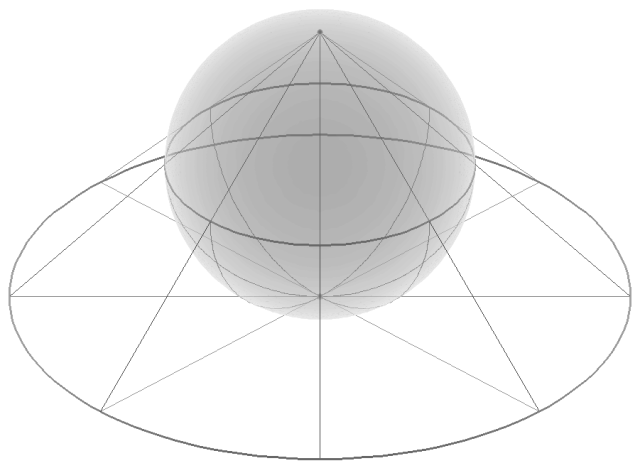
実際の指数写像や対数写像は(関数$e^{±θ}$(θ=0→π)の振る舞いを見れば分かる様に)球表面に従って連続的に進行する。
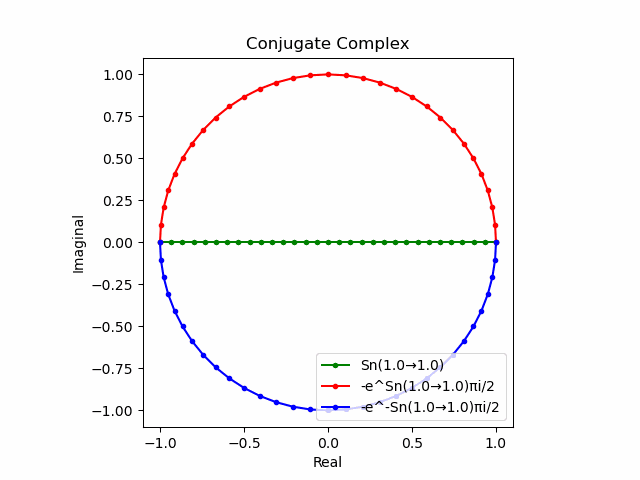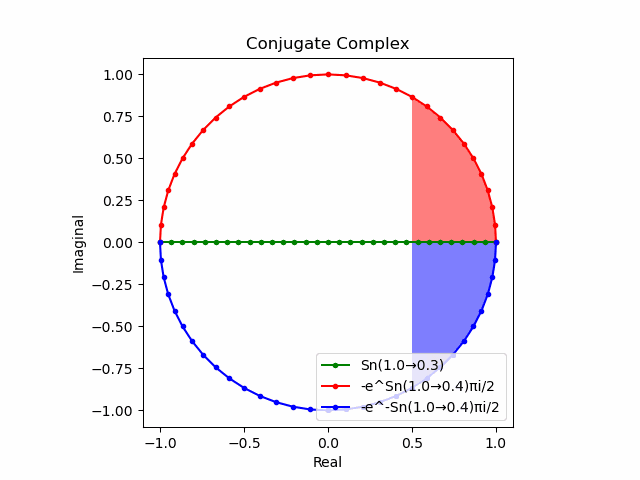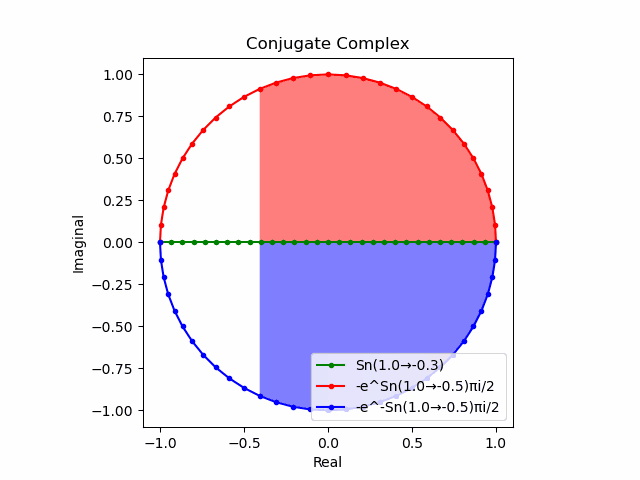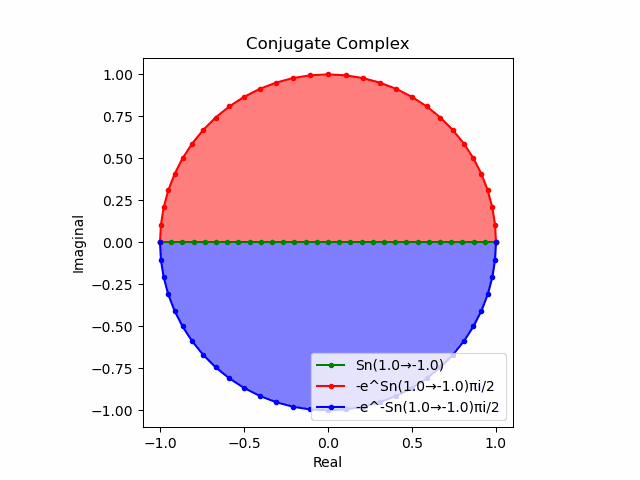
68747470733a2f2f71696974612d696d6167652d73746f72652e73332e61702d6e6f727468656173742d312e616d617a6f6e6177732e636f6d2f302f3539373737322f36336665663638302d353662312d343437382d616363352d3966313962643662333033612e676966.gif
そう、さながらみたらし団子かマーブリング製品の量産工場の様に…

さらにコンピューター上で線だけで球面を描く場合のは細かい螺旋構造を使います。
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303431322f32303231303431323039323934332e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303431322f32303231303431323039313135392e676966.gif
68747470733a2f2f63646e2d616b2e662e73742d686174656e612e636f6d2f696d616765732f666f746f6c6966652f6f2f6f6368696d7573686130312f32303231303431322f32303231303431323039313735392e676966.gif

%matplotlib nbagg
import math as m
import cmath as c
import numpy as num
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation

#円柱データ作成
c0=num.linspace(0,m.pi*120,1201,endpoint = True)
s0=[]
for nm in range(len(c0)):
    s0.append(complex(m.cos(c0[nm]),m.sin(c0[nm])))
s1=num.array(s0)
z0=num.linspace(-1,1,1201,endpoint = True)

#断面線(z)
cutz0=num.linspace(-1,1,61,endpoint = True)
cutz=cutz0[::-1]
cutx=num.sqrt(1-cutz**2)
cuty=num.repeat(0,61)

#「曲率」を計算
cv0=num.linspace(-1,1,1201,endpoint = True)
cv1=num.sqrt(1-cv0**2)

#単位円データ作成
u0=num.linspace(0,m.pi*2,61,endpoint = True)
u1=[]
for nm in range(len(u0)):
    u1.append(complex(m.cos(u0[nm]),m.sin(u0[nm])))
uc=num.array(u1)
uz0=num.repeat(-1,61)
uz1=num.repeat(0,61)
uz2=num.repeat(1,61)

#断面円
ucv0=num.linspace(-1,1,61,endpoint = True)
ucv=num.sqrt(1-ucv0**2)

#グラフ表示
plt.style.use('default')
fig = plt.figure()
ax = Axes3D(fig)

#関数定義
def unit_cylinder(n):
    plt.cla()
    ucutz=num.full(61,cutz[n])
    #円柱描画
    ax.plot(s1.real*cv1,s1.imag*cv1,z0,color="gray",lw=0.5)
    #スポーク描画
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[0,0],color="gray",lw=0.5)
    #for num in range(len(uc)):
    #    ax.plot([0,uc[num].real],[0,uc[num].imag],[1,1],color="gray",lw=0.5)
    for nm in range(len(uc)):
        ax.plot([0,uc[nm].real*ucv[n]],[0,uc[nm].imag*ucv[n]],[cutz[n],cutz[n]],color="black",lw=0.5)
    #単位円描画
    ax.plot(uc.real,uc.imag,uz0,color="red",lw=1)
    ax.plot(uc.real,uc.imag,uz1,color="green",lw=1)
    ax.plot(uc.real,uc.imag,uz2,color="blue",lw=1)
    #実数線追加
    ax.plot([0,0],[0,0],[-1,1],color="black",lw=1.5)
    ax.plot([0,1],[0,0],[-1,-1],color="red",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[0,cutz[n]],color="purple",lw=1)
    ax.plot([0,cutx[n]],[0,cuty[n]],[cutz[n],cutz[n]],color="purple",lw=1)
    ax.plot([0,cuty[n]],[0,cutx[n]],[0,cutz[n]],color="blue",lw=1)
    ax.plot([0,cuty[n]],[0,-1*cutx[n]],[0,cutz[n]],color="red",lw=1)
    ax.plot([0,1],[0,0],[0,0],color="purple",lw=1)
    ax.plot([0,0],[0,1],[0,0],color="blue",lw=1)
    ax.plot([0,0],[0,-1],[0,0],color="red",lw=1)
    ax.plot([0,1],[0,0],[1,1],color="blue",lw=1)
    ax.plot([1,1],[0,0],[-1,0],color="red",lw=1)
    ax.plot([1,1],[0,0],[0,1],color="blue",lw=1)
    #断面線描画
    ax.plot(cutx,cuty,cutz,color="purple",lw=1)
    ax.plot(cuty,cutx,cutz,color="blue",lw=1)
    ax.plot(cuty,-1*cutx,cutz,color="red",lw=1)
    #断面円描画
    ax.plot(uc.real*ucv[n],uc.imag*ucv[n],ucutz,color="black",lw=1)
    #諸元追加
    ax.set_ylim([-1.1,1.1])
    ax.set_xlim([-1.1,1.1])
    ax.set_zlim([-1.1,1.1])
    ax.set_title("Unit Cylinder")
    ax.set_xlabel("Real")
    ax.set_ylabel("Imaginal")
    ax.set_zlabel("Cycle")
    # グラフを回転(elev=0にすると水平表示に)
    ax.view_init(elev=45, azim=Time_code[n])

Time_code0=num.arange(0,360,6)  
Time_code=Time_code0[::-1]  
#unit_cylinder(len(s1))
#plt.show()

ani = animation.FuncAnimation(fig, unit_cylinder, interval=50,frames=len(Time_code))
ani.save("output521.gif", writer="pillow")

互いに逆数となる複素平面２枚を貼り合わせて球面を表現するリーマン球面への入り口と言える。
複素円筒座標系リーマン球面へ
image.png
そんな感じで以下続報…

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0